Integrated multistage supply chain inventory model of multiple retailers with imperfect production and inspection systems

Abstract

An integrated multistage supply chain inventory model containing a single manufacturer and multiple retailers is proposed to consider deteriorating raw materials and finished products with imperfect production and inspection systems. The main purpose is to jointly determine the manufacturer’s production and delivery strategies and the retailers’ replenishment strategies to maximize the integrated total profit. First, the individual total profit functions of the manufacturer and multiple retailers are established and are integrated to form the total profit function of the supply chain system. Then, to address the model complexity, an algorithm is proposed to obtain the optimal solution. Several practical numerical examples are presented to demonstrate the solution procedure, and a sensitivity analysis is performed on the major parameters. From the numerical results, several findings that differ from those in the previous literature were observed. First, retailers with larger market scale, better cost control, and/or inspection capabilities guarantee higher individual and integrated total profits. Second, increasing the deterioration rates of raw materials and finished products has different effects on the order quantity of raw materials. Third, the manufacturer’s shipping strategy is rigid and not easily changed except for significant changes (increase or decrease by 20%) to the production rate or selling price. The performance of the proposed model has several meaningful management implications.

1 Introduction

For supply chain systems, inventory management is a core activity of operation management. Efficient inventory management is essential to the healthy operation of the supply chain system, and decisions will intensively affect the financial performance, operational efficiency, and service level of the whole system (Nemati and Alavidoost 2019). Inventory operations span the whole supply chain from manufacturer to retailer, including the processes of storing raw materials and finished products. The managers of a supply chain system must make a tradeoff between reactivity and cost where holding a large amount of inventory allows the overall supply chain to effectively respond to market changes; nevertheless, the demand for storage of inventory generates a series of costs. Therefore, effectively integrating manufacturers and retailers in an appropriate production–inventory model and jointly determining the optimal production and ordering strategies are important issues for supply chain management to minimize the total inventory-related cost and maximize the total profit.

Traditional economic order quantity (EOQ) and economic production quantity (EPQ) models were both developed from the perspective of a single retailer or a single manufacturer. In recent years, inventory management studies have tended to consider the entire supply chain membership to establish an integrated production–inventory model. Integrated production–inventory models are an important direction of current inventory research (e.g., Darma Wangsa and Wee 2018; Venegas and Ventura 2018; Hayrutdinov et al. 2019). However, most of the previous models assumed that only a single manufacturer and single retailer are included in the production–inventory system. In fact, several large manufacturers deal with multiple retailers, and retailers of different scales and characteristics have competitive and coordinated relationships, for example, Nestlé cooperates with Walmart, Carrefour, Tesco, and other retailers. Therefore, considering the supply chain issues of multiple retailers can better reflect actual practice.

In inventory management, an important consideration is the deterioration of most types of products. Generally, deterioration is defined as the damage, spoilage, dryness, vaporization, or another process that reduces the usefulness of a product. Controlling and maintaining the inventories of deteriorating items are important issues for modern corporations (Wu et al. 2006). In the early literature, inventory models did not consider the deterioration of items, but researchers in the last decade have incorporated the deterioration of items in inventory models as a basic assumption (Dhandapani and Uthayakumar 2017; Soni and Suthar 2019). Regarding the deterioration of items in the supply chain inventory, previous studies only considered the deterioration of finished products (Tiwari et al. 2018; Mishra et al. 2018; Maihami et al. 2019). However, inventory in the supply chain system exists in different forms, such as raw materials or finished products. Therefore, the deterioration of raw materials should also be considered in supply chain inventory models.

In a competitive industrial environment, defective products may be produced due to incomplete production procedures, old equipment, or human negligence. In recent years, imperfect production systems and inventory management of defective products have been widely discussed (Ullah and Kang 2014; Kundu and Chakrabarti 2015; Barzegar and Sajadieh 2017; Mohanty et al. 2018). However, most studies that considered the inventory model of defective products have assumed no error in the inspection process which implies the inspection is 100% correct. In reality, the negligence of inspectors, old equipment, or outdated inspection techniques can lead to mistakes in the inspection results (Khan et al. 2011; Sarkar and Saren 2016; Khalilpourazari et al. 2019a). Thus, models that consider the issue of defective products should also consider the probability of inspection errors.

Based on the context described above, a model was developed in the present study for the production and inventory problem of deteriorating raw materials and finished products with imperfect production and inspection systems from the perspective of supply chain integration. A single manufacturer and multiple retailers were considered. The aim was to jointly determine the manufacturer’s production and delivery strategies and the retailers’ replenishment strategies to maximize the total profit of the entire supply chain system. First, the total profit functions were individually established for the manufacturer and retailers. The total profit functions were then integrated and solved mathematically. A unique algorithm was developed to obtain the optimal solution to address the model complexity. The model was applied to several realistic numerical examples to illustrate the solution procedure, and a sensitivity analysis was conducted on the main model parameters to obtain useful management implications for decision makers. The contributions of this study are as follows:

• (1) The inventory problem of deteriorating raw materials and finished products in a multistage supply chain system which has not been discussed so far are proposed.

• (2) Multiple retailers are included in the supply chain system, and the influence of the relative market size, cost control and inspection capability between retailers are explored.

• (3) A unique algorithm is developed to obtain the optimal solutions, and the properties of the optimal solutions are numerically proved.

• (4) A sensitivity analysis is performed on the major model parameters to illustrate the effects of these parameters on the optimal solutions.

The rest of this paper is organized as follows. The related literature is briefly reviewed in Sect. 2. The notation and assumptions used throughout are listed in Sect. 3. The formula system and algorithm for obtaining the optimal solution are established in Sect. 4. In Sect. 5, numerical calculations are presented to explain the solution process and verify the concavity of the proposed model, along with the sensitivity analysis of the main parameters. Finally, conclusions and suggestions for future works are provided in Section 6.

2 Literature review

In this section, we conduct a literature review on the main topics closed related to this study included integrated supply chain inventory models, inventory models of deteriorating items and inventory models considering defective products.

2.1 Integrated supply chain inventory models

Goyal (1976) first developed an integrated inventory model on the basis of the traditional EOQ model to determine the optimal joint inventory policy for a single vendor and a single buyer. Banerjee (1986) developed a joint economic lot size model, in which a vendor produces to order for a buyer on a lot-for-lot basis. Lu (1995) subsequently extended this model to a single vendor and multiple buyers for an integrated inventory model. Ha and Kim (1997) recognized that products should be delivered during production to comply with the spirit of just-in-time (JIT) manufacturing. Kelle et al. (2003) proposed the concept of multiple shipments for batch delivery. Since then, other researchers (e.g., Ho et al. 2008; Lin 2009; Wu and Chen 2010; Lin and Ho 2011; Lou and Wang, 2013) have continued to explore strategies for integrated inventory models. Zhao et al. (2016) explored an integrated multistage supply chain with time-varying demand over a finite planning horizon. Wu and Zhao (2016) discussed supply chain models for two retailers and one supplier with a default risk under trade credit policy. Hariga et al. (2017) proposed a multistage cold supply chain model with carbon tax regulation. Du and Lei (2018) discussed the competition and coordination of a supply chain with a single supplier and multiple retailers. Kogan (2019) studied the effect of wholesale prices with a quantity discount offered by a supplier to multiple retailers engaged in a Cournot–Nash competition. Recently, a new integrated production–transportation–ordering–inventory holding problems for multi-client was developed by Goodarzian et al. (2021). Although multi-retailer inventory models have been proposed, they usually consider only the inventory of finished products; the inventory of raw materials is not considered simultaneously.

2.2 Inventory models of deteriorating items

Ghare and Schrader (1963) first included deteriorating items in the EOQ model and assumed that the deterioration is subject to exponential decay. Fujiwara (1993) discussed deteriorating items and proposed an EOQ model related to freshness. Wu et al. (2006) discussed an optimal replenishment policy for deteriorating items on the basis of stock-dependent demand and partial backlogging. Hsu et al. (2006) considered an optimal lot sizing model for deteriorating items with expiration dates. Lee and Dye (2012) proposed the preservation technology cost as a decision variable for deteriorated items. He and Huang (2013) discussed seasonally deteriorating products. Yang et al. (2015) proposed the optimal dynamic trade credit and preservation technology allocation for a deteriorating inventory model. Geetha and Udayakumar (2016) considered the residual value of deteriorating items. Mishra et al. (2017) developed an inventory model for deteriorating items with controllable deterioration rate under trade credit policy. Tiwari et al. (2018) considered a two-echelon supply chain model for deteriorating items in which the demand rate is assumed as dependent on the stock level. Shah et al. (2019) analyzed the inventory deterioration under dynamic prices. Khan et al. (2019b) proposed an inventory model for deteriorating items considering price-dependent demand. Shaikh et al. (2019) developed a two-warehouse deteriorating inventory model with advanced payment, partial backlogged shortages. Chakraborty et al. (2020) further explored a multi-item inventory model for non-instantaneous deteriorating items with multiple warehouses. Maihami et al. (2019) discussed a three-echelon supply chain model of items with probabilistic deterioration rates. Agi and Soni (2020) proposed a deteriorating inventory model with age-, stock-, and price-dependent demand rates. However, the above studies only discussed the impact of the deterioration characteristics of finished products on the inventory and did not consider the deterioration of raw materials.

2.3 Inventory models considering defective products

Porteus (1986) found that defective products are related to the probability of processes going out of control and regarded product quality as a decision variable for production process issues. Salameh and Jaber (2000) extended the traditional EPQ/EOQ model by accounting for imperfect quality items. Huang (2004) discussed an integrated production–inventory model that considers process unreliability and defective items. Sana (2010) discussed imperfect quality items and rework. Khan et al. (2011) considered the possibility of errors during defective product inspection and established an EOQ model that accounts for imperfect items and inspection errors. Ouyang et al. (2012) discussed an EOQ model with defective items and partially permissible delay in payments. Vishkaei et al. (2014) discussed optimal lot sizing for screening processes with returnable defective items. Ullah and Kang (2014) discussed the effects of defects, inspection, and reworking on inventory. Chen et al. (2016) considered the effect of the product warranty period of imperfect production systems on the selling price. Taleizadeh et al. (2016) proposed an inventory model that considers imperfect products and partial backordering. Khalilpourazari et al. (2016) developed a bi-objective EPQ model where defective products produce with a random rate while shortage are allowed. Zhou et al. (2016) considered trade credits, shortages, imperfect quality, and inspection errors to establish a synergic EOQ model. Barzegar and Sajadieh (2017) considered improving the quality of defective products in an integrated production–inventory model. Priyan and Manivannan (2017) discussed an inventory model that considers quality inspection errors and a fuzzy defective rate. Nobil et al. (2018) considered an imperfect production system in an integrated procurement-production-inventory problem, and discussed two cases for being with and without shortage. Cheikhrouhou et al. (2018) established an inventory model that includes the quality inspection and return of defective items; to model the problem, they introduced misclassification errors (Types I and II). Jain et al. (2018) designed a fuzzy imperfect production and repair inventory model with time dependent demand, production and repair rates. Khan et al. (2019a) established an integrated supply chain model that includes inspection errors and purchase and repair options. Recently, Tiwari et al. (2020) developed a stochastic supply chain model where quality issues and inspection errors affect its coordination. Zahedi et al. (2021) designed a closed-loop supply chain system which includes suppliers, production and distribution in the forward direction, and inspection, recycling and disposing in the reverse direction, and presented an integrated objective function to maximize the total profit of the supply chain. These previous studies did not consider the inventory management of multiple retailers with different inspection capabilities. In the present study, an integrated supply chain inventory model was developed to consider the imperfect production system of a single manufacturer and different imperfect inspection systems of multiple retailers.

2.4 Research gap analysis

Table 1 reveals the main differences between the present study and previous studies in the relevant literature. Although previous studies have sufficiently considered the deterioration of finished products, they have generally focused on EPQ/EOQ models and given less attention to production–inventory models. To our knowledge, no study has considered the deterioration of raw materials and finished products simultaneously when developing a supply chain inventory model. Similarly, no study has considered both imperfect production and inspection systems in an integrated multistage supply chain system with multiple retailers. The present study fills the above research gaps and is the first to discuss an integrated multistage supply chain inventory model for multiple retailers with imperfect production and inspection systems.

Table 1 Major characteristics of previous relevant research and our proposed model

3 Notation and assumptions

The notation and assumptions that were used to develop the multistage production–inventory model are described below.

3.1 Notation

k	Number of retailers, $k \in {\mathbb{Z}}^{ + }$
$i$	The $i$th retailer, where $i \in \left\{ {1, \ldots ,k} \right\}$
$D_{i}$	Market demand rate for retailer i
$P$	Manufacturer’s production rate
$A_{i}$	Ordering cost of finished products per order for retailer i
$O$	Manufacturer’s ordering cost of raw material per order
$r$	Amount of raw materials required to produce one unit of the finished product
$S$	Manufacturer’s setup cost per production cycle
$s_{i}$	Unit inspection cost for retailer i
$g$	Manufacturer’s unit raw material cost
$c$	Manufacturer’s unit production cost
$v$	Manufacturer’s unit selling price (retailers’ unit purchase price)
$p$	Retailers’ unit selling price of the finished product
$h_{{b_{i} }}$	Unit holding cost of finished products per unit time for retailer i
$h_{m}$	Manufacturer’s unit holding cost of raw material per unit time
$h_{v}$	Manufacturer’s unit holding cost of finished products per unit time
$w_{i}$	Unit treatment cost (including penalty cost) of defective products returned by customers for retailer i
$u$	Manufacturer’s handling cost for defective products returned by retailers
$F_{i}$	Fixed shipping cost per shipment for retailer i
$f_{i}$	Variable shipping cost per unit for retailer i
$\alpha_{i}$	Type I inspection error rate for retailer i, where $0 < \alpha_{i} < 1$
$\beta_{i}$	Type II inspection error rate for retailer i, where $0 < \beta_{i} < 1$
$\theta_{m}$	Deterioration rate of raw materials
$\theta_{v}$	Deterioration rate of finished products
$\lambda$	Defective rate of finished products, where $\lambda \in \left( {0,1} \right)$
$Q_{i}$	Order quantity of finished products for retailer i
$Q_{{m_{i} }}$	Order quantity of raw materials for retailer i
$n_{i}$	Number of shipments from the manufacturer to retailer i during a production cycle
$q_{i}$	Quantity shipped from the manufacturer to retailer i per shipment
$T_{{v_{i} }}$	Length of the manufacturer’s production cycle for retailer i
$T_{{s_{i} }}$	Length of the manufacturer’s production period for retailer i
$T_{{p_{i} }}$	Length of time for the manufacturer to produce and deliver the first batch of finished products to retailer i
$T_{{b_{i} }}$	Length of replenishment cycle for retailer i
*	The superscript represents the optimal value

3.2 Assumptions

• 1. The multistage supply chain system comprises a single manufacturer, multiple retailers, a single raw material, and a single product.

• 2. The finished products produced by the manufacturer contain defective items should be inspected by the retailers. Based on Khan et al. (2011), Sarkar and Saren (2016), Cheikhrouhou et al. (2018), and Khan et al. (2019a), Type I and Type II errors occur during the inspection process. Table 2 shows the inspection error ratio matrix for retailer i, where $i \in \left\{ {1,2, \ldots ,k} \right\}$.

• 3. The manufacturer’s production rate of non-defective products is finite and greater than the sum of the retailers’ demand rates; thus, it satisfies $\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]P > \mathop \sum \nolimits_{i = 1}^{k} D_{i}$. Otherwise, no inventory problems would occur (see Chen et al. 2016; Zhou et al. 2016; Jain et al. 2018; Mohanty et al. 2018).

• 4. Retailer i orders $Q_{i}$ quantity of finished products each time and allows the manufacturer to divide the order into $n_{i}$ consignments (see Ouyang et al. 2012; Darma Wangsa and Wee 2018). In each shipment, the manufacturer may ship $q_{i}$ units to ensure that retailer i receives $\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]q_{i}$ units of non-defective products inspected.

• 5. After inspection, the retailers immediately return all defective products to the manufacturer; the defective products sold due to Type II inspection errors should also be returned by the customer.

• 6. Shortages are not allowed for either the manufacturer or the retailers.

• 7. Type I and Type II error ratios of retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ are denoted by $\alpha_{i}$ and $\beta_{i}$, respectively. In practice, they can be estimated by using data from past inspection procedures. To facilitate the establishment of the model, $\alpha_{i}$ and $\beta_{i}$ are assumed to be known constants.

Table 2 Inspection error matrix for retailer i

4 Model formulation and solution

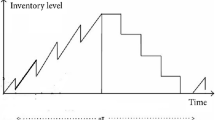
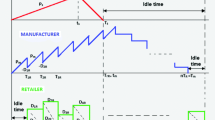
In the present study, a multistage integrated supply chain production–inventory model that considers deteriorating items, defective products, and inspection errors has been established. Figure 1 depicts the production, delivery, and inventory processes of the entire multistage supply chain system with a single manufacturer and multiple retailers. In this system, each retailer has an order of $Q_{i}$ units; the manufacturer must deliver the order in $n_{i}$ batches, and each shipment quantity is $q_{i}$ (the freight cost is borne by retailers), where $i \in \left\{ {\left. {1,2, \ldots ,k} \right|k \in {\mathbb{Z}}^{ + } } \right\}$. Since the finished products contain defective products at a defective rate of $\lambda$ and the retailer will have inspection errors, the total shipment quantity, which is judged as non-defective by retailer i for a production cycle (period length of $T_{{v_{i} }}$), is $\left[ {(1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda ]Q_{i}$, and the quantity judged as non-defective for each shipment is $\left[ {(1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda ]q_{i}$ (see Fig. 2a). To comply with the JIT inventory system, the manufacturer begins shipping during the production period and ships to retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ when the production quantity reaches $q_{i}$ units for the first time (period length of $T_{{p_{i} }}$). The manufacturer then ships $q_{i}$ units at regular intervals (period length of $T_{{b_{i} }}$). Furthermore, based on the assumption that the manufacturer’s production rate is greater than the total demand rate, it may stop producing (period length is $T_{{s_{i} }}$) the product but continue to ship them regularly until the entire ordered quantity has been shipped. Figure 2b presents the inventory level of the manufacturer’s finished products in a complete production cycle. On the other hand, when the manufacturer receives an order from retailer i, it also places an order with the raw material supplier and immediately purchases sufficient raw materials to supply a production cycle. These raw materials will be used up just at the end of production ($T_{{s_{i} }}$) and the inventory level can be shown as in Fig. 2c.

Fig. 1

Multistage supply chain of a single manufacturer and multiple retailers considering defective products

Fig. 2

Inventory levels of materials and finished products in a production cycle

The above notation and assumptions were used to establish the total profits per unit time of the retailers and the manufacturer.

4.1 Total profit per unit time for retailer i

Since the finished products from the manufacturer contain defective items in each shipment, retailer i immediately inspects the items upon receipt. Due to possible inspection errors, a ratio of $\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]$ products per order will be judged as non-defective and sold, and a ratio of $\left[ {\alpha_{i} \left( {1 - \lambda } \right) + \left( {1 - \beta_{i} } \right)\lambda } \right]$ products per order will be judged as defective and returned to the manufacturer immediately. Moreover, items will deteriorate during storage, so the inventory for retailer i $i \in \left\{ {1,2, \ldots ,k} \right\}$ will be reduced by sales and deterioration, as shown in Fig. 1. The dynamic change in the inventory level for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ during the time period $[0, T_{{b_{i} }} ]$ can be expressed by the following differential equation:

$$ \frac{{{\text{d}}I_{{R_{i} }} \left( t \right)}}{{{\text{d}}t}} + \theta_{v} I_{{R_{i} }} \left( t \right) = - D_{i} ,\quad 0 \le t \le T_{{b_{i} }} . $$

(1)

Assuming the boundary condition $I_{{R_{i} }} \left( {T_{{b_{i} }} } \right) = 0$, Eq. (1) transforms into

$$ I_{{R_{i} }} \left( t \right) = \frac{{D_{i} }}{{\theta_{v} }}\left[ {e^{{\theta_{v} \left( {T_{{b_{i} }} - t} \right)}} - 1} \right],\quad t \le T_{{b_{i} }} . $$

(2)

Since the quantity judged as non-defective per order is $\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]q_{i}$, Eq. (2) can be used to obtain the quantity of non-defective items shipped from the manufacturer to retailer i $\in \left\{ {1,2, \ldots ,k} \right\}$ per shipment $q_{i} = I_{{R_{i} }} \left( 0 \right)$ as follows:

$$ \left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]q_{i} = I_{{R_{i} }} \left( 0 \right) = \frac{{D_{i} }}{{\theta_{v} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right). $$

(3)

From Eq. (3), the quantity $q_{i}$ is given by

$$ q_{i} = \frac{{D_{i} }}{{\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]\theta_{v} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right). $$

(4)

The total profit per unit time for retailer i is determined by the sales revenue, ordering cost, inspection cost, purchasing cost, transportation cost, holding cost, and defective product disposal cost. These are evaluated as follows:

• 1. Sales revenue The sales revenue per replenishment cycle for retailer i $\in \left\{ {1,2, \ldots ,k} \right\}$ is $pD_{i} T_{{b_{i} }}$. However, due to Type II errors during the inspection process, $\beta_{i} \lambda q_{i}$ defective products are returned by customers. Therefore, the sales revenue per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is $pD_{i} - \beta_{i} \lambda q_{i} /T_{{b_{i} }} k$.

• 2. Ordering cost The ordering cost per replenishment cycle for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is $A_{i}$. Hence, the ordering cost per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is $A_{i} /T_{{b_{i} }}$.

• 3. Inspection cost The inspection cost per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is

  $$ \frac{{s_{i} q_{i} }}{{T_{{b_{i} }} }} = \frac{{s_{i} D_{i} \left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right)}}{{\left[ {(1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda ]\theta_{v} T_{{b_{i} }} }}. $$

  (5)

• 4. Purchasing cost The manufacturer sends the quantity $q_{i}$ to retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ per replenishment, where $\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]q_{i}$ gives the products judged as non-defective and the rest are judged as defective products and returned to the manufacturer immediately. Thus, the purchasing cost per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is

  $$ \frac{{v\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]q_{i} }}{{T_{{b_{i} }} }} = vD_{i} \left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right)/\theta_{v} T_{{b_{i} }} . $$

  (6)

• 5. Holding cost The inventory holding cost per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ can be obtained as follows:

  $$ \frac{{h_{{b_{i} }} }}{{T_{{b_{i} }} }}\mathop \int \limits_{0}^{{T_{{b_{i} }} }} I_{{R_{i} }} \left( t \right){\text{d}}t = \frac{{h_{{b_{i} }} D_{i} }}{{\theta_{v}^{2} T_{{b_{i} }} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - \theta_{v} T_{{b_{i} }} - 1} \right). $$

  (7)

• 6. Transportation cost The transportation cost per replenishment cycle for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ comprises the fixed cost $F_{i}$ and variable cost $f_{i} q_{i}$ and is given by

  $$ F_{i} + \frac{{f_{i} D_{i} }}{{\left[ {(1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda ]\theta_{v} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right). $$

  (8)

  Hence, the transportation cost per unit time is

  $$ \frac{1}{{T_{{b_{i} }} }}\left\{ {F_{i} + \frac{{f_{i} D_{i} }}{{\left[ {(1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda ]\theta_{v} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right)} \right\}. $$

  (9)

• 7. Defective product disposal cost For retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$, $\beta_{i} \lambda q_{i}$ units will be misjudged as non-defective during the inspection and sold and then will be returned by customers due to Type II errors. This results in handling costs for defective products, which includes penalty costs, freight costs, and loss of goodwill. If the handling cost for defective products per unit is $w_{i}$, the handling cost per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is $w_{i} \beta_{i} \lambda q_{i} /T_{{b_{i} }}$.

Based on these details, the total profit per unit time for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ can be obtained and is denoted as $TP_{i} \left( {T_{{b_{i} }} } \right)$:

$$ TP_{i} \left( {T_{{b_{i} }} } \right) = \frac{{\left( {\theta_{v} p + h_{{b_{i} }} } \right)D_{i} }}{{\theta_{v} }} - \frac{1}{{T_{{b_{i} }} }}\left\{ {A_{i} + F_{i} + \frac{{\left( {p\beta_{i} \lambda + w_{i} \beta_{i} \lambda + s_{i} + f_{i} } \right)D_{i} }}{{\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 + \lambda } \right) + \beta_{i} \lambda } \right]\theta_{v} }}(e^{{\theta_{v} T_{{b_{i} }} }} - 1) + \frac{{\theta_{v} v + h_{{b_{i} }} )D_{i} }}{{\theta_{v}^{2} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right)} \right\}. $$

(10)

4.2 Total profit per unit time for manufacturer

Within a production cycle, once the manufacturer receives an order from retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ for $Q_{i}$ units, it places an order with the raw material supplier and purchases enough raw materials for that production cycle. As each unit of finished products requires $r$ units of raw materials, the manufacturer needs at least $rQ_{i}$ units of raw materials for one production cycle. Raw materials also deteriorate during storage. In the interval [0,$T_{{s_{i} }}$], the raw material inventory level decreases on account of production and deterioration, as shown in Fig. 2. The dynamic changes in the manufacturer’s raw material inventory level can be expressed by the following differential equation:

$$ \frac{{{\text{d}}I_{{M_{i} }} \left( t \right)}}{{{\text{d}}t}} + \theta_{m} I_{{M_{i} }} \left( t \right) = - rP, \quad 0 \le t \le T_{{s_{i} }} . $$

(11)

Under the boundary condition $I_{{M_{i} }} \left( {T_{{s_{i} }} } \right) = 0$, the manufacturer’s inventory level of raw materials per production cycle is given by

$$ I_{{M_{i} }} \left( t \right) = \frac{rP}{{\theta_{m} }}\left[ {e^{{\theta_{m} \left( {T_{{s_{i} }} - t} \right)}} - 1} \right],\quad 0 \le t \le T_{{s_{i} }} . $$

(12)

From Eq. (12), the quantity of raw materials $Q_{{m_{i} }}$ is given by

$$ Q_{{m_{i} }} = \frac{rP}{{\theta_{m} }}\left( {e^{{\theta_{m} T_{{s_{i} }} }} - 1} \right). $$

(13)

To comply with the spirit of JIT manufacturing, as the manufacturer produces $q_{i}$ units of finished products, it delivers products to retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ immediately at the beginning of the production cycle. Then, a fixed shipment of $q_{i}$ units is repeated at intervals of $T_{{b_{i} }}$, and $n_{i}$ shipments take place in a production cycle, as shown in Fig. 2. For each shipment, $\left[ {\alpha_{i} \left( {1 - \lambda } \right) + \left( {1 - \beta_{i} } \right)\lambda } \right]q_{i}$ units of defective products are returned by the retailer and discarded. The manufacturer’s inventory level of finished products changes by reason of production and deterioration during the interval $\left[ {0,T_{{s_{i} }} } \right]$. As the manufacturer’s production rate for non-defective products is finite and greater than the demand rate, the manufacturer stops production once the inventory reaches a certain level $I_{max}$, and the inventory level is only affected by the deterioration in the interval $\left[ {T_{{s_{i} }} ,T_{{v_{i} }} } \right]$. The manufacturer’s inventory level of finished products at time t during the interval $\left[ {0,T_{{s_{i} }} } \right]$ can be expressed by the following differential equation:

$$ \frac{{{\text{d}}I_{{p_{i} }} \left( t \right)}}{{{\text{d}}t}} + \theta_{v} I_{{p_{i} }} \left( t \right) = P, \quad 0 \le t \le T_{{s_{i} }} . $$

(14)

Under the boundary condition $I_{{p_{i} }} \left( 0 \right) = 0$, the manufacturer’s inventory level of finished products per production cycle is given by

$$ I_{{p_{i} }} \left( t \right) = \frac{P}{{\theta_{v} }}\left( {1 - e^{{ - \theta_{v} t}} } \right), \quad 0 \le t \le T_{{s_{i} }} . $$

(15)

After the first $q_{i}$ units are completed at time $T_{{p_{i} }}$, the manufacturer immediately ships the products to retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$. This is governed by the relation $I_{{p_{i} }} \left( {T_{{p_{i} }} } \right) = \frac{{P\left( {1 - e^{{ - \theta_{v} T_{{p_{i} }} }} } \right)}}{{\theta_{v} }} = q_{i}$ from Eq. (3), which implies that

$$ T_{{p_{i} }} = \frac{1}{{\theta_{v} }}\ln \left[ {\frac{P}{{P - \theta_{v} q_{i} }}} \right]. $$

(16)

Hence, at $\left[ {T_{{s_{i} }} ,T_{{v_{i} }} } \right]$, since the manufacturer is no longer making products, the inventory changes are only due to item deterioration. At a certain time $t$, the inventory level of the finished products is governed by the following differential equation:

$$ \frac{{{\text{d}}I_{{d_{i} }} \left( t \right)}}{{{\text{d}}t}} + \theta_{v} I_{{d_{i} }} \left( t \right) = 0, \quad T_{{s_{i} }} \le t \le T_{{v_{i} }} . $$

(17)

Under the boundary condition $I_{{d_{i} }} \left( {T_{{v_{i} }} } \right) = n_{i} q_{i}$, Eq. (17) can be solved to determine the inventory level during the interval $\left[ {T_{{s_{i} }} ,T_{{v_{i} }} } \right]$:

$$ I_{{d_{i} }} \left( t \right) = n_{i} q_{i} e^{{\theta_{v} (T_{{v_{i} }} - t)}} ,\quad T_{{s_{i} }} \le t \le T_{{v_{i} }} . $$

(18)

Equations (15) and (18) and the boundary condition $I_{{p_{i} }} \left( {T_{{s_{i} }} } \right) = I_{{d_{i} }} \left( {T_{{s_{i} }} } \right)$ can be used to obtain

$$ T_{{s_{i} }} = \frac{1}{{\theta_{v} }}ln\left[ {\frac{{P + n_{i} q_{i} \theta_{v} e^{{\theta_{v} T_{{v_{i} }} }} }}{P}} \right]. $$

(19)

For retailer i, the manufacturer’s total profit includes the sales revenue, setup cost, material purchasing cost, production cost, raw material cost, holding cost, and defective product disposal cost. These are evaluated as follows:

• 1. Sales revenue With a ratio of $\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]$ products in the quantity $Q_{i}$ delivered by the manufacturer to retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ per production cycle will be judged as non-defective, the manufacturer’s total sales revenue for a production cycle is

  $$ v\left[ {\left( {1 - \alpha_{i} } \right)\left( {1 - \lambda } \right) + \beta_{i} \lambda } \right]Q_{i} = \frac{{vn_{i} D_{i} }}{{\theta_{v} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right). $$

  (20)

  As the production cycle has a duration of $T_{{v_{i} }}$, the sales revenue per unit time is $\frac{{vn_{i} D_{i} }}{{\theta_{v} T_{{v_{i} }} }}\left( {e^{{\theta_{v} T_{{b_{i} }} }} - 1} \right)$.

• 2. Setup cost The manufacturer’s setup cost per unit time for the order from retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is $\frac{S}{{T_{{v_{i} }} }}$.

• 3. Raw material purchasing cost The manufacturer’s purchasing cost per unit time for the order from retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ is $\frac{O}{{T_{{v_{i} }} }}$.

• 4. Production cost For retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$, the manufacturer’s production cost order per unit time is $\frac{{cPT_{{s_{i} }} }}{{T_{{v_{i} }} }}$.

• 5. Raw material cost The manufacturer’s raw material cost for retailer $i \in \left\{ {1,2, \ldots ,k} \right\}$ per production cycle is $gQ_{{m_{i} }} = \frac{grP}{{\theta_{m} }}\left( {e^{{\theta_{m} T_{{s_{i} }} }} - 1} \right)$, so the raw material cost for retailer i per unit time is $\frac{grP}{{\theta_{m} T_{{v_{i} }} }}\left( {e^{{\theta_{m} T_{{s_{i} }} }} - 1} \right)$.

• 6. Holding cost The manufacturer’s inventory holding cost for retailer i $\in \left\{\mathrm{1,2},\ldots ,k\right\}$ comprises two parts: raw materials and finished products. The holding cost per unit time for raw materials is

  $$\frac{{h}_{m}}{{T}_{{v}_{i}}}{\int }_{0}^{{T}_{{s}_{i}}}{I}_{{M}_{i}}\left(t\right)dt=\frac{{h}_{m}rP}{{\theta }_{m}^{2}}\left({e}^{{\theta }_{m}{T}_{{s}_{i}}}-{\theta }_{m}{T}_{{s}_{i}}-1\right).$$

  (21)

  For the holding cost of finished products, the manufacturer’s cumulative inventory per production cycle can be obtained as follows:

  $${\int }_{0}^{{T}_{{s}_{i}}}{I}_{{P}_{i}}\left(t\right)dt+{\int }_{{T}_{{s}_{i}}}^{{T}_{{v}_{i}}}{I}_{{d}_{i}}\left(t\right)dt-{q}_{i}{T}_{{b}_{i}}\left[1+2+\ldots +\left({n}_{i}-1\right)\right].$$

  (22)

  Therefore, the holding cost of finished products per unit time is

  $$\frac{{h}_{v}}{{T}_{{v}_{i}}}\left\{{\int }_{0}^{{T}_{{s}_{i}}}{I}_{{P}_{i}}(t)dt+{\int }_{{T}_{{s}_{i}}}^{{T}_{{v}_{i}}}{I}_{{d}_{i}}\left(t\right)dt-{q}_{i}{T}_{{b}_{i}}\left[1+2+\ldots +\left({n}_{i}-1\right)\right]\right\}=\frac{{h}_{v}}{{T}_{{v}_{i}}}\left\{\frac{P}{{\theta }_{v}^{2}}({e}^{-{\theta }_{v}{T}_{{s}_{i}}}+{\theta }_{2}{T}_{{s}_{i}}-1)+\frac{{n}_{i}{q}_{i}}{{\theta }_{v}}[{e}^{{\theta }_{v}{(T}_{{v}_{i}}-{T}_{{s}_{i}})}-1]-\frac{{n}_{i}\left({n}_{i}-1\right){D}_{i}{T}_{{b}_{i}}}{2\left[{(1-\alpha }_{i})(1-\lambda )+{\beta }_{i}\lambda \right]{\theta }_{v}}\left({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1\right)\right\}.$$

  (23)

  The above can be used to obtain the inventory holding cost per unit time of the manufacturer:

  $$\frac{1}{{T}_{{v}_{i}}}\left\{\frac{{h}_{m}rP\left({e}^{{\theta }_{m}{T}_{{s}_{i}}}-{\theta }_{m}{T}_{{s}_{i}}-1\right)}{{\theta }_{m}^{2}}+{h}_{v}\left\{\frac{P\left({e}^{-{\theta }_{v}{T}_{{s}_{i}}}+{\theta }_{v}{T}_{{s}_{i}}-1\right)}{{\theta }_{v}^{2}}+\frac{{n}_{i}{q}_{i}\left[{e}^{{\theta }_{v}{(T}_{{v}_{i}}-{T}_{{s}_{i}})}-1\right]}{{\theta }_{v}}-\frac{{n}_{i}\left({n}_{i}-1\right){D}_{i}{T}_{{b}_{i}}\left({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1\right)}{2\left[{(1-\alpha }_{i})(1-\lambda )+{\beta }_{i}\lambda \right]{\theta }_{v}}\right\}\right\}.$$

  (24)

• 7. Defective product disposal cost Due to the fact that a quantity of $[{\alpha }_{i}(1-\lambda )+(1-{\beta }_{i})\lambda ]{q}_{i}$ products per shipment is judged as defective by retailer i$\in \left\{\mathrm{1,2},\ldots ,k\right\}$ and returned directly, the manufacturer’s handling cost per unit time for defective products from retailer i is

  $$\frac{u}{{T}_{{v}_{i}}}\left[{\alpha }_{i}\left(1-\lambda \right)+\left(1-{\beta }_{i}\right)\lambda \right]{{n}_{i}q}_{i}=\frac{{n}_{i}\left[{\alpha }_{i}\left(1-\lambda \right)+\left(1-{\beta }_{i}\right)\lambda \right]{n}_{i}}{[\left(1-{\alpha }_{i}\right)\left(1-\lambda \right)+{\beta }_{i}\lambda ]{\theta }_{v}{T}_{{v}_{i}}}({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1).$$

  (25)

According to the above, for retailer i, the manufacturer’s total profit per unit time is denoted by $T{P}_{{v}_{i}}\left({T}_{{v}_{i}},{T}_{{s}_{i}},{n}_{i}\right)$ and is given by

$$T{P}_{{v}_{i}}\left({T}_{{v}_{i}},{T}_{{s}_{i}},{n}_{i}\right)=\frac{1}{{T}_{{v}_{i}}}\left\{\frac{v{n}_{i}{D}_{i}}{{\theta }_{v}}\left({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1\right)-(S+O)-(c-\frac{{h}_{m}r}{{\theta }_{m}}+\frac{{h}_{v}}{{\theta }_{v}})P{T}_{{s}_{i}}-\frac{{{(\theta }_{m}g+h}_{m})rP\left({e}^{{\theta }_{m}{T}_{{s}_{i}}}-1\right)}{{\theta }_{m}^{2}}+\frac{{{h}_{v}n}_{i}\left({n}_{i}-1\right){D}_{i}{T}_{{b}_{i}}\left({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1\right)}{2\left[{(1-\alpha }_{i})(1-\lambda )+{\beta }_{i}\lambda \right]{\theta }_{v}}-\{u[{\alpha }_{i}(1-\lambda )+(1-{\beta }_{i})\lambda ]{-\frac{{h}_{v}}{{\theta }_{v}}\}n}_{i}{q}_{i}\right\}.$$

(26)

${T}_{{v}_{i}}={T}_{{p}_{i}}+{n}_{i}{T}_{{b}_{i}}$; according to Eqs. (16) and (19), Eq. (26) can be simplified to $T{P}_{{v}_{i}}({T}_{{b}_{i}},{n}_{i})$. Based on the above, the total profit per unit time integrated for the multistage supply chain system is denoted by $JTP\left({T}_{b},n\right)$ and is given by

$$JTP\left({T}_{b},n\right)=\sum_{i=1}^{k}\left[T{P}_{i}\left({T}_{{b}_{i}}\right)+T{P}_{i}\left({T}_{{b}_{i}},{n}_{i}\right)\right]=\sum_{i=1}^{k}\left\{\frac{({\theta }_{v}p+{h}_{{b}_{i}}){D}_{i}}{{\theta }_{v}}-\right.\frac{1}{{T}_{{b}_{i}}}\left\{{A}_{i}+{F}_{i}+\frac{\left({p{\beta }_{i}\lambda +{w}_{i}{\beta }_{i}\lambda +s}_{i}+{f}_{i}\right){D}_{i}}{\left[\left(1-{\alpha }_{i}\right)\left(1+\lambda \right)+{\beta }_{i}\lambda \right]{\theta }_{v}}{(e}^{{\theta }_{v}{T}_{{b}_{i}}}-1)+\frac{{{(\theta }_{v}v+h}_{{b}_{i}}{)D}_{i}}{{\theta }_{v}^{2}}({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1)\right\} +\left.\frac{1}{{T}_{{v}_{i}}({T}_{{b}_{i}})}\left\{\frac{v{n}_{i}{D}_{i}}{{\theta }_{v}}\left({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1\right)-(S+O)-(c-\frac{{h}_{m}r}{{\theta }_{m}}+\frac{{h}_{v}}{{\theta }_{v}})P{T}_{{s}_{i}}({T}_{{b}_{i}})-\frac{{{(\theta }_{m}g+h}_{m})rP}{{\theta }_{m}^{2}}[{e}^{{\theta }_{m}{T}_{{s}_{i}}({T}_{{b}_{i}})}-1]+\frac{{{h}_{v}n}_{i}\left({n}_{i}-1\right){D}_{i}{T}_{{b}_{i}}}{2\left[{(1-\alpha }_{i})(1-\lambda )+{\beta }_{i}\lambda \right]{\theta }_{v}}\left({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1\right)-\frac{{{n}_{i}D}_{i}\{{\theta }_{v}u[{\alpha }_{i}(1-\lambda )+(1-{\beta }_{i})\lambda ]-{h}_{v}\}}{[\left(1-{\alpha }_{i}\right)\left(1-\lambda \right)+{\beta }_{i}\lambda ]{\theta }_{v}^{2}}({e}^{{\theta }_{v}{T}_{{b}_{i}}}-1)\right\}\right\}$$

(27)

Owing to the complexity of the model and integer value of $n_{i}$, finding closed-form solutions for $T_{b}$ and $n$ is difficult, where ${\varvec{T}}_{{\varvec{b}}}$ = {$T_{{b_{1} }} , T_{{b_{2} }} , \ldots ,T_{{b_{k} }}$}, ${\varvec{n}}$ = {$n_{1} , n_{2} , \ldots ,n_{k} \}$. The necessary conditions for maximizing $JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)$ for a given $n$ are obtained by solving the equation $\partial JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)/\partial T_{{b_{i} }} = 0$. $JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)$ is at its maximum when the Hessian matrix is negative definite. The matrix is defined as

$$ H = \left[ {\frac{{\partial^{2} JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)}}{{\partial T_{{b_{1} }}^{2} }} \ldots \frac{{\partial^{2} JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)}}{{\partial T_{{b_{1} }} \partial T_{{b_{k} }} }} \vdots \ddots \vdots \frac{{\partial^{2} JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)}}{{\partial T_{{b_{k} }} \partial T_{{b_{1} }} }} \ldots \frac{{\partial^{2} JTP\left( {{\varvec{T}}_{{\varvec{b}}} ,{\varvec{n}}} \right)}}{{\partial T_{{b_{k} }}^{2} }} } \right]. $$

(28)

Due to the high-power expression of the exponential function in Eq. (27), the concavity property of the total profit per unit time cannot be proved through mathematical analysis. Alternatively, the concavity for a given $n_{i}$ can be verified through numerical analysis, as given in the following section. The following algorithm was developed to optimize $n_{i}$.

5 Numerical examples and sensitivity analysis

This section presents the results of applying the proposed model to reasonable data and a sensitivity analysis of major parameters. All numerical examples are coded by Mathematica 12.0 which is a scientific computing software to obtain the optimal solutions based on the proposed algorithm.

5.1 Numerical examples

Example 1

To illustrate the solution process and verify the proposed model, we first consider a supply chain system with one manufacturer and two retailers in this example. Based on assumptions and reality, the relatively reasonable parameters of Retailers 1 and 2 are as follows:

• 1. Demand parameter ${D}_{1}=2000$, ${D}_{2}=1500$ (Retailer 1 has a market advantage over Retailer 2);

• 2. Cost parameters ${A}_{1}=\$100$/order, ${A}_{2}=\$150$/order; ${F}_{1}=\$100$/ship, ${F}_{2}=\$150$/ship; ${f}_{1}=\$0.6$/unit, ${f}_{2}=\$0.9$/unit;${h}_{{b}_{1}}=\$0.4$/unit/year, ${h}_{{b}_{2}}=\$0.6$/unit/year; ${s}_{1}=\$0.2$/unit, ${s}_{2}=\$0.3$/unit;${w}_{1}=\$10$/unit, and ${w}_{2}=\$15$/unit (Retailer 1 has an cost control advantage over Retailer 2);

• 3. Inspection parameters ${\alpha }_{1}=0.04$, ${\alpha }_{2}=0.06$; ${\beta }_{1}=0.08$, ${\beta }_{2}=0.12$ (Retailer 1 over Retailer 2 in inspection capabilities).

The other parameters are set to the following values: $P=8000$, $O=\$300$/order, $S=\$500$/setup, ${h}_{m}=\$0.1$/unit/year, ${h}_{v}=\$0.3$/unit/year, $u=\$3$/unit, $g=\$0.5$/unit, $c=\$1$/unit, $r=1$, ${\theta }_{m}=0.05$, ${\theta }_{v}=0.05$, $\lambda =0.05$, $p=\$50$/unit, and $v=\$20$/unit. The above realistic values are used to demonstrate the manufacturer’s optimal production and shipping policies and the two retailers’ ordering policies, as well as the integrated total profit per unit time. The above algorithm is used to obtain the solution procedure of the proposed model, as given in Table 3. All computations are implemented on a Core i7-7700 CPU @ 3.60 GHz 12 GB processor desktop computer and the calculation time of the numerical results in Table 3 is 1.641 s.

Table 3 Solution procedure of Example 1 with the proposed algorithm

From Table 3, it is obvious that for given value of${n}_{1}$, the integrated total profit per unit time is the concave in ${n}_{2}$ and for given value of${n}_{2}$, the integrated total profit per unit time is the concave in${n}_{1}$. Therefore, we can find an optimal solution of (${n}_{1}$,${n}_{2}$) to maximize the integrated total profit per unit time. The results indicate that the manufacturer should prepare ${n}_{1}^{*}=13$ and ${n}_{2}^{*}=9$ shipments to Retailers 1 and 2 in a production cycle, respectively, with corresponding shipping quantities of ${q}_{1}^{*}=442.164$ and${q}_{2}^{*}=532.572$. The order quantities for Retailers 1 and 2 per production cycle are ${Q}_{1}^{*}=$5748.14 and${Q}_{2}^{*}=4793.15$, respectively. Finally, the optimal integrated total profit per unit time for the multistage supply chain system ${JTP}^{*}$ is$\$\mathrm{156,860.07}$. Further, to verify the characteristics of the optimal solutions, we calculate the Hessian matrix at the point $({T}_{{b}_{1}}$,${T}_{{b}_{2}}$) = (0.2015, 0.3167) for given value of (${n}_{1}$,${n}_{2}$) = (13, 9) as follows:

$$H=\left[\begin{array}{cc}-64365.2& 0\\ 0& -24526.5\end{array}\right],$$

It is obvious that the Hessian matrix at the point $({T}_{{b}_{1}}$,${T}_{{b}_{2}}$) = (0.2015, 0.3167) for given value of (${n}_{1}$,${n}_{2}$) = (13, 9) is negative definite. Figure 3 displays the graphical illustration of the joint total profit function with respect to ${T}_{{b}_{1}}$ and $T_{{b_{2} }}$ for ($n_{1}$, $n_{2}$) = (9, 13), and Figs. 4 and 5 illustrate the graphical illustrations of the joint total profit function versus $n_{1}$ and $n_{2}$, respectively. Based on the above, the concavity of the joint total profit function can be verified, and the obtained solutions are optimal for maximizing the joint total profit function.

Fig. 3

Graphical illustration of $JTP\left( {T_{{b_{1} }} ,T_{{b_{2} }} ,n_{1} , n_{2} } \right)$ with respect to $T_{{b_{1} }}$ and $T_{{b_{2} }} ,$ for ($n_{1}$, $n_{2}$) = (13, 9)

Fig. 4

Graphical illustration $JTP\left( {T_{{b_{1} }} ,T_{{b_{2} }} ,n_{1} , n_{2} } \right)$ versus $n_{1}$ for ($T_{{b_{1} }} ,T_{{b_{2} }} , n_{2}$) = (0.2015, 0.3167, 9)

Fig. 5

Graphical illustration of $JTP\left( {T_{{b_{1} }} ,T_{{b_{2} }} ,n_{1} , n_{2} } \right)$ versus $n_{2}$ for ($T_{{b_{1} }} ,T_{{b_{2} }} ,n_{1}$) = (0.2015, 0.3167, 13)

Example 2

To explore the influence of the relative size of the parameters between retailers on the model, this example focuses on retailers with different demand scale parameter ($D_{i}$), cost control parameters ($A_{i}$, $h_{{b_{i} }}$, $C_{{T_{i} }}$,$C_{{t_{i} }}$,$s_{i}$, $w_{i}$), and inspection capability parameters ($\alpha_{i}$, $\beta_{i}$). The optimal decisions and total profits of the supply chain system in each situation are obtained. For clarity, Table 4 describes the different situations considered in this example. Table 5 presents the optimal solutions for each situation. Please note that Situation 1 indicates that the demand, cost control and inspection capability of Retailer 1 are more advantageous than retailer 2. Situations 2–4 indicate that Retailer 1 has at least two advantages over Retailer 2. Situations 5–7 indicate that one of Retailer 1’s demand, cost control or inspection capability of Retailer 1 is better than Retailer 2. Situation 1 indicates that the demand, cost control and inspection capability of Retailer 1 is the same as that of Retailer 2.

Table 4 Description of each situation with different parameters for the retailers

Table 5 Optimal solutions for situations depending on the retailers’ parameters

Comparing the results of different situations in Table 5 leads to the following insights:

• 1. Given the same cost and inspection parameters (for example, Situation 5), the retailer with a larger demand has a larger optimal order quantity and total profit. The practical explanation is that the retailer with a larger market requires more inventory, which increases the total profit.

• 2. Given the same demand and inspection parameters (for example, Situation 6), the retailer with lower cost parameters has a lower optimal order quantity but larger total profit. This indicates that a retailer who is more able to control costs can reduce the amount of inventory required and increase the total profit.

• 3. Given the same demand and cost parameters (for example Situation 7), the retailer with lower rates of inspection errors has a lower optimal order quantity but a larger total profit. Thus, a retailer who is more capable of judging good/defective products can reduce the amount of inventory required, which increases the total profit. This result is similar to that of Khan et al. (2019a), who found that improving the inspection capability has a positive impact on the profits of both buyers and sellers. The difference is that the present study further compared the optimal decisions and total profits of different retailers depending on their inspection capabilities.

• 4. Comparing Situations 1–4 and 8 indicates that with the increase of the demand (for example, $D_{1}$ is increased from 1750 to 2000) or the decreases of the cost and inspection parameters (for example $A_{1}$ is decreased from 125 to 100 or $\alpha_{1}$ is decreased from 0.05 to 0.04), the number of shipments from the manufacturer, the optimal profits of the manufacturer and retailers and optimal total profit of the supply chain system increase accordingly. For the management of the supply chain system, this indicates that the manufacturer’s shipping strategy and total profit and integrated total profit are also affected by the market size of the retailer and the retailer’s cost control and inspection capabilities. Increasing the market size, cost control, or inspection capability increases the number of shipments from the manufacturer, which increases the total profit of the manufacturer and integrated total profit.

• 5. By comparing Situations 1 and 5–8, it is found that changes to the demand parameters have the greatest impact on the retailers’ order quantity and total profits, followed by the cost parameters. The inspection parameters have the smallest impact. Regarding the integrated total profit of the supply chain system, changes in cost parameters have the greatest impact, followed by demand parameters. Inspection parameters again have the smallest impact.

Example 3

In real life, the supply chain contains more than three retailers; hence, to make the model more realistic, this example extends example 1 to consider three retailers. The parameters are the same as example 1 except $\{ D_{3} , A_{3} ,F_{3} , f_{3} ,h_{{b_{3} }} ,s_{3} ,w_{3} , \alpha_{3} ,\beta_{3} ) = \left\{ {1400, 160, 160, 1, 0.7, 0.4, 16, 0.07, 0.13} \right\}$. The results indicated that the manufacturer should prepare $n_{1}^{*} = 13$, $n_{2}^{*} = 10$ and $n_{3}^{*} = 7$ shipments to Retailers 1, 2 and 3, respectively, with corresponding shipping quantities of $q_{1}^{*} = 442.164$, $q_{2}^{*} = 466.999$ and $q_{3}^{*} = 676.225$. The order quantities for Retailers 1, 2 and 3 are $Q_{1}^{*} =$ 5748.14, $Q_{2}^{*} = 4469.99$ and $Q_{3}^{*} = 4733.57$, respectively. Finally, the optimal integrated total profit per unit time for the multistage supply chain system $JTP^{*}$ is $\$ 218,244$.35.

5.2 Sensitivity analysis

In this subsection, a sensitivity analysis is performed on the major model parameters. For convenience, the data are the same as the values used in Example 1. Each of the parameters changes by − 20%, − 10%, + 10% and + 20%, one parameter at a time while keeping all the remaining parameters unchanged. Table 6 presents the numerical results for the effects of these parameters on the optimal solutions. The following observations can be made:

• 1. Increasing the manufacturer’s production rate or retailer’s selling price reduced the retailers’ order quantities of finished products and the manufacturer’s order quantities of raw materials while increasing the integrated total profit. The increase in the integrated total profit of the supply chain with increased productivity and selling price is intuitive. However, it is interesting that productivity had a significant impact on the procurement of raw materials and ordering of finished products but no significant impact on the integrated profit, which is the opposite of the result for the selling price. In addition, the percentage of change in integrated total profit exceeds that of price fluctuations. For example, if the price is increased by 20%, the integrated total profit will increase by 22.1924% (> 20%).

• 2. Increasing the manufacturer’s ordering cost of raw materials, setup cost, or defective rate of finished products increased both the retailers’ order quantities of finished products and the manufacturer’s order quantities of raw materials while reducing the integrated total profit. Khan et al. (2019a) found that the inspection rate directly affects the cost of disposing of defective products and the strategic relationship between the seller and buyer. Similarly, the present study found that increasing the defective rate of finished products increased the burden on the supply chain system, which caused the manufacturer and retailers to increase purchases to meet demand. The circulation and return of more defective products caused related wastes, which ultimately reduced the integrated total profit.

• 3. Increasing the manufacturer’s holding cost of raw materials or finished products, raw material cost, production cost, selling price, disposal cost for defective products, or deterioration rate of finished products reduced the retailers’ order quantities of finished products and the manufacturer’s order quantities of raw materials, which reduced the integrated total profit.

• 4. Increasing the amount of raw materials required to produce one unit of a finished product or the deterioration rate of raw materials increased the manufacturer’s order quantities of raw materials and reduced the retailers’ order quantities of finished products and the integrated total profit. Increasing the consumption of raw materials naturally increases the purchase volume of the manufacturer, and the increase in related costs reduces the integrated total profit of the supply chain system. Thus, if the loss rate or deterioration rate of raw materials can be effectively reduced, the integrated total profit will be increased.

• 5. The results in the previous literature (Fujiwara 1993; Hsu et al. 2006; Geetha and Udayakumar 2016) showed that increasing the deterioration rate of items reduced the order quantity of finished products to avoid losses due to the deterioration of excess orders. However, the present study considered the deteriorations of raw materials and finished products at the same time. Increasing the deterioration rates of raw materials and finished products had different effects on the order quantity of raw materials. Increasing the deterioration rate of raw materials increased the purchase quantity; however, increasing the deterioration rate of finished products decreased the purchase quantity. Further, the deterioration rate of finished products has a significantly higher impact on the optimal solutions than the deterioration rate of raw materials.

• 6. The manufacturer’s shipping strategy was affected by changes to the manufacturer’s production rate, ordering cost of raw materials, setup cost, holding cost of finished products, selling price, raw material cost, the amount of raw materials required to produce one unit of a finished product, and the deterioration rate of finished products. The number of shipments increased with the manufacturer’s ordering cost of raw material, setup cost, or selling price. For the retailer with inferior status, the manufacturer’s shipping strategy was not easily changed, except for obvious changes (for example, increase or decrease by 20%) to the production rate or selling price.

Table 6 Sensitivity analysis of other parameters for optimal solutions

6 Conclusions and future work

The present study explored the practicality of an integrated multistage supply chain inventory model with multiple retailers and imperfect production and inspection systems. The model expresses the imperfect production and inspection systems according to the ratio of defective products produced by the manufacturer and Types I and II error rates of the retailers’ inspection system. Raw materials in the inventory stage and the deterioration of raw materials and products were also considered to improve the suitability of the model to actual situations. The present study aimed to clearly determine the manufacturer’s production and delivery strategies and the retailers’ replenishment strategies to maximize the total profit of the entire supply chain system. An algorithm was proposed to mathematically analyze the manufacturer’s optimal production and shipping strategies and the retailers’ optimal replenishment strategies. Numerical examples and sensitivity analysis were conducted to verify the characteristics of the optimal solutions and obtain managerial insights as follows:

• 1. By comparing the optimal decisions and total profits under different retailer markets and cost control and demand inspection capabilities, highlight insights were obtained: (1) Retailers with larger markets and better cost control and inspection capabilities guarantee a high integrated total profit for the supply chain system. (2) Changes in cost parameters have the greatest impact on the integrated total profit of the supply chain system, followed by demand parameters. Inspection parameters have the smallest impact.

• 2. The manufacturer’s production rate has a significant impact on the procurement of raw materials and the ordering of finished products, but it has no significant impact on the integrated profit. The retailers’ selling price has no significant impact on the procurement of raw materials and ordering of finished products, but it has a significant impact on the integrated profit. The percentage of change in integrated total profit (22.19%) exceeds that of price fluctuations (20%).

• 3. In contrast to previous research, the proposed model considers the deterioration of raw materials and finished products. The results showed that increasing the deterioration rates of materials and finished products have different effects on the order quantity of raw materials. Increasing the deterioration rate of materials increases the purchase quantity, whereas increasing the deterioration rate of finished products decreases the purchase quantity. If the deterioration rate of finished products can be effectively reduced, the integrated total profit will be increased. Such improvement requires preservation technology investment, which may be an interesting issue for future research.

• 4. The manufacturer’s shipping strategy is relatively rigid. Changes in part of the manufacturer's parameters (production rate, ordering cost of raw materials, setup cost, holding cost of finished products, selling price, raw material cost, the amount of raw materials required to produce one unit of a finished product, and deterioration rate of finished products) will slightly affect the delivery strategy of the dominant retailers to achieve the optimal joint total profit, while the delivery strategy of the weak retailers in the market remains stable.

The conclusions of this study can serve as a useful reference for decision makers in practical applications. Future research may focus on evaluating how different retailers can reduce the deterioration rate of finished products by investing in warehousing. The proposed model can also be extended by incorporating game theory, setting the manufacturer or one retailer as the leader and other retailers as followers, expanding demand rates as functions of time or inventory, or allowing shortages. In addition, for more complex multi-retailer models, using heuristic, metaheuristic, fuzzy, and evolutionary optimization approaches, such as the parallel heuristic local search algorithm and the parallel multithreaded $A^{*}$ heuristic search algorithm (Al-Adwan et al. 2019; Khalilpourazari and Mohammadi 2018; Mahafzah 2014), the genetic algorithm, simulated annealing, particle swarm, chemical reaction optimizer, grey wolf optimizer and most valuable player algorithm (Al-Shaikh et al. 2019; Al-Shraideh et al. 2013; Bhunia et al. 2017; Ghezavati and Nia 2015; Khattab et al. 2019; Mahafzah et al. 2021; Mohammadi and Khalilpourazari 2017), and fuzzy mathematical model (Alavidoost et al. 2021; Khalilpourazari et al. 2019b) to solve the models and reduce the time complexity of searching is worth investigated in future research.