Optimizing a multi-item economic order quantity problem with imperfect items, inspection errors, and backorders

Abstract

This paper proposes a multi-item economic order quantity model with imperfect items in supply deliveries. The inspection process to classify the items is not perfect and involves two types of error: Type-I and Type-II. To cope with the uncertainty involved in real-world applications and to bring the problem closer to reality, operational constraints are assumed stochastic. The aim is to determine the optimal order and back order sizes of the items in order to achieve maximum total profit. As the proposed mathematical model is a constrained nonlinear programming, three different solution methods including an exact method named the interior-point and two novel meta-heuristics named grey wolf optimizer (GWO) and moth-flame optimization (MFO) algorithms are utilized to solve the problem. In order to demonstrate the most efficient solution method, the performance of the three solution methods is evaluated when they solve some test problems of different sizes. Various comparison measures including percentage relative error, relative percentage deviation, and computation time are used to compare the solution methods. Based on the results, MFO performs better in small and medium instances in terms of percentage relative error; meanwhile, GWO shows a better performance in terms of relative percentage deviation in large-size test problems. In the end, sensitivity analyses are carried out to investigate how any parameter change affects the objective function value of the mathematical model in order to determine the most critical parameter.

1 Introduction

Economic order quantity (EOQ) model is one of the most widely used approaches in production and service systems. The classical EOQ model was first proposed by Harris (1913). Aiming to minimize total inventory costs, this model determines the optimal order size of an item (Kundu et al. 2016). Although the EOQ is a commonly used inventory control methods, it has some unrealistic assumptions which limit its applicability (Dye 2012). One of the most inherent assumptions in this model is that all the supply deliveries are perfect with no defective items. In real-world situations, however, it is hard to find a supply process with no defective items. In many manufacturing processes, such as high-tech manufacturing processes producing sensitive products, it is important to ensure that all the supply deliveries are of the best quality and contain no defective items. This is because of the very high additional costs imposed by entering defective items into the system. In the last decades, this problem motivated many researchers to develop new versions of the EOQ model which takes the presence of imperfect items (the ones that cannot meet customers’ expectation) into account in supply deliveries.

One of the first researchers who considered imperfect items in the EOQ model was Salameh and Jaber (2000). They assumed that the supply batches are inspected by a 100% inspection policy upon arrival, based on which the withdrawn defective items are sold at a lower price in a single batch. Cárdenas-Barrón (2000) modified the formulation proposed by Salameh and Jaber (2000) by adding a parameter which was missing from the economic order size formulation. In addition, Goyal and Cárdenas-Barrón (2002) aimed to propose a new simple approach to calculate economic order size in the model proposed by Salameh and Jaber (2000). Eroglu and Ozdemir (2007) developed a new EOQ formulation with defective items. They assumed that the defective items are withdrawn by a 100% inspection process. In recent years, Khan et al. (2011) proposed an EOQ model considering imperfect items. Their main contribution was to consider the inspection as an imperfect process as well. Therefore, a non-defective item could be classified defective and vice versa. In other words, an inspector may commit Type-I and Type-II errors during the inspection process. Hsu and Hsu (2013) extended the model proposed by Khan et al. (2011) by allowing back orders. Similar to Khan et al. (2011), they considered a sale return in their model. In another research, Nasr et al. (2013) proposed an EOQ model under the assumption of random supply. They showed that the correlation between the qualities of the items decreases the optimal order quantity. Arqub and Abo-Hammour (2014) introduced a continuous genetic algorithm as an efficient solver for systems of second-order boundary value problems where smooth solution curves were used throughout the evolution of the algorithm to obtain the required nodal values of the unknown variables. The proposed methodology was based on representing each derivative in the system of differential equations by its finite difference approximation. Abo-Hammour et al. (2014) proposed an optimization algorithm for solving systems of singular boundary value problems. In their work, the system was formulated as an optimization problem by the direct minimization of the overall individual residual error subject to the given constraints boundary conditions and was then solved using the continuous genetic algorithm in the sense that each of the derivatives was replaced by an appropriate difference quotient approximation. Skouri et al. (2014) developed an EOQ model with backorders and defective supply batches. They assumed that the supply batches are inspected upon arrival using a 100% inspection policy, based on which if at least one defective item in the supplied batch is found, the whole batch will be returned to the supplier.

The presence of imperfect items is studied extensively in the EPQ model. To make it brief, Table 1 shows some research aimed to develop EOQ and EPQ models with defective items and states the place the current work stands with regard to the previous works.

Table 1 Literature review of the EOQ and EPQ models with defective items

The motivation behind this research is twofold. First, while most of the EOQ and EPQ models concerning imperfect items presented in the literature are developed for a single-item inventory system, the current research proposes a multi-item version of the EOQ model with imperfect quality items to bring the problem more applicable. Second, as there are many real-world operational constraints which can significantly influence the economic order and back ordering sizes, an attempt is also made in this research to have an EOQ model with stochastic operational constraints (the constraints with adjustable stochastic satisfaction level).

This research is a direct extension of the work presented by Hsu and Hsu (2013), based on which a mathematical model for a multi-item economic order quantity model is proposed with the presence of defective items in supply deliveries. Each delivery is inspected using a 100% inspection policy, in which the operator is subject to committing a Type-I error (the operator recognizes a non-defective item as a defective item) or a Type-II error (he/she recognizes a defective item as a non-defective item). Both Type-I and Type-II errors impose additional costs on the inventory system. In addition, sales return occurs. This means that the customer returns defective items to the system. In the considered EOQ model, the shortages are fully back ordered. In order to develop a more realistic and applicable EOQ model, in this paper, various operational constraints such as warehouse capacity and budget are added to the model. As most of the main parameters of the developed model in real-world environments are uncertain, all the operational constraints of the proposed model are considered stochastic. The goal of the proposed mathematical model is to determine the optimal order and back order sizes of the items in order to maximize the expected total profit. Due to the complexity of the proposed mathematical model, an exact solution methodology named the interior-point method alongside two novel meta-heuristics called grey wolf optimizer (GWO) and moth-flame optimization (MFO) algorithms is utilized to solve the problem. Moth-flame is a novel algorithm that is successfully implemented in a variety of fields and presented promising results (Acharyulu et al. 2019; Reddy et al. 2018; Ebrahim et al. 2018; Khalilpourazari and Pasandideh 2017). It has also been highly recommended by many researchers to solve complex optimization problems (Precup et al. 2017; Rodríguez et al. 2017; Heidari and Pahlavani 2017; Khalilpourazari and Khalilpourazary 2018a). Both GWO and MFO have several advantages over classical methods. One of the most important advantages of these algorithms is that they can modify the exploration and exploitation of the solution space iteratively. In other words, in first iterations they aim at explorations and as the iterations pass on, they focus of exploitation more. Moreover, these algorithms use efficient operators that avoid trapping in local optima as well as generating efficient solutions in each iteration. By solving various test problems, the performances of the three solution methods are evaluated. To compare the solution methods, different measures including percentage relative error (PRE), relative percentage deviation (RPD), and computation time are considered. A single factor ANOVA and the Tukey’s multiple comparison tests are used to determine significant differences in the performance of the solution methods. Finally, sensitivity analyses are carried out to determine the effect of any change in the main parameters of the proposed mathematical model on the objective function value to determine the most critical parameters.

The remainder of the paper is organized as follows: Sect. 2 first presents a definition of the problem and assumptions and then proposes the mathematical model of the problem. In Sect. 3, the solution methods are illustrated. In Sect. 4, the performances of the solution methods in terms of different metrics are compared when they solve various test problems. In Sect. 5, sensitivity analyses are carried out to determine the most critical parameters of the problem. Finally, Sect. 6 concludes the paper.

2 Mathematical formulation

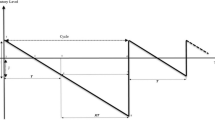
The general behavior of the classical single-item EOQ problem with inspection error and defective items investigated by Hsu and Hsu (2013) and Khan et al. (2011) is shown in Fig. 1.

Fig. 1

Behavior of the considered EOQ problem

Hsu and Hsu (2013) assumed that when the ordered batch arrives, it should first be used to meet the back ordered demand during (0 − t₁). Then, the screening process and fulfilling the usual demands occur in (t₂ − t₁) simultaneously. As the screening process is imperfect with inspection errors (the errors that occur during the inspection process by the operators), some non-defective items are classified defective and some defective items are classified non-defective (Type-I and Type-II errors). The defective items (B₁) are collected and withdrawn from the process at the time (t₂). The remaining items, which are classified as non-defective items, are used to satisfy the demand. Note in this case that some defective items are delivered to the customers. Hsu and Hsu (2013) assumed that the customers will return the defective items with a probability of 1. Therefore, the defective items (B₂) are returned to the system. At the end of the screening process, the defective items are separated and considered as a single batch to be sold in secondary markets.

To illustrate the cost function presented by Hsu and Hsu (2013), the following notations are first considered.

Parameters
$D$	Demand rate
$p$	The probability that each item is defective
$h$	Holding cost per unit time
$k$	Fixed ordering cost
$b$	The back ordering cost per unit per time
$s$	Selling price of each non-defective unit
$v$	Selling price of each defective unit
$x$	Screening rate of products
$m_{1}$	Probability of Type-I error in product i (determining a non-defective product as defective product)
$m_{2}$	Probability of Type-II error in product i (determining a defective product as a non-defective product)
$f(p)$	Probability density function of $p$
$f(m_{1} )$	Probability density function of $m_{1}$
$f(m_{2} )$	Probability density function of $m_{2}$
$C_{\text{r}}$	Rejection cost of a non-defective product
$C_{\text{a}}$	Accepting the cost of a defective product
Decision variables
$Q$	Order size
$B$	Maximum back ordering level

Now, based on the inventory behavior we have:

$$ B_{1} = Q\left( {1 - p} \right)m_{1} + Qp\left( {1 - m_{2} } \right). $$

(1)

In addition, the number of returned products can be obtained as follows:

$$ B_{2} = Qpm_{2} . $$

(2)

Then we have:

$$ t_{1} = \frac{{Q\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\} - B}}{D} = \frac{{Q\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{D} - \frac{B}{D}, $$

(3)

$$ t_{2} = \frac{B}{D}, $$

(4)

$$ t_{3} = \frac{B}{{x\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\} - D}}, $$

(5)

and

$$ T = t_{1} + t_{2} = \frac{{Q\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{D}. $$

(6)

Based on the above-mentioned equations alongside the quantities of backordered demand and inventory level, the total cost function for a given cycle can be formulated as follows.

$$ \begin{aligned} {\text{TC}}\left( {Q,B} \right) &= K + cQ + dQ + c_{\text{r}} Q\left( {1 - p} \right)m_{1} + c_{\text{a}} Qpm_{2} \\ & \quad + \frac{1}{2}bB^{2} \left( {\frac{1}{D} + \frac{1}{{x\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\} - D}}} \right) \\ & \quad + \frac{h}{2}\left\{ {\frac{{QB\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{{x\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\} - D}} + \frac{{Q^{2} }}{D}\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}^{2} } \right\} \\ & \quad + \frac{h}{2}\left\{ { - \frac{{QB\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}^{2} }}{{D(\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}} - \frac{{QB\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{D} + \frac{{B^{2} \left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{{D(\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}}} \right\} \\ & \quad + h\left\{ {\frac{{Q^{2} }}{x}\left\{ {p + m_{1} - p\left( {m_{1} + m_{2} } \right)} \right\} + \frac{{Q^{2} pm_{2} \left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{2D}} \right\} \\ \end{aligned} $$

(7)

Then, the expected profit function of the EOQ problem for a given cycle follows.

$$ \begin{aligned} E\left[ {{\text{TP}}\left( {Q,B} \right)} \right] &= E\left[ {{\text{TR}}\left( {Q,B} \right)} \right] - E\left[ {{\text{TC}}\left( {Q,B} \right)} \right] \\ & \quad = E\left[ {sQ\left( {1 - p} \right)\left( {1 - m_{1} } \right) + vQ\left( {1 - p} \right)m_{1} + vQp - K - cQ - dQ - c_{\rm r} Q\left( {1 - p} \right)m_{1} - c_{\rm a} Qpm_{2} } \right. \\ & \quad \quad - \frac{1}{2}bB^{2} \left( {\frac{1}{D} + \frac{1}{{x\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\} - D}}} \right) \\ & \quad \quad - \frac{h}{2}\left\{ {\frac{{QB\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{{x\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\} - D}} + \frac{{Q^{2} }}{D}\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}^{2} } \right\} \\ & \quad \quad - \frac{h}{2}\left\{ { - \frac{{QB\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}^{2} }}{{D(\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}} - \frac{{QB\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{D}} \right. \\ &\quad \quad \left. { + \frac{{B^{2} \left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{{D(\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}}} \right\} \\ & \quad \quad \left. { - h\left\{ {\frac{{Q^{2} }}{x}\left\{ {p + m_{1} - p\left( {m_{1} + m_{2} } \right)} \right\} + \frac{{Q^{2} pm_{2} \left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}}}{2D}} \right\}} \right]. \\ \end{aligned} $$

(8)

Moreover, the expected cycle length is calculated by

$$ E\left[ T \right] = \frac{{Q\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}{D} . $$

(9)

To obtain the expected annual profit function, Hsu and Hsu (2013) used the renewal reward theorem and obtained the following function.

$$ \begin{aligned} & {\text{ETPU}}\left( {Q,B} \right) \\ & = \frac{{sD\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right)}}{{\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}} + \frac{{vD\left( {\left( {1 - E\left[ p \right]} \right)E\left[ {m_{1} } \right] + E\left[ p \right]} \right)}}{{\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}} \\ & \quad - \frac{{D\left( {\frac{K}{Q} + c + d + c_{\rm r} \left( {1 - E\left[ p \right]} \right)E\left[ {m_{1} } \right] + c_{\rm a} E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}{{\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}} \\ & \quad - \frac{{bB^{2} }}{{2Q\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}\left( {1 + \frac{{E\left[ {\frac{1}{{\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}}} \right]D}}{x}} \right) \\ & \quad - \frac{h}{2}\left\{ {\frac{{BDE\left[ {\frac{{\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} }}{{\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}}} \right]/x + Q(E\left[ {\left( {1 - p} \right)^{2} } \right]E\left[ {\left( {1 - m_{1} } \right)^{2} } \right] + 2E\left[ {p^{2} } \right]E\left[ {m_{2}^{2} } \right]}}{{\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}} \right. \\ & \quad \left. { + \frac{{3\left( {E\left[ p \right] - E\left[ {p^{2} } \right]} \right)E\left[ {\left( {1 - m_{1} } \right)} \right]E\left[ {m_{2} } \right]}}{{\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}} \right\} \\ & \quad - \frac{h}{2}\left\{ { - \frac{{BE\left[ {\frac{{\left\{ {\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} } \right\}^{2} }}{{\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}}} \right]}}{{\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}} - B + \frac{{B^{2} E\left[ {\frac{{\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} }}{{\left( {1 - p} \right)\left( {1 - m_{1} } \right) + pm_{2} - D/x}}} \right]}}{{Q\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}} \right\} \\ & \quad - hQ\left\{ {\frac{{D\left\{ {E\left[ p \right] + E\left[ {m_{1} } \right] - E\left[ p \right]\left( {E\left[ {m_{1} } \right] + E\left[ {m_{2} } \right]} \right)} \right\}}}{{x\left( {\left( {1 - E\left[ p \right]} \right)\left( {1 - E\left[ {m_{1} } \right]} \right) + E\left[ p \right]E\left[ {m_{2} } \right]} \right)}}} \right\}. \\ \end{aligned} $$

(10)

As mentioned earlier, some of the main assumptions used by Hsu and Hsu (2013) make the problem unrealistic. For example, they only considered a single-item inventory system which is far from a real-world application. Another point to mention is that they did not take into account any operational constraints. As such, referring to the profit function proposed by Hsu and Hsu (2013), in this study a constrained multi-item economic order quantity model that accounts for inspection errors, back orders, and defective items is proposed. To develop a more applicable EOQ model, different operational constraints such as maximum desirable holding and back ordering constraints, warehouse capacity and budget constraints are considered. Besides, as most of the main parameters of the problem are uncertain in real-world applications, all the above-mentioned constraints are considered stochastic.

The following notations are used to develop the mathematical model of the problem.

Parameters
$D_{i}$	Demand rate of product i (units per time)
$p_{i}$	The probability that an item of product i is defective
$h_{i}$	Holding cost of product i per unit time
$k_{i}$	Fixed ordering cost of product i per order
$b_{i}$	The back ordering cost for product i per unit per time
$s_{i}$	Selling price of a non-defective unit of product i
$v_{i}$	Selling price of a defective unit of product i
$x_{i}$	Screening rate of product i
$m_{i1}$	Probability of Type-I inspection error of product i (classifying a non-defective product as defective)
$m_{i2}$	Probability of Type-II inspection error of product i (classifying a defective product as a non-defective)
$f(p_{i} )$	Probability density function of $p_{i}$
$f(m_{i1} )$	Probability density function of $m_{i1}$
$f(m_{i2} )$	Probability density function of $m_{i2}$
$C_{\text{r}}$	Rejection cost of a non-defective product
$C_{\text{a}}$	Accepting the cost of a defective product
Budget	Total available budget to purchase products
Ca	Total available capacity to keep products in stock
$f_{i}$	Space required for storing product i per unit
$C_{i}$	Purchasing cost of product i
$T^{ + }$	Portion of the cycle length in which the inventory is positive
$T^{ - }$	Portion of the cycle length in which inventory is negative
G	Minimum acceptable ratio of the portion of the cycle length in which the inventory is positive $T^{ + }$ to portion of the cycle length in which the inventory is negative $T^{ - }$
TCB	Maximum desirable back ordering costs
TCH	Maximum desirable holding costs
ETPU	Expected total annual profit
Decision variables
$Q_{i}$	Order size of product i
$B_{i}$	Maximum back ordering level of product i

The following assumptions are made to model the problem:

• The sales return rate is a known constant

• Supply deliveries are inspected using a 100% inspection policy

• Demand rates are known and constant.

• The probability density function of Type-I and Type-II errors is a uniform distribution.

• The probability of an item being defective follows a uniform distribution

• The budget is limited.

• The warehouse capacity is constrained.

• Shortages are fully back ordered.

• No shortages occur during the inspection process.

The multi-item mathematical model of the problem with stochastic constraints is presented as:

$$ \begin{aligned} \max {\text{ETPU}}\left( {Q_{i} ,B_{i} } \right) = &\mathop \sum \limits_{i = 1}^{n} \frac{{s_{i} D_{i} \left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right)}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad + \mathop \sum \limits_{i = 1}^{n} \frac{{v_{i} D_{i} \left( {1 - E\left[ {p_{i} } \right]} \right)E\left[ {m_{i1} } \right] + E\left[ {p_{i} } \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{D_{i} (\frac{{k_{i} }}{{Q_{i} }} + c_{i} + d_{i} + c_{ri} \left( {1 - E\left[ {p_{i} } \right]} \right)E\left[ {m_{i1} } \right] + c_{{{\text{a}}i}} E\left[ {p_{i} } \right]E\left[ {m_{2i} } \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{b_{i} B_{i}^{2} }}{{2Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad \times \left( {1 + \frac{{E\left[ {\frac{1}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]D_{i} }}{{x_{i} }}} \right) \\ & \quad - \sum\limits_{i = 1}^{n} {\frac{{h_{i} }}{2}} \left\{ {\frac{{\frac{{B_{i} D_{i} E\left[ {\frac{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} }}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]}}{{x_{i} }}}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right. \\ & \quad \left. { + \frac{{Q_{i} (E\left[ {\left( {1 - p_{i} } \right)^{2} } \right]E\left[ {\left( {1 - m_{i1} } \right)^{2} } \right] + 2E\left[ {p_{i}^{2} } \right]E\left[ {m_{2i}^{2} } \right] + 3\left( {E\left[ {p_{i} } \right] - E\left[ {p_{i}^{2} } \right]} \right)E\left[ {\left( {1 - m_{i1} } \right)} \right]E\left[ {m_{i2} } \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right\} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} }}{2}\left\{ { - \frac{{B_{i} E\left[ {\frac{{\left\{ {\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} } \right\}^{2} }}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} - B_{i} } \right. \\ & \quad \left. { + \frac{{B_{i}^{2} E\left[ {\frac{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} }}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]}}{{Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right\} \\ & \quad - h_{i} D_{i} \left\{ {\frac{{D_{i} \left\{ {E\left[ {p_{i} } \right] + E\left[ {m_{i1} } \right] - E\left[ {p_{i} } \right]\left( {E\left[ {m_{i1} } \right] + E\left[ {m_{i2} } \right]} \right)} \right\}}}{{x_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right\}. \\ \end{aligned} $$

(11)

$$ \begin{aligned} & {\text{s.t.}} \\ & P\left\{ {\mathop \sum \limits_{i = 1}^{n} f_{i} \left( {Q_{i} - B_{i} } \right) \le Ca} \right\} \ge \xi . \\ \end{aligned} $$

(12)

$$ P\left\{ {\mathop \sum \limits_{i = 1}^{n} c_{i} Q_{i} \le {\text{Budget}}} \right\} \ge \alpha . $$

(13)

$$ P\left\{ {\frac{{Q_{i} \left\{ {\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E[m_{i1} ]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\} - B_{i} }}{{B_{i} }} \ge G} \right\} \ge \beta , \quad \forall i . $$

(14)

$$ \begin{aligned} & P\left\{ {\mathop \sum \limits_{i = 1}^{n} \frac{{D_{i} }}{{Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right. \\ & \quad \left. { \times \frac{1}{2}b_{i} B_{i}^{2} \left( {\frac{1}{{D_{i} }} + \frac{1}{{x_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{2i} } \right]} \right\} - D_{i} }}} \right) \le {\text{TCB}}} \right\} \ge \gamma . \\ \end{aligned} $$

(15)

$$ \begin{aligned} & P\left\{ {\sum\limits_{i = 1}^{n} {\frac{{D_{i} }}{{Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} } \right. \\ & \quad \quad \times \left\{ \begin{aligned} &\frac{{h_{i} }}{2}\left\{ {\frac{{Q_{i} B_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{x_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{2i} } \right]} \right\} - D_{i} }} + \frac{{Q_{i}^{2} }}{{D_{i} }}\left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}^{2} } \right\} \hfill \\ \quad + \frac{{h_{i} }}{2}\left\{ {\begin{array}{*{20}c} { - \frac{{Q_{i} B_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}^{2} }}{{D_{i} \left\{ {\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}} \right\}}} - \frac{{Q_{i} B_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{D_{i} }}} \\ { + \frac{{B_{i}^{2} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{D_{i} \left\{ {\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}} \right\}}}} \\ \end{array} } \right\} \hfill \\\quad +\, h_{i} \left\{ {\begin{array}{*{20}c} {\frac{{Q_{i}^{2} }}{{x_{i} }}\left\{ {E\left[ {p_{i} } \right] + E\left[ {m_{1i} } \right] - E\left[ {p_{i} } \right]\left( {E\left[ {m_{1i} } \right] + E\left[ {m_{2i} } \right]} \right)} \right\}} \\ { + \frac{{Q_{i}^{2} E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]\left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{2D_{i} }}} \\ \end{array} } \right\} \hfill \\ \end{aligned} \right\} \\ & \quad \left. { \le {\text{TCH}}} \right\} \ge \delta . \\ \end{aligned} $$

(16)

$$ Q_{i} ,B_{i} \ge 0,\quad i = 1,2, \ldots ,n. $$

(17)

The objective function in Eq. (11) aims to maximize the expected total annual profit of the inventory system considering inspection error costs, sales return, backorders, holding, and ordering costs for a multi-item EOQ model. Constraint (12) ensures that there is enough warehouse space to store all products under uncertainty. Constraint (13) guarantees that purchasing costs of products do not exceed the budget under uncertainty. Constraint (14) ensures that the division of $T^{ + }$ by $T^{ - }$ is not less than a specific percent for all products with a probability greater than or equal $\beta$. Constraint (15) holds with a probability greater than or equal $\gamma .$ Constraint (15) determines that the total backordering cost should not exceed the maximum desirable backordering costs under uncertainty. Constraint (16) guarantees that the total holding costs are less than the maximum desirable holding costs under uncertainty. Finally, the decision variables alongside their possible values are defined in Constraint (17). Note that $\xi$, $\gamma$, and $\delta$ are percentages that show the satisfaction levels of the stochastic constraints.

As all the constraints in the above mathematical formulation are stochastic, assuming a normal distribution for each of their right-hand-side parameters, the model of the problem becomes:

$$ \begin{aligned} \max {\text{ETPU}}\left( {Q_{i} ,B_{i} } \right) = &\mathop \sum \limits_{i = 1}^{n} \frac{{s_{i} D_{i} \left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right)}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad + \mathop \sum \limits_{i = 1}^{n} \frac{{v_{i} D_{i} \left( {1 - E\left[ {p_{i} } \right]} \right)E\left[ {m_{i1} } \right] + E\left[ {p_{i} } \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{D_{i} (\frac{{k_{i} }}{{Q_{i} }} + c_{i} + d_{i} + c_{ri} \left( {1 - E\left[ {p_{i} } \right]} \right)E\left[ {m_{i1} } \right] + c_{ai} E\left[ {p_{i} } \right]E\left[ {m_{2i} } \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{b_{i} B_{i}^{2} }}{{2Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad \times \left( {1 + \frac{{E\left[ {\frac{1}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]D_{i} }}{{x_{i} }}} \right) \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} }}{2}\left\{ {\frac{{\frac{{B_{i} D_{i} E\left[ {\frac{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} }}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]}}{{x_{i} }}}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right. \\ & \quad \left. { + \frac{{Q_{i} (E\left[ {\left( {1 - p_{i} } \right)^{2} } \right]E\left[ {\left( {1 - m_{i1} } \right)^{2} } \right] + 2E\left[ {p_{i}^{2} } \right]E\left[ {m_{2i}^{2} } \right] + 3\left( {E\left[ {p_{i} } \right] - E\left[ {p_{i}^{2} } \right]} \right)E\left[ {\left( {1 - m_{i1} } \right)} \right]E\left[ {m_{i2} } \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right\} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} }}{2}\left\{ { - \frac{{B_{i} E\left[ {\frac{{\left\{ {\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} } \right\}^{2} }}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]}}{{(\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} - B_{i} } \right. \\ & \quad + \frac{{B_{i}^{2} E\left[ {\frac{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} }}{{\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}}}} \right]}}{{Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad - h_{i} D_{i} \left\{ {\frac{{D_{i} \left\{ {E\left[ {p_{i} } \right] + E\left[ {m_{i1} } \right] - E\left[ {p_{i} } \right]\left( {E\left[ {m_{i1} } \right] + E\left[ {m_{i2} } \right]} \right)} \right\}}}{{x_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}}} \right\}. \\ \end{aligned} $$

(18)

$$ \begin{aligned} & {\text{s.t.:}}\\ & \mathop \sum \limits_{i = 1}^{n} f_{i} \left( {Q_{i} - B_{i} } \right) + z_{\xi } \sigma_{Ca} \le \mu_{Ca} . \\ \end{aligned} $$

(19)

$$ \mathop \sum \limits_{i = 1}^{n} c_{i} Q_{i} + z_{\alpha } \sigma_{\text{Budget}} \le \mu_{\text{Budget}} . $$

(20)

$$ \frac{{Q_{i} \left\{ {\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E[m_{i1} ]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\} - B_{i} }}{{B_{i} }} + z_{\beta } \sigma_{G} \ge \mu_{G} ,\quad \forall i . $$

(21)

$$ \begin{aligned} & \mathop \sum \limits_{i = 1}^{n} \frac{{D_{i} }}{{Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad \times \frac{1}{2}b_{i} B_{i}^{2} \left( {\frac{1}{{D_{i} }} + \frac{1}{{x_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{2i} } \right]} \right\} - D_{i} }}} \right) \\ & \quad + z_{\gamma } \sigma_{\text{TCB}} \le \mu_{\text{TCB}} . \\ \end{aligned} $$

(22)

$$ \begin{aligned} & \mathop \sum \limits_{i = 1}^{n} \frac{{D_{i} }}{{Q_{i} (\left( {1 - E\left[ {p_{i} } \right]} \right)\left( {1 - E\left[ {m_{i1} } \right]} \right) + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]}} \\ & \quad \times \left\{ {\begin{array}{l} {\frac{{h_{i} }}{2}\left\{ {\frac{{Q_{i} B_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{x_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{2i} } \right]} \right\} - D_{i} }} + \frac{{Q_{i}^{2} }}{{D_{i} }}\left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}^{2} } \right\}} \\ \quad { + \frac{{h_{i} }}{2}\left\{ {\begin{array}{*{20}c} { - \frac{{Q_{i} B_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}^{2} }}{{D_{i} \left\{ {\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}} \right\}}} - \frac{{Q_{i} B_{i} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{D_{i} }}} \\ { + \frac{{B_{i}^{2} \left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{D_{i} \left\{ {\left( {1 - p_{i} } \right)\left( {1 - m_{i1} } \right) + p_{i} m_{i2} - {\raise0.7ex\hbox{${D_{i} }$} \!\mathord{\left/ {\vphantom {{D_{i} } {x_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{i} }$}}} \right\}}}} \\ \end{array} } \right\}} \\\quad { + h_{i} \left\{ {\begin{array}{*{20}c} {\frac{{Q_{i}^{2} }}{{x_{i} }}\left\{ {E\left[ {p_{i} } \right] + E\left[ {m_{1i} } \right] - E\left[ {p_{i} } \right]\left( {E\left[ {m_{1i} } \right] + E\left[ {m_{2i} } \right]} \right)} \right\}} \\ { + \frac{{Q_{i}^{2} E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]\left\{ {E\left[ {1 - p_{i} } \right]E\left[ {1 - m_{i1} } \right] + E\left[ {p_{i} } \right]E\left[ {m_{i2} } \right]} \right\}}}{{2D_{i} }}} \\ \end{array} } \right\}} \\ \end{array} } \right\} \\ & \quad + z_{\delta } \sigma_{\text{TCH}} \le \mu_{\text{TCH}} . \\ \end{aligned} $$

(23)

$$ Q_{i} ,B_{i} \ge 0,\quad i = 1,2, \ldots ,n . $$

(24)

Note that $z$ in the above formulation is the critical percentile of the standard normal distribution. In addition, $\sigma_{\text{Ca}}$, $\sigma_{\text{Budget}}$, $\sigma_{\text{G}}$, and $\sigma_{\text{TCH}}$ are the standard deviations (SD) of the warehouse capacity, the SD of available budget, the SD of the minimum acceptable ratio of the portion of the cycle length in which the inventory is positive T⁺ to portion of the cycle length in which the inventory is negative T⁻, and the SD of the maximum desirable backordering costs, respectively. Also, $\mu_{\text{Ca}}$, $\mu_{\text{Budget}}$, $\mu_{\text{G}}$, and $\mu_{\text{TCH}}$ are the average warehouse capacity, average available budget, the average minimum acceptable ratio of the portion of the cycle length in which the inventory is positive T⁺ to portion of the cycle length in which the inventory is negative T⁻, and the average maximum desirable backordering costs, respectively.

3 Solution methods

The model developed in the previous section is a constrained nonlinear programming (CNLP) problem, which is hard to solve using an exact method. This is due to the nonlinearity of the objective function and constraints and existence of too many local minima. In the last decade, many meta-heuristic algorithms mostly inspired by nature, animals’ behavior, or other physical phenomena have been proposed in the literature to find near-optimum solutions of various complex NLP problems. Water cycle algorithm (WCA), mine blast algorithm (MBA), multi-verse optimization (MVO) algorithm, particle swarm optimization (PSO) algorithm, whale optimization algorithm (WOA), dragonfly algorithm (DA), ant lion optimizer (ALO), grey wolf optimizer (GWO), crow search algorithm (CSA), the gravitational search algorithm (GSA), stochastic fractal search (SFS), sine cosine algorithm (SCA), moth-flame optimization (MFO), and genetic algorithm (GA) are just a few. In this paper, a well-known exact solution method, i.e., the interior-point method is used to solve the problem. As large-size problems cannot be solved using the exact method in a reasonable computational time, GWO and MFO due to their good performances are utilized as well to solve large instances.

3.1 Interior-point method

The interior-point method is one the most efficient and commonly used algorithms to solve complex NLP problems. Interested readers are referred to Byrd et al. (1999, 2000), and Waltz et al. (2006) for more information on this method.

3.2 Grey wolf optimizer

The GWO algorithm is a relatively new meta-heuristic that was proposed by Mirjalili et al. (2014) for the first time. GWO mimics the behavior of the grey wolves in nature to perform optimization. Usually, 5–12 grey wolves live together and form a pack. One of the most interesting things about the grey wolves is their social hierarchy in the pack which is shown graphically in Fig. 2. The Alpha wolf in Fig. 2 acts as the leader which is responsible for making decisions about when to sleep or how to hunt. All the other wolves must follow Alpha. The Beta wolf is the wolf that helps Alpha in managing the pack. The Omega wolves are the lowest in rank and must follow Alpha, Beta and Delta wolves. The other wolves are called Delta who helps Alpha and Beta in managing the pack. Considering this hierarchy of the grey wolves, the GWO performs optimization by mimicking the hunting approach of the grey wolves (Mirjalili et al. 2014; Guha et al. 2016). GWO considers the position of the prey as the optimal solution of the problem. Then, using the social hierarchy of the grey wolves, GWO tries to find the position of the prey.

Fig. 2

Grey wolves’ hierarchy and their responsibilities

There are three steps in the hunting process of the grey wolves illustrated as follows.

3.2.1 Encircling prey

In nature, the grey wolves start the hunting process by encircling the prey. In GWO, the hunting process starts with encircling the prey as well. The following formulation is used to update the position of the grey wolves in the encircling process (Khalilpourazari and Khalilpourazary 2018a).

$$ \vec{D} = \left| {\vec{C}.\vec{X}_{\text{p}} (t) - \vec{X}(t)} \right|, $$

(25)

$$ \bar{X}(t + 1) = \vec{X}_{\text{p}} (t) - \vec{A}.\vec{D}, $$

(26)

where $\vec{C}$ and $\vec{A}$ are coefficients, $\vec{X}_{\text{p}}$ is the position of prey, while, $\vec{X}$ is the position of the grey wolves (Mirjalili et al. 2014). In the above formulation, the Parameter $\vec{A}$ has a prominent role, since it determines the search radius of the grey wolves. These coefficients are calculated in each iteration of the GWO algorithm as follows.

$$ \vec{A} = 2\vec{a}. \vec{r}_{1} - \vec{a}, $$

(27)

$$ \vec{C} = 2. \vec{r}_{2} , $$

(28)

where $\vec{a}$ decreases from two to zero over the course of iterations, and the parameters $\vec{r}_{1}$ and $\vec{r}_{2}$ are random numbers between 0 and 1. The above formulae allow the grey wolves to update their positions around the prey, efficiently. Figure 3 demonstrates how these formulations allow the grey wolves to update their positions around the prey in 2D and 3D views.

Fig. 3

Encircling the prey in 2D and 3D views

3.2.2 Hunting

In the hunting process, the Alpha Wolf estimates the position of the prey and the Beta and Delta wolves follow him/her. Therefore, the positions of the Alpha, Beta, and Delta wolves are the best approximation of the position of the prey. As such, the Omega wolves update their position based on the position of the dominant wolves. The following equations are considered to update the position of the Omega wolves.

$$ \vec{D}_{\alpha } = \left| {\vec{C}_{1} .\vec{X}_{\alpha } - \vec{X}} \right|, \vec{D}_{\beta } = \left| {\vec{C}_{2} .\vec{X}_{\beta } - \vec{X}} \right|, \vec{D}_{\delta } = \left| {\vec{C}_{3} .\vec{X}_{\delta } - \vec{X}} \right|, $$

(29)

$$ \bar{X}_{1} = \vec{X}_{\alpha } - \vec{A}_{1} .\vec{D}_{\alpha } , \bar{X}_{2} = \vec{X}_{\beta } - \vec{A}_{2} .\vec{D}_{\beta } , \bar{X}_{3} = \vec{X}_{\delta } - \vec{A}_{3} .\vec{D}_{\delta } , $$

(30)

$$ \bar{X}(t + 1) = \frac{{\vec{X}_{1} + \vec{X}_{2} + \vec{X}_{3} }}{3}. $$

(31)

3.2.3 Attacking prey

By decreasing the value of the $\vec{a}$ over the course of iterations, the grey wolves update their positions toward the prey. The pseudo-code of the GWO algorithm is presented as follows.

Knowing that each meta-heuristic algorithm needs to make a proper trade-off between its exploration and exploitations abilities to perform efficiently, by decreasing the search radius of the grey wolves in GWO an appropriate trade-off between exploration and exploitation phases is obtained.

3.3 Moth-flame optimization

Moths are small and beautiful insects with a very intelligent approach to fly. They use the moonlight at night to fly in long straight paths by keeping a fixed angle with the moon (light source). This efficient approach for flying is called transverse orientation (Gaston et al. 2013; Frank 2006; Mirjalili 2015). When the light source is close to the moth, by keeping a fixed angle with respect to the light source, moth starts flying in a spiral path around the light source (Khalilpourazari and Pasandideh 2017). After a while, the spiral fly path of the moth converges to the light source. The moth-flame optimization algorithm (MFO), firstly proposed by Mirjalili (2015), mimics this behavior of moths to perform optimization.

Similar to most of the meta-heuristic algorithms, the MFO starts the optimization process by generating a set of random solutions. The following equation shows the first population of the moths.

$$ {\text{IP}} = \left[ {\begin{array}{*{20}c} {u_{1,1} } & {u_{1,2} } & \cdots & {u_{1,n - 1} } & {u_{1,n} } \\ {u_{2,1} } & \ddots & \cdots & \cdots & {u_{2,n} } \\ \vdots & \cdots & \ddots & \cdots & \vdots \\ {u_{{{\text{npop}} - 1,1}} } & \cdots & \cdots & \ddots & {u_{{{\text{npop}} - 1,n}} } \\ {u_{{{\text{npop}},1}} } & {u_{{{\text{npop}},2}} } & \cdots & {u_{{{\text{npop}},n - 1}} } & {u_{{{\text{npop}},n}} } \\ \end{array} } \right]. $$

(32)

In Eq. (32), each row presents a moth where $u_{{{\text{npop}},n}}$ is nth decision variable of npopth moth. Moreover, npop is an input parameter of the MFO which determines the number of moths in the initial population and n is the number of decision variables. As MFO mimics the spiral flying of the moths around light sources (flame), one needs to generate a set of random solutions exactly in the size of the initial population named flame matrix. The flame matrix is shown by the following equation.

$$ F = \left[ {\begin{array}{*{20}c} {l_{1,1} } & {l_{1,2} } & \cdots & {l_{1,n - 1} } & {l_{1,n} } \\ {l_{2,1} } & \ddots & \cdots & \cdots & {l_{2,n} } \\ \vdots & \cdots & \ddots & \cdots & \vdots \\ {l_{{{\text{npop}} - 1,1}} } & \cdots & \cdots & \ddots & {l_{{{\text{npop}} - 1,n}} } \\ {l_{{{\text{npop}},1}} } & {l_{{{\text{npop}},2}} } & \cdots & {l_{{{\text{npop}},n - 1}} } & {l_{{{\text{npop}},n}} } \\ \end{array} } \right]. $$

(33)

In Eq. (33), each row presents a flame where $l_{{{\text{npop}},n}}$ is nth decision variable of npopth flame. The difference between the initial population (IP) and the flame matrix (F) is that each row in IP shows a moth in the solution space, while each row in F shows the corresponding flame of each moth. Moreover, each flame presents the best solution obtained so far by each moth in the solution space of the problem.

To mimic the spiral fly behavior of the moths around their corresponding flame, a logarithmic spiral function is proposed (Mirjalili 2015; Khalilpourazari and Khalilpourazary 2017).

$$ {\text{IP}}_{i}^{X + 1} = \left| {{\text{IP}}_{i}^{X} - F_{i} } \right|.e^{bt} .\cos \left( {2\pi t} \right) + F_{i} , $$

(34)

where ${\text{IP}}_{i}^{X + 1}$ is updated position of the moth,${\text{IP}}_{i}^{X}$ is the current position of the moth,$F_{i}$ is the position of the flame, and $e$, and $b$ are coefficients. Moreover, t is a coefficient in [− 1, 1] which determines the distance of the moth from its corresponding flame in its next position. Figure 4 presents the spiral fly of the moths around their corresponding flame.

Fig. 4

Spiral fly path of the moths around their corresponding flame

As mentioned earlier, each meta-heuristic algorithm needs to make an appropriate trade-off between its exploration and exploitation abilities to perform well in optimization. The MFO algorithm decreases the value of the parameter t over the iterations to force the moths to update their position toward their corresponding flame using the following equations (Mirjalili 2015; Khalilpourazari and Pasandideh 2017).

$$ a = - 1 + {\text{Current}}\; {\text{iteration}}\left( {\frac{ - 1}{{\max \;{\text{iterations}}}}} \right), $$

(35)

$$ t = (a - 1) \times {\text{rand}} + 1, $$

(36)

where ${\text{Current}}\; {\text{iteration}}$ is the current iteration number and $\max \;{\text{iterations}}$ is the maximum number of iterations. Mirjalili (2015) named the parameter $a$ as the convergence constant. The above equations guarantee that the moths converge to their corresponding flame at the last iterations. Figure 5 presents the possible positions of the moths over the iterations of the MFO algorithm, where the blue and red moths present the possible positions of the search agents around their corresponding flames in the first and last iterations, respectively.

Fig. 5

The positions of the moths in the first and last iterations of the MFO algorithm

The pseudo-code of the MFO algorithm is presented as follows.

4 Numerical examples and performance evaluation

In this section, the performances of the three solution methods are evaluated by solving various test problems with different sizes in small, medium and large, since the performance of a meta-heuristic algorithm varies depending on the size of the problem it solves. The problems with up to 7 items are considered small, the ones with more than 7 items up to 90 items are assumed medium, and the problems with 100 items and more are considered large size. For all test problems, the values of the main parameters of the mathematical formulation are generated randomly using uniform distributions shown in Table 2.

Table 2 The uniform distribution of the randomly generated parameters

4.1 Comparing measures

Three performance measures are used in this section to evaluate the efficiency of the algorithms. In problems with small and medium sizes for which the optimal order and back ordering sizes can be obtained using the interior-point method, and hence the optimal objective function value is in hand, the percentage relative error (PRE) is defined in Eq. (30) to quantify the gap between the solutions provided by the two meta-heuristics and the optimal solution (Kayvanfar and Teymourian 2014; Khalilpourazari et al. 2016; Fazli-Khalaf et al. 2017).

$$ {\text{PRE}} = \frac{{M_{\text{sol}} - {\text{Opt}}}}{\text{opt}}. $$

(37)

In Eq. (37), $M_{\text{sol}}$ is the objective function value of a solution found by a meta-heuristic and Opt is the optimal objective function value determined using the interior-point approach.

As the optimal value of the objective function for large-size problems cannot be determined by the interior-point method in a reasonable computational time, the relative percentage deviation (RPD) is utilized in Eq. (38) to evaluate the performance of the GWO and MFO (Khalilpourazari and Pasandideh 2017; Khalilpourazari and Khalilpourazary 2018b)

$$ {\text{RPD}} = \frac{{M_{\text{sol}} - {\text{Best}}_{\text{sol}} }}{{{\text{Best}}_{\text{sol}} }} , $$

(38)

where ${\text{Best}}_{\text{sol}}$ is the best solution obtained by either GWO or MFO and $M_{\text{sol}}$ is the solution provided by each algorithm.

The above two measures compare the solution methods in terms of the solution quality. However, further measures are needed to make the comparison fairer. The next performance measure is the computational time (CT) in seconds needed for each solution method to solve a problem. Note that, based on the suggestions provided in the literature, a fixed number of evaluations (NFE) should be considered for both meta-heuristics to solve small, medium, and large-size problems.

In what follows in Sects. 4.2–4.4, the solution algorithms are compared together in terms of the above three measures in small, medium, and large problems, respectively.

4.2 Small-size test problems

In this subsection, the performance of the three solution methods is evaluated in small-size test problems. Table 3 presents the computational results.

Table 3 Percentage relative error and computation time of the algorithms in small-size test problems

The three solution methods solve 6 small-size problems, each with 5 scenarios of randomly generated parameters in Table 3. In other words, each solution algorithm solves 30 different test problems in 10 runs, based on which the average computation time (CT_Ave) and the average percentage relative error (PRE_Ave) are reported. Note that the interior-point method finds a unique optimal solution in all the 10 runs of a problem with a specific scenario. However, its computation time strongly depends on the starting point. Therefore, various starting points are chosen in 10 runs in order to obtain the required average computation time of the interior-point method. The performance of the three solution methods in solving small-size test problems is graphically depicted in Fig. 6.

Fig. 6

a The best solution obtained by each solution methods, b the average percentage relative error of MFO and GWO, c standard deviation of the best solutions of MFO and GWO, d computation time of the solution methods

From Table 3, it is clear that the three solution methods are completely competitive. Thus, more analyses are needed to make a correct conclusion. In this research, a one-way analysis of variance (ANOVA) is implemented to find significant differences in the performance of the three solution methods. The ANOVA is carried out at a 95% confidence level. Table 4 presents the ANOVA results to compare the means of the computation times.

Table 4 Analysis of variance for average computation time measure

As the P value in Table 4 is less than 0.05, implying significant differences among the means of the required computation times, a post hoc analysis based on Tukey’s multiple comparison tests is employed to find specific differences (Mohammadi and Khalilpourazari 2017). Table 5 contains the results.

Table 5 Tukey’s multiple comparison tests to determine the differences among the average computation times

Considering the value of the adjusted P values, it is clear that the performance of the interior-point method is significantly different from the ones of both MFO and GWO. Therefore, both MFO and GWO are faster than the interior-point method. In addition, there is no significant difference between MFO and GWO. Figure 7 shows this conclusion pictorially.

Fig. 7

Results of the Tukey’s multiple comparison tests for CT in small-size test problems

Another statistical test is implemented on the average PRE values of the two meta-heuristic algorithms to find a significant difference at a 95% confidence level. Table 6 presents the results.

Table 6 Statistical comparison of the two meta-heuristics in terms of the PRE measure in small-size problems

As the P value in Table 6 is far more than 0.05, there is no significant difference in terms of the quality of the solution between MFO and GWO. Figure 8 presents the Boxplot of the average PRE of the MFO and GWO.

Fig. 8

The Boxplot of the average PRE of the MFO and GWO in small-size test problems

To conclude all the above-mentioned analyses, the interior-point was able to solve small-size problems in reasonable computational times. Moreover, MFO and GWO were able to solve the problem efficiently, where the average gaps of the MFO and GWO were 0.004 and 0.002%, respectively. In addition, the interior-point method, as it should, is the best in terms of the solution quality provided for small-size problems. However, in terms of the computational time, MFO was the best. The main goal of comparing MFO and GWO in small-size test problems was to show that the solution quality of MFO and GWO is considerably well and competitive with a well-known exact solution method such as the interior-point. Table 7 presents the ranking of the three solution methods in small-size test problems.

Table 7 Ranking the three solution methods in small-size test problems

4.3 Medium-size test problems

Similar to small-sized problems solved in Sect. 4.2, the performances of the solution methods in terms of solution quality and required computational time are compared together when they solve medium-sized test problems. Table 8 summarizes the results.

Table 8 Percentage relative error and computation time of the algorithms in medium-size test problems

The results in Table 8 indicate that as the number of variables is increased significantly in medium size compared to small-size problems, obtaining a solution using a classical method such as the interior-point becomes harder. As a result, the computational time of the interior-point method increases significantly. Meanwhile, the performances of the two meta-heuristics that are shown in Table 8 indicate that they are completely competitive. Figure 9 presents the convergence plot, the average penalty of the solutions, the average objective function value and the value of the convergence parameters of the GWO and MFO in each iteration.

Fig. 9

Infeasibility, best solution and the values of the main parameters of the GWO and MFO over iterations

Figure 9 shows that GWO is able to reach the feasible solution space of the problem much faster than MFO. This is because the average penalty value of the solutions in GWO decreases faster than MFO. In addition, the average objective function value of the GWO increases constantly comparing to MFO. This shows that GWO is able to find better solutions and update the position of the search agents, intelligently. Figure 10 presents the best solution, the average standard deviation of the best solutions, the average PRE, and the average computational times of the solution methods, graphically.

Fig. 10

a The best solution, b the average percentage relative error, c average standard deviation, d computation time of the solution methods in medium-size test problems

First of all, Fig. 10 shows that both MFO and GWO are able to provide solutions with a significantly low deviation from the optimal solution. Besides, Fig. 10 depicts that MFO is able to provide better solutions than GWO. In other words, MFO is more efficient in the exploitation of the solution space. Moreover, the average standard deviation of the solutions obtained by MFO within different repetitions is significantly smaller than the one in GWO. Therefore, it can be concluded that MFO is more robust in solution compared to GWO in solving medium-size test problems.

Once again, to find significant statistical differences among the solution methods in terms of their required average computational times, a single factor ANOVA is utilized, based on which the results are summarized in Table 9.

Table 9 ANOVA results to compare average computation time in medium-sized problems

As the P value in Table 9 is smaller than 0.05, implying significant differences among the solution methods in terms of their required average computational times at 95% confidence level, a post hoc analysis using the Tukey’s multiple comparisons is performed here to find out which algorithm performs significantly different. The results that are given in Table 10 show that the average computation time of the interior-point method is significantly different from the ones of MFO and GWO. This shows the merit of the MFO and GWO in solving medium-size test problems against a classical method. Figure 11 presents the Boxplot and the results obtained by the Tukey’s test.

Table 10 Tukey’s simultaneous tests for differences of the means of the computation times of the algorithms

Fig. 11

Results of Tukey’s multiple comparison tests for CT_Ave in medium-size test problems

To compare the performance of MFO and GWO, another statistical analysis is performed here to find significant differences in average PRE of these two solution methods in medium-size problems. Table 11 presents the results.

Table 11 Analysis of variance for PRE in medium-size test problems

As Table 11 shows, there is a significant difference between MFO and GWO in obtaining solutions for medium-size test problems. Figure 12 presents the Boxplot of the average PRE of these algorithms.

Fig. 12

The Boxplot of the average PRE of the MFO and GWO in medium-size test problems

To make a conclusion from the computational results in this subsection, Table 12 is presented to rank the solution methods based on their efficiency in solving the medium-size test problems.

Table 12 Ranking the three solution methods in medium-size test problems

4.4 Large-size test problems

In this section, the performance of the two novel meta-heuristic algorithms is investigated for large-size test problems. Due to the complexity and nonlinearity of the mathematical model, the interior-point method could not solve large-size test problems in less than 5000 s. Therefore, to compare the efficiency of MFO and GWO, the relative percentage deviation (RPD) measure is utilized. Table 13 presents the computational results containing the best solutions (Best_MFO and Best_GWO), the average RPDs, and the average computational time (CT_Ave) in each test problem.

Table 13 Average relative percentage deviation and CT_Ave of the algorithms in large-size test problems

The results in Table 13 show that the performances of the two meta-heuristics are very competitive in terms of the required computational time. Conversely, the performance of GWO in terms of RPD is considerably better. This implies that GWO is able to find better solutions compared to MFO. Figure 13 presents a schematic view of the results presented in Table 13.

Fig. 13

a The best solution, b the average relative percentage deviation, c average standard deviation, d average computation time of the solution methods in large-size test problems

The average RPD and the standard deviation of the best solution obtained by GWO are considerably low compared to MFO, implying GWO the better algorithm (see Fig. 14). The question which arises here is that MFO performed well in both small and medium-size test problems in terms of PRE. However, why in large-size problems MFO is the weaker algorithm to find the best solution? To answer this question, one should focus on the fundamentals of the two algorithms and analyze them in details. To this aim, consider Fig. 14 which shows the detailed information of the performance of the two meta-heuristics for different problem sizes in terms of the number of items. The left-hand-side plot (the first plot) in Fig. 14 shows the convergence paths of the algorithms to find the best solution obtained so far over the course of iterations. The second plot presents the average penalty of the infeasible search agents in each iteration. The third plot presents the average fitness of the search agents over the course of iterations, and the last plot in each row shows the convergence constant of each algorithm.

Fig. 14

Infeasibility, best solution and the values of the main parameters of GWO and MFO over iterations

From Fig. 14, one can see that the average penalty of the search agents in GWO decreases over the iterations and reaches to zero very fast. In contrast, the average penalty of MFO remains positive over the course of iterations. In addition, the average fitness of the search agents in GWO increases constantly over the iterations, but in MFO the average fitness of the search agents changes abruptly and becomes better or worst over the iterations. As the solutions are generated randomly in the first iteration within the lower and the upper bound of the decision variables, almost all the solutions are infeasible. Considering the basic concept of GWO, the Omega wolves follow the Alpha, Beta and Delta wolves. In the first iteration, the best three infeasible solutions with minimum constraints violation level are considered as Alpha, Beta, and Delta. Therefore, all the Omega wolves move toward the solutions which have the least violation level. When the Alpha wolf becomes feasible (reaches the feasible solution space), the other wolves start to follow him/her instantly. This is why the average objective function value of the grey wolves increases constantly in the third plot of Fig. 14. Note that the reason behind using the static penalty approach was to use the information of the infeasible solutions, which, here one can see that this approach significantly increases the efficiency of GWO.

Now consider the basic concept behind MFO. In MFO, the search agents do not share the information of the best solution obtained so far, because each moth goes around its corresponding flame. In other words, the position of the best solution has no effect on the flying path of the other moths. Therefore, when the best flame (best solution) becomes feasible, it has no effect on the flying patch of the other moths. Thus, it takes too much time for all flames to become feasible. That is why the average penalty for the search agents in MFO is always positive in Fig. 14. The third plot of Fig. 14 shows the average fitness of feasible search agents over the iterations. Consider a specific iteration in which the average fitness of the search agents in the feasible solution space is 1000. In the next iteration, one of the flames in MFO becomes feasible and finds a solution with the value of 10. This causes a significant decrease in the average fitness value of MFO. This is why the average fitness of the search agents abruptly increases and decreases over the course of iterations. This shows that GWO is much robust and reliable compared to MFO in solving the problems.

For a statistical comparison between MFO and GWO, the single factor ANOVA is utilized one more time for both computational time and RPD measures. Table 14 presents the results. Since the P values are less than 0.05 for both comparisons, there are significant differences between GWO and MFO in terms of both RPD and CT. Figure 15 presents the Boxplot for the average RPD and CT of the two algorithms.

Table 14 ANOVA results to compare the mean computation times and RPD for large-size test problems

Fig. 15

a The Boxplot of the average CT of the MFO and GWO in large-size test problems, b the Boxplot of the average RPD of the MFO and GWO in large-size test problems

From Fig. 15 it is clear that GWO performs significantly better than MFO in solving the problems. To make a conclusion, Table 15 is presented to rank the algorithms based on their performance measures in large-size test problems. Although the CT of the MFO is significantly smaller than the one of the GWO, GWO performs significantly better than MFO to provide better quality solutions.

Table 15 Ranking the two solution methods in large-size test problems

5 Sensitivity analyses

The effects of the changes in the main parameters of the proposed mathematical model on the objective function value are investigated in this section for a test problem with five products. These analyses involve simultaneous changes in the parameters of all products at − 50%, − 25%, + 25%, + 50% rates. The GAMS software is employed to solve the test problem. Note that $f(p_{i} )$, $f(m_{i1} )$ and $f(m_{i2} )$ are considered to follow uniform distributions in $[0,\beta ]$, $[0,\lambda ]$ and $[0,\eta ]$, respectively. The results are presented in Table 16.

Table 16 The results of sensitivity analyses

The results in Table 16 indicate that the demand parameter D_i has the highest effect on the objective function value. The second most critical parameter is $\lambda_{i}$ which determines the upper bound of the distribution of the Type-I error. Therefore, by minimizing the probability of Type-I error, the total annual profit of the system can significantly increase. The third, the fourth and the fifth critical parameters are K_i, $\beta_{i}$, and $\eta_{i}$ parameters. These results reveal that the probability of Type-I and Type-II errors have a considerable effect on the objective function value. Thus, minimizing the errors involved in the inspection process is the first step to increase the total annual profit of the system. Figure 16 presents a schematic view of the results obtained in the above sensitivity analyses.

Fig. 16

Results of the sensitivity analyses

6 Conclusion

This research aimed to propose a new multi-item economic order quantity model in the presence of imperfect items in supply batches. The supply batches were inspected upon arrival. The inspection process was considered imperfect. Thus, two types of inspection errors (Type-I and Type-II errors) were involved. Various operational constraints were involved to develop a more applicable mathematical model. As most of the parameters of the model are under uncertainty in real-world situations, the operational constraints were assumed stochastic. The goal was to determine the optimal order and back order sizes of the items in order to achieve the maximum total profit. Due to the complexity of the mathematical model, three different solution methods including the interior-point method, the grey wolf optimizer, and the moth-flame optimization algorithm were utilized to solve the problem. In order to demonstrate the most efficient solution method, the performances of the three solution methods were evaluated by solving various test problems in different sized. Various comparison measures were also utilized to compare solution methods. Besides, sensitivity analyses that were performed to investigate the effect of changes in the main parameters of the mathematical model on the total expected profit indicated that the inspection errors were the most influential factor.

For future research, it would be interesting to develop robust models of the proposed model. Considering other objective functions such as reliability is another extension of this work.