Development of an optimization model for product returns using genetic algorithms and simulated annealing

Abstract

Product returns have become a significant management issue and an unavoidable cost for a business. This situation made firms to consider the possibility of managing product returns in a more cost-efficient way. In this paper, we develop a mixed integer non-linear programming model of a three-stage logistics network to optimize the number and location of collection/inspection centers and recovery centers as well as collection frequency with the objective of minimizing the total costs which include the reverse logistics shipping costs and fixed costs of opening facilities. We propose two solution algorithms based on genetic algorithm (GA) and simulated annealing (SA). Numerical experiments are used to illustrate the effectiveness and efficiency of the proposed solution approaches and compare the results with the previous works.

1 Introduction

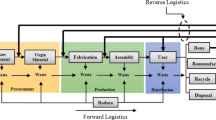
Reverse logistics is the process of planning, implementing and controlling the efficient, effective inbound flow and storage of secondary goods and related information opposite to the traditional supply chain directions for the purpose of recovering value and proper disposal (Rogers and Tibben-Lembke 1999). Many activities are included in reverse logistics concept such as the reuse of used products, disassembly, and processing of excess inventory of products, parts, and/or materials (Daugherty et al. 2005). Typically, a product return involves the collection of returned products at designated regional distribution centers or retail outlets, the transfer and consolidation of returned products at centralized return centers, the asset recovery of returned products through repairs, refurbishing, and remanufacturing, and the disposal of returned products with no commercial value (Min et al. 2006a). Logical planning should set collection options that provide consumers with the motivation to return products with any extra hassle such as finding a collection center. Implementation of reverse logistics especially in product returns would allow not only for savings in inventory carrying cost, transportation cost, and waste disposal cost due to returned products, but also for the improvement of customer loyalty and future sales (Lee et al. 2009).

The collection of used products is very difficult and needs a well-estimated structure in reverse logistics (Lee and Dong 2009).

In this paper, after reviewing of the literature, we develop a mixed integer non-linear programming (MINLP) model for a three-stage logistics network to optimize the number and location of collection/inspection centers and recovery centers as well as collection frequency with the objective of minimizing the total costs which include the reverse logistics shipping costs and fixed costs of opening facilities. We propose two solution algorithms based on genetic algorithm (GA) and simulated annealing (SA). Finally, numerical experiments are used to illustrate the effectiveness and efficiency of the proposed solution approaches and compare the results with the previous works.

2 Literature review

In this section, we review different types of reverse logistic problems in some categories including: Reverse logistic network design, Closed-loop supply chain network design, genetic algorithms in reverse logistic networks, and simulated annealing algorithm in reverse logistic networks.

2.1 Reverse logistic network design

Fleischmann et al. (1997) presented a comprehensive review on the application of mathematical modeling in reverse logistics management, as one of the seminal works in reverse supply chain network design. Barros et al. (1998) conducted a case study for the design of a logistics network for recycling sand coming from processing construction waste in the Netherlands. A heuristic algorithm was also used to solve the problem.

2.1.1 The problems with optimizing strategic decisions

This section includes the papers that aim to improve and optimize the efficiency of the strategic decisions through decision-making process in the reverse logistic network design.

Louwers et al. (1999) proposed a non-linear programming model procedure to determine the location and size of regional recycling centers for a carpet waste management network with a linear approximation solution.

Realff et al. (1999) proposed a multi-level capacitated facility location mixed integer programming model to support reverse logistics network design for carpet recycling.

Aras et al. (2008) also formulated a mixed integer nonlinear facility location-allocation model to determine both the optimal locations of the collection centers and the optimal incentive values for each return type so as to maximize the profit gained by the returns. They developed a heuristic approach based on tabu search to solve the model. Alumur et al. (2012) formulated a mixed integer linear programming model which was flexible to incorporate most of the reverse network structures reasonable in practice.

2.1.2 The problems with optimizing tactical decisions

This section includes the papers whose purpose is to improve and optimize the efficiency of the tactical decisions through decision- making process in the reverse logistic network design.

Jayaraman et al. (1999) developed a MILP model for reverse logistics network design under a pull system based on customer demands for recovered products. The objective of the proposed model was to minimize the total costs. Also, Krikke et al. (1999a) proposed another MILP model for the multi-echelon product recovery network design which focused on the remanufacturing of a certain type of photocopier.

Jayaraman et al. (2003) extended their prior work to solve the single product two-level hierarchical location problem involving the reverse supply chain operations of hazardous products. They also developed a heuristic to handle relatively large-sized problems.

2.1.3 Stochastic models

This section describes papers in which assume some parameters to be uncertain. In this way, stochastic parameters can be continuous or describe a set of discrete scenarios.

Listes and Dekker (2001) proposed a stochastic mixed integer programming model for a sand recycling network design to maximize the total profit. Jayant et al. (2011) have developed modeling and simulation in a reverse logistics network for collection of end of life products for XYZ Limited Company in North India. Mixed integer linear programming (MILP) models have become a standard approach for network design.

2.1.4 Multi-objective decision making

Pati et al. (2008) proposed a mixed integer goal programming model for paper recycling logistics network design. The objectives included: minimizing the positive deviation from the planned budget allocated for reverse logistics activities, minimizing the positive deviation from the maximum limit of non-relevant wastepaper and minimizing the negative deviation from the minimum desired waste collection. Lee and Dong (2009) found that a business specializing in the recovery of used electronic personal computer products was estimated to have a value bar.

2.2 Closed-loop supply chain network design

The concept of closed-loop supply chains is now widely garnering attention as a result of the recognition that both the forward and reverse supply chains need to be managed jointly. The configuration of both forward and reverse logistic has a strong influence on the performance of each other. Therefore, the design of the forward and reverse networks should be integrated (Pishvaee et al. 2010a). Fleischmann et al. (2001) developed a generic model for the design of closed-loop logistics networks. They considered the forward flow together with the reverse flow, allowing the simultaneous definition of the optimal distribution and recovery networks. A MILP formulation was proposed that constitutes an extension of the traditional warehouse location problem.

Salema et al. (2007) proposed a mixed integer formulation using standard branch and bound techniques in a reverse logistics network with capacity limits, multi-product management, and uncertainty on product demands and returns. Using Tabu search, a logistics network was designed for end-of-lease computer product recovery by developing a deterministic programming model for systematic management (Lee and Dong 2009).

Lu and Bostel (2007) considered a two-level location problem with three types of facilities to be located in a remanufacturing network. They proposed a mixed integer programming model considering both the forward and reverse flows and their interactions at the same time. A Lagrangian-based heuristic was developed to solve the proposed model. Pishvaee et al. (2009) developed a mixed integer linear programming model for integrated forward/reverse logistics using scenario-based stochastic approach.

Finally, Pishvaee et al. (2010a) proposed a bi-objective MILP model maximizing the network responsiveness and minimizing the total costs in a closed-loop supply chain network including both forward and reverse flows. To solve the proposed bi-objective MILP model, a mimetic algorithm was developed. Pishvaee et al. (2011) developed a deterministic mixed integer linear programming model and proposed a robust optimization approach for closed-loop supply chain network design under uncertainty.

Ramezani et al. (2012) presented a stochastic multi-objective model for forward/reverse logistic network design under an uncertain environment including three echelons in forward direction and two echelons in backward direction and demonstrate a method to evaluate the systematic supply chain configuration maximizing the profit, customer responsiveness and quality as objectives of the logistic network. Chen et al. (2013) considered a model where there are multiple suppliers and customers in a single cross-docking center. They formulated the optimal route selection problems from the suppliers to the cross-docking center and from the cross-docking center to the customers as the respective VRPs. They integrated the two VRP models to optimize the overall traveling time, distance, and waiting time at the cross-docking center. In addition, they proposed a novel mixed 0/1 integer linear programming model by which the complexity of the problem can be reduced significantly.

2.3 Genetic algorithms in reverse logistic networks

Min et al. (2006a) proposed a genetic algorithm approach to develop the multi-echelon reverse logistics network for product returns. The proposed model was designed to find the optimal location, number and size of both initial collection points and centralized return centers in the reverse logistics network under capacity limits and service requirements.

Ko and Evans (2007) used a mixed integer nonlinear programming model for the design of a dynamic integrated distribution network to account for the integrated aspect of optimizing the forward and return network simultaneously using genetic algorithms.

Lieckens and Vandaele (2007) combined the traditional MILP models with queuing models to deal with high degree of uncertainty and some dynamic aspects in a reverse logistics network design problem. A genetic algorithm was also developed to solve the proposed model.

Lee et al. (2009) proposed a mathematical model of remanufacturing system as three-stage logistics network model for minimizing the total of costs to reverse logistics shipping cost and fixed opening cost of the disassembly centers and processing centers. They considered a multi-stage, multi-product and some attach condition for disassembly centers and processing centers, respectively. For solving the problem, they proposed a genetic algorithm (GA) with priority-based encoding method consisting of 1st and 2nd stages that combined a new crossover operator called as weight mapping crossover (WMX).

Min and Ko (2008) proposed a multi-period MILP model for determining the number and location of repair facilities, where returned products from retailers or end-customers were inspected, repaired, and refurbished for redistribution. To solve the model, a genetic algorithm was developed.

Hu et al. (2013) addressed two implementation scenarios of TAS: static TAS (STAS) and dynamic TAS (DTAS). A non-stationary $M(t)/Ek/c(t)$ queuing model was used to analyze a terminal gate system, and solved with a new approximation approach. They proposed a genetic algorithm to optimize the hourly quota of entry appointments in STAS for the derived queuing model and they presented the concept of DTAS that can assist individual trucker in making appointment by providing real-time estimation of waiting time based on existing appointments.

Diabat et al. (2013) modified the model proposed by Min et al. (2006a) by transforming the renting and shipping cost terms in the objective function, and the proposed mixed integer nonlinear programming problem was solved using genetic algorithm and artificial immune system.

2.4 Simulated annealing algorithm in reverse logistic networks

Pishvaee et al. (2010b) proposed a mixed integer linear programming model to minimize the transportation and fixed opening costs in a multistage reverse logistics network. To solve the model, they used a simulated annealing (SA) algorithm with special neighborhood search mechanisms. They also applied exact methods in a set of problems to compare with SA algorithm and presentation of the high-quality performance of the applied SA algorithm.

Pan and Choi (2013) considered a make-to-order fashion supply chain in which the downstream manufacturer and the upstream supplier are cooperative on due date and competitive on price. They proposed a two-phase negotiation agenda based on such characteristics, and goal to find an optimal solution to deal with the negotiation problem considering production cost and mutual benefit. They build an agent-based two-phase negotiation system where agents are used to represent the two parties to enhance communication. In the cooperative phase, a simulated annealing-based intelligent algorithm was used to minimize the total supply chain cost. In the competitive phase, the two parties bargained on the pricing issue using concession-based methods.

In this paper, we develop a mixed integer non-linear programming (MINLP) model of a three-stage logistics network to optimize the number and location of collection/inspection centers and recovery centers as well as collection frequency with the objective of minimizing the total costs which include the reverse logistics shipping costs and fixed costs of opening facilities. The model was presented by Diabat et al. (2013) in single-product case. In this paper, we develop it to a multi-product problem. We propose two solution algorithms based on genetic algorithm (GA) and simulated annealing (SA) and compare the proposed algorithms with those proposed by Diabat et al. (2013). Numerical experiments are used to illustrate the effectiveness and efficiency of the proposed solution approaches and compare the results with the previous works.

3 Mathematical model

Prior to developing the nonlinear mixed integer programming model for reverse logistics network design, we consider it as multi-product and multi-period model. We make the following assumptions:

(1) The direct shipment from customers to a recovery center is not possible. (2) Collection/inspection centers have sufficient capacity to hold returned products during the consolidation process. (3) The location/allocation plan covers a planning horizon within which no substantial changes are incurred in customer demands and in the transportation infrastructure.

3.1 Indices

$i$ :

Index for customers; $i\in I$

$j$ :

Index for collection/inspection centers; $j \in J$

$k$ :

Index for potential recovery centers; $k \in K$

$p$ :

Index for products; $p\in P$

3.2 Parameters

$a_{j}$ :

Annual cost to rent collection/inspection center $j$

$b_{ijp}$ :

Daily inventory carrying cost per unit product $p$ between customer $i$ and collection/inspection center $j$

$w$ :

Annual working days

$r_{ip}$ :

Daily volume of products $p$ returned by customer $i$

$q_{k}$ :

Cost of establishing recovery center $k$

$m_{k}$ :

Maximum capacity of recovery center $k$

$d_{{ ij}}$ :

Distance between customer $i$ and collection/inspection center $j$

$d_{jk}$ :

Distance between collection/inspection center $j$ and recovery center $k$

$l$ :

Maximum allowable distance between customer $i$ and collection/inspection center $j$

$h$ :

Cost of handling one unit of product per day

$z$ :

Minimum number of established collection/inspection centers

$g$ :

Minimum number of established centralized return centers

$M$ :

Arbitrarily large number

$E_{jkp}$ :

Carrying cost per unit product $p$ between collection/inspection center $j$ and recovery center $k$

$\alpha$ :

Discount rate depended on the shipping volume $X_{jk}$ between collection/inspection center $j$ and recovery center $k$

$\beta$ :

Penalty rate depended on the distance $d_{jk}$ between collection/inspection center $j$ and recovery center $k$

$p_1 ,p_2$ :

Volume breakpoints used in the calculation of $\alpha$

$q_1 ,q_2$ :

Distance breakpoints used in the calculation of $\beta$

$$\begin{aligned} \alpha = {\left\{ \begin{array}{ll} 1&{} {\mathrm{for }}\,{x}_{{j0}} \le p_1 \\ \alpha _1 &{} \mathrm{for }\,{p}_{1} \le {x}_{j0}\le p_2 \\ \alpha _2 &{} \mathrm{for}\,{x}_{j0}>p_2 \\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \beta = {\left\{ \begin{array}{ll} 1 &{} \hbox {for }{d}_{j0} \le q_1 \\ \beta _1 &{} \hbox {for }{q}_{1} \le d_{j0}\le q_2 \\ \beta _2 &{} \hbox {for }{d}_{j0}>q_2 \\ \end{array}\right. } \end{aligned}$$

3.3 Decision variables

$X_{jkp}$ :

Volume of product $p$ returned from collection/inspection center $j$ to recovery center $k$

$T_{j}$ :

Maximum holding (collection) time (in days) at collection/inspection center $j$

$Y_{ij} = 1,$ :

If customer $i$ is allocated to collection/inspection center $j$; 0, otherwise

$Z_{j} = 1,$ :

If a collection/inspection center is established at site $j$; 0, otherwise

$G_{k}= 1,$ :

If a recovery center is established at site $k$; 0, otherwise.

3.4 Objective function

In this paper, a MINLP model is developed to minimize the total reverse logistics cost including renting, inventory carrying, setup, material handling and shipping costs for different products. Some companies have begun to consider mapping the process of reverse logistics involving product returns and creating opportunities for cost savings and service improvements. These companies include e-tailers that have grown with increases in online sales, but were often overwhelmed by the scope and complexity of sending returned products back to their distributors or manufacturers for credit. The rate of product returns is usually higher for books, magazines, apparel, greeting cards, CD-ROMs and electronics. In particular, mail catalogue or online sales are more vulnerable to product returns. A work in Modern Material Handling estimated that 30 % of online sales would be returned to e-retailers (Min et al. 2006a). This high rate of returns would cost e-tailers $1.8 to $2.5 billion a year. Typical reasons for product returns may include: defects, in-transit damage, trade-ins, product upgrades, exchanges for other products, refunds, repair, recalls, and order errors.

The objective function (1) has a nonlinear form, because both inventory carrying and shipping costs are affected by the collection period. It is described as follows:

Minimize

$$\begin{aligned}&a\sum \limits _{j} {z}_{j} +w\sum \limits _{j} {\left\{ {\sum \limits _{i} {\sum \limits _{p} {r_{ip} } b_{p} Y_{ij} \frac{T_{j} +1}{2}} } \right\} }\nonumber \\&\quad +wh\sum \limits _{i} {r_{i}} +\sum \limits _{k} {q_{k} G_{k}} \nonumber \\&\quad +\sum \limits _{k} {\left\{ {G_{k} \sum \limits _{j} {\left( {\sum \limits _{p} {X_{jkp} } \frac{W}{T_j +1}E_{jkp} \alpha \beta }\right) } } \right\} } \end{aligned}$$

(1)

3.5 Constraints

$$\begin{aligned}&\sum \limits _{j} {Y_{ij} } =1,\quad \forall i\in I \end{aligned}$$

(2)

$$\begin{aligned}&\sum \limits _{j} {Y_{ij} } \le M. Z_{j}, \quad \forall j \in J \end{aligned}$$

(3)

$$\begin{aligned}&\sum \limits _{i} \sum \limits _{p} {r_{ip} } Y_{ij} T_{j } =\sum \limits _{k} {\sum \limits _{p} {X_{jkp}}},\quad \forall j\in J \end{aligned}$$

(4)

$$\begin{aligned}&\sum \limits _{j} {\sum \limits _{p} {X_{jkp} } } \le m_{k} G_k ,\quad \forall k \in K \end{aligned}$$

(5)

$$\begin{aligned}&d_{ij} Y_{ij} \le l,\quad \forall i \in I, \; \forall j \in J \end{aligned}$$

(6)

$$\begin{aligned}&g \le \sum \limits _{k} {G_{k},} \end{aligned}$$

(7)

$$\begin{aligned}&z \le \sum \limits _{j} {z_{j}}, \end{aligned}$$

(8)

$$\begin{aligned}&T_{j} \in ( {0,1,2,3,4,5,6,7}),\quad \forall j\in J \end{aligned}$$

(9)

$$\begin{aligned}&X_{jk} \ge 0, \, \forall j \in J, \quad \forall k \in K \end{aligned}$$

(10)

$$\begin{aligned}&Y_{ij},Z_{j},G_{k} \in (0,1),\quad \forall i \in I,\; \forall j \in J, \;\forall k \in K \end{aligned}$$

(11)

Constraint (2) assures that each customer is assigned to exactly one collection/inspection center.

Constraint (3) prevents any return flow from a closed collection/inspection center. Constraint (4) requires the incoming flow to equal the outgoing flow at a collection/inspection center.

Constraint (5) ensures that the total volume of products returned from collection/inspection center does not exceed the maximum capacity of a centralized return center. Constraint (6) ensures that each collection/inspection center should be located within a certain allowable proximity to customers. Constraints (7, 8) ensure a minimum number of recovery centers and collection/inspection centers for product returns, respectively. In Constraint (9), the integrality of decision variables $T_{j}$ and its possible values are mentioned. Constraint (10) preserves the non-negativity of decision variables. And finally, Constraint (11) ensures the binary integrality of decision variables $Y_{ij}, Z_{j}, G_{k}.$

4 Solution methodology

The formulation given in Eq. (1) is a non-linear integer programming (NILP) model and belongs to the class of NP-hard problems. We used the genetic algorithm (GA) and simulated annealing (SA) approaches to solve the model. These approaches are described below.

4.1 First solution approach: genetic algorithm

GA is a stochastic search and heuristic optimization technique, which has been widely adopted by many researchers to solve various problems. This algorithm was first developed by Holland (1975). GA is introduced as a stochastic solution search procedure that is designed to solve combinatorial problems using the concept of evolutionary computation imitating the natural selection and biological reproduction of animal species (Goldberg 1989; Gen and Cheng 2000). GA is getting special attention in supply chain management research studies (Cheng et al. 1998). Many researchers have used GA in reverse logistics network design (Aras et al. 2008; Lee and Dong 2009; Min and Ko 2008; Lee et al. 2009). The parameters of GA are described as follows (Pasandideh et al. 2011):

Population size ($N$): It is the number of the chromosomes or scenarios that are kept in each generation.

Crossover rate ($P_\mathrm{c}$): This is the probability of performing a crossover in the GA method.

Mutation rate ($P_\mathrm{m}$): This is the probability of performing mutation in the GA method. In the following, the proposed GA is described in detail.

4.1.1 The chromosomes

In this paper, we have represented the chromosome using a one-dimensional array of binary values, representing decision variables related to collection/inspection centers, centralized return centers, and collection periods (i.e., holding time for consolidation at the collection/inspection center), as illustrated in Fig. 1. The chromosome consists of 10 collection/inspection centers, 7 days of collection periods at collection/inspection centers, and 5 recovery centers. Each collection/inspection center is described by four bits: the first bit is 1 if the collection/inspection center is open and 0 if it is closed, the remaining three bits represent the collection period for that collection/inspection center, so that eight possible collection periods (0–7) are possible. Each recovery center is described by one bit which is 1 if it is open and 0 if it is closed (Diabat et al. 2013).

Fig. 1

Chromosome representation

4.1.2 Evaluation

The fitness value is a measure of the goodness of a solution with respect to the original objective function and the “degree of infeasibility” (Santos et al. 2010). Decoding the chromosome generates a candidate solution and determines its fitness value (Min et al. 2006b; Ko and Evans 2007). We consider it in two steps. The first step is used to obtain total daily demand of the opened collection/inspection centers. All customers should be allocated to the nearest collection/inspection centers. We assign algorithm since we assumed that there is enough capacity of each collection/inspection center owing to small volume of returns. The mathematical representation is as follows (Diabat et al. 2013):

Minimize

$$\begin{aligned} a\sum \limits _{j} {z_{j} } +w\sum \limits _{j} {\left\{ {\sum \limits _{i} {\sum \limits _{p} {r_{{ip}} } b_{p} Y_{ij} \frac{T_{j} +1}{2}} } \right\} } \end{aligned}$$

Subject to

$$\begin{aligned} \sum \limits _{j} {Y_{ij} } =1, \quad \forall i\in I \end{aligned}$$

$$\begin{aligned} \sum \limits _{j} {Y_{{ij}} } \le M.Z_{j} , \quad \forall j\in J \end{aligned}$$

$$\begin{aligned} d_{ij} Y_{ij} \le l, \quad \forall i \in I, \, \forall j \in J, \end{aligned}$$

$$\begin{aligned} Y_{ij} \in ( {0,1}) , \quad \forall i \in I, \forall j \in J, \end{aligned}$$

In the second step, we assign open collection/inspection centers to a recovery center taking into account capacity limitations. This step is solved using the simplex method (Diabat et al. 2013):

Minimize

$$\begin{aligned}&wh\sum \limits _{i} {r_{i} } +\sum \limits _{k} q_{k} G_{k }\\&\quad +\sum \limits _{k} {\left\{ {G_{k} \sum \limits _{j} {\left( {\sum \limits _{p} {X_{jkp}} \frac{W}{T_{j} +1}E_{jkp} \alpha \beta }\right) } } \right\} } \end{aligned}$$

Subject to

$$\begin{aligned} \sum \limits _{j} {\sum \limits _{p} {X_{jkp} } } \le m_{k} G_{k}, \quad \forall k\in K \end{aligned}$$

$$\begin{aligned} \sum \limits _{i} {\sum \limits _{p} {r_{ip} } Y_{ij} T_{j} } =\sum \limits _{k} {\sum \limits _{p} {X_{jkp}} }, \quad \forall j\in J \end{aligned}$$

$$\begin{aligned} X_{jkp} \ge 0, \forall j \in J, \quad \forall k\in K \end{aligned}$$

The fitness function is formed by adding a penalty to the original objective function. The following penalty function was used (Diabat et al. 2013):

$$\begin{aligned} \hbox {Penalty function}&= \sum \limits _{j} {\sum \limits _{k} {p_\mathrm{v}}} \times g( {X_{jk} ,m_{k} ,G_{k} }) \nonumber \\&\quad +\sum \limits _{i} \sum \limits _{j} {p_\mathrm{v}}\times {h(d_{ij,} Y_{ij}, l_{k} )} \end{aligned}$$

where ${p_\mathrm{v}}$ is the penalty value;

$$\begin{aligned} g(X_{jk},m_{k},G_{k})=\hbox {1, \, if \,} \sum X_{jk} >m_{k} G_{k}; \hbox {0,\,otherwise.} \end{aligned}$$

$$\begin{aligned} h(d_{ij},Y_{ij}, l_{k})=1,\quad \mathrm{if \,} d_{ij} Y_{ij} >l; \mathrm{0,\,otherwise}. \end{aligned}$$

4.1.3 Initial population

In this step, a collection of chromosomes is randomly generated.

4.1.4 Chromosomes’ selection

In genetic algorithms, the selection operator is used to guide the search process towards more promising regions in a search space. Several selection methods, such as roulette wheel, tournament, ranking, and elitist are discussed in Michalewicz (1996). Since in the roulette wheel selection, there is possibility of confronting with convergence suddenly, here we used three-chromosome tournament method to select the chromosomes of this research. We form two groups of chromosomes. Each group consists of three chromosomes randomly selected from the current population. Three chromosomes are randomly selected from the current population. From each group, the best chromosome is chosen to be a parent. Diabat et al. (2013) chose two-chromosome tournament method.

4.1.5 Crossover operator

The crossover operator generates offspring by combining the information contained in the chromosomes of the parents so that new chromosomes will have the good parts of the parents’ chromosomes. A crossover probability indicates how often crossover will be performed. There are several types of crossovers, including single-point crossover, multi-point crossover, and uniform crossover (Gen and Cheng 1997). Here, we applied the uniform crossover. In this way, we generate a binary crossover mask with the same length as the chromosome. The value of the mask bits tells whether to use the information of which parents. The bits are swapped with a fixed probability, 0.5. Figure 2 shows the crossover mechanism. Unlike one- and two-point crossover, the uniform crossover enables the parent chromosomes to contribute the gene level rather than the segment level. Diabat et al. (2013) chose two-point crossover.

Fig. 2

Uniform crossover

The crossover code which has been applied, is shown below:

4.1.6 Mutation operator

In GA, mutation is the second operation for exploring new solutions. Mutation adds new information in a random way to the genetic search process and ultimately helps to avoid getting trapped at local optima (Awan et al. 2008). Mutation is a background operator which produces spontaneous random changes in various chromosomes. Similar to crossover, mutation is done to prevent the premature convergence and explores new solution space (Gen and Cheng 2000; Lee et al. 2009). In our genetic algorithm, in each selected chromosome, one bit is randomly selected and flipped. In research of Diabat et al. (2013), mutation only operates either on the bits within the region of the chromosome that determines initial collection points, or on the bits within the region of the chromosome that determines centralized return centers. Since the model is multi-product and multi -period, the number of genes in each generation is too much and if the mutation rate is small, the genes almost will be similar to other and we must consider it not very small.

4.2 Second solution approach: simulated annealing

SA is a metaheuristic method developed to solve optimization problems. It is one of the stochastic search algorithms designed by the Kirkpatrick et al. (1983). It has been used in wide areas, as it performs well on most optimization problems and its implementation is not hard. The powerfulness of the method originates from good selection scheme and annealing technique, i.e., the technique of gradual temperature reducing.

SA technique generally involves three main activities: an objective function should be determined; a scheme for cooling process should be specified; and a neighborhood should be generated. In single objective problems, the famous acceptance probability functions are Metropolis and logistic functions. A good overview of theoretical development and application domains of SA has been presented in the Eglese (1990), Fleischer (1995), Romeo and Sangiovanni-Vincentelli (1991). In the current solution, a candidate solution is selected from its neighbors. If the candidate has a better objective function value (less cost value) than the current solution, then the solution is updated and the candidate solution replaces the current one. Otherwise, the solution does not change and the candidate is rejected; however, it may be selected as the current solution with some probability.

In any iteration, a discrete optimization problem is applied. The cost value for the new solution is calculated and compared with the current solution. This comparison results in one of the following two situations:

• 1. The new solution (new cost) is better than the current one (cost); then, the current solution is replaced by the new solution and the reference for the next iteration will be the new generated solution.

• 2. The new solution is worse than the current one; then, the reference solution is selected according to the acceptance probability function.

The algorithm stops at the frozen state.

4.2.1 Encoding

We encode the problem similar to the chromosome represented in Sect. 4.1.1.

4.2.2 Solution initiation

To start the solution algorithm, a feasible solution should be identified to the problem. The initial solution is randomly generated.

4.2.3 Neighborhood generation

The neighborhood of a solution is the set of all feasible solutions obtained by a single transformation in some solution characteristics. Two points are randomly selected along the array, then the segment between two points is replaced with a binary code randomly selected. Figure 3 shows the way of generating neighbors.

Fig. 3

Generating neighborhood

4.2.4 Acceptance probability function

Any solution with inferior or superior total cost may be selected with a probability to be the reference. If the new solution (new cost) is worse than the current one (cost), the reference solution is selected according to the acceptance probability function as follows:

$$\begin{aligned} p=e^{-\frac{\mathrm{new \ cost }- \mathrm{cost}}{k\times T}} \end{aligned}$$

where $T$ is defined as current temperature and $k$ is considered as a big constant to compare it with a random value in (0, 1).

The simulated annealing solution procedure is summarized as follows:

5 Computational experiment

We divide this section into four parts. In the first part, we compare proposed algorithms in this paper with algorithms in the literature by Diabat et al. (2013) in single-product case. For this purpose, we choose the example presented by Diabat et al. (2013). In the second part, we compare proposed GA with proposed SA in multi-product case. In the third part, we present effectiveness and robustness of the GA and SA algorithm. In the last part, we present sensitivity analysis. The algorithms are coded using MATLAB 7.0 and implemented on a PC with a 2.1 GHz processor with 4 GB of RAM. Table 3 gives the output of the solution algorithm.

5.1 Comparing proposed algorithms with the literature

In this part, we compare proposed GA and SA algorithms proposed in this paper with GA and AIS algorithms in the literature by Diabat et al. (2013). For this purpose, we choose the example presented by Diabat et al. (2013). The example considers the problem in single-product case. Here, we also consider the problem in single-product case and compare their results with each other.

5.1.1 Comparing proposed GA with GA in the literature

In this section, we compare proposed GA in this paper with GA in the literature by Diabat et al. (2013). In Table 1, we compare these two solutions when different examples are taken. To estimate the gap between them, we use this ratio: $\Delta$ = (objective function in literature GA $-$ objective function in proposed GA)/objective function in proposed GA). In Table 1, from these computational results, we see that the gap is 4.270 % $\le \Delta \le$ 10.108 %. It is observed the proposed GA has better result than the GA in the literature.

Table 1 Comparing proposed GA with GA in literature

5.1.2 Comparing proposed SA with GA in literature

In this part, we compare proposed SA in this paper with GA in literature by Diabat et al. (2013).

In Table 2, we compare these two solutions when different examples are taken. To estimate the gap between them, we use this ratio: $\Delta$ = (objective function in literature GA $-$ objective function in proposed SA)/objective function in proposed SA). In Table 2, from these computational results, we see that the gap is 9.443 % $\le \Delta \le$ 15.851 %. It is observed the result of the proposed SA is better than the GA in literature.

Table 2 Comparing proposed SA with GA in literature

5.1.3 Comparing proposed GA with AIS in literature

In this section, we compare proposed GA in this paper with AIS in the literature by Diabat et al. (2013). In Table 3, we compare these two solutions when different examples are taken. In order to estimate the gap between them we use this ratio: $\Delta$ = (objective function in literature AIS $-$ objective function in proposed GA)/objective function in proposed GA). In Table 3, from these computational results, we see that the gap is 0.182 % $\le \Delta \le$ 1.548 %. It is observed the proposed GA has better result than the AIS in literature.

Table 3 Comparing proposed GA with AIS in literature

5.1.4 Comparing proposed SA with AIS in the literature

In this section, we compare proposed SA in this paper with AIS in literature by Diabat et al. (2013).

In Table 4, we compare these two solutions when different examples are taken. To estimate the gap, we use this ratio: $\Delta$ = (objective function in literature AIS $-$ objective function in proposed SA)/ objective function in proposed SA). In Table 4, from these computational results, we see that the gap is 5.088 % $\le \Delta \le$ 6.658 %. It is observed the proposed SA has better result than the AIS in literature.

Table 4 Comparing proposed SA with AIS in literature

5.2 Comparing proposed algorithms: GA and SA

In this section, we compare solutions obtained from our GA with our SA and finally compute the gap between them. We solve six examples and we describe one of them in detail and present final results for the others. Here, we expand the example presented by Diabat et al. (2013) to the three-product case and add some parameters to that as follows:

• $b_{ijA=0.1}$: daily inventory carrying cost per unit product $A$

• $b_{ijB=0.11}$: daily inventory carrying cost per unit product $B$

• $b_{ijC=0.12}$: daily inventory carrying cost per unit product $C$

• $E_{jkA=1}$: carrying cost per unit product $A$ between collection/inspection center $j$ and recovery center $k$

• $E_{jkB=1.2}$: carrying cost per unit product $B$ between collection/inspection center $j$ and recovery center $k$

• $E_{jkC=1.1}$: carrying cost per unit product $C$ between collection/inspection center $j$ and recovery center $k$

Also, Table 5 shows the number of different types of returned products including $A, B$ and $C$ by customers:

Table 5 Number of the returned products

This problem is solved using our GA proposed solution algorithm. The parameters are: population size = 20; number of generations = 100; crossover rate = 80 %; mutation rate = 30 %. Table 6 gives the output of the solution algorithm.

This problem is solved using our SA proposed solution algorithm. The initial temperature is 100 and decreased by a rate of 0.98. The final temperature is assumed to occur at 0.0001 and the number of iterations at each temperature is five. Table 7 gives the output of the solution algorithm.

Table 6 Solution by proposed GA

Table 7 Solution by proposed SA

Final results for the other examples are presented in Table 8. In Table 8, we compare GA and SA solutions when different problems are taken. To estimate the gap we use this ratio: $\Delta =$ (objective function in literature GA $-$ objective function in proposed SA)/objective function in proposed SA). As we see behavior of SA is better than SA. In Table 8, from these computational results, we see that the gap is 6.00 % $\le \Delta \le$ 6.42 %. It is observed the proposed SA has better result than the GA in literature.

Table 8 Result of different examples

5.3 Measuring robustness of the proposed algorithms

In this section, to prove the effectiveness and robustness of the proposed algorithms, we compare solutions with each algorithm when different parameters are taken. We consider each algorithm in following parts.

5.3.1 Measuring robustness of the proposed GA

We compare solutions with GA algorithm in Table 9 when different parameters are taken. It appears that the differences among all costs are negligible. To estimate it, we present a parameter: $\Delta$. We define it as: $\Delta$ = (Objective value $-$ the best objective value)/the best objective value, where the best objective value is the least one of all the ten minimal costs obtained. From these computational results, we see that the maximal percent of the gap does not exceed 1.784 % when different parameters are chosen. Therefore, the genetic algorithm is also robust to the parameter settings and effective to solve model.

Table 9 Measuring robustness of the proposed GA

5.3.2 Measuring robustness of the proposed SA

We compare solutions with SA algorithm in Table 10 when different parameters are taken. It appears that the differences among all costs are negligible. To estimate it, we present a parameter: $\Delta$. We define it as: $\Delta$ = (Objective value $-$ the best objective value)/the best objective value, where the best objective value is the least one of all the ten minimal costs obtained. From these computational results, we see that the maximal percent of the gap does not exceed 1.123 % when different parameters are chosen. Therefore, the genetic algorithm is also robust to the parameter settings and effective to solve model.

Table 10 Measuring robustness of the proposed SA

5.4 Sensitivity analysis

Finding the accurate values assigned to the numerical components of a model is a challenging task in the decision analysis. The collection of true values for real problems requires relevant data, which can sometimes be difficult (Diabat et al. 2013). We carry out a sensitivity analysis to investigate the holding period, location of collection centers, and capacity of recovery centers. As the SA algorithm has better result, the sensitivity analysis is conducted with SA algorithm.

5.4.1 A sensitivity analysis of the maximum collection period

Longer holding period increases products carrying costs, but it can reduce total reverse logistics costs. To examine the sensitivity of the holding period to total reverse logistics costs, we experimented on the model by changing the holding period. Table 11 shows the results of sensitivity analysis with four different holding periods (1, 2, 3, and 5 days). The numerical experiments indicated that as the holding period increased, the total reverse logistics cost. In particular, we noticed a dramatic cost saving in total reverse logistics costs after setting the holding period to three days. Figure 4 shows this trend. In particular, we noticed a dramatic cost saving in total reverse logistics costs after setting the maximum holding period at three days.

Table 11 A sensitivity analysis of the collection period

Fig. 4

A sensitivity analysis of the maximum collection period

5.4.2 A sensitivity analysis of locations of collection centers

The proximity of collection centers to customer centers can enhance the level of customer service due to easy access to customers’ locations. But to reduce distances between collection centers and customers, we need a larger number of collection centers and this increases total reverse logistics costs. We carry out a sensitivity analysis to determine the suitable proximity of collection centers to customers. Table 12 shows the sensitivity analysis results with four different possibilities of proximity (15, 20, 25, and 29 miles). As it was expected, as the distance between collection centers and customer locations increased, the total reverse logistics cost decreased and the longer distance between collection centers and customer locations led to reduction in the total number of collection centers and the subsequent savings in total reverse logistics cost. Figure 5 shows this trend.

Compromising total reverse logistics cost and customer service, we suggest about 25 miles between initial collection points and customers as the ideal distance.

Table 12 A sensitivity analysis of locations of collection centers

Fig. 5

A sensitivity analysis of locations of collection centers

5.4.3 A sensitivity analysis of capacity of recovery centers

We carry out a sensitivity analysis to determine the suitable capacity of recovery centers. Table 13 shows the sensitivity analysis results with four different possibilities of capacity (800, 900, 1,000, and 1,200 units). It is observed, as the capacity decreased, the total reverse logistics cost increased because the number of collection centers need to be established increases. We noticed a dramatic cost saving in total reverse logistics costs after setting the capacity to 1,000. Figure 6 shows this trend.

Table 13 A sensitivity analysis of capacity of recovery centers

Fig. 6

A sensitivity analysis of capacity of recovery centers

6 Conclusions

Because of the increasing importance of network costs in supply chain management and reverse logistics activities, this paper developed a mixed integer non-linear programming (MINLP) model for reverse logistics network design. In this paper, two solution algorithms were introduced using metaheuristic methods, SA and GA, to optimize the number and location of collection/inspection centers and recovery centers as well as collection frequency with the objective of minimizing the total costs including the reverse logistics shipping costs and fixed costs of opening facilities A numerical example has been discussed to illustrate the efficiency and the effectiveness of the algorithms. In addition, the quality of the obtained results has been evaluated through a comparative study.

Since there has not been enough logistic research solved by SA, we applied it as an almost new method and we compare it with GA through different problem and we got better result.

We compare proposed GA and SA algorithms in this paper with GA and AIS algorithms in the literature by Diabat et al. (2013). We found better results by the proposed algorithms. Also, we compared solutions obtained from our GA with our SA and finally computed the gap between them. We solved six examples and we described one of them in more detail and presented final results for the others. We found the SA algorithm has better behavior than the GA. To prove the effectiveness and robustness of the proposed algorithms, we compared solutions with each algorithm when different parameters were taken. The results showed that the algorithms are robust.

We reach significant good results and since they were found through different problems and we tested their robustness, they are trustable and can be used in return products and improve business management by saving cost which used to be wasted by inappropriate management before.

For future researches in this field, we recommend the followings:

• (a) The proposed algorithm can be further explored considering other objectives such as minimizing transportation risk, storage risk, response time, market potential and speedy returns.

• (b) The consideration of what-if scenarios involving changes in parameter values over time may be explored in the future.

• (c) The consideration of other heuristics such as Lagrangian relaxation, heuristic concentration, and tabu search methods may be explored in future studies.