1 Introduction

Since the establishment of the economic order quantity (EOQ) model by Harris (1913), this model has become a “well-known” inventory problem and many studies have followed and studied this problem. Andriolo et al. (2014) developed a good review of all the research that has been taken for this last century. Throughout its evolution, the EOQ model keeps receiving attention for several research studies and publications, which tried to fill the weaknesses of the model’s assumptions that are never met.

One of these assumptions stated that the received items are perfect quality. This problem has received considerable attention for the last thirty years. Porteus (1986) first considered investments for the quality improvement problem and setup cost reduction. He believed that the number of defective items in a lot depends of the probability of the production process (machine) becoming out of control and he concluded that quality of items can be improved by reducing lot sizes. After dealing with the same issue, Rosenblatt and Lee (1986) came to the same conclusion.

After almost a decade, Salameh and Jaber (2000) worked on this similar problem of quality related issue with a different approach. Instead of focusing on how to reduce defective items in production, they tried to determine how to compensate this quality problem on the traditional EOQ model. They suggested a model where the lot is 100% screened. At the end of the inspection, the items of imperfect quality are not considered defective, but they are sold as a single batch with a discounted price.

However, in some modern supply chains areas, the inspection of each product or component is nowadays no longer possible. The quantities of products have increased significantly; the inspection cost of each item might be too high. A sampling method is then required and applied in most of these sectors. Another reason for using sampling methods is in the requirement of a sample inspection, i.e., after inspection of a product might render it unmarketable. Some examples of industries requiring this method are for example food products, hygiene products or even matches.

Another trend in today’s industry concerns the quality warranty from suppliers. As the power of retailer is increasing, some suppliers could offer the possibility of returning back the defective lots. This usually occurs when the retailer obtains strict quality requirements from the customers and can’t sell the defective items at a lower price in the market.

This study fills the gap described previously; it presents an inventory model, in which defective lots are detected through a sampling inspection. As soon as the inspection reduction from the whole shipment is concluded, defective lots are sent back to the supplier and are not charged. The mathematical model develops in this paper to determine the optimal order size and the optimal sample size, which minimizes the system costs, taking into account this quality related problem. The items used in the sampling inspection are no more marketable and withdraw from the supply chain stream. This study doesn’t investigate the policy to accept or reject a lot. It simply supposes that a lot accepted by the quality office contains only perfect quality items. This last assumption is applicable in sectors, where the probability of having identical items throughout the lot is high, (examples: products issued from the same recipe process or same raw material).

This proposed study is extended from Salameh and Jaber’s (2000) model, described previously. Since 17 years, this publication has received a lot of interest. Cárdenas-Barrón (2000) updated this study, Goyal and Cárdenas-Barrón (2002) simplified the model, and Rezaei (2005) made an extension by allowing shortages. Huang (2002) extended the model into a two-echelon vendor-buyer supply chain. Papachristos and Konstantaras (2006) clarified a point about the conditions ensuring that shortages will not occur in the original model of Salameh and Jaber (2000) they also propose an extension, supposing that the withdrawing of defectives takes place at the end of the planning horizon. Skouri et al. (2014) built a model illustrating what would happened if there is a probability that the entire shipment may be defective. In short, Khan et al. (2011a, b) gave a good review of the research areas and extensions of this model.

Most of the research always considered that the items are subject to a 100% screening. Tai (2015) proposed a model, where items are subject to multiple of successive 100% screening. However, only a few models have considered a sampling process. Moussawi-Haidar et al. (2013) investigated the case, where only a sample is inspected instead of the whole lot. If the number of defective items is below a certain “acceptance number”, the lot is accepted. Otherwise, the lot is subject to a 100% screening. They determined the optimal lot size and the optimal sampling plan to achieve the requirements of quality established. However, they obtained a profit significantly higher when compared to the optimal profit using Salameh and Jaber’s (2000) model, but couldn’t guarantee a zero defective item on the output quality.

Al-Salamah (2011) developed an inventory model with a sample inspection, and an acceptance sampling and possible Type II errors of miss-classification, but didn’t consider the Type I errors. He assumed that a lot could be classified as non-defective if it is less than a certain percentage of items that are found as defective items. It means that a lot could still present defective items even though it has passed the inspection process. Finally according to his model, defective lots are withdrawn as soon as detected and sold.

Many studies have reflected about other solutions to make efficient use of the defective items rather than selling as second quality goods. Chan et al. (2003) proposed a production-inventory model, extension to the Salameh and Jaber’s (2000) model, and provided a framework to integrate three possible uses of the defectives: sell at a lower price/rework/reject. Jaber et al. (2014) proposed an inventory model as defective items are either sent for reworking or replaced by good ones from a local supplier. They found that there exists a threshold value to the replacement unit cost and the fraction of defectives to which it is more beneficial to either buy or repair. Yu et al. (2012) established an inventory model, where a portion of the defective items (called the acceptable defective parts) can be used as perfect quality.

However, only some studies have already investigated some models which return defected items as soon as detected. Only Hsu and Yu (2011) proposed an inventory model in which all items are immediately returned back, as soon as they are detected. Yu et al. (2013) proposed the same model with an integrated policy. However, we consider in our proposed model that the retailer is still responsible for the safekeeping of the defective lots during the inspection. Indeed, the retailer has to keep defective lots, and send them back to the supplier as soon as the inspection phase for all the lots is concluded.

Khan et al. (2011a, b) proposed an extension by considering that the inspector may commit errors while screening. They build an inventory to depict this scenario. However, this model is based again on a 100% screening process and the defectives are sold at a lower price. This model has been updated by Hsu (2012a, b) and extended by allowing shortages in Hsu and Hsu (2013a) model. The same approach has been used to build the analogue production-inventory model (Hsu and Hsu 2013b). Thereafter, Khan et al. extended the model of Khan et al. (2011a, b) for a two-echelon vendor-buyer supply chain, similar as Huang’s (2002) model with the incorporation of learning in production.

Sarkar (2013) addressed a production-inventory model with defective items, but those defective items were due to deterioration. Due to improvement of the quality of defective products, Sarkar and Moon (2014), Sarkar et al. (2015a, b) developed integrated inventory models. Even though the system contains defective products, how the service level can be maintained, that is given by Sarkar et al. (2015a, b). During transportations of products (perfect or defective), how transportations cost and carbon emission cost effect on total cost, that is discussed by Sarkar et al. (2015a, b). In this direction, several research are done by Skouri et al. (2011), De and Sana (2013), Cárdenas-Barrón et al. (2014, 2015), Sarkar et al. (2015a, b), Roy et al. (2015), Wang et al. (2015), Lashgari et al. (2015), Sarkar (2016), Jaggi et al. (2016), Sarkar and Saren (2016), Taleizadeh et al. (2016a, b), Sarkar et al. (2016), Tayyab and Sarkar (2016), Sarkar and Lee (2017), Mishra et al. (2017).

This study extends the model of Salameh and Jaber (2000). The model considers a sampling process to identify and reject the defective lots. It includes Type I and Type II errors resulting from an imperfect inspection, following the approach of Khan et al. (2011a, b). However, this model doesn’t consider sales return. After the inspection process, the defective lots follow two scenarios. In the first one, defectives are immediately returned back to the supplier by the retailer. In the second scenario, defective items are kept in inventory and are taken back during the next shipment from the supplier. We don’t allow shortages and don’t consider an integrated supply chain model.

Table 1 summarizes the contribution of this study compared with other models from the literature review.

Table 1 Literature review
Full size table

The remainder of this paper is organized as follows: Sect. 2 gives a list of assumptions and nomenclatures used in our study; Sect. 3 presents the mathematical model itself. A numerical example and managerial insights are given for illustration in Sect. 4 and a sensitivity analysis is given in Sect. 5. Finally, some concluding remarks about the study are provided in Sect. 6.

2 Assumptions and notation

The assumptions, taken in this paper, are as follows:

  1. 1.

    The study considers an inventory model for single-type of products with a certain percentage of imperfect quality product’s shipments. Based on Sarkar et al. (2014), the model assumes the rate of defective production follows a random variable, which follows any probability distribution (for this model, it is assumed as uniform distribution).

  2. 2.

    Shipment of product contains several lots without inspection as supplier sends products without inspection and the retailer inspects to ensure the brand image of retailer in the market.

  3. 3.

    As soon as the shipment is received, a sampling process is applied. A quality inspection to n items in each lot is applied. If the lot passes the quality inspection, one can consider that all items in the lot are of perfect quality. Otherwise, the lot is intended to return to the supplier. The inspection is not error-free. During inspections, some imperfect products are accepted and some perfect products are wrongly rejected, thus Type I and Type II errors are incorporated within the model.

  4. 4.

    Lots, which do not meet the quality standard, have to be kept in inventory until they are sent back to the supplier. Either defective lots are sent back immediately after inspection, or the supplier will take them back in the next shipment.

  5. 5.

    The inspection phase and the demand proceed simultaneously. However, the study considers that the number of perfect lots identified is greater than the demand rate.

  6. 6.

    The demand rate is constant and uniform over the entire planning horizon.

  7. 7.

    Shortages are not allowed and the time horizon is infinite.

3 Mathematical model

The study develops an inventory model with imperfect items. The items are detected with 100% inspection process is not possible during delivery time. This model emphasizes about a sample inspection to avoid maximum possibility of Type I and Type II errors of defective items. The mathematical model analyzes two ways how to reduce defective lots. Retailer chooses the way, after inspection of defective items, they are immediately sent back to the supplier or wait for next shipment from supplier to send defective items. The model mainly stands on two major factors: order size (\(y^{*})\) and sample size (\(n^{*})\), which are related each other. Actually, products depend on taking quantity of sample products and number of quantity lots, which are ordered from supplier. Applying both related factors, the model obtains the total profit (TP) of retailer.

In this section, the mathematical model is introduced. Let y represents the order quantity size of lots, a new constant L is introduced, which represents the number of items per lots.

In order to satisfy the demand D of items per year, a shipment containing several lots is received every T unit of time. In a perfect model and without defected items, the relation \(\hbox {D}=yL/T\) is established in the stationary state, where T represents the cycle time. To calculate the total cost of the model, the following costs hand to be calculated.

3.1 Inspection costs

Upon receiving an order, an inspection based on a sample is applied. Let n represents sample size and satisfying constraint \(\mathrm {1}\le n \le \mathrm {L }\) and \(n \in {\mathbb {N}}\) . It is supposed that the arbitrary number of items used for the inspection is sufficient to provide a trustfully test. In other words, there isn’t a single defected item in the lot inspected if the inspection phase had been successful. It is also considered that the inspection time for a shipment \(t_{l}\) depends from the order size and from the number of samples used for inspection. Thus, one can obtain relation \(t_{l}= \frac{yn}{X}\), where X is the screening rate (constant).

A unit inspection cost \(c_{l}\) is introduced, which represents the cost for applying a quality inspection on an item. The inspection cost (\({\mathrm {IC}})\) for a shipment is

$$\begin{aligned} \mathrm {IC\,=\,}{\mathrm {c}}_{{\mathrm {l}}}{\mathrm {n}}\,\hbox {y} \end{aligned}$$
(1)

3.2 Inspection errors

As described in the model by Khan et al. (2011a, b), their screening process is assumed to be error free. But it is quite realistic to account for Type I and Type II errors committed by inspectors as it is offline inspection by the inspectors, thus there is a chance for accepting imperfect products as perfect and rejecting perfect product as imperfect. For this reason, the increased number of samples permits to reduce the risk of falsely qualifying a lot. Depending on the sample size n, inspectors classify some non-defective lots as defectives, i.e. \((1-{\uprho })m_{1}^{n}\), while some defective units as non-defectives, i.e. \({\uprho }\;m_{2}^{n}\). For this reason, the percentage of defective items perceived by the retailer \({\uprho }_{e}\) is different from the actual one \({\uprho }\). Thus, the fraction of defectives units perceived can be obtained as

$$\begin{aligned} E\left[ {\uprho }_{e} \right] =\left( 1-E[{\uprho ]} \right) {E{[}m_{1}]}^{n}+ E[{\uprho ]( 1-}{E{[}m_{2}]}^{n}) \end{aligned}$$

It is considered a cost of misclassification due to an insufficient number of samples to qualify the quality of the lot. One can assume that the number of items, which goes into Type I error (false rejection) is dependent on n. The inspectors falsely reject a lot if the inspectors have a Type I error, which happens on each non-defective item from the sample.

$$\begin{aligned} y\left( 1-E\left[ {\uprho } \right] \right) {E[m_{1}]}^{n} \end{aligned}$$

The number of items, that goes into Type II error (false acceptation), is dependent on n. The inspectors falsely accept a lot if they have a Type II error, which happens on each defective item from the sample.

$$\begin{aligned} yE\left[ {\uprho } \right] {E[m_{2}]}^{n} \end{aligned}$$

Let \(c_{r}\) and \({c}_{a}\), respectively be the cost of rejecting a non-defective lot (Type I error) and the cost accepting a defective lot (Type II error). In case of critical products, such as food, medical, or parts of an aircraft, the cost of acceptance \(c_{a}\) is much more than that of a false rejection (see for reference Raouf et al. 1983). Costs of inspection error \((\mathrm {IEC)}\) per cycle can be expressed as

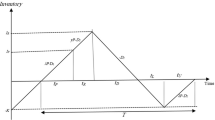
$$\begin{aligned} \mathrm {IEC=}\,c_{a}yE\left[ {\uprho } \right] {E[m_{2}]}^{n}+c_{r}y\left( 1-E\left[ {\uprho } \right] \right) {E[m_{1}]}^{n} \end{aligned}$$

Figure 1 represents the behavior of the inventory level. It can be noticed that the number of items that are withdrawn from the inventory is \({\uprho }_{e}\mathrm {yL+ny}\left( \mathrm {1-}{\uprho }_{e} \right) \), which represents the number of defective lots plus the number of items used for the inspection in the accepted lots. Under this condition, the inventory cycle \({\mathrm {T}}_{0}\) is determined as

$$\begin{aligned} {\mathrm {T}}_{0}\mathrm \,{=}\,\frac{yL-(pyL+ny(1-{\uprho }_{e}))}{D}=\frac{y(1-{\uprho }_{e})(L-n)}{D} \end{aligned}$$
(2)

The remainder of the model is subdivided in two cases. The first case (Case 1) considers a special transport is organized to send the defective lots back to the supplier. The model has an additional transport costs \({\mathrm {K}}_{d},\) but the defective products are no longer stored in the warehouse to avoid additional holding costs. The second case (Case 2) considers that for the sake of convenience, the supplier can take back the defective items in the next shipment. These two cases are the more efficient possibilities as it is logically be more expensive to send a transportation cost not immediately after the screening process (because of the holding costs of defective items).

3.3 Case 1 Defective items are immediately sent back to supplier with an additional transportation cost

Fig. 1
figure 1

Behavior of the inventory model sub-case (1)

Full size image

As h is the holding cost per unit per item, the holding costs per cycle for the first case \(\mathrm {(}{{\mathrm {HC}}}_{1}\mathrm {)}\) can be determined from the Fig. 1 (summing the 2 areas, see “Appendix 1” for the complete development) as

$$\begin{aligned} {{\mathrm {HC}}}_{1}=h\left( \frac{y^{\mathrm {2}}{\mathrm {(1-}{\uprho }_{e}\mathrm {)}}^{\mathrm {2}}{\mathrm {(}L-n\mathrm {)}}^{\mathrm {2}}}{\mathrm {2}D}\mathrm {+ }\frac{y^{\mathrm {2}}n\mathrm {L(}{\uprho }_{e}\mathrm {L+}n\mathrm {(1-\uprho ))}}{X} \right) \end{aligned}$$
(3)

In this case, the defective lots are sent back to the supplier with an additional cost for transportation cost \({{\mathrm {K}}}_{d}\). The purchasing costs (PC) per cycle is determined as

$$\begin{aligned} {{\mathrm {PC}}}_{1}={\mathrm {K}}_{d}\,\mathrm {+}\,y\left( \mathrm {1-}{\uprho }_{e} \right) c_{U} \end{aligned}$$
(4)

Total revenue (TR) in a cycle is

$$\begin{aligned} {\mathrm {TR= }}\,P\left( yL-{\uprho }_{e}\mathrm {yL-}\left( \mathrm {1-}{\uprho }_{e} \right) ny \right) {\mathrm {=P}}y\mathrm {((}L-n\mathrm {)(1-}{\uprho }_{e}\mathrm {))} \end{aligned}$$
(5)

where P is the unit’s selling price. Total profit \({\mathrm {TP}}\left( \mathrm {y,n} \right) \) is the total revenue per cycle less the total cost per cycle divided by the cycle time, and is given as follows:

$$\begin{aligned} {{\mathrm {TP}}}_{1}(y, n)= & {} \frac{\mathrm {TR-}\,{{\mathrm {PC}}}_{1}\,\mathrm {-\,IC\,-\,IEC\,-\,}{{\mathrm {HC}}}_{1}}{{{\mathrm {T}}}_{\mathrm {0}}}\nonumber \\= & {} \hbox {PD}-\frac{Dc_{U}}{\left( L-n \right) }-\frac{c_{l}nD}{\left( L-n \right) \left( 1-{\mathrm {E}}[\uprho _{e}] \right) }-\frac{\left( {\mathrm {K}}+{\mathrm {K}}_{d} \right) D}{y(\mathrm {1}-E[{\uprho }_{e}])(L-n)}\nonumber \\&\qquad -\,\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( \mathrm {1-E}[{\uprho }_{e}] \right) \left( L-n \right) }-\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( \mathrm {1-E}[{\uprho }_{e}] \right) \left( L-n \right) }\nonumber \\&\qquad -\,h\frac{y\left( \mathrm {1-E}[{\uprho }_{e}] \right) \left( L-n \right) }{\mathrm {2}} -h\frac{DLyn\left( {\mathrm {E}}[\uprho _{e}]\hbox {L}+n\left( \mathrm {1-E}[{\uprho }_{e}] \right) \right) }{X\left( \mathrm {1-}{\mathrm {E}}[\uprho _{e}] \right) \left( L-n \right) } \end{aligned}$$
(6)

For maximization of the profit, by taking partial derivatives with respect to y and n,  one can obtain

$$\begin{aligned} \frac{\delta {{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta y}= & {} \frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{2}\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) }-h\frac{\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) }{\mathrm {2}}\nonumber \\&\quad -\,h\frac{DLn\left( {\mathrm {E[\uprho }}_{e}\mathrm {]L+}n\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \right) }{X\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) } \end{aligned}$$
(7)

and

$$\begin{aligned} \frac{\delta {{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta n}= & {} -\frac{Dc_{U}}{\left( L-n \right) ^{2}}-\frac{c_{l}DL}{\left( 1-E\left[ {\uprho }_{e} \right] \right) \left( L-n \right) ^{2}}-\frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y\left( \mathrm {1-E}\left[ {\uprho }_{e} \right] \right) \left( L-n \right) ^{2}}\nonumber \\&\quad -\,\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( \mathrm {1-E}\left[ {\uprho }_{e} \right] \right) \left( L-n \right) } \left[ \frac{1}{\left( L-n \right) }\mathrm {+}\ln \left( E\left[ m_{2} \right] \right) \right] \nonumber \\&\quad -\,\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) (L-n)}\left[ \frac{1}{\left( L-n \right) }\mathrm {+}\ln \left( E\left[ m_{1} \right] \right) \right] \mathrm {+}h\frac{y\left( \mathrm {1-E[}{\uprho }_{e}] \right) }{\mathrm {2}}\nonumber \\&\quad -\,h\frac{DLy\left( {\mathrm {E[\uprho }}_{e}]{\mathrm {L}}^{2}\mathrm {+ 2}nL\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) -n^{2}\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \right) }{X\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{2}} \end{aligned}$$
(8)

For sufficient condition, the second order derivative can be obtained as follows:

All terms of Hessian matrix are obtained as follows:

$$\begin{aligned} \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta y}^{2}}= & {} -\frac{2\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{3}\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) }< 0 \end{aligned}$$
(9)
$$\begin{aligned} \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta n\delta y}= & {} \frac{\delta {{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta y\delta n}\nonumber \\= & {} \frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{2}\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) ^{2}}\mathrm {+}h\frac{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) }{\mathrm {2}}\nonumber \\&\quad -\,h\frac{DL\left( {\mathrm {L}}^{2}{\mathrm {E[\uprho }}_{e}\mathrm {]+2}Ln\left( \mathrm {1-E[}{\uprho }_{e}] \right) -n^{2}\left( \mathrm {1-E[}{\uprho }_{e}] \right) \right) }{X\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{2}} \end{aligned}$$
(10)
$$\begin{aligned} \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta n}^{2}}= & {} -\frac{2Dc_{U}}{\left( L-n \right) ^{3}}-\frac{2c_{l}DL}{\left( 1-{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{3}}-\frac{2\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{3}}\nonumber \\&\quad -\,\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( \mathrm {1-E}\left[ {\uprho }_{e} \right] \right) \left( L-n \right) }\times \left[ \frac{2}{\left( L-n \right) ^{2}}\mathrm {+}\frac{\ln \left( E\left[ m_{2} \right] \right) }{\left( L-n \right) }\mathrm {+}\ln \left( E\left[ m_{2} \right] \right) ^{2} \right] \nonumber \\&\quad -\,\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) (L-n)}\left[ \frac{2}{\left( L-n \right) ^{2}}\mathrm {+}\frac{\ln \left( E\left[ m_{1} \right] \right) }{\left( L-n \right) }\mathrm {+}\ln \left( E\left[ m_{1} \right] \right) ^{2} \right] \nonumber \\&\quad -\,h\frac{2DyL^{3}}{X\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) ^{3}}{<}0 \end{aligned}$$
(11)

Proposition 1

For \(n<L\) and for X more than 1, the expected profit function \({{TP}}_{1}\left( y,n \right) \) is concave. Thus, there always exist an order size y and a sample size n which maximizes the total profit.

Proof

The function TP (y, x) is concave and have the global maximum if the principal minors are alternating in sign. For the 1st principal minor, it is found that \(\frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta n}^{2}}\) and \(\frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta y}^{2}}\) are negative definite. Thus if the 2nd principal minor is positive definite, then the profit function has the global maximum. \(\square \)

To prove, the 2nd condition, the relation \({\frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta y}^{2}}\times \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta n}^{2}}-\left( \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta n\delta y} \right) }^{2}>0\) should be verified. As the terms\( \frac{\delta {{\mathrm {TPU}}}_{1}\left( y,n \right) }{\delta y\delta y}\) and \(\frac{\delta {{\mathrm {TPU}}}_{1}\left( y,n \right) }{\delta n\delta n}\) are always strictly negative according to the conditions, the determinant is negative if:

  1. 1.
    $$\begin{aligned} \left| \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta y}^{2}} \right| >\left| \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta n\delta y} \right| \end{aligned}$$

    and

  2. 2.
    $$\begin{aligned} \left| \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta n}^{2}} \right| >\left| \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta n\delta y} \right| \end{aligned}$$

The 1st condition is obviously true for every \(y>1\). The complete explanation of the 2nd condition is provided in “Appendix 2”. Consequently, it could be stated that the function is always concave and has a solution, which maximizes the total profit.

Fig. 2
figure 2

Behavior of the inventory, subcase (2)

Full size image

3.4 Case 2 Supplier will take back defective lots in the next shipment

In this case, the holding costs are the same as in Eq. 3 increased by an additional term corresponding to the holing costs of the defective items (grey area on Fig. 2). The holding costs are determined as

$$\begin{aligned} {{\mathrm {HC}}}_{2}= & {} h\left[ \frac{y^{\mathrm {2}}{\mathrm {(1-}{\uprho }_{e}\mathrm {)}}^{\mathrm {2}}{\mathrm {(}L-n\mathrm {)}}^{\mathrm {2}}}{\mathrm {2}D}\mathrm {+ }\frac{{Ly}^{\mathrm {2}}\mathrm {(}{\uprho }_{e}\mathrm {L+}n\mathrm {(1-}{\uprho }_{e}\mathrm {))}}{X} \right] \nonumber \\&\quad +\,h_{d}\left[ \frac{y^{\mathrm {2}}{\uprho }_{e}\mathrm {(1-}{\uprho }_{e}\mathrm {)}{\mathrm {(}L-n\mathrm {)}}^{\mathrm {2}}}{D}\mathrm {+ }\frac{{\mathrm {L}}y{\uprho }_{e}\mathrm {(L+}n\mathrm {)}}{X} \right] \end{aligned}$$
(12)

Supplier takes back defective items in the next shipment. Thus, there isn’t any additional cost for transportation. The purchase costs (PC) per cycle is determined as

$$\begin{aligned} {{\mathrm {PC}}}_{2}=y\left( \mathrm {1-}{\uprho }_{e} \right) c_{U} \end{aligned}$$
(13)

Total profit \({\mathrm {TP}}\left( y,n \right) \) is determined in the same way and is given as

$$\begin{aligned} {{\mathrm {TP}}}_{2}\left( y,n \right)= & {} \frac{\mathrm {TR-}{{\mathrm {PC}}}_{2}\mathrm {-IC-}{{\mathrm {HC}}}_{2}}{{\mathrm {T}}_{\mathrm {0}}}=\hbox {PD}-\frac{Dc_{U}}{\left( L-n \right) }-\frac{c_{l}nD}{\left( L-n \right) }-\,\frac{{\mathrm {K}}D}{y\left( \mathrm {1-E}\left[ {\uprho }_{e} \right] \right) \left( L-n \right) }\nonumber \\&\quad -\,\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) }-\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) }-h\frac{y\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) }{\mathrm {2}}\nonumber \\&\quad -\,h\frac{DLy\left( {\mathrm {E[\uprho }}_{e}\mathrm {]L+}n\left( \mathrm {1-\uprho } \right) \right) }{X\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) }-h_{d}y{\mathrm {E[\uprho }}_{e}]\left( \mathrm {L-}n \right) \nonumber \\&\quad -\,h_{d}\frac{DL{\mathrm {E[\uprho }}_{e}\mathrm {](L+}n\mathrm {)}}{X\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) } \end{aligned}$$
(14)

If one can consider a transportation cost is zero and a holding cost of the defective lots is zero, i.e. \({\mathrm {K}}_{d}=0\) and \({h}_{d}=0\), one can observe that Eqs. 6 and  14 are the same, supporting the evidence that the two cases are based on the same model.

A similar statement on Proposition 1 can be proposed regarding the existence of a maximum for the \({{\mathrm {TPU}}}_{2}\left( y,n \right) \) function.

Proposition 2

Based on this model, there exists a threshold value of \({{K}}_{d}\) consider \({{K}}_{d}^{*}\), after which it is more profitable to conduct a transporting of defective items to a supplier rather than to keep the defective items in a warehouse. This threshold value is dependent from the optimal couple (y, n) and is given by

$$\begin{aligned} {\mathrm {K}}_{d}^{*}<h_{d}\left( \frac{y^{\mathrm {2}}{\mathrm {E[\uprho }}_{e}\mathrm {](1-}{\mathrm {E[\uprho }}_{e}\mathrm {])}{\mathrm {(}L-n\mathrm {)}}^{\mathrm {2}}}{D}\mathrm {+ }\frac{{\mathrm {L}}y{\mathrm {E[\uprho }}_{e}\mathrm {](L+}n\mathrm {)}}{X} \right) \end{aligned}$$
(15)

Proof

As Eq. 6 shows the total profit \({{\mathrm {TP}}}_{1}\left( y,n \right) \) and Eq. 14 shows explicitly \({{\mathrm {TPU}}}_{2}\left( y,n \right) \). The validity of the theorem that \({{{\mathrm {TP}}}_{1}\left( y,n \right) \mathrm {-TP}}_{2}\left( y,n \right) >0\). After an arrangement of the terms, the Eq. 15 is obtained. Hence, this implies the proof. \(\square \)

3.5 NBBARY algorithm

As the solutions are dependent to each other, thus we need an algorithm for the numerical study. Here one can present a procedure in order to find the optimal solution of the problem.

  • Step 1 Find the maximum values of \({{\mathrm {TP}}}_{1}\left( y,n \right) \mathrm { }\)and \({{\mathrm {TP}}}_{2}\left( y,n \right) \mathrm { }\)by solving the zero value of gradients, using Newton- Raphson’s method.

  • Step 2 Compare both cases and select the more profitable one. If the two cases give profits then more profitable case can be accepted and less profitable case can be rejected. Otherwise, Step 3 must be applied for both cases.

  • Step 3 Let \(\left( y^{*},n^{*} \right) \) be the optimal values obtained corresponding to the optimal total profit function. The aim is to obtain an integer value of n and y corresponding to convenient practical cases. Compute the values of \({\mathrm {TP}}\left( \left\lfloor y \right\rfloor ,\left\lfloor n \right\rfloor \right) \), \({\mathrm {TP}}\left( \left\lfloor y \right\rfloor +1 ,\left\lfloor n \right\rfloor \right) \), \({\mathrm {TP}}\left( \left\lfloor y \right\rfloor \mathrm {, }\left\lfloor n \right\rfloor +1 \right) \) and \(\mathrm {TP}\left( \left\lfloor y \right\rfloor +1, \left\lfloor n \right\rfloor +1 \right) \), choose finally between the four results with the twin value which gives the highest profit.

4 Numerical examples

In this section, the behavior of mathematical model is presented for practical cases. Five relevant numerical experiments are conducted. In the first numerical example, parametric values, similar to the numerical example by Salameh and Jaber (2000), are considered. The above solution procedure in order to obtain the optimal twin \((y^{*},n^{*})\) is applied. In the second numerical example, the ratios between the total profits \((\mathrm {TP)}\) of both cases are observed, while varying the holding costs and transport costs of defective items. In the third numerical example, the behavior of the optimal values \((y^{*},n^{*})\) are analyzed, while varying the lot size. On the fourth example, the implication of ordering costs and inventory costs are observed on the optimal values \( (y^{*},n^{*})\). Finally, the same scenario is replicated on the fifth example, while varying the screening rate.

Example 1

NBBARY algorithm to obtain the optimal order size and sample size is applied. Table 2 gives the values adopted by this numerical example; similar to the work of Salameh and Jaber (2000). A lot size of 300 has been arbitrary chosen, the remaining values are adjusted in order to correspond with the same range of costs.

Table 2 Standard values adopted for the numerical example
Full size table

Prior to computing the \({\mathrm {TP}}\left( y,n \right) \) and find the optimal twin \((y^{*},n^{*})\), it is necessary to compute

$$\begin{aligned} E\left[ {\uprho } \right] \mathrm {= }\int _a^b {\rho f\mathrm {(\uprho )}} \rho d\rho =\int _a^b {\rho \frac{1}{b-a}} d\rho = \frac{b+a}{2}=\frac{0.04+0}{2}=0.02 \end{aligned}$$
(16)

Following the same process, the values of \(E\left[ m_{1} \right] {=0.025}\) and \(E\left[ m_{2} \right] {=0.05}\) are obtained. Finally,

$$\begin{aligned} E\left[ {\uprho }_{e} \right] = 0.98\times {0.005}^{n}+ 0.02 {( 1-}{0.01}^{n}) \end{aligned}$$
(17)

By numerical experiment, a maximum profit of 248,291 occurs for an order size y of 47.04 and a sample size n of 2.48. The second case has a maximum profit of 278,924 for an order size of 37.45 and a sample size of 2.79. The second case is consequently the model to adopt as in these conditions it is more profitable to keep defective lots in inventory until the next shipment. After analyzing the four possible values of integer parameters, the optimum combination of decision variables reveals to be \((y^{*},n^{*}) = ( 2 , 37)\) with a profit of 278,924. It can be found from the results that with such parameters, the total profit among all four values is almost the same. In order to validate these results, the curve of the profit function is represented on Fig. 3.

Fig. 3
figure 3

Total profit (TP) behavior for parameters issued from Table 2

Full size image

Example 2

The ratio between the two total profits for relatively different values of the ratio \(K_{b}/h_{d}\) is represented (\(K_{b}\) is fixed in this numerical example). The results are represented for three fixed values of the lot size L, the lot purchase costs \(c_{u}\) has been adapted in each case in order to maintain the proportionality to the lot size. All others parameters remain unchanged from Table 2.

One can notice from the results of Fig. 4 that the bigger the lot sizes, the more the ratio between the two cases differ. Also, one can observe on the same figure that the bigger lot sizes, the more profitable the first case is (\(TP1/TP2>1)\). This deduction is quite intuitive as it can be more expensive to conduct the second sub-case. Thus, the holding costs considerably increase with bigger lot sizes.

Fig. 4
figure 4

Ratio of total profit while varying the parameters \(\hbox {K}_{{\mathrm {d}}}\) and \(\hbox {h}_{{\mathrm {d}}}\)

Full size image

Example 3

The optimal order size and the optimal sample size are represented on Fig. 5 for different levels of lot sizes. The results are obtained with the application of the NBBARY algorithm. In order to interpret the model and study specifically the values resulting from the increase of the lot size, the lot purchase price \(c_{u}\) has been adapted and set proportional to the lot size. In that way, there is no misunderstanding with other parameters, which can be compared with the essential results.

The exponentially decreasing behavior of curve from the optimal order size \(y^{*}\) can be noticed. However, there’s a sudden fall of the curve for a lot size around 100. This corresponds to a change in the optimal sample size from 3 samples to 2 samples. This behavior is intuitive as, in this Example 3, the cost of accepting a lot is constant whatever the lot size is. Naturally, the model considers that one should take a higher number of samples in order to prevent a too costly error in the wrong classification of the lot.

Fig. 5
figure 5

Optimal order size and sample while varying the lot size

Full size image

Example 4

The optimal order size is represented for different ratios of ordering costs versus holding costs K / h. Two curves are represented on Fig. 6, illustrating the results obtained for two fixed values of K. The other parameters remain unchanged from those of Table 2. These results are obtained for successive applications of the solution algorithm. It could be noticed the increasing value of the optimal order size \(y^{*}\) as K became high based on the value of h. Also, the higher K and h are, the lower the optimum order size is. The sample size is not represented in this numerical example as it stays constant at value of \({n}^{*}=2\) for both cases.

Fig. 6
figure 6

Optimal order size while varying the ratio K/h

Full size image

Example 5

The optimal order size and the optimal sample size are represented on the same figure for different values of the expected Type II errors \(E[m_{2}]\). These results, observed on Fig. 7, are obtained for successive applications of the NBBARY algorithm. It could be noticed that the optimal sample size \(n^{*}\)increases as \(E[m_{2}]\) became high. However, for every change of \(n^{*}\), the optimal order size \(y^{*}\) changes itself also and follows a decreasing curve. One of the reasons for such behavior is that for a higher Type II error, there are much more defective items, which will be classified as non-defective, thus it starts to decrease the fraction of defective items perceived.

Fig. 7
figure 7

Optimal sample size versus expected Type II error

Full size image

4.1 Managerial insight

As always full inspection is not possible, the managers of different industries have problems to inspect items and they cannot take decision that after getting defective items, they immediately send to the supplier or wait for next lot arrival. For the second case, the retailer does not have to pay the transportation cost, but the retailer has to pay the holding cost for carrying defective items. If the retailer sends immediately after receiving from the system as defective products, the retailer has to pay the transportation cost. Therefore, there is a trade-off between the extra holding cost for carrying the defective products or invested transportation cost for transporting the defective products. The results, obtained by this proposed model, suggest that the retailer should transport defective products immediately after the detection as defective through lot inspection. If the input data of the numerical results are changed, the results may vary with the existing one.

For many plastic industries, the inspection are done by checking all of its chemical components and the capacities for which it is made. To check the product is harmful or not for human health, it is tested through several process. For those tests, the plastic products have to melt into liquid forms. In the liquid form, they are tested and after testing they cannot be used any more for general use. Therefore, full inspection is never be possible for these types of products. Lot inspection is the best policy for those industries. The proposed model gives the solution for the managers for those industries.

As lot inspection is conducted, there is a chance for inspection errors, it means that defective lot may be considered as perfect or perfect lot may be considered as imperfect. Thus Type-I and Type-II error are introduced, which gives the accurate results for industry manager to predict the chances or percentages of errors.

Table 3 Sensitivity analysis of the model in a numerical example for sub-case 1
Full size table

5 Sensitivity analysis

In this section, the results of our sensitivity analysis are discussed. Table 3 presents the sensitivity analysis of the parameters representing costs in the model for the first case. The values from the parameters used in this analysis are those from Table 2.

It can be observed from the results that an increasing value of costs has a negative influence on the TP, which is intuitive. However, the optimal sample size \(n^{*}\) and the optimal order size \(y^{*}\) don’t follow always the same behavior. For example, increasing value of the cost \(c_{a}\) (cost of falsely accepting a defective lot) has a positive effect on the optimal sample size \(y^{*}\). Also, the increasing value of the cost K(order cost) has a positive effect on the optimal order size \(y^{*}\).

The cost \(c_{a}\) (cost of falsely accepting a defective lot) is the parameter, which less influences the total profit. For an increment of 50%,  the total profit only decreases by 0.006%. On the contrary, the cost \(c_{U}\) (lot purchase cost) is the parameter, which more influences the total profit. For an increment of 50%, the total profit decreases by 16.9%. However, these results can slightly differ from other parameters and should be analyzed with precautions.

6 Conclusions

This paper developed an economic order quantity model for a sampling, sample quality inspection, and a returned policy of defective items. This model filled the research gap in the literature in providing a model, which took into account the impairment loss resulting from the sample inspection. It also highlighted the strong link between order sizes, sample sizes, and lot sizes. Thus, these values were considered all together to obtain the optimal twin \((y^{*},n^{*})\). Two cases were discussed with two policies of returning defective items. The return of defective items to a supplier was relevant nowadays as it might occur in several supplies chain sectors in which retailers maintained strict quality requirements.

A threshold value was defined upon which the first case was obtained as more profitable and a solution procedure to find the best couple (y, n) was provided. Numerical examples were conducted and a sensitivity analysis was established. From numerical study, it was found that global optimal results gave several conditions for the policy related solutions and amount of defective products. This work can be enhanced in a number of ways. There are still plenty of hypothesis that cannot always be considered yet by any researches. A model with shortages can be developed. Another direction is to extend the model by considering stochastic demand rates or integrate this model in a two-level supply chain (Sarkar et al. 2015a, b). This paper does not consider any inspection errors with warranty cost i.e., Type-I and Type-II errors with warranty cost (Sarkar and Saren 2016). For further research work, this paper can be extended by introducing these two types of errors with warranty cost. Warranty cost and machine breakdown can be added to this model for further extension. It will be a nice contribution if this model will assume finite inspection time during production run. Variable transportation costs along with carbon-emission costs can be introduced to this model for future study [see for reference Sarkar et al. (2016)].