Optimal Lot Sizing Policy for Non-instantaneous Deteriorating Items with Price and Advertisement Dependent Demand Under Partial Backlogging

Abstract

This article deals with an economic order quantity model for non-instantaneous deteriorating items with price and advertisement dependent demand pattern. The salvage value for deteriorating items is considered in this model. Shortages are allowed and partially backlogged. The backlogging rate depends upon the waiting time for the next replenishment. A mathematical model is framed to obtain the optimal replenishment policy which aids the retailer to minimize the total inventory cost. The necessary and sufficient condition for the existence and uniqueness of the optimal solution are also derived with useful theoretical results. Numerical examples are provided to illustrate the results obtained. Sensitivity analyses are carried out. The managerial implications and the effects of key parameters are studied to analyze the behavior of the model.

Introduction

Deterioration is defined as decay, damage or spoilage such that the items are not in a condition of being used for its original purpose. Foodstuffs, medicine, volatile liquids, blood, grains, gasoline are examples of deteriorating items. The problem of managing deteriorating inventory has received considerable attention in recent years. Ghare and Schrader [1] made the first attempt to describe the optimal ordering policies for such items having constant rate of deterioration. Covert and Philip [2] formulated an economic order quantity (EOQ) model for item with Weibull distribution deterioration. Philip [3] generalized this model by taking three parameter Weibull distributions. Goyal and Giri [4] gave a detailed review of deteriorating inventory literature. Chung et al. [5] gave a note on EOQ models for deteriorating items under stock dependent selling rate. Dye and Ouyang [6] developed an EOQ model for perishable items under stock dependent selling rate and time-dependent partial backlogging. Jaggi and Aggarwal [7] developed an EOQ model for deteriorating items with salvage values. Recently, Annadurai [8] derived an optimal replenishment policy for decaying items with shortages and salvage value. Teng et al. [9] described an optimal replenishment policy for deteriorating items with time varying demand and partial backlogging. Skouri and Papachristos [10] developed an optimal stopping and restarting production times for an EOQ model with deteriorating items and time dependent partial backlogging. Musa and Sani [11] developed inventory ordering policies of delayed deteriorating items under permissible delay in payments. Duan et al. [12] presented inventory models for perishable items with inventory level dependent demand rate. Cheng et al. [13] gave the optimal policy for deteriorating items with trapezoidal type demand and partial backlogging.

The above said researchers assumed that the deterioration of the items in inventory starts from the instant of their arrival. But items such as fruits, vegetables, fish, meat etc., remain fresh for a certain period. During that period, the items do not deteriorate. Wu et al. [14] defined the phenomenon as “non-instantaneous deterioration”. In this direction, Ouyang et al. [15] gave a study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments. Chung [16] derived a complete proof on the solution procedure for non-instantaneous deteriorating items with permissible delay in payments. Geetha and Uthayakumar [17] developed an economic design of an inventory policy for non-instantaneous deteriorating items under permissible delay in payments. Liao [18] discussed an EOQ model with non-instantaneous receipt and exponentially deteriorating items under two level trade credits.

All these models and many more treated the demand rate as constant or time-dependent. In real-life situation, lower selling price exposures demand and its effectiveness, while high selling prices decline demand records to zero. Due to the reason, researchers considered the demand as a function of the selling price. Yang [19] developed pricing strategy for deteriorating items using quantity discount when demand is price sensitive. Ray et al. [20] developed joint pricing and inventory policies for make-to-stock products with deterministic price sensitive demand. Teng and Chang [21] formulated an economic production quantity models for deteriorating items with price and stock dependent demand. You and Hseih [22] developed an EOQ model with stock and price sensitive demand. Mukhopadhyay et al. [23] established the joint pricing and ordering policy for a deteriorating inventory. Palanivel and Uthayakumar [24] derived a finite horizon EOQ model for non-instantaneous deteriorating items with price and advertisement dependent demand and partial backlogging under inflation. Khouja and Robbins [25] were derived the model with linking advertising and quantity decisions in the single period inventory. Mondal et al. [26] investigated the finite replenishment inventory model for defective items incorporating marketing decisions with variable production cost. Recently, Shah et al. [27] obtained an optimizing inventory and marketing policy for non-instantaneous deteriorating items with generalized type deterioration and holding cost rates.

However, we must acknowledge that consumption rate is also dependent on selling price in a practical environment. In addition to the selling price, the other marketing parameter, which affects the demand, is advertisement. It is commonly seen that a product is promoted through advertisements in well-known print or electronic media or by other means to attract customers. The purpose of this type of advertisement is to raise the demand for the product. Hence, in this article, we developed an EOQ model for non-instantaneous deteriorating items with price and advertisement dependent demand pattern. Shortages are allowed and are partially backlogged in this model. Some useful theoretical results have been derived to characterize the optimal solutions. Numerical examples are provided to demonstrate the developed model and the solution procedure. Sensitivity analysis of the optimal solution with respect to major parameters of the system is carried out, and their results, with managerial implications, are discussed.

Notations and Assumptions

Notations

The following notations are used throughout this paper:

k :

ordering cost per order ($/order)

h :

unit stock holding cost (($/unit /unit time)

c :

unit purchasing cost ($/unit)

s :

shortage cost for backlogged item($/unit /unit time)

$\pi$ :

the unit cost of lost sales

$\theta$ :

the deterioration rate, where $0\le \theta \le 1$

$\delta$ :

the backlogging parameter which is a positive constant, where $0\le \delta \le \,1$

$\gamma$ :

salvage value parameter $0\le \gamma \le 1$, associated with deteriorated units during the cycle time

$I_m$ :

the maximum inventory level for each replenishment cycle

S :

the maximum amount of demand backlogged per cycle

T :

inventory cycle length (decision variable)

$t_d$ :

the length of time in which the product has no deterioration

$t_1$ :

the time at which the inventory level falls to zero (decision variable)

$I\left( t \right)$ :

inventory level at time t

$I_1 \left( t \right)$ :

the inventory level at time $t,0\le t\le t_d$

$I_2 \left( t \right)$ :

the inventory level at time $t,t_d \le t\le t_1$

$I_3 \left( t \right)$ :

the inventory level at time $t,t_1 \le t\le T$

$TC\left( {t_1 ,T} \right)$ :

the total annual inventory cost per unit time of inventory system

Q :

the retailer’s order quantity

Assumptions

To develop the mathematical model, the following assumptions are being made.

• i. A single item is considered in the inventory system.

• ii. The demand rate D is a deterministic function of selling price p, and advertisement cost $A_C$ per unit item i.e. $D\left( {A_C ,p} \right) =A_C^\eta ap^{-b},a>0,b>1,0\le \eta <1, a$ is the scaling factor, b is the index of price elasticity and $\eta$ is the shape parameter.

• iii. Replenishment occurs instantaneously at an infinite rate and the lead time is negligible.

• iv. Shortages are allowed to occur and are partially backlogged. During the stock-out period, the backlogging rate is variable and is dependent on the length of the waiting time for the next replenishment. So, the backlogging rate for negative inventory is denoted as $B\left( t \right) =\frac{1}{1+\delta \left( {T-t} \right) }$, where $\delta$ is the backlogging parameter $0\le \delta \le 1$, the remaining fraction $1-B\left( t \right)$ is lost.

• v. It is assumed that during certain period of time the product has no deterioration (i.e., fresh product time). After this period, a constant fraction, $\theta \left( {0\le \theta \le 1} \right)$ of the on-hand inventory deteriorates and there is no repair or replacement for the deteriorated units.

• vi. The salvage value $\gamma$, where $0\le \gamma \le 1$, is associated with deteriorated units during the cycle time.

Mathematical Model

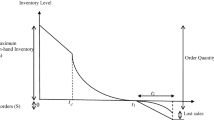
In this section, the mathematical modeling of the inventory system with the above assumptions is given. The retailer orders and receives Q units of a single product from the supplier at the beginning of the cycle at time $t=0$. During the time $[0,t_d ]$, there was no deterioration occurring. Therefore the inventory level decreases owing to demand alone. The inventory level is depleted gradually to zero due to demand and deterioration in the time interval [$t_d ,t_1$]. At time $t=t_1$ the inventory level reaches zero. Thereafter, shortages are allowed to occur and the demand during the period $[t_1 ,T]$ is partially backlogged. This model is demonstrated in Fig. 1.

Fig. 1

Graphical representation of the inventory system

Hence the change of inventory level $I\left( t \right)$ with respect to time can be given by the differential equation

$$\begin{aligned} \frac{dI\left( t \right) }{dt}=\left\{ {{\begin{array}{lll} -D \quad \quad &{} if &{}\quad 0 \le t \le t_d , \\ -D-\theta I\left( t \right) \quad \quad &{} if &{}\quad t_d \le t\le t_1 , \\ \frac{-D}{1+\delta \left( {T-t} \right) } \quad \quad &{} if &{}\quad t_1 \le t\le T, \\ \end{array}}} \right. \end{aligned}$$

(1)

with the boundary condition $I\left( 0 \right) =I_m ,I\left( {t_1 } \right) =0$.

The solution of Eq. (1) is

$$\begin{aligned} I\left( t \right) =\left\{ {{\begin{array}{lll} I_1 \left( t \right) \quad &{} \quad if &{}\quad 0\le t\le t_d , \\ I_2 \left( t \right) \quad &{} \quad if &{} \quad t_d \le t\le t_1 , \\ I_3 \left( t \right) \quad &{} \quad if &{}\quad t_1 \le t\le T, \\ \end{array}}} \right. \end{aligned}$$

where

$$\begin{aligned} I_1 \left( t \right)= & {} \frac{D}{\theta }\left[ {e^{\theta \left( {t_1 -t_d } \right) }-\theta \left( {t-t_d } \right) -1} \right] , \end{aligned}$$

(2)

$$\begin{aligned} I_2 \left( t \right)= & {} \frac{D}{\theta }\left[ {e^{\theta \left( {t_1 -t} \right) }-1} \right] \end{aligned}$$

(3)

$$\begin{aligned} I_3 \left( t \right)= & {} \frac{D}{\delta }\left[ {\ln \left[ {1+\delta \left( {T-t} \right) } \right] -\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] } \right] \end{aligned}$$

(4)

At $t=t_d ,I_1 \left( {t_d } \right) =I_2 \left( {t_d } \right)$, the maximum inventory level for each cycle is obtained by

$$\begin{aligned} I_m =Dt_d +\frac{D}{\theta }\left[ {e^{\theta \left( {t_1 -t_d } \right) }-1} \right] \end{aligned}$$

(5)

The maximum amount of demand backlogged per cycle is given by

$$\begin{aligned} S=-I_3 \left( t \right) =\frac{D}{\delta }\left[ {\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] } \right] \end{aligned}$$

(6)

From Eqs. (5) and (6), we can obtain the order quantity per cycle as

$$\begin{aligned} Q=I_m +S \quad =Dt_d +\frac{D}{\theta }\left[ {e^{\theta \left( {t_1 -t_d } \right) }-1} \right] +\frac{D}{\delta }\left[ {\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] } \right] \end{aligned}$$

(7)

The total annual inventory cost which is a function of $t_1$ and T is given by (see Appendix 1)

$$\begin{aligned} TC\left( {t_1 ,T} \right)= & {} \frac{D}{T}\left\{ \frac{k}{D}+\left( {\frac{h+\left( {c-\gamma } \right) \theta }{\theta }} \right) \left[ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right] \right. \nonumber \\&\left. +\left( {\frac{s+\pi \delta }{\delta }} \right) \left[ {\left( {T-t_1 } \right) -\frac{\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] }{\delta }} \right] \right\} \end{aligned}$$

(8)

Theoretical Results and Optimal Solutions

In this section, we shall determine the optimal shortage point and the optimal replenishment cycle time that minimizes the total cost per unit time as follows. The necessary conditions for the total cost per unit time $TC\left( {t_1 ,T} \right)$ to be minimum are

$$\begin{aligned} \frac{\partial TC\left( {t_1 ,T} \right) }{\partial t_1 }=0 \hbox { and } \frac{\partial TC\left( {t_1 ,T} \right) }{\partial T}=0 \end{aligned}$$

which give

$$\begin{aligned} \frac{\partial TC\left( {t_1 ,T} \right) }{\partial t_1 }= & {} \frac{D}{T}\left\{ \left( {\frac{h+\left( {c-\gamma } \right) \theta }{\theta }} \right) \left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] \right. \nonumber \\&\left. +\left( {\frac{s+\pi \delta }{\delta }} \right) \left[ {\frac{1}{1+\delta \left( {T-t_1 } \right) }-1} \right] \right\} =0 \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial TC\left( {t_1 ,T} \right) }{\partial T}= & {} \frac{D}{T^{2}}\left\{ \left( {\frac{s+\pi \delta }{\delta }} \right) \left[ {\frac{\left( {T-t_1 } \right) \left( {\delta t_1 -1} \right) }{1+\delta \left( {T-t_1 } \right) }+\frac{\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] }{\delta }} \right] \right. \nonumber \\&\left. -\left( {\frac{h+\left( {c-\gamma } \right) \theta }{\theta }} \right) \left[ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right] -\frac{k}{D} \right\} =0\nonumber \\ \end{aligned}$$

(10)

For notational convenience, let

$$\begin{aligned} U=\left( {\frac{s+\pi \delta }{\delta }} \right) >0 \;and\; V=\left( {\frac{h+\left( {c-\gamma } \right) \theta }{\theta }} \right) >0, \end{aligned}$$

then Eqs. (9) and (10) becomes

$$\begin{aligned} T=t_1 +\frac{V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] }{\delta \left[ {U-V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] } \right] } \end{aligned}$$

(11)

and

$$\begin{aligned}&U\left[ {\frac{\left( {T-t_1 } \right) \left( {\delta t_1 -1} \right) }{1+\delta \left( {T-t_1 } \right) }+\frac{\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] }{\delta }} \right] \nonumber \\&\quad -\,V\left[ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_1 } \right] -\frac{k}{D}=0 \end{aligned}$$

(12)

respectively. Substituting Eq. (11) in (12) we have

$$\begin{aligned}&\left( {\frac{1-\delta t_1 }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] +\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta t_1 }-1} \right) }} \right] } \right) \nonumber \\&\quad -\,V\left[ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right] -\frac{k}{D}=0 \end{aligned}$$

(13)

Now we give the following results.

Theorem 1

(a) If

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {ln\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -\,V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}\le 0, \end{aligned}$$

then the solution of $\left( {t_1 ,T} \right)$ which satisfies Eqs. (11) and (12) not only exists but also is unique.

(b) If

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {ln\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -\,V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}>0, \end{aligned}$$

then the solution of $\left( {t_1 ,T} \right)$ which satisfies Eqs. (11) and (12) does not exist.

Proof of Part (a)

By assumptions and notations, we have $T>t_1$. Hence from Eq. (11), we get

$$\begin{aligned} \frac{V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] }{\delta \left[ {U-V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] } \right] }>0. \end{aligned}$$

Because the numerator part:

$$\begin{aligned} V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] =\left( {\frac{h+\left( {c-\gamma } \right) }{\theta }} \right) \left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] >0, \end{aligned}$$

thus, the denominator part: $\delta \left[ {U-V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] } \right] >0$, or equivalently, $\left[ {U-V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] } \right] >0,$ which implies $t_1 <t_d +\frac{1}{\theta }\ln \left[ {\frac{U+V}{V\left( {\theta t_d +1} \right) }} \right] \equiv t_1^b$.

From Eq. (13), we let

$$\begin{aligned} F\left( x \right)= & {} \left( {\frac{1-\delta x}{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {x-t_d } \right) }-1} \right] +\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta x}-1} \right) }} \right] } \right) \nonumber \\&-V\left[ {e^{\theta \left( {x-t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-x} \right] -\frac{k}{D},x\ge t_d \end{aligned}$$

(14)

Taking the first order derivative of $F\left( x \right)$ with respect to $x\in \left[ {t_d ,t_1^b } \right)$, we have $\frac{dF\left( x \right) }{dx}>0$. Thus, $F\left( x \right)$ is a strictly increasing function with respect to x in the interval $[t_d ,t_1^b )$. Furthermore, by using assumption, we have,

$$\begin{aligned} F\left( {t_d } \right)= & {} \left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&-V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}\le 0 \end{aligned}$$

and it can be shown that $\mathop {\lim }\nolimits _{x\rightarrow t_1^b -} F\left( x \right) =+\infty$. Therefore, by using intermediate value theorem, there exists a unique $t_1^{*}\in [t_d ,t_1^b )$ such that $F\left( {t_1^{*}} \right) =0$, which implies $t_1 ^{*}$ is the unique solution of Eq. (14). Once we obtain the value $t_1^{*},$ the value of T(denoted by $T^{*})$ can be found using Eq. (11) and is given by

$$\begin{aligned} T^{*}=t_1^{*}+\frac{V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] }{\delta \left[ {U-V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] } \right] }. \end{aligned}$$

Proof of Part (b)

If

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}>0, \end{aligned}$$

then from Eq. (14) we have, $F\left( {t_d } \right) >0$. Since $F\left( x \right)$ is a strictly increasing function of $x\in \left[ {t_d ,t_1^b } \right)$, which implies $F\left( x \right) >0$ for all $x\in \left[ {t_d ,t_1^b } \right)$. Thus we cannot find a value $t_1 \in \left[ {t_d ,t_1^b } \right)$ such that $F\left( {t_1} \right) =0$.

Theorem 2

(a) If

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {ln\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}\le 0, \end{aligned}$$

then the total cost $TC\left( {t_1 ,T} \right)$ is convex and reaches its global minimum at the point $(t_1^{*},T^{*})$, where $(t_1^{*},T^{*})$ is the point which satisfies the Eqs. (11) and (12).

(b) If

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {ln\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}>0, \end{aligned}$$

then the total cost $TC\left( {t_1 ,T} \right)$ has a minimum value at the point $(t_1^{*},T^{*}),$ where $t_1^{*}=t_d$ and

$$\begin{aligned} T^{*}=t_d +\frac{t_d \left[ {h+\left( {c-\gamma } \right) \theta } \right] }{\left( {s+\pi \delta } \right) -\delta t_d \left[ {h+\left( {c-\gamma } \right) \theta } \right] }. \end{aligned}$$

Proof of Part (a)

Taking the second derivative of $TC\left( {t_1 ,T} \right)$ with respect to $t_1$ and T, and then finding the values of these functions at point $(t_1^{*},T^{*})$, we obtain

$$\begin{aligned} \left. {\frac{\partial ^{2}TC\left( {t_1 ,T} \right) }{\partial t_1 ^{2}}} \right| _{(t_1^{*},T^{*})}= & {} \frac{D}{T^{*}}\left\{ {\theta V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 ^{*}-t_d } \right) }} \right] +\frac{s+\pi \delta }{\left[ {1+\delta \left( {T^{*}-t_1^{*}} \right) } \right] ^{2}}} \right\} >0,\nonumber \\ \left. {\frac{\partial ^{2}TC\left( {t_1 ,T} \right) }{\partial T^{2}}} \right| _{(t_1^{*},T^{*})}= & {} \frac{D}{T^{*}}\left\{ {\frac{s+\pi \delta }{\left[ {1+\delta \left( {T^{*}-t_1^{*}} \right) } \right] ^{2}}} \right\} >0\nonumber \\ \left. {\frac{\partial ^{2}TC\left( {t_1 ,T} \right) }{\partial t_1 \partial T}} \right| _{(t_1^{*},T^{*})}= & {} \frac{D}{T^{*}}\left\{ {\frac{s+\pi \delta }{\left[ {1+\delta \left( {T^{*}-t_1^{*}} \right) } \right] ^{2}}} \right\} \end{aligned}$$

(15)

and

$$\begin{aligned}&\left. {\frac{\partial ^{2}TC\left( {t_1 ,T} \right) }{\partial t_1 ^{2}}} \right| _{(t_1^{*},T^{*})} \left. {\frac{\partial ^{2}TC\left( {t_1 ,T} \right) }{\partial T^{2}}} \right| _{(t_1 ^{*},T^{*})} -\left[ {\left. {\frac{\partial ^{2}TC\left( {t_1 ,T} \right) }{\partial t_1 \partial T}} \right| _{(t_1 ^{*},T^{*})}} \right] ^{2}\nonumber \\&\quad =\left( {\frac{D}{T^{*}}} \right) ^{2}\left\{ {\theta V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1^{*}-t_d } \right) }} \right] +\frac{s+\pi \delta }{\left[ {1+\delta \left( {T^{*}-t_1^{*}} \right) } \right] ^{2}}} \right\} >0. \end{aligned}$$

(16)

From Eqs. (15), (16) and Theorem 1, we can see easily that $(t_1^{*},T^{*})$ is the global minimum point of $TC\left( {t_1 ,T} \right)$.

Proof of Part (b)

If

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}>0, \end{aligned}$$

then we know that $F\left( x \right) >0$ for all $x\in \left[ {t_d ,t_1^b } \right)$. Thus,

$$\begin{aligned} \frac{\partial TC\left( {t_1 ,T} \right) }{\partial T}\!= & {} \!\frac{D}{T^{2}}\left\{ \left( {\frac{1-\delta x}{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {x-t_d } \right) }-1} \right] \!+\!\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta x}-1} \right) }} \right] } \right) \right. \\&\left. -V\left[ {e^{\theta \left( {x-t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-x} \right] -\frac{k}{D} \right\} \\= & {} \frac{DF\left( {t_1 } \right) }{T^{2}}>0,\forall t_1 \in \left[ {t_d ,t_1^b } \right) \end{aligned}$$

which implies $TC\left( {t_1 ,T} \right)$ is a strictly increasing function of T. Thus, $TC\left( {t_1 ,T} \right)$ has a minimum value when T is minimum. On the other hand, from Eq. (11), we can see that T has a minimum value of

$$\begin{aligned} t_d +\frac{t_d \left[ {h+\left( {c-\gamma } \right) \theta } \right] }{\left( {s+\pi \delta } \right) -\delta t_d \left[ {h+\left( {c-\gamma } \right) \theta } \right] } \end{aligned}$$

as $t_1 =t_d$. Therefore, $TC\left( {t_1 ,T} \right)$ has a minimum value at the point $(t_1^{*},T^{*})$, where $t_1^{*}=t_d$ and

$$\begin{aligned} T^{*}=t_d +\frac{t_d \left[ {h+\left( {c-\gamma } \right) \theta } \right] }{\left( {s+\pi \delta } \right) -\delta t_d \left[ {h+\left( {c-\gamma } \right) \theta } \right] }. \end{aligned}$$

This completes the proof. $\square$

The optimal order quantity $Q\left( {\hbox {which is denoted by} \,Q^{*}} \right)$ and the total annual inventory cost function $TC^{*}\left( {t_1^*,T^{*}} \right)$ can be obtained from

$$\begin{aligned} Q^{*}= & {} Dt_d +\frac{D}{\theta }\left[ {e^{\theta \left( {(t_1 ^{*}-t_d } \right) }-1} \right] +\frac{D}{\delta }\left[ {\ln \left[ {1+\delta \left( {T^{*}-t_1^{*}} \right) } \right] } \right] \\ TC\left( {t_1^*,T^{*}} \right)= & {} \frac{D}{T}\left\{ \frac{k}{D}+\left( {\frac{h+\left( {c-\gamma } \right) \theta }{\theta }} \right) \left[ {e^{\theta \left( {t_1^*-t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1^*} \right] \right. \\&\left. +\left( {\frac{s+\pi \delta }{\delta }} \right) \left[ {\left( {T^{*}-t_1^*} \right) -\frac{\ln \left[ {1+\delta \left( {T^{*}-t_1^*} \right) } \right] }{\delta }} \right] \right\} \end{aligned}$$

where $(t_1^{*},T^{*})$ denotes the optimal values of $t_1$ and $\,T$. The convexity of the total annual inventory cost function $TC\left( {t_1^*,T^{*}} \right)$ can be established graphically (see Appendix 2).

Computational Algorithm to Find the Optimal Values

To find the optimal length of the inventory interval with positive inventory $t_1^*$ and the optimal length of order cycle $T^{*}$, we follow the decision policy shown in the flowchart representation (Fig. 2) using the summarized above results.

Let

$$\begin{aligned} \Delta= & {} \left( {\frac{1-\delta t_1 }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) e^{\theta \left( {t_1 -t_d } \right) }-1} \right] +\frac{U}{\delta }\left( {\hbox {ln}\left[ {\frac{U}{U-V\left( {e^{\theta t_1 }-1} \right) }} \right] } \right) \\&-V\left[ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right] -\frac{k}{D} \end{aligned}$$

Fig. 2

Flowchart representation of optimal decision policy

Numerical Examples

In this section we find the optimal solutions to illustrate the solution procedure with the following numerical examples.

Example 1

Consider an inventory system with the following data:

$k=650, h=0.5,c=1.5, \gamma =0.08, t_d=0.0833, s=6, \delta =0.1, \pi =1.5, \theta =0.1, A_C=150, \eta =0.4, a= 40,000, b=2.5, p=20$ in appropriate units. We first check the condition

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\ln \left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}=-2.8520<0 \end{aligned}$$

Thus, the optimal length of the inventory interval with positive inventory $t_1^*$ and the optimal length of order cycle $T^{*}$ can be obtained by solving Eqs. (11) and (12), and are given by $t_1^*= 0.3616$ and $T^{*} = 0.7205$. Hence, the optimal order quantity per cycle is $Q^{*} = 119.15$ and the minimum total cost per unit time is $TC^{*}\left( {t_1^*,T^{*}} \right) = 1001.02$.

Example 2

Let us consider another inventory system with the following data: $k=650, h=0.5, c=0.75, \gamma =0.1, t_d=0.0833, s=8, \delta = 0.1, \pi =2, \theta =0.1, A_C=150, \eta =0.4, a=40,000, b=2.5, p=20$ in appropriate units. Similarly, we first check the condition

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\ln \left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}=-2.9798<0 \end{aligned}$$

Thus, the optimal length of the inventory interval with positive inventory $t_1^*$ and the optimal length of order cycle $T^{*}$ can be obtained by solving Eqs. (11) and (12), and are given by $t_1^*= 0.4369$ and $T^{*} = 0.7466$. Hence, the optimal order quantity per cycle is $Q^{*} = 124.16$ and the minimum total cost per unit time is $TC^{*}\left( {t_1^*,T^{*}} \right) = 968.31$.

Example 3

We consider another inventory system with the following data:

$k=850, h=3, c=2.5, \gamma =0.08, t_d=0.1522, s=0.5, \delta =0.086, \pi =2, \theta =0.2, A_C=150, \eta =0.4, a=40000, b=2.5, p=20$ in appropriate units. Here we check the condition

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\ln \left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}=7.6604>0 \end{aligned}$$

Thus, from Theorem 2(b), the optimal length of the inventory interval with positive inventory $t_1^*=t_d = 0.1522$ and the optimal length of the order cycle is $T^{*} = 1.0197$. Hence, the optimal order quantity per cycle is $Q^{*} = 164.10$ and the minimum total cost per unit time is $TC^{*}\left( {t_1^*,T^{*}} \right) = 879.38$.

Example 4

Let us take the data as $k = 900, h = 1.5, c = 0.4, \gamma = 0.09, t_d = 0.2586, s = 0.4, \delta = 0.092, \pi = 2, \theta = 0.2, A_C = 150, \eta = 0.4, a = 40,000, b = 2.5, p = 20$ in appropriate units. Here we check the condition

$$\begin{aligned}&\left( {\frac{1-\delta t_d }{\delta }} \right) V\left[ {\left( {\theta t_d +1} \right) -1} \right] +\frac{U}{\delta }\left( {\ln \left[ {\frac{U}{U-V\left( {e^{\theta t_d }-1} \right) }} \right] } \right) \\&\quad -V\left[ {\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_d } \right] -\frac{k}{D}=3.4699>0 \end{aligned}$$

Thus, from Theorem 2(b), the optimal length of the inventory interval with positive inventory $t_1^*=t_d = 0. 2586$ and the optimal length of the order cycle is $T^{*} = 0.9973$. Hence, the optimal order quantity per cycle is $Q^{*} = 161.49$ and the minimum total cost per unit time is $TC^{*}\left( {t_1^*,T^{*}} \right) = 936.51$.

Sensitivity Analysis

In this section, we study the effect of changes in the major parameters of the system on the optimal length of inventory interval with positive inventory $t_1^*$, the optimal length of order cycle $T^{*}$, the optimal order quantity per cycle $Q^{*}$, and the minimum total cost $TC^{*}\left( {t_1^*,T^{*}} \right)$ on the optimal replenishment policy of the Example 1. We change one parameter at a time keeping the other parameters unchanged. The sensitivity analyses are performed and the results are summarized in Tables 1 and 2.

Table 1 Effect of change in various parameters of the inventory model

Table 2 Computational results for various values of the demand $D\left( {A_C ,p} \right)$

It is important to discuss the influence of key model parameters on the optimal solutions. The effects of changing the parameters are shown graphically in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. Based on these, we have the following inferences.

• 1. When the rate of ordering cost k increases, there is an increase in the optimal order quantity $Q^{*}$ and decrease in the total cost $TC^{*}$.

• 2. Increasing the rate of holding cost h, the optimal order quantity $Q^{*}$ decreases and the total cost $TC^{*}$ increases.

• 3. There is a negative change in the optimal order quantity $Q^{*}$ and a positive change in the total cost $TC^{*}$, when the purchasing cost c increases.

• 4. When the rate of salvage value $\gamma$ increases, the optimal order quantity $Q^{*}$ increases and the total cost $TC^{*}$ decreases.

• 5. Increasing the fresh-product time $t_d$, decrease the optimal order quantity $Q^{*}$ and increases the total cost $TC^{*}$.

• 6. Changes in the shortage cost s result in a negative change in the optimal order quantity $Q^{*}$ and a positive change in the total cost $TC^{*}$.

• 7. Increasing the backlogging parameter $\delta$ increases, the optimal order quantity $Q^{*}$ and the cycle length while there is a decrease in the total cost $TC^{*}$.

• 8. When the deterioration rate $\theta$ increases, the optimal order quantity $Q^{*}$ decreases and the total cost $TC^{*}$increases.

• 9. When the advertisement cost $A_C$ increases, there is a decrease in the optimal order quantity $Q^{*}$ and increase in the total cost $TC^{*}$.

Fig. 3

Effect of change in h on the optimal solution

Fig. 4

Effect of change in k on the optimal solution

Fig. 5

Effect of change in c on the optimal solution

Fig. 6

Effect of change in $\gamma$ on the optimal solution

Fig. 7

Effect of change in $t_d$ on the optimal solution

Fig. 8

Effect of change in s on the optimal solution

Fig. 9

Effect of change in $\delta$ on the optimal solution

Fig. 10

Effect of change in $\theta$ on the optimal solution

Fig. 11

Effect of change in $A_c$ on the optimal solution

Fig. 12

Graphical representation of total cost with respect to changes in major parameters of the inventory system

Managerial Implications

In this section, we have discussed the managerial insights from the results obtained in the sensitivity analysis.

• (a) Figures 3 and 10 shows that, the optimal length of inventory interval with positive inventory $t_1^*$, the optimal length of order cycle $T^{*}$ and the optimal order quantity $Q^{*}$ per cycle decrease, while the minimum total cost $TC^{*}$ increases with increase in the value of the parameter h and $\theta$. This shows that from managerial point of view, it is reasonable that when the holding cost increases, the retailer will shorten the cycle time. If the retailer can effectively reduce the deteriorating rate of the item by improving equipment of storehouse, the total cost will be lowered.

• (b) In Fig. 9, if the backlogging parameter $\delta$ is increased then the total cost $TC^{*}$ will be decreased and the optimal order quantity $Q^{*}$ increases. That is, in order to minimize the cost, the retailer should increase the backlogging parameter.

• (c) From Fig. 4, we infer that when the ordering cost k increases, the optimal replenishment cycle time $T^{*}$ significantly increases and the total cost $TC^{*}$ decreases. From the managerial view point, if the ordering cost is higher, it is reasonable that the retailer lengths the cycle time to reduce the frequency of replenishment and can marginally increases the selling price.

• (d) Increasing the salvage value parameter $\gamma$ decreases the total cost $TC^{*}$ of the inventory system. When the salvage value is incorporated into the deteriorating items, the total inventory cost can be effectively minimized. The results obtained are shown in Fig. 6.

• (e) When the length of fresh product time is decreasing, the total cost $TC^{*}$ decreases. Since the order quantity $Q^{*}$ is reduced, automatically the holding cost of the items will also be reduced. So, the retailer will attain minimum total cost. Figure 7 shows the variation of the parameter $t_d$ in the inventory system. Furthermore, if the retailer manages the non-instantaneous deteriorating items instead of instantaneous deteriorating items then their total cost will be lowered.

• (f) From Table 2, it shows that when the selling price p increases, there is a marginal increase in the total cost $TC^{*}$. The larger the value of p, the smaller value of the optimal cycle time $T^{*}$ and the optimal order quantity $Q^{*}$. That is, from managerial point of view, when the unit selling price is increasing, the retailer will order less quantity more frequently.

• (g) When the advertisement cost $A_C$ is increasing, the total cost $TC^{*}$ is highly increasing and the optimal order quantity $Q^{*}$ decreases. Figure 11 shows that the minimum advertisement cost will minimize the total cost of the retailer but more advertisement cost implies more demand as well as less ordering quantity.

• (h) With increase in the value of the parameter $a,b,\eta$, from Table 2 we find that, there is an increase in the total cost $TC^{*}$ and decrease in the optimal order quantity $Q^{*}$ and the optimal length of the replenishment cycle $T^{*}$. Moreover, for non-instantaneous deteriorating items, the longer the length of no-deterioration time is, the lower selling price, while the higher order quantity per replenishment cycle time minimize the total cost.

Special Cases

The important special cases that influence the optimal value of total cost are described as follows:

• If we take $t_d =0$ and $\delta =0$, our model reduces to the EOQ model for instantaneous deteriorating items without any shortages, which becomes the model of Jaggi and Aggarwal [7].

• If we let $\gamma =0, t_d =0$ and $\delta =0$, then our model reduces to the EOQ model for instantaneous deteriorating items and complete backlogging. Hence, the derived model reduces to that of Ghare and Schrader [1].

• Also if $\delta = 0$ in the proposed model, i.e., $B\left( t \right) = 1$, we obtain the EOQ model for non-instantaneous deteriorating items with completely backlogging.

• When $\delta \rightarrow \infty$, we have $T\approx t_1$ from Eq. (11). Thus, the model becomes the case without shortages.

Conclusion

Based on present real-life situations, it is a common belief that a product is promoted through advertisement to raise the demand from the customers. In this view, we have discussed a realistic inventory model for non-instantaneous deteriorating items with price and advertisement dependent nature of demand. In our study, we have incorporated several realistic features. First, allowing shortages and time proportional backlogging rate, where the backlogging rate is considered to be a decreasing function of the waiting time for the next replenishment is a natural phenomenon. Secondly, incorporating salvage value with the deteriorated units will lead to minimization of the total cost. Thirdly, demand is considered as a function of advertisement cost which is an influential factor when determining the optimal replenishment policy. The necessary and sufficient condition for the existence and uniqueness of the optimal solutions has been derived for the system. Useful theoretical results derived will help the retailer to determine the optimal replenishment policy under various decision-making situations. Furthermore, the model proposed here is a general framework that includes numerous previous models [1, 7, 8] as special cases. Finally, we provide several numerical examples to illustrate the results obtained with some managerial insights. The outcome shows that the retailer can reduce the total inventory cost by ordering lower order quantity, raising the length of time in which the product has no deterioration or improving storage conditions for non-instantaneous deteriorating items and increasing the backlogging rate.

Appendices

Appendix 1

Total Cost Calculations

The total cost of the inventory system per unit time is composed of the following costs:

• (a) the ordering cost per order $=\frac{k}{T}$

• (b) the inventory holding cost per unit time

  $$\begin{aligned}= & {} \frac{h}{T}\left\{ {\mathop \int \nolimits _0^{t_d } I_1 \left( t \right) dt+\mathop \int \nolimits _{t_d }^{t_1 } I_2 \left( t \right) dt} \right\} \\= & {} \frac{Dh}{T\theta }\left\{ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right\} \end{aligned}$$

• (c) the cost due to deterioration per unit time

  $$\begin{aligned} =\frac{c\theta }{T}\mathop \int \nolimits _{t_d }^{t_1 } I_2 \left( t \right) dt=\frac{cD}{T}\left\{ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right\} \end{aligned}$$

• (d) the shortage cost due to backlogging

  $$\begin{aligned} =\frac{s}{T}\mathop \int \nolimits _{t_1 }^T -I_3 \left( t \right) dt=\frac{sD}{\delta T}\left\{ {\left( {T-t_1 } \right) -\frac{\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] }{\delta }} \right\} \end{aligned}$$

• (e) the opportunity cost due to lost sales

  $$\begin{aligned} =\frac{\pi }{T}\mathop \int \nolimits _{t_1 }^T D\left[ {1-B\left( {T-t} \right) } \right] dt=\frac{\pi D}{T}\left\{ {\left( {T-t_1 } \right) -\frac{\ln \left[ {1+\delta \left( {T-t_1 } \right) } \right] }{\delta }} \right\} \end{aligned}$$

• (f) the salvage value of deteriorated items per unit time

  $$\begin{aligned} =\frac{\gamma D}{T}\left\{ {e^{\theta \left( {t_1 -t_d } \right) }\left( {t_d +\frac{1}{\theta }} \right) +\frac{\theta t_d ^{2}}{2}-\frac{1}{\theta }-t_1 } \right\} \end{aligned}$$

Appendix 2

We can show graphically that, the total cost ${\mathbf {TC}}^{*} \left( {\mathbf {t}}_{1}^{*} ,{\mathbf {T}}^{*} \right)$ is convex. The values given in the example 1 are plotted and the three dimensional graph obtained is given below.

See Fig. 13.

Fig. 13

Graphical representation of the total cost for Example 1