A fuzzy bi-objective MILP approach to integrate sales, production, distribution and procurement planning in a FMCG supply chain

Abstract

Sales and operations are the heart of today’s businesses, and the decisions made in these areas will intensively affect the financial performance, operational efficiency and service level of the whole organization. This manuscript is going to develop three multiobjective fuzzy mixed integer linear programming models of sales and operations planning process. Then, the performance of the fully integrated fuzzy model is compared to the similar crisp model, in terms of total supply chain’s cost and customer service level. All the models are developed for a multisite manufacturing company, which is coping with different raw material suppliers and third-party logistics, distribution centers and customers with a wide range of product families. Finally, the models are applied to a real case in a FMCG manufacturing company in Iran. The final results approve the superiority of the fuzzy model over the crisp one. Furthermore, a sensitivity analysis is carried out to analyze the effect of some key factors on the benefits of the SC planning integration.

1 Introduction

Facing with competitive markets in extremely dynamic economic environment, companies are forced to promote their manufacturing systems by more efficient and effective planning and concentrating on their supply chains. Supply chain is about gathering around traditionally disconnected divisions from the whole business, in order to orchestrate the processes and activities in a more efficient way (Alavidoost et al. 2015a). Under supply chain management (SCM) and supply chain planning (SCP) paradigms as umbrella, S&OP is spreading worldwide as a supply chain planning integration concept. S&OP is a monthly planning process at tactical level which is leaded by the company’s top management, and its function is to balance demand and supply in order to maximize production, distribution and procurement utilization and analyze their financial impacts, so that the top manager ensures the alignment and coordination of the functional divisions with enterprise’s global strategy. In fact, S&OP is a mid-term planning process that evaluates and integrates the operational plans from all functional divisions to present the output as set of compatible plans to coordinate, balance and control the performance of the total chain (Ling 2002).

Sales and operations are the heart of today’s businesses, and the decisions made in these areas will intensively affect the financial performance, operational efficiency and service level of the whole organization (Nemati et al. 2017b). In broader scope, supply chain includes four essential functions: sales, distribution, production and procurement (Fleischmann et al. 2015). Traditionally, these steps are coupled with each other by “stocks.” Discrete governance environment implies that the decisions being made independently in each functional division. Although this approach may reduce the amount of complexity, it ignores the inter-dependencies among functional areas and eliminates the cost reduction opportunities and in worth case, and it can lead to inapplicable decisions.

Since 1980, the concept of S&OP expanded and sales planning attached to operations planning part. Thus, S&OP consists of two distinct pieces: production planning, where issues such as inventory and capacity needs as well as back-order levels have been considered and demand-based sales planning (Olhager et al. 2001; Wallace 2004). This concept of S&OP is still being used by a lot of authors and researchers. The relationship between operations and sales functional areas and the role and importance of each one is pointed by Wahlers and Cox (1994). They propose that the collaboration between these two functions can be considered as an important competitive criterion for further improvements in organization’s total performance.

Until today, the researches around S&OP were mainly focused on its definitions, processes, activities, implementation procedures and practical case studies, and very few works have investigated the benefits of implementing S&OP from mathematical modeling point of view. Considering the difficulties that fast moving consumer good (FMCG) manufacturing companies deal with in traditional planning and decision-making process, and taking into account the many opportunities that integrated supply chain planning would bring for such companies, we are persuaded enough to fill this gap through presenting a mathematical modeling approach to quantitatively evaluate and compare the benefits of fully integrated S&OP process with no and less integrated planning approaches. Hence, three different planning approaches will be considered in this article in order to compare the past, present and future situation of the studied company from SCP point of view: FI-S&OP, PI-S&OP and DP approaches. Also, the advantages of the fuzzy models over the similar crisp one are going to be investigated through comparing the outputs and a solid sensitivity analysis.

This paper proceeds as follows: we start Sect. 2 with a literature review, where the fundamentals of S&OP are presented along with current trends review. In Sect. 3, three fuzzy multiobjective models will be developed representing the FI-S&OP, PI-S&OP and DP approaches, in the context of a multisite FMCG network. Furthermore, the crisp model for the FI-S&OP model is going to be developed for the purpose of the comparison. The implementation of the mentioned models in a real industrial condition in a dairy company will be presented in section along with the numerical results and sensitivity analysis of the models. Finally, the conclusions followed by future research opportunities will be available in Sect. 6.

2 Literature review

Reviewing the recent studies indicates an increasing trend in utilizing S&OP in supply chain coordination and value creation. These studies look at S&OP as a coordination and synchronization mechanism that adopts customer demand with supply capabilities through confronting it to marketing, production, procurement, logistic and financial activities and decisions. This idea developed by Cecere et al. (2006) proposes that S&OP must synchronize customer demand with supply capacity, aligned with the business strategy in a profitable way. The plans should reflect all the constraints including distribution, production, warehousing and purchasing, while linking these constraints with demand and supply management strategies (in an aggressive or reactive way).

In spite of rapid development of S&OP concept in recent years, there are little studies that systematically address the S&OP functionality in the form of mathematical modeling through pre-implementation analysis. Until today, the expanded models of S&OP were mostly APP-based models that determine the amount to be produced, inventory and back-order levels and the needed amount of manpower based on forecast, in order to minimize the minimum production cost (Feng et al. 2013; Olhager et al. 2001).

Although the concepts of SCP and S&OP are relatively new, the idea of coordinated planning can be traced back to as early as 1960 by Clark and Scarf (1960), who studied multiechelon inventory—distribution systems. Since that time, research on coordination of various partial sections of the supply chain has been conducted.

Williams (1983) studied the coordinated scheduling of production and distribution using a dynamic programming approach, which simultaneously determined the production and distribution batch sizes that minimize the costs in an assembly and distribution network. Chandra and Fisher (1994) measured the added value of integrated distribution routing with production scheduling to reduce the distribution cost, production setup cost and inventory holding cost. Youssef and Mahmoud (1996) proposed a nonlinear programming model to measure production economies of scale from establishing balance between production and distribution costs and investigated the effects on centralization and decentralization decisions. Fumero and Vercellis (1999) presented an integrated production–distribution planning model to optimize capacity, in a multiperiod truck routing problem. The feasible solution was compared to the decoupled planning approach solution. The results revealed undeniable advantages of integration over decoupled planning approach. Dhaenens-Flipo (2000) presented a production distribution planning case in a can manufacturing company, where the production sites were geographically dispersed from each other and each site had different unrelated production lines. The proposed hierarchical approach broke the main problem apart into multiple sub-problems and enabled the total production allocation and scheduling problem to perform coordinately.

Feng et al. (2013) dealt with an optimization model in order to maximize total supply chain profit to solve the S&OP problem in oriented strand board industry assuming deterministic demand in a make to order environment. The results indicated superior performance of integrated supply chain-based planning approach over the discrete planning one. Kopanos et al. (2011) have proposed a new mixed discrete/continuous MILP model to solve a resource-constrained production planning problem in semicontinuous multiproduct yoghurt production facility. Guan and Philpott (2011) have applied multistage stochastic programming to a production planning problem for a dairy company in New Zealand, under uncertain milk supply, price–demand curves and contracting conditions. Kopanos et al. (2012a) presented an efficient mixed integer programming (MIP) continuous-time model, in order to address the simultaneous optimization of all processing stages to facilitate the interaction among the different departments of a food production facility. Kopanos et al. (2012b) developed a discrete-/continuous-time mixed integer programming model, based on the product families, and tested the efficiency of the model by solving two industrial-size case studies, for an emerging real-life Greek dairy industry. Bilgen and Çelebi (2013) addressed the production scheduling and distribution planning problem in a yoghurt production line of the multiproduct dairy plants. The MILP objective function was trying to maximize the benefit by considering the shelf life-dependent pricing component and costs such as processing, setup, storage, overtime, backlogging and transportation costs. Pauls-Worm et al. (2014) have studied the practical production planning problem of a food producer with perishable products. They have generated a MILP model to generate approximate solutions. Baumann and Trautmann (2014) have presented a novel hybrid method for the short-term scheduling of FMCG production processes. They have presented strategies for integrating MILP models into the construction and improvement phases of the hybrid method to efficiently solve the scheduling. Sel and Bilgen (2015) provided a critical review on quantitative supply chain models within the dairy industry, considering solution approaches, problem and model characteristics and decision levels. Pant et al. (2015) have studied three prevalent types of dairy supply chains in India and presented a framework for transparency, traceability and information flow for management of dairy supply chain networks. Bilgen and Dogan (2015) addressed a production planning problem in a multistage production system consisting of continuous processing resources separated by finite-capacity storage tanks, stimulated by a particular case study in the dairy industry. Sel et al. (2015) have studied an integrated planning and scheduling problem of set yoghurt production. They have proposed a MILP formulation to integrate tactical and operational decisions, and also a heuristic approach is proposed to solve the problem. Wari and Zhu (2016) have presented a multiweek MILP scheduling model for an ice cream processing facility. Kır and Yazgan (2016) have studied on a scheduling problem of a single machine producing dairy products. They have proposed an integrated algorithm (by integration of tabu search and genetic algorithm) to solve the problem. Touil et al. (2016) have developed a mixed integer linear programming (MILP) model for a production scheduling problems in a multistage, multiproduct milk processing facility. Nemati et al. (2017a) investigated the benefits of S&OP by proposing three MIP models by three levels of planning integration of sales, production, distribution and procurement for a multisite manufacturing company. The models were solved through CPLEX 12 optimizer in GAMS software. The results demonstrate the superiority of fully integrated model over less integrated approaches.

Although many studies have been conducted around coordination of different functional areas in supply chain, very few studies have been dedicated to address the integration of sales, production, distribution and procurement planning simultaneously and most of the studies are focused on some selected functions (mostly production and distribution) at planning and scheduling levels. Besides, to our best knowledge, no research exists on modeling fully integrated S&OP in fuzzy environment, so far.

Reviewing the upcoming literature, our study is going to formulate a multiobjective model of the “fully integrated sales and operations planning process” to quantitatively evaluate the added value of fuzzy mathematical programming over the crisp approaches in a manufacturing supply chain. After that, the models will be challenged through a real case study in FMCG industry in Iran. In the next step, a sensitivity analysis will take place, in order to evaluate the benefits of the fuzzy model over the crisp one.

3 Model development

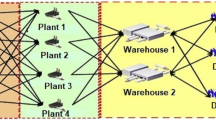
As mentioned, building on the previous studies, we intent to propose a modeling approach to measure the added value of implementing S&OP. Inspired by the supply chain planning matrix proposed by Fleischmann et al. (2015), and based on the analysis of fundamental elements of S&OP, the whole process of S&OP is depicted in Fig. 1. This framework can be expanded to a multisite model. In this study, three multisite S&OP models can be presented, to reflect the effort through integrated cooperation and accommodation of sales, production, distribution and procurement planning in an organization, seeking to optimize total chain’s performance. The centralized FI-S&OP model will propose a specific plan for each manufacturing site. According to the specified plans, each site can prepare its operation scheduling as well.

Fig. 1

The fully integrated S&OP in supply chain planning context

To formulate the model, we consider the FMCG industry, where the products’ consumption period is mostly limited with a predefined shelf life. The target company has three alternative factories in different geographical locations. This company has two different sales organizations. One of them is responsible for domestic sales, and the other one is responsible for the export markets. The unsatisfied demand may be considered as backlog in future period. When there is surplus capacity, the noncontract demand is absorbed by the excess capacity. Both the contractual and noncontractual demands follow seasonality.

Production orders are passed to each factory which has a finite specified capacity for each product family. Production is carried out in batch, based on a bill of material (BOM) and routing, each product family contains specific raw materials with different amounts, while the major components for most of the products are milk and cream. Most of the product families have their specific production lines, while a few ones use common production lines; thus, there would be a change over time (setup time) for changing the line to produce another product family. The setup time and naturally setup cost are different for each production line. Each production family consists of numerous products. Production is based on MTS procedure, and the warehousing capacity is limited in each site.

Finished products distribution is carried out by two shipping suppliers as 3PL by trucks. Finished products are delivered to customers (which are all wholesalers) straightly from the factory or through the DCs. The company has owned 16 DCs in different geographical locations with different capacities.

About 11 different product families are being produced in this company through, including yoghurt, cream cheese, processed cheese, pizza cheese, natural cheese, dough (a kind of local drink), dessert, butter, milk, cream and curd.

In procurement, raw materials are being supplied by two major suppliers. These two suppliers are dealing with many small or big second-hand suppliers, preferring long-term contracts with them. The procurement lead time will vary depending on the origination of the resources (domestic or importation) and supplier capacity, from 3 days to 6 months. Based on the strategic importance of the raw materials, factory keeps a defined amount of safety stock to cover variations in supply amount and lead time.

3.1 Model components introduction

Based on the above explanations, indices, sets, parameters and decision variables of the models are as below:

Indexes and Sets:
$f\in F$	Set of factories
$i\in I$	Set of product families
$t\in T$	Set of time periods
$b\in T$	Set of times of batch production
$c\in C$	Set of customers
$s\in S$	Set of raw material suppliers
$m\in M$	Set of raw materials
$j\in J$	Set of raw material categories $( {m\in j})$
$o\in O$	Set of outbound shipping suppliers
$d\in D$	Set of distribution centers
$v\in V$	Set of vehicle types
$r\in R_{fd}$	Set of routes from factory f to DC d
$r\in R_{fc}$	Set of routes from factory f to customerc
$r\in R_{dc}$	Set of routes from DC d to customer c
$r\in R$	Set of all routes, $R=R_{f,d} \cup R_{f,c} \cup R_{d,c}$
Parameters:
Sales:
$d_{ict}$	Demand for product family i from customer $c( {c\in C} )$ in period t
$dmin_{ict}$	Minimum demand quantity of product family i from customer $c ( {c\in C} )$ in period t
Production:
$pCap_{ift}$	Production capacity for product family i at factory f in period t
$epCap_{ift}$	Estimated production capacity for product family i at factory f in period t

$\alpha _{ift}$	Capacity consumption for producing one batch of product family i at factory f in period t
$\beta _{ift}$	Production batch size of product family i at factory f at period t
${\widetilde{pC}}_{ift}$	Unit production cost to produce product family i at factory f in period t
${\widetilde{sC}}_{ift}^1$	Expected setup cost for product family i at factory f in period t
$st_{ift}$	Expected setup time for product family i at factory f in period t
${\widetilde{hC}}_{ift}^1$	Inventory holding cost for unit quantity of product family i at factory f in period t
${\widetilde{boC}}_{ift}$	Backlog cost for unit quantity of product family i at factory f in period t
$I_{if0}^-$	Initial backlog quantity of product family i at factory f in period $t=0$
$hCap_f^1$	Finished goods warehouse inventory capacity at factory f
G	Big number
Distribution:
${\widetilde{tfC}}_{rov}$	Shipping fixed cost on route r of supplier $o ( {o\in O} )$ using vehicle type v
${\widetilde{tvC}}_{irov}$	Shipping variable cost for product family i on route r of supplier $o ( {o\in O})$ using vehicle type v
$a_{iv}$	Vehicle capacity absorption coefficient per unit of product family i
${\widetilde{hC}}_{id}^2$	Inventory holding cost for unit quantity of product family i at DC d
$hCap_d^2$	Inventory holding capacity of DC d
${\widetilde{trC}}_{id}$	Transshipment cost of unit quantity of product family i through DC d
$trCap_{otv}$	Shipping capacity of supplier $o({o\in O} )$ in period t with vehicle v
$vCap_v$	Vehicle capacity of vehicle type v
$KCap_{fv}$	Expedition capacity of factory f for vehicle category v
Procurement:
$u_{mif}$	Consumption of raw material m for producing unit quantity of product family i at factory f
$mCap_{jf}$	Inventory capacity of raw material category j at factory f
$sCap_{st}$	Supply capacity of supplier $s({s\in S} )$ in period t
$Qmin_{ms}$	Minimum purchase quantity for raw material m from supplier $s ( {s\in CS} )$
$SS_{mf}$	Safety stock of raw material m at factory f
${\widetilde{purC}}_{mst}$	Unit purchase cost of raw material m from supplier $s ( {s\in S} )$ in period t
${\widetilde{sC}}_{mst}^2$	Setup cost of purchasing raw material m from supplier $s ( {s\in S} )$ in period t
${\widetilde{hC}}_{mf}^3$	Unit inventory holding cost of raw material m at factory f
$L_{ms}$	Lead time of procuring raw material m from supplier $s ( {s\in S} )$
Decision Variables:
Sales:
$sQ_{ict}$	Sales quantity of product family i to customer $c ( {c\in C} )$ in period t
$bsQ_{ict}$	Backlogged sales quantity for product family i to customer $c ( {c\in C} )$ in period t
$K_{ict}$	Binary variable; 1, if demand is more than minimum demand size; 0, otherwise.

Production:
$pQ_{ift}$	Production quantity of product family i at factory f in period t
$pbN_{ift}$	Number of production batches of product family i at factory f in period t
$I_{iftb}^+$	Inventory quantity of product family i from batch production date b in factory f at the end of period t
$I_{ift}^-$	Backlog quantity of product family i in factory f at the end of period t
$X_{ift}$	Binary variable; 1, if setup is required to produce product family i at factory f in period t; 0, otherwise
Distribution:
$trQ_{irovt}$	Shipping quantity of product family i by supplier $o ( {o\in O} )$ on route r using vehicle v in period t
$tN_{rovt}$	Number of truckload requirements from supplier $o ( {o\in O} )$ on route r using vehicle v in period t
$I_{idtb}^1$	Inventory of product family i from batch production date b in DC d at the end of period t
Procurement:
$purQ_{msft}$	Purchasing quantity of raw material m from supplier $s ( {s\in S} )$ by factory f in period t
$I_{mft}$	Inventory of raw material m at factory f at the end of period t
$y_{mst}$	Binary variable; 1, if purchase is made for material m from supplier $s ( {s\in S} )$ in period t; 0, otherwise
Objective Functions:
${\widetilde{TC}}_{FI}$	Fuzzy total SC cost of fully integrated supply chain
${\widetilde{TC}}_{PI}$	Fuzzy total SC cost of partially integrated supply chain
${\widetilde{TC}}_{DP}$	Fuzzy total SC cost of decoupled supply chain
$TC_{FI}$	Crisp total SC cost of fully integrated supply chain
$CSL_{FI}$	Customer service level of fully integrated supply chain
$CSL_{PI}$	Customer service level of partially integrated supply chain
$CSL_{DP}$	Customer service level of decoupled supply chain

3.2 The fuzzy FI-S&OP model

Now we can present our multiobjective f-MILP S&OP model through the integration of sales, production, distribution and procurement planning at enterprise level. The aims are to minimize the total SC cost and to minimize the customer service level (CSL) of the entire company. The fuzzy model is formulated as below:

Objective Function:

$$\begin{aligned}&{\widetilde{TC}}_{FI}=\hbox {min}\left( \left\{ \sum \limits _{i\in I} \sum \limits _{f\in F} \sum \limits _{t\in T} \left( {\widetilde{pC}} _{ift}\cdot pQ_{ift}+{\widetilde{sC}}_{ift}^1 \cdot X_{ift} \right. \right. \right. \nonumber \\&\quad \left. \left. \left. +\,{\widetilde{hC}} _{ift}^1\cdot \sum \limits _{b=1}^t I_{ift}^+ +{\widetilde{boC}} _{ift} \cdot I_{ift}^-\right) \right\} \right. \nonumber \\&\quad +\left\{ \sum \limits _{i\in I}\sum \limits _{r\in R_{f,d} \cup R_{f,c} \cup R_{d,c} } \sum \limits _{o\in O} \sum \limits _{v\in V} \sum \limits _{t\in T} ({\widetilde{tvC}}_{irov} \cdot trQ_{irovt}\right. \nonumber \\&\quad +\,{\widetilde{tfC}}_{rov}\cdot tN_{rovt} )+\sum \limits _{i\in I} \sum \limits _{r\in R_{f,d} } \sum \limits _{o\in O} \sum \limits _{v\in V} \sum \limits _{t\in T}\nonumber \\&\times \left( {\widetilde{trC}_{ir} \cdot trQ_{irovt}}\right) \nonumber \\&\quad \left. +\sum \limits _{i\in I} \sum \limits _{d\in D} \sum \limits _{t\in T} \left( {\widetilde{hC} _{id}^2\cdot \sum \limits _{b=1}^t I_{idtb}^1 } \right) \right\} \nonumber \\&\quad +\left. \left\{ \sum \limits _{m\in M} \sum \limits _{s\in S} \sum \limits _{f\in F} \sum \limits _{t\in T} \left( {\widetilde{purC} _{mst}\cdot purQ_{msft} } \right) \right. \right. \nonumber \\&\quad \left. \left. +\sum \limits _{m\in M} \sum \limits _{s\in S} \sum \limits _{t\in T} \left( {\widetilde{sC} _{mst}^2 \cdot y_{mst} } \right) \right. \right. \nonumber \\&\quad \left. \left. +\sum \limits _{m\in M} \sum \limits _{f\in F} \sum \limits _{t\in T} \left( {\widetilde{hC} _{mf}^3 \cdot I_{mft} } \right) \right\} \right) \end{aligned}$$

(1)

$$\begin{aligned}&CSL_{FI} =\hbox {max} \left\{ {1-\left( {\frac{\sum _{i\in I} \sum _{c\in C} \sum _{t\in T} \left( {d_{ict} -sQ_{ict} } \right) }{\sum _{i\in I} \sum _{c\in C} \sum _{t\in T} d_{ict}}}\right) }\right\} \nonumber \\ \end{aligned}$$

(2)

Constraints:

Sales:

$$\begin{aligned} dmin_{ict}\le & {} d_{ict} +\left( {1-K_{ict} } \right) G\forall c\in C,i,t \end{aligned}$$

(3)

$$\begin{aligned} sQ_{ict}\le & {} d_{ict} {*}K_{ict} \forall c\in C,i,t \end{aligned}$$

(4)

$$\begin{aligned} sQ_{ict}\ge & {} dmin_{ict} {*}K_{ict} \forall c\in C,i,t \end{aligned}$$

(5)

Production:

$$\begin{aligned}&\sum \limits _{f\in F} \left( pQ_{ift} +\sum \limits _{b=t-shl_i }^{t-1} I_{ift-1,b}^+\right. \nonumber \\&\left. \quad -I_{ift-1}^- -\sum \limits _{b=t-shl_i }^t I_{iftb}^+ +I_{ift}^- \right) \nonumber \\&\quad +\sum \limits _{d\in D} \left( {\sum \limits _{b=t-shl_i }^{t-1} I_{idt-1,b}^1 -\sum \limits _{b=t-shl_i}^t I_{idtb}^1} \right) \nonumber \\&\quad =\sum \limits _{c\in C} sQ_{ict} \quad \forall i,t \end{aligned}$$

(6)

$$\begin{aligned}&I_{iftb}^+ \le I_{ift-1,b}^+\quad \forall b\le t-1,i,f,t \end{aligned}$$

(7)

$$\begin{aligned}&I_{iftb}^+ \le pQ_{ift} \quad \forall ,i,f,t,b=t \end{aligned}$$

(8)

$$\begin{aligned}&I_{idtb}^1 \le I_{idt-1,b}^1 \quad \forall b\le t-1,i,d,t \end{aligned}$$

(9)

$$\begin{aligned}&I_{idtb}^1 \le \sum \limits _{o\in O} \sum \limits _{r\in R_{f,d} } \sum \limits _{v\in V} trQ_{irovt} \quad \forall ,i,d,t,b=t\end{aligned}$$

(10)

$$\begin{aligned}&\sum \limits _{f\in F} I_{ift}^- =\sum \limits _{c\in C} bsQ_{ict} \quad \forall i,t \end{aligned}$$

(11)

$$\begin{aligned}&pQ_{ift} =pbN_{ift} \cdot \beta _{ift}\quad \forall i,f,t \end{aligned}$$

(12)

$$\begin{aligned}&G\cdot X_{ift} \ge pQ_{ift} \quad \forall i,f,t \end{aligned}$$

(13)

$$\begin{aligned}&\alpha _{ift}\cdot pbN_{ift} +st_{ift}\cdot X_{ift} \le pCap_{ift} \quad \forall f,t \end{aligned}$$

(14)

$$\begin{aligned}&\sum \limits _{i\in \mathrm{I}} \sum \limits _{b=t-shl_i }^t I_{iftb}^+ \le hCap_f^1\quad \forall f,t \end{aligned}$$

(15)

$$\begin{aligned}&I_{ift=0}^- =I_{ift=T}^- =I_{ifo}^-\quad \forall i,f \end{aligned}$$

(16)

Distribution:

$$\begin{aligned}&sQ_{ict} +bsQ_{ict-1} -bsQ_{ict} \nonumber \\&\quad =\sum \limits _{o\in O} \sum \limits _{r\in R_{f,c} \cup R_{d,c} } \sum \limits _{v\in V} trQ_{irovt} \quad \forall c\in C,i,t \end{aligned}$$

(17)

$$\begin{aligned}&pQ_{ift} +\sum \limits _{b=t-shl_i }^{t-1} I_{ift-1,b}^+ -\sum \limits _{b=t-shl_i }^t I_{ift,b}^+ \nonumber \\&\quad =\sum \limits _{o\in O} \sum \limits _{r\in R_{f,d} \cup R_{f,c} } \sum \limits _{v\in V} trQ_{irovt}\quad \forall i,f,t \end{aligned}$$

(18)

$$\begin{aligned}&\sum \limits _{o\in O} \sum \limits _{r\in R_{f,d} } \sum \limits _{v\in V} trQ_{irovt} +\sum \limits _{b=t-shl_i }^{t-1} I_{idt-1,b}^1-\sum \limits _{b=t-shl_i }^t I_{idtb}^1 \nonumber \\&\quad =\sum \limits _{o\in O} \sum \limits _{r\in R_{d,c} } \sum \limits _{v\in V} trQ_{irovt} \quad \forall i,d,t \end{aligned}$$

(19)

$$\begin{aligned}&tN_{rovt} \ge \sum \limits _{i\in I} \frac{a_{iv} \cdot trQ_{irovt} }{vCap_v }\quad \forall o\in O,r,v,t \end{aligned}$$

(20)

$$\begin{aligned}&\sum \limits _{r\in R} tN_{rovt} \le trCap_{otv}\quad \forall o\in O,v,t \end{aligned}$$

(21)

$$\begin{aligned}&\sum \limits _{r\in R_{d,f} } \sum \limits _{o\in O} \sum \limits _{v\in V} tN_{rovt} \le KCap_{fv}\quad \forall f,t \end{aligned}$$

(22)

Procurement:

$$\begin{aligned}&\sum \limits _{s\in S} purQ_{msft-L_{ms} } +I_{mft-1}^2 -I_{mft}^2 \nonumber \\&\quad =\sum \limits _{i\in I} u_{mif}\cdot pQ_{ift}\quad \forall m,f,t=1-L_{m,s},\ldots ,T \end{aligned}$$

(23)

$$\begin{aligned}&I_{mft}^2 -SS_{mf} \ge 0\quad \forall m,f,t \end{aligned}$$

(24)

$$\begin{aligned}&\sum \limits _{m\in j} I_{mft}^2 \le mCap_{jf}\quad \forall j,f,t \end{aligned}$$

(25)

$$\begin{aligned}&\sum \limits _{m\in M} \sum \limits _{f\in F} purQ_{msft} \le sCap_{st} \quad \forall s\in S,t \end{aligned}$$

(26)

$$\begin{aligned}&G\cdot y_{mst} \ge \sum \limits _{f\in F} purQ_{msft} \quad \forall s\in S,m,t \end{aligned}$$

(27)

$$\begin{aligned}&\sum \limits _{f\in F} \sum \limits _{t\in T} purQ_{msft} \ge Qmin_{ms} \quad \forall s\in CS\end{aligned}$$

(28)

$$\begin{aligned}&sQ_{ict},bsQ_{ict} ,pQ_{ift},I_{iftb}^+,I_{ift}^-,trQ_{irovt},\nonumber \\&\quad I_{idtb}^1 ,purQ_{msft},I_{m,f,t}^2 \ge 0\nonumber \\&\quad tN_{rovt} \text { is positive integer, and }X_{ift} \in \left\{ {0,1} \right\} ,\nonumber \\&\quad y_{mst} \in \left\{ {0,1} \right\} \nonumber \\&\quad \forall c,i,f,t,r,v,d,m,o\left( {o\in O} \right) , s\left( {s\in S} \right) \end{aligned}$$

(29)

In objective function (Eq. (1)), the first bracket covers production, setup, inventory holding and back-order costs. The second brackets represent the total transportation costs of finished products from factory to DCs, factory to customers and DCs to customers, as well as the inventory holding costs in DCs. The inventory of DCs is included in the model to give us the flexibility to absorb the excess production capacity, when facing idle capacity, as well as reducing the lost sales impact, when facing procurement capacity shortage. When considering DC simply as docking station, this capacity will be set as zero. Finally, the last bracket states the raw materials purchasing, ordering and holding cost.

Equation (2) represents the service level of the supply chain, which is equal to the subtraction of demand and sales quantity, divided by the demand, for all product families.

Equations (3)–(5) address the sales decisions and the fact that all demands must be greater than minimum demands else they are rejected and if demands are accepted, sales quantities are less than demands and greater than minimum demands. In this case, the sales managers can decide whether to accept the demand as back-order $(I_{ift}^- )$ and satisfy it in next period or reject them.

Equation (6) is coupling constraint, jointing the production, distribution and sales decisions to each other, and they define a smooth consolidated physical flow over the chain. This constraint expresses that the accepted demand should be satisfied from the production or inventory of all sites and DCs so that storage time of these products must not be greater than their shelf life. To satisfy shelf life limitations, we have developed Eqs. (6)–(10) and Eqs. (18)–(19). Equation (7) expresses that the amount of inventory from each production batch in period t, at factory f, should be lower than or equal to the amount of inventory from the same production batch in previous period. Equation (8) guarantees that the amount of inventory from each production batch in period t is lower than or equal to the amount of production in the same period. Equation (9) expresses that the amount of inventory from each production batch in period t and DC d is lower than or equal to the amount of inventory from the same production batch in previous period. Equation (10) implies that the amount of inventory from each production batch in period t is lower than or equal to the amount of shipping products to DC d in the same period.

Equation (11) converts the backlogs into backlogged sales $bsQ_{ict}$, which itself is subtracted from the shipping quantity of period t as shown in Eq. (17). Equation (12) ensures that production is always done in batch sizes. Equation (13) examines whether a setup cost is imposed to start producing product family i. Equation (14) is the production capacity constraint, stating that the sum of production and setup time should not exceed the total available time in period t. Equation (15) defines the finished goods warehouse’s capacity. The amount of opening and closing backlog conditions is presented in Eq. (16).

Equation (17) weaves the sales and distribution decisions together and insures the stock balance in customer point (Fig. 2). It means that the product delivered to the customers in period t should be equal to the sales amount in period t plus the backlogged sales of period $t-1$ minus the backlogged sales of period t. Equation (18) links the production and distribution decisions together and insures the inventory balance in factory point (Fig. 2). It means that the products delivered from the factories should be equal to the amounts produced plus the opening stock minus the closing stock. Equation (19) addresses the balance of inventory flow in DCs, where the total delivery to a DC, plus the opening stock, minus the closing stock should be equal to total delivery from the DC. Equation (20) measures the needed number of vehicles of each types from each shipping suppliers. This constraint specifies which type of vehicle and how many, in what configuration of products have to be arranged for which destination. If the delivery could be arranged with less numbers of trucks, then the objective function forces this variable to take the minimum possible integer. Equation (21) shows the shipping supplier capacity limitation, and Eq. (22) depicts the loading and dispatching capacity of each factory.

Equation (23) joints the procurement and production decisions together, through the inventory balance of raw materials in factory point. This constraint describes that the delivery of raw materials—which is equal to the purchased raw materials in period $t-L_{ms}$ plus the opening stock minus the closing stock—should be equal to the consumption of raw materials. Holding policy of raw material is described in Eq. (24), and the warehousing capacity of raw material inventories is addressed in Eq. (25). Equation (26) describes the procurement limitations of raw materials as a function of t, so that it can cover the demand seasonality. Equation (27) is the raw materials ordering constraint which assumes demands can be allocated to the production sites, in a way that the total ordering cost stays at minimum. Equation (28) implies that the purchasing amount from the suppliers should be at least equal to the minimum committed amount. Equation (29) defines the domain of each decision variables.

3.3 The fuzzy PI-S&OP model

Multisite PI-S&OP model addresses the state that sales and production planning are executed jointly in a multisite environment and distribution and procurement planning are done in each site locally. Hence, the PI-S&OP model consists of two sub-models: a multisite sales and production planning and a single-site distribution and procurement planning model. Each of these sub-models has its own objective function which seeks for its local optimality. The total cost of the enterprise will be measured through summing up the cost of production, distribution and procurement of all sites. Sales and backlogged sales of each site are depicted through the multisite sales and production sub-model in order to be used in distribution sub-model. In distribution sub-model, DCs are looked only as docking stations. Since all factories are linked to all DCs, the distribution planning of each site is performed separately and independently. The three sub-models are defined as follows:

3.3.1 Sales-production sub-model

The first objective of this sub-model is to minimize the sales and production cost, considering the production, setup, inventory and backlogged sales costs (Eq. (30)). The second objective is to maximize the customer service level of the entire supply chain, through fulfilling as much as orders as factories can produce.

Objective Function:

$$\begin{aligned} \widetilde{TC} _{PIc}= & {} \hbox {Min}\left( \sum \limits _{i\in I} \sum \limits _{f\in F}\sum \limits _{t\in T} \left( {\widetilde{pC}}_{ift} \cdot pQ_{ift} +{\widetilde{sC}}_{ift}^1 \cdot X_{ift} \right. \right. \nonumber \\&\quad \left. \left. +{\widetilde{hC}}_{ift}^1 \cdot \sum \limits _{b=t-shl}^t I_{iftb}^+ +{\widetilde{boC}} _{ift} \cdot I_{ift}^- \right) \right) \end{aligned}$$

(30)

$$\begin{aligned} CSL_{PI}= & {} \max \left\{ 1-\left( {\frac{\sum \nolimits _{i\in I} \sum \nolimits _{c\in C} \sum \nolimits _{t\in T} \left( {d_{ict} -\sum \nolimits _{f\in F} sQ_{icft} } \right) }{\sum \nolimits _{i\in I} \sum \nolimits _{c\in C} \sum \nolimits _{t\in T} d_{ict} }} \right) \right\} \nonumber \\ \end{aligned}$$

(31)

Subject to following constraint plus (3), (7) and (9)–(14):

$$\begin{aligned}&\sum \limits _{f\in F} sQ_{icft} \le d_{ict} {*}K_{ict} \quad \forall c\in C,i,t \end{aligned}$$

(32)

$$\begin{aligned}&\sum \limits _{f\in F} sQ_{icft} \ge dmin_{ict} {*}K_{ict} \quad \forall c\in C,i,t \end{aligned}$$

(33)

$$\begin{aligned}&pQ_{ift} +\sum \limits _{b=t-shl_i }^{t-1} I_{ift-1,b}^+ -I_{ift-1}^- \nonumber \\&\quad -\sum \limits _{b=t-shl_i }^t I_{iftb}^+ +I_{ift}^- =\sum \limits _{c\in C} sQ_{icft} \quad \forall i,f,t \end{aligned}$$

(34)

$$\begin{aligned}&I_{i,f,t}^- =\sum \limits _{c\in C} bsQ_{icft} \quad \forall i,f,t \end{aligned}$$

(35)

$$\begin{aligned}&sQ_{icft},bsQ_{icft},pQ_{ift},I_{iftb}^+,\nonumber \\&\quad I_{ift}^- \ge 0,pbN_{ift}~\textit{is positive integer, and} \nonumber \\&\quad sQ_{ift} \in \left\{ {0,1} \right\} \quad \forall c,i,f,t \end{aligned}$$

(36)

Equation (31) represents the service level of the supply chain, which is equal to the subtraction of demand and sales quantity, divided by the demand, for all product families. Equations (32)–(33) are the modification of Eqs. (4)–(5), where sales and backlogged sales are specified before in each site. Equations (34) and (35) are modified Eqs. (6) and (11), which transfer the inventories of DCs, while focusing on the inventory balance, through the sales and backlogged sales decisions. Equation (36) is the modified positive constraints which include only sales and production decisions.

3.3.2 Distribution sub-model

Based on the sales and backlogged sales information, the single-site distribution sub-model decides about which type of transportation vehicle and how many, from which shipping supplier is needed to deliver products. Objective function (Eq. (37)) tries to minimize the total shipping and transshipment costs.

Objective Function

$$\begin{aligned} {\widetilde{TC}}_{PId}= & {} \hbox {Min}\left( \sum \limits _{f\in F} \sum \limits _{o\in O} \sum \limits _{i\in I} \sum \limits _{v\in V} \sum \limits _{t\in T} \right. \nonumber \\&\left. \left\{ \sum \limits _{r\in R} \left( {{\widetilde{tvC}} _{irov}\cdot trQ_{irovt} +{\widetilde{tfC}}_{rov}\cdot tN_{rovt} } \right) \right. \right. \nonumber \\&\quad \left. \left. +\sum \limits _{r\in R_{f,d} } \widetilde{trC} _{id}\cdot trQ_{irovt} \right\} \right) . \end{aligned}$$

(37)

Subject to following constraint plus (18)–(20):

$$\begin{aligned}&\sum \limits _{f\in F} \left( {sQ_{ifct} +bsQ_{ifct-1} -bsQ_{ifct} } \right) \nonumber \\&\quad =\sum \limits _{o\in O} \sum \limits _{r\in \left( {R_{f,c} \cup R_{d,c} } \right) } \sum \limits _{v\in V} trQ_{irovt} \quad \forall c\in C,i,t \end{aligned}$$

(38)

$$\begin{aligned}&\sum \limits _{o\in O} \sum \limits _{r\in R_{f,d} } \sum \limits _{v\in V} trQ_{irovt} \nonumber \\&\quad =\sum \limits _{o\in O} \sum \limits _{r\in R_{d,c} } \sum \limits _{v\in V} trQ_{irovt} \quad \forall i,d,t \end{aligned}$$

(39)

$$\begin{aligned}&trQ_{irovt} \ge 0~\textit{and}~tN_{srvt}~\textit{is positive integer}\nonumber \\&\quad \forall o\in O,i,r,v,t \end{aligned}$$

(40)

Equation (38) is the modification of Eq. (17), where the sales and backlogged sales decision variables are set in each manufacturing site, independently. Equation (39) is the modification of Eq. (15), where inventory of DCs is ignored. Equation (40) just defines the domain of distribution decision variables. Noted that, the sales and backlogged sales in Eq. (37) are the parameter that had been set before by the sales-production sub-model and the distribution sub-model has no influence on them.

3.3.3 Procurement sub-model

Based on the production information extracted from the sales-production sub-model, the procurement sub-model decides about how much of what material from which suppliers needed to be purchased and how much inventory of them needed to be kept. The aim is to minimize the total purchasing, ordering and raw material inventory costs.

Objective Function

$$\begin{aligned} {\widetilde{TC}}_{PIs}= & {} \hbox {Min}\left\{ \sum \limits _{f\in F} \left( \sum \limits _{m\in M} \sum \limits _{s\in S} \sum \limits _{t\in T} {\widetilde{purC}} _{mst} \cdot purQ_{msft}\right. \right. \nonumber \\&\quad \left. \left. +\sum \limits _{m\in M} \sum \limits _{t\in T} {\widetilde{hC}} _{mf}^3\cdot I_{mft}^2 \right) \right. \nonumber \\&\quad \left. +\sum \limits _{m\in M} \sum \limits _{s\in S} \sum \limits _{t\in T} {\widetilde{sC}} _{mst}^2\cdot y_{mst} \right\} . \end{aligned}$$

(41)

Subject to constraints (21)–(23) plus:

$$\begin{aligned}&\sum \limits _{m\in M} \sum \limits _{f\in F} purQ_{msft} \le sCap_{st} \quad \forall s\in S,t \end{aligned}$$

(42)

$$\begin{aligned}&G\cdot y_{mst} \le purQ_{msft} \quad \forall s\in S,m,f,t \end{aligned}$$

(43)

$$\begin{aligned}&\sum \limits _{m\in M} \mathop \sum \limits _{t\in T} purQ_{msft} \ge Qmin_{msf} \quad \forall s\in CS,f \end{aligned}$$

(44)

$$\begin{aligned}&purQ_{msft},I_{mft}^2 \ge 0\textit{ and }y_{smt} \in \left\{ {0,1} \right\} \nonumber \\&\quad \forall s\in S,m,f,t \end{aligned}$$

(45)

Equation (41) tries to minimize the total procurement cost. Equation (42) is the modification of Eq. (22), where the purchased amount of raw materials is set in each manufacturing site, independently. Ordering cost in Eq. (43) is now applied to each factory, separately. Parameter $Qmin_{ms}$ in Eq. (24) is now converted to $Qmin_{msf}$ in Eq. (44), which is applied on the determined share of factory f. Equation (45) is modified Eq. (25), which includes procurement decision variables only.

3.4 The fuzzy DP model

The multisite decoupled planning model states the traditional approach of discrete planning, where sales planning is performed centrally and production, distribution and procurement planning are performed separately in each manufacturing site. The model has four sub-models which represent the sales, production, distribution and procurement planning, respectively, and each planning model is seeking its local optimality. In this section, we just address the sales and production sub-models, as not to repeat the distribution and procurement sub-models, which have been described in PI-S&OP model.

3.4.1 Sales sub-model

In decoupled planning approach, the sales decisions are being made based on aggregated demand, determined production cost of production and the supply capacity of each factory (mostly by weight). The aim is to minimize the estimated production cost, using sales amounts. The backlogged sale is inevitable and is addressed by production sub-model.

Objective Function:

$$\begin{aligned} {\widetilde{TC}}_{DPc}= & {} \hbox {Min}\left( {\sum \limits _{i\in I} \sum \limits _{f\in F} \sum \limits _{t\in T} \sum \limits _{c\in C} \left( {{\widetilde{epC}} _{ift} \cdot sQ_{icft} } \right) } \right) \end{aligned}$$

(46)

$$\begin{aligned} CSL_{DP}= & {} \max \left\{ {1-\left( {\frac{\sum \nolimits _{i\in I} \sum \nolimits _{c\in C} \sum \nolimits _{t\in T} \left( {d_{ict} -\sum \nolimits _{f\in F} sQ_{icft} } \right) }{\sum \nolimits _{i\in I} \sum \nolimits _{c\in C} \sum \nolimits _{t\in T} d_{ict} }} \right) } \right\} \nonumber \\ \end{aligned}$$

(47)

Subject to following constraints plus Eqs. (3) and (32):

$$\begin{aligned}&\sum \limits _{i\in I} \sum \limits _{c\in C} sQ_{icft} \le epCap_{ift} \quad \forall ,m,t \end{aligned}$$

(48)

$$\begin{aligned}&sQ_{icft} \ge 0\quad \forall c\in C,i,f,t \end{aligned}$$

(49)

Equation (46) tries to minimize total production cost of the goods sold, using the estimated production cost. Equation (47) represents the service level of the supply chain, which is equal to the subtraction of demand and sales quantity, divided by the demand, for all product families. Equation (48) is the capacity constraint. Equation (49) defines the domain of sales decision variables.

3.4.2 Production sub-model

Based on the sales decisions, the production sub-model decides about the lot size, inventory levels and back orders/back sales. Due to dissociation of planning process in this approach, production decisions are being made by the determination of the capacity; thus, backlogs would be inevitable. Production has no effect on sales decisions, and outsourcing is not possible. The aim is to minimize the production, setup, inventory holding, backlog and lost sale costs at the end of time horizon T. Objective Function:

$$\begin{aligned}&{\widetilde{TC}}_{DPp} =\hbox {Min}\left( \sum \limits _{f\in F} \sum \limits _{i\in I} \sum \limits _{t\in T} \left\{ {\widetilde{pC}}_{ift}\cdot pQ_{ift} +{\widetilde{sC}} _{ift}^1\cdot X_{ift}\right. \right. \nonumber \\&\quad \left. \left. +{\widetilde{hC}}_{ift}^1\cdot \sum \limits _{b=t-shl_i }^t I_{iftb}^+ +\widetilde{boC} _{ift}\cdot I_{ift}^- \right. \right. \nonumber \\&\quad \left. \left. +\left( {\sum \limits _{c\in C} \widetilde{sP} _{icT}\cdot bsQ_{icT} } \right) \right\} \right) \end{aligned}$$

(50)

Subject to Eqs. (8), (33)–(35) and (10)–(13) plus:

$$\begin{aligned}&\sum \limits _{f\in F} \left( {pQ_{ift} +\sum \limits _{b=t-shl_i }^{t-1} I_{ift-1,b}^+ -I_{ift-1}^- } \right) \nonumber \\&\quad \ge \sum \limits _{c\in CC} \left( {dmin_{ict} {*}K_{ict} } \right) \quad \forall i,t \end{aligned}$$

(51)

$$\begin{aligned}&I_{ift}^- =I_{if0}^- \quad \forall i,f \end{aligned}$$

(52)

$$\begin{aligned}&bsQ_{icT},pQ_{ift},I_{iftb}^+ ,I_{ift}^- \ge 0,pbN_{ift} \nonumber \\&\quad \textit{is positive integer, and}~X_{ift} \in \left\{ {0,1} \right\} \nonumber \\&\quad \forall c\in C,i,f,t. \end{aligned}$$

(53)

Equation (51) forces Eq. (32) to satisfy the demands to minimum committed amount. Equation (52) modifies Eq. (12) through defining the opening backlog amount, where the closing backlog $({I_{ift}^-})$ is out of control. The closing backlog at the end of period T is taking into account as lost sales, and the penalty of lost sales is considered as lost sales revenue in Eq. (50). This penalty forces the lost sales $({bs_{cifT}})$—in this case $({I_{ifT}^-})$—to be in production capacity intervals. Equation (53) is the nonnegative constraints which solely dedicate to production decision variables.

3.5 The crisp FI-S&OP model

Multisite crisp S&OP model addresses the state that all the cost parameters of sales, production, procurement and distribution are assumed to be deterministic. Hence, the crisp model should be different in objective function, while the rest of the constraints will be defined as the same of the fuzzy model.

Objective Function:

$$\begin{aligned}&TC_{FI}=\hbox {Min}\left( \left\{ \sum \limits _{i\in I} \sum \limits _{f\in F} \sum \limits _{t\in T} (pC_{ift} \cdot pQ_{ift} \right. \right. \nonumber \\&\quad \left. \left. +sC_{ift}^1\cdot X_{ift} +hC_{ift}^1\cdot \sum \limits _{b=1}^t I_{ift}^+ +boC_{ift}\cdot I_{ift}^- ) \right\} \right. \nonumber \\&\quad \left. +\left\{ \sum \limits _{i\in I} \mathop \sum \limits _{r\in R_{f,d} \cup R_{f,c} \cup R_{d,c} } \sum \limits _{o\in O}\right. \right. \nonumber \\&\quad \left. \left. \sum \limits _{v\in V} \sum \limits _{t\in T} \left( {tvC_{irov}\cdot trQ_{irovt} +tfC_{rov}\cdot tN_{rovt} } \right) \right. \right. \nonumber \\&\quad \left. \left. + \sum \limits _{i\in I}\sum \limits _{r\in R_{f,d} } \sum \limits _{o\in O}\sum \limits _{v\in V} \sum \limits _{t\in T} \left( {trC_{ir}\cdot trQ_{irovt} } \right) \right. \right. \nonumber \\&\quad \left. \left. + \sum \limits _{i\in I} \sum \limits _{d\in D} \sum \limits _{t\in T} \left( {hC_{id}^2\cdot \sum \limits _{b=1}^t I_{idtb}^1 } \right) \right\} \right. \nonumber \\&\quad \left. +\left\{ \sum \limits _{m\in M} \sum \limits _{s\in S} \sum \limits _{f\in F} \sum \limits _{t\in T} \left( {purC_{mst}\cdot purQ_{msft} } \right) \right. \right. \nonumber \\&\quad \left. \left. + \sum \limits _{m\in M} \sum \limits _{s\in S} \sum \limits _{t\in T} \left( {sC_{mst}^2\cdot y_{mst} } \right) \right. \right. \nonumber \\&\quad \left. \left. +\sum \limits _{m\in M} \sum \limits _{f\in F} \sum \limits _{t\in T} \left( {hC_{mf}^3\cdot I_{mft} } \right) \right\} \right) \end{aligned}$$

(54)

where the first bracket covers production, setup, inventory holding and back-order costs. The second brackets represent the total transportation costs of finished products from factory to DCs, factory to customers and DCs to customers, as well as the inventory holding costs in DCs. and the third bracket addresses the raw materials purchasing, ordering and holding cost. As we described earlier, the rest of the model is the same as the fuzzy model, so we do not repeat it.

4 How to solve the model?

In this paper, as shown in Fig. 2, triangular fuzzy numbers (TFNs) are used to present all operational costs. A TFN can be characterized by three parameters $\tilde{C}=({c^{p},c^{m},c^{o}})$ (Shermeh et al. 2016; Tarimoradi et al. 2015; Zarandi et al. 2015a, b).

Fig. 2

A triangular fuzzy numbers (TFNs)

The reason of using triangulated data in this paper is because of its computational simplicity in comparison with other fuzzy data, as its considered calculations in Eq. (16) (Alavidoost et al. 2015b, 2017; Alavidoost 2017):

$$\begin{aligned} \tilde{A} +\tilde{B}= & {} \left( {A_1 +B_1,A_2 +B_2 ,A_3 +B_3 } \right) . \nonumber \\ \tilde{A} -\tilde{B}= & {} \left( {A_1 -B_3,A_2 -B_2 ,A_3 -B_1 } \right) \nonumber \\ \tilde{A} \times \tilde{B}= & {} \left( {A_1 \times B_1 ,A_2 \times B_2,A_3 \times B_3 } \right) \nonumber \\ \tilde{A} /\tilde{B}= & {} \left( {A_1 /B_3,A_2 /B_2 ,A_3 /B_1 } \right) \end{aligned}$$

(55)

For defuzzification of TFNs, we use Eq. (17), as follows:

$$\begin{aligned} \textit{Defuzzification}\left( {\tilde{A} } \right) =\frac{\left( {A_1 +2\times A_2 +A_3 } \right) }{4}. \end{aligned}$$

(56)

A two-phase approach has been utilized in this article in order to solve the problem. In the first phase, the model will be defuzzified through transforming the original problem into an auxiliary crisp multiple objective mixed integer linear programming (MOMILP), which is equal to the original problem. Then in second phase, a two-phase interactive fuzzy programming approach is utilized to achieve a satisfactory compromise solution.

4.1 Phase I: an auxiliary crisp MOMILP model

In this work, TFNs are employed in order to account uncertainty associated with the task processing times. Generally, a triangular fuzzy processing time is defined by a triplet points. As can be seen from Fig. 2, a fuzzy triangular MF consists of three main elements including:

• The most optimistic value $({c^{o}})$

• The most possible value $({c^{m}})$

• The most pessimistic value $({c^{p}})$

The most optimistic and pessimistic values have the lowest membership degree $( {\mu _{\tilde{c} } ( {c^{o}} )=\mu _{\tilde{c} } ( {c^{p}} )=0} )$. The most possible value is posited within the interval and has the maximum degree of membership $( {\mu _{\tilde{c}} ( {c^{m}} )=1} )$. It is assumed that all other points located between these three points have membership degree whose values vary linearly between [0, 1].

According to the descriptions, the financial parameters of the model will be defined as below:

$$\begin{aligned} \widetilde{sP} _{ict}= & {} \left( {sP_{ict}^o,sP_{ict}^m ,sP_{ict}^p } \right) \nonumber \\ \widetilde{pC} _{ift}= & {} \left( {pC_{ift}^o,pC_{ift}^m ,pC_{ift}^p } \right) \nonumber \\ \widetilde{sC} _{ift}^1= & {} \left( {sC_{ift}^{o1},sC_{ift}^{m1} ,sC_{ift}^{p1} } \right) \nonumber \\ \widetilde{hC} _{ift}^1= & {} \left( {hC_{if}^{o1},hC_{if}^{m1} ,hC_{if}^{p1} } \right) \nonumber \\ \widetilde{boC} _{ift}= & {} \left( {boC_{ift}^o,boC_{ift}^m ,boC_{ift}^p } \right) \nonumber \\ \widetilde{tvC} _{irov}= & {} \left( {tvC_{irov}^o,tvC_{irov}^m ,tvC_{irov}^p } \right) \nonumber \\ \widetilde{tfC} _{rov}= & {} \left( {tfC_{rov}^o,tfC_{rov}^m ,tfC_{rov}^p } \right) \nonumber \\ \widetilde{trC} _{ir}= & {} \left( {trC_{ir}^o,trC_{ir}^m ,trC_{ir}^p } \right) \nonumber \\ \widetilde{hC} _{id}^2= & {} \left( {hC_{id}^{o2},hC_{id}^{m2} ,hC_{id}^{p2} } \right) \nonumber \\ \widetilde{purC} _{mst}= & {} \left( {purC_{mst}^o,purC_{mst}^m ,purC_{mst}^p } \right) \nonumber \\ \widetilde{sC} _{mst}^2= & {} \left( {sC_{mst}^{o2},sC_{mst}^{m2} ,sC_{mst}^{p2} } \right) \nonumber \\ \widetilde{hC} _{mf}^3= & {} \left( {hC_{mf}^{o3},hC_{mf}^{m3} ,hC_{mf}^{p3} } \right) \end{aligned}$$

(57)

Given that all the three presented models are composed of multiple TFNs, the related objective function can be defined as follows:

FI-S&OP objective function

$$\begin{aligned} \widetilde{TC} _{FI}= & {} \left( {TC_{FI} ^{o},TC_{FI} ^{m},TC_{FI} ^{p}} \right) \end{aligned}$$

(58)

PI-S&OP objective functions

$$\begin{aligned} \widetilde{TC} _{PIc}= & {} \left( {TC_{PIc} ^{o},TC_{PIc} ^{m},TC_{PIc} ^{p}} \right) \end{aligned}$$

(59)

$$\begin{aligned} \widetilde{TC} _{PId}= & {} \left( {TC_{PId} ^{o},TC_{PId} ^{m},TC_{PId} ^{p}} \right) \end{aligned}$$

(60)

$$\begin{aligned} \widetilde{TC} _{PIs}= & {} \left( {TC_{PIs} ^{o},TC_{PIs} ^{m},TC_{PIs} ^{p}} \right) \end{aligned}$$

(61)

DP objective functions

$$\begin{aligned} \widetilde{TC} _{DPc}= & {} \left( {TC_{DPc} ^{o},TC_{DPc} ^{m},TC_{DPc} ^{p}} \right) \end{aligned}$$

(62)

$$\begin{aligned} \widetilde{TC} _{DPp}= & {} \left( {TC_{DPp} ^{o},TC_{DPp} ^{m},TC_{DPp} ^{p}} \right) \end{aligned}$$

(63)

$$\begin{aligned} \widetilde{TC} _{DPd}= & {} \left( {TC_{DPd} ^{o},TC_{DPd} ^{m},TC_{DPd} ^{p}} \right) \end{aligned}$$

(64)

$$\begin{aligned} \widetilde{TC} _{DPs}= & {} \left( {TC_{DPs} ^{o},TC_{DPs} ^{m},TC_{DPs} ^{p}} \right) \end{aligned}$$

(65)

The above objectives are defined by a TFN $( \tilde{f}=\min ( {\widetilde{TC} } )=\min ( {c^{p},c^{m},c^{o}} ) )$. There have been several methods proposed to deal with optimizing fuzzy objective functions in which they are represented by fuzzy numbers. According to method suggested by Lai and Hwang (1992), in order to solve a fuzzy integer programming problem, an auxiliary multiobjective linear programming (MOLP) approach with converting a fuzzy objective into three independent crisp ones is applied. According to this strategy, we intend to simultaneously minimize the most possible value of the total supply chain cost; $f_1 =\{ {min( {c^{m}} )} \}$ maximize the possibility of obtaining lower objective value, $f_2 =\{ {max( {c^{m}-c^{o}} )} \}$, and minimize the risk of obtaining higher objective value $f_3 =\{ {min( {c^{p}-c^{m}} )} \}$. As one can see in Fig. 3 compared with A, objective function B is much preferable as it simultaneously meets the requirements of all three objectives.

Fig. 3

The minimization strategy for a fuzzy objective

Therefore, FI-S&OP objective function (Eq. (1)) will be transformed into three objectives (Eqs. (66)–(68)). Similarly, PI-S&OP objective functions (Eq. (30)) will be transformed into six objectives (Eqs. (69)–(76)). And the DP original objectives will be converted into twelve defuzzified objectives (Eqs. (77)–(89)).

Converted FI-S&OP objectives

$$\begin{aligned} \widetilde{TC} _{FI}= & {} \left( {TC_{FI} ^{o},TC_{FI}^{m},TC_{FI} ^{p}} \right) \nonumber \\ TC_{FI_1 }= & {} Min\left( {TC_{{FI}_1}^m } \right) \end{aligned}$$

(66)

$$\begin{aligned} TC_{FI_2 }= & {} Max\left( {TC_{FI}^m -TC_{FI}^o } \right) \end{aligned}$$

(67)

$$\begin{aligned} TC_{FI_3 }= & {} Min\left( {TC_{FI}^p -TC_{FI}^m } \right) \end{aligned}$$

(68)

Converted PI-S&OP objectives

$$\begin{aligned} \widetilde{TC} _{PIc}= & {} \left( {TC_{PIc} ^{o},TC_{PIc} ^{m},TC_{PIc} ^{p}} \right) \nonumber \\ TC_{PIc_1 }= & {} Min\left( {TC_{PIc}^m } \right) \end{aligned}$$

(69)

$$\begin{aligned} TC_{PIc_2 }= & {} Max\left( {TC_{PIc}^m -TC_{PIc}^o } \right) \end{aligned}$$

(70)

$$\begin{aligned} TC_{PIc_3 }= & {} Min\left( {TC_{PIc}^p -TC_{PIc}^m } \right) \end{aligned}$$

(71)

$$\begin{aligned} \widetilde{TC} _{PId}= & {} \left( {TC_{PId} ^{o},TC_{PId} ^{m},TC_{PId} ^{p}} \right) \nonumber \\ TC_{PId_1 }= & {} Min\left( {TC_{PId} ^{m}} \right) \end{aligned}$$

(72)

$$\begin{aligned} TC_{PId_2 }= & {} Max\left( {TC_{PId} ^{m}-TC_{PId} ^{o}} \right) \end{aligned}$$

(73)

$$\begin{aligned} TC_{PId_3 }= & {} Min\left( {TC_{PId} ^{p}-TC_{PId} ^{m}} \right) \end{aligned}$$

(74)

$$\begin{aligned} \widetilde{TC} _{PIs}= & {} \left( {TC_{PIs} ^{p},TC_{PIs} ^{m},TC_{PIs} ^{o}} \right) \nonumber \\ TC_{PIs_1 }= & {} Min\left( {TC_{PIs} ^{m}} \right) \end{aligned}$$

(75)

$$\begin{aligned} TC_{PIs_2 }= & {} Max\left( {TC_{PIs} ^{m}-TC_{PIs} ^{o}} \right) \end{aligned}$$

(76)

$$\begin{aligned} TC_{PIs_3 }= & {} Min\left( {TC_{PIs} ^{p}-TC_{PIs} ^{m}} \right) \end{aligned}$$

(77)

Converted DP objectives

$$\begin{aligned} \widetilde{TC} _{DPc}= & {} \left( {TC_{DPc} ^{p},TC_{DPc} ^{m},TC_{DPc} ^{o}} \right) \nonumber \\ TC_{DPc_1 }= & {} Min\left( {TC_{DPc}^m } \right) \end{aligned}$$

(78)

$$\begin{aligned} TC_{DPc_2 }= & {} Max\left( {TC_{DPc}^m -TC_{DPc}^o } \right) \end{aligned}$$

(79)

$$\begin{aligned} TC_{DPc_3 }= & {} Min\left( {TC_{DPc}^p -TC_{DPc}^m } \right) \end{aligned}$$

(80)

$$\begin{aligned} \widetilde{TC} _{DPp}= & {} \left( {TC_{DPp} ^{p},TC_{DPp} ^{m},TC_{DPp} ^{o}} \right) \nonumber \\ TC_{DPp_1 }= & {} Min\left( {TC_{DPp} ^{m}} \right) \end{aligned}$$

(81)

$$\begin{aligned} TC_{DPp_2 }= & {} Max\left( {TC_{DPp}^m -TC_{DPp}^o } \right) \end{aligned}$$

(82)

$$\begin{aligned} TC_{DPp_3 }= & {} Min\left( {TC_{DPp}^p -TC_{DPp}^m } \right) \end{aligned}$$

(83)

$$\begin{aligned} TC_{DPd}= & {} \left( {TC_{DPd} ^{p},TC_{DPd} ^{m},TC_{DPd} ^{o}} \right) \nonumber \\ TC_{DPd_1 }= & {} Min\left( {TC_{DPd} ^{m}} \right) \end{aligned}$$

(84)

$$\begin{aligned} TC_{DPd_2 }= & {} Max\left( {TC_{DPd} ^{m}-TC_{DPd} ^{o}} \right) \end{aligned}$$

(85)

$$\begin{aligned} TC_{DPd_2 }= & {} Min\left( {TC_{DPd} ^{p}-TC_{DPd} ^{m}} \right) \end{aligned}$$

(86)

$$\begin{aligned} \widetilde{TC} _{PIs}= & {} \left( {TC_{PIs} ^{p},TC_{PIs} ^{m},TC_{PIs} ^{o}} \right) \nonumber \\ TC_{DPs_1 }= & {} Min\left( {TC_{DPs} ^{m}} \right) \end{aligned}$$

(87)

$$\begin{aligned} TC_{DPs_2 }= & {} Max\left( {TC_{DPs} ^{m}-TC_{DPs} ^{o}} \right) \end{aligned}$$

(88)

$$\begin{aligned} TC_{DPs_2 }= & {} Min\left( {TC_{DPs} ^{p}-TC_{DPs} ^{m}} \right) \end{aligned}$$

(89)

Now, every single fuzzy objective has been transformed into a defuzzified multiobjective problem. In the next section, the interactive fuzzy programming will be presented, in order to solve the multiobjective problems.

4.2 Phase II: interactive fuzzy programming approach

4.2.1 Fuzzy programming

In this paper, an efficient interactive fuzzy programming approach is used to achieve an efficient compromise solution. Different methodologies are developed for solving multiobjective optimization problems such as the weighted-sum method, the constraint method, the goal-programming method and fuzzy method (Alavidoost et al. 2015a). Fuzzy decision making and fuzzy programming are two methods that have been proposed by Bellman and Zadeh (1970) and Zimmermann (1978), respectively, to solve MOLP in which both methods tend to obtain the positive ideal solutions (PIS) and the negative ideal solutions (NIS) of all the corresponding objective functions. These values are determined either by the DM’s preferences (between the worst and best values of each function) or are equal to the worst and best values of each function, as follows:

NIS&PIS for FI-S&OP objectives

$$\begin{aligned} TC_{FI_1 }^{PIS}= & {} Min\left( {TC_{{FI} _1}^m } \right) \end{aligned}$$

(90)

$$\begin{aligned} TC_{FI_1 }^{NIS}= & {} Max\left( {TC_{{FI} _1}^m } \right) \end{aligned}$$

(91)

$$\begin{aligned} TC_{FI_2 }^{PIS}= & {} Min\left( {TC_{FI}^m -TC_{FI}^o } \right) \end{aligned}$$

(92)

$$\begin{aligned} TC_{FI_2 }^{NIS}= & {} Max\left( {TC_{FI}^m -TC_{FI}^o } \right) \end{aligned}$$

(93)

$$\begin{aligned} TC_{FI_3 }^{PIS}= & {} Min\left( {TC_{FI}^p -TC_{FI}^m } \right) \end{aligned}$$

(94)

$$\begin{aligned} TC_{FI_3 }^{NIS}= & {} Max\left( {TC_{FI}^p -TC_{FI}^m } \right) \end{aligned}$$

(95)

$$\begin{aligned} CSL_{FI}^{PIS}= & {} Max\left( {CSL_{FI} } \right) \end{aligned}$$

(96)

$$\begin{aligned} CSL_{FI}^{NIS}= & {} Min\left( {CSL_{FI} } \right) \end{aligned}$$

(97)

The similar procedure will be applied for the PI-S&OP and DP objective functions. Each objective function corresponds to an equivalent linear MF which can be obtained using Eqs. (98)–(99).

$$\begin{aligned} \mu (x)= & {} \left\{ {\begin{array}{ll} 1 &{}\quad \hbox {if}\quad F\le F^{PIS} \\ \frac{F^{NIS}-F}{F^{NIS}-F^{PIS}}&{}\quad \hbox {if}\quad F^{PIS}\le F\le F^{NIS} \\ 0&{}\quad \hbox {if}\quad F\ge F^{NIS} \\ \end{array} } \right. \end{aligned}$$

(98)

$$\begin{aligned} \mu (x)= & {} \left\{ {\begin{array}{ll} 0&{}\quad \hbox {if}\quad F\le F^{NIS} \\ \frac{F-F^{NIS}}{F^{PIS}-F^{NIS}}&{}\quad \hbox {if}\quad F^{NIS}\le F\le F^{PIS} \\ 1&{}\quad \hbox {if}\quad F\ge F^{PIS} \\ \end{array} } \right. \end{aligned}$$

(99)

4.2.2 The interactive fuzzy programming approach

The significant advantage of interactive approaches is related to their ability to provide a systematic framework enabling the DM to interactively adjust the parameters according to his/her preferences until an efficient satisfactory solution is reached. In other words, the DM adjusts interactively the search direction during the solution procedure, until the efficient solution satisfies the DM’s preferences (El-Wahed and Lee 2006). In this article, we used the fuzzy programming approach proposed by Alavidoost et al. (2016). This approach consists of ten steps which includes the following steps:

Step 1 Specify an appropriate pattern of triangular possibility distribution for all uncertain data and construct the fuzzy MOLP problem.

Step 2 Transform the fuzzy objectives in to crisp ones according to procedure described in 4.1.

Step 3 Convert the fuzzy constraints in to crisp ones.

Step 4 Perform the optimization process for each objective function. If the solutions obtained from this process are equal, then select one of them and deliver to the DM and go to step 10. Otherwise, go ahead and continue the procedure on step 5.

Step 5 Considering the obtained solutions resulted from previous step, having the PIS value associated with each objective, determine the negative ideal solution (NIS) for each objective function by solving the corresponding MILP model.

Step 6 Specify the linear MF to correspond to each objective function according to Eqs. (98)–(99).

Step 7 Transform the MOMILP problem into an equivalent MILP by means of the following proposed auxiliary crisp formulation (Eq. (100)) and solve it.

$$\begin{aligned}&\hbox {Max}\lambda (x)=\lambda _0 +\delta \mathop \sum \limits _{k=1}^K \theta _z \lambda _z\nonumber \\&\qquad \quad \hbox {S.t}:\quad \theta _z \left( {\lambda _0 } \right) +\lambda _z \le \mu _z (x),z=1\ldots Z \nonumber \\&\,\,\qquad \qquad \qquad x\in F(x) \end{aligned}$$

(100)

where $\mu _k (x)$ refers to the satisfaction level of objective and $\delta$ denotes small positive number which is normally set to 0.01. Additionally, the relative importance of kth objective is represented by $\theta _k$ which is determined according to DM’s preference so that $\sum \nolimits _{k=1}^K \theta _z =1,\theta _k >0$. Moreover, in the above formulation, the compromise degree among the objectives and the minimum satisfaction level of objectives is controlled by $\lambda _0$. x indicates decision variables, and F(x) should be interpreted as feasible region which covers all the constraints.

Step 8 Deliver the obtained solution to the DM; if the solution meets the preference of the DM, then it is considered as compromise solutions and go to step 10. Otherwise, go to step 9.

Step 9 The model should be interactively revised according to DM’s preference to reach the desirable solution. This process repeats until the solution approach leads to produce the satisfactory solution. In this regard, the changes, which are permitted, are as follows:

• For maximization objectives, increase the NIS.

• For minimization objectives, decrease the PIS.

• Changes in weights of objective.

It should be noted that since any changes in the NIS value can lead to the large variation in the obtained result, the size of change in the NIS should be as small as possible to prevent from locating in infeasible region.

Step 10 Stop, the algorithm has reached to the compromise solution.

5 Implementation in dairy industry

5.1 Case description

The described models in section three are taking into a real-world challenge through implementation in a dairy production company. The enterprise has three factories in three different geographical positions in Iran. This section will be dedicated to the implementation of S&OP concept and mathematical models in a multisite environment.

Table 1 Total validation result of three fuzzy models (most possible value)

The scope of the problem consists of three manufacturing sites in different geographical positions, producing 11 different product families, which consume about 114 raw materials from two major suppliers. Two shipping suppliers are responsible for delivering the finished products to 44 customers, by 5 different vehicle types, through 16 DCs.

The factory consists of multiple production lines, each producing one or more product families. In the production lines, different raw materials, which mainly consist of fresh milk and cream, are being mixed together with different ratios. The process and production cycle time differs from one product to another, but on the whole, a typical dairy process consists of five steps: milk (and cream) reception, mixing, fermentation, filling and packaging. Each product family consists of a unique BOM $( {u_{imf} } )$ and a routing based on a specific cycle time. Any change over in production lines imposes us a setup time.

In distribution channel, the fleets consist of 5 different road transportation vehicle types, being provided by two 3PLs. The products reach the hands of the customers through DCs or directly from the factories. DCs are used for different purposes, as transshipping, break-bulking, mixing, stockpiling, etc.

On the purchasing side, more than 50% of the average finished cost of products is dedicated to milk, which is collected by one supplier from numerous farms. About 70% of the purchased milk is industrial milk, which is acquired from long-term contracts. The remained 30% is obtained noncontractually, collecting from milk gathering stations in different location, mostly from country side. Almost all the purchasing of the remaining raw materials is through contracts. Only in the time of shortage, there would be buying on the market possibilities. In this article, we supposed that all the transportation of raw materials is handled by the supplier itself and the shipping cost is considered in ordering cost.

The MIP models are programmed using general algebraic modeling system (GAMS) mathematical programming software and solved by CPLEX 12 optimizer. The programs are run on Windows platform using quad core 2.40 GHz core i7 CPU, 4 GB of RAM and Windows 7 professional edition version 2012.

5.2 Results

The total validation results of the three fuzzy models are presented in Table 1. Noting that the values for each cost item are the most possible value ($c^{m})$ of the three models. The results show that all the three models yield satisfying answers. Close to 100% of the sales/demand ratio supports this claim, as well. Little difference between the sales amounts of three models is due to the different planning approaches. Finally, the capacity utilization of capacity in all the three models is around 70%, which indicates that 30% of the capacity is idle for probable breakdowns or raw material out of stocks. This is aligned with the company’s policy to reserve this amount for machine breakdowns and other system unreliabilities. All the results support the validity of our models. It should be noted the results are being calculated for equal weights for CSL and SC cost objectives.

The evaluation of the benefits of the FI-S&OP model over the PI-S&OP and DP models is performed through the following KPIs: total SC cost, customer service level (CSL) and operational utilization (OU). As shown in Table 1, the financial results are stated in Islamic Republic Rial (IRR) and percentage.

Fig. 4

Total SC cost of each model for 95% CSL

As we expected, the FI-S&OP model obtains the least and DP delivers the highest total SC cost, while PI-S&OP stands in between, very close to FI-S&OP. On the other hand, the DP model delivers higher CSL and naturally higher OU than the other two. This comes from the decoupled sales and production planning of the DP model, where the model accepts as much orders as it can, without considering the downstream operation capacity, while the PI-S&OP rejects the orders which are beyond the production capacity and FI-S&OP goes even further by rejecting the orders which cannot be processed by procurement and distribution divisions. So they may accept fewer orders, in order to face less back sales and back orders. On the whole with the equal weight of the two objectives, which are SC cost and CSL, the integrated S&OP approaches deliver obviously superior results over the decoupled planning approach.

The detailed result of the models is addressed next. According to the first objective function, the cost analysis of three values—pessimistic, optimistic and the most possible value—of the fuzzy models is presented in Figs. 4, 5,, 6, 7, 8, 9, 10 and 11. As can be seen in Fig. 4, the total SC cost of the DP model is higher than PI-S&OP and much higher than the FI-S&OP model. As depicted in Figs. 7 and 8, the higher back-order and back-sales cost leads to higher total cost, addressing the lack of joint sales-production planning in DP model. Also, as can be seen in Fig. 11, more setups are the cause of imposing more higher setup cost, which is originating from decoupling of sales and production planning.

Fig. 5

Production cost of each model for three TFN points

Fig. 6

Purchase cost of each model for three TFN points

Fig. 7

Back-order cost of each model for three TFN points

The benefits of the fully integrated over the partially integrated model are not that much outstanding, due to the integration of sales and production planning in both. Slightly higher total SC cost of PI-S&OP over the FI-S&OP model can be explained in the lack of integration in distribution and procurement planning, causing higher purchasing cost (Fig. 6) as well as higher inventory holding (Fig. 10).

Fig. 8

Back-sales cost of each model for three TFN points

Fig. 9

Transportation cost of each model for three TFN points

Fig. 10

Inventory holding cost of each model for three TFN points

Fig. 11

Setup cost of each model for three TFN points

Based on the second objective, Fig. 12 addresses the service level result of the three models. No surprise that the DP model delivers more service level over the other two. As can be guessed, lack of integration between sales and production caused the model to accept as much orders as it can, without production capacity considerations, leading to more back-order and back-sales cost.

As a notification, the operational utilization (OU) of the system is depicted in Fig. 13. Again, the decoupled model includes higher OU than the partially integrated and fully integrated models. OU indicates the level of the capacity saturation of the factory, which is about 720,000 kilotons per year. So obviously, more production means more capacity saturation of the system.

Fig. 12

Customer service level (CSL) of the three fuzzy models

Fig. 13

Operational utilization (OU) of the three fuzzy models

5.3 Sensitivity analysis

In this section, a sensitivity analysis is carried out in order to find the effect of the objectives weight on the behavior of the three developed models. The results of the sensitivity analysis are illustrated in Table 2, representing the benefits of the FI-S&OP model on PI-S&OP and DP models, respectively. It should be noted again that all the calculations are based on the most possible value of the cost parameters.

Fig. 14

Service level versus a SC cost trade-off

Fig. 15

The behavior of the three fuzzy models with different objective weights

Table 2 Sensitivity analysis results for different objective weights

As can be seen in Table 2, the results approve the fact that along with increase in CSL, the SC cost will increase, exponentially. So, we should find a way to achieve a compromise solution between CSL and SC cost, which keeps both objectives in balance (Fig. 14).

Fig. 16

The behavior of fuzzy FI-S&OP model under different weights of three equivalent crisp objectives

Fig. 17

The behavior of fuzzy and crisp FI-S&OP objective under different weights of three equivalent crisp objectives

The benefits of the FI-S&OP model over DP are completely intense, while the superiority of the model over the PI-S&OP model is moderate. As discussed earlier, the savings in transportation cost from integrated sales and distribution planning were reported in numerous studies, before (Chandra and Fisher 1994; Fumero and Vercellis 1999). However, the benefits from integration of sales decisions in supply chain planning context are not well documented.

As depicted in Fig. 15, our sensitivity analysis approves that the behavior of fully integrated and partially integrated models is pretty similar to different objective weights. This is because of the integrated sales and production decisions, which prevents accepting excessive orders and imposing back-order and back-sales cost, consequently. On the other side, the benefits of fully integrated and partially integrated models over the decoupled planning model are pretty intense, under all objective weights. As can be seen, the SC cost is going to increase dramatically, when decision maker (DM) desires to tune the system for achieving CSL over 95%, while the CSL of 95%—which is very common in SC design—in fully integrated and even partially integrated models is easily achievable with a reasonable cost.

In order to compare our fuzzy model with the crisp one, we can evaluate the impact of fuzzy modeling from two aspects: maximizing the possibility of obtaining lower cost and minimizing the risk of obtaining higher cost. As we mentioned, each fuzzy objective is equivalent to three crisp objectives which should be optimized, simultaneously as follows:

• $f_1 =\left\{ {min\left( {c^{m}} \right) } \right\} :$ minimizing the most possible value of the total supply chain cost;

• $f_2 =\left\{ {max\left( {c^{m}-c^{o}} \right) } \right\} :$ maximizing the possibility of obtaining lower objective value;

• $f_3 =\left\{ {min\left( {c^{p}-c^{m}} \right) } \right\} :$ minimizing the risk of obtaining higher objective value.

Unlike the crisp modeling, we will have different results under different weights for above three objectives. Meaning that based on the preference of the DM, the model will produce different compromised solutions.

In order to show the above advantage, we applied four different weights for the mentioned three equivalent crisp objectives (Table 3).

Table 3 Weights of three equivalent crisp objectives

The behavior of the fuzzy FI-S&OP model under different weights of three equivalent objectives is depicted in Fig. 16, where the DM can select the compromised solution, based on his/her preferences. Also Fig. 17 shows the difference between the result of the fuzzy FI-S&OP model and the crisp one, in terms of SC cost.

6 Conclusion and future research

Three different bi-objective f-MILP models were developed in this study, in order to show different planning integration levels. Each model tries to minimize the total SC cost, while maximizing the CSL, simultaneously: a fully integrated S&OP (FI-S&OP) approach, which integrates the planning functions of sales, production, distribution and procurement; a partially integrated S&OP (PI-S&OP), which sales and production planning are carried out jointly and centrally, while distribution and procurement planning is performed discretely in each site; and a decoupled planning (DP) approach which demonstrate the traditional planning condition, where the sales planning takes place centrally and the other planning functions are being executed separately in each site. After that, we evaluated the functionality of the models, using real data, through a case study in massive size dairy manufacturing supply chain. Finally, a sensitivity analysis took place in order to investigate the benefits of planning integration, by trading off between the two objectives of the models, which are SC cost and CSL. Also, a comparison between the fuzzy and crisp modeling was executed to show the advantages of the fuzzy mathematical modeling.

The results demonstrate the absolute dominance of FI-S&OP model over DP and slight superiority over the PI-S&OP model, under different weights of the objective functions. According to this and by considering the pre-requisites of implementing the planning integration over the whole chain, including hardware and software infrastructures, skills and qualifications, cultural issues, etc., the companies in FMCG segment are being recommended to move along the integration track, no matter they have the capability of achieving the best in class, full integration, at least they can benefit from the partial integration of sales and production.

The mathematical models of this study were developed through the MTS logic. Thus, there will be possibility to develop FI-S&OP model in make to order (MTO) or even more sophisticated environments such as build to order (BTO). In real world, at tactical planning level, the production decisions in both MTS and MTO systems are being made using forecasts. Therefore, other suggestions of this study can be the investigation of the effect of the demand forecast error on FI-S&OP benefits over the PI-S&OP and DP models in stable demand environment. On the other hand, since the pricing procedure is being taken place in marketing division, the integration of marketing decisions, including fixed or dynamic pricing in S&OP, could be addressed in another study. Furthermore, since the output of S&OP, as a set of aligned demand and supply decisions, should be affordable by the company, including the financial review of the S&OP scenarios, by assuming the budget limitations can be considered as an extension of this study. Finally, the new product development (NPD) as an undeniably permanent part of the strategic decision-making process in pioneer companies can be included in mathematical modeling of the S&OP.