An inventory model under price and stock dependent demand for controllable deterioration rate with shortages and preservation technology investment

Abstract

This paper develops an EOQ inventory model that considers the demand rate as a function of stock and selling price. Shortages are permitted and two cases are studied: (i) complete backordering and (ii) partial backordering. The inventory model is for a deteriorating seasonal product. The product’s deterioration rate is controlled by investing in the preservation technology. The main purpose of the inventory model is to determine the optimum selling price, ordering frequency and preservation technology investment that maximizes the total profit. Additionally, the paper proves that the total profit is a concave function of selling price, ordering frequency and preservation technology investment. Therefore, a simple algorithm is proposed to obtain the optimal values for the decision variables. Several numerical examples are solved and studied along with a sensitivity analysis.

1 Introduction

The economic order quantity (EOQ) inventory model was introduced a century ago by Harris (1913). It is well known that the EOQ balances inventory holding and setup costs in order to determine the optimal lot size. It is worth mentioning that the EOQ inventory model is still applied in many organizations today. Furthermore, the EOQ inventory model has been extended considering the deterioration effect. Deterioration means spoilage, decay or damage. Therefore, it is necessary to consider the deterioration rate in the development of inventory models. In the recent years, the management of stock level of deteriorating products considering shortages has attracted a considerable interest of some researchers and academicians around the world because the majority of the products deteriorate thru time. Thus, the damage due to deterioration must not be ignored. Consequently, the deterioration of products in inventory is an actual characteristic that is necessary to study its effect on inventory. Goyal and Giri (2001) proposed several tendencies of the modelling of deteriorating inventory. On the one hand, there exist several inventory models that take into account constant deterioration rate, Weibull deterioration rate, and linear time fluctuating demand. These inventory models were developed by Goswami and Chaudhuri (1991), Chakrabarti and Chaudhuri (1997), Giri et al. (2000), Yang (2010), Skouri et al. (2011), Mishra (2015), Shah (2015), Taleizadeh et al. (2016), among others. On the other hand, Jalan and Chaudhuri (1999) developed inventory models with constant deterioration, constant demand, and instantaneous replenishment. Furthermore, there also exist inventory models with a fixed deteriorating rate and an exponential time fluctuating demand and these were derived by Hariga and Benkherouf (1994) and Wee (1995). The situation of deterioration and permissible shortages is dealt in Jamal et al. (1997) and Chang and Dye (2001).

Wee (1997) built a replenishment policy for products with a price dependent demand and variable deterioration rate. At the same time, Burwell et al. (1997) derived an economic lot size model for price dependent demand considering quantity and freight discounts. Afterwards, Lin et al. (2000) presented an EOQ inventory model with time fluctuating demand, partial backordering, and linear time dependent deterioration rate. After, Mondal et al. (2003) proposed an inventory model for ameliorating products considering price dependent demand. Later, You (2005) developed an inventory model with price and time dependent demand.

In many situations of real life the selling price may not be constant. Therefore, it is significant for a retailer to select worthy pricing and replenishment policies when the demand rate is stock dependent and sensitive with regard to selling price. In this direction, Datta and Paul (2001) developed a finite horizon inventory model with stock dependent and price sensitive demand rate. Teng and Chang (2005) proposed an economic production quantity (EPQ) inventory model for deteriorating products whose demand is a function of selling price and the stock. In addition, they imposed a ceiling on the number of display stocks due to limited shelf space. One year later, Hou (2006) presented an inventory model for deteriorating products with stock dependent consumption rate and shortages under inflation and time discounting for a finite horizon time. However, Hou (2006) did not consider the potential profit from increased demand due to the stock on display. In this line, Hou and Lin (2006) extended Hou (2006)’s inventory model taking into account that the demand is a function of both stock level and selling price. Afterwards, Yang (2010) extended Hou (2006)’s inventory model to permit shortages with partial backlogging but with known selling price. Conversely, Dye and Hsieh (2011) derived a deterministic ordering policy with price and stock dependent demand under fluctuating cost and limited capacity permitting shortages. Later, Pal et al. (2014) developed an inventory model that permits shortages with full backlogging taking into account price and stock dependent demand rate with deterioration under inflation and delay in payment. Sarkar et al. (2014) proposed an EPQ inventory model for deteriorating items with two-level trade credit for fixed lifetime products. Jaggi et al. (2017) developed two-warehouse inventory model for non-instantaneous deteriorating items under trade credit policy.

Nevertheless, the deterioration rate in the research articles mentioned previously is addressed as an exogenous variable, either constant or varying thru time, which is not under control. In fact, several organizations have recognized that it is not worthy to manage and control the product’s deterioration rate and have implemented several actions, for example process improvement and enhancing storage technology in order to control and reduce the deterioration effects. Furthermore, thru an effective investment in decreasing the deterioration rate, the organizations avoid unnecessary waste and reduce obviously economic losses and therefore improve their business competitiveness.

Hsu et al. (2010) built a deterioration inventory model considering constant demand, deterioration rate, and preservation technology investment that reduces the deterioration rate of products. After, Dye and Hsieh (2012) extended Hsu et al. (2010)’s inventory model permitting time varying deterioration rate. The central purpose of their inventory model is to derive the optimal replenishment and preservation technology investment policies. Later, Hsieh and Dye (2013) proposed a production inventory model with controllable deterioration rate and time dependent demand. They determined the optimal production and preservation technology investment policies that minimize the total cost by applying a particle swarm optimization algorithm. One year later, Dye (2013) presented a preservation technology investment in a non-instantaneous deteriorating inventory model under the fraction of shortages. Afterwards, Zhang et al. (2014) proposed a pricing policy for deteriorating products with preservation technology investment without shortage and stock. Recently, Mishra (2015) established an inventory model for deteriorating products under trapezoidal type demand and controllable deterioration rate considering that the demand is not dependent on stock.

Notice that almost all products are price sensitive. Some of them are highly price sensitive and others are less. Consequently, a more general and representative inventory model is one that considers the demand as a function of both stock level and selling price. Evidently, the demand is a decreasing function of selling price and an increasing function of stock level. In this case, the problem is to fix the selling price of products to determine the order quantity and the reorder level that minimizes the total cost. Sometimes, it is necessary to sell the product within a prescribed time period, after which there is no substantial demand or the product converts obsolete. The research work’s motivation is to develop a more general inventory model for deteriorating seasonal product that includes: (a) price and stock dependent demand rate, and (b) shortages with complete and partial backordering. In this inventory model the deterioration rate is controlled by preservation technology investment. The decision variables of the inventory model are the selling price, the ordering frequency, and the preservation technology investment. A research work related to this paper is the study of He and Huang (2013). They developed an inventory and pricing policy for seasonal deteriorating products with preservation technology investment but their inventory model does not consider shortages, stock dependent demand and deterioration cost. This paper includes the three issues previously mentioned. Therefore, the present paper is a general model and He and Huang (2013) is a special case. Liu et al. (2015) studied the joint effect of dynamic pricing and preservation technology for a price and quality dependent demand. Zhang et al. (2015, 2016) dealt with an integrated supply chain model for deteriorating items, in which both manufacturer and retailer cooperatively invest in preservation technology in order to reduce their deterioration cost under different realistic scenarios. Liu et al. (2015) developed an inventory model for deteriorating items which jointly determines the selling price, preservation technology investment, cycle length and dynamic service investment. Lu et al. (2016) were the first to study the joint dynamic pricing and replenishment policy for a deteriorating item under limited capacity. Table 1 presents some related research to this paper.

Table 1 Summary of the related research

The rest of the paper is organized as follows. Section 2, provides the fundamental notations and assumptions of the proposed inventory model. Section 3 discusses the two mathematical models for the inventory system (i) with complete backordering and (ii) with partial backordering. Section 4 derives theoretical results and optimal solutions. Section 5 presents special cases which can be obtained from proposed inventory model. Section 6 presents and solves some numerical examples in order to illustrate the proposed inventory model. Section 7 does a sensitivity analysis. Finally, Sect. 8 gives some conclusions suggestions for future research.

2 Notation and assumptions

2.1 Notation

The notation is given below:

Decision variables
n	Ordering frequency (an integer number)
$\alpha$	Cost of preservation technology investment per unit time ($/unit/time unit)
p	Selling price ($/unit)
Dependent decision variables
Q	Ordering quantity (units)
$D_\tau$	Total number of products that become deteriorated during the interval $\left[ {0,t_1 } \right]$ (units)
Constant parameters
$t_1$	Time when the inventory level comes down to zero (time unit)
T	Inventory cycle length (time unit)
$\lambda (\alpha )$	Deterioration rate when there is investing on preservation technology (units/time unit)
$\lambda _0$	Deterioration rate without preservation technology investment (units/time unit)
$\delta$	Sensitive parameter of investment to the deterioration rate
$\beta$	Stock dependent consumption rate parameter
D(p, t)	Demand rate function is a function of instantaneous stock level I(t) and the selling price p (units/time unit)
D(p)	Market demand (units/time unit)
a	Demand scale
b	Price sensitive parameter
d	Deterioration cost ($/unit)
c	Buying cost ($/unit)
h	Inventory holding cost ($/unit/time unit)
s	Shortage cost ($/unit/time unit)
$c_{1}$	Unit opportunity cost due to lost sale, if the shortage is lost ($/unit)
A	Ordering cost per order ($/order)
$\eta$	Backordering parameter
I(t)	Inventory level at a time point (units)
S(T / n)	Maximum shortage level for complete backordering (units)
B(t)	Backorder level at any time t for partial backordering (units)
L(t)	Number of lost sales at any time t (units)
B(T / n)	Maximum backorder level for partial backordering (units)
SR	Sales revenue ($/time unit)
PC	Purchase cost ($/time unit)
HC	Holding cost ($/time unit)
SC	Shortage cost ($/time unit)
LSC	Lost sale cost ($/time unit)
DC	Deterioration cost ($/time unit)
OC	Ordering cost ($/time unit)
PTC	Preservation technology cost ($/time unit)
TP	Total profit of the selling season ($/time unit)

2.2 Assumptions

The inventory model is developed considering the following assumptions:

• (1) A single supplier, a single manufacturer and a single product are considered.

• (2) The demand rate function D(p, t) is a function of instantaneous stock level I(t) and the selling price p. The function D(p, t) is given by:

  $$\begin{aligned} D(p,t)=\left\{ {\begin{array}{ll} D(p)+\beta I(t) ,&{} I(t)>0, \\ D(p) , &{}I(t)\le 0, \\ \end{array}} \right. \end{aligned}$$

  $\beta$ is stock dependent consumption rate parameter and it is within the interval $0\le \beta \le 1.$ Here, two type of demand functions are considered: (1) $D(p)=a-bp$ where a is demand scale and b is price sensitive parameter and (2) $D(p)=ap^{-r}$ where a is demand scale and r is price sensitive parameter.

• (3) The demand only exists in a finite time horizon T.

• (4) Shortages are permitted and these can be complete backordered or partial backordered.

• (5) Lead time is zero.

• (6) The relationship of deterioration rate and the preservation technology investment parameter satisfies the following $\partial \lambda (\alpha )/\partial \alpha <0 ,\partial ^{2}\lambda (\alpha )/\partial \alpha ^{2}>0$. Therefore, this research work considers that $\lambda (\alpha )=\lambda _0 e^{-\delta \alpha }$; where,$\lambda (\alpha )$ is the deterioration rate when there is investing on preservation technology, $\lambda _0$ is the deterioration rate without preservation technology investment, and $\delta$ is the sensitive parameter of investment to the deterioration rate.

• (7) The cost of preservation technology investment per unit time is constrained to $\alpha \in \left[ {0,\bar{{\alpha }}} \right]$.

3 Mathematical model

Given the above notation and assumptions, the proposed EOQ inventory models have two situations: (i) with shortages and complete backordering and (ii) with shortages and partial backordering. The detailed derivation of these EOQ inventory models are given below.

3.1 The EOQ inventory model with complete backordering

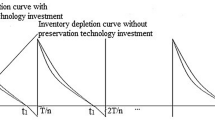
The inventory model has two trade-offs. The first one is the trade-off among the ordering frequency and the ordering cost per order. Obviously, when the order frequency is increased, the deteriorating cost decreases. However, the ordering cost rises. The second one is the trade-off among the preservation technology investment and the deteriorating cost. Clearly, if the preservation technology investment is incremented then the deteriorating cost decrements. Basically, this paper derives a single retailer’s inventory policy considering that the deterioration rate is changed by the preservation technology investment. Thus, a mathematical model is proposed in order to obtain the optimal selling price, ordering frequency and preservation technology investment that maximize the total profit for an inventory system with controllable deteriorating products when the demand is stock and price dependent and shortages permitted. Here, I(t) represents the inventory level at any time in the interval $0\le t\le T/n$. It is important to remark that the inventory level I(t) diminishes due to both the demand and deterioration of the product within of period $\left[ {0,t_1 } \right]$ and finally drops to zero at $t=t_1$. Subsequently, shortages are permitted to happen and whole demand in the period $\left[ {t_1 ,T/n} \right]$ is entirely backordered. According to the notation and assumptions mentioned previously, the behaviour of inventory system at any time is shown in Fig. 1.

Fig. 1

Graphical representation of the inventory system with complete backordering

The differential equations which represent the inventory level are expressed below;

$$\begin{aligned} \frac{dI(t)}{dt}+\lambda (\alpha )I(t)=-D(p,t)-\beta I(t) , \quad if\; 0\le t\le t_1 , \end{aligned}$$

(1)

and

$$\begin{aligned} \frac{dI(t)}{dt}=-D(p), \quad { if}\; t_1 \le t\le T/n \end{aligned}$$

(2)

Considering the boundary condition $I(t)=0$ at $t=t_1.$ The solutions of Eqs. (1) and (2) are given by;

$$\begin{aligned} \frac{dI(t)}{dt}=\left\{ {\begin{array}{ll} \frac{D(p)}{\lambda (\alpha )+\beta } \left( {e^{\left( {\lambda (\alpha )+\beta } \right) \left( {t_1 -t} \right) }-1} \right) ,&{} { if}\; 0\le t\le t_1 \\ D(p)(t_1 -t) , &{}{ if}\; t_1 \le t\le T/n \\ \end{array}} \right. \end{aligned}$$

(3)

The initial inventory level (S) for each cycle is calculated with

$$\begin{aligned} S=I(0)=\frac{D(p)}{\lambda (\alpha )+\beta } \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-1} \right) \end{aligned}$$

(4)

The total number of products that become deteriorated during the interval $\left[ {0,t_1 } \right]$, say $D_\tau$, is computed as

$$\begin{aligned} D_\tau =S-\int _0^{t_1 } {D(p)dt=S-D(p)t_1 } =\frac{D(p)}{\lambda (\alpha )+\beta } \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 -t_1 } \right) \end{aligned}$$

(5)

Therefore, the order quantity per cycle is determined with $Q=D_\tau +\int _0^{T/n} {D(p)dt=} D_\tau +\frac{D(p)T}{n}$

$$\begin{aligned} \Rightarrow Q=\frac{D(p)}{\lambda (\alpha )+\beta } \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 +\frac{\left( {\lambda (\alpha )+\beta } \right) T}{n}-t_1 } \right) \end{aligned}$$

(6)

The maximum amount of shortages per cycle is

$$\begin{aligned} S(T/n)=D\left( p \right) \left( {\frac{T}{n}-t_1 } \right) \end{aligned}$$

(7)

Now, the total profit of the inventory system is calculated using the following components:

$$\begin{aligned} \mathrm{(1)}\ \text {Sales revenue: }{} \textit{SR}=pD(p)T \end{aligned}$$

(8)

$$\begin{aligned} \mathrm{(2)}\ \text {Purchase cost:}{} \textit{PC}=ncQ=\frac{ncD(p)}{\lambda (\alpha )+\beta } \left\{ {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 +\frac{\left( {\lambda (\alpha )+\beta } \right) T}{n}-t_1 } \right\} \nonumber \\ \end{aligned}$$

(9)

$$\begin{aligned} \mathrm{(3)}\ \text {Holding cost: } \textit{HC}=hnD(p)\int \limits _0^{t_1 } {I(t)dt} =hnD(p)\left\{ {\frac{e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-t_1 \left( {\lambda (\alpha )+\beta } \right) -1}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}} \right\} \nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned} \mathrm{(4)}\ \text {Shortage cost:}{} \textit{SC}=ns\int \limits _{t_1 }^{T/n} {I(t)dt=nsD(p)\left( {\frac{t_1 T}{n}-\frac{t_1 ^{2}}{2}-\frac{T^{2}}{n^{2}}} \right) } \end{aligned}$$

(11)

(5) Deterioration cost: $\textit{DC}=nd\left[ {Q-\int \limits _0^{t_1 } {(D(p)+\beta I(t))dt} } \right]$

$$\begin{aligned} \Rightarrow \textit{DC}= & {} \frac{ndD(p)}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}\left\{ {\left( {\lambda (\alpha )+\beta } \right) e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 +\left( {\lambda (\alpha )+\beta } \right) T/n} \right. \nonumber \\&\left. {-t_1 -t_1 \left( {\lambda (\alpha )+\beta } \right) -\beta \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-t_1 \left( {\lambda (\alpha )+\beta } \right) -1} \right) } \right\} \end{aligned}$$

(12)

$$\begin{aligned} \mathrm{(6)}\ \text {Ordering cost: }{} \textit{OC}=nA \end{aligned}$$

(13)

$$\begin{aligned} \mathrm{(7)}\ \text {Preservation technology cost: }{} \textit{PTC}=\alpha T \end{aligned}$$

(14)

Hence, the total profit of the inventory system is expressed by

$$\begin{aligned} \textit{TP}= & {} \textit{SR}-(\textit{PC}+\textit{HC}+\textit{SC}+\textit{DC}+\textit{OC}+\textit{PTC})\nonumber \\ \Rightarrow \textit{TP}= & {} pD(p)T-\frac{ncD(p)}{\lambda (\alpha )+\beta } \left\{ {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 +\frac{\left( {\lambda (\alpha )+\beta } \right) T}{n}-t_1 } \right\} \nonumber \\&-\,hnD(p)\left\{ {\frac{e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-t_1 \left( {\lambda (\alpha )+\beta } \right) -1}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}} \right\} -nsD(p)\left\{ {\frac{t_1 T}{n}-\frac{t_1 ^{2}}{2}-\frac{T^{2}}{n^{2}}} \right\} \nonumber \\&-\,\frac{ndD(p)}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}\left\{ {\left( {\lambda (\alpha )+\beta } \right) e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 +\left( {\lambda (\alpha )+\beta } \right) T/n} \right. \nonumber \\&\left. {-\,t_1 -t_1 \left( {\lambda (\alpha )+\beta } \right) -\beta \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-t_1 \left( {\lambda (\alpha )+\beta } \right) -1} \right) } \right\} -nA-\alpha T \end{aligned}$$

(15)

Let $t_1 =\frac{\gamma T}{n} , 0<\gamma <1$. Thus, the total profit function is;

$$\begin{aligned}&\textit{TP}(n,\alpha ,p)\nonumber \\&\quad =pD(p)T-\frac{ncD(p)}{\lambda (\alpha )+\beta } \left\{ {e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}+\frac{\left( {\lambda (\alpha )+\beta } \right) T}{n}-\frac{\gamma T}{n}} \right\} \nonumber \\&\qquad -\,hnD(p)\left\{ {\frac{e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\frac{\gamma T}{n}\left( {\lambda (\alpha )+\beta } \right) -1}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}} \right\} -nsD(p)\left\{ {\frac{\gamma T^{2}}{n^{2}}-\frac{\gamma ^{2}T^{2}}{2n^{2}}-\frac{T^{2}}{n^{2}}} \right\} \nonumber \\&\qquad -\,\frac{ndD(p)}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}\left\{ {\left( {\lambda (\alpha )+\beta } \right) e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}+\left( {\lambda (\alpha )+\beta } \right) T/n} \right. \nonumber \\&\qquad \left. {-\,\frac{\gamma T}{n}-\frac{\gamma T}{n}\left( {\lambda (\alpha )+\beta } \right) -\beta \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\frac{\gamma T}{n}\left( {\lambda (\alpha )+\beta } \right) -1} \right) } \right\} -nA-\alpha T\nonumber \\ \end{aligned}$$

(16)

Hence, the non-linear optimization problem is as follows:

$$\begin{aligned}&\max \textit{TP}(n,\alpha ,p) \\&\text {subject to} \\&D(p)>0 \\&p>0 \\&n\ge 1\text { and discrete} \\&0\le \alpha \le \bar{{\alpha }} \\ \end{aligned}$$

It is worthwhile mentioning here that in order to optimize the above non-linear optimization problem first the objective function is simplified and then some theorems and algorithm are proposed.

For a small x value, the Taylor series says that the exponential function has an approximation of $e^{x}\approx 1+x+\frac{x^{2}}{2!}$.Using this result into Eq. (16), it is obtained the following:

$$\begin{aligned} \textit{TP}(n,\alpha ,p)= & {} pD(p)T-\frac{cD(p)}{\lambda (\alpha )+\beta }\left\{ {n+\frac{\gamma ^{2}T^{2}}{2n}\left( {\lambda (\alpha )+\beta } \right) ^{2}+\left( {\lambda (\alpha )+\beta } \right) T-\gamma T} \right\} \nonumber \\&-\,hD(p)\left( {\frac{\gamma ^{2}T^{2}}{2n}} \right) -sD(p)\left( {\frac{\gamma T^{2}}{n}-\frac{\gamma ^{2}T^{2}}{2n}-\frac{T^{2}}{n}} \right) \nonumber \\&-\frac{dD(p)}{\lambda (\alpha )+\beta }\left\{ n+\frac{\gamma ^{2}T^{2}}{2n}\left( {\lambda (\alpha )+\beta } \right) ^{2}+\left( {\lambda (\alpha )+\beta } \right) T-\gamma T \right\} \nonumber \\&-\,dD(p)\gamma T-\frac{\beta dD(p)\gamma ^{2}T^{2}}{2n}-nA-\alpha T \end{aligned}$$

(17)

Fig. 2

Graphical representation of the inventory system with partial backordering

3.2 The EOQ inventory model with partial backordering

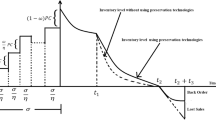
In this inventory model the first differential equation representing inventory level during period $\left[ {0,t_1 } \right]$ is similar to Sect. 3.1. Additionally (Fig. 2),

$$\begin{aligned} \frac{dB\left( t \right) }{dt}=D(p)e^{-\eta \left( {\frac{T}{n}-t} \right) } ,\; if\; t_1 \le t\le T/n . \end{aligned}$$

(18)

Using boundary conditions $B(t_1 )=0$ the solutions of the above differential equation is

$$\begin{aligned} B\left( t \right) =\frac{D\left( p \right) }{\eta }\left\{ {e^{-\eta \left( {\frac{T}{n}-t} \right) }-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right\} ,\quad { if}\; t_1 \le t\le T/n \end{aligned}$$

(19)

The number of lost sales at time t is given by

$$\begin{aligned} L(t)= & {} \int \limits _{t_1 }^t {D\left( p \right) \left\{ {1-e^{-\eta \left( {\frac{T}{n}-t} \right) }} \right\} dt};\quad { if}\; t_1 \le t\le T/n\nonumber \\ L(t)= & {} D\left( p \right) \left\{ {\left( {t-t_1 } \right) -\frac{1}{\eta }\left( {e^{-\eta \left( {\frac{T}{n}-t} \right) }-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) } \right\} \end{aligned}$$

(20)

Putting $t=\frac{T}{n}$ into Eq. (19), the maximum backorder level per cycle is

$$\begin{aligned} B\left( {\frac{T}{n}} \right) =\frac{D\left( p \right) }{\eta }\left( {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) \end{aligned}$$

(21)

Therefore, the order quantity over the replenishment cycle is determined as

$$\begin{aligned} Q= & {} S+B\left( {\frac{T}{n}} \right) \nonumber \\ Q= & {} \frac{D(p)}{\lambda (\alpha )+\beta } \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-1} \right) +\frac{D\left( p \right) }{\eta }\left( {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) \end{aligned}$$

(22)

The shortage cost (SC) is $ns\int _{t_1 }^{T/n} {B\left( t \right) dt}$

$$\begin{aligned} \textit{SC}=\frac{nsD\left( p \right) }{\eta }\left\{ {\frac{1}{\eta }\left( {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) -\left( {\frac{T}{n}-t_1 } \right) e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right\} \end{aligned}$$

(23)

The opportunity cost due to lost sale (LSC) $=nc_1 \int _{t_1 }^{T/n} {\left\{ {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right\} D\left( p \right) dt}$

$$\begin{aligned} \textit{LSC}=nc_1 D\left( p \right) \left\{ {\left( {\frac{T}{n}-t_1 } \right) -\frac{1}{\eta }\left( {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) } \right\} \end{aligned}$$

(24)

Hence, the total profit of the inventory system is expressed by

$$\begin{aligned} \textit{TP}= & {} \textit{SR}-(\textit{PC}+\textit{HC}+\textit{SC}+\textit{LSC}+\textit{DC}+\textit{OC}+\textit{PTC})\nonumber \\ \Rightarrow \textit{TP}= & {} pD(p)T-\frac{ncD(p)}{\lambda (\alpha )+\beta } \left\{ {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 +\frac{\left( {\lambda (\alpha )+\beta } \right) T}{n}-t_1 } \right\} \nonumber \\&-\,hnD(p)\left\{ {\frac{e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-t_1 \left( {\lambda (\alpha )+\beta } \right) -1}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}} \right\} \nonumber \\&-\,\frac{nsD\left( p \right) }{\eta }\left\{ {\frac{1}{\eta }\left( {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) -\left( {\frac{T}{n}-t_1 } \right) e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right\} \nonumber \\&-\,nc_1 D\left( p \right) \left\{ {\left( {\frac{T}{n}-t_1 } \right) -\frac{1}{\eta }\left( {1-e^{-\eta \left( {\frac{T}{n}-t_1 } \right) }} \right) } \right\} \nonumber \\&-\,\frac{ndD(p)}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}\left\{ {\left( {\lambda (\alpha )+\beta } \right) e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-\left( {\lambda (\alpha )+\beta } \right) t_1 } \right. \nonumber \\&\left. {+\,\left( {\lambda (\alpha )+\beta } \right) T/n-t_1 -t_1 \left( {\lambda (\alpha )+\beta } \right) -\beta \left( {e^{\left( {\lambda (\alpha )+\beta } \right) t_1 }-t_1 \left( {\lambda (\alpha )+\beta } \right) -1} \right) } \right\} \nonumber \\&-\,nA-\alpha T \end{aligned}$$

(25)

Let $t_1 =\frac{\gamma T}{n} , 0<\gamma <1$. Thus, the total profit function is;

$$\begin{aligned} \textit{TP}(n,\alpha ,p)= & {} pD(p)T-\frac{ncD(p)}{\lambda (\alpha )+\beta } \left\{ e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}\right. \nonumber \\&\left. +\,\frac{\left( {\lambda (\alpha )+\beta } \right) T}{n}-\frac{\gamma T}{n} \right\} \nonumber \\&-\,hnD(p)\left\{ {\frac{e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\frac{\gamma T}{n}\left( {\lambda (\alpha )+\beta } \right) -1}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}} \right\} \nonumber \\&-\,\frac{nsD\left( p \right) }{\eta }\left\{ {\frac{1}{\eta }\left( {1-e^{-\eta \left( {1-\gamma } \right) \frac{T}{n}}} \right) -\left( {1-\gamma } \right) \frac{T}{n}e^{-\eta \left( {1-\gamma } \right) \frac{T}{n}}} \right\} \nonumber \\&-\,nc_1 D\left( p \right) \left\{ {\left( {1-\gamma } \right) \frac{T}{n}-\frac{1}{\eta }\left( {1-e^{-\eta \left( {1-\gamma } \right) \frac{T}{n}}} \right) } \right\} \nonumber \\&-\,\frac{ndD(p)}{\left( {\lambda (\alpha )+\beta } \right) ^{2}}\left\{ {\left( {\lambda (\alpha )+\beta } \right) e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}} \right. \nonumber \\&+\,\left( {\lambda (\alpha )+\beta } \right) T/n-\frac{\gamma T}{n}-\frac{\gamma T}{n}\left( {\lambda (\alpha )+\beta } \right) \nonumber \\&\left. -\,\beta \left( {e^{\left( {\lambda (\alpha )+\beta } \right) \frac{\gamma T}{n}}-\frac{\gamma T}{n}\left( {\lambda (\alpha )+\beta } \right) -1} \right) \right\} -nA-\alpha T \end{aligned}$$

(26)

Remember that for a small x value, the Taylor series establishes that the exponential function can be approximated to $e^{x}\approx 1+x+\frac{x^{2}}{2!}$. As a direct consequence of using this result into Eq. (26), it is derived the following:

$$\begin{aligned} \textit{TP}(n,\alpha ,p)= & {} pD(p)T-\frac{cD(p)}{\lambda (\alpha )+\beta }\left\{ {n+\frac{\gamma ^{2}T^{2}}{2n}\left( {\lambda (\alpha )+\beta } \right) ^{2}+\left( {\lambda (\alpha )+\beta } \right) T-\gamma T} \right\} \nonumber \\&-\,hD(p)\left( {\frac{\gamma ^{2}T^{2}}{2n}} \right) -snD(p)\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{n^{2}}-nc_1 D(p)\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{n^{2}}\nonumber \\&-\,\frac{dD(p)}{\lambda (\alpha )+\beta }\left\{ {\begin{array}{l} n+\frac{\gamma ^{2}T^{2}}{2n}\left( {\lambda (\alpha )+\beta } \right) ^{2} \\ +\left( {\lambda (\alpha )+\beta } \right) T-\gamma T \\ \end{array}} \right\} \nonumber \\&-\,dD(p)\gamma T-\frac{\beta dD(p)\gamma ^{2}T^{2}}{2n}-nA-\alpha T \end{aligned}$$

(27)

4 Theoretical results and optimal solution

This section establishes some theoretical theorems which prove the concavity of retailer’s total profit TP(n, $\alpha$, p). First, the case of shortages with complete backordering is discussed, and then the case in which shortages are partially backordered.

4.1 The EOQ inventory model with complete backordering

Theorem 1

When selling price p and preservation cost $\alpha$ are fixed, the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (17) is concave with respect to ordering frequency n.

Proof

Refer to “Appendix 1”. $\square$

Theorem 2

For known n and fixed p, the following is stated:

• (1) If $\Delta _1 (n,p)\le 0\; \mathrm{then}\; \textit{TP}(n,\alpha ,p)$ reaches its maximum value at $\alpha ^{*}=0.$

• (2) If $\Delta _2 (n,p)\ge 0\; \mathrm{then}\; \textit{TP}(n,\alpha ,p)$ attains its maximum value at $\alpha =\bar{{\alpha }}.$

• (3) If $\Delta _1 (n,p)>0 ,\; and\; \Delta _2 (n,p)<0\; \mathrm{then} \; \textit{TP}(n,\alpha ,p)$ is concave and achieves its global maximum at point $\alpha ^{*}\in (0,\bar{{\alpha }})$ when $\frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial \alpha }=0$.

Proof

Refer to “Appendix 2”. $\square$

It is worth mentioning that while the initial deterioration rate is very low or the efficiency of the invested capital is small then there is not necessary to spend money in preservation technology because it is not beneficial. Moreover, if there exists a constraint of the investment capital then there might be a possibility for the organization to acquire more profit.

Theorem 3

There exists a unique $p^{*}$ that maximizes profit function $\textit{TP}(n,\alpha ,p)$ for fixed values of n and $\alpha$.

Proof

Refer to “Appendix 3”. $\square$

Theorem 4

For fixed n, the optimal solution $(\alpha ^{*},p^{*})$ which maximizes the profit function $\textit{TP}(n,\alpha ,p)$ exists and is unique.

Proof

The optimal solution is easily obtained thru an iterative algorithm. $\square$

Using the four theorems obtained previously, the following iterative algorithm is developed. Notice that this algorithm is similar to the He and Huang (2013)’s algorithm.

Algorithm

• Step 1. Initialize $n=1.$

• Step 2. Initialize $m=1$and set the value of $p^{m}=p_0 .$

• Step 3. Compute $\Delta _1 (n,p),\Delta _2 (n,p)$ and perform any one of the following three cases 1, 2 or 3.

  • (1) If $\Delta _1 (n,p)\le 0,$ then $\alpha _1^m =0$. Determine $p_1^m$ from Eq. (34).

  • (2) If $\Delta _2 (n,p)\ge 0,$ then $\alpha _1^m =\bar{{\alpha }}$. Calculate $p_1^m$ from Eq. (34).

  • (3) If $\Delta _1 (n,p)>0$ and $\Delta _2 (n,p)<0$, Compute $\alpha _1^m$ by solving (32). Substitute the value of $\alpha _1^m$ into Eq. (34) and determine the corresponding value for $p_1^m$.

  Set $p^{m+1}=p_1^m$ and $\alpha ^{m}=\alpha _1^m$.

• Step 4. If $\left| {p^{m+1}-p^{m}} \right| \le 10^{-4}$, then $(\alpha ^{*},p^{*})=(\alpha ^{m},p^{m+1})$ and go to Step 5. Otherwise, set $m=m+1$ and go to Step 3.

• Set 5. Compute $\textit{TP}(n,\alpha ^{*},p^{*})$with Eq. (17) which is the maximum for the profit function for a fixed value of n.

• Step 6. Set ${n}'=n+1$, repeat Step 2 to 5 and find $\textit{TP}({n}',\alpha ^{*},p^{*})$ with Eq. (17). Go to Step 7.

• Step 7. If $\textit{TP}({n}',\alpha ^{*},p^{*})\ge \textit{TP}(n,\alpha ^{*},p^{*})$, set $n={n}'$. Go to Step 6. Otherwise go to Step 8.

• Step 8. Set $(n^{*},\alpha ^{*},p^{*})=(n,\alpha ^{*},p^{*})$ and $\textit{TP}(n,\alpha ^{*},p^{*})$as the optimal solution.

• Step 9. Compute the order quantity Q with Eq. (6).

• Step 10. Calculate shortage level using Eq. (7).

• Step 11. Determine the quantity of deteriorated items with Eq. (5).

4.2 The EOQ inventory model with partial backordering

Theorem 5

If the selling price p and preservation cost $\alpha$ are given then the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (27) is concave with respect to ordering frequency n.

Proof

Refer to “Appendix 4”.

Theorem 6

For known n and fixed p, the following is established:

• (1) If $\Delta _1 (n,p)\le 0\; \mathrm{then}\; \textit{TP}(n,\alpha ,p)$ achieves its maximum value at $\alpha ^{*}=0.$

• (2) If $\Delta _2 (n,p)\ge 0\; \mathrm{then}\; \textit{TP}(n,\alpha ,p)$ reaches its maximum value at $\alpha =\bar{{\alpha }}.$

• (3) If $\Delta _1 (n,p)>0 , and\; \Delta _2 (n,p)<0 \;\mathrm{then}\; \textit{TP}(n,\alpha ,p)$ is concave and has its global maximum at point $\alpha ^{*}\in (0,\bar{{\alpha }})$ when $\frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial \alpha }=0$.

Proof

The proof is omitted because it is similar to that of Theorem 2. $\square$

Theorem 7

There exists a unique $p^{*}$ that maximizes profit function $\textit{TP}(n,\alpha ,p)$ for fixed values of n and $\alpha$.

Proof

Refer to “Appendix 5”. $\square$

Theorem 8

For fixed n, the optimal solution $(\alpha ^{*},p^{*})$ that maximizes the profit function $\textit{TP}(n,\alpha ,p)$ exists and is unique.

Proof

The optimal solution is without difficulty determined with an iterative algorithm similar to given for complete backordering case with some slight modifications in its steps. The algorithm is shown in “Appendix 6”. $\square$

5 Special cases

This section discusses several special cases that can be obtained from the two proposed EOQ inventory models:

• (i) When b = 0 and $\beta =0$ (i.e. demand is constant), deterioration rate is time-dependent, and planning horizon is infinite $\left( {\mathrm{i.e.} n=0} \right)$, the EOQ inventory model with partial backordering of the present paper reduces to Dye and Hsieh (2012).

• (ii) If $D(p,t)=D\left( t \right)$ (i.e. demand is time dependent only), $\lambda (\alpha )=\lambda _0$ (i.e. deterioration rate is constant), $s \rightarrow \infty$ (i.e. no shortage), and planning horizon is infinite $\left( {\mathrm{i.e.} n=0} \right)$ then both EOQ inventory models of the present paper converts to Hsieh and Dye (2013).

• (iii) Considering that the demand is price dependent only $\left( {\mathrm{i.e.}\;\beta =0} \right)$, $\lambda (\alpha )=\lambda _0$ (i.e. deterioration rate is constant), $s \rightarrow \infty$ (i.e. no shortage), and planning horizon is infinite $\left( {\mathrm{i.e.}\; n=0} \right)$, both EOQ inventory models of this paper transforms to Zhang et al. (2014).

• (iv) Taking into account that the demand is price dependent only $\left( {\mathrm{i.e.}\;\beta =0} \right)$, $\lambda (\alpha )=0$ (i.e. no deterioration), $s \rightarrow \infty$ (i.e. no shortage), and planning horizon is infinite $\left( {\mathrm{i.e.}\;n=0} \right)$, both EOQ inventory models of the current paper changes to He and Huang (2013).

• (v) When b = 0 and $\beta =0$ (i.e. demand is constant), $\lambda (\alpha )=0$ (i.e. no deterioration) and no preservation technology, $s \rightarrow \infty$ (i.e. no shortage), and planning horizon is infinite $\left( {\mathrm{i.e.} \;n=0} \right)$, both EOQ inventory models of the present paper converges to traditional EOQ inventory model with shortages.

6 Numerical examples

In order to illustrate the two proposed EOQ inventory models and the application of the algorithms several numerical examples are solved. The numerical examples corresponds to complete and partial backordering considering two different demand functions. For each case, four numerical examples are given and solved. The first example in each case is a base that corresponds to a benchmark for the other three examples. The first example illustrates the situation in which the constraint of investment capital is not active; in other words the optimal solution for $\alpha$ is on the interval $\left[ {0,\bar{{\alpha }}} \right]$. The second example imposes a constraint for the investment capital $(\bar{{\alpha }})$; this means that it is an active constraint. The third example considers that initial deterioration rate ($\lambda _0 )$ is pretty small and the fourth example takes into account that the sensitivity parameter of investment to deterioration rate ($\delta )$ is pretty small.

6.1 Completely backordering when $D(p)=a-bp$

Example 1

Consider the following parameter values $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={\$} 10$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\lambda _0 =0.02,\delta =0.5$ and $\bar{{\alpha }}=12$. For distinct values of n, the optimal profit is computed. As it is presented in Table 2, the profit function is concave with respect to ordering frequency (n). Note that when $n=9$, the profit function attains its maximum. Therefore, the maximum value for profit is $\textit{TP}={\$} 98006.10$. In this example, the upper bound of investment in preservation cost is unlimited. In other words, there is not a constraint on investment in preservation cost. Notice that the optimal solution is not on the boundary. Figure 3 schemes the total profit with respect to preservation cost and selling price. It is easy to see that profit function (TP) is jointly concave in preservation cost and selling price.

Table 2 The optimal solution is a global maximum at $n=9$

Fig. 3

The total profit function with respect to preservation cost $(\alpha )$ and selling price (p) for fixed $n=9$ for example 1

Example 2

This example considers the same parameter values of Example 1, but here the upper bound on the investment of preservation cost is $\bar{{\alpha }}=1.85$. From Table 3, it can be observed that the optimal solution is $\alpha ^{*}=1.85$. Note that the solution is on the boundary and the profit is smaller than that of Example 1; as it is expected. Therefore, the maximum capital of preservation technology investment has a significant effect on profit.

Table 3 Optimal solution at $\bar{{\alpha }}=1.85$

Example 3

Now, consider the following parameter values $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={{\$}} 10$ per unit, $d={{\$}}5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\lambda _0 =0.0002,\delta =0.5$ and $n=9$. Taking into account that the initial deterioration rate value is pretty small, for example $\lambda _0 =0.0002$, then according to the algorithm, $\Delta _1 (n,p)<0$, therefore the optimal investment capital is $\alpha ^{*}=0$; as it is expected. This shows that invest in preservation technology is not beneficial when the initial deterioration rate value is pretty small.

Example 4

Here, $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={\$} 10$ per unit, $d={\$} 5$ per unit, $h={\$}0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\lambda _0 =0.02,\delta =0.005$ and $n=9$. According to the algorithm, $\Delta _1 (n,p)<0$, thus the optimal investment capital is $\alpha ^{*}=0$. This also specifies that when the value of the sensitivity parameter of investment to deterioration rate $(\delta )$ is small, it is not beneficial to invest in preservation technology.

6.2 Completely backordering when $D(p)=ap^{-r}$

Example 5

The input data values are as follows: $T=80$ weeks, $A={\$} 400$ per order,$a=30$ units, $c={\$} 10$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2$, $\gamma =0.5,\lambda _0 =0.02,\delta =0.5,r=0.4$ and $\bar{{\alpha }}=12$. For some values of n, the optimal profit is determined. As it is exposed in Table 4, the profit function is concave with respect to ordering frequency (n). Also, note that when $n=9$ the profit function reaches its maximum. Consequently, the maximum value for profit is $\textit{TP}={\$} 14238.00$.

Table 4 The optimal solution is a global maximum at $n=9$

Example 6

This example has the same parameter values of Example 5 but here $\bar{{\alpha }}=1.45$. From Table 5, it can be noted that the optimal solution is $\alpha ^{*}=1.45$. It is important to remark that the solution is on the boundary and the profit is smaller than that of Example 5; as it is expected. Thus, the maximum capital of preservation technology investment has a relevant impact on profit.

Table 5 Optimal solution at $\bar{{\alpha }}=1.45$

Example 7

In this example the data values are: $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $c={\$} 10$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2, \gamma =0.5,\lambda _0 =0.0002$, $\delta =0.5,r=0.4$ and $n=9$. Taking into consideration that the initial deterioration rate value is pretty small, for example $\lambda _0 =0.0002$, the algorithm reports that $\Delta _1 (n,p)<0$, consequently the optimal investment capital is $\alpha ^{*}=0$. This demonstrates that invest in preservation technology is not valuable when the initial deterioration rate value is pretty small.

Example 8

Here, $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={\$} 10$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\lambda _0 =0.02$, $\delta =0.005,r=0.4$ and $n=9$. According to the algorithm, $\Delta _1 (n,p)<0$, thus the optimal investment capital is $\alpha ^{*}=0$. This means that when the value of $\delta$ is small, it is not advantageous to make an investment in preservation technology.

6.3 Partial backordering when $D(p)=a-bp$

Example 9

Consider the following parameter values $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={\$} 10$ per unit, $c_1 ={\$} 20$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\eta =0.2,\lambda _0 =0.02$, $\delta =0.5$ and $\bar{{\alpha }}=12$.For different values of n, the optimal profit is calculated. As it is shown in Table 6, the profit function is concave with respect to ordering frequency (n). Notice that the profit function has its maximum when $n=11$. Then, the maximum value for profit is $\textit{TP}={\$} 92,237.5$.

Table 6 The optimal solution is a global maximum at $n=11$

Example 10

This example contains the same data values of Example 9 but here $\bar{{\alpha }}=1.05$. From Table 7, it is easy to see that the optimal solution is $\alpha ^{*}=1.05$. Given that the solution is on the boundary then the profit is smaller than that of Example 9. In fact, the maximum capital of preservation technology investment affects significantly to the profit.

Table 7 Optimal solution at $\bar{{\alpha }}=1.05$

Table 8 The optimal solution is a global maximum at $n=10$

Example 11

Now, the parameter values are: $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={\$} 10$ per unit, $c_1 ={\$} 20$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\eta =0.2,\lambda _0 =0.0002,\delta =0.5,r=0.4$ and $n=11$. Considering the initial deterioration rate value is pretty small, for example $\lambda _0 =0.0002$ thus the algorithm says that $\Delta _1 (n,p)<0$, for that reason the optimal investment capital is $\alpha ^{*}=0$. This confirms that when the initial deterioration rate value is pretty small then invest in preservation technology is not useful.

Example 12

Here, $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $b=0.2$ units, $c={\$} 10$ per unit, $c_1 ={\$} 20$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\eta =0.2,\lambda _0 =0.02,\delta =0.005,r=0.4$ and $n=11$. According to the algorithm, $\Delta _1 (n,p)<0$, thus the optimal investment capital is $\alpha ^{*}=0$. This also specifies that when $\delta$ is small, it is not favourable to invest in preservation technology.

6.4 Partial backordering when $D(p)=ap^{-r}$

Example 13

The information for this example is as follows: $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $r=0.4$ units, $c={\$} 10$ per unit, $c_1 ={\$} 20$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\eta =0.2$, $\lambda _0 =0.02,\delta =0.5$ and $\bar{{\alpha }}=12$. For several values of n, the optimal profit is computed. As it is presented in Table 8, the profit function is concave with respect to ordering frequency (n). When $n=10$ the profit function achieves its maximum. Therefore, the maximum value for profit is $\textit{TP}={\$} 24,335.00$. In this example, the upper bound of investment in preservation cost is unlimited.

Example 14

This example uses the same parameter values of Example 13 but here $\bar{{\alpha }}=2.5$. From Table 9, it is clear that the optimal solution is $\alpha ^{*}=2.5$. Note that this solution is on the boundary and the profit is smaller than that of Example 13. In fact, the maximum capital of preservation technology investment has a significant influence on profit.

Table 9 Optimal solution at$\bar{{\alpha }}=2.5$

Example 15

Now, consider the following parameter values $T=80$ weeks, $A={\$} 400$ per order, $a=30$ units, $r=0.4$ units, $c={\$} 10$ per unit, $c_1 ={\$} 20$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2$, $\gamma =0.5,\eta =0.2,\lambda _0 =0.002,\delta =0.5,r=0.4$ and $n=10$. When the initial deterioration rate value is pretty small, for example, $\lambda _0 =0.0002$, according to the algorithm, $\Delta _1 (n,p)<0$, hence the optimal investment capital is $\alpha ^{*}=0$. This certify that an investment in preservation technology is not beneficial when the initial deterioration rate value is pretty small.

Example 16

Here, $T=80$ weeks, $A={\$} 400$ per order, $a=30$units, $r=0.4$ units, $c={\$} 10$ per unit,$c_1 ={\$} 20$ per unit, $d={\$} 5$ per unit, $h={\$} 0.02$ per unit/week, $s={\$} 2$ per unit/week, $\beta =0.2,\gamma =0.5,\eta =0.2,\lambda _0 =0.02$, $\delta =0.005$, $r=0.4$ and $n=10$. According to the algorithm, $\Delta _1 (n,p)<0$, thus the optimal investment capital is $\alpha ^{*}=0$. This means that when $\delta$ is small, it is not valuable to make an investment in preservation technology.

7 Sensitive analysis

The total profit function represents real solutions in which the system parameters are considered as static values. This is significant from a practical point of view since the managers are capable to take the best decisions with respect to the situation at hand and how the objectives change. For this purpose, a sensitivity analysis of several system parameters ($a, b, c, d, h,s, \beta ,\gamma ,\lambda _0$ and $\delta$) is made by changing each of the parameters by $\pm 50\%$ and $\pm 25\%$ taking one parameter at a time and maintaining the rest of the parameters without change.

Table 10 Sensitivity analysis for Example 1

Based on the results of Table 10, the following observations are made.

• i. ${ TP}^{*}$ increases with an increase in the values of parameters a, c, d, h, $\gamma$ and $\delta$ while ${ TP}^{*}$ decreases with an increase in the value of b, s, $\beta$ and $\lambda _0$. ${ TP}^{*}$ is highly sensitive to changes in a, b and $\gamma$. It is less sensitive to changes in c, s, $\beta$ and d; and very less sensitive to changes in h, $\lambda _0$ and $\delta$.

• ii. $Q^{*}$ increases with an increase in the values of parameters a, b, c, d, h and $\delta$ while $Q^{*}$ decreases with an increase in the value of s, $\beta$ and $\gamma$. $Q^{*}$is highly sensitive to changes in a and $\beta$. It is less sensitive to changes in b, $\textit{c d}$, h, $\delta$, s, and $\gamma$ and no changes in $\lambda _0$.

Managerial implications

Based on the results of Table 10, the following managerial insights are stated:

• (a) When the value of scaling factor a rises and other parameters’ values are fixed, it can be concluded that the optimal total profit per unit time $\textit{TP}{*}$, the optimal selling price $p{*}$, the optimal preservation technology investment $\alpha ^{*}$ and the optimal order quantity $Q{*}$ increase. This indicates that when the scaling factor a rises, the market demand rate will rise, making that the organization increases the order quantity per replenishment cycle and shorten the replenishment cycle to satisfy the increasing market requirement. Furthermore, the organization will place the selling price higher to get more profit. The organization will also spend more funds into the improvement of preservation technology to decrease the product’s deterioration rate, therefore the organization can sell more products.

• (b) When the price elasticity b rises, the optimal,$p{*}$ and $\textit{TP}{*}$ decrease, while the optimal preservation technology investment $\alpha ^{*}$ and the optimal order quantity $Q{*}$ rises. It suggests that, as price elasticity b rises, the organization will bring down the selling price to avoid the demand rate decreases dramatically. And with lowering the selling price, the order quantity will decrease and the total profit per unit time will shrink significantly. Further, the organization has an incentive to rise the preservation technology investment.

• (c) The preservation cost is increasing in c, $\lambda _0$ and h. This implies that when the buying cost and initial deterioration rate are high then the retailer must spend more in order to reduce the deteriorating cost. But when the holding cost rate is high, the retailer can decrease the cost by ordering more frequently in place of spending more on preservation cost.

8 Conclusions

This paper develops an inventory model for simultaneously determining the optimal ordering frequency, optimal pricing and the optimal preservation technology investment policies for deteriorating products whose deterioration rate is controlled by investing in the preservation technology. Here, some useful properties characterizing the optimal solution are formulated and an algorithm is developed to determine jointly the optimal ordering frequency, optimal pricing and the optimal preservation technology investment. Some numerical examples are provided to illustrate the inventory model and the solution procedure. Additionally, sensitivity analysis is done with regard to parameters to get remarkable managerial insights.

The two proposed EOQ inventory models can help the manufacturer and retailer in determining the optimal ordering frequency, pricing, preservation technology investment, quantity and profit. Likewise, the two proposed EOQ inventory models can be used in inventory control of certain products such as food products, seasonal products, among others.

This research can further be extended by taking more realistic assumptions such as stochastic demand or demand with uncertainty, linear increasing demand, price, and advertising-dependent demand or power-demand. This research can be also extended by considering the limited capacity of shelf space. One another extension can be considered in the direction of trade credit policy.

Appendices

Appendix 1: Proof of Theorem 1

The first and second partial derivatives of the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (17) with respect to n are given below:

$$\begin{aligned} \frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial n}= & {} -\frac{cD(p)}{\lambda (\alpha )+\beta }\left( {1-\frac{\gamma ^{2}T^{2}}{2n^{2}}(\lambda (\alpha )+\beta )^{2}} \right) +hD(p)\left( {\frac{\gamma ^{2}T^{2}}{2n^{2}}} \right) \nonumber \\&-sD(p)\left( {-\frac{\gamma T^{2}}{n^{2}}+\frac{\gamma ^{2}T^{2}}{2n^{2}}+\frac{T^{2}}{n^{2}}} \right) -\frac{dD(p)}{\lambda (\alpha )+\beta }\left( {1-\frac{\gamma ^{2}T^{2}}{2n^{2}}(\lambda (\alpha )+\beta )^{2}} \right) ,\nonumber \\&+\frac{\beta dD(p)\gamma ^{2}T^{2}}{2n^{2}}-A \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial ^{2}(\textit{TP}(n,\alpha ,p))}{\partial n^{2}}= & {} -cD(p)\left( {\frac{\gamma ^{2}T^{2}}{n^{3}}(\lambda (\alpha )+\beta )} \right) -hD(p)\left( {\frac{\gamma ^{2}T^{2}}{n^{3}}} \right) -\frac{\beta dD(p)\gamma ^{2}T^{2}}{n^{3}} \nonumber \\&-\frac{sD(p)T^{2}}{n^{3}}\left( {2+\gamma (\gamma -2)} \right)<0 ,\; 0<\gamma <1. \end{aligned}$$

(29)

Clearly, from Eq. (29) it is concluded that the profit function given by Eq. (17) is concave in n. Notice that n must be an integer number. Thus, the determination of the optimal n is reduced to obtain a local optimal solution for n.

This completes the Proof of Theorem 1. $\square$

Appendix 2: Proof of Theorem 2

The first and second partial derivatives of the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (17) with respect to $\alpha$ are as follows,

$$\begin{aligned} \frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial \alpha }= & {} \frac{(c+d)\gamma ^{2}T^{2}\delta \lambda (\alpha )D(p)}{2n}-T, \end{aligned}$$

(30)

$$\begin{aligned} \frac{\partial ^{2}(\textit{TP}(n,\alpha ,p))}{\partial \alpha ^{2}}= & {} -\frac{(c+d)\gamma ^{2}T^{2}\delta ^{2}\lambda (\alpha )D(p)}{2n}-T<0. \end{aligned}$$

(31)

For straightforwardness, set $H(\alpha )=\frac{(c+d)\gamma ^{2}T^{2}\delta \lambda (\alpha )D(p)}{2n}-T$

$$\begin{aligned} \mathrm{State}\; \Delta _1 (n,p)= & {} \left. {H(\alpha )} \right| _{\alpha =0} =\frac{(c+d)\gamma ^{2}T^{2}\delta \lambda _0 D(p)}{2n}-T\\ \mathrm{and } \Delta _2 (n,p)= & {} \left. {H(\alpha )} \right| _{\alpha =\bar{{\alpha }}} =\frac{(c+d)\gamma ^{2}T^{2}\delta \lambda (\bar{{\alpha }})D(p)}{2n}-T. \end{aligned}$$

It is understandable that ${H}'(\alpha )<0$. Consequently $H(\alpha )$ is strictly decreasing in $\alpha$.

• (1) $If\;\Delta _1 (n,p)\le 0, H(\alpha )\le 0$ and $\forall \alpha \in \left[ {0,\bar{{\alpha }}} \right]$ then $\textit{TP}(n,\alpha ,p)$ is decreasing in $\alpha \in \left[ {0,\bar{{\alpha }}} \right]$. Thus, the optimal preservation cost is $\alpha ^{*}=0.$

• (2) $If\;\Delta _2 (n,p)\ge 0, H(\alpha )\ge 0$ and $\forall \alpha \in \left[ {0,\bar{{\alpha }}} \right]$ then $\textit{TP}(n,\alpha ,p)$ is increasing in $\alpha \in \left[ {0,\bar{{\alpha }}} \right]$.Therefore, the optimal preservation cost is $\alpha ^{*}=\bar{{\alpha }}.$

• (3) $If\;\Delta _1 (n,p)>0$ and $\Delta _2 (n,p)<0$ then, according to the intermediate value theorem, there is an unique value $\alpha \in \left( {0,\bar{{\alpha }}} \right)$ that satisfies $H(\alpha ^{*})=0 ,$ Thus,

  $$\begin{aligned} \frac{(c+d)\gamma ^{2}T^{2}\delta \lambda (\alpha ^{*})D(p)}{2n}-T=0. \end{aligned}$$

  (32)

This completes the Proof of Theorem 2. $\square$

Appendix 3: Proof of Theorem 3

The first and second partial derivatives of the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (17) with respect to p are presented below:

$$\begin{aligned} \begin{aligned} \frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial p}=&(a-2bp)T+\frac{cb}{\lambda (\alpha )+\beta }\left( {n+\frac{\gamma ^{2}T^{2}}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )T-\gamma T} \right) \\&+\,hb\left( {\frac{\gamma ^{2}T^{2}}{2n}} \right) +sb\left( {\frac{\gamma T^{2}}{n}-\frac{\gamma ^{2}T^{2}}{2n}-\frac{T^{2}}{n}} \right) +\frac{db}{\lambda (\alpha )+\beta }\\&\left\{ {n+\frac{\gamma ^{2}T^{2}}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )T-\gamma T} \right\} bd\gamma T+\frac{\beta db\gamma ^{2}T^{2}}{2n} \\ \end{aligned} \end{aligned}$$

(33)

Set $\frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial p}=0$ and solve it for the optimal $p^{*}$;

$$\begin{aligned}&\begin{aligned} \Rightarrow p^{*}=&\frac{c}{2(\lambda (\alpha )+\beta )}\left( {\frac{n}{T}+\frac{\gamma ^{2}T}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )-\gamma } \right) +\frac{h}{2}\left( {\frac{\gamma ^{2}T}{2n}} \right) \\&+\,\frac{s}{2}\left( {\frac{\gamma T}{n}-\frac{\gamma ^{2}T}{2n}-\frac{T}{n}} \right) +\frac{d}{2(\lambda (\alpha )+\beta )}\\&\left( {\frac{n}{T}+\frac{\gamma ^{2}T}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )-\gamma } \right) +\frac{d\gamma }{2}+\frac{\beta d\gamma ^{2}T}{4n}+\frac{a}{2b} . \\ \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned}&\frac{\partial ^{2}\left( {\textit{TP}\left( {n,\alpha ,p} \right) } \right) }{\partial p^{2}}=-2bT<0 \end{aligned}$$

(35)

Hence, $p^{*}$ is the global optimal that maximizes the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (17) for fixed values of n and $\alpha$.

This completes the Proof of Theorem 3. $\square$

Appendix 4: Proof of Theorem 5

The first and second partial derivatives of the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (27) with respect to n are given below:

$$\begin{aligned}&\begin{aligned} \frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial n}=&-\frac{cD(p)}{\lambda (\alpha )+\beta }\left( {1-\frac{\gamma ^{2}T^{2}}{2n^{2}}(\lambda (\alpha )+\beta )^{2}} \right) +hD(p)\left( {\frac{\gamma ^{2}T^{2}}{2n^{2}}} \right) \\&+\,sD(p)\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{2n^{2}}+c_1 D(p)\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{2n^{2}} \\&-\frac{dD(p)}{\lambda (\alpha )+\beta }\left( {1-\frac{\gamma ^{2}T^{2}}{2n^{2}}(\lambda (\alpha )+\beta )^{2}} \right) +\frac{\beta dD(p)\gamma ^{2}T^{2}}{2n^{2}}-A \\ \end{aligned} \end{aligned}$$

(36)

$$\begin{aligned}&\begin{aligned} \frac{\partial ^{2}(\textit{TP}(n,\alpha ,p))}{\partial n^{2}}=&-cD(p)\left( {\frac{\gamma ^{2}T^{2}}{n^{3}}(\lambda (\alpha )+\beta )} \right) -hD(p)\left( {\frac{\gamma ^{2}T^{2}}{n^{3}}} \right) -\frac{\beta dD(p)\gamma ^{2}T^{2}}{n^{3}} \\&-\,\left( {s+c_1 } \right) D(p)\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{n^{3}}<0 ,\; 0<\gamma <1. \\ \end{aligned} \end{aligned}$$

(37)

Clearly, the profit function given by Eq. (27) is concave in n.

This completes the Proof of Theorem 5. $\square$

Appendix 5: Proof of Theorem 7

The first and second partial derivatives of the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (27) with respect to p are presented below:

$$\begin{aligned} \begin{aligned} \frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial p}=&(a-2bp)T+\frac{cb}{\lambda (\alpha )+\beta }\left( {n+\frac{\gamma ^{2}T^{2}}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )T-\gamma T} \right) \\&+\,hb\left( {\frac{\gamma ^{2}T^{2}}{2n}} \right) +\left( {s+c_1 } \right) nb\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{n^{2}} \\&+\frac{db}{\lambda (\alpha )+\beta }\left\{ {n+\frac{\gamma ^{2}T^{2}}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )T-\gamma T} \right\} \\&bd\gamma T+\frac{\beta db\gamma ^{2}T^{2}}{2n} \end{aligned} \end{aligned}$$

(38)

Set $\frac{\partial (\textit{TP}(n,\alpha ,p))}{\partial p}=0$ and solve it for the optimal $p^{*}$;

$$\begin{aligned}&\begin{aligned} \Rightarrow p^{*}=&\frac{c}{2(\lambda (\alpha )+\beta )}\left( {\frac{n}{T}+\frac{\gamma ^{2}T}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )-\gamma } \right) +\frac{h}{2}\left( {\frac{\gamma ^{2}T}{2n}} \right) \\&+\,\left( {s+c_1 } \right) n\left( {1-\gamma } \right) ^{2}\frac{\eta T^{2}}{n^{2}}+\frac{d}{2(\lambda (\alpha )+\beta )}\\ {}&\left( {\frac{n}{T}+\frac{\gamma ^{2}T}{2n}(\lambda (\alpha )+\beta )^{2}+(\lambda (\alpha )+\beta )-\gamma } \right) +\frac{d\gamma }{2}+\frac{\beta d\gamma ^{2}T}{4n}+\frac{a}{2b} . \\ \end{aligned} \end{aligned}$$

(39)

$$\begin{aligned}&\frac{\partial ^{2}\left( {\textit{TP}\left( {n,\alpha ,p} \right) } \right) }{\partial p^{2}}=-2bT<0 \end{aligned}$$

(40)

Hence, $p^{*}$ is the global optimal that maximizes the profit function $\textit{TP}(n,\alpha ,p)$ given by Eq. (27) for fixed values of n and $\alpha$.

This completes the Proof of Theorem 7. $\square$

Appendix 6: Algorithm for partial backlogging

Algorithm for partial backlogging

• Step 1. Initialize $n=1.$

• Step 2. Initialize $m=1$ and set the value of $p^{m}=p_0 .$

• Step 3. Compute $\Delta _1 (n,p),\Delta _2 (n,p)$ and perform any one of the following three cases 1, 2 or 3.

  • (1) If $\Delta _1 (n,p)\le 0,$ then $\alpha _1^m =0$. Determine $p_1^m$ from Eq. (39).

  • (2) If $\Delta _2 (n,p)\ge 0,$ then $\alpha _1^m =\bar{{\alpha }}$. Calculate $p_1^m$ from Eq. (39).

  • (3) If $\Delta _1 (n,p)>0$ and $\Delta _2 (n,p)<0$, Compute $\alpha _1^m$ by solving (32). Substitute the value of $\alpha _1^m$ into Eq. (39) and determine the corresponding value for $p_1^m$.

  Set $p^{m+1}=p_1^m$ and $\alpha ^{m}=\alpha _1^m$.

• Step 4. If $\left| {p^{m+1}-p^{m}} \right| \le 10^{-4}$, then $(\alpha ^{*},p^{*})=(\alpha ^{m},p^{m+1})$ and go to Step 5. Otherwise, set $m=m+1$ and go to Step 3.

• Set 5. Compute $\textit{TP}(n,\alpha ^{*},p^{*})$ with Eq. (27) which is the maximum for the profit function for a fixed value of n.

• Step 6. Set ${n}'=n+1$, repeat Step 2 to 5 and find $\textit{TP}({n}',\alpha ^{*},p^{*})$ with Eq. (27). Go to Step 7.

• Step 7. If $\textit{TP}({n}',\alpha ^{*},p^{*})\ge \textit{TP}(n,\alpha ^{*},p^{*})$, set $n={n}'$. Go to Step 6. Otherwise go to Step 8.

• Step 8. Set $(n^{*},\alpha ^{*},p^{*})=(n,\alpha ^{*},p^{*})$ and $\textit{TP}(n,\alpha ^{*},p^{*})$ as the optimal solution.

• Step 9. Compute the order quantity Q with Eq. (22).

• Step 10. Calculate shortage level using Eq. (21).

• Step 11. Determine the quantity of deteriorated items with Eq. (5).