1 Introduction

Quantum science has been attracting much attention in recent years. Quantum teleportation (QT) [1] is one of the most important protocols of quantum information theory. QT is a type of quantum communication, where by using entanglement and classical information, one of the users from one place teleport an unknown quantum state to the other user in the other place. This kind of protocol was presented in 1993. Bennett et al. [2] proposed the first protocol of QT by using Einstein-Podolsky-Rosen (EPR) pair. Since 1993, several QT schemes have been proposed so far [3,4,5,6,7,8,9,10,11] by using other entangled states as a quantum channel including Greenberger—Horne—Zeilinger (GHZ) state, W state, GHZ-like state, and etc, where the only difference among these protocols is the quantum channel.

A different kind of QT protocols was proposed in 1998 by Karlsson and Bourennane [12]. This type of QT is a controlled quantum teleportation (CQT), in which the sender transmits an unknown state to a remote receiver under the control of the supervisor. After that, several CQT protocols have been proposed [13,14,15,16,17] by using one or more than one controller. In these protocols the third person controls the qubits of users by applying measurement on his qubits.

Several experiments have been performed for realizing quantum teleportation. In pioneering work the teleportation protocol was implemented with single photons [18] over lab-scale distances and later also over km-scale distances in free space [19,20,21,22].

One of the most important subfields of QT is bidirectional quantum teleportation (BQT). In BQT, two users can teleport qubits to each other and two users play sender role and receiver role, simultaneously. In 2013, the first CBQT was proposed by Zha et al. [23]. After that, several BCQT protocols have been proposed [24,25,26,27,28]. Yan [24] and Sun et al. [25] proposed two protocols of BQCT by using six-qubit cluster state and six-qubit maximally-entangled state as a quantum channel, respectively. Li and Nie [26] presented a protocol of BQCT via five-qubit composite GHZ-Bell state as a quantum channel but Shukla et al. [27] showed that the Li’s protocol [26] is not a BQCT scheme. Then, Li et al. [28] proposed a protocol via five-qubit entangled state. All of those protocols were proposed in 2013.

In 2014, Fu et al. [29] presented a BQT scheme by using a four-qubit cluster state as a quantum channel. In this scheme, users can simultaneously exchange their single-qubit states by applying Hadamard operation. In the same year, Chen [30], Duan et al. [31] and Duan and Zha [32], proposed new schemes of BCQT by using five-qubit entangled state, seven-qubit entangled state, and six-qubit entangled state, as a quantum channel, respectively. In Duan et al.’s scheme [31], Charlie improves the security of the protocol by performing single-qubit measurements three times. In the next study, Duan and Zha [32] improved the security of their protocol by applying two single-qubit measurements.

In 2015, different schemes of BCQT by using six-qubit genuine state [33], GHZ-type state [34], eight-qubit entangled state [35], and six-qubit entangled state [36] as a quantum channel were proposed. The scheme in [35] is better than the previous ones in terms of quantum resource consumptions. In Hassanpour’s scheme [36], the quantum channel is easier to prepare.

In all mentioned protocols, Alice and Bob can only teleport an arbitrary single-qubit state to each other. In 2016, two different protocols of BCQT by using seven-qubit entangled state as a quantum channel were proposed, that Alice can teleport an arbitrary single-qubit state to Bob and Bob can teleport an arbitrary two-qubit state to Alice [37, 38]. The same year in February, a BQT protocol by using six-qubit entangled state as a quantum channel was presented [39]. In this protocol, Alice and Bob can teleport a pure EPR state to each other. Then a BCQT protocol was proposed by using nine-qubit entangled state as a quantum channel, where Alice and Bob can teleport an arbitrary two-qubit state to each other [40]. In June 2016, a BCQT protocol by using six-qubit cluster state as a quantum channel was proposed [41]. In this protocol, Alice can teleport an arbitrary two-qubit state to Bob and Bob can teleport an arbitrary single-qubit state to Alice. In [42], a new scheme of bidirectional quantum teleportation (BQT) making use of an eight-qubit entangled state as the quantum channel is presented, where Alice and Bob can teleport two-qubit states to each other simultaneously.

In this study, for the first time, a BQT protocol is presented by which n-qubit states (as (1) and (2) shows) can be teleported simultaneously. This protocol utilizes (2n + 2)-qubit entangled state as a channel. In this protocol, each user applies one CNOT gate and (n + 1) single-qubit unitary gates as well as performing n measurements in X basis.

The rest of the paper is organized as follows. In Section 2, the proposed protocol is explained. Section 3, includes summary and analysis of previous research. Conclusion and future work are presented in Section 4.

2 Description of the Presented Protocol

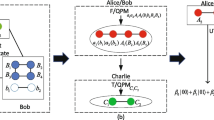
The proposed scheme is a BQT protocol, where Alice and Bob as two legitimate users want to teleport an n-qubit state as (1) and (2) to each other. (It should be noted that EPR and GHZ states are examples of states in (1) and (2).)

$$ \left|\emptyset \right\rangle_{A_{1} A_{2} {\ldots} A_{n}} =\alpha_{0}\left| q_{1}q_{2}\ldots q_{n}\right\rangle+\alpha_{1}\left| \bar{q}_{1}\bar{q}_{2}{\ldots} \bar{q}_{n}\right\rangle, $$
(1)
$$ \left|\emptyset \right\rangle_{B_{1} B_{2} {\ldots} B_{n}} =\beta_{0}\left\vert q_{1}q_{2}{\ldots} q_{n}\right\rangle+\beta_{1}\left\vert \bar{q}_{1}\bar{q}_{2}{\ldots} \bar{q}_{n}\right\rangle, $$
(2)

where |α 0|2 +|α 1|2 = 1, |β 0|2 +|β 1|2 = 1 and q 1 q 2…q n ∈ {0,1} and q bar is the flipped state of q.

2.1 Preparation Phase

In this protocol, two users teleport their qubits by using (2n + 2)-qubit entangled state as a quantum channel,

$$\begin{array}{@{}rcl@{}} \left\vert G\right\rangle_{a_{1}b_{1}b_{2}{\ldots} b_{n}a_{2}a_{3}{\ldots} a_{n+1}b_{n+1}}&=& \frac{1}{2}\left[ \left| 0q_{1}q_{2}\ldots q_{n}q_{1}q_{2}{{\ldots} q}_{n}0\right\rangle +\left| 0q_{1}q_{2}{{\ldots} q}_{n}\bar{q}_{1}\bar{q}_{2}\ldots \bar{q}_{n}1\right\rangle\right.\\ &&\left. +\left| 1\bar{q}_{1}\bar{q}_{2}{\ldots} \bar{q}_{n}q_{1}q_{2}{{\ldots} q}_{n}0\right\rangle +\left|1\bar{q}_{1}\bar{q}_{2}{\ldots} \bar{q}_{n}\bar{q}_{1}\bar{q}_{2}{\ldots} \bar{q}_{n}1\right\rangle \right],\\ \end{array} $$
(3)

Alice generates the N states described in (3). She keeps qubits a 1…a n+1 for herself and sends the qubits b 1…b n+1 to Bob.

2.2 Security Checking Phase

For making sure that qubits of (3) are shared without eavesdropping, Alice selects randomly enough states of sequence as checking qubits. The remaining qubits are used as teleporting qubits. To measure the checking qubits, she randomly selects one of the Z or X bases for each checking qubits. Then she announces the orders and the bases of the checking qubits to her Bob. Bob measures the corresponding qubits under the same measuring bases. Then, he announces their measurement results to Alice.

If there is no Eve interference and the channel is secure, the measurement results must be correlated. As an example suppose q 1 = q 2 = ⋯ = q n = 0.

Table 1 shows the correlation of Alice and Bob measurement results where n − indicates the number of the qubits that are collapsed to |−〉 when measured in X basis. It should be noted that:

$$\left|0\right\rangle =\frac{\left|+\right\rangle +\left|-\right\rangle} {\sqrt 2} ,\left|1\right\rangle =\frac{\left|+\right\rangle -\left|-\right\rangle} {\sqrt 2} $$

If the error rate is more than the threshold, they discard and abort the communication; otherwise they continue the communication and execute the next phase.

Table 1 Measurement bases and measurement results
Full size table

2.3 Main Protocol

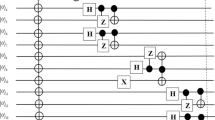
In this subsection the steps of the protocol is described. Figure 1 illustrates the protocol.

  1. Step 1.

    After Alice and Bob share a (2n + 2)-qubit entangled state as (3), as a quantum channel, the initial state of the whole system can be expressed as (4),

    $$ \left|\varphi \right\rangle_{a_{1} b_{1} {\ldots} b_{n} a_{2} {\ldots} a_{n+1} b_{n+1} A_{1} {\ldots} A_{n} B_{1} {\ldots} B_{n}} \!\,=\,\left|G\right\rangle_{a_{1} b_{1} {\ldots} b_{n} a_{2} {\ldots} a_{n+1} b_{n+1}} \otimes \left|\emptyset \right\rangle_{A_{1} {\ldots} A_{n}} \otimes \left|\emptyset \right\rangle_{B_{1} {\ldots} B_{n}} , $$
    (4)

    where the qubits a 1…a n+1 and A 1…A n belong to Alice and qubits b 1…b n+1 and B 1…B n belong to Bob, respectively.

  2. Step 2.

    In this step, Alice and Bob apply a controlled-not operation with A 1 and B 1 as control qubits and qubits a 1 and b n+1 as target respectively. Now the state will be in the form of (5) (without loss of generality suppose q 1 = 0).

    $$\begin{array}{@{}rcl@{}} &&\left|\varphi_{1} \right\rangle_{a_{1} b_{1} {\ldots} b_{n} a_{2} \ldots a_{n+1} b_{n+1} A_{1} {\ldots} A_{n} B_{1} {\ldots} B_{n}} \\ &=&\frac{1}{2}\left[\vphantom{\left|\overline{q}_{1}\right.} {\alpha_{0} \beta_{0}} \right.\left|0q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} 0\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle\\ &&+\alpha_{0} \beta_{0} \left|0q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 1\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle \\ &&+\alpha_{0} \beta_{0} \left|1\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} 0\right\rangle \left| q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle\\ && +\alpha_{0} \beta_{0} \left|1\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 1\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle \\ &&+\alpha_{0} \beta_{1} \left|0q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} 1\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle\\ &&+\alpha_{0} \beta_{1} \left|0q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 0\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle \\ &&+\alpha_{0} \beta_{1} \left|1\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} 1\right\rangle \left| {q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n}} \right\rangle\\ && +\alpha_{0} \beta_{1} \left|1\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 0\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle \\ &&+\alpha_{1} \beta_{0} \left|1q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} 0\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle\\ &&+\alpha_{1} \beta_{0} \left|1q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 1\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle \\ &&+\alpha_{1} \beta_{0} \left|0\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} 0\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle\\ && +\alpha_{1} \beta_{0} \left|0\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 1\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle \\ &&+\alpha_{1} \beta_{1} \left|1q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} 1\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} \ldots \overline{q}_{n} \right\rangle\\ && +\alpha_{1} \beta_{1} \left|1q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} \ldots q_{n} 0\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle \\ &&+\alpha_{1} \beta_{1} \left|0\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} 1\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle\\ &&\left. +\alpha_{1} \beta_{1} \left|0\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} 0\right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle \right]. \end{array} $$
    (5)
  3. Step 3.

    In this step, Alice and Bob perform a single-qubit measurement in the Z-basis on qubits a 1 and b n+1 respectively. According to Table 2, the remaining particles may collapse into one of the 4 possible states with 25% probability.

  4. Step 4.

    After Alice and Bob tell their measurement results to each other, they apply suitable unitary operation as is shown in Table 3.

    After users applied unitary operation on their qubits, all of the 4 states will be in the form of (6).

    $$\begin{array}{@{}rcl@{}} &&\left( \alpha_{0} \beta_{0} \left| q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n}\right\rangle \left|q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle\right.\\ &&~\left.+\alpha_{0} \beta_{1} \left|q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} \ldots \overline{q}_{n} \right\rangle\left|q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle\right.\\ &&~\left.+\alpha_{1} \beta_{0} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle\right.\\ &&~\left.+\alpha_{1} \beta_{1} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle\right)_{b_{1} {\ldots} b_{n} a_{2} {\ldots} a_{n+1} A_{1} {\ldots} A_{n} B_{1} {\ldots} B_{n}}.\\ \end{array} $$
    (6)
  5. Step 5.

    In this step, Alice and Bob perform n single-qubit measurement in the X-basis on qubits A 1…A n and B 1…B n respectively. The remaining particles may collapse into one of the 2n possible states with the same probability as described in Table 4, where n − and m − are the numbers of |−〉 in the collapsed state after the Alice’s measurement and Bob’s measurement respectively.

  6. Step 6.

    In this step, Alice and Bob can reconstruct the n-qubit state by applying suitable unitary operation as shown in Table 5.

    Fig. 1
    figure 1

    Steps of the protocol

    Full size image
    Table 2 The (Z-basis) measurement results of users and the corresponding collapsed state
    Full size table
    Table 3 Applying suitale unitary operations
    Full size table
    Table 4 The (X-Basis) measurement results of users and the corresponding collapsed state
    Full size table
    Table 5 Required unitary operations
    Full size table

After applying the unitary operators in Table 5, the state will be as below:

$$\begin{array}{@{}rcl@{}} &&\alpha_{0} \beta_{0} \left|q_{1} q_{2} {\ldots} q_{n} q_{1} q_{2} {\ldots} q_{n} \right\rangle \,+\,\alpha_{0} \beta_{1} \left|q_{1} q_{2} {\ldots} q_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle\\ &&+\alpha_{1} \beta_{0} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} q_{1} q_{2} \ldots q_{n} \right\rangle \,+\,\alpha_{1} \beta_{1} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle\\ \!&=&\!\left( \beta_{0} \left|q_{1} q_{2} {\ldots} q_{n} \right\rangle \,+\,\beta_{1} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle \right)_{a_{2} {\ldots} a_{n+1}} \!\otimes\! \left( \alpha_{0} \left|q_{1} q_{2} {\ldots} q_{n} \right\rangle \,+\,\alpha_{1} \left|\overline{q}_{1} \overline{q}_{2} \ldots \overline{q}_{n} \right\rangle \right)_{b_{1} {\ldots} b_{n}},\\ \end{array} $$
(7)

Now, Alice and Bob reconstruct the n-qubit state, and the bidirectional teleportation is successfully finished which is shown in (8) and (9).

$$ \left|\emptyset\right\rangle_{a_{2} {\ldots} a_{n+1}} =\beta_{0} \left|q_{1} q_{2} \ldots q_{n} \right\rangle +\beta_{1} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle $$
(8)
$$ \left|\emptyset\right\rangle_{b_{1} {\ldots} b_{n}} =\alpha_{0} \left|q_{1} q_{2} {\ldots} q_{n} \right\rangle +\alpha_{1} \left|\overline{q}_{1} \overline{q}_{2} {\ldots} \overline{q}_{n} \right\rangle $$
(9)

Considering that the protocol is based on quantum teleportation and no qubit is transmitted in the channel, the protocol is secure against attacks such as intercept-resend.

3 Comparison

The most important advantage of the proposed protocol is that Alice and Bob can simultaneously teleport an n-qubit state in the form of (1) and (2) to each other. In the best approach previously proposed [40], the users can transmit only two-qubit states while in the proposed protocol in this paper, the users can teleport as many qubits as they desire through the bidirectional quantum teleportation.

Consider m u the number of transmitted qubits, q k the number of used qubits in the channel and b k the number of transmitted bits, the efficiency is calculated as the following relation:

$$ {\eta} =\frac{m_{u}} {q_{k} +b_{k}} . $$
(10)

By setting the values of these parameters, we will have:

$$ m_{u} =2n,q_{\mathrm{k}} =2n+2, b_{\mathrm{k}} =16,\eta =\frac{m_{\mathrm{u}}} {q_{\mathrm{k}} +b_{\mathrm{k}}} =\frac{2n}{2n+18}, $$
(11)

which implies that by increasing the value of n, the efficiency of this protocol gets closer to one.

4 Conclusions

The advantage of this protocol is that users can simultaneously teleport an n-qubit state to each other. In the best case of previous protocols the users can only teleport a two-qubit state simultaneously. In this protocol, only single-qubit measurements are required so it is more simple and feasible in experiment. As a future work, this protocol can be extended to transmitting an arbitrary n-qubit state. Further, the effects of the amplitude-damping noise and the phase-damping noise for BQT process could be investigated. The other direction for a future work is to include a third party as a controller in the protocol, where without controller’s cooperation Alice and Bob cannot recover the teleported quantum states.