1 Introduction

Quantum teleportation(QT) as a significant part in quantum communication and quantum information theory, which allows the transmission of unknown states between two or more legitimate participants through the pre-shared entanglement, classical communication and local unitary operations [1]. Since the initial QT protocol was introduced by Bennett et al. [1], it has been attracting the attention of many researchers both theoretically and experimentally. Several experimental implementations of QT in different quantum systems have been reported, such as optical and photonic systems [2,3,4,5,6,7]. From then on, various schemes of QT have been presented [8,9,10,11,12,13,14,15,16,17,18]. Thereinto, controlled QT adds a supervisor to controll the whole communication process [19,20,21,22,23,24,25], simultaneous QT ensures that the receivers can acquire their information respectively and simultaneously [26,27,28]. In 2013, Zha et al. [29] presented the bidirectional controlled quantum teleportation (BCQT) for the first time, where two participants Alice and Bob can exchange a single particle via a five-qubit cluster state.

As we all know, BCQT can accomplish the transmission of information between two parties under the control of third party. A more general view was presented by Shukla et al. [30] about five-qubit cluster. In 2016, Li et al. [31] realized a protocol transmitting an arbitrary two-qubit state by utilizing a nine-qubit entangled state. In 2020, Zhou et al. [32] presented a BCQT scheme via a seven-qubit state in noisy environment. Owing to the advantages and characteristic of BCQT, many BCQT references have been introduced [33,34,35,36,37]. For the optimal success probability and fidelity, most BCQT proposals can be completed by using the maximally entangled channels. However, most of the time, it is difficult to generate or maintain a maximally entangled state. Apparently, it is necessary to research BCQT via non-maximally entangled quantum channel.

In this paper, we propose a BCQT protocol of arbitrary two-qubit via a ten-qubit entangled state. In this scheme, Alice and Bob have an unknown two-qubit respectively and want to transmit the information to each other. In order to obtain the messages, the receivers need the controller Charlie’s permission and collaborate. Besides, we analyze the effects of amplitude-damping noise and phase-damping noise in our protocol. It is worth emphasizing that the fidelities of the output states in these two noisy environments only affected by the amplitude parameter of the initial state and the decoherence noisy rate. Finally, we give a comparison between the presented protocol and previous BCQT protocols to illustrate the advantages of our protocol.

2 Bidirectional Controlled Quantum Teleportation of Arbitrary Two-qubit States

Our scheme can be described as follows. Suppose Alice has an arbitrary two-qubit state, which is given by

$$\vert\varphi\rangle_{a_{1}a_{2}}=\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle+\alpha_{2}\vert10\rangle+\alpha_{3}\vert11\rangle$$
(1)

And that Bob has particles in an unknown two-qubit state, which has the form

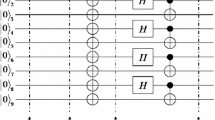
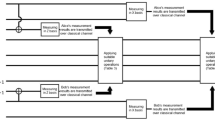
$$\vert\varphi\rangle_{b_{1}b_{2}}=\beta_{0}\vert00\rangle+\beta_{1}\vert01\rangle+\beta_{2}\vert10\rangle+\beta_{3}\vert11\rangle$$
(2)

Now Alice wants to transmit the state of particles a1 and a2 to Bob and Bob wants to transmit the state of particles b1 and b2 to Alice under the control of supervisor Charlie. The detailed steps of the proposed BCQT protocol are shown in Fig. 1.

Fig. 1
figure 1

The schematic of the proposed BCQT scheme, where a solid circle stands for a particle, the solid line represents an entanglement between the particles. A ten-qubit entangled state is utilized as the quantum channel. F-QPM and T-QPM represent the four- and two-qubit projective measurements. UT represents the appropriate unitary transformation

Full size image

We consider the quantum channel shared between Alice, Bob, and controller Charlie consisting of a ten-qubit entangled state which can be given by [38],

$$\begin{array}{@{}rcl@{}} \vert\psi\rangle_{123...8910}&=&\frac{1}{4}(\vert0000000000\rangle+\vert0001000001\rangle +\vert0010000010\rangle+\vert0011000011\rangle\\ &+&\vert0100010100\rangle+\vert0101010101\rangle +\vert0110010110\rangle+\vert0111010111\rangle\\ &+&\vert1000101000\rangle+\vert1001101001\rangle +\vert1010101010\rangle+\vert1011101011\rangle\\ &+&\vert1100111100\rangle+\vert1101111101\rangle +\vert1110111110\rangle\\ &+&\vert1111111111\rangle)_{123...8910} \end{array}$$
(3)

The particles 1,2,3,4 and 7,8,9,10 belong to Alice and Bob, respectively. The controller Charlie owns the particles 5,6. Therefore, the quantum channel can also be expressed as:

$$\begin{array}{@{}rcl@{}} \vert\psi\rangle_{A_{1}A_{2}A_{3}A_{4}C_{1}C_{2}B_{1}B_{2}B_{3}B_{4}}&=&\frac{1}{4}(\vert0000000000\rangle +\vert0001000001\rangle+\vert0010000010\rangle\\ &+&\vert0011000011\rangle+\vert0100010100\rangle+\vert0101010101\rangle\\ &+&\vert0110010110\rangle+\vert0111010111\rangle+\vert1000101000\rangle\\ &+&\vert1001101001\rangle+\vert1010101010\rangle+\vert1011101011\rangle\\ &+&\vert1100111100\rangle+\vert1101111101\rangle+\vert1110111110\rangle\\ &+&\vert1111111111\rangle)_{A_{1}A_{2}A_{3}A_{4}C_{1}C_{2}B_{1}B_{2}B_{3}B_{4}} \end{array}$$
(4)

Hence, the initial state of the whole system can be written as

$$\vert\psi\rangle_{s}=\vert\varphi\rangle_{a_{1}a_{2}}\otimes\vert\varphi\rangle_{b_{1}b_{2}}\otimes\vert\psi\rangle_{A_{1}A_{2}A_{3}A_{4}C_{1}C_{2}B_{1}B_{2}B_{3}B_{4}}$$
(5)

In order to realize the bidirectional controlled quantum teleportation, Alice measures her qubits a1,a2,A1 and A3 in an appropriate basis, Bob measures his qubits b1,b2,B2 and B4 in an appropriate basis, which has the form

$$\begin{array}{@{}rcl@{}} \vert\psi_{1}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0000\rangle+\vert0101\rangle+\vert1010\rangle +\vert1111\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{2}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0000\rangle+\vert0101\rangle-\vert1010\rangle -\vert1111\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{3}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0000\rangle-\vert0101\rangle+\vert1010\rangle -\vert1111\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{4}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0000\rangle-\vert0101\rangle-\vert1010\rangle +\vert1111\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{5}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0001\rangle+\vert0100\rangle+\vert1011\rangle +\vert1110\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{6}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0001\rangle+\vert0100\rangle-\vert1011\rangle -\vert1110\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{7}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0001\rangle-\vert0100\rangle+\vert1011\rangle -\vert1110\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{8}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0001\rangle-\vert0100\rangle-\vert1011\rangle +\vert1110\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{9}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0010\rangle+\vert0111\rangle+\vert1000\rangle +\vert1101\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{10}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0010\rangle+\vert0111\rangle-\vert1000\rangle -\vert1101\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{11}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0010\rangle-\vert0111\rangle+\vert1000\rangle -\vert1101\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{12}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0010\rangle-\vert0111\rangle-\vert1000\rangle +\vert1101\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{13}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0011\rangle+\vert0110\rangle+\vert1001\rangle +\vert1100\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{14}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0011\rangle+\vert0110\rangle-\vert1001\rangle -\vert1100\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{15}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0011\rangle-\vert0110\rangle+\vert1001\rangle -\vert1100\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}\\ \vert\psi_{16}\rangle_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})}&=&\frac{1}{2}(\vert0011\rangle-\vert0110\rangle-\vert1001\rangle +\vert1100\rangle)_{a_{1}a_{2}A_{1}A_{3}(b_{1}b_{2}B_{2}B_{4})} \end{array}$$
(6)

For example, from (6), we know, if Alice’s and Bob’s measurement results are \(\vert \psi _{1}\rangle _{a_{1}a_{2}A_{1}A_{3}}\) and \(\vert \psi _{1}\rangle _{b_{1}b_{2}B_{2}B_{4}}\), the state of particles (A2A4C1C2B1B3) as shown by (6) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\psi^{{~}_{11}}\rangle_{A_{2}A_{4}C_{1}C_{2}B_{1}B_{3}}&=&{~}_{b_{1}b_{2}B_{2}B_{4}}\langle\psi_{1}\vert_{a_{1}a_{2}A_{1}A_{3}}\langle\psi_{1}\vert\psi\rangle_{s}\\ &=&\frac{1}{16}(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle +\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert00\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle)_{B_{1}B_{3}} (\beta_{2}\vert10\rangle +\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert01\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{2}\vert10\rangle+\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle +\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert10\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{2}\vert10\rangle+\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{2}\vert10\rangle +\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert11\rangle_{C_{1}C_{2}} \end{array}$$
(7)

if Alice’s and Bob’s measurement results are \(\vert \psi _{1}\rangle _{a_{1}a_{2}A_{1}A_{3}}\) and \(\vert \psi _{2}\rangle _{b_{1}b_{2}B_{2}B_{4}}\), the state of particles (A2A4C1C2B1B3) as shown by (6) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\psi^{{~}_{12}}\rangle_{A_{2}A_{4}C_{1}C_{2}B_{1}B_{3}}&=&{~}_{b_{1}b_{2}B_{2}B_{4}}\langle\psi_{2}\vert_{a_{1}a_{2}A_{1}A_{3}}\langle\psi_{1}\vert\psi\rangle_{s}\\ &=&\frac{1}{16}(a_{0}\vert00\rangle+a_{1}\vert01\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle +\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert00\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle)_{B_{1}B_{3}} (-\beta_{2}\vert10\rangle -\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert01\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{2}\vert10\rangle+\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle +\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert10\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{2}\vert10\rangle+\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (-\beta_{2}\vert10\rangle -\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert11\rangle_{C_{1}C_{2}} \end{array}$$
(8)

if Alice’s and Bob’s measurement results are \(\vert \psi _{2}\rangle _{a_{1}a_{2}A_{1}A_{3}}\) and \(\vert \psi _{3}\rangle _{b_{1}b_{2}B_{2}B_{4}}\), the state of particles (A2A4C1C2B1B3) as shown by (6) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\psi^{{~}_{23}}\rangle_{A_{2}A_{4}C_{1}C_{2}B_{1}B_{3}}&=&{~}_{b_{1}b_{2}B_{2}B_{4}}\langle\psi_{3}\vert_{a_{1}a_{2}A_{1}A_{3}}\langle\psi_{2}\vert\psi\rangle_{s}\\ &=&\frac{1}{16}(\alpha_{0}\vert00\rangle+a_{1}\vert01\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle -\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert00\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle)_{B_{1}B_{3}} (\beta_{2}\vert10\rangle -\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert01\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(-\alpha_{2}\vert10\rangle-\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle -\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert10\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(-\alpha_{2}\vert10\rangle-\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{2}\vert10\rangle -\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert11\rangle_{C_{1}C_{2}} \end{array}$$
(9)

if Alice’s and Bob’s measurement results are \(\vert \psi _{3}\rangle _{a_{1}a_{2}A_{1}A_{3}}\) and \(\vert \psi _{3}\rangle _{b_{1}b_{2}B_{2}B_{4}}\), the state of particles (A2A4C1C2B1B3) as shown by (6) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\psi^{{~}_{33}}\rangle_{A_{2}A_{4}C_{1}C_{2}B_{1}B_{3}}&=&{~}_{b_{1}b_{2}B_{2}B_{4}}\langle\psi_{3}\vert_{a_{1}a_{2}A_{1}A_{3}}\langle\psi_{3}\vert\psi\rangle_{s}\\ &=&\frac{1}{16}(\alpha_{0}\vert00\rangle-\alpha_{1}\vert01\rangle)_{B_{1}B_{3}}(\beta_{0}\vert00\rangle -\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert00\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{0}\vert00\rangle-\alpha_{1}\vert01\rangle)_{B_{1}B_{3}}(\beta_{2}\vert10\rangle -\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert01\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{2}\vert10\rangle-\alpha_{3}\vert11\rangle)_{B_{1}B_{3}}(\beta_{0}\vert00\rangle -\beta_{1}\vert01\rangle)_{A_{2}A_{4}}\vert10\rangle_{C_{1}C_{2}}\\ &+&\frac{1}{16}(\alpha_{2}\vert10\rangle-\alpha_{3}\vert11\rangle)_{B_{1}B_{3}}(\beta_{2}\vert10\rangle -\beta_{3}\vert11\rangle)_{A_{2}A_{4}}\vert11\rangle_{C_{1}C_{2}} \end{array}$$
(10)

Next, Charlie has to perform a two-qubit von-Neumann measurement on qubits C1,C2, the measurement basis chosen by Charlie is a set of mutually orthogonal basis vectors, which can be presented as:

$$\begin{array}{@{}rcl@{}} \vert\varphi^{1}\rangle_{C_{1}C_{2}}&=&\frac{1}{2}(\vert0\rangle+\vert1\rangle)_{C_{1}}(\vert0\rangle+\vert1\rangle)_{C_{2}}\\ \vert\varphi^{2}\rangle_{C_{1}C_{2}}&=&\frac{1}{2}(\vert0\rangle+\vert1\rangle)_{C_{1}}(\vert0\rangle-\vert1\rangle)_{C_{2}}\\ \vert\varphi^{3}\rangle_{C_{1}C_{2}}&=&\frac{1}{2}(\vert0\rangle-\vert1\rangle)_{C_{1}}(\vert0\rangle+\vert1\rangle)_{C_{2}}\\ \vert\varphi^{4}\rangle_{C_{1}C_{2}}&=&\frac{1}{2}(\vert0\rangle-\vert1\rangle)_{C_{1}}(\vert0\rangle-\vert1\rangle)_{C_{2}} \end{array}$$
(11)

If Charlie’s measurement result is \(\vert \varphi ^{1}\rangle _{C_{1}C_{2}}\), the state of particles (B1B3,A2A4) as shown by (7) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\varphi^{11,1}\rangle_{B_{1}B_{3}A_{2}A_{4}}&=&(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle+\alpha_{2}\vert10\rangle +\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle+\beta_{1}\vert01\rangle\\ &+&\beta_{2}\vert10\rangle+\beta_{3}\vert11\rangle)_{A_{2}A_{4}} \end{array}$$
(12)

After gaining the outcome of Charlie, Alice(Bob) performs appropriate unitary operation \(I_{A_{2}}(_{B_{1}})\otimes I_{A_{4}}(_{B_{3}})\) to restore the teleported state.

If Charlie’s measurement result is \(\vert \varphi ^{2}\rangle _{C_{1}C_{2}}\), the state of particles (B1B3,A2A4) as shown by (8) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\varphi^{12,2}\rangle_{B_{1}B_{3}A_{2}A_{4}}&=&(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle+\alpha_{2}\vert10\rangle +\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle+\beta_{1}\vert01\rangle\\ &+&\beta_{2}\vert10\rangle+\beta_{3}\vert11\rangle)_{A_{2}A_{4}} \end{array}$$
(13)

After obtaining the outcome of Charlie, the collaspsed state of Alice and Bob are as the same as the (12). The protocol is finished by executing the same operations as in the last example.

If Charlie’s measurement result is \(\vert \varphi ^{3}\rangle _{C_{1}C_{2}}\), the state of particles (B1B3,A2A4) as shown by (9) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\varphi^{23,3}\rangle_{B_{1}B_{3}A_{2}A_{4}}&=&(\alpha_{0}\vert00\rangle+\alpha_{1}\vert01\rangle+\alpha_{2}\vert10\rangle +\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle-\beta_{1}\vert01\rangle\\ &+&\beta_{2}\vert10\rangle-\beta_{3}\vert11\rangle)_{A_{2}A_{4}} \end{array}$$
(14)

After acquiring the outcome of Charlie, Alice performs proper unitary operation \(I_{A_{2}}\otimes \sigma _{A_{4z}}\) to get the prepared state, Bob applies proper unitary operation \(I_{B_{1}}\otimes I_{B_{3}}\) to regain the prepared state.

If Charlie’s measurement result is \(\vert \varphi ^{4}\rangle _{C_{1}C_{2}}\), the state of particles (B1B3,A2A4) as shown by (10) will collapse into

$$\begin{array}{@{}rcl@{}} \vert\varphi^{33,4}\rangle_{B_{1}B_{3}A_{2}A_{4}}&=&(\alpha_{0}\vert00\rangle-\alpha_{1}\vert01\rangle-\alpha_{2}\vert10\rangle +\alpha_{3}\vert11\rangle)_{B_{1}B_{3}} (\beta_{0}\vert00\rangle-\beta_{1}\vert01\rangle\\ &-&\beta_{2}\vert10\rangle+\beta_{3}\vert11\rangle)_{A_{2}A_{4}} \end{array}$$
(15)

After receiving the outcome of Charlie, Alice(Bob) executes corresponding unitary operation \(\sigma _{A_{2z}}(_{B_{1}})\otimes \sigma _{A_{4z}}(_{B_{3}})\) on her(his) qubits to construct the prepared state. Therefore, the bidirectional controlled quantum teleportation is successfully realized. Analogously, for other cases, according to the measurement results by Alice, Bob and Charlie, the receivers Alice and Bob can operate appropriate unitary transformation, the bidirectional controlled quantum teleportation can be easily realized. (there are 256 results and 4 examples are displayed)

3 Effects of Channel Noises on the Proposed BCQT Scheme

Obviously, there is no noiseless environment in actual communication. In practice, a real quantum system will inevitably interact with its environment. Thus, it is necessary to discuss the impact of noises. Here, we will illustrate the proposed BCQT scheme with amplitude-damping noise and phase-damping noise.

The BCQT scheme is considered as follows. In Section 2, a BCQT scheme is presented by using a pure ten-qubit entangled state |ψ〉. The corresponding density matrix can be obtained as ρ = |ψ〉〈ψ|. However, after being transmitted via the noisy channel, the corresponding density matrix |ψ〉 can be reexpressed as

$$\begin{array}{@{}rcl@{}} \xi^{r}(\rho)&=&\sum\limits_{m}({E_{m}^{r}})_{A_{1}}({E_{m}^{r}})_{A_{3}}({E_{m}^{r}})_{B_{2}}({E_{m}^{r}})_{B_{4}} ({E_{m}^{r}})_{A_{2}} ({E_{m}^{r}})_{A_{4}}({E_{m}^{r}})_{B_{1}}({E_{m}^{r}})_{B_{3}} \\ &\times&\rho({E_{m}^{r}})_{A_{1}}^{\dagger}({E_{m}^{r}})_{A_{3}}^{\dagger} ({E_{m}^{r}})_{B_{2}}^{\dagger}({E_{m}^{r}})_{B_{4}}^{\dagger} ({E_{m}^{r}})_{A_{2}}^{\dagger} ({E_{m}^{r}})_{A_{4}}^{\dagger}({E_{m}^{r}})_{B_{1}}^{\dagger} ({E_{m}^{r}})_{B_{3}}^{\dagger} \end{array}$$
(16)

where r ∈ {A, P}. If r = A, for amplitude-damping noise, then m = 0, 1; if r = P, for phase-damping noise, then m = 0, 1, 2. The Kraus operators Em satisfy \(\sum \limits _{m}E_{m}^{\dagger } E_{m}=I\). We suppose that the qubits (A1,A2,A3,A4,B1,B2,B3,B4) teleported through the noisy environment between the sender Alice and the receiver Bob are affected by the same Kraus operator. Although the controller Charlie generates the quantum channel and owns the qubits C1,C2, the qubits C1,C2 are not transmitted via the quantum channel. Therefore, we discuss the shared state which is composed of these qubits in the following.

3.1 The Amplitude-damping Noise

The amplitude-damping noise can be expressed in terms of Kraus operators [39]

$${E_{0}^{A}}= \begin{bmatrix} 1 & 0\\ 0 & \sqrt{1-P_{A}} \end{bmatrix}, {E_{1}^{A}}= \begin{bmatrix} 0 & \sqrt{P_{A}}\\ 0 & 0 \end{bmatrix}$$
(17)

where PA(0 ≤ PA ≤ 1) represents the decoherence rate of amplitude-damping noise. It describes the probability of missing a photon. Due to the interaction with the surrounding noise environment, energy dissipation occurs in the quantum system. After the qubits (A1,A2,A3,A4,B1,B2,B3,B4) transmitted via the amplitude-damping channel, we can rewrite the density matrix ρ as ξA(ρ)

$$\begin{array}{@{}rcl@{}} \xi^{A}(\rho)&=&\frac{1}{16}\big\{[\vert0000000000\rangle +(1-P_{A})\vert0001010000\rangle +(1-P_{A})\vert0100000100\rangle\\ &+&(1-P_{A})^{2}\vert0101010100\rangle +(1-P_{A})\vert0010100001\rangle +(1-P_{A})^{2}\vert0011110001\rangle\\ &+&(1-P_{A})^{2}\vert0110100101\rangle +(1-P_{A})^{3}\vert0111110101\rangle +(1-P_{A})\vert1000001010\rangle\\ &+&(1-P_{A})^{2}\vert1001011010\rangle +(1-P_{A})^{2}\vert1100001110\rangle +(1-P_{A})^{3}\vert1101011110\rangle\\ &+&(1-P_{A})^{2}\vert1010101011\rangle +(1-P_{A})^{3}\vert1011111011\rangle +(1-P_{A})^{3}\vert1110101111\rangle\\ &+&(1-P_{A})^{4}\vert1111111111\rangle] \times [\langle0000000000\vert +(1-P_{A})\langle0001010000\vert\\ &+&(1-P_{A})\langle0100000100\vert +(1-P_{A})^{2}\langle0101010100\vert +(1-P_{A})\langle0010100001\vert\\ &+&(1-P_{A})^{2}\langle0011110001\vert +(1-P_{A})^{2}\langle0110100101\vert +(1-P_{A})^{3}\langle0111110101\vert\\ &+&(1-P_{A})\langle1000001010\vert +(1-P_{A})^{2}\langle1001011010\vert +(1-P_{A})^{2}\langle1100001110\vert\\ &+&(1-P_{A})^{3}\langle1101011110\vert +(1-P_{A})^{2}\langle1010101011\vert +(1-P_{A})^{3}\langle1011111011\vert\\ &+&(1-P_{A})^{3}\langle1110101111\vert +(1-P_{A})^{4}\langle1111111111\vert]\\ &+&{P_{A}^{8}}(\vert0000000000\rangle \langle0000000000\vert) \big\} \end{array}$$
(18)

In order to recover the desired state, Alice and Bob need to implement corresponding unitary operations on their qubits (B1,B3,A2,A4). Subsequently, the density matrix of the output state becomes

$$\begin{array}{@{}rcl@{}} \rho_{out}^{A}&=&\big\{[\alpha_{0}\beta_{0}\vert0000\rangle +(1-P_{A})\alpha_{0}\beta_{1}\vert0001\rangle +(1-P_{A})\alpha_{1}\beta_{0}\vert0100\rangle\\ &+&(1-P_{A})^{2}\alpha_{1}\beta_{1}\vert0101\rangle +(1-P_{A})\alpha_{0}\beta_{2}\vert0010\rangle +(1-P_{A})^{2}\alpha_{0}\beta_{3}\vert0011\rangle\\ &+&(1-P_{A})^{2}\alpha_{1}\beta_{2}\vert0110\rangle +(1-P_{A})^{3}\alpha_{1}\beta_{3}\vert0111\rangle +(1-P_{A})\alpha_{2}\beta_{0}\vert1000\rangle\\ &+&(1-P_{A})^{2}\alpha_{2}\beta_{1}\vert1001\rangle +(1-P_{A})^{2}\alpha_{3}\beta_{0}\vert1100\rangle +(1-P_{A})^{3}\alpha_{3}\beta_{1}\vert1101\rangle\\ &+&(1-P_{A})^{2}\alpha_{2}\beta_{2}\vert1010\rangle +(1-P_{A})^{3}\alpha_{2}\beta_{3}\vert1011\rangle +(1-P_{A})^{3}\alpha_{3}\beta_{2}\vert1110\rangle\\ &+&(1-P_{A})^{4}\alpha_{3}\beta_{3}\vert1111\rangle] \times [\alpha_{0}\beta_{0}\langle0000\vert +(1-P_{A})\alpha_{0}\beta_{1}\langle0001\vert\\ &+&(1-P_{A})\alpha_{1}\beta_{0}\langle0100\vert +(1-P_{A})^{2}\alpha_{1}\beta_{1}\langle0101\vert +(1-P_{A})\alpha_{0}\beta_{2}\langle0010\vert\\ &+&(1-P_{A})^{2}\alpha_{0}\beta_{3}\langle0011\vert +(1-P_{A})^{2}\alpha_{1}\beta_{2}\langle0110\vert +(1-P_{A})^{3}\alpha_{1}\beta_{3}\langle0111\vert\\ &+&(1-P_{A})\alpha_{2}\beta_{0}\langle1000\vert +(1-P_{A})^{2}\alpha_{2}\beta_{1}\langle1001\vert +(1-P_{A})^{2}\alpha_{3}\beta_{0}\langle1100\vert\\ &+&(1-P_{A})^{3}\alpha_{3}\beta_{1}\langle1101\vert +(1-P_{A})^{2}\alpha_{2}\beta_{2}\langle1010\vert +(1-P_{A})^{3}\alpha_{2}\beta_{3}\langle1011\vert\\ &+&(1-P_{A})^{3}\alpha_{3}\beta_{2}\langle1110\vert +(1-P_{A})^{4}\alpha_{3}\beta_{3}\langle1111\vert]\\ &+&{P_{A}^{8}}{\alpha_{3}^{2}}{\beta_{3}^{2}}(\vert0000\rangle \langle0000\vert)_{B_{1}B_{3}A_{2}A_{4}} \big\} \end{array}$$
(19)

When we consider our scheme in an ideal situation, the output state is \(\vert {\Omega }\rangle =(\alpha _{0}\vert 00\rangle +\alpha _{1}\vert 01\rangle +\alpha _{2}\vert 10\rangle +\alpha _{3}\vert 11\rangle )_{B_{1}B_{3}}(\beta _{0}\vert 00\rangle +\beta _{1}\vert 01\rangle +\beta _{2}\vert 10\rangle +\beta _{3}\vert 11\rangle )_{A_{2}A_{4}}\), However, in the noisy environment, the desired state is impossible to be restored. Taking into account the information loss of the amplitude-damping channel, we calculate the fidelity of the output state. Applying the (19), it can be obtained as

$$\begin{array}{@{}rcl@{}} F^{A}&=&\langle{\Omega}\vert\rho_{out}^{A}\vert{\Omega}\rangle\\ &=&\big\{[{\alpha_{0}^{2}}{\beta_{0}^{2}}+(1-P_{A}){\alpha_{0}^{2}}{\beta_{1}^{2}}+(1-P_{A}){\alpha_{1}^{2}}{\beta_{0}^{2}} +(1-P_{A})^{2}{\alpha_{1}^{2}}{\beta_{1}^{2}}\\ &+&(1-P_{A}){\alpha_{0}^{2}}{\beta_{2}^{2}} +(1-P_{A})^{2}{\alpha_{0}^{2}}{\beta_{3}^{2}}+(1-P_{A})^{2}{\alpha_{1}^{2}}{\beta_{2}^{2}} +(1-P_{A})^{3}{\alpha_{1}^{2}}{\beta_{3}^{2}}\\ &+&(1-P_{A}){\alpha_{2}^{2}}{\beta_{0}^{2}} +(1-P_{A})^{2}{\alpha_{2}^{2}}{\beta_{1}^{2}}+(1-P_{A})^{2}{\alpha_{3}^{2}}{\beta_{0}^{2}} +(1-P_{A})^{3}{\alpha_{3}^{2}}{\beta_{1}^{2}}\\ &+&(1-P_{A})^{2}{\alpha_{2}^{2}}{\beta_{2}^{2}} +(1-P_{A})^{3}{\alpha_{2}^{2}}{\beta_{3}^{2}}+(1-P_{A})^{3}{\alpha_{3}^{2}}{\beta_{2}^{2}} +(1-P_{A})^{4}{\alpha_{3}^{2}}{\beta_{3}^{2}}]^{2}\\ &+&{P_{A}^{8}}{\alpha_{0}^{2}}{\alpha_{3}^{2}}{\beta_{0}^{2}}{\beta_{3}^{2}}\big\} \end{array}$$
(20)

3.2 The Phase-damping Noise

The phase-damping noise can be characterized by Kraus operators [39]

$${E_{0}^{P}}=\sqrt{1-P_{P}} \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}, {E_{1}^{P}}=\sqrt{P_{P}} \begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix}, {E_{2}^{P}}=\sqrt{P_{P}} \begin{bmatrix} 0 & 0\\ 0 & 1 \end{bmatrix}$$
(21)

where PP(0 ≤ PP ≤ 1) represents the decoherence rate of phase-damping noise. As a result of the phase-damping noisy environment, we can rewrite the density matrix ρ as ξP(ρ)

$$\begin{array}{@{}rcl@{}} \xi^{P}(\rho)&=&\frac{1}{16}\big\{[(1-P_{A})^{8}\vert0000000000\rangle +\vert0001010000\rangle +\vert0100000100\rangle\\ &+&\vert0101010100\rangle +\vert0010100001\rangle +\vert0011110001\rangle +\vert0110100101\rangle\\ &+&\vert0111110101\rangle +\vert1000001010\rangle +\vert1001011010\rangle +\vert1100001110\rangle\\ &+&\vert1101011110\rangle +\vert1010101011\rangle +\vert1011111011\rangle +\vert1110101111\rangle\\ &+&\vert1111111111\rangle] \times [\langle0000000000\vert +\langle0001010000\vert +\langle0100000100\vert\\ &+&\langle0101010100\vert +\langle0010100001\vert +\langle0011110001\vert +\langle0110100101\vert\\ &+&\langle0111110101\vert +\langle1000001010\vert +\langle1001011010\vert +\langle1100001110\vert\\ &+&\langle1101011110\vert +\langle1010101011\vert +\langle1011111011\vert +\langle1110101111\vert\\ &+&\langle1111111111\vert] +{P_{P}^{8}}(\vert0000000000\rangle \langle0000000000\vert)\\ &+&{P_{P}^{8}}(\vert1111111111\rangle \langle1111111111\vert) \big\} \end{array}$$
(22)

The density matrix of the output state turns to

$$\begin{array}{@{}rcl@{}} \rho_{out}^{P}&=&\big\{[(1-P_{P})^{8} \alpha_{0}\beta_{0}\vert0000\rangle +\alpha_{0}\beta_{1}\vert0001\rangle +\alpha_{1}\beta_{0}\vert0100\rangle +\alpha_{1}\beta_{1}\vert0101\rangle\\ &+&\alpha_{0}\beta_{2}\vert0010\rangle +\alpha_{0}\beta_{3}\vert0011\rangle +\alpha_{1}\beta_{2}\vert0110\rangle +\alpha_{1}\beta_{3}\vert0111\rangle +\alpha_{2}\beta_{0}\vert1000\rangle\\ &+&\alpha_{2}\beta_{1}\vert1001\rangle +\alpha_{3}\beta_{0}\vert1100\rangle +\alpha_{3}\beta_{1}\vert1101\rangle +\alpha_{2}\beta_{2}\vert1010\rangle +\alpha_{2}\beta_{3}\vert1011\rangle\\ &+&\alpha_{3}\beta_{2}\vert1110\rangle +\alpha_{3}\beta_{3}\vert1111\rangle] \times [\alpha_{0}\beta_{0}\langle0000\vert +\alpha_{0}\beta_{1}\langle0001\vert +\alpha_{1}\beta_{0}\langle0100\vert\\ &+&\alpha_{1}\beta_{1}\langle0101\vert +\alpha_{0}\beta_{2}\langle0010\vert +\alpha_{0}\beta_{3}\langle0011\vert +\alpha_{1}\beta_{2}\langle0110\vert +\alpha_{1}\beta_{3}\langle0111\vert\\ &+&\alpha_{2}\beta_{0}\langle1000\vert +\alpha_{2}\beta_{1}\langle1001\vert +\alpha_{3}\beta_{0}\langle1100\vert +\alpha_{3}\beta_{1}\langle1101\vert +\alpha_{2}\beta_{2}\langle1010\vert\\ &+&\alpha_{2}\beta_{3}\langle1011\vert +\alpha_{3}\beta_{2}\langle1110\vert +\alpha_{3}\beta_{3}\langle1111\vert] +{P_{P}^{8}}{\alpha_{0}^{2}}{\beta_{0}^{2}}\vert0000\rangle \langle0000\vert\\ &+&{P_{P}^{8}}{\alpha_{3}^{2}}{\beta_{3}^{2}}\vert1111\rangle \langle1111\vert_{B_{1}B_{3}A_{2}A_{4}}\big\} \end{array}$$
(23)

According to (23), we can calculate the fidelity of the output state as below

$$\begin{array}{@{}rcl@{}} F^{P}&=&\langle{\Omega}\vert\rho_{out}^{P}\vert{\Omega}\rangle\\ &=&(1-P_{P})^{8}+{P_{P}^{8}}{\alpha_{0}^{4}}{\beta_{0}^{4}}+{P_{P}^{8}}{\alpha_{3}^{4}}{\beta_{3}^{4}} \end{array}$$
(24)

From the above fidelity calculation results, it is not difficult to see that the fidelities for these two noise scenarios only related to the amplitude parameter of the initial state and the decoherence rate. Exactly, the effect of amplitude-damping (phase-damping) noise on the fidelity FA(FP) and variation of the fidelity with amplitude parameter of the initial state and the decoherence rate Pr are clearly displayed in Fig. 2a-f. It is evidently that the fidelity FA and FP always decrease with decoherence PA and PP, respectively. (Figure 2a, b, d, e).

Fig. 2
figure 2

The effect of noise on BCQT scheme reflected through variation of fidelity FA (for amplitude-damping noise) and FP (for phase-damping noise) with regard to amplitude information of the states to be teleported and decoherence rates for various situations: (a) amplitude-damping noise with \(a = \alpha _{0}, \beta _{0} = \beta _{3} = \frac {\sqrt {2}}{2}, \alpha _{1} = \alpha _{2} = \beta _{1} = \beta _{2} = 0,\) (b) amplitude-damping noise with \(b = \beta _{0}, \alpha _{1} = \alpha _{2} = \frac {\sqrt {2}}{2}, \alpha _{0} = \alpha _{3} = \beta _{1} = \beta _{2} = 0,\) (c) amplitude-damping noise with b = β0,PA = 1,a = α0,α1 = α2 = β1 = β2 = 0, (d) phase-damping noise with a = α0,β0 = 1,α1 = α2 = β1 = β2 = 0, (e) phase-damping noise with \(b = \beta _{0}, \alpha _{0} = \frac {1}{2}, \alpha _{1} = \alpha _{2} = \beta _{1} = \beta _{2} = 0, \alpha _{3} = \frac {\sqrt {3}}{2},\) (f) phase-damping noise with a = α0,α1 = α2 = β1 = β2 = 0,b = β0,PP = 1

Full size image

In Fig. 3, we can observe the trend of the fidelity FA and FP with the change of the decoherence rate PA and PP. We hypothesize that PA = PP = P, and \(\alpha _{0}=\alpha _{1}=\alpha _{2}= \alpha _{3}=\frac {1}{2}\), \(\beta _{0}=\beta _{1}=\beta _{2}= \beta _{3}=\frac {1}{2}\). (α0,α1,α2,α3,β0,β1,β2,β3 ∈ R) This situation demonstrates the fidelity of amplitude-damping channel (solid line in Fig. 3a) is always higher than that of the phase-damping channel (dashed line in Fig. 3a) for the same value of decoherence rate P. Therefore, we can conclude that for this special choice of the amplitude parameter of the initial state, the information loss is less when the travel qubits are transmitted through the amplitude-damping channel compared with the phase-damping channel. However, as shown in Fig. 3b, we can notice that for P > 0.6677 and \(\alpha _{0}=\beta _{0}=\frac {1}{2}, \alpha _{3}= \beta _{3}=\frac {\sqrt {3}}{2}, \alpha _{1}=\alpha _{2}=0, \beta _{1}=\beta _{2}=0\), the fidelity of phase-damping channel is more than amplitude-damping channel, so the effect of amplitude-damping noise is more.

This figure reveals that in the actual communication situation, the fidelity decreases as the decoherence rate increases. Surprisingly, even the system interacts with the noisy environment, BCQT may be achieved with unit fidelity, if the states with particular αi and βj are to be transmitted. Figure 2c, f indicates this fact.

Fig. 3
figure 3

The relationship between the fidelities of amplitude-damping noise, phase-damping noise and the decoherence rate P. The red solid line denotes amplitude-damping noise, the blue dashed line denotes phase-damping noise

Full size image

4 Discussion and Comparison

In this section, we compare our presented scheme with other BCQT schemes. The method for calculating intrinsic efficiency [40] of QT schemes is given by

$$\eta=\frac{c}{q}$$
(25)

where c indicates the number of qubits for preparing, q denotes the number of qubits utilized as quantum channel. Table 1 shows a comparison of five aspects: type of protocol (TP), the qubits composed of quantum information to be transmitted (QIBT), the number of qubits used in the quantum channel (QC), discussion of noise environment (NA), intrinsic efficiency (IE).

Table 1 Comparison with some other BCQT protocols
Full size table

It appears from the Table 1 that our scheme has the highest intrinsic efficiency among the compared schemes. Our scheme has the remarkable advantages: (1) compared with the maximally entangled channel, the non-maximum entangled channel is easy to construct; (2) it is unnecessary to employ C-NOT gates and Hadamard gates to generate the quantum channel in our scheme, the complexity of quantum channel construction is reduced; (3) the support of ancillary qubit is not required in our scheme. Thus, our scheme is more suitable for BCQT.

5 Conclusion

In summary, we have proposed a BCQT scheme of arbitrary two-qubit. In the scheme, Alice has particles a1,a2 in an unknown arbitrary two-qubit state, she wants to transmit the state of particles a1,a2 to Bob. Bob also has particles b1,b2 in an unknown arbitrary two-qubit state and he wants to transmit the state of particles b1,b2 to Alice at the same time. The whole communication process is under the control of supervisor Charlie. So the desired states can be exchanged by operating appropriate basis measurement and unitary transformation. Then, we assess our scheme in amplitude-damping noise and phase-damping noise. It is noted that the fidelities of the output states are only related to the amplitude parameter of original state and decoherence rate. In addition, we compare our protocol with previous works in several aspects to show the advantages of our protocol. In order to reduce the complexity of teleportation, the quantum channel is easier to construct in our scheme. Gate transformations and auxiliary particles are not required to construct the quantum channel.

The proposed scheme improves high efficiency via quantum transformation and reduces the waste of resources. We hope that BCQT will offer more significant advantages in quantum information tranportation.