1 Introduction

Quantum teleportation (QT) is a communication protocol that transmits the state of quantum system from some place to other place without transmitting the system itself. In 1993, Bennett et al. first showed that quantum entanglement, which represents a distinctive feature of quantum mechanics [1, 2], can be used to teleport an unknown quantum state via an Einstein-Podolsky-Rosen (EPR) pair with the help of some classical information [3]. Later, a number of theoretical and experimental studies [4–12] on QT have been done, some authors have demonstrated QT protocol that transmit an unknown single photon polarized state utilizing standard bi-photonic Bell states [13, 14], atomic qubit using bipartite atomic Bell states [15, 16] and unknown quantum state of nucleus [17] in the experiment.

Communication is duplex, bidirectional quantum teleportation has attracted a number of authors [18–21]. However, in the existing schemes of bidirectional teleportation, they all select a special quantum state as the quantum channel, it does not give a method of selecting quantum channels. Does there exist a general method for choosing channel in bidirectional quantum teleportation? The answer is affirmative and we do it in this paper. Lately, a tensor representation method about teleportation was put forward [22–24], this tensor representation shows the intrinsic link among Bell basis measurement matrix T α and channel parameter matrix (CPM) R. By analyzing some underlying relationship between quantum channel parameter matrix R and measurement matrix T α, a quantum state that can be employed as quantum channel for bidirectional teleportation satisfy necessary condition, which is determined by the channel parameter matrix R in the Bell basis measurement. This necessary condition is a criterion of quantum channel for realizing bidirectional teleportation, which can be used to judge whether a quantum state can be employed as quantum channel or not in bidirectional teleportation. In terms of the criterion, a general method selecting quantum channel and a theoretical scheme of bidirectional quantum teleportation via four-particle cluster state as the quantum channel is proposed. This general method provides a theoretical basis for quantum channel selection and flexible choice in the bidirectional quantum experiments.

2 The Condition of Selecting Quantum Channel for Bidirectional Teleportation

Suppose Alice wants to teleport an unknown state |φ〉 A to Bob; at the same time, Bob wants to teleport an unknown state |φ〉 B to Alice, with the help of tensor representation, |φ〉 A and |φ〉 B can be expressed as

$$\begin{aligned} |\varphi\rangle_{A}=x^{i}|i\rangle,\qquad |\varphi\rangle_{B}=y^{j}|j\rangle,\quad ij\in0,1, \end{aligned}$$
(1)

where it implicits summation when an index is repeated and the unknown coefficients x i, y j satisfy \({x^{i}}{x^{*}_{i}}=1\) and \({y^{i}}{y^{*}_{i}}=1\). We assume a general four-qubit state as quantum channel, which has the following form:

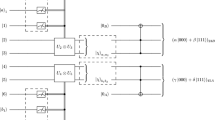
$$\begin{aligned} &|\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}}=R^{lmst}|lmst\rangle \\ &\phantom{|\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}}}= R^{0000}|0000\rangle+R^{0001}|0001\rangle + \cdots+R^{1110}|1110\rangle+R^{1111}|1111\rangle, \\ &\quad{} l,m,s,t\in 0,1, \end{aligned}$$
(2)

where \({R^{lmst}}{R^{*}_{lmst}}=1\), the particles A 1 and A 2 belong to Alice, the particles B 1 and B 2 belong to Bob. There are two kinds of forms for the quantum channel consisting of the four-qubit state: the single channel which is composed of a genuine quantum entangled state [25] is illustrated in Fig. 1(a). the double channel which is composed of two single channel is illustrated in Figs. 1(b) and (c). According to collapse principle of state when it being measured, after Alice (Bob) performing a Bell basis measurement on his particles (A,A 1) ((B,B 1)) via the single channel in Fig. 1(a), the state of particle A can collapse to particle B 2 and the state of particle B can collapse to particle A 2 probably, the single channel can realize the bidirectional teleportation. If selecting the double channel in Fig. 1(b), when Alice (Bob) performs a Bell basis measurement on his particles (A,A 1) ((B,B 1)), obviously, it can not realize the bidirectional teleportation; if selecting the double channel in Fig. 1(c), after Alice and Bob performing a Bell basis measurement on their particles (A,A 1) and (B,B 1), respectively, although it can exchange two states, this is two uncorrelated unidirectional teleportation. So, the quantum channel of bidirectional teleportation must select a single channel which is composed of a genuine quantum entangled state. Next we further analyze that this single channel must satisfy condition for bidirectional teleportation.

Fig. 1
figure 1

Quantum channel of bidirectional teleportation: the single channel (a); the double channel (b) and (c). The black line represents quantum entanglement channel, the shorter blue dot curve represents a Bell basis measurement

Full size image

The total state of the system is as follow

$$\begin{aligned} |\varPsi\rangle_{T} =&|\varphi\rangle_{A}\otimes|\varphi\rangle_{B}\otimes |\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}} \\ =&x^{i}|i\rangle_{A}y^{j}|j\rangle_{B}R^{lmst}|lmst\rangle _{A_{1},B_{1},B_{2},A_{2}}, \end{aligned}$$
(3)

Alice and Bob will decompose |Ψ〉 T with Bell basis \(\phi_{ij}^{\alpha}\) through transformation matrix T which is between computation basis |ij〉 and Bell basis \(\phi_{ij}^{\alpha}\), where α∈1,2,3,4 and \(\phi_{ij}^{1,2}=\frac{1}{\sqrt {2}}(|00\rangle\pm |11\rangle),\phi_{ij}^{3,4}=\frac{1}{\sqrt{2}} (|01\rangle\pm|10\rangle)\), the T has the following form:

$$\begin{aligned} T=\left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} T_{00}^{1} &T_{00}^{2} &T_{00}^{3} &T_{00}^{4}\\ T_{01}^{1} &T_{01}^{2} &T_{01}^{3} &T_{01}^{4}\\ T_{10}^{1} &T_{10}^{2} &T_{10}^{3} &T_{10}^{4}\\ T_{11}^{1} &T_{11}^{2} &T_{11}^{3} &T_{11}^{4}\\ \end{array} \right ) =\frac{1}{\sqrt{2}}\left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 &1 &0 &0\\ 0 &0 &1 &1\\ 0 &0 &1 &-1\\ 1 &-1 &0 &0\\ \end{array} \right ). \end{aligned}$$
(4)

Under the Bell basis representation, the total state |Ψ〉 T can be transformed into

$$\begin{aligned} &|\varPsi\rangle_{T}=x^{i}y^{j}R^{lmst}T^{\alpha}_{il}T^{\beta}_{jm}| \alpha\rangle|\beta\rangle |st\rangle_{{B_2}{A_2}},\quad (\alpha,\beta\in1,2,3,4) \\ &\phantom{|\varPsi\rangle_{T}}=x^{i}y^{j}\sigma^{\alpha\beta}_{iljm}|\alpha \rangle|\beta\rangle |st\rangle_{{B_2}{A_2}}, \end{aligned}$$
(5)
$$\begin{aligned} &R^{lmst}=\left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} R^{0000} &R^{0100} &R^{1000} &R^{1100}\\ R^{0001} &R^{0101} &R^{1001} &R^{1101}\\ R^{0010} &R^{0110} &R^{1010} &R^{1110}\\ R^{0011} &R^{0111} &R^{1011} &R^{1111}\\ \end{array} \right ), \end{aligned}$$
(6)
$$\begin{aligned} &T^{\alpha}=\left ( \begin{array}{c@{\quad}c} T_{00}^{\alpha} &T_{10}^{\alpha}\\ T_{01}^{\alpha} &T_{11}^{\alpha}\\ \end{array} \right ),\qquad T^{\beta}=\left ( \begin{array}{c@{\quad}c} T_{00}^{\beta} &T_{10}^{\beta}\\ T_{01}^{\beta} &T_{11}^{\beta}\\ \end{array} \right ), \end{aligned}$$
(7)
$$\begin{aligned} &\sigma^{\alpha\beta}_{iljm}=R^{lmst}T^{\alpha}_{il}T^{\beta}_{jm} \end{aligned}$$
(8)

where R is the quantum CPM, T α and T β is measurement matrix, \(\sigma^{\alpha\beta}_{iljm}\) is an element of the transmission matrix σ αβ. In terms of Eq. (4), the four Bell basis measurement matrix T α can be described by

$$\begin{aligned} T^{1}=\frac{1}{\sqrt{2}}I,\qquad T^{2}=\frac{1}{\sqrt{2}} \sigma_{z},\qquad T^{3}=\frac{1}{\sqrt{2}}\sigma_{x},\qquad T^{4}=-i\frac{1}{\sqrt{2}}\sigma_{y} =\frac{1}{\sqrt{2}}\sigma_{x}\sigma_{z}. \end{aligned}$$
(9)

After Alice and Bob finishing the Bell state measurement on their particles (A,A 1) and (B,B 1), respectively, the total state of the system collapses into particles A 2 and B 2, the remanent state has the next form:

$$\begin{aligned} |\varPsi^{\alpha\beta}\rangle_{T} =&x^{i}y^{j}\sigma^{\alpha\beta}|s\rangle_{B_{2}}|t\rangle_{A_{2}} \end{aligned}$$
(10)

where the transmission matrix σ αβ is

$$\begin{aligned} \sigma^{\alpha\beta}=R\bigl( T^{\alpha}\otimes T^{\beta}\bigr) \end{aligned}$$
(11)

Here the quantum CPM R is 4×4 complex matrix, T α and T β are 2×2 complex matrix.

In order to perfectly realize their quantum state interchanged, firstly, the transformation matrix σ αβ must be a unitary matrix; secondly, by reason of the two particles A 2 and B 2 belong individually to Alice and Bob, Alice and Bob have to perform individually a unitary transformation on particles A 2 and B 2 to perfectly swap their quantum state, so the matrix R must be reduced into a direct product form of two unitary matrix R 1 and R 2, which are 2×2 unitary matrices. The transmission matrix σ αβ can be remarked as

$$\begin{aligned} \sigma^{\alpha\beta} =&R\bigl( T^{\alpha}\otimes T^{\beta}\bigr)=(R_{1}\otimes R_{2}) \bigl(T^{\alpha}\otimes T^{\beta}\bigr) \\ =&\bigl(R_{1}T^{\alpha}\bigr)\otimes\bigl(R_{2}T^{\beta}\bigr)=\sigma^{\alpha}\sigma^{\beta}. \end{aligned}$$
(12)

The residual state |Ψ αβ〉 T can be expressed as

$$\begin{aligned} |\varPsi^{\alpha\beta}\rangle_{T} = x^{i}y^{j}\sigma^{\alpha} \sigma^{\beta}|st\rangle_{B_{2}A_{2}}, \end{aligned}$$
(13)

In this case, the matrix \(\sqrt{2}T^{\alpha}\) is unitary, the two matrices R 1 and R 2 are also unitary, the bidirectional quantum teleportation can be realized when Alice (Bob) operates an appropriate unitary transformation (σ β)−1 ((σ α)−1) on the residual state |Ψ αβ〉 T .

From the above analysis, we find a criterion which can be used to judge whether a quantum state can be regarded as quantum channel or not for bidirectional teleportation, namely, the quantum channel of realizing bidirectional teleportation must satisfy the following necessary condition:

  1. (i)

    the quantum channel must be a single channel which is composed of a genuine quantum entangled state.

  2. (ii)

    the quantum channel parameter matrix can be reduced into direct product form of two unitary matrices. If realizing a probabilistic bidirectional teleportation, the quantum channel parameter matrix can be reduced into direct product form of two invertible matrices.

3 A General Method of Selecting Four-Qubit Entangled State as Quantum Channel in Bidirectional Teleportation

3.1 A General Quantum Channel Consisting of the Four-Qubit Entangled State

In accordance with the above condition of selecting quantum channel to realize bidirectional teleportation, we choose a genuine four-qubit entangled state as quantum channel, where the CPM is composed of two general unitary matrices U 1 and U 2, which have the following form:

$$\begin{aligned} U_{1}=\left ( \begin{array}{c@{\quad}c} \cos\theta_{1} &\sin\theta_{1}\\ \sin\theta_{1}&-\cos\theta_{1}\\ \end{array} \right ),\qquad U_{2}=\left ( \begin{array}{c@{\quad}c} \cos\theta_{2} &\sin\theta_{2}\\ \sin\theta_{2}&-\cos\theta_{2}\\ \end{array} \right ),\quad 0\leq \theta_{1,2}\leq2\pi, \end{aligned}$$
(14)

without loss of generality, let \(\theta_{1}=\theta_{2}=\frac{\pi}{4}\), then U 1 and U 2 is given by:

$$\begin{aligned} U_{1}=H_{1}=\frac{1}{\sqrt{2}}\left ( \begin{array}{c@{\quad}c} 1 &1\\ 1&-1\\ \end{array} \right ),\qquad U_{2}=H_{2}= \frac{1}{\sqrt{2}}\left ( \begin{array}{c@{\quad}c} 1 &1\\ 1&-1\\ \end{array} \right ), \end{aligned}$$
(15)

in this case, U 1 and U 2 are Hadamard operation. Because coefficients of quantum channel satisfy standard normalization, the channel parameter will be suitably adjusted, from Eq. (6), the quantum channel parameter matrix R can be selected as

$$\begin{aligned} R=\frac{1}{2}H_{1}\otimes H_{2}= \frac{1}{4} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 &1 &1 &1\\ 1 &-1 &1 &-1\\ 1 &1 &-1 &-1\\ 1 &-1 &-1 &1\\ \end{array} \right ), \end{aligned}$$
(16)

the quantum channel consisting of the four-qubit entangled state is

$$\begin{aligned} |\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}} =&\frac{1}{4}\bigl(|0000\rangle +|0100\rangle+|1000\rangle+|1100\rangle \\ &{}+|0001\rangle-|0101\rangle+|1001\rangle-|1101\rangle \\ &{}+|0010\rangle+|0110\rangle-|1010\rangle-|1110\rangle \\ &{}+|0011\rangle-|0111\rangle-|1011\rangle+|1111\rangle\bigr). \end{aligned}$$
(17)

Obviously, \(|\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}}\) is a genuine quantum entangled state. The system state of the six particles is given by

$$\begin{aligned} |\varPsi\rangle_{T}=|\varphi\rangle_{A}\otimes |\varphi \rangle_{B}\otimes|\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}} \end{aligned}$$
(18)

After Alice and Bob performing a standard Bell basis measurement on their particles (A,A 1) and (B,B 1), respectively, if Alice’s and Bob’s measurement result are ϕ 1, the whole system state |Ψ〉 T will be collapsed into the following state

$$\begin{aligned} |\varPsi^{11}\rangle_{T} =&\bigl\langle \phi^{1}_{A,A_{1}}\bigr|\phi^{1}_{B,B_{1}}|\varPsi_{T}\rangle \\ =&\frac{1}{8}\bigl[\bigl(x^{0}y^{0}+x^{1}y^{0}+x^{0}y^{1}+x^{1}y^{1}\bigr)|00\rangle \\ &{}+\bigl(x^{0}y^{0}+x^{1}y^{0}-x^{0}y^{1}-x^{1}y^{1}\bigr)|01\rangle \\ &{}+\bigl(x^{0}y^{0}-x^{1}y^{0}+x^{0}y^{1}-x^{1}y^{1}\bigr)|10\rangle \\ &{}+\bigl(x^{0}y^{0}-x^{1}y^{0}-x^{0}y^{1}+x^{1}y^{1}\bigr)|11\rangle\bigr], \end{aligned}$$
(19)

in order to achieve bidirectional quantum teleportation, Alice, Bob have to operate an Hadamard transformation on their particles A 2 and B 2, respectively, the final state is

$$\begin{aligned} H_2^{A_2}H_1^{B_2}\bigl|\varPsi^{11}\bigr\rangle _{T} =&\frac{1}{4}\bigl(x^{0}y^{0}|00\rangle+x^{1}y^{0}|10 \rangle +x^{0}y^{1}|01\rangle+x^{1}y^{1}|11\rangle\bigr)_{B_{2},A_{2}} \\ =&\frac{1}{4}\bigl(x^{0}|0\rangle+x^{1}|1\rangle\bigr)_{B_{2}}\otimes \bigl(y^{0}|0\rangle+y^{1}|1\rangle\bigr)_{A_{2}}, \end{aligned}$$
(20)

the bidirectional quantum teleportation is successfully achieved. For the other 15 kinds of Bell basis \(\phi_{A}^{\alpha}\phi_{B}^{\beta}\) measurement results, Alice and Bob operate an appropriate unitary transformation on their particles to swap their quantum states. We give measurement results and the corresponding unitary transformation of Alice and Bob in Table 1.

Table 1 Alice, Bob, Charlie’s measurement results and appropriate unitary transformation of Alice and Bob after H transformation, where σ x , σ y , σ z are Pauli matrices
Full size table

3.2 A Simple Quantum Channel Consisting of the Four-Qubit Entangled State

Before Alice and Bob performing standard Bell basis measurement, the whole system state |Ψ〉 T can be rewrite in the following form:

$$\begin{aligned} |\varPsi\rangle_{T} =&x^{i}y^{j}R \bigl(T^\alpha\otimes T^\beta\bigr)|\alpha\rangle|\beta\rangle |st\rangle_{{B_2}{A_2}} \\ =&\frac{1}{2}x^{i}y^{j}({U_1} \otimes{U_2}) \bigl(T^\alpha\otimes T^\beta \bigr)| \alpha\rangle|\beta\rangle|st\rangle_{{B_2}{A_2}}. \end{aligned}$$
(21)

If Alice, Bob operate a unitary transformation \((U_{2})^{-1}_{A_{2}}\), \((U_{1})^{-1}_{B_{2}}\) on the whole system state |Ψ〉 T , respectively, the system state |Ψ〉 T is converted into the following form

$$\begin{aligned} |\varPsi\rangle_{T}^{U} =& (U_2)^{-1}_{A_2}(U_1)^{-1}_{B_2}|\varPsi\rangle_{T} \\ =&\frac{1}{2}x^{i}y^{j}\bigl((U_1)^{-1}(U_1) \otimes(U_2)^{-1}(U_2)\bigr)\bigl(T^\alpha \otimes T^\beta\bigr)|\alpha\rangle|\beta \rangle|st\rangle_{{B_2}{A_2}} \\ =&\frac{1}{2}x^{i}y^{j}(I) \bigl(T^\alpha\otimes T^\beta\bigr)|\alpha\rangle|\beta \rangle|st\rangle_{{B_2}{A_2}}, \end{aligned}$$
(22)

where the matrix I is a 4×4 identity matrix. Form Eqs. (16) and (17), we can select a simple quantum channel consisting of the four-qubit entangled state, which CPM is

$$\begin{aligned} R'=\frac{1}{2}\left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 &0 &0 &0\\ 0 &1 &0 &0\\ 0 &0 &1 &0\\ 0 &0 &0 &1\\ \end{array} \right ), \end{aligned}$$
(23)

and the quantum channel can be expressed as

$$\begin{aligned} |\varphi\rangle_{A_{1},B_{1},B_{2},A_{2}}=\frac{1}{2}\bigl(|0000\rangle +|0101\rangle+|1010\rangle+|1111\rangle\bigr) \end{aligned}$$
(24)

Evidently, this is a simple genuine four-qubit entangled state, which is just composed of state of diagonal element the channel parameter matrix R.

After Alice and Bob performing Bell basis measurement, if Alice’s and Bob’s measurement result are ϕ 2 and ϕ 3, the final state |Ψ αβ〉 T has the form:

$$\begin{aligned} |\varPsi^{23}\rangle_{T} =&\frac{1}{2}x^{i}y^{j}\bigl(T^{2}\otimes T^{3}\bigr) |s\rangle_{B_{2}}|t\rangle_{A_{2}} \\ =&\frac{1}{4}x^{i}y^{j}(\sigma_z\otimes\sigma_x) |s\rangle_{B_{2}}|t\rangle_{A_{2}}, \end{aligned}$$
(25)

the bidirectional quantum teleportation have realized when Alice (Bob) operate \((\sigma_{x}^{A})^{-1}\) (\((\sigma_{z}^{B})^{-1}\)) on his particle A 2 (B 2). For the other 15 kinds of Bell basis measurement results, Alice and Bob operate an appropriate unitary transformation to exchange their quantum states.

For the above-mentioned quantum channel expressed Eqs. (17) and (24), one can operate a unitary transformation on any a particle to obtain many kinds of available simple quantum channels.

4 Conclusion

How to choose the quantum channel is very important in teleportation. In this paper, we suggest a necessary condition of quantum channels to achieve bidirectional quantum teleportation via four-particle entangled state as the quantum channel. If the channel parameter matrix R consisting of a genuine quantum entangled state can be decomposed into the direct product forms of two unitary matrices U 1 and U 2, the bidirectional teleportation can be perfectly realized, we obtain a criterion which can be used to judge whether quantum state can be regarded as quantum channel or not for bidirectional teleportation. More than that, we provide a general method of selecting quantum channel for bidirectional quantum teleportation according to this criterion, and give a general quantum channel and a simple quantum channel consisting of a genuine four-qubit entangled state, this simple quantum channel is just composed of diagonal element the CPM R, i.e. the \(\operatorname{diag}[0000,0101,1010,1111]\). the method tells us how to choose proper and simple quantum channel to realize bidirectional teleportation and provide flexible choices for the bidirectional quantum experiments. By the way, the criterion of selecting a available quantum channel to realize bidirectional teleportation is a necessary condition. we find that realizing bidirectional teleportation is decided by not only available quantum channel but also selection of Alice’s and Bob’s Bell basis measurement on their particles, we will take about it in the future.