1 Introduction

Entanglement plays an important role in quantum information processing tasks. Quantum state teleportation is a significant application of quantum entanglement. In 1993, Bennettet al.[1] proposed the first quantum teleporatation protocol, after that, quantum teleportation of single and multiqubit state in theory is a hot topic [2–23], experimental research of teleportation has been reported [24, 25]. Recently, attention has been turned towards bidirectional quantum controlled teleportation (BQCT). In 2013, Zha et al. [26] firstly presented a BQCT protocol with five-qubit cluster state, up to now, some BQCT protocols have been investigated by multi-partie state as quantum channel, such as five-qubit entangled state[27–30], six-qubit maximally entangled state[31], six-qubit cluster state [32].

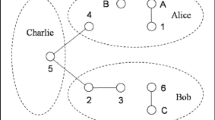
In 2006, Chen et al. [33] introduced a genuinely six-qubit entangled state, this entangled state is not decomposable into pairs of Bell states, it is can be utilized as quantum channel for perfectly teleporting an arbitrary three-qubit state. In this paper, we employ this six-qubit entangled state to investigate a BQCT scheme, at the beginning, the six-qubit entangled state as quantum channel is shared by the agents Alice, Bob and supervisor Charlie. Consider that agent Alice owns particle a in an unknown state, she wants to transmit this unknown state to Bob; at the same time, Bob has particle b in an unknown state, he wants to transmit this state to Alice. We prove that Alice and Bob can transmit the arbitrary single-qubit quantum state to each other simultaneously via Charlie’s control with shared entanglement and local operations and classical communications (LOCC).

2 Bidirectional Quantum Controlled Teleportation

Let us describe our scheme in detail. Assume that Alice holds an arbitrary single-qubit state, which is given by

$$ |\varphi\rangle_{a}=a_{0}|0\rangle+a_{1}|1\rangle $$
(1)

and that Bob owns an arbitrary single-qubit state

$$ |\varphi\rangle_{b}=b_{0}|0\rangle+b_{1}|1\rangle $$
(2)

Now Alice wants to transmit the state of qubit a to Bob and Bob wants to transmit the state of qubit b to Alice. The quantum channel shared among Alice, Bob and Charlie is

$$\begin{array}{@{}rcl@{}} |\psi_{s}\rangle_{123456}&=&\frac{1}{2\sqrt{2}}(|000000\rangle+|001101\rangle+|010110\rangle+|011011\rangle \\ &&+|100010\rangle+|101111\rangle+|110100\rangle+|111001\rangle)\\ \end{array} $$
(3)

Alice owns qubit pair 1 and 2, Bob possesses qubits 4 and 5, Charlie holds qubits 3 and 6. So the entangled state can also be represented as

$$\begin{array}{@{}rcl@{}} |\psi_{s}\rangle_{A_{1}A_{2}B_{1}B_{2}C_{1}C_{2}} &=&\frac{1}{2\sqrt{2}}[(|0000\rangle+|0111\rangle+|1001\rangle+|1110\rangle)_{A_{1}A_{2}B_{1}B_{2}}|00\rangle_{C_{1}C_{2}} \\ &&+(|0010\rangle+|0101\rangle+|1011\rangle+|1100\rangle)_{A_{1}A_{2}B_{1}B_{2}}|11\rangle_{C_{1}C_{2}}] \\ \end{array} $$
(4)

So the state of the composite system can be written in the following form of direct product

$$\begin{array}{@{}rcl@{}} |\psi\rangle_{t}=|\psi\rangle_{A_{1}A_{2}B_{1}B_{2}C_{1}C_{2}ab}=|\psi_{s}\rangle_{A_{1}A_{2}B_{1}B_{2}C_{1}C_{2}}\otimes|\psi\rangle_{a}\otimes |\psi\rangle_{b} \end{array} $$
(5)

Firstly, Bob executes an unitary operation \(U_{B_{1}B_{2}}\) on qubits B 1 and B 2. \(U_{B_{1}B_{2}}\) takes the following form

$$ U_{B_{1}B_{2}}= \left(\begin{array} {cccc} 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} \right) $$
(6)

As a consequence, the quantum state of the total system turns into

$$\begin{array}{@{}rcl@{}} |\psi^{\prime}\rangle_{t}=U_{B_{1}B_{2}}|\psi\rangle_{t} &=&\frac{1}{2\sqrt{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{a}(b_{0}|0\rangle+b_{1}|1\rangle)_{b}[(|0001\rangle+|0100\rangle \\ &&+|1011\rangle+|1110\rangle)_{A_{1}A_{2}B_{1}B_{2}}|00\rangle_{C_{1}C_{2}}+(|0010\rangle+|0111\rangle \\ &&+|1000\rangle+|1101\rangle)_{A_{1}A_{2}B_{1}B_{2}}|11\rangle_{C_{1}C_{2}}] \\ \end{array} $$
(7)

Subsequently, Alice takes a Bell-state measurement on particles (a, A 1) and Bob makes the same operation on (b, B 2) as Alice, the four Bell states are

$$ |\phi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle),|\varphi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|01\rangle+|10\rangle) $$
(8)

after the measurement, they announce the measurement results to each other via classical communication. According to Alice and Bob’s measurement outcomes, the corresponding collapses states of qubits A 2, B 1, C 1 and C 2 are listed in Table 1.

Table 1 Alice and Bob’s measurement outcomes, the corresponding collapses state of qubits (A 2, B 1, C 1, C 2)
Full size table

In Table 1, the states |η i〉(i = 0, ... 15) are given by

$$\begin{array}{@{}rcl@{}} |\eta^{0}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{1}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{2}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{3}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{4}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{5}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{6}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{7}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{8}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{9}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{10}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{11}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle+a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{12}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{13}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{14}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle+b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle+b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$
$$\begin{array}{@{}rcl@{}} |\eta^{15}\rangle_{A_{2}B_{1}C_{1}C_{2}}&=&(b_{0}|0\rangle-b_{1}|1\rangle)_{A_{2}}(a_{0}|1\rangle-a_{1}|0\rangle)_{B_{1}}|00\rangle _{C_{1}C_{2}} \\ &&+(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}}(a_{0}|0\rangle-a_{1}|1\rangle)_{B_{1}}|11\rangle_{C_{1}C_{2}} \end{array} $$

Without loss of generality, assume that Alice’s measurement outcome is \(|\phi ^{-}\rangle _{aA_{1}}\), Bob’s measurement outcome is \(|\varphi ^{-}\rangle _{bB_{2}}\), the collapsed state of qubits A 2, B 1, C 1 and C 2 will be \(|\eta ^{7}\rangle _{A_{2}B_{1}C_{1}C_{2}}\).

Afterwards, Charlie carries out a two-qubit von Neumann measurement on qubits (C 1, C 2) with the bases {|00〉, |11〉} and then publishes her measurement results. Having obtained the outcomes of Charlie, Alice and Bob can reconstruct the the original unknown single qubit state by applying appropriate unitary transformation on particles A 2 and B 1 respectively. Alice and Bob’s corresponding operations according to the Alice, Bob and Charlie’s measurement results are shown in Table 2.

Table 2 Alice, Bob and Charlie’s measurement outcomes and Alice and Bob’s corresponding operations
Full size table

Suppose Alice’s measurement outcome is \(|\phi ^{+}\rangle _{aA_{1}}\), Bob’s measurement outcome is \(|\varphi ^{-}\rangle _{bB_{2}}\), Charlie’s result is \(|11\rangle _{C_{1},C_{2}}\), then the state of qubits A 2 and B 1 will collapse into the state

$$\begin{array}{@{}rcl@{}} |\varsigma\rangle_{A_{2}}&=&(b_{0}|1\rangle-b_{1}|0\rangle)_{A_{2}} \\ |\varsigma\rangle_{B_{1}}&=&(a_{0}|1\rangle+a_{1}|0\rangle)_{B_{1}} \\ \end{array} $$
(9)

Next Alice should implement the unitary operation \(i\sigma _{A_{2}y}\) on qubit A 2, similarly, Bob makes the Pauli operator \(\sigma _{B_{1}x}\) on qubit B 1, As a result, the state of qubit a has been reconstructed on qubit B 1, at the same time, the state of qubit b has also been regenerated on qubit A 2. Consequently, the bidirectional quantum controlled teleportation has been successfully achieved.

3 Discussion and Conclusion

Let’s describe briefly the present and previous work about bidirectional quantum controlled teleportation (BQCT). By far, BQCT protocols are investigated by multiqubit entangled states, such as five-qubit entangled state [27–30] and six-qubit entangled state [31, 32]. In reference [29], the authors give a generalized conclusion for BQCT protocol by using five-qubit state. That is, the five entangled states that are utilized for BQCT can be expressed by

$$ |\psi\rangle_{12345}=\frac{1}{\sqrt{2}}(|\psi_{1}\rangle_{A_{1}B_{1}}|\psi_{2}\rangle_{A_{2}B_{2}}|a\rangle_{C_{1}} \pm|\psi_{3}\rangle_{A_{1}B_{1}}|\psi_{4}\rangle_{A_{2}B_{2}}|b\rangle_{C_{1}}) $$
(10)

where single qubit states |a〉 and |b〉 satisfy 〈a|b〉 = δ a, b , |ψ i 〉 ∈ {|ϕ +〉, |ϕ −〉, |φ +〉, |φ −〉}; |ϕ +〉, |ϕ −〉, |φ +〉, |φ −〉 are Bell states and the subscripts A, B and C stand for the qubits of Alice, Bob and Charlie respectively. In a similar way, we can extend their idea to the situation in which the six-qubit states are utilized for BQCT. In fact, the modified six-qubit cluster state for BQCT by An [32] can be described by

$$\begin{array}{@{}rcl@{}} |\psi^{\prime}_{An}\rangle&=&\frac{1}{\sqrt{2}}(|\phi^{+}\rangle_{A_{1}B_{1}}|\phi^{+}\rangle_{A_{2}B_{2}}|++\rangle_{C_{1}C_{2}} +|\phi^{+}\rangle_{A_{1}B_{1}}|\varphi^{-}\rangle_{A_{2}B_{2}}|+-\rangle_{C_{1}C_{2}} \\ &&+|\varphi^{-}\rangle_{A_{1}B_{1}}|\phi^{+}\rangle_{A_{2}B_{2}}|-+\rangle_{C_{1}C_{2}} +|\varphi^{-}\rangle_{A_{1}B_{1}}|\varphi^{-}\rangle_{A_{2}B_{2}}|--\rangle_{C_{1}C_{2}}) \end{array} $$
(11)

Besides, it is found that the modified six-qubit entangled state in this paper can be rewritten as:

$$ |\psi^{\prime}_{s}\rangle=\frac{1}{\sqrt{2}}(|\phi^{+}\rangle_{A_{1}B_{1}}|\varphi^{+}\rangle_{A_{2}B_{2}})|00\rangle_{C_{1}C_{2}} +|\varphi^{+}\rangle_{A_{1}B_{1}}|\phi^{+}\rangle_{A_{2}B_{2}}|11\rangle_{C_{1}C_{2}} $$
(12)

this can be seen from (7). As a result, the supervisor Charlie in reference [32] makes a single qubit measurement on particles C 1 and C 2 with the bases {|+〉, |−〉} respectively. Analogously, the supervisor Charlie in our protocol performs a two-qubit Von Neumann measurement on his particles C 1 and C 2 with the bases {|00〉, |11〉}. Actually, The (11) can be expressed in the following form

$$\begin{array}{@{}rcl@{}} |\psi^{\prime}_{s}\rangle&=&\frac{1}{\sqrt{2}}\left(|\phi^{+}\rangle_{A_{1}B_{1}}|\varphi^{+}\rangle_{A_{2}B_{2}}|0\rangle_{C_{1}}|+\rangle_{C_{2}} +|\phi^{+}\rangle_{A_{1}B_{\text{}1}}|\varphi^{+}\rangle_{A_{2}B_{2}}\right)|0\rangle_{C_{1}}|-\rangle_{C_{2}} \\ &&+|\varphi^{+}\rangle_{A_{1}B_{1}}|\phi^{+}\rangle_{A_{2}B_{2}}|1\rangle_{C_{1}}|+\rangle_{C_{2}} -|\varphi^{+}\rangle_{A_{1}B_{1}}|\phi^{+}\rangle_{A_{2}B_{2}}|1\rangle_{C_{1}}|-\rangle_{C_{2}}) \end{array} $$
(13)

Hence, Charlie can also make a single qubit measurement on C 1 in the bases {|0〉, |1〉} and on C 2 in the bases {|+〉, |−〉} respectively. Moreover, the measurement of controller Charlie improves the security of schemes.

In conclusion, we have presented a protocol for bidirectional quantum controlled teleportation with a six-qubit entangled state as quantum channel. In our scheme, Alice and Bob are not only senders but also receivers, Charlie is the supervisor. Based on local operations and classical communications (LOCC), Alice and Bob can teleport simultaneously an arbitrary single-qubit quantum state to each other with three participants’ right measurement,Charlie’s measurement improves the security of this protocol. Furthermore, theoretical study for generation of this six-partite entangled state in trapped-ion system has been explored [34], when considering the advance of future quantum information technology, we hope our scheme can be realized experimentally.