Bidirectional quantum controlled teleportation of unique four-qubit states by newly entangled 15-qubit state

Abstract

Using fifteen qubits entangled state, we proposed a theoretically novel protocol for Bidirectional Quantum Controlled Teleportation for a unique four-qubit state. The specialty of the proposed protocol is that in order to minimize resource consumption, users can apply only a few GHZ-state measurements in the entire protocol. The entangled state of 15-qubit acts as the quantum channel in which two users simultaneously teleport a four-qubit state under the controller as a third party. Following that, the protocol efficiency and security are computed and evaluated, concluding that protocol security is ensured.

1 Introduction

Quantum entanglement is a key component of quantum information processing that has been used as a quantum resource to execute a variety of quantum communication tasks such as quantum teleportation (Bennett et al. 1993), quantum key distribution (Bennett et al. 1992; Ekert 1991; Kwek et al. 2021; Liu et al. 2022a; Li and Wei 2022), quantum secure direct communication (Long and Liu 2002; Deng et al. 2003; Liu et al. 2022b; Zhou and Sheng 2022), Quantum remote state preparation (Bennett et al. 2001; Zhou et al. 2021; Lu et al. 2022; Feng et al. 2022), Hierarchical controlled remote state preparation (Jin et al. 2023; Wang et al. 2010). An important aspect of quantum communication is quantum teleportation (QT), which enables two or more users to teleport unknown quantum states using classical communication and previously shared entanglement. The first QT protocol was proposed by Bennett et al. (1993) in 1993 utilizing Einstein–Podolsky–Rosen (EPR) pair as the quantum channel. Following that, several QT protocols (Zhang et al. 2016; Wang and Zha 2010; Yu and Zhu 2009; Tian et al. 2008; Nie et al. 2011; Tsai and Hwang 2010; Huelga et al. 2001) using EPR pairs, W-states, Greenberger–Horne–Zeilinger (GHZ) states, and other entangled states as a quantum channel were proposed. Later, Bidirectional Quantum Teleportation (BQT) (Hassanpour and Houshmand 2016; Kazemikhah and Aghababa 2021; Verma 2020; Sadeghi Zadeh et al. 2017; Mafi et al. 2022) was proposed in which two users exchange their quantum information simultaneously, achieving the great attention of many researchers.

Bidirectional Controlled Quantum Teleportation (BCQT) protocol was proposed in 2013, where two communicators exchanged quantum information, namely each communicator acts as sender and receiver at the same time under the controller. A five-qubit cluster state was used as the quantum channel in the first BCQT protocol proposed by Zha et al. (2013). After that, different BCQT protocols using the multi-qubit entangled state as a quantum channel were proposed (Yan 2013; Duan et al. 2014; Sarvaghad-Moghaddam et al. 2018; Zhou et al. 2020a; Jiang et al. 2020; Choudhury and Samanta 2021; Kazemikhah et al. 2022). The asymmetric BCQT (ABCQT) protocol was proposed by Wen-qin Hong in 2016 (Hong 2016) that allows more than single qubits to be transmitted. In the protocol, Alice sends Bob a single-qubit state, and Bob sends Alice a two-qubit state through the seven-qubit entangled state with Charlie acts as the controller. After that, various ABCQT protocol (Hong 2016; Zhang et al. 2015a, b; Zhou et al. 2019; Choudhury and Samanta 2017) was proposed using different types of entangled channel.

In 2019, Zhou et al. (2020b) proposed BQT of the two-qubit state based on GHZ-state measurement of three particles using entangled six-qubit states as a quantum channel. In 2021, Jiang et al. (2021) presented a BCQT protocol in which two users can exchange a special three-qubit state via an eleven-qubit entangled state as a quantum channel.

This paper proposes a BQCT protocol that employs an entangled fifteen-qubit state as the quantum channel in which two users, Alice and Bob, act simultaneously as sender and receiver and each user teleport a unique four-qubit state under the controller David. The quantum channel is constructed using two GHZ states, four Bell states and a single qubit state. The teleportation can be realized by using GHZ and Bell-state measurement (BSM) orderly followed by David’s single-qubit measurement (SQM). And by using classical communication, both users apply a specified unitary operation on their qubits to reconstruct their original state. Then, we calculate the protocol’s efficiency and evaluate its security.

The sections of this paper are as follows: In Sect. 2, we proposed the BQCT protocol of the four-qubit state in detail. In Sect. 3, we compute the protocol's efficiency. Section 4 examines the proposed quantum channel’s security by taking into account two eavesdropper attacks, namely the eavesdropping attack and the intercept-resend attack, and in Sect. 5, we conclude the paper.

2 Description of the proposed protocol

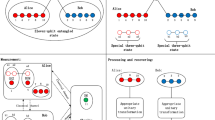
The proposed BQCT protocol is outlined as follows. There are three parties: two users Alice and Bob, and a controller David. Alice has a unique four-qubit entangled state $\left| \phi \right\rangle$ in her qubits $a_{1},\,\,a_{2},\,\,a_{3},\,a_{4}$, and Bob has another unique four-qubit entangled state $\left| \varphi \right\rangle$ in his qubits $b_{1},\,\,b_{2},\,\,b_{3},\,b_{4}$. Assuming the generalized forms of four-qubit states $\left| \phi \right\rangle_{{a_{1} a_{2} a_{3} a_{4} }} ,\left| \varphi \right\rangle_{{b_{1} b_{2} b_{3} b_{4} }}$ are expressed as follows:

$$\begin{aligned} \left| \phi \right\rangle_{{a_{1} a_{2} a_{3} a_{4} }} & = \alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle\\ &\quad + \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle \\ \left| \varphi \right\rangle_{{b_{1} b_{2} b_{3} b_{4} }} & = \beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle \\ &\quad+ \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle \end{aligned}$$

(1)

where it satisfies $\left| {\alpha_{0} } \right|^{2} + \left| {\alpha_{1} } \right|^{2} + \left| {\alpha_{2} } \right|^{2} + \left| {\alpha_{3} } \right|^{2} + \left| {\alpha_{4} } \right|^{2} + \left| {\alpha_{5} } \right|^{2} + \left| {\alpha_{6} } \right|^{2} + \left| {\alpha_{7} } \right|^{2} = 1$ and $\left| {\beta_{0} } \right|^{2} + \left| {\beta_{1} } \right|^{2} + \left| {\beta_{2} } \right|^{2} + \left| {\beta_{3} } \right|^{2} + \left| {\beta_{4} } \right|^{2} + \left| {\beta_{5} } \right|^{2} + \left| {\beta_{6} } \right|^{2} + \left| {\beta_{7} } \right|^{2} = 1$

Detailed steps of the protocol are followed as:

• Step 1 Under the controller, Alice intends to teleport her four-qubit state $\left| \phi \right\rangle_{{a_{1} a_{2} a_{3} a_{4} }}$ to Bob, and simultaneously, Bob intends to transmit his four-qubit state $\left| \varphi \right\rangle_{{b_{1} b_{2} b_{3} b_{4} }}$ to Alice. To accomplish this, Alice, Bob and David pre-share an entangled fifteen-qubit state $\left| \chi \right\rangle_{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}$, which is used as the quantum channel in the proposed protocol which is expressed as:

  $$\begin{aligned} \left| \chi \right\rangle_{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15} & = \left| {\eta^{1} } \right\rangle_{123} \left| {\phi^{ + } } \right\rangle_{45} \left| {\phi^{ + } } \right\rangle_{67} \left| {\eta^{3} } \right\rangle_{8910} \left| {\phi^{ + } } \right\rangle_{1112} \left| {\phi^{ + } } \right\rangle_{1314} \left| 0 \right\rangle_{15} \\ &\quad+ \left| {\eta^{5} } \right\rangle_{123} \left| {\psi^{ + } } \right\rangle_{45} \left| {\psi^{ + } } \right\rangle_{67} \left| {\eta^{7} } \right\rangle_{8910} \left| {\psi^{ + } } \right\rangle_{1112} \left| {\psi^{ + } } \right\rangle_{1314} \left| 1 \right\rangle_{15} \end{aligned}$$

  where Alice possesses qubits 1, 4, 6, 9, 10, 12, 14, Bob possesses qubits 2, 3, 5, 7, 8, 11, 13 and qubit 15 belongs to David. Then quantum channel can be rewritten as

  $$\begin{aligned} \left| \chi \right\rangle_{{X_{1} Y_{1} Y_{2} X_{2} Y_{3} X_{3} Y_{4} Y_{5} X_{4} X_{5} Y_{6} X_{6} Y_{7} X_{7} D}} & = \left| {\eta^{1} } \right\rangle_{{X_{1} Y_{1} Y_{2} }} \left| {\phi^{ + } } \right\rangle_{{X_{2} Y_{3} }} \left| {\phi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \left| {\eta^{3} } \right\rangle_{{Y_{5} X_{4} X_{5} }} \left| {\phi^{ + } } \right\rangle_{{Y_{6} X_{6} }} \left| {\phi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \left| 0 \right\rangle_{D} \\ &\quad+ \,\,\,\left| {\eta^{5} } \right\rangle_{{X_{1} Y_{1} Y_{2} }} \left| {\psi^{ + } } \right\rangle_{{X_{2} Y_{3} }} \left| {\psi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \left| {\eta^{7} } \right\rangle_{{Y_{5} X_{4} X_{5} }} \left| {\psi^{ + } } \right\rangle_{{Y_{6} X_{6} }} \left| {\psi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \left| 1 \right\rangle_{D} \end{aligned}$$

  (2)

  This quantum channel consists of two GHZ-states, four Bell-states, and one single qubit state (Fig. 1).

  Fig. 1

  

  Illustration of quantum circuit of the proposed fifteen-qubit entangled state

  The GHZ state can be given as

  $$\begin{gathered} \left| {\eta^{1} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\eta^{3} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {001} \right\rangle + \left| {110} \right\rangle } \right) \hfill \\ \left| {\eta^{5} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {010} \right\rangle + \left| {101} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\eta^{7} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {011} \right\rangle + \left| {100} \right\rangle } \right) \hfill \\ \end{gathered}$$

  (3)

  The Bell state can be given as

  $$\left| {\phi^{ + } } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\psi^{ + } } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {01} \right\rangle + \left| {10} \right\rangle } \right)$$

  (4)

  The entire quantum system may be expressed as a tensor product:

  $$\left| \tau \right\rangle_{{_{{a_{{_{1} }} a_{{_{2} }} a_{{_{3} }} a_{{_{4} }} b_{1} b_{2} b_{3} b_{4} X_{1} Y_{1} Y_{2} X_{2} Y_{3} X_{3} Y_{4} Y_{5} X_{4} X_{5} Y_{6} X_{6} Y_{7} X_{7} D}} }} = \left| \phi \right\rangle_{{a_{1} a_{2} a_{3} a_{4} }} \otimes \left| \varphi \right\rangle_{{b_{1} b_{2} b_{3} b_{4} }} \otimes \left| \chi \right\rangle_{{X_{1} Y_{1} Y_{2} X_{2} Y_{3} X_{3} Y_{4} Y_{5} X_{4} X_{5} Y_{6} X_{6} Y_{7} X_{7} D}}$$

  (5)

  To simplify the task, we put the position of the particle in measured form, which will not modify the system's information. As a result, we rewrite it as

  $$\begin{aligned} & \left| \tau \right\rangle_{{a_{1} a_{2} a_{3} a_{4} b_{1} b_{2} b_{3} b_{4} X_{1} Y_{1} Y_{2} X_{2} Y_{3} X_{3} Y_{4} Y_{5} X_{4} X_{5} Y_{6} X_{6} Y_{7} X_{7} D}} \\ & \quad = \frac{1}{2}\left[ \begin{gathered} \left( \begin{gathered} \left( {\left| {000} \right\rangle \left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle } \right) + \left| {111} \right\rangle \left( {\alpha_{4} \left| {1100} \right\rangle + \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)} \right) \hfill \\ \left( {\left| {001} \right\rangle \left( {\alpha_{0} \left| {1100} \right\rangle + \alpha_{1} \left| {1101} \right\rangle + \alpha_{2} \left| {1110} \right\rangle + \alpha_{3} \left| {1111} \right\rangle } \right) + \left| {110} \right\rangle \left( {\alpha_{4} \left| {0000} \right\rangle + \alpha_{5} \left| {0001} \right\rangle + \alpha_{6} \left| {0010} \right\rangle + \alpha_{7} \left| {0011} \right\rangle } \right)} \right) \hfill \\ \end{gathered} \right)_{{a_{1} a_{2} X_{1} Y_{1} Y_{2} a_{3} a_{4} }} \otimes \left| {\phi^{ + } } \right\rangle_{{X_{2} Y_{3} }} \otimes \left| {\phi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \hfill \\ \left( \begin{gathered} \left( {\left| {010} \right\rangle \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle } \right) + \left| {101} \right\rangle \left( {\beta_{4} \left| {1000} \right\rangle + \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)} \right) \hfill \\ \left( {\left| {011} \right\rangle \left( {\beta_{0} \left| {1000} \right\rangle + \beta_{1} \left| {1001} \right\rangle + \beta_{2} \left| {1010} \right\rangle + \beta_{3} \left| {1011} \right\rangle } \right) + \left| {100} \right\rangle \left( {\beta_{4} \left| {0100} \right\rangle + \beta_{5} \left| {0101} \right\rangle + \beta_{6} \left| {0110} \right\rangle + \beta_{7} \left| {0111} \right\rangle } \right)} \right) \hfill \\ \end{gathered} \right)_{{b_{1} b_{2} Y_{5} X_{4} X_{5} b_{3} b_{4} }} \otimes \left| {\phi^{ + } } \right\rangle_{{Y_{6} X_{6} }} \otimes \left| {\phi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \hfill \\ \end{gathered} \right] \otimes \left| 0 \right\rangle_{D} \\ & \quad \quad + \left[ \begin{gathered} \left( \begin{gathered} \left( {\left| {000} \right\rangle \left( {\alpha_{0} \left| {1000} \right\rangle + \alpha_{1} \left| {1001} \right\rangle + \alpha_{2} \left| {1010} \right\rangle + \alpha_{3} \left| {1011} \right\rangle } \right) + \left| {111} \right\rangle \left( {\alpha_{4} \left| {0100} \right\rangle + \alpha_{5} \left| {0101} \right\rangle + \alpha_{6} \left| {0110} \right\rangle + \alpha_{7} \left| {0111} \right\rangle } \right)} \right) \hfill \\ \left( {\left| {001} \right\rangle \left( {\alpha_{0} \left| {0100} \right\rangle + \alpha_{1} \left| {0101} \right\rangle + \alpha_{2} \left| {0110} \right\rangle + \alpha_{3} \left| {0111} \right\rangle } \right) + \left| {110} \right\rangle \left( {\alpha_{4} \left| {1000} \right\rangle + \alpha_{5} \left| {1001} \right\rangle + \alpha_{6} \left| {1010} \right\rangle + \alpha_{7} \left| {1011} \right\rangle } \right)} \right) \hfill \\ \end{gathered} \right)_{{a_{1} a_{2} X_{1} Y_{1} Y_{2} a_{3} a_{4} }} \otimes \left| {\psi^{ + } } \right\rangle_{{X_{2} Y_{3} }} \otimes \left| {\psi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \hfill \\ \left( \begin{gathered} \left( {\left| {010} \right\rangle \left( {\beta_{0} \left| {1100} \right\rangle + \beta_{1} \left| {1101} \right\rangle + \beta_{2} \left| {1110} \right\rangle + \beta_{3} \left| {1111} \right\rangle } \right) + \left| {101} \right\rangle \left( {\beta_{4} \left| {0000} \right\rangle + \beta_{5} \left| {0001} \right\rangle + \beta_{6} \left| {0010} \right\rangle + \beta_{7} \left| {0011} \right\rangle } \right)} \right) \hfill \\ \left( {\left| {011} \right\rangle \left( {\beta_{0} \left| {0000} \right\rangle + \beta_{1} \left| {0001} \right\rangle + \beta_{2} \left| {0010} \right\rangle + \beta_{3} \left| {0011} \right\rangle } \right)} + \left| {100} \right\rangle \left( \beta_{4} \left| {1100} \right\rangle + \beta_{5} \left| {1101} \right\rangle + \beta_{6} \left|1110\right\rangle + \beta_{7} \left|1111\right\rangle \right) \right) \hfill \\ \end{gathered} \right)_{{b_{1} b_{2} Y_{5} X_{4} X_{5} b_{3} b_{4} }} \otimes \left| {\psi^{ + } } \right\rangle_{{Y_{6} X_{6} }} \otimes \left| {\psi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \hfill \\ \end{gathered} \right] \otimes \left| 1 \right\rangle_{D} \\ \end{aligned}$$

  (6)

• Step 2 Alice and Bob performs GHZ-state measurement on their qubits $\left( {a_{1} ,a_{2} ,X_{1} } \right)$ and $\left( {b_{1} ,b_{2} ,Y_{5} } \right)$ and communicate their measurement result to each other. Alice selects one of the four GHZ states at random as their measuring result. Four different GHZ states are as follows:

  $$\begin{gathered} \left| {\eta^{1} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\eta^{2} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {000} \right\rangle - \left| {111} \right\rangle } \right)\, \hfill \\ \left| {\eta^{3} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {001} \right\rangle + \left| {110} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\eta^{4} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {001} \right\rangle - \left| {110} \right\rangle } \right) \hfill \\ \end{gathered}$$

  (7)

  whereas Bob chooses one of the four different GHZ states at random as their measurement result. Four different GHZ states are as follows:

  $$\begin{gathered} \left| {\eta^{5} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {010} \right\rangle + \left| {101} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\eta^{6} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {010} \right\rangle - \left| {101} \right\rangle } \right)\, \hfill \\ \,\left| {\eta^{7} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {011} \right\rangle + \left| {100} \right\rangle } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\eta^{8} } \right\rangle = \frac{1}{\sqrt 2 }\left( {\left| {011} \right\rangle - \left| {100} \right\rangle } \right) \hfill \\ \end{gathered}$$

  (8)

  Let Alice and Bob get $\left| {\eta^{1} } \right\rangle \,_{{a_{1} a_{2} X_{1} }}$ and $\,\left| {\eta^{5} } \right\rangle_{{b_{1} b_{2} Y_{5} }}$ as their measurement result, the remaining qubits $\left( {Y_{1} ,\,Y_{2} ,\,a_{3} ,\,a_{4} ,\,X_{2} ,\,Y_{3} ,\,X_{3} ,\,Y_{4} ,\,X_{4} ,\,X_{5} ,\,b_{3} ,\,b_{4} ,\,Y_{6} ,\,X_{6} ,\,Y_{7} ,\,X_{7} ,\,D} \right)$ are collapsed into Eq. (9)

  $$\begin{aligned} &_{{a_{1} a_{2} X_{1} }} \left\langle {\eta^{1} } \right|\,_{{b_{1} b_{2} Y_{1} }} \left\langle {{\eta^{5} }} \mathrel{\left | {\vphantom {{\eta^{5} } \tau }} \right. \kern-0pt} {\tau } \right\rangle_{{Y_{1} Y_{2} a_{3} a_{4} X_{2} Y_{3} X_{3} Y_{4} \,X_{4} X_{5} \,b_{3} b_{4} Y_{6} X_{6} Y_{7} X_{7} D}} \\ & \quad \left[ \begin{aligned} &\left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle }\right. \\ &\quad \left. {+ \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)_{{Y_{1} Y_{2} a_{3} a_{4} }} \otimes \left| {\phi^{ + } } \right\rangle_{{X_{2} Y_{3} }} \otimes \left| {\phi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \\ & \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle }\right. \\ & \quad\left.{+ \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)_{{X_{4} X_{5} \,b_{3} b_{4} }} \otimes \left| {\phi^{ + } } \right\rangle_{{Y_{6} X_{6} }} \otimes \left| {\phi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \end{aligned} \right]\left| 0 \right\rangle_{D} \\ & \quad \quad + \left[ \begin{aligned} &\left( \alpha_{0} \left| {1000} \right\rangle + \alpha_{1} \left| {1001} \right\rangle + \alpha_{2} \left| {1010} \right\rangle + \alpha_{3} \left| {1011} \right\rangle + \alpha_{4} \left| {0100} \right\rangle\right. \\ &\quad \left. + \alpha_{5} \left| {0101} \right\rangle + \alpha_{6} \left| {0110} \right\rangle + \alpha_{7} \left| {0111} \right\rangle \right)_{{Y_{1} Y_{2} a_{3} a_{4} }} \otimes \left| {\psi^{ + } } \right\rangle_{{X_{2} Y_{3} }} \otimes \left| {\psi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \\ & \left( \beta_{0} \left| {1100} \right\rangle + \beta_{1} \left| {1101} \right\rangle + \beta_{2} \left| {1110} \right\rangle + \beta_{3} \left| {1111} \right\rangle + \beta_{4} \left| {0000} \right\rangle\right. \\ &\quad \left. + \beta_{5} \left| {0001} \right\rangle + \beta_{6} \left| {0010} \right\rangle + \beta_{7} \left| {0011} \right\rangle \right)_{{X_{4} X_{5} \,b_{3} b_{4} }} \otimes \left| {\psi^{ + } } \right\rangle_{{Y_{6} X_{6} }} \otimes \left| {\psi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \end{aligned} \right]\left| 1 \right\rangle_{D} \\ \end{aligned}$$

  (9)

  Both Alice and Bob had four different measurement choices, the remaining qubits $\left( {Y_{1} ,\,Y_{2} ,\,a_{3} ,\,a_{4} ,\,X_{2} ,\,Y_{3} ,\,X_{3} ,\,Y_{4} ,\,X_{4} ,\,X_{5} ,\,b_{3} ,\,b_{4} ,\,Y_{6} ,\,X_{6} ,\,Y_{7} ,\,X_{7} ,\,D} \right)$ would be collapsed with equal probability into 16 distinct qubits states. In the appendix, Table 2 presents the measurement results for Alice and Bob and their corresponding collapsed states (Fig. 2).

  Fig. 2

  

  The systematic demonstration of fifteen-qubit entangled state as quantum channel for BQCT protocol. Here solid circle represents the qubits of the quantum channel and hollow circle represents the qubits to be transmitted

• Step 3 After the implementation of GHZ-states measurement, both users simultaneously implement BSM on qubits $\left( {a_{3} ,\,X_{2} } \right)$ and $\left( {b_{3} ,\,Y_{6} } \right)$. They choose one of four different BSM as their result. Four Bell-states are as follows:

  $$\begin{gathered} \left| \phi \right\rangle^{ + } = \frac{1}{\sqrt 2 }(\left| {00} \right\rangle + \left| {11} \right\rangle )\quad \left| \phi \right\rangle^{ - } = \frac{1}{\sqrt 2 }(\left| {00} \right\rangle - \left| {11} \right\rangle ) \hfill \\ \left| \psi \right\rangle^{ + } = \frac{1}{\sqrt 2 }(\left| {01} \right\rangle + \left| {10} \right\rangle )\quad \left| \psi \right\rangle^{ - } = \frac{1}{\sqrt 2 }(\left| {01} \right\rangle - \left| {10} \right\rangle ) \hfill \\ \end{gathered}$$

  (10)

  Let Alice and Bob get $\left| {\phi^{ + } } \right\rangle_{{a_{3} X_{2} }}$ and $\left| {\phi^{ + } } \right\rangle_{{b_{3} Y_{6} }}$ as their measurement result, then the remaining qubits $\left( {Y_{1} ,\,Y_{2} ,\,Y_{3} ,a_{4} ,\,X_{3} ,\,Y_{4} ,\,X_{4} ,\,X_{5} ,X_{6} ,b_{4} ,\,Y_{7} ,\,X_{7} ,\,D} \right)$ are collapsed into Eq. (11)

  $$\begin{gathered}_{{a_{1} a_{2} X_{1} }} \left\langle {\eta^{1} } \right|\,_{{b_{1} b_{2} Y_{1} }} \left\langle {\eta^{5} } \right|\,\,\,\,\,_{{a_{3} X_{2} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{3} Y_{6} }} \left\langle {{\phi^{ + } }} \mathrel{\left | {\vphantom {{\phi^{ + } } \tau }} \right. \kern-0pt} {\tau } \right\rangle_{{Y_{1} Y_{2} Y_{3} a_{4} X_{3} Y_{4} \,X_{4} X_{5} \,X_{6} b_{4} Y_{7} X_{7} D}} \hfill \\ \,\,\,\,\left[ \begin{gathered} \left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle + \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} a_{4} }} \otimes \left| {\phi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle + \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)_{{X_{4} X_{5} X_{6} a_{4} }} \otimes \left| {\phi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \hfill \\ \end{gathered} \right]\left| 0 \right\rangle_{D} \hfill \\ + \left[ \begin{gathered} \left( {\alpha_{0} \left| {1010} \right\rangle + \alpha_{1} \left| {1011} \right\rangle + \alpha_{2} \left| {1001} \right\rangle + \alpha_{3} \left| {1001} \right\rangle + \alpha_{4} \left| {0110} \right\rangle + \alpha_{5} \left| {0111} \right\rangle + \alpha_{6} \left| {0100} \right\rangle + \alpha_{7} \left| {0101} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} a_{4} }} \otimes \left| {\psi^{ + } } \right\rangle_{{X_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {1110} \right\rangle + \beta_{1} \left| {1111} \right\rangle + \beta_{2} \left| {1100} \right\rangle + \beta_{3} \left| {1101} \right\rangle + \beta_{4} \left| {0010} \right\rangle + \beta_{5} \left| {0011} \right\rangle + \beta_{6} \left| {0000} \right\rangle + \beta_{7} \left| {0001} \right\rangle } \right)_{{X_{4} X_{5} X_{6} a_{4} }} \otimes \left| {\psi^{ + } } \right\rangle_{{Y_{7} X_{7} }} \hfill \\ \end{gathered} \right]\left| 1 \right\rangle_{D} \hfill \\ \end{gathered}$$

  (11)

  Both Alice and Bob communicate their measurement results to each other and to the controller David via the classical channel. Based on the GHZ measurement results of Alice and Bob, i.e. $\left| {\eta^{1} } \right\rangle \,_{{a_{1} a_{2} X_{1} }}$ and $\,\left| {\eta^{5} } \right\rangle_{{b_{1} b_{2} Y_{5} }}$, all the BSM choices and their corresponding 16 different collapsed states of qubits $\left( {Y_{1} ,\,Y_{2} ,Y_{3} ,a_{4} ,\,X_{3} ,\,Y_{4} ,\,X_{4} ,\,X_{5} ,\,X_{6} ,b_{4} ,\,Y_{7} ,\,X_{7} ,\,D} \right)$ are given in the appendix of Table 3.

• Step 4 Both users again implement BSM on qubit pairs $\left( {a_{4},\,\,X_{3} } \right)\,$ and $\left( {b_{4},\,\,Y_{7} } \right)$. If the measurement result of Alice and Bob is $\left| {\phi^{ + } } \right\rangle_{{a_{4} X_{3} }}$ and $\left| {\phi^{ + } } \right\rangle_{{b_{4} Y_{7} }}$, then the remaining qubits $\left( {Y_{1} ,\,Y_{2} ,\,Y_{3} ,\,Y_{4} ,\,X_{4} ,\,X_{5} ,\,X_{6} ,\,\,X_{7} ,\,D} \right)$ are collapsed into Eq. (12)

  $$\begin{gathered}_{{a_{1} a_{2} X_{1} }} \left\langle {\eta^{1} } \right|\,_{{b_{1} b_{2} Y_{1} }} \left\langle {\eta^{5} } \right|\,\,\,\,\,_{{a_{3} X_{2} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{3} Y_{6} }} \left\langle {\phi^{ + } } \right|\,_{{a_{4} X_{3} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{4} Y_{7} }} \left\langle {{\phi^{ + } }} \mathrel{\left | {\vphantom {{\phi^{ + } } \tau }} \right. \kern-0pt} {\tau } \right\rangle_{{Y_{1} Y_{2} Y_{3} Y_{4} \,X_{4} X_{5} \,X_{6} X_{7} D}} \hfill \\ \,\,\,\,\left[ \begin{gathered} \left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle + \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle + \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered} \right]\left| 0 \right\rangle_{D} \hfill \\ + \left[ \begin{gathered} \left( {\alpha_{0} \left| {1011} \right\rangle + \alpha_{1} \left| {1010} \right\rangle + \alpha_{2} \left| {1001} \right\rangle + \alpha_{3} \left| {1000} \right\rangle + \alpha_{4} \left| {0111} \right\rangle + \alpha_{5} \left| {0110} \right\rangle + \alpha_{6} \left| {0101} \right\rangle + \alpha_{7} \left| {0100} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {1111} \right\rangle + \beta_{1} \left| {1110} \right\rangle + \beta_{2} \left| {1101} \right\rangle + \beta_{3} \left| {1100} \right\rangle + \beta_{4} \left| {0011} \right\rangle + \beta_{5} \left| {0010} \right\rangle + \beta_{6} \left| {0001} \right\rangle + \beta_{7} \left| {0000} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered} \right]\left| 1 \right\rangle_{D} \hfill \\ \end{gathered}$$

  (12)

  After applying BSM they communicate the measurement results to each other and to the supervisor David. Based on BSM results $\left| {\phi^{ + } } \right\rangle_{{a_{3} X_{2} }}$ and $\left| {\phi^{ + } } \right\rangle_{{b_{3} Y_{6} }}$, all the BSM choices and their corresponding 16 collapsed states of qubits $\left( {Y_{1} ,Y_{2} ,Y_{3} ,Y_{4},\,X_{4} ,X_{5},\,X_{6} ,X_{7} ,D} \right)$ are given in the appendix of Table 4.

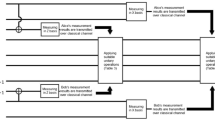
• Step 5 Now the system becomes a nine-qubit entangled state of qubits $\left( {Y_{1} ,Y_{2} ,Y_{3} ,Y_{4},\,X_{4} ,X_{5},\,X_{6} ,X_{7} ,D} \right)$. So, in this step David performs SQM operation on his qubit and measures his particle in the Z-basis $\left[ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right]$ and tells the measurement results to both communicators Alice and Bob. Based on David’s outcome, both users apply unitary operations on their qubits for reconstruct their original state.

  If the outcome of David is $\left| 0 \right\rangle_{D}$, then the remaining eight qubits $\left( {Y_{1} ,Y_{2} ,Y_{3} ,Y_{4},\,X_{4} ,X_{5},\,X_{6} ,X_{7} } \right)$ are collapsed into Eq. (13)

  $$\begin{gathered}_{{a_{1} a_{2} X_{1} }} \left\langle {\eta^{1} } \right|\,_{{b_{1} b_{2} Y_{1} }} \left\langle {\eta^{5} } \right|\,\,\,\,\,_{{a_{3} X_{2} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{3} Y_{6} }} \left\langle {\phi^{ + } } \right|\,_{{a_{4} X_{3} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{4} Y_{7} }} \left\langle {\phi^{ + } } \right|\,_{D} \left\langle {0} \mathrel{\left | {\vphantom {0 \tau }} \right. \kern-0pt} {\tau } \right\rangle_{{Y_{1} Y_{2} Y_{3} Y_{4} \,X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle + \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} \,}} \hfill \\ \otimes \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle + \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered}$$

  (13)

  And the unitary operation applied by Alice and Bob is

  $$\left( {I \otimes I \otimes I \otimes I \otimes I \otimes I \otimes I \otimes I} \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} \,X_{4} X_{5} \,X_{6} X_{7} }}$$

  Otherwise, the qubits are collapsed into $\left| 1 \right\rangle_{D}$,

  $$\begin{gathered}_{{a_{1} a_{2} X_{1} }} \left\langle {\eta^{1} } \right|\,_{{b_{1} b_{2} Y_{1} }} \left\langle {\eta^{5} } \right|\,\,\,\,\,_{{a_{3} X_{2} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{3} Y_{6} }} \left\langle {\phi^{ + } } \right|\,_{{a_{4} X_{3} }} \left\langle {\phi^{ + } } \right|\,\,_{{b_{4} Y_{7} }} \left\langle {\phi^{ + } } \right|\,_{D} \left\langle {1} \mathrel{\left | {\vphantom {1 \tau }} \right. \kern-0pt} {\tau } \right\rangle_{{Y_{1} Y_{2} Y_{3} Y_{4} \,X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \left( {\alpha_{0} \left| {1011} \right\rangle + \alpha_{1} \left| {1010} \right\rangle + \alpha_{2} \left| {1001} \right\rangle + \alpha_{3} \left| {1000} \right\rangle + \alpha_{4} \left| {0111} \right\rangle + \alpha_{5} \left| {0110} \right\rangle + \alpha_{6} \left| {0101} \right\rangle + \alpha_{7} \left| {0100} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \otimes \left( {\beta_{0} \left| {1111} \right\rangle + \beta_{1} \left| {1110} \right\rangle + \beta_{2} \left| {1101} \right\rangle + \beta_{3} \left| {1100} \right\rangle + \beta_{4} \left| {0011} \right\rangle + \beta_{5} \left| {0010} \right\rangle + \beta_{6} \left| {0001} \right\rangle + \beta_{7} \left| {0000} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered}$$

  (14)

  And the unitary operation applied by Alice and Bob is

  $$\left( {X \otimes I \otimes X \otimes X \otimes X \otimes I \otimes X \otimes X} \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} \,X_{4} X_{5} \,X_{6} X_{7} }}$$

Based on the Alice and Bob GHZ-state measurement results $\left| {\eta^{1} } \right\rangle \,_{{a_{1} a_{2} X_{1} }}$ and $\left| {\eta^{5} } \right\rangle_{{b_{1} b_{2} Y_{5} }}$, the specified BSM results, $\left| {\phi^{ + } } \right\rangle_{{a_{3} X_{2} }} ,\,\,\left| {\phi^{ + } } \right\rangle_{{b_{3} Y_{6} }} ,\left| {\phi^{ + } } \right\rangle_{{a_{4} X_{3} }} ,\,\left| {\phi^{ + } } \right\rangle_{{b_{4} Y_{7} }}$, and David’s SQM results, Table 5 lists the unitary operators implemented by Alice and Bob to transform the four qubit state into the desired state.

3 Efficiency of protocol

The protocol proposes a BCQT of transmitting two four-qubit states by employing two GHZ-state measurement, four BSM, and SQM utilizing a fifteen-qubit entangled state as the quantum channel. The efficiency of the protocol is defined as (Yuan et al. 2008)

$$\eta = \frac{{q_{t} }}{{q_{c} + b_{t} }}$$

(15)

where $q_{t}$ is the number of qubits being sent, $q_{c}$ denotes the number of qubits used as quantum channel, $b_{t}$ denotes the number of classical bits communicated. Hence, the efficiency of the proposed protocol is

$$\eta = \frac{8}{15 + 13} = 28.57\%$$

In Table 1, we have compared the performance of proposed BCQT protocol with the previous BCQT schemes in terms of five aspects, including the type of protocol, the quantum resource consumption (QRC), the classical resource consumption (CRC), number of qubits transmitted (QBIT), and intrinsic efficiency ($\eta$).

Table 1 Comparison of proposed protocol with various previous studies

4 Security analysis

In quantum teleportation, quantum information is not transmitted in a quantum channel, so it cannot be intercepted during the transmission process. Therefore, the quantum channels are attacked during distribution of qubits. The two of the most common quantum channel attacks are eavesdropping and intercept-resend attack.

4.1 Eavesdropping attack

Assume Charlie, the eavesdropper, performing eavesdropping attack. Charlie entangled their four auxiliary qubits $E_{1} ,\,E_{2} ,\,E_{3} \,and\,E_{4}$ with David’s qubit. Then Charlie applies measurements on their particle to steal the information. Let us suppose that the measurement result of Alice and Bob is $\left| {\eta^{1} } \right\rangle \,_{{a_{1} a_{2} X_{1} }}$,$\left| {\eta^{5} } \right\rangle_{{b_{1} b_{2} Y_{5} }}$, $\left| {\phi^{ + } } \right\rangle_{{a_{3} X_{2} }} ,\,\,\left| {\phi^{ + } } \right\rangle_{{b_{3} Y_{6} }} ,\left| {\phi^{ + } } \right\rangle_{{a_{4} X_{3} }} ,\,\left| {\phi^{ + } } \right\rangle_{{b_{4} Y_{7} }}$. Then the state will collapse into Eq. (16)

$$\begin{gathered} \,\,\,\,\left[ \begin{gathered} \left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle + \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle + \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered} \right]\left| {00000} \right\rangle_{{DE_{1} E_{2} E_{3} E_{4} }} \hfill \\ + \left[ \begin{gathered} \left( {\alpha_{0} \left| {1011} \right\rangle + \alpha_{1} \left| {1010} \right\rangle + \alpha_{2} \left| {1001} \right\rangle + \alpha_{3} \left| {1000} \right\rangle + \alpha_{4} \left| {0111} \right\rangle + \alpha_{5} \left| {0110} \right\rangle + \alpha_{6} \left| {0101} \right\rangle + \alpha_{7} \left| {0100} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {1111} \right\rangle + \beta_{1} \left| {1110} \right\rangle + \beta_{2} \left| {1101} \right\rangle + \beta_{3} \left| {1100} \right\rangle + \beta_{4} \left| {0011} \right\rangle + \beta_{5} \left| {0010} \right\rangle + \beta_{6} \left| {0001} \right\rangle + \beta_{7} \left| {0000} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered} \right]\left| {11111} \right\rangle_{{DE_{1} E_{2} E_{3} E_{4} }} \hfill \\ \end{gathered}$$

(16)

If the measurement outcome of David is $\left| 0 \right\rangle_{D}$, then the state collapsed into:

$$\left[ \begin{gathered} \left( {\alpha_{0} \left| {0000} \right\rangle + \alpha_{1} \left| {0001} \right\rangle + \alpha_{2} \left| {0010} \right\rangle + \alpha_{3} \left| {0011} \right\rangle + \alpha_{4} \left| {1100} \right\rangle}\right. \hfill \\ \left. {+ \alpha_{5} \left| {1101} \right\rangle + \alpha_{6} \left| {1110} \right\rangle + \alpha_{7} \left| {1111} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {0100} \right\rangle + \beta_{1} \left| {0101} \right\rangle + \beta_{2} \left| {0110} \right\rangle + \beta_{3} \left| {0111} \right\rangle + \beta_{4} \left| {1000} \right\rangle} \right. \hfill \\ \left.{+ \beta_{5} \left| {1001} \right\rangle + \beta_{6} \left| {1010} \right\rangle + \beta_{7} \left| {1011} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered} \right] \otimes \left| {0000} \right\rangle_{{E_{1} E_{2} E_{3} E_{4} }}$$

And if the measurement result of David is $\left| 1 \right\rangle_{D}$, then the state will collapse into:

$$\left[ \begin{gathered} \left( {\alpha_{0} \left| {1011} \right\rangle + \alpha_{1} \left| {1010} \right\rangle + \alpha_{2} \left| {1001} \right\rangle + \alpha_{3} \left| {1000} \right\rangle + \alpha_{4} \left| {0111} \right\rangle + \alpha_{5} \left| {0110} \right\rangle + \alpha_{6} \left| {0101} \right\rangle + \alpha_{7} \left| {0100} \right\rangle } \right)_{{Y_{1} Y_{2} Y_{3} Y_{4} }} \hfill \\ \left( {\beta_{0} \left| {1111} \right\rangle + \beta_{1} \left| {1110} \right\rangle + \beta_{2} \left| {1101} \right\rangle + \beta_{3} \left| {1100} \right\rangle + \beta_{4} \left| {0011} \right\rangle + \beta_{5} \left| {0010} \right\rangle + \beta_{6} \left| {0001} \right\rangle + \beta_{7} \left| {0000} \right\rangle } \right)_{{X_{4} X_{5} \,X_{6} X_{7} }} \hfill \\ \end{gathered} \right]\,\, \otimes \left| {1111} \right\rangle_{{DE_{1} E_{2} E_{3} E_{4} }}$$

Therefore, regardless of the results of David's measurement, Charlie's state cannot be entangled with the Alice’s and Bob’s combined state, implying that Charlie cannot steal information about the desired state from them.

4.2 Intercept-resend attack

Assume Charlie, an eavesdropper intercepts the qubit during entanglement distribution and preparing another set of entangled fifteen-qubit state to transmit to Alice. Before entanglement distribution, David generates some single-qubit decoy states in the basis $\left\{ {\left| + \right\rangle ,\,\left| - \right\rangle ,\,\left| 0 \right\rangle ,\,\left| 1 \right\rangle } \right\}$, where $\left| + \right\rangle$ and $\left| - \right\rangle$ are measured in the X-basis, and $\left| 0 \right\rangle$ and $\left| 1 \right\rangle$ are measured in the Z-basis. After that, David sequenced the single-qubit decoy states in the specific order $\left\{ {X_{1} ,\,X_{2} ,\,X_{3} ,\,X_{4} ,\,X_{5} ,\,X_{6} ,\,X_{7} } \right\}$ that Charlie doesn't know. Upon receiving Charlie's qubit sequence, Alice notifies David, who then announces the position of decoy state and measurement basis to Alice through classical channel. After measuring the decoy states correctly, Alice sends David the measurement results. Using the measurement results, David can determine whether an eavesdropper exist. After that, Charlie's fifteen-qubit entangled state will be destroyed when Alice measures the decoy states. Therefore, the intercept–resend attack can be detected and no quantum information can be intercepted by Charlie.

Briefly, the proposed protocol is secured.

5 Conclusion

In summary, we have proposed a novel BQCT protocol that utilizes entangled fifteen-qubit state as quantum channels for simultaneous teleportation of a unique four-qubit state between users under the controller. For fulfill the task, Alice and Bob first implement GHZ and BSM orderly, and David finally implements SQM. Using classical communication and unitary operations, both users can send and receive four-qubit state. Our proposed BCQT protocol is different in the sense that the two unique four-qubit states are teleported simultaneously with good efficiency and the quantum channel is constructed using GHZ state, Bell state and single qubit state.

And, the security of the proposed protocol is guaranteed.

Appendix

See Tables 2, 3, 4, 5.

Table 2 GHZ measurement result of Alice and Bob and associated collapsed state $\left( {Y_{1} ,\,Y_{2} ,\,a_{3} ,\,a_{4} ,\,X_{2} ,\,Y_{3} ,\,X_{3} ,\,Y_{4} ,\,X_{4} ,\,X_{5} ,\,b_{3} ,\,b_{4} ,\,Y_{6} ,\,X_{6} ,\,Y_{7} ,\,X_{7} ,\,D} \right)$

Table 3 Based on the GHZ measurement result $\left| {\eta^{1} } \right\rangle \,_{{a_{1} a_{2} X_{1} }}$ and $\,\,\left| {\eta^{5} } \right\rangle_{{b_{1} b_{2} Y_{5} }}$ of Step 2, the collapsed states of qubits correspond to Alice’s and Bob’s Bell-state measurement results of Step 3

Table 4 Based on the BSM result $\left| {\phi^{ + } } \right\rangle_{{a_{3} X_{2} }}$ and $\left| {\phi^{ + } } \right\rangle_{{b_{3} Y_{6} }}$ of Step 3, the collapsed states of qubits $\left( {Y_{1} ,Y_{2} ,Y_{3} ,Y_{4},\,X_{4} ,X_{5},\,X_{6} ,X_{7} ,D} \right)$ correspond to Alice’s and Bob’s Bell-state measurement results of Step 4

Table 5 Based on BSM result of Alice and Bob of step 4, the specific unitary operation required to transmit collapsed state of qubits $\left( {Y_{1} ,Y_{2} ,Y_{3} ,Y_{4},\,X_{4} ,X_{5},\,X_{6} ,X_{7} } \right)$ into the desired state corresponds to David’s single-qubit measurement results