1 Introduction

Quantum teleportation has been attracting great attention both in theoretical and experimental aspects in recent years, which is regarded as one of the most striking results of quantum information. Since the original protocol of quantum teleportation was proposed by using an entangled channel of Einstein-Podolsky-Rosen (EPR) pair [1]. Many theoretical and experimental protocols of quantum teleportation have been reported [2–9]. In 2013, since the first bidirectional quantum controlled teleportation (BQCT) protocol is presented [10], a number of BQCT protocols have been devised with the help of different kinds of entangled states including five-qubit entangled state [11–13], six-qubit entangled state [14], six-qubit cluster state [15], and seven-qubit entangled state [16].

In this work, we present an experimentally feasible scheme for implementing BQCT by using a seven-qubit entangled state as quantum channel. Suppose that Alice has qubit A in an unknown state, she wants to transmit an arbitrary single qubit state of qubit A to Bob; at the same time, Bob has two qubits B and C in an unknown state, he wants to transmit the state of qubits B and C to Alice. To achieve this BQCT task, besides appropriate unitary transformation and classical communications, it is necessary that three parties perform proper measurement, that is, Alice and Bob make the Bell-state measurement respectively, and Charlie must perform single-qubit measurement.

2 Bidirectional Quantum Controlled Teleportation

Our scheme can be described as follows. Suppose Alice has an arbitrary single-qubit state, which is described by

$$ \left|\psi\right\rangle_{A} =a_{0} \left|0\right\rangle +a_{1} \left|1\right\rangle, $$
(1)

and that Bob has qubits B and C in an unknown state,

$$ \left|\psi\right\rangle_{BC} =b_{00} \left|00\right\rangle +b_{01} \left|01 \right\rangle +b_{10} \left|10\right\rangle +b_{11} \left|11\right\rangle . $$
(2)

Now Alice wants to transmit the state of qubit A to Bob and Bob wants to transmit the state of qubits B and C to Alice. Assume that Alice, Bob and Charlie share a seven-qubit entangled state, which has the form

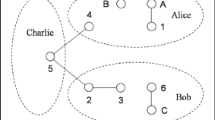
$$ \begin{array}{c} \left|\psi\right\rangle_{1234567} =\frac{\sqrt 2} {4}\left({\left|0000000\right\rangle +\left|0000011\right\rangle +\left|0001101 \right\rangle +\left|0001110 \right\rangle} \right. \\ \left. {+\left|1110001\right\rangle +\left|1110010\right\rangle +\left|1111100\right\rangle +\left|1111111\right\rangle} \right)_{1234567} , \end{array} $$
(3)

where the qubits A, 1, 5 and 7 belong to Alice, qubit 2 belongs to Charlie and qubits B, C, 3, 4 and 6 belong to Bob, respectively. The initial state of the total system can be expressed as

$$ \left|{\Psi}\right\rangle_{1234567\,ABC} =\left|\psi\right\rangle_{1234567} \otimes \left|\psi\right\rangle_{A} \otimes \left|\psi\right\rangle_{BC} . $$
(4)

To achieve the purpose of BQCT, then Alice and Bob perform a Bell-state measurement on own qubit pairs (A, 1), (B, 4) and (C, 6), respectively. It is known that one may obtain one of the 64 kinds of possible measured results with equal probability, and the residual qubits system may collapse into one of the following 64 states,

$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Phi}^{\pm} } \right|_{B4} \left\langle {{\Phi}^{\pm} } \right|_{A1} \left\langle {{\Phi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0}} \right.\left({b_{00} \left|0000\right\rangle \pm_{3} b_{01} \left|0001\right\rangle \pm_{2} b_{10} \left|0011\right\rangle \pm_{3} \pm_{2} b_{11} \left|0010\right\rangle} \right)\\ \left. {+a_{1} \left({\pm_{1} b_{00} \left|1101\right\rangle \pm_{3} \pm_{1} b_{01} \left|1100 \right\rangle \pm_{2} \pm_{1} b_{10} \left|1110\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|1111\right\rangle} \right)} \right]_{2357} , \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Psi}^{\pm} } \right|_{B4} \left\langle {{\Phi}^{\pm} } \right|_{A1}\left\langle {{\Phi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left| 0001\right\rangle \pm_{3} b_{01} \left|0000 \right\rangle \pm_{2} b_{10} \left|0010\right\rangle \pm_{3} \pm_{2} b_{11} \left|0011\right\rangle} \right)} \right.\\ +a_{1} \left. {\left({\pm_{1} b_{00} \left|1100\right\rangle \pm_{3} \pm_{1} b_{01} \left|1101\right\rangle \pm_{2} \pm_{1} b_{10} \left|1111\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|1110\right\rangle} \right)} \right]_{2357} , \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} {}~_{C6}\left\langle {{\Phi}^{\pm} } \right|_{B4} \left\langle {{\Psi}^{\pm} } \right|_{A1} \left\langle {{\Phi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left|0011 \right\rangle \pm_{3} b_{01} \left|0010 \right\rangle \pm_{2} b_{10} \left|0000\right\rangle \pm_{3} \pm_{2} b_{11} \left|0001\right\rangle} \right)} \right.\\ \left. {+a_{1} \left({\pm_{1} b_{00} \left|1110\right\rangle \pm_{3} \pm_{1} b_{01} \left|1111\right\rangle \pm_{2} \pm_{1} b_{10} \left|1101\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|1100\right\rangle} \right)} \right]_{2357}, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Psi}^{\pm}}\right|_{B4} \left\langle {{\Psi}^{\pm} } \right|_{A1} \left\langle {{\Phi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left|0010 \right\rangle \pm_{3} b_{01} \left|0011 \right\rangle \pm_{2} b_{10} \left|0001\right\rangle \pm_{3} \pm_{2} b_{11} \left|0000\right\rangle} \right)} \right. \\ +\left. {a_{1} \left({\pm_{1} b_{00} \left|1111\right\rangle \pm_{3} \pm_{1} b_{01} \left|1110\right\rangle \pm_{2} \pm_{1} b_{10} \left|1100\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|1101\right\rangle} \right)} \right]_{2357} , \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Phi}^{\pm} } \right|_{B4} \left\langle {{\Phi}^{\pm} } \right|_{A1} \left\langle {{\Psi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left|1101 \right\rangle \pm_{3} b_{01} \left|1100 \right\rangle \pm_{2} b_{10} \left|1110\right\rangle \pm_{3} \pm_{2} b_{11} \left|1111\right\rangle} \right)} \right. \\ +\left. {a_{1} \left({\pm_{1} b_{00} \left|0000\right\rangle \pm_{3} \pm_{1} b_{01} \left|0001\right\rangle \pm_{2} \pm_{1} b_{10} \left|0011\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|0010\right\rangle} \right)} \right]_{2357} , \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Psi}^{\pm} } \right|_{B4} \left\langle {{\Phi}^{\pm} } \right|_{A1} \left\langle {{\Psi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left|1100 \right\rangle \pm_{3} b_{01} \left|1101 \right\rangle \pm_{2} b_{10} \left|1111\right\rangle \pm_{3} \pm_{2} b_{11} \left|1110\right\rangle} \right)} \right. \\ +a_{1} \left. {\left({\pm_{1} b_{00} \left|0001\right\rangle \pm_{3} \pm_{1} b_{01} \left|0000\right\rangle \pm_{2} \pm_{1} b_{10} \left|0010\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|0011\right\rangle} \right)} \right]_{2357} , \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Phi}^{\pm} } \right|_{B4} \left\langle {{\Psi}^{\pm} } \right|_{A1} \left\langle {{\Psi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left|1110 \right\rangle \pm_{3} b_{01} \left|1111 \right\rangle \pm_{2} b_{10} \left|1101\right\rangle \pm_{3} \pm_{2} b_{11} \left|1100\right\rangle} \right)} \right. \\ +\left. {a_{1} \left({\pm_{1} b_{00} \left|0011\right\rangle \pm_{3} \pm_{1} b_{01} \left|0010\right\rangle \pm_{2} \pm_{1} b_{10} \left|0000\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|0001\right\rangle} \right)} \right]_{2357} , \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} {~}_{C6}\left\langle {{\Psi}^{\pm}}\right|_{B4} \left\langle {{\Psi}^{\pm} } \right|_{A1} \left\langle {{\Psi}^{\pm} } \right|\left|{\Psi}\right\rangle =\frac{1}{8}\left[ {a_{0} \left({b_{00} \left|1111 \right\rangle \pm_{3} b_{01} \left|1110 \right\rangle \pm_{2} b_{10} \left|1100\right\rangle \pm_{3} \pm_{2} b_{11} \left|1101\right\rangle} \right)} \right. \\ \left. {+a_{1} \left({\pm_{1} b_{00} \left|0010\right\rangle \pm_{3} \pm_{1} b_{01} \left|1101\right\rangle \pm_{2} \pm_{1} b_{10} \left|0001\right\rangle \pm_{3} \pm_{2} \pm_{1} b_{11} \left|0000\right\rangle} \right)} \right]_{2357}, \end{array} $$
(12)

where \(\left |{\Phi }^{\pm }\right \rangle =\frac {1}{\sqrt {2}}\left (\left |00\right \rangle \pm \left |11\right \rangle \right )\) and \(\left |{\Psi }^{\pm }\right \rangle =\frac {1}{\sqrt {2}}\left (\left |01\right \rangle \pm \left |10\right \rangle \right )\) are Bell states. In the above equations, the notes “ ±1”, “ ±2” and “ ±3” from right to left correspond to the Bell-state measurements of qubit pairs (A, 1), (B, 4) and (C, 6) in the basis of \(\left \{ {\left |{\Phi }^{\pm }\right \rangle }, \left |{\Psi }^{\pm }\right \rangle \right \}\), respectively, and they mean multiplication of ± signs.

Then Alice (Bob) tells the result to Bob (Alice) and Charlie. If Charlie allows Bob and Alice to reconstruct the initial unknown state, he needs to carry out a single-qubit measurement in the basis of \({\left |\pm \right \rangle =(\left |0 \right \rangle \pm \left |1\right \rangle )} / {\sqrt 2}\) on qubit 2, and then tells the receivers his result. By combining information from Alice, Bob and Charlie, Alice and Bob can co-operate and make two controlled-NOT gates on own qubits with the qubits 3, 5 as controlled qubits and the qubit 7 as target qubit, and then they can obtain the secret quantum information with an appropriate unitary transformation on the qubits at hand, the BQCT is easily realized.

In order to simplify our descriptions but without loss of generality, we take the outcome \(\left |{\Phi }^{\pm }\right \rangle _{A1}\left |{\Phi }^{\pm }\right \rangle _{A4}\left |{\Phi }^{\pm }\right \rangle _{A6}\) as an example to show the principle of this BQCT protocol, where the residual qubits system collapses into the state,

$$\begin{array}{@{}rcl@{}} \left|\phi\right\rangle_{2357} &=&\left[a_{0} \left(b_{00} \left|0000\right\rangle +b_{01} \left|0001\right\rangle +b_{10} \left|0011\right\rangle +b_{11} \left|0010\right\rangle\right)+a_{1} \left(b_{00} \left|1101\right\rangle +b_{01} \left|1100\right\rangle\right.\right.\\ &&\left.\left.+ b_{10} \left|1110\right\rangle+b_{11} \left|1111\right\rangle\right)\right]_{2357}\\ {\kern46pt}&=&\frac{\sqrt 2} {2}\left\{\left|+\right\rangle_{2} \left[a_{0} \left(b_{00} \left|000\right\rangle +b_{01} \left|001\right\rangle +b_{10} \left|011\right\rangle +b_{11} \left|010\right\rangle\right)_{357} + a_{1} \left(b_{00} \left|101\right\rangle +b_{01} \left|100\right\rangle \right.\right.\right.\\ &&\left.\left.\left.+ b_{10}\left|110\right\rangle +b_{11} \left|111\right\rangle\right)_{357}\right]\right.\\ &+&\left|-\right\rangle_{2} \left.\left[a_{0} \left(b_{00} \left|000\right\rangle +b_{01} \left|001\right\rangle +b_{10} \left|011\right\rangle +b_{11} \left|010\right\rangle \right)_{357} -a_{1} \left(b_{00} \left|101\right\rangle +b_{01} \left|100\right\rangle \right.\right.\right.\\ &&\left.\left.\left.+b_{10} \left|110\right\rangle +b_{11} \left|111\right\rangle\right)_{357}\right]\right\}, \end{array} $$

where \(\left \{ {\left |\pm \right \rangle _{2} =\frac {1}{\sqrt 2} \left ({\left |0 \right \rangle \pm \left |1\right \rangle } \right )_{2}} \right \}\). Charlie can make a single-qubit measurement on qubit 2 in the basis of \(\left \{ {\left |\pm \right \rangle _{2}} \right \}\), and then he sends the result of his measurement to Alice and Bob. If the result of the single qubit is \(\left |+\right \rangle _{2}\) or \(\left |-\right \rangle _{2} \), the qubits 3, 5 and 7 will collapse into one of the following state, respectively,

$$\begin{array}{@{}rcl@{}} \left|\phi_{1}\right\rangle_{357}&=&a_{0} \left(b_{00} \left|000\right\rangle +b_{01} \left|001\right\rangle +b_{10} \left|011\right\rangle +b_{11} \left|010\right\rangle \right)_{357}+a_{1} \left(b_{00} \left|101\right\rangle +b_{01} \left|100\right\rangle\right.\\ &&\left.+ b_{10} \left|110\right\rangle +b_{11} \left|111\right\rangle\right)_{357} \end{array} $$
(13)

or

$$\begin{array}{@{}rcl@{}} \left|\phi_{1}\right\rangle_{357}&=&a_{0} \left(b_{00} \left|000\right\rangle +b_{01} \left|001\right\rangle +b_{10} \left|011\right\rangle +b_{11} \left|010\right\rangle \right)_{357}-a_{1} \left(b_{00} \left|101\right\rangle +b_{01} \left|100\right\rangle\right.\\ &&\left.+ b_{10} \left|110\right\rangle +b_{11} \left|111\right\rangle\right)_{357} . \end{array} $$
(14)

In order to obtain the BQCT easily, firstly, Bob performs a corresponding single qubit unitary operation I 3 or \({\sigma _{3}^{z}} \) on the qubit 3 to transfer its state into

$$ a_{0} \left({b_{00} \left|000\right\rangle +b_{01} \left|001\right\rangle +b_{10} \left|011\right\rangle +b_{11} \left|010\right\rangle} \right)_{357} +a_{1} \left({b_{00} \left| 101\right\rangle +b_{01} \left|100\right\rangle +b_{10} \left|110\right\rangle +b_{11} \left|111\right\rangle} \right)_{357} . $$
(15)

Then Alice and Bob can co-operate and make two controlled-NOT gates on own qubits with the qubits 3, 5 as controlled qubits and the qubit 7 as target qubit, then the (15) becomes

$$ \left({a_{0} \left|0\right\rangle +a_{1} \left|1\right\rangle} \right)_{3} \otimes \left({b_{00} \left|00 \right\rangle +b_{01} \left|01\right\rangle +b_{10} \left|10\right\rangle +b_{11} \left|11\right\rangle} \right)_{57} . $$
(16)

After doing those operations, Alice and Bob may successfully reconstruct the original unknown state.

3 Conclusion

In summary, we have demonstrated that a seven-qubit entangled state can be used as the quantum channel to realize the deterministic BQCT. In our scheme, Alice may transmit an arbitrary single-qubit state of qubit A to Bob and at same time Bob may transmit an arbitrary two-qubit state of qubits B and C to Alice via the control of the supervisor Charlie. However, if one agent is dishonest, the receiver cannot acquire the valid information. We hope our scheme will be implemented experimentally in the future.