1 Introduction

Since a scheme was proposed for implementation of quantum secure direct communication (QSDC) [1], its importance and applications have been investigated extensively in quantum information theory [2–10]. The original quantum teleportation (QT) introducing by Bennett et al. [11], for example, was improved and modified as quantum information splitting [12], controlled teleportation [13, 14], quantum operation sharing [15–17] and quantum secret sharing [18, 19].

According to the QT, some new QSDC schemes have been devised with the help of multi-particle entangled states, such as EPR state [20], W state [21], GHZ state [22], cluster state [23], and six-qubit entangled state [24].

As discussed in ref. [25] for the bidirectional QT scheme, Alice and Bob can simultaneously send an unknown quantum state each other after performing an appropriate unitary operator. And the bidirectional QT can be used to implement a quantum remote control or a nonlocal quantum gate, where Alice can transmit an arbitrary single qubit state of qubit A to Bob and Bob can also transmit an arbitrary single qubit state of qubit B to Alice. Recently, Zha et al. [26] and Li et al. [27] reported tripartite schemes for bidirectional controlled QT by using different five-qubit states as the quantum channel. On the other hand, when Charlie is boss and Alice and Bob are his subordinates who are semihonest, Alice and Bob may require to implement the quantum remote control for a specific task. In this case, Alice and Bob are allowed to implement the quantum remote control only when Charlie permits them to do so. In such a scenario we need a scheme for the bidirectional controlled QT. Thus, a quantum cryptographic switch was introduced recently [28] by using the bidirectional controlled QT. These previous knowledge and experiences have motivated us to investigate that how to use bidirectional controlled QT to implement bidirectional controlled QSDC.

In this paper, we propose a five-qubit entangled quantum channel that can be used to implement a bidirectional controlled QT. It is interesting in noting that our five-qubit entangled resource can be prepared from a five-qubit Brown state [29–34] by using a quantum controlled phase gate (QCPG) operation and a controlled-NOT operation. In fact, we find that a five-qubit Brown state can be used to implement a bidirectional controlled QT. But the receivers (i.e., Alice and Bob) must co-operate and make a two-qubit unitary transformation to exchange their secret quantum information. Therefore, it is difficult to be operated to realize based on present technique. After measured a qubit by the controller, our five-qubit state becomes a direct couple of two Bell states. Thus, it is easy to implement the bidirectional QT tasks. In our scheme, Alice may transmit an arbitrary single qubit A to Bob and Bob may also transmit an arbitrary single qubit B to Alice via the control of the supervisor Charlie. For a bidirectional controlled QT protocol, thus, only two Bell-state and a single qubit are necessary to be measured. Furthermore, we propose a bidirectional controlled QSDC protocol. Under the case of insuring the security of the quantum channel, Alice (Bob) encodes the secret message directly on a sequence of qubit states and transmits them to Bob (Alice) supervised by Charlie. Bob (Alice) can read out the encoded message directly by the measurement on his (her) qubit. In our QSDC scheme, the qubits carrying the secret message do not need to be transmitted in quantum channel. At last, we show this bidirectional controlled QSDC scheme may be determinate and secure.

2 Five-qubit entangled quantum channel

In order to generate the five-qubit entangled state \(\left| \Xi \right\rangle _{12345} \) as a quantum channel, firstly, we prepare a five-qubit Brown state, i.e.,

$$\begin{aligned} \left| \psi \right\rangle _{12345}&= \frac{\sqrt{2}}{4}\left[ {\left| {001} \right\rangle _{123} \left( {\left| {01} \right\rangle -\left| {10}\right\rangle }\right) _{45}}\right. +\left| {010} \right\rangle _{123} \left( {\left| {00} \right\rangle -\left| {11} \right\rangle }\right) _{45}\nonumber \\&\quad \left. +\left| {100} \right\rangle _{123} \left( {\left| {01} \right\rangle +\left| {10} \right\rangle } \right) _{45} +\left| {111} \right\rangle _{123} \left( {\left| {00} \right\rangle +\left| {11} \right\rangle } \right) _{45} \right] . \end{aligned}$$
(1)

It is obvious that the five-qubit entangled channel \(\left| \Xi \right\rangle _{12345} \) can be obtained from the state \(\left| \psi \right\rangle _{12345} \) in Eq. (1) by performing a QCPG operation and a controlled-NOT operation. Under a QCPG operation on qubits 3 (set as a target qubit) and 4 (set as a control qubit), for example, the state \(\left| \psi \right\rangle _{12345} \) becomes

$$\begin{aligned} \left| {\psi ^{\prime }} \right\rangle _{12345}&= \frac{\sqrt{2}}{4}\left[ {\left| {001} \right\rangle _{123} \left( {\left| {01} \right\rangle +\left| {10} \right\rangle } \right) _{45} } \right. +\left| {010} \right\rangle _{123} \left( {\left| {00} \right\rangle -\left| {11} \right\rangle } \right) _{45}\nonumber \\&\quad \left. {+\left| {100} \right\rangle _{123} \left( {\left| {01} \right\rangle +\left| {10} \right\rangle } \right) _{45} +\left| {111} \right\rangle _{123} \left( {\left| {00} \right\rangle -\left| {11} \right\rangle } \right) _{45} } \right] , \end{aligned}$$
(2)

then we perform a controlled-NOT operation on qubits 3 (set as a target qubit) and 4 (set as a control qubit), the five-qubit quantum channel can be written as

$$\begin{aligned} | \Xi \rangle _{12345}&= \frac{\sqrt{2}}{4}( {| {00101} \rangle +| {00010} \rangle +| {01000} \rangle } -| {01111} \rangle +| {10001} \rangle +| {10110} \rangle \nonumber \\&+| {11100} \rangle -| {11011} \rangle )_{12345} \nonumber \\&= \frac{\sqrt{2}}{4}[ {( {| {01} \rangle \!+\!| {10} \rangle } )_{13} ( {| {00} \rangle \!-\!| {11} \rangle } )_{24} | 1 \rangle _5 \!+\!( {| {01} \rangle \!+\!| {10} \rangle } )_{13} ( {| {00} \rangle \!+\!| {11} \rangle } )_{24} | 0 \rangle _5 } ].\nonumber \\ \end{aligned}$$
(3)

Next, we implement bidirectional controlled QT by using the above five-qubit entangled state as the quantum channel.

3 Bidirectional controlled QT protocol

Our scheme can be described as follows. Suppose Alice has an arbitrary single qubit state \(\left| \psi \right\rangle _A =a_0 \left| 0 \right\rangle +a_1 \left| 1 \right\rangle \) and Bob has a qubit B in an unknown state \(\left| \psi \right\rangle _B =b_0 \left| 0 \right\rangle +b_1 \left| 1 \right\rangle .\) Sequently, Alice transmits the state \(\left| \psi \right\rangle _A \) of qubit A to Bob and Bob transmits the state \(\left| \psi \right\rangle _B \) of qubit B to Alice. Assume that Alice, Bob and Charlie share a genuine five-qubit entangled state \(\left| \Xi \right\rangle _{12345} \) in Eq. (3), where the qubits 1 and 4 belong to Alice, qubit 5 belongs to Charlie and qubits 2 and 3 belong to Bob, respectively. The initial state of the total system can be expressed as

$$\begin{aligned} \left| \Psi \right\rangle _{12345AB} =\left| \Xi \right\rangle _{12345} \otimes \left| \psi \right\rangle _A \otimes \left| \psi \right\rangle _B. \end{aligned}$$
(4)

To achieve a bidirectional controlled QT, Alice and Bob perform a Bell-state measurement (BSM) on own qubit pairs (A, 1) and (B, 2), respectively. Thus, one may obtain one of the 16 kinds of possible measured results with equal probability, and the remaining qubits may collapse into one of the 16 states after the measurement.

$$\begin{aligned} { }_{B2}\left\langle {\Phi ^{\pm }} \right| _{A1} \left\langle {\Phi ^{\pm }} \right| \left| {\Psi } \right\rangle _{12345AB}&= \frac{1}{4}\left[ {a_0 b_0 \left( {\left| {101} \right\rangle +\left| {010} \right\rangle } \right) \pm +a_1 b_0 \left( {\left| {001} \right\rangle +\left| {110} \right\rangle } \right) } \right. \nonumber \\&\quad \left. +\pm a_0 b_1 \left( {\left| {000} \right\rangle -\left| {111} \right\rangle } \right) \pm \pm a_1 b_1 \left( {\left| {100} \right\rangle -\left| {011} \right\rangle } \right) \right] _{345},\qquad \end{aligned}$$
(5)
$$\begin{aligned} { }_{B2}\left\langle {\Psi ^{\pm }} \right| _{A1} \left\langle {\Phi ^{\pm }} \right| \left| {\Psi } \right\rangle _{12345AB}&= \frac{1}{4}\left[ {a_0 b_0 \left( {\left| {000} \right\rangle -\left| {111} \right\rangle } \right) \pm +a_1 b_0 \left( {\left| {100} \right\rangle -\left| {011} \right\rangle } \right) } \right. \nonumber \\&\quad \left. +\pm a_0 b_1 \left( {\left| {101} \right\rangle +\left| {010} \right\rangle } \right) \pm \pm a_1 b_1 \left( {\left| {001} \right\rangle +\left| {110} \right\rangle } \right) \right] _{345},\end{aligned}$$
(6)
$$\begin{aligned} { }_{B2}\left\langle {\Phi ^{\pm }} \right| _{A1} \left\langle {\Psi ^{\pm }} \right| \left| {\Psi } \right\rangle _{12345AB}&= \frac{1}{4}\left[ {a_0 b_0 \left( {\left| {001} \right\rangle +\left| {110} \right\rangle } \right) \pm +a_1 b_0 \left( {\left| {101} \right\rangle +\left| {010} \right\rangle } \right) } \right. \nonumber \\&\quad \left. {+\pm a_0 b_1 \left( {\left| {100} \right\rangle -\left| {011} \right\rangle } \right) \pm \pm a_1 b_1 \left( {\left| {000} \right\rangle -\left| {111} \right\rangle } \right) } \right] _{345},\end{aligned}$$
(7)
$$\begin{aligned} { }_{B2}\left\langle {\Psi ^{\pm }} \right| _{A1} \left\langle {\Phi ^{\pm }} \right| \left| {\Psi } \right\rangle _{12345AB}&= \frac{1}{4}\left[ {a_0 b_0 \left( {\left| {100} \right\rangle -\left| {011} \right\rangle } \right) \pm +a_1 b_0 \left( {\left| {000} \right\rangle -\left| {111} \right\rangle } \right) } \right. \nonumber \\&\quad \left. +\pm a_0 b_1 \left( {\left| {001} \right\rangle +\left| {110} \right\rangle } \right) \pm \pm a_1 b_1 \left( {\left| {101} \right\rangle +\left| {010} \right\rangle } \right) \right] _{345},\qquad \quad \end{aligned}$$
(8)

where \(\left| {\Phi ^{\pm }} \right\rangle =\frac{1}{\sqrt{2}}\left( {\left| {00} \right\rangle \pm \left| {11} \right\rangle } \right) \) and \(\left| {\Psi ^{\pm }} \right\rangle =\frac{1}{\sqrt{2}}\left( {\left| {01} \right\rangle \pm \left| {10} \right\rangle } \right) \) are Bell states. In Eqs. (5)–(8), the notes “\(\pm \)” or “+” from right to left correspond to the Bell-state measurements (BSMs) of qubits ‘A1’ and ‘B2’, respectively, and they mean multiplication of \(\pm \) signs.

Then Alice (Bob) tells the result to Bob (Alice) and Charlie. It is dependent on the controller Charlie for the situation of that Bob and Alice exchange their secret quantum information. If Charlie allows for Bob and Alice to reconstruct the initial unknown state, he needs to carry out the single qubit measurement in the basis of \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \) on qubit 5 and tells the receivers. By combining information from Alice, Bob and Charlie, the two unknown single qubit states can be exchanged if Alice and Bob make an appropriate unitary transformation on the qubit at hand, the bidirectional controlled QT is easily realized. The appropriate unitary transformation for Bob and Alice for different scenarios are presented in the Appendix.

As an example, let us demonstrate the principle of this bidirectional controlled QT protocol. Suppose Alice’s measured outcome is \(\left| {\Phi ^{+}} \right\rangle _{A1} \)and Bob’s one is \(\left| {\Phi ^{+}} \right\rangle _{B2} \) at the same time, then the state of the remaining qubits collapse into the following state,

$$\begin{aligned} \left| \varphi \right\rangle _{345}&= \frac{1}{2}\left[ {\left| 0 \right\rangle _5 } \right. \left( {a_0 \left| 0 \right\rangle +a_1 \left| 1 \right\rangle } \right) _3 \left( {b_0 \left| 1 \right\rangle +b_1 \left| 0 \right\rangle } \right) _4\nonumber \\&\quad \left. +\left| 1 \right\rangle _5 \left( {a_0 \left| 1 \right\rangle +a_1 \left| 0 \right\rangle } \right) _3 \left( b_0 \left| 0 \right\rangle -b_1 \left| 1 \right\rangle \right) _4 \right] . \end{aligned}$$
(9)

Next, Charlie measures the single qubit 5 in the basis of \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \) and sends his result to both Bob and Alice with two possible results, i.e., \(\left| 0 \right\rangle _5 \) or \(\left| 1 \right\rangle _5 \). Then Alice and Bob need to apply a corresponding local unitary operation with the operators \(\sigma _4^x \otimes I_3\) or \(\sigma _4^z \otimes \sigma _3^x \), respectively. After their operations, Alice and Bob can successfully exchange their secret quantum information, i.e., the bidirectional controlled QT is successfully realized.

It is important to discuss the security problem against certain eavesdropping attacks. Assume that an eavesdropper (say Eve) has entangled an ancilla qubit with Charlie’s one, then she tries to measure the ancilla qubit to gain message about the unknown qubit state. Suppose that all the three participants are unaware of this attack of Eve, then after Alice and Bob perform the BSM on own qubit pairs, respectively, the compound state from Alice, Bob, Charlie and Eve collapses into a four-qubit entangled state. After Charlie measure his qubit 5 under the classical basis \(\left\{ {0,1} \right\} \), however, the Alice-Bob-Eve compound system collapses into a product state, leaving Eve without the message about the unknown qubit. To see this scenario more explicitly, assume the ancillia qubit entangles with the qubit 5 possessed by Charlie, i.e., \(\left| 0 \right\rangle _E \). If Alice’s measured outcome is \(\left| {\Phi ^{+}} \right\rangle _{A1} \)and Bob’s one is \(\left| {\Phi ^{+}} \right\rangle _{B2} \) at the same time, the compound state of Alice, Bob, Charlie and Eve’s qubits system would be

$$\begin{aligned} \left| \mathrm{Z} \right\rangle _{345E}&= \frac{1}{2}\left[ {\left| {00} \right\rangle _{5E} } \right. \left( {a_0 \left| 0 \right\rangle +a_1 \left| 1 \right\rangle } \right) _3 \left( {b_0 \left| 1 \right\rangle +b_1 \left| 0 \right\rangle } \right) _4\nonumber \\&\quad \left. {+\left| {11} \right\rangle _{5E} \left( {a_0 \left| 1 \right\rangle +a_1 \left| 0 \right\rangle } \right) _3 \left( {b_0 \left| 0 \right\rangle -b_1 \left| 1 \right\rangle } \right) _4 } \right] . \end{aligned}$$

Suppose that Charlie obtains the \(\left| 0 \right\rangle _5 \), then Alice–Bob–Eve system collapses into a product state,

$$\begin{aligned} \left| \Psi \right\rangle _{34E}&= \left( {a_0 \left| 0 \right\rangle +a_1 \left| 1 \right\rangle } \right) _3 \otimes \left( {b_0 \left| 1 \right\rangle +b_1 \left| 0 \right\rangle } \right) _4 \otimes \left| 0 \right\rangle _E. \end{aligned}$$

It is evident that Eve’s state is unaltered leaving no chance for her to gain any information about the unknown qubit state, so this bidirectional controlled QT scheme is secure.

4 Bidirectional controlled QSDC protocol

It is necessary to realize a bidirectional controlled QSDC scheme. Let us describe our bidirectional controlled QSDC protocol in detail as follows:

  1. (1)

    In order to implement a direct communication, Alice and Bob agree the coding method with single qubit state, i.e. \(\left| + \right\rangle =\frac{1}{\sqrt{2}}\left( {\left| 0 \right\rangle +\left| 1 \right\rangle } \right) \rightarrow 0, \left| - \right\rangle =\frac{1}{\sqrt{2}}\left( {\left| 0 \right\rangle -\left| 1 \right\rangle } \right) \rightarrow 1\).

  2. (2)

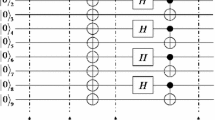
    Charlie prepares an ordered sequence of five-qubit entangled states \(\left| {\Xi ^{i}} \right\rangle _{12345} \) and enough one-qubit states, where the five-qubit entangled states are used as quantum channel, and the one-qubit states are used for generating disturbance. Then Alice should divide the ordered sequence of five-qubit entangling states into three ordered sequences. The first ordered sequence, called the sequence \(P_{14}^i \), is composed of qubits 1 and 4 from each five-qubit entangling state, the second ordered sequence \(P_{23}^i \) is composed of qubits 2 and 3, the remaining qubits compose the another ordered sequence \(P_5^i \). In our approach, Charlie reserves \(P_5^i \), and sends \(P_{14}^i \) and \(P_{23}^i \) to Alice and Bob, respectively. For sake of against eavesdropping, these qubits of one-qubit states are arbitrarily mixed in the sequence \(P_{14}^i \) and it’s position are known by Charlie before \(P_{14}^i \) is sent to Alice. One of modes for mixing one-qubit states in the sequence \(P_{14}^i \) is shown in Fig. 1. And then Charlie sends \(P_{23}^i \) to Bob by using the same method.

Fig. 1
figure 1

The sketch of mixing one-qubit

Full size image
  1. (3)

    After confirming that Alice and Bob have received the entire sequence, Charlie tells the positions of disturbing one-qubit states to Alice and Bob. Thus, Alice and Bob find out these disturbing one-qubit states and discard them.

  2. (4)

    Alice randomly chooses sufficient qubits 1 and 4 from \(P_{14}^i \) to apply the single qubit measurements in the basis of \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \). Then Alice tells the positions and measured results for each sampling qubits to Bob and Charlie. Corresponding to the positions in the sequence \(P_5^i \), Charlie make the single qubit measurements in the basis of \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \) on his qubits. With the information, Alice measures the corresponding qubits 2 and 3 in the sequence \(P_{23}^i \) under the basis of \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \) and compares the outcomes with Charlie’s and Bob’s. If their outcomes are completely correlated according to Eq. (3), Charlie can sure that the quantum channel is security and continue to the next step. Otherwise, they must abandon the communication and repeat the procedure from the beginning.

  3. (5)

    Alice and Bob prepare an ordered sequence of encoding state from \(\left| {\psi ^{i}} \right\rangle _A =a_0 \left| 0 \right\rangle +a_1 \left| 1 \right\rangle =\left| \pm \right\rangle _A^i \) or \(\left| {\psi ^{i}} \right\rangle _B =b_0 \left| 0 \right\rangle +b_1 \left| 1 \right\rangle =\left| \pm \right\rangle _B^i \) with \(a_0 =b_0 =\frac{\sqrt{2}}{2}\) and \(a_1 =b_1 =\pm \frac{\sqrt{2}}{2}\) according to the encoded rules and the secret message sequence. Then Alice and Bob make a BSM on the qubit pairs (A, 1) and (B, 2) according to the order of the secret message sequence. Next, Alice sends the measured results to Bob and Charlie by using a classical channel. At the same time, Bob sends the measured results to Alice and Charlie by the classical channel. Subsequently, Charlie applies the single qubit measurements on his qubit in the basis of \(\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \), and sends the measured results to Alice and Bob. By combining all messages from Alice, Bob and Charlie, the single qubit states \(\left| {\psi ^{i}} \right\rangle _B \) and \(\left| {\psi ^{i}} \right\rangle _A \) can be exchanged if Alice and Bob apply an appropriate unitary transformations on the qubits at hand. The corresponding appropriate unitary transformations for Bob and Alice for different scenarios are shown in the Appendix.

  4. (6)

    Finally, Alice performs a measurement on the basis of \(\left\{ {\left| + \right\rangle ,\left| - \right\rangle } \right\} \) on the qubits 4 to read out the messages that Bob wants to transmit to her. At the same time, Bob measures the basis \(\left\{ {\left| + \right\rangle ,\left| - \right\rangle } \right\} \) on his qubits 3 and extracts the secret information that Alice wants to transmit to him according to the encoded rules. And the process of that Alice (Bob) transmits the secret information to Bob (Alice) is completed.

Therefore, three spatially separated parties have realized a deterministic bidirectional controlled QSDC.

5 Security analysis of the bidirectional controlled QSDC protocol

Because the qubits carrying information are not transmitted in quantum channel, it is impossible for Eve to intercept the qubits during message transmission process, i.e., interruption of communication. A unique approach for Eve to attack the quantum channel between Alice and Bob is when Charlie sends \(P_{14}^i \) and \(P_{23}^i \) to Alice and Bob, respectively. Therefore, the safety requirement of this scheme is that the quantum channel is secure. If only quantum channel is secure, the secret message will not be leaked, and the communication is secure. Thus, we only analyze the security of quantum channel as following.

We first assume that Eve performs an intercept-resend attack. The process as follows: Eve intercepts the sequence \(P_{14}^i \) in which Charlie sends to Alice, and then Charlie prepares other ordered sequence of five-qubit entangled states and sends the sub-sequence of qubit pairs (1, 4) to Alice. Fortunately, this case can be found by checking of Charlie and Alice. Because Alice has mixed sufficient disturbing one-qubit states in the sequence \(P_{14}^i \) before he sends the sequence \(P_{14}^i \) to Alice. The positions of these disturbing one-qubit states are only known by Charlie, and Eve do not know. After receiving the sub-sequence of qubit pairs (1, 4) from Eve, Alice informs the result to Charlie by a classical channel. Then Charlie tells the positions of disturbing one-qubit states to Alice, and Alice finds out these disturbing one-qubit states and then discards them. In this case, the correlativity of five-qubit entangled states are destroyed and can be detected. Therefore, Eve’s intercept-resend attack is invalid.

Similarly, an entanglement attack is one possible attack strategy in quantum cryptography. We suppose that Eve introduces an auxiliary sequence \(P_{67}^i \), each particle of the auxiliary sequence is in the initial state \(\left| 0 \right\rangle \). And Eve has entangled his qubits 6, 7 with the qubits 2, 3 of quantum channel by performing C-NOT operation, respectively. In this case, Eve’s qubits 6, 7 with the state \(\left| 0 \right\rangle \) are target qubits and the qubits 2, 3 are controller qubit. Then the quantum channel becomes

$$\begin{aligned} \left| {\Omega ^{i}} \right\rangle _{1234567}&= \frac{\sqrt{2}}{4}\left( {\left| {0010101} \right\rangle +\left| {0001000} \right\rangle +\left| {0100010} \right\rangle } \right. -\left| {0111111} \right\rangle \nonumber \\&\quad \left. \!+\!\left| {1000100} \right\rangle +\left| {1011001} \right\rangle \!+\!\left| {1110011} \right\rangle \!-\!\left| {1101110} \right\rangle \right) _{1234567}.\qquad \end{aligned}$$
(10)

According to Eq. (10), it is evident that now Eve and Bob are in an equivalent position. But this case can be ruled out. Because Alice and Bob as well as Charlie may choose randomly some corresponding qubits to make the single qubit measurements and then compare their measured results, they will find that the probability of an uncorrelated result is 50 %. According to this result, one knows that our scheme is secure under a specific type of Eve’s attack.

Therefore, our QSDC scheme may be reliable, deterministic and secure.

6 Conclusions

In this paper, the construction of a five-qubit entangled state channel is discussed. We show that such a five-qubit entangled state can be used as the quantum channel to realize the deterministic bidirectional controlled QT. In our approach, Alice may transmit an arbitrary single qubit state of qubit A to Bob and at same time Bob may also transmit an arbitrary single qubit state of qubit B to Alice via the control of the supervisor Charlie, where only two BSMs and a single qubit measurement are needed so as to be more simple and feasible in experiment.

By using this bidirectional controlled QT, we propose a bidirectional controlled QSDC protocol. After insuring the security of the quantum channel, Alice (Bob) encodes the secret message directly on a sequence of qubit states and transmits them to Bob (Alice) supervised by Charlie. Bob (Alice) can read out the encoded message directly by the measurement on his qubit. In our scheme, all qubits carrying the secret message do not need to be transmitted in quantum channel. And we show this bidirectional controlled QSDC scheme may be determinate and secure.

It is well-known that the two Bell states can be utilized to implement the bidirectional QT tasks. From Eq. (3), it is evident that our five-qubit entangled state is concerted a couple of two Bell states if the controller measures the qubit in the hand. It is an essential reason why the five-qubit entangled states introduced in our scheme can be used as quantum channels to accomplish the bidirectional QT tasks. Especially, it may be to obtain such a state by using present technique. For example, Wang et al. presented a method to generate the five-qubit Brown state in cavity QED [35]. In addition the BSMs, two-qubit control gates and the single qubit unitary operations have already been realized in various quantum systems, such as the cavity QED system [36], ion-trap system [37], optical system [38], and so on. Thus, the proposed bidirectional controlled QSDC scheme may be implemented based on current technology. More importantly, our bidirectional controlled QSDC scheme is important for many applications including two-way quantum key distribution [39] and realizations of quantum interactive proof systems [40]. We hope that such a bidirectional controlled QSDC scheme can be realized experimentally with photons in the future.