1 Introduction

Quantum entanglement has been exploited as a quantum resource to carry out different types of quantum information processing including quantum teleportation [1], controlled teleportation [2], quantum state sharing [3], hierarchical quantum communication [4], remote state preparation [5–10], quantum operation sharing [11, 12], and quantum secure direct communication [13]. As pointed out by Zha et al. [14], especially, a five-qubit cluster state can be used for bidirectional quantum controlled teleportation (BQCT). Thus the BQCT protocols have been attracting an increasing attention [15–22] in the field of quantum information theory.

As we know, the BQCT can be used to implement a quantum remote control or a nonlocal quantum gate, where Alice can transmit an arbitrary single-qubit state of qubit A to Bob and Bob can also transmit an arbitrary single-qubit state of qubit B to Alice via the control of the supervisor Charlie [22]. And a quantum cryptographic switch was introduced recently [23] by using the BQCT.

In this paper, we propose a nine-qubit entangled quantum channel that can be used to implement a BQCT. It is interesting to note that our nine-qubit entangled resource can be prepared from nine single-qubit product states \(|{\psi _0}\rangle =|0 \rangle _1\otimes |0\rangle _2\otimes |0\rangle _3\otimes |0 \rangle _4 \otimes |0\rangle _5\otimes |0\rangle _6\otimes |0 \rangle _7 \otimes |0\rangle _8\otimes |0\rangle _9\) by using Hadamard gates and controlled-NOT operations [24]. In our scheme, Alice may transmit an arbitrary two-qubit state of qubits \(A_{1}\) and \(A_{2}\) to Bob; and at the same time, Bob may also transmit an arbitrary two-qubit state of qubits \(B_{1}\) and \(B_{2}\) to Alice via the control of the supervisor Charlie. For our BQCT protocol, only four Bell states and a single-qubit state are necessary to be measured. Moreover, we analytically derive the fidelities of the BQCT process under the amplitude-damping noise and the phase-damping noise. We consider that noise only affects the travel qubits of the quantum channel. Interestingly, it is found that the fidelities in these two cases only depend on the amplitude parameter of the initial state and the decoherence noisy rate.

2 Preparation of nine-qubit entangled state

The nine-qubit entangled state \(|\psi \rangle \) is not only theoretically existent but also practically feasible. As showed by a quantum circuit in Fig. 1, an input state is prepared by

$$\begin{aligned} |{\psi _0}\rangle =|0 \rangle _1\otimes |0\rangle _2\otimes |0 \rangle _3\otimes |0\rangle _4\otimes |0\rangle _5\otimes |0 \rangle _6\otimes |0\rangle _7\otimes |0\rangle _8\otimes |0 \rangle _9. \end{aligned}$$
(1)
Fig. 1
figure 1

A quantum circuit to generate the nine-qubit entangled state \(|\psi \rangle \)

Full size image

After sending the qubit 1 through the Hadamard gate, we have

$$\begin{aligned} |{\psi _1}\rangle =\frac{\left( {|0 \rangle +|1\rangle } \right) _1}{\sqrt{2}}\otimes |0\rangle _2\otimes |0\rangle _3 \otimes |0 \rangle _4\otimes |0\rangle _5\otimes |0\rangle _6 \otimes |0 \rangle _7\otimes |0\rangle _8\otimes |0\rangle _9 . \end{aligned}$$
(2)

Through the eight controlled-NOT operations with qubit 1 as controlled qubit and each of eight qubits 2, 3, 4, 5, 6, 7, 8, 9 as target qubit, the state of all the nine qubits becomes

$$\begin{aligned} |{\psi _2}\rangle =\frac{1}{\sqrt{2}}\left( {|{000000000} \rangle +|{111111111} \rangle }\right) _{123456789}, \end{aligned}$$
(3)

and one sends the qubit 2 through the Hadamard gate and then carries out a controlled-NOT operation with the qubit 2 as controlled qubit and the qubit 3 as target qubit. One does the same things on the qubits (4, 5), (6, 7), and (8, 9).

Finally, one can obtain the nine-qubit entangled state, which is given by

$$\begin{aligned} |\psi \rangle \!=\!\frac{1}{\sqrt{2}}\left[ {|{\Phi ^{+}} \rangle _{23}|{\Phi ^{+}} \rangle _{45}|{\Phi ^{+}} \rangle _{67}|{\Phi ^{+}} \rangle _{89}|0 \rangle _1 \!+\!|{\Psi ^{-}} \rangle _{23}|{\Psi ^{-}} \rangle _{45}|{\Psi ^{-}} \rangle _{67}|{\Psi ^{-}} \rangle _{89}|1 \rangle _1 } \right] ,\nonumber \\ \end{aligned}$$
(4)

where \(|{\Phi ^{+}} \rangle =\frac{1}{\sqrt{2}}\left( {|{00} \rangle +|{11} \rangle }\right) \) and \(|{\Psi ^{-}} \rangle =\frac{1}{\sqrt{2}}\left( {|{01} \rangle -|{10} \rangle }\right) .\)

Thus, we can prepare such a nine-qubit entangled state as a quantum communication channel in our BQCT protocol.

3 BQCT protocol

Our scheme can be described as follows. Suppose Alice has two qubits \(A_{1}\) and \(A_{2}\) in an arbitrary two-qubit state \(|\psi \rangle _{A_1 A_2}=\sum _{i_{A_1 }, i_{A_2} =0}^1 {a_{i_{A_1 } i_{A_2}}}|{i_{A_1}, i_{A_2}}\rangle _{A_1 A_2}\), where \(\sum _{i_{A_1},i_{A_2} =0}^1{|{a_{i_{A_1}i_{A_2}}}|}^{2}=1\), and Bob has two qubits \(B_{1}\) and \(B_{2}\) in an arbitrary two-qubit state \(|\psi \rangle _{B_1 B_2 } =\sum _{j_{B_1 }, j_{B_2 } =0}^1 {b_{j_{B_1 } j_{B_2 } } }|{j_{B_1 }, j_{B_2 } } \rangle _{B_1 B_2} \), where \(\sum _{j_{B_1 }, j_{B_2 } =0}^1 {|{b_{j_{B_1 } j_{B_2 }}}|} ^{2}=1\). Sequently, Alice transmits the state \(|\psi \rangle _{A_1 A_2}\) of qubits \(A_{1}\) and \(A_{2}\) to Bob and Bob transmits the state \(|\psi \rangle _{B_1 B_2}\) of qubits \(B_{1}\) and \(B_{2}\) to Alice. Assume that Alice, Bob, and Charlie share a nine-qubit entangled state \(|\psi \rangle \) in Eq. (4), where the qubits 2, 4, 7, and 9 belong to Alice, qubit 1 belongs to Charlie and qubits 3, 5, 6, and 8 belong to Bob, respectively. The initial state of the total system can be expressed as

$$\begin{aligned} |\Psi \rangle _{123456789A_1 A_2 B_1 B_2 } =|\psi \rangle _{123456789} \otimes |\psi \rangle _{A_1 A_2 } \otimes |\psi \rangle _{B_1 B_2 } . \end{aligned}$$
(5)

To achieve the BQCT, Alice and Bob perform Bell-state measurements (BSMs) on own qubit pairs (A1, 2), (A2, 4), (B1, 6), and (B2, 8), respectively. Alice’s and Bob’s BSMs outcomes may be \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\) or \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }} \rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }} \rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }} \rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }} \rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }} \rangle _{B_2 8} \) and \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }} \rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }} \rangle _{B_2 8}\), where \(|{\Phi ^{\pm }}\rangle =\frac{1}{\sqrt{2}}\left( {|{00}\rangle \pm |{11}\rangle }\right) \) and \(|{\Psi ^{\pm }}\rangle =\frac{1}{\sqrt{2}}\left( {|{01}\rangle \pm |{10} \rangle }\right) \) are Bell states.

Next Alice (Bob) tells her (his) BSMs results to Bob (Alice) and Charlie via a classical channel. It is dependent on the controller Charlie for the situation of that Bob and Alice exchange their secret quantum information. If Charlie allows for Bob and Alice to reconstruct the initial unknown state, he needs to carry out the single-qubit measurement in the basis of \(\left\{ {|0 \rangle ,|1 \rangle } \right\} \) on qubit 1 and tells his measured result to the receivers Alice and Bob. By combining information from Alice, Bob, and Charlie, the two arbitrary two-qubit states can be exchanged if Alice and Bob make the appropriate unitary transformations on the qubits at hand, the BQCT is easily realized. We have summarized the all possible Alice’s and Bob’s possible Bell-state measurement result, Charlie’s possible single-qubit measurement result, all the corresponding unitary operation for Alice and Bob in the “Appendix.”

As an example, let us demonstrate the principle of this BQCT protocol. Suppose Alice’s measured outcome is \(|{\Phi ^{+}} \rangle _{A_1 2}|{\Phi ^{+}} \rangle _{A_2 4}\) and Bob’s measured outcome is \(|{\Phi ^{+}} \rangle _{B_1 6}|{\Phi ^{+}} \rangle _{B_2 8}\) at the same time, then the state of the remaining qubits collapse into the following state,

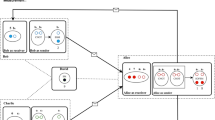
$$\begin{aligned} |\varphi \rangle _{13579}= & {} \frac{\sqrt{2}}{2}\sum _{l,i_3,i_5,j_7,j_9 =0}^1{\left( {-1}\right) ^{l{\bullet }\left( {i_3 \oplus i_5 } \right) }a_{i_3 i_5 } }|{i_3 \oplus l,i_5 \oplus l} \rangle _{35} \otimes \left( {-1}\right) ^{l{\bullet }\left( {j_7 \oplus j_9} \right) }\nonumber \\&\,\times b_{j_7 j_9 }|{j_7 \oplus l,j_9 \oplus l} \rangle _{79} \otimes |l \rangle _1, \end{aligned}$$
(6)

where \(\oplus \) is an addition mod 2. Equation (6) implies that for the outcomes of Charlie’s measurement under the basis \(|0\rangle _1\) and \(|1\rangle _1 \), Charlie sends his result to both Bob and Alice with two possible results, i.e., \(|0\rangle _1\) or \(|1\rangle _1\). Then Alice and Bob need to apply a corresponding local unitary operation with the operators \(I_{3}{\otimes } I_{5}{\otimes }I_{7}{\otimes }I_{9}\) or \(i\sigma _3^{y}{\otimes } i\sigma _{5}^{y}{\otimes } i\sigma _{7}^{y}\otimes i\sigma _{9}^{y}\), respectively. After their operations, Alice and Bob can successfully exchange their secret quantum information, i.e., the BQCT is successfully realized. The other situations may similarly obtain from \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8} \), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Phi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Phi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Phi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Phi ^{\pm }}\rangle _{B_2 8}\), \(|{\Psi ^{\pm }}\rangle _{A_1 2}|{\Psi ^{\pm }}\rangle _{A_2 4}|{\Psi ^{\pm }}\rangle _{B_1 6}|{\Psi ^{\pm }}\rangle _{B_2 8}\). And the processing of our BQCT protocol is shown in Fig. 2.

Fig. 2
figure 2

A BQCT protocol is shown for exchanging secret quantum information, where a solid circle represents a qubit and the solid line an entanglement between qubits, where a Alice holds a two-qubit state \(|\psi \rangle _{A_1 A_2}\), and Bob holds a two-qubit state \(|\psi \rangle _{B_1 B_2}\). In addition, she shares a nine-qubit entangled state \(|\psi \rangle \) with Bob and Charlie, b after Alice’s and Bob’s BSMs with outcomes (\(A_{1}\), 2), (\(A_{2}\), 4), (\(B_{1}\), 6) and (\(B_{2}\), 8), and the qubits 1, 3, 5, 7, and 9 compound system become entangling states and c after Charlie measures his qubit 1, Alice’s (Bob’s) two qubits may preserve all information of Bob’s (Alice’s) original secret two-qubit state

Full size image

It is important to discuss the security problem on our scheme. Because the qubits carrying information are not transmitted in quantum channel, it is impossible for Eve to intercept the qubits during message transmission process, i.e., interruption of communication. A unique approach for Eve to attack the quantum channel between Alice and Bob is when Charlie sends the qubits (2, 4, 7, 9) and the qubits (3, 5, 6, 8) to Alice and Bob, respectively. Therefore, the safety requirement of this scheme is that the quantum channel is secure. If only quantum channel is secure, the secret message will not be leaked, and the communication is secure. Thus we only analyze the security of quantum channel as following.

We first assume that Eve performs an intercept-resend attack. The process as follows: Eve intercepts the qubits (2, 4, 7, 9) in which Charlie sends to Alice, and then Charlie prepares other ordered sequence of nine-qubit entangled states and sends the subsequence of qubits (2, 4, 7, 9) to Alice. Fortunately, this case can be found by checking of Charlie and Alice. Because Alice has mixed sufficient disturbing one-qubit states in the sequence of qubits (2, 4, 7, 9) before he sends the sequence of qubits (2, 4, 7, 9) to Alice. The positions of these disturbing one-qubit states are only known by Charlie, and Eve do not know. After receiving the subsequence of qubits (2, 4, 7, 9) from Eve, Alice informs the result to Charlie by a classical channel. Then Charlie tells the positions of disturbing one-qubit states to Alice, and Alice finds out these disturbing one-qubit states and then discards them. In this case, the correlativity of nine-qubit entangled state is destroyed and can be detected. Therefore, Eve’s intercept–resend attack is invalid.

Similarly, an eavesdropping attack is one possible attack strategy. We assume that an eavesdropper (say Eve) has managed to entangle two ancilla qubits with Bob’s one, so that she can measure the ancilla qubits to gain information about the unknown qubit states. Under situation of that all the three participants are unaware of this attack, if Alice and Bob make the BSMs, the compound state possessed by Alice, Bob, Charlie, and Eve collapses into a seven-qubit entangled state. After Charlie measure his qubit 1 under the basis \(\left\{ {|0 \rangle ,|1 \rangle } \right\} \), however, the Alice–Bob–Eve compound system collapses into a product state, leaving Eve with no information about the unknown qubits. To see this scenario more explicitly, we let the ancilla qubits entangle with the qubit 1 under the entangled channel possessed by Charlie, i.e., \(|{00}\rangle _{E_1 E_2}\). If Alice and Bob get the result \(|{\Phi ^{+}}\rangle _{A_1 2}|{\Phi ^{+}} \rangle _{A_2 4}\) and \(|{\Phi ^{+}}\rangle _{B_1 6}|{\Phi ^{+}} \rangle _{B_2 8}\), the compound state of Alice, Bob, Charlie, and Eve’s qubits system would be

$$\begin{aligned} |E \rangle _{13579E_1 E_2}= & {} \frac{\sqrt{2}}{2}\left( {\sum _{l,i_3,i_5,j_7,j_9 =0}^1 {\left( {-1} \right) ^{l{\bullet }\left( {i_3 \oplus i_5 }\right) }a_{i_3 i_5 } }|{i_3 \oplus l,i_5 \oplus l} \rangle _{35} } \right. \nonumber \\&\left. {\otimes \left( {-1}\right) ^{l{\bullet }\left( {j_7 \oplus j_9 }\right) }b_{j_7 j_9 }|{j_7 \oplus l,j_9 \oplus l} \rangle _{79} \otimes |{lll} \rangle _{1E_1 E_2 } }\right) , \end{aligned}$$
(7)

From Eq. (7), we see that if Charlie obtains the qubits \(|0\rangle _1 \) or \(|1 \rangle _1 \), the Alice–Bob–Eve qubits compound system collapses correspondingly into the following product state according to Eq. (7), i.e., \(\sum _{i_3,i_5 =0}^1 {a_{i_3 i_5 }}|{i_3,i_5} \rangle _{35} \otimes \sum _{j_7,j_9 =0}^1 {b_{j_7 j_9}}|{j_7,j_9 } \rangle _{79} \otimes |{00} \rangle _{E_1 E_2 }\) or \(\sum _{i_3,i_5 =0}^1 {(-1)^{i_3 \oplus i_5 }a_{i_3 i_5 } }|{i_3 \oplus 1,i_5\oplus 1} \rangle _{35} \otimes \sum _{j_7,j_9 =0}^1 {(-1)^{j_7 \oplus j_9 }b_{j_7 j_9 } }|j_7 \oplus \) \( 1,j_9 \oplus 1 \rangle _{79} \otimes |{11} \rangle _{E_1 E_2}\), which imply that Eve’s state is unaltered leaving no chance for her to gain any information from the Bob’s and Alice’s initial states. Therefore, our BQCT protocol is secure.

Then, we will generalize the above ideal protocol to a realistic situation. In the above BQCT scheme, the three participants will share a nine-qubit entangled state \(|\psi \rangle \) with each other before the communication. However, in a realistic situation, it needs one participant, for example, the Charlie to generate the state \(|\psi \rangle \) in his laboratory at first. Then he keeps the qubit 1 with him and sends the qubits (2, 4, 7, 9) and the qubits (3, 5, 6, 8) to Alice and Bob via the noisy channel, respectively. Due to the interaction with the environment, the state \(|\psi \rangle \) will do some changes. Here we will consider the effects of the amplitude-damping noise and the phase-damping noise on the BQCT process.

4 Effects of the amplitude-damping noise and the phase-damping noise on the BQCT process

In this section, we consider the effect of noise on the BQCT process when the travel qubits pass through either the amplitude-damping noisy environment or the phase-damping noisy environment. The amplitude-damping noise model is characterized by the following Kraus operators [25]

$$\begin{aligned} E_{0}^{A}=\left[ {{\begin{array}{cc} 1&{}0\\ 0&{}{\sqrt{1-\eta _A}} \\ \end{array}}} \right] , E_{1}^{A} =\left[ {{\begin{array}{cc} 0&{} {\sqrt{\eta _A}} \\ 0&{} 0 \\ \end{array} }} \right] , \end{aligned}$$
(8)

where \(\eta _A \left( {0\le \eta _A \le 1}\right) \) describes the probability of error due to amplitude-damping noisy environment when a travel qubit passes through it, and \(\eta _{A}\) is the decoherence rate. Similarly, phase-damping noise model is characterized by the following Kraus operators [25]

$$\begin{aligned} E_{0}^{p} =\sqrt{1-\eta _P }I,E_{1}^{P}=\sqrt{\eta _P }\left[ {{\begin{array}{ll} 1&{} 0 \\ 0&{} 0 \\ \end{array}}}\right] ,E_{2}^{P}=\sqrt{\eta _P }\left[ {{\begin{array}{ll} 0&{} 0 \\ 0&{} 1 \\ \end{array}}}\right] , \end{aligned}$$
(9)

where \(\eta _{P}\left( {0\le \eta _{P}\le 1}\right) \) is the decoherence rate for the phase-damping noise.

In Sect. 3, we have proposed a scheme for BQCT by using a nine-qubit entangled state \(|\psi \rangle \). As the state is pure, it is straightforward to obtain the corresponding density matrix \(\rho =|\psi \rangle \langle \psi |\). Now the effect of the noisy environment described by (8) or (9) on the density operator \(\rho \) is

$$\begin{aligned} \xi ^{r}(\rho )= & {} \sum _m {\left( {E_m^{r2} }\right) } \left( {E_m^{r4} } \right) \left( {E_m^{r7} }\right) \left( {E_m^{r9} }\right) \left( {E_m^{r3} }\right) \left( {E_m^{r5} }\right) \left( {E_m^{r6} } \right) \left( {E_m^{r8} }\right) \rho \nonumber \\&\left( {E_m^{r2}}\right) ^{\dagger }\left( {E_m^{r4} } \right) ^{\dagger }\left( {E_m^{r7} }\right) ^{\dagger }\left( {E_m^{r9} }\right) ^{\dagger }\left( {E_m^{r3} } \right) ^{\dagger }\left( {E_m^{r5} }\right) ^{\dagger }\left( {E_m^{r6} }\right) ^{\dagger }\left( {E_m^{r8} }\right) ^{\dagger },\nonumber \\ \end{aligned}$$
(10)

where \(r\in \{A,P\}\). For \(r=A\), i.e., for amplitude-damping noise \(m\in \{0,1\}\), while for \(r=P\), i.e., for phase-damping noise \(m\in \{0,1,2\}\), and the superscripts (2, 4, 7, 9, 3, 5, 6, 8) represent the operator E act on which qubit, \(\xi \) denotes a quantum operation which maps from \(\rho \) to \(\xi ^{r}(\rho )\) due to the noise. In the construction of (10), we have considered that the qubit 1 is not affected by the noise as they are not transmitted through the noisy environment. Further, it is assumed that both the qubits sent to Alice and Bob are affected by the same Kraus operator. As a consequence of the noisy environment, we know that the shared state would become a mixed state after the distribution of the qubits, which are given by

$$\begin{aligned}&\xi ^{A}\left( \rho \right) _{247935681}\!=\!\frac{1}{32}\left\{ {\left[ {|{000000000} \rangle \!+\!\left( {1\!-\!\eta _A }\right) |{000100010} \rangle \!+\!\left( {1\!-\!\eta _A }\right) |{001000100} \rangle } \right. } \right. \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}|{001100110} \rangle +\left( {1-\eta _A }\right) |{010001000} \rangle +\left( {1-\eta _A }\right) ^{2}|{010101010} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}|{011001100} \rangle +\left( {1-\eta _A }\right) ^{3}|{011101110} \rangle +\left( {1-\eta _A }\right) |{100010000} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}|{100110010} \rangle +\left( {1-\eta _A }\right) ^{2}|{101010100} \rangle +\left( {1-\eta _A }\right) ^{3}|{101110110} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}|{11001100} \rangle +\left( {1-\eta _A }\right) ^{3}|{110111010} \rangle +\left( {1-\eta _A }\right) ^{3}|{111011100} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{4}|{111111110} \rangle +\left( {1-\eta _A }\right) ^{2}|{001111001} \rangle -\left( {1-\eta _A }\right) ^{2}|{001011011} \rangle \nonumber \\&\quad -\left( {1-\eta _A }\right) ^{2}|{000111101} \rangle +\left( {1-\eta _A }\right) ^{2}|{000011111} \rangle -\left( {1-\eta _A }\right) ^{2}|{011110001} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}|{011010011} \rangle +\left( {1-\eta _A }\right) ^{2}|{010110101} \rangle -\left( {1-\eta _A }\right) ^{2}|{01001011} \rangle \nonumber \\&\quad -\left( {1-\eta _A }\right) ^{2}|{101101001} \rangle +\left( {1-\eta _A }\right) ^{2}|{101001011} \rangle +\left( {1-\eta _A }\right) ^{2}|{100101101} \rangle \nonumber \\&\quad -\left( {1-\eta _A }\right) ^{2}|{100001111} \rangle +\left( {1-\eta _A }\right) ^{2}|{111100001} \rangle -\left( {1-\eta _A }\right) ^{2}|{111000011} \rangle \nonumber \\&\quad \left. {-\left( {1-\eta _A }\right) ^{2}|{110100101} \rangle +\left( {1-\eta _A }\right) ^{2}|{110000111} \rangle } \right] \times \left[ {\langle {000000000}|} \right. \nonumber \\&\quad +\left( {1-\eta _A }\right) \langle {000100010}|+\left( {1-\eta _A }\right) \langle {001000100}|+\left( {1-\eta _A }\right) ^{2}\langle {001100110}|\nonumber \\&\quad +\left( {1-\eta _A }\right) \langle {010001000}|+\left( {1-\eta _A }\right) ^{2}\langle {010101010}|+\left( {1-\eta _A }\right) ^{2}\langle {011001100}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{3}\langle {011101110}|+\left( {1-\eta _A }\right) \langle {100010000}|+\left( {1-\eta _A }\right) ^{2}\langle {100110010}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}\langle {101010100}|+\left( {1-\eta _A }\right) ^{3}\langle {101110110}|+\left( {1-\eta _A }\right) ^{2}\langle {11001100}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{3}\langle {110111010}|+\left( {1-\eta _A }\right) ^{3}\langle {111011100}|+\left( {1-\eta _A }\right) ^{4}\langle {111111110}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}\langle {001111001}|-\left( {1-\eta _A }\right) ^{2}\langle {001011011}|-\left( {1-\eta _A }\right) ^{2}\langle {000111101}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}\langle {000011111}|-\left( {1-\eta _A }\right) ^{2}\langle {011110001}|+\left( {1-\eta _A }\right) ^{2}\langle {011010011}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}\langle {010110101}|-\left( {1-\eta _A }\right) ^{2}\langle {01001011}|-\left( {1-\eta _A }\right) ^{2}\langle {101101001}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}\langle {101001011}|+\left( {1-\eta _A }\right) ^{2}\langle {100101101}|-\left( {1-\eta _A }\right) ^{2}\langle {100001111}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}\langle {111100001}|-\left( {1-\eta _A }\right) ^{2}\langle {111000011}|-\left( {1-\eta _A }\right) ^{2}\langle {110100101}|\nonumber \\&\quad \left. {+\left( {1-\eta _A }\right) ^{2}\langle {110000111}|} \right] \left. {+\eta _A^8|{000000000} \rangle \langle {000000000}|} \right\} . \end{aligned}$$
(11)

And

$$\begin{aligned}&\xi ^{P}\left( \rho \right) _{247935681}\nonumber \\&\quad =\frac{1}{32}\left\{ {\left( {1-\eta _P }\right) ^{8}\left[ {|{000000000} \rangle +|{000100010} \rangle +|{001000100} \rangle } \right. } \right. +|{001100110} \rangle \nonumber \\&\qquad +\,|{010001000} \rangle +|{010101010} \rangle +|{011001100} \rangle +|{011101110} \rangle +|{100010000} \rangle \nonumber \\&\qquad +\,|{100110010} \rangle +|{101010100} \rangle +|{101110110} \rangle +|{11001100} \rangle +|{110111010} \rangle \nonumber \\&\qquad +\,|{111011100} \rangle +|{111111110} \rangle +|{001111001} \rangle -|{001011011} \rangle -|{000111101} \rangle \nonumber \\&\qquad +\,|{000011111} \rangle -|{011110001} \rangle +|{011010011} \rangle +|{010110101} \rangle -|{01001011} \rangle \nonumber \\&\qquad -\,|{101101001} \rangle +|{101001011} \rangle +|{100101101} \rangle -|{100001111} \rangle +|{111100001} \rangle \nonumber \\&\qquad \left. {-|{111000011} \rangle -|{110100101} \rangle \!+\!|{110000111} \rangle } \right] \times \left[ {\langle {000000000}|\!+\!\langle {000100010}|} \right. \nonumber \\&\qquad +\,\langle {001000100}|+\langle {001100110}|+\langle {010001000}|+\langle {010101010}|+\langle {011001100}|\nonumber \\&\qquad +\,\langle {011101110}|+\langle {100010000}|+\langle {100110010}|+\langle {101010100}|+\langle {101110110}|\nonumber \\&\qquad +\,\langle {11001100}|+\langle {110111010}|+\langle {111011100}|+\langle {111111110}|+\langle {001111001}|\nonumber \\&\qquad -\,\langle {001011011}|-\langle {000111101}|+\langle {000011111}|-\langle {011110001}|+\langle {011010011}|\nonumber \\&\qquad +\,\langle {010110101}|-\langle {01001011}|-\langle {101101001}|+\langle {101001011}|+\langle {100101101}|\nonumber \\&\qquad \left. {-\,\langle {100001111}|\!+\!\langle {111100001}|-\langle {111000011}|-\langle {110100101}|\!+\!\langle {110000111}|} \right] \nonumber \\&\qquad \left. {+\,\eta _P^8|{000000000} \rangle \langle {000000000}|+\,\eta _P^8|{111111110} \rangle \langle {111111110}|} \right\} . \end{aligned}$$
(12)

According to Alice’s and Bob’s and Charlie’s measurement results described in Sect. 3, Alice and Bob can perform appropriate operation on own qubits to recover the original state. Afterward, the density matrix of the final state can be expressed as

$$\begin{aligned} \rho _\mathrm{out}^r =Tr_{A_1 A_2 B_1 B_2 12468} \left\{ {U\left[ {\rho _{A_1 A_2 } \otimes \rho _{B_1 B_2 } \otimes \xi ^{r}\left( \rho \right) } \right] U^{\dagger }} \right\} , \end{aligned}$$
(13)

where \(Tr_{A_1 A_2 B_1 B_2 12468}\) is the partial trace over qubits \((A_{1}, A_{2}, B_{1}, B_{2}, 1, 2, 4, 6, 8)\), and U is a unitary operation to describe the BQCT process, which is given by

$$\begin{aligned} U= & {} \left\{ {I_{A_1 2A_2 4} \otimes I_{B_1 6B_2 8} \otimes I_1 \otimes \sigma _{3579}^{nklsy} } \right\} \left\{ {I_{A_1 2A_2 4} \otimes I_{B_1 6B_2 8} \otimes |{\phi ^{y}} \rangle _1 \langle {\phi ^{y}}|_1 \otimes I_{3579} } \right\} \nonumber \\&\left\{ |{\phi ^{s}} \rangle _{B_2 8} \langle {\phi ^{s}}|_{B_2 8} \otimes |{\phi ^{l}} \rangle _{B_1 6} \langle {\phi ^{l}}|_{B_1 6} \otimes |{\phi ^{k}} \rangle _{A_2 4} \langle {\phi ^{k}}|_{A_2 4} \otimes |{\phi ^{n}} \rangle _{A_1 2} \langle {\phi ^{n}}|_{A_1 2}\right. \nonumber \\&\left. \otimes I_1 \otimes I_{3579} \right\} , \end{aligned}$$
(14)

where \(n,k,l,s\in \{1,2,3,4\}\), \(y\in \{1,2\}\), with \(|{\phi ^{k}} \rangle _{A_2 4}\langle {\phi ^{k}}|_{A_2 4}\otimes |{\phi ^{n}} \rangle _{A_1 2}\langle {\phi ^{n}}|_{A_1 2}\) denotes Alice’s joint Bell-state measurement result, \(|{\phi ^{s}}\rangle _{B_2 8} \langle {\phi ^{s}}|_{B_2 8} \otimes |{\phi ^{l}}\rangle _{B_1 6} \langle {\phi ^{l}}|_{B_1 6}\) denotes Bob’s joint Bell-state measurement result, \(|{\phi ^{y}}\rangle _{1}\langle {\phi ^{y}}|_{1}\) represents Charlie’s single-qubit state measurement result. \(\sigma _{3579}^{nklsy} \) is Alice’s and Bob’s recover operation, which depends on Alice’s and Bob’s and Charlie’s measurement results.

Depending upon the choice, we may have to obtain the final quantum state \(\rho _\mathrm{out}^{r}\) which is the product of the quantum states produced on the side of the receivers Alice and Bob in a noisy environment. Thus, the expected final state in the absence of noise is a product state where Alice will have qubits \(\sum _{j_7 ,j_9 =0}^1 {b_{j_7 j_9}}|{j_7,j_9}\rangle _{79}\) in her possession and Bob will have \(\sum _{i_3, i_5 =0}^1 {a_{i_3 i_5}}|{i_3 ,i_5} \rangle _{35}\) in his possession. As a consequence, in the ideal situation (i.e., in the absence of noise) in all successful cases of BQCT the final state would be \(|\Phi \rangle =\sum _{j_7,j_9 =0}^1 {b_{j_7 j_9 } }|{j_7,j_9 } \rangle _{79} \otimes \sum _{i_3,i_5 =0}^1 {a_{i_3 i_5 } }|{i_3,i_5 } \rangle _{35} \).

We can visualize the effect of noise by comparing the quantum state \(\rho _\mathrm{out}^{r}\) in the noisy environment with the state \(|\Phi \rangle \) by using fidelity

$$\begin{aligned} F=\langle \Phi |\rho _\mathrm{out}^{r}|\Phi \rangle , \end{aligned}$$
(15)

which is square of the usual definition of fidelity of two quantum states \(\rho \) and \(\sigma \) defined as \(F\left( {\rho , \sigma } \right) =Tr\sqrt{\rho ^{1/2}\sigma \rho ^{1/2}}\). In the present paper, we have used (15) as the definition of fidelity. Thus \(F=1\) means the perfect communication. If F becomes smaller and smaller, it indicates that we have lost more and more information in this BQCT process.

According to (13) and (14), it can be easy to get the resultant state \(\rho _\mathrm{out}^{r}\). From (11) and (12), we can intuitively see that the \(\rho _\mathrm{out}^{r}\) is related to three participants’ measurement results n, k, l, s and y. However, after calculation we get that output state \(\rho _\mathrm{out}^{r}\) is independent of three participants’ measurement results. And the \(\rho _\mathrm{out}^{r}\) is shown as follows

$$\begin{aligned}&\left( {\rho _\mathrm{out}^A }\right) _{7935} =\left\{ {\left[ {a_{00} b_{00}|{0000} \rangle +\left( {1-\eta _A }\right) a_{00} b_{01}|{0100} \rangle +\left( {1-\eta _A }\right) a_{00} b_{10}|{1000} \rangle } \right. } \right. \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}a_{00} b_{11}|{1100} \rangle +\left( {1-\eta _A }\right) a_{01} b_{00}|{0001} \rangle +\left( {1-\eta _A }\right) ^{2}a_{01} b_{01}|{0101} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}a_{01} b_{10}|{1001} \rangle +\left( {1-\eta _A }\right) ^{3}a_{01} b_{11}|{1101} \rangle +\left( {1-\eta _A }\right) a_{10} b_{00}|{0010} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}a_{10} b_{01}|{0110} \rangle +\left( {1-\eta _A }\right) ^{2}a_{10} b_{10}|{1010} \rangle +\left( {1-\eta _A }\right) ^{3}a_{10} b_{11}|{1110} \rangle \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}a_{11} b_{00}|{0011} \rangle +\left( {1-\eta _A }\right) ^{3}a_{11} b_{01}|{0111} \rangle +\left( {1-\eta _A }\right) ^{3}a_{11} b_{10}|{1011} \rangle \nonumber \\&\quad \left. {+\left( {1-\eta _A }\right) ^{4}a_{11} b_{11}|{1111} \rangle } \right] \times \left[ {a_{00} b_{00} \langle {0000}|+\left( {1-\eta _A }\right) a_{00} b_{01} \langle {0100}|} \right. \nonumber \\&\quad +\left( {1-\eta _A }\right) a_{00} b_{10} \langle {1000}|+\left( {1-\eta _A }\right) ^{2}a_{00} b_{11} \langle {1100}|+\left( {1-\eta _A }\right) a_{01} b_{00} \langle {0001}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}a_{01} b_{01} \langle {0101}|+\left( {1-\eta _A }\right) ^{2}a_{01} b_{10} \langle {1001}|+\left( {1-\eta _A }\right) ^{3}a_{01} b_{11} \langle {1101}|\nonumber \\&\quad +\left( {1-\eta _A }\right) a_{10} b_{00} \langle {0010}|+\left( {1-\eta _A }\right) ^{2}a_{10} b_{01} \langle {0110}|+\left( {1-\eta _A }\right) ^{2}a_{10} b_{10} \langle {1010}|\nonumber \\&\quad +\left( {1-\eta _A }\right) ^{3}a_{10} b_{11} \langle {1110}|+\left( {1-\eta _A }\right) ^{2}a_{11} b_{00} \langle {0011}|+\left( {1-\eta _A }\right) ^{3}a_{11} b_{01} \langle {0111}|\nonumber \\&\quad \left. {\!+\,\left( {1-\eta _A }\right) ^{3}a_{11} b_{10} \langle {1011}|\!+\!\left( {1-\eta _A }\right) ^{4}a_{11} b_{11} \langle {1111}|} \right] \left. {\!+\!\eta _A^8 a_{11}^2 b_{11}^2|{0000} \rangle \langle {0000}|} \right\} .\nonumber \\ \end{aligned}$$
(16)

And

$$\begin{aligned}&\left( {\rho _\mathrm{out}^P }\right) _{7935}\nonumber \\&\quad =\left\{ {\left( {1-\eta _P }\right) ^{8}\left[ {a_{00} b_{00}|{0000} \rangle +a_{00} b_{01}|{0100} \rangle +a_{00} b_{10}|{1000} \rangle } \right. } \right. +a_{00} b_{11}|{1100} \rangle \nonumber \\&\qquad +\,a_{01} b_{00}|{0001} \rangle +a_{01} b_{01}|{0101} \rangle \!+\!a_{01} b_{10}|{1001} \rangle \!+\!a_{01} b_{11}|{1101} \rangle \!+\!a_{10} b_{00}|{0010} \rangle \nonumber \\&\qquad +\,a_{10} b_{01}|{0110} \rangle +a_{10} b_{10}|{1010} \rangle \!+\!a_{10} b_{11}|{1110} \rangle +a_{11} b_{00}|{0011} \rangle +a_{11} b_{01}|{0111} \rangle \nonumber \\&\qquad \left. +\,{a_{11} b_{10}|{1011} \rangle +a_{11} b_{11}|{1111} \rangle } \right] \times \left[ {a_{00} b_{00} \langle {0000}|+a_{00} b_{01} \langle {0100}|\!+\!a_{00} b_{10} \langle {1000}|} \right. \nonumber \\&\qquad +\,a_{00} b_{11} \langle {1100}|+a_{01} b_{00} \langle {0001}|+a_{01} b_{01} \langle {0101}|\!+\!a_{01} b_{10} \langle {1001}|\!+\!a_{01} b_{11} \langle {1101}|\nonumber \\&\qquad +\,a_{10} b_{00} \langle {0010}|+a_{10} b_{01} \langle {0110}|+a_{10} b_{10} \langle {1010}|+a_{10} b_{11} \langle {1110}|\nonumber \\&\qquad \left. {+\,a_{11} b_{00} \langle {0011}|+a_{11} b_{01} \langle {0111}|+a_{11} b_{10} \langle {1011}|+a_{11} b_{11} \langle {1111}|} \right] \nonumber \\&\qquad \left. {+\,\eta _P^8 a_{00}^2 b_{00}^2|{0000} \rangle \langle {0000}|+\eta _P^8 a_{11}^2 b_{11}^2|{1111} \rangle \langle {1111}|} \right\} . \end{aligned}$$
(17)

Using (15) and (16), we obtain the fidelity of the quantum state teleportation by using the proposed BQCT scheme under amplitude-damping noise as

$$\begin{aligned}&F^{A}=\left[ {a_{00}^2 b_{00}^2 +\left( {1-\eta _A } \right) a_{00}^2 b_{01}^2 +\left( {1-\eta _A }\right) a_{00}^2 b_{10}^2+\left( {1-\eta _A }\right) ^{2}a_{00}^2 b_{11}^2 } \right. \nonumber \\&\quad +\left( {1-\eta _A }\right) a_{01}^2 b_{00}^2 +\left( {1-\eta _A }\right) ^{2}a_{01}^2 b_{01}^2 +\left( {1-\eta _A }\right) ^{2}a_{01}^2 b_{10}^2 +\left( {1-\eta _A}\right) ^{3}a_{01}^2 b_{11}^2\nonumber \\&\quad +\left( {1-\eta _A }\right) a_{10}^2 b_{00}^2 +\left( {1-\eta _A }\right) ^{2}a_{10}^2 b_{01}^2 \nonumber \\&\quad +\left( {1-\eta _A }\right) ^{2}a_{10}^2 b_{10}^2 +\left( {1-\eta _A }\right) ^{3}a_{10}^2 b_{11}^2 +\left( {1-\eta _A}\right) ^{2}a_{11}^2 b_{00}^2 +\left( {1-\eta _A } \right) ^{3}a_{11}^2 b_{01}^2\nonumber \\&\quad \left. {+\left( {1-\eta _A }\right) ^{3}a_{11}^2 b_{10}^2+\left( {1-\eta _A }\right) ^{4}a_{11}^2 b_{11}^2 } \right] ^{2}+\eta _A^8 a_{00}^2 a_{11}^2 b_{00}^2 b_{11}^2. \end{aligned}$$
(18)

Similarly, by using (15) and (16), we obtain the fidelity of the quantum state teleportation by using the proposed BQCT scheme under phase-damping noise as

$$\begin{aligned} F^{P}=\left( {1-\eta _P}\right) ^{8}+\eta _P^8 a_{00}^4 b_{00}^4 +\eta _P^8 a_{11}^4 b_{11}^4 . \end{aligned}$$
(19)

From (18) and (19), we can see that the fidelities for both of the two cases only depend on the amplitude parameter of the initial state and the decoherence rate. Specifically, Fig. 3a–f clearly illustrates the effect of amplitude-damping (phase-damping) noise on the fidelity \(F_{A}\) (\(F_{P}\)) and variation of the fidelity with amplitude parameter of the initial state and the decoherence rate \(\eta _{r}\). We can easily observe that fidelity \(F_{A}\) and \(F_{P}\) always decrease with decoherence \(\eta _A\) and \(\eta _P\), respectively (cf. Fig. 3a, b, e).

Similar nature is also observed in Fig. 4, where we have compared the effect of amplitude-damping noise with phase-damping noise by assuming \(\eta _A =\eta _P=\eta \) and \(a_{00}=a_{01} =a_{10} =a_{11} =1/2\), \(b_{00}=b_{01}=b_{10}=b_{11}=1/2\) (Here \(a_{00} ,a_{01},a_{10},a_{11}, b_{00},b_{01},b_{10},b_{11} \in R\)). In this situation, fidelity of amplitude-damping channel (solid line in Fig. 4a) is always more than that of the phase-damping channel (dashed line in Fig. 4a) for the same value of decoherence rate \(\eta \). Thus, we see that for this particular choice of the amplitude parameter of the initial state, information loss is less when the travel qubits are transferred through the amplitude-damping channel as compared to the phase-damping channel. However, this is not true in general as illustrated through Fig. 4b, where we can see that for \(\eta >0.671836\) and \(a_{00} =b_{00} =1/2,a_{11} ={b_{11} =\sqrt{3}}/{2,}a_{01} =a_{10} =0,b_{01} =b_{10} =0\), effect of phase-damping channel on fidelity is less than that of amplitude-damping channel.

Fig. 3
figure 3

Effect of noise on BQCT scheme is visualized through variation of fidelity \(F_{A}\) (for amplitude-damping noise model) and \(F_{P}\) (for phase-damping noise model) with respect to amplitude information of the states to be teleported and decoherence rates for various situations: a amplitude-damping noise with \(a=a_{00} \), \(b_{00} =b_{11} ={\sqrt{2}}/2\), \(a_{01} =a_{10} =b_{01} =b_{10} =0\), b amplitude-damping noise with \(b=b_{00} \), \(a_{01} =a_{10} ={\sqrt{2}}/2\), \(a_{00} =a_{11} =b_{01} =b_{10} =0\), c amplitude-damping noise with \(b=b_{00} \), \(\eta _A =1\),\(a=a_{00} \), \(a_{01} =a_{10} =b_{01} =b_{10} =0\), d phase-damping noise with \(a=a_{00} \), \(b_{00} =1\), \(a_{01}=a_{10} =b_{01} =b_{10} =0\), e phase-damping noise with \(b=b_{00}\), \(a_{00} =1/2, a_{01} =a_{10} =b_{01} =b_{10} =0\), \(a_{11} ={\sqrt{3}}/2\), f phase-damping noise with \(a=a_{00}, a_{01} =a_{10} =0\), \(b=b_{00},b_{01} =b_{10} =0\), \(\eta _P =1\)

Full size image
Fig. 4
figure 4

The fidelities of amplitude-damping noise and phase-damping noise. The solid line stands for the amplitude-damping noise, the dashed line stands for the phase-damping noise

Full size image

Thus in a real physical scenario, fidelity decreases with increased noise. However, even in a noisy environment, BQCT may be implemented with unit fidelity, if states with particular \(a_{i_3 i_5}\) and \(b_{j_7 j_9}\) are to be teleported. This fact can be visualized through the peaks of Fig. 3c, f.

5 Discussions and comparisons

Now let us briefly consider the feasibility of this scheme in experiment. It is found that the necessary local unitary operation in the protocol contains controlled-NOT operations and Hadamard operations, and the employed measurement includes Bell-state measurements and single-qubit measurement. It is well known that Bell-state measurements can be decomposed into an ordering combination of a single-qubit Hadamard operation and a two-qubit CNOT operation as well as two single-qubit measurements. Up to now, the BSMs, two-qubit control gates, and the single-qubit unitary operations have already been realized in various quantum systems, such as the cavity QED system [26], ion-trap system [27], and optical system [28]. More importantly, our BQCT protocol is important for many applications including two-way quantum key distribution [29] and realizations of quantum interactive proof systems [30]. In addition, the nine-qubit entangled state in our scheme has not been reported in experiment, but when combined with the advances in quantum information technology, we hope that our scheme will be implemented in the future.

Then let us make some comparisons among our scheme and other schemes [14–20]. Comparisons are made from the four aspects, namely the quantum resource consumption, the classical resource consumption, transmitted quantum information bits and the intrinsic efficiency. They are summarized in Table 1.

From Table 1, one can see that the quantum resource consumption, quantum information bits transmitted and efficiency are equal in Refs. [17–19]. Comparison with Duan scheme [20], the six schemes [14–19] have consumed fewer quantum and classical resources and possessed higher intrinsic efficiency. Comparison with the four schemes [17–19], Refs. [14–16] schemes have consumed fewer quantum and classical resources, and possessed higher intrinsic efficiency. Comparison with the schemes in Ref. [14] and Ref. [15], quantum channel in Ref. [16] scheme is much easier to generate in experiment. In all, the scheme [16] is more optimal and economic. Comparing the scheme [16] with our scheme, we will be readily to see the following three differences: (1) the quantum resource consumption in the scheme [16] is less than it in our scheme; (2) the nine-qubit entangled state channel in our scheme is more difficult than the scheme [16]; and (3) the remarkable advantages in our scheme transmit arbitrary two-qubit state and possess higher intrinsic efficiency. In this sense, our scheme is better for BQCT.

Table 1 Comparison between eight protocols
Full size table

The intrinsic efficiency of the communication scheme is defined [31] as \(\eta ={q_s }/{(q_u +b_t)}\), where \(q_s\) is the number of qubits that consist of the quantum information to be exchanged, \(q_u \) is the number of the qubits which are used as the quantum channel (except for those chosen for security checking), \(b_{t}\) is the classical bits transmitted. And QRC (quantum resource consumption), NO (necessary operations), BS (Bell states), CS (cluster state), CRC (classical resource consumption), BSMs (Bell-state measurements), SMs (single-qubit measurements), QIBT (quantum information bits transmitted), Q (qubit), ES (entangled state), UOs (unitary operations), CNOTs (controlled-NOT operation), PoP (permutation of particles), PO (permutation operator).

Furthermore, comparing our scheme with Ref. [20], our protocol exploits the nine-qubit entangled state as quantum channel which may improve greatly the security of the scheme. If the quantum channel is not safe, the probability that the eavesdropper simultaneously gets the right information of Alice and Bob’s is 1/512, and Ref. [20] is 1/128.

6 Conclusions

In this paper, the construction of the nine-qubit entangled state channel is discussed. We show that such a nine-qubit entangled state can be used as the quantum channel to realize the deterministic BQCT. In our approach, Alice may transmit an arbitrary two-qubit state of qubits \(A_1\) and \(A_2\) to Bob and at same time Bob may also transmit an arbitrary two-qubit state of qubits \(B_1\) and \(B_2\) to Alice via the control of the supervisor Charlie, where only four BSMs and a single-qubit measurement are needed so as to be more simple and feasible in experiment. And we have compared our scheme with other schemes on quantum and classical resource consumptions, quantum information bits transmitted, and efficiencies. We think our scheme is better than other schemes.

Further, the effects of the amplitude-damping noise and the phase-damping noise for BQCT process are investigated, which makes the present work much more realistic compared to the existing works as in practice we cannot have a noise-free quantum channel. Moreover, the method used here for the study of effect of noise is quite general and it is possible to apply this approach to study the effect of noise in other similar schemes of quantum communication. However, how to reduce, furthermore, to eliminate the influence of these noise to improve the transmission efficiency should be a more important thing, and it is our future work.