1 Introduction

Since the first creation of quantum teleportation protocol by Bennett [1], research on quantum teleportation has been attracting much attention both in theoretical and experimental aspects in recent years due to its important applications in quantum calculation and quantum communication. Several experimental implementations of teleportation have been reported [2–4] and some schemes of quantum teleportation have also been presented [5–22]. Thereinto, one branch of the extension is controlled teleportation first presented by Karlsson and Bourennane [23] in 1998. In 2004,Yang et al. presented a multiparty controlled teleportation protocol to teleport multi-qubit quantum information [24]. In 2005, Deng et al. introduced a symmetric multiparty controlled teleportation scheme for an arbitrary two particle entangled state [25]. Up to now teleportation, many teleportation and controlled teleportation scheme have been reported [23–30], but no bidirectional quantum controlled teleportation has not yet been presented.

In this paper, we present a scheme of bidirectional quantum controlled teleportation in which a five-qubit cluster state [31] quantum channel initially shared by the sender (receiver) Alice, Bob and supervisor Charlie. Suppose that Alice has particle a in an unknown state, she wants to transmit the state of particle a to Bob; at the same time, Bob has particle b in an unknown state, he wants to transmit the state of particle b to Alice. We show that the original state of each qubit can be restored by the receiver as long as sender Alice (Bob) make a C-not measurement and a single-qubit measurements on the sender’s side and operate an appropriate unitary transformation on the receiver’s side with the cooperation of the supervisor Charlie.

2 Bidirectional Quantum Controlled Teleportation

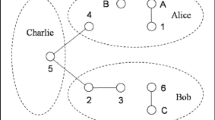
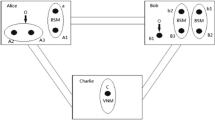
Let us assume that the quantum channel between the sender Alice (Bob), the receiver Bob (Alice) and the supervisor Charlie, is a one-dimensional five-qubit cluster state, which has the form:

$$ \vert \psi \rangle_{12345} = \frac{1}{2}\bigl(\vert 00000 \rangle + \vert 00111 \rangle + \vert 11010 \rangle + \vert 11101 \rangle\bigr)_{12345} $$
(1)

If Alice, Bob, and Charlie have particles 13,25,4, respectively, the quantum channel can be expressed as:

$$ | \psi_{5} \rangle_{A_{1}B_{1}A_{2}CB_{2}} = \frac{1}{2}\bigl(| 00000 \rangle + | 00111 \rangle + | 11010 \rangle + | 11101 \rangle\bigr)_{A_{1}B_{1}A_{2}CB_{2}} $$
(2)

Suppose that Alice has particle a in an unknown state:

$$ | \chi\rangle_{a} = \bigl(a_{0}| 0 \rangle + a_{1}| 1 \rangle\bigr)_{a} $$
(3a)

And that Bob has particle b in an unknown state:

$$ | \chi\rangle_{b} = \bigl(b_{0}| 0 \rangle + b_{1}| 1 \rangle\bigr)_{b} $$
(3b)

Alice wants to transmit the state of particle a to Bob and Bob wants to transmit the state of particle b to Alice.

The system state of the seven particles can be expressed as:

(4)

In order to realize quantum state swapping, Bob make a C-not operation with the particle b as the control qubit and the particle B 2 as the target. Which will transform Eq. (4) to the result

(5)

On the other hand, Alice make a C-not operation with the particle a as the control qubit and the particle A 1 as the target, which will transform Eq. (5) to the result

(6)

Charlie performs a Von Neumann measurement on his single qubit. Then, if Charlie’s Von Neumann measurement result is |+〉 c , the corresponding collapsed state of particle aA 1 A 2,bB 1 B 2 will be

(7)

Then Alice carries out measurement on qubit A 1, if Alice’s Von Neumann measurement result is \(| 0 \rangle_{A_{1}}\) the corresponding collapsed state of particle aA 2,bB 1 B 2 will be

(8)

Subsequently, Bob operates measurement on qubit B 2, if Bob’s Von Neumann measurement result is \(|0 \rangle_{B_{2}}\) the corresponding collapsed state of particle aA 2,bB 1 will be

(9)

Finally, Alice and Bob have to perform Von Neumann measurement on their qubits a, b, with measurement base

$$ | \pm\rangle_{a( b )} = \frac{1}{\sqrt{2}} \bigl( | 0 \rangle\pm| 1 \rangle\bigr)_{a( b )} $$
(10)

For example, if Alice’s measurements result is |+〉 a , Bob’s measurements result is |+〉 b , the corresponding collapsed state of particle B 1,A 2 will be

(11)

The Bidirectional quantum controlled teleportation is successfully realized.

Similarly, if Charlie’s Von Neumann measurement result is |−〉 c , the corresponding collapsed state of particle aA 1 A 2,bB 1 B 2 will be

(12)

Then Alice measurements on qubit A 1, if Alice’s Von Neumann measurement result is \(| 1 \rangle_{A_{1}}\)the corresponding collapsed state of particle aA 2,bB 1 B 2 will be

(13)

Subsequently, Bob measurements on qubit B 2, if Bob’s Von Neumann measurement result is \(| 1 \rangle_{B_{2}}\)the corresponding collapsed state of particle aA 2,bB 1 will be

(14)

Then, if Alice’s measurements result is |+〉 a , Bob’s measurements result is |+〉 b , the corresponding collapsed state of particle B 1,A 2 will be

(15)

The Bidirectional quantum controlled teleportation is successfully realized.

Analogously, for other cases, according to measurement result by Alice, Bob and Charlie, Alice and Bob operate an appropriate unitary transformation; the Bidirectional quantum controlled teleportation is easily realized.

3 Conclusions

In summary, we have proposed a scheme for Bidirectional quantum controlled teleportation by five cluster state. Namely, Suppose that Alice wants to transmit a entangled state of particle a to Bob and at same time Bob wants to transmit a entangled state of particle b to Alice via the control of the supervisor Charlie. The two unknown states can be exchanged if Alice and Bob operate Von Neumann measurement and appropriate unitary transformation with the help of Charlie. However, if one agent does not cooperate, the receiver can not fully recover the original state of each qubit. We hope that the scheme will be experimentally realized in the future.