1 Introduction

Feynman R.P. first proposed the concept of simulating physics with computers, i.e., quantum computers (Feynman 1982). The information is stored in quantum systems and regarded as quantum bits (qubits) (Stajic 2013). Due to the inherent properties of quantum mechanics such as coherence, entanglement, and superposition of qubits, quantum information processing (QIP) is deemed to precede its classical counterparts in aspects of information storage, parallel computing and security (Michael and Isaac 2000). Although a real physical quantum computer has not been realized yet, it seems very necessary to develop quantum image processing tasks on account of that a quantum computer will inevitably need images displaying and processing ability. With the rapid development of QIP in recent years, classical image processing tasks are naturally extended to quantum scenarios named as quantum image processing (QImP). QImP is an emerging sub-discipline that focuses on extending conventional image processing tasks and operations to the quantum computing framework (Iliyasu 2013; Yan et al. 2016, 2017). Compared to image processing algorithm implemented within classical computers in a conventional way, an efficient quantum image encryption algorithm based on the principle of quantum mechanics are assumed to improve the computational cost greatly, and can guarantee high security in theoretical. At present, the development of QImP can be classified into two aspects: quantum image representation and quantum image processing algorithm.

Quantum image representation encodes digital images within quantum computers. Many representation models of quantum images are investigated. Qubit Lattice is deemed as the first quantum image representation model (Venegas-Andraca 2003), which stores a \(2^{n} \times 2^{n}\) color image in quantum systems with \(2^{2n}\) qubits. To reduce the number of qubits used for encoding the quantum images, the flexible representation of quantum images (FRQI) proposed in (Li et al. 2018) stores a \(2^{n} \times 2^{n}\) grayscale image with 2n + 1 qubits, which stores pixel’s coordinate information into 2n-qubit computational basis states and encodes the pixel’s color information into a single qubit via angle encoding. For the convenience of color processing, the novel enhanced quantum representation (NEQR) of digital images (Zhang et al. 2013a) improves the FRQI model, which utilizes q-qubit computational basis state to store pixel’s gray value ranged \([0,2^{q} - 1]\). Next, the flexible quantum representation for gray-level images (FQRGI) was proposed by (Yang et al. 2014) that encode pixel’s gray-level information within single qubit phases. A normal arbitrary quantum superposition state (NAQSS) was proposed by (Li et al. 2014) to store a k-dimensional color digital image using amplitudes of computational basis state. Inspired by NEQR model, some quantum image representation models use computational basis states to store pixel’s gray value information were proposed, such as quantum log-polar image (QUALPI) (Zhang et al. 2013b) and novel quantum representation of color digital images (NCQI) (Sang et al. 2017). To further improve the storage performance, quantum image representation models based on bit-plane was also proposed in (Li et al. 2018; Wang et al., 2019; Li et al. 2019). Quantum image representation based on bit-planes (BRQI) presented in (Li et al. 2018) uses (n + 4) and (n + 6) qubits to store a grayscale or RGB color image of \(2^{n}\) pixels, respectively. The quantum representation model of color digital images (QRCI) in (Wang et al. 2018) stores a \(2^{n} \times 2^{n}\) color image with 2n + 6 qubits. The generalized model of NEQR (GNEQR) presented in (Li et al. 2019) uses 2n + 10 qubits to encode a \(2^{n} \times 2^{n}\) RGB color image. Based on the coding method of pixel information, quantum image representation models described above can be classified into three categories: the first encodes pixel information via amplitude of qubit that includes Qubit Lattice and FRQI (Venegas-Andraca 2003; Li et al. 2018); the second utilizes the phase of qubit encoding pixel information that contains FQRGI and NAQSS (Yang et al. 2014; Li et al. 2014); the third using the basis states of qubits stores the pixel information, which includes NEQR, QUALPI, NCQI, BRQI, QRCI and GNEQR (Zhang et al. 2013a; Zhang et al. 2013b; Sang et al. 2017; Li et al. 2018; Wang et al., 2019; Li et al. 2019).

Image encryption aims at providing information secrecy in public environment through disturbing an image into meaningless form using different methods. Up to now, quantum image encryption has gained researchers’ considerable interest and mainly classified into following two classes: (1) image encryption in spatial domain based on quantum transformations; (2) image encryption based on chaos theory. In first category, a series of quantum encryption algorithms were investigated, such as quantum image scrambling based on Arnold, Fibonacci and Hilbert transforms (Jiang et al. 2014a, b; Jiang and Wang 2014), quantum image encrypted based on quantum Fourier transform and double phase encoding (Yang et al. 2014; Li et al. 2018a, b, c), quantum image encrypted based on generalized Arnold transform and double random-phase encoding (Zhou et al. 2015), quantum image encrypted based on block geometric transformation and bit-plane scrambling (Li et al. 2019). In second category, Liang et al. investigated quantum image encryption based on generalized affine transform and Logistic map (Liang et al. 2016). Tan et al. proposed a quantum color image encryption algorithm based on a hyper-chaotic system and quantum Fourier transform (Tan et al. 2016). Ran et al. proposed the quantum color image encryption based on coupled hyper-chaotic Lorenz system (Ran et al. 2018). Subsequently, more quantum image encryption algorithms based on chaos theory were also reported in (Li et al. 2017; Zhou et al. 2018; Jiang et al. 2019).

However, above-mentioned quantum transformation based image encryption scheme only disturbing the coordinate information have several disadvantages. Such as the histogram graphs are unchanged, and the quantum transformations need to perform many times to obtain a better encryption effect. On the other hand, chaos theory based quantum image encryption algorithms described above are similar to the "one-time pad" encryption, which involves high complexity in processing the pixel step-by-step according to the specific key stream. Furthermore, the former chaos-based quantum image encryption literatures also not provide the intact quantum implementation circuit.

To conquer the disadvantage of quantum transformation based quantum image encryption algorithms and improve the computational efficiency of chaos theory based quantum image encryption algorithms, an enhanced quantum image encryption scheme that combines generalized Arnold transform and Logistic map technologies are investigated. The main contributions of our work can be stated as: (1) twice scrambling based on generalized Arnold transform are implemented to simultaneously encrypt the image coordinate information and pixel gray value; (2) the complete quantum circuit implementation for encrypting the image information based on quantum key image (generated via Logistic map) are constructed and illustrated, which can process all image pixel’s information in parallel. On the basis of computational complexity and experimental result analysis demonstrated in latter, it proves that our investigated quantum encryption scheme has lower complexity and high security.

The rest of this paper is organized as follows: In Sect. 2, we provide the basic knowledges needed for the proposed algorithm, including quantum qubits and gates, NEQR and GNEQR models, twice scrambling based on generalized Arnold transform, Logistic map and some quantum circuit modules. Section 3 describes the proposed quantum encryption and decryption algorithms in detailed. Section 4 analyses the quantum cost and time complexity of the quantum implementation circuits, and comparisons with related references in terms of quantum cost. Experimental results and numerical analyses are demonstrated in Sect. 5. Finally, the conclusion works are stated in Sect. 6.

2 Preliminaries

2.1 Quantum bits and gates

2.1.1 Quantum bits

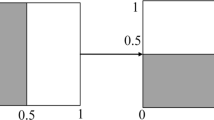
The quantum bit (qubit) is the elementary memory unit in a quantum computer. Quantum information can be stored, manipulated and measured via qubits. The state of single qubit can be mathematically described by a unit vector in two-dimensional Hilbert space. One useful picture in thinking about single qubit is the Bloch sphere as shown in Fig. 1 (Michael and Isaac 2000). A single qubit \(\left| \psi \right\rangle\) can be expressed as:

$$\begin{gathered} \left| \psi \right\rangle = \cos \frac{\theta }{2}\left| 0 \right\rangle + e^{i\varphi } \sin \frac{\theta }{2}\left| 1 \right\rangle \hfill \\ \;\;\;\;\; = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle , \hfill \\ \end{gathered}$$
(1)

where \(\theta \in [0,\;\pi ],\;\varphi \in [0,\;2\pi ]\), and \(\left| \alpha \right|^{2} + \left| \beta \right|^{2} = 1\) subjects to the normalization condition.

Fig. 1
figure 1

Bloch sphere representation of a qubit

Full size image

The qubit states \(\left| 0 \right\rangle = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]^{T}\) and \(\left| 1 \right\rangle = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]^{T}\) are called as the computational basis state spanning \(H^{2}\) in 2-D Hilbert space. The tensor product, denoted by \(\otimes\), is utilized to put the small vector spaces together forming a larger vector space in Hilbert space. Let A be a \(n \times n\) matrix and B be a \(m \times m\) matrix, then the tensor product A \(\otimes\) B is a \(nm \times nm\) block matrix defined as:

$$A \otimes B = \left[ {\begin{array}{*{20}c} {A_{0,0} B} & \cdots & {A_{0,n - 1} B} \\ \vdots & \ddots & \vdots \\ {A_{n - 1,0} B} & \cdots & {A_{n - 1,n - 1} B} \\ \end{array} } \right].$$
(2)

Suppose that \(\left| i \right\rangle\) is the computational basis state in a \(2^{n} { - }D\) Hilbert space, where the state \(\left| i \right\rangle \;\left( {i = 0,\;1,\;2,\; \cdot \cdot \cdot ,\;2^{n} - 1} \right)\) consists of the tensor products of the n computational basis states defined as:

$$\left| i \right\rangle = \left| {i_{n - 1} } \right\rangle \otimes \left| {i_{n - 2} } \right\rangle \otimes \cdot \cdot \cdot \otimes \left| {i_{1} } \right\rangle \otimes \left| {i_{0} } \right\rangle = \left| {i_{n - 1} i_{n - 2} \cdot \cdot \cdot i_{1} i_{0} } \right\rangle ,$$
(3)

where \(i = \sum\nolimits_{j = 0}^{n - 1} {i_{j} \times 2^{j} }\), \(i_{0} ,\;i_{1} ,\; \cdot \cdot \cdot ,\;i_{n - 1} \; \in \left\{ {0,\;1} \right\}\). Thus, the quantum system of n-qubit can be described as a superposition state of \(2^{n}\) quantum computational basis states:

$$\left| \psi \right\rangle = \sum\limits_{k = 0}^{n - 1} {a_{k} } \left| k \right\rangle ,\;k = k_{n - 1} k_{n - 2} \cdot \cdot \cdot k_{1} k_{0} ,\;k_{i} \in \left\{ {0,\;1} \right\},$$
(4)

and also satisfying the normalization condition \(\sum\limits_{k = 0}^{n - 1} {\left| {a_{k} } \right|^{2} } = 1\).

2.1.2 Quantum gates

Quantum gates are the necessary elements in constructing the quantum circuit. Some basic quantum gates and their corresponding matrices are demonstrated in Fig. 2.

Fig. 2
figure 2

Notations for some basic quantum gates with their corresponding matrices expression

Full size image

Quantum Identity (\(I_{2}\)) gate denotes the quantum circuit line of single qubit. Similarly, \(\left( {I_{2} } \right)^{ \otimes n} = I_{{2^{n} }}\) denotes the quantum circuit line of n qubits.

Quantum NOT (also denoted as X) gate is similar to classical NOT operation, expressed as \(X\left| a \right\rangle = \left| {\overline{a} } \right\rangle\),\(a \in \{ 0,1\} ,\)\(\;\overline{a} = 1 - a\).

Quantum Hadamard (H) gate operated on single qubit \(\left| 0 \right\rangle\) and \(\left| 1 \right\rangle\) can transform the quantum state into an equal superposition state, i.e., \(H\left( {\left| 0 \right\rangle } \right) = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}\left( {\left| 0 \right\rangle + \left| 1 \right\rangle } \right)\), \(H\left( {\left| 1 \right\rangle } \right) =\)\({1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-\nulldelimiterspace} {\sqrt 2 }}\left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right)\).

Quantum Controlled-NOT (CNOT) gate is usually used to realize the similar function of the classical XOR operation, which has two input qubits: control qubit and target qubit. It has two different forms 1-CNOT and 0-CNOT, which mean the control qubit in state of \(\left| 1 \right\rangle\) and \(\left| 0 \right\rangle\), respectively. Thus \(1{ - }CNOT\left( {\left| {a,b} \right\rangle } \right) = \left| {a,a \oplus b} \right\rangle\) and \(0{ - }CNOT\left( {\left| {a,b} \right\rangle } \right) = \left| {a,\overline{a} \oplus b} \right\rangle\).

The Swap gate is used to interchange the two qubit state, i.e., \(Swap\left( {\left| {a,b} \right\rangle } \right) = \left| {b,a} \right\rangle\), and it can be decomposed into three 1-CNOT gates.

2.2 NEQR and GNEQR

Quantum image representation model NEQR (Zhang et al. 2013a, b) uses two entangled qubit sequences to encode the whole image information into a normalized superposition state. For a \({2}^{n} \times 2^{n}\) quantum image with grayscale ranged \({[0,}\;{2}^{q} - 1]\), the representative expression is expressed as:

$$\left| I \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {I_{YX} } \right\rangle \left| {YX} \right\rangle } } = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{K = 0}^{q - 1} } } \left| {I_{YX}^{K} } \right\rangle \left| Y \right\rangle \left| X \right\rangle ,$$
(5)

where the binary sequence \(I_{YX} = I_{YX}^{0} I_{YX}^{1} \cdot \cdot \cdot I_{YX}^{q - 2} I_{YX}^{q - 1}\) encodes the pixel’s gray value in corresponding position \((Y,\;X)\). \(Y = y_{n - 1} \cdot \cdot \cdot y_{1} y_{0}\) and \(X = x_{n - 1} \cdot \cdot \cdot x_{1} x_{0}\) denote the pixel’s location information in vertical and horizontal directions, respectively.

When q = 8, \(\left| I \right\rangle\) represents a grayscale image. As an example, Fig. 3 gives a \(2 \times 2\) NEQR grayscale image, its quantum circuit line, and the representative expression.

Fig. 3
figure 3

A \(2 \times 2\) NEQR image

Full size image

A RGB color image can be decomposed into three channels of Red, Green, Blue, and each channel is a grayscale image defined as:

$$\begin{gathered} \left| {I_{R} } \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {R_{YX} } \right\rangle \left| {YX} \right\rangle } } = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{K = 0}^{q - 1} } } \left| {R_{YX}^{K} } \right\rangle \left| Y \right\rangle \left| X \right\rangle , \hfill \\ \left| {I_{G} } \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {G_{YX} } \right\rangle \left| {YX} \right\rangle } } = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{K = 0}^{q - 1} } } \left| {G_{YX}^{K} } \right\rangle \left| Y \right\rangle \left| X \right\rangle , \hfill \\ \left| {I_{B} } \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {B_{YX} } \right\rangle \left| {YX} \right\rangle } } = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{K = 0}^{q - 1} } } \left| {B_{YX}^{K} } \right\rangle \left| Y \right\rangle \left| X \right\rangle , \hfill \\ \end{gathered}$$
(6)

where \(\left| {I_{R} } \right\rangle ,\;\;\left| {I_{G} } \right\rangle ,\;\;\left| {I_{B} } \right\rangle\) encode the grayscale image in channels of Red, Green, and Blue, respectively.

Based on three components of grayscale image within RGB color image, the generalized model of NEQR (GNEQR) (Li et al. 2019) that represents a quantum RGB color image is defined as:

$$\begin{gathered} \left| G \right\rangle = \frac{1}{\sqrt 3 }\left( {\left| {I_{R} } \right\rangle \left| {01} \right\rangle + \left| {I_{G} } \right\rangle \left| {10} \right\rangle + \left| {I_{B} } \right\rangle \left| {11} \right\rangle } \right) \hfill \\ = \frac{1}{\sqrt 3 } \times \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left( {\left| {R_{YX} } \right\rangle \left| {YX} \right\rangle \left| {01} \right\rangle + \left| {G_{YX} } \right\rangle \left| {YX} \right\rangle \left| {10} \right\rangle } \right.} } \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { + \left| {B_{YX} } \right\rangle \left| {YX} \right\rangle \left| {11} \right\rangle } \right) \hfill \\ \end{gathered}$$
(7)

Figure 4 illustrates the quantum circuit implementation for GNEQR image, where the quantum oracle NEQR (i.e., a quantum black box) prepares a NEQR quantum image (Zhang et al. 2013a, b), and the unitary operation \(R_{x} \left( {\arctan \sqrt 2 } \right)\) is defined as:

$$\begin{gathered} R_{x} (\arctan \sqrt 2 ) = \left[ {\begin{array}{*{20}c} {\cos (\arctan \sqrt 2 )} & {\sin (\arctan \sqrt 2 )} \\ {\sin (\arctan \sqrt 2 )} & { - \cos (\arctan \sqrt 2 )} \\ \end{array} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}} & {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}} \\ {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}} & {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$
(8)
Fig. 4
figure 4

Quantum circuit for the preparation of GNEQR image and its quantum circuit line

Full size image

2.3 Twice scrambling based on generalized Arnold transform

Arnold transform, also called as cat map, was proposed by (Arnold and Avez, 1968) in the research of ergodic theory. Dyson and Falk quoted the transform as an image scrambling method (Dyson and Falk, 1992). On the basis of Arnold transform, the two-dimension generalized Arnold transform (Zhou et al. 2015) is defined as:

$$\left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & t \\ m & {t \cdot m + 1} \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right]\;\left( {\bmod N} \right),$$
(9)

where \((x,y)\) and \((x^{\prime},y^{\prime})\) are the pixel’s coordinates of the original image and scrambled image, respectively. N is the size of the square image, t and m are the positive integers.

The generalized Arnold transform in the form of coordinates can be expressed as:

$$\begin{gathered} x^{\prime} = \left( {x + t \cdot y} \right)\bmod N, \hfill \\ y^{\prime} = \left[ {m \cdot x + \left( {t \cdot m + 1} \right)y} \right]\bmod N. \hfill \\ \end{gathered}$$
(10)

Accordingly, the inverse generalized Arnold transform is defined as:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & t \\ m & {t \cdot m + 1} \\ \end{array} } \right]^{ - 1} \;\left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right]\left( {\bmod N} \right) \hfill \\ \;\;\;\;\; = \left[ {\begin{array}{*{20}c} {t \cdot m + 1} & { - t} \\ { - m} & 1 \\ \end{array} } \right]\;\;\left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right]\left( {\bmod N} \right). \hfill \\ \end{gathered}$$
(11)

The inverse generalized Arnold transform in the form of coordinates is expressed as:

$$\begin{gathered} x = \left[ {\left( {t \cdot m + 1} \right)x^{\prime} - t \cdot y^{\prime}} \right]\bmod N, \hfill \\ y = \left( {y^{\prime} - m \cdot x^{\prime}} \right)\bmod N. \hfill \\ \end{gathered}$$
(12)

Only implementing the generalized Arnold transform on the image’s coordinate information do not changes histogram graph of the scrambled image. To enhance the security of the scrambled image, the generalized Arnold transform also can be used to scramble the pixel’s gray value. Assume that the pixel’s grayscale information \(I_{YX}\) shown in Eq. (5) is divided into following two parts:

$$\begin{gathered} I_{YX} = I1_{YX} I2_{YX} , \hfill \\ I1_{YX} = I_{YX}^{0} I_{YX}^{1} I_{YX}^{2} I_{YX}^{3} ,\;\;\;I2_{YX} = I_{YX}^{4} I_{YX}^{5} I_{YX}^{6} I_{YX}^{7} . \hfill \\ \end{gathered}$$
(13)

Then the generalized Arnold transform and its inverse transform implemented on grayscale space can be defined as:

$$\begin{gathered} \left\{ \begin{gathered} I1_{YX}^{\prime } = (I1_{YX} + t \cdot I2_{YX} )\bmod 16 \hfill \\ I2_{YX}^{\prime } = \left( {m \cdot I1_{YX} + (t \cdot m + 1) \cdot I2_{YX} } \right)\bmod 16 \hfill \\ \end{gathered} \right., \hfill \\ \left\{ \begin{gathered} I1_{YX} = \left[ {\left( {t \cdot m + 1} \right)I1_{YX}^{\prime } - t \cdot I2_{YX}^{\prime } } \right]\bmod 16 \hfill \\ I2_{YX} = \left( {I2_{YX}^{\prime } - m \cdot I1_{YX}^{\prime } } \right)\bmod 16 \hfill \\ \end{gathered} \right., \hfill \\ \end{gathered}$$
(14)

where \(I_{YX}^{\prime } = I1_{YX}^{\prime } I2_{YX}^{\prime } = I_{YX}^{0 \prime } I_{YX}^{1 \prime } I_{YX}^{2 \prime } I_{YX}^{3 \prime } I_{YX}^{4 \prime } I_{YX}^{5 \prime } I_{YX}^{6 \prime } I_{YX}^{7 \prime }\) is the pixel’s color information of encrypted image in position (Y,X).

2.4 Logistic map

The chaotic Logistic map (Jafarizadeh and Behnia 2011) is widely studied in dynamic system, which is defined as:

$$x_{k + 1} = \mu \cdot x_{k} (1 - x_{k} ),$$
(15)

where \(0 \le \mu \le 4,\;k = 0,1,2,3,\; \cdot \cdot \cdot ,\;n\) and \(0 < x_{0} < 1\).

The study of chaotic dynamics shows that the Logistic map is in chaos when \(3.56 < \mu \le 4\). As an example, Logistic map curves under two different initial values with 100 iteration times are illustrated in Fig. 5, from which it is easily to find that the Logistic map curves are very sensitive to the initial values.

Fig. 5
figure 5

Two Logistic map curves under different initial values within 100 iteration times

Full size image

2.5 Quantum circuit modules

In this subsection, some quantum circuit modules are introduced, which play a key element to construct the quantum circuit for the presented quantum scheme.

2.5.1 ADDER module

The quantum ADDER originally introduced in (Vedral et al. 1996) is used to add two integers. Figure 6 illustrates the quantum circuit implementation for ADDER, which calculates the sum of two binary numbers A and B, where \(A = a_{n - 1} a_{n - 2} \cdot \cdot \cdot a_{2} a_{1} a_{0}\) and \(B = b_{n - 1} b_{n - 2} \cdot \cdot \cdot b_{2} b_{1} b_{0}\), \(a_{i} ,\;b_{i} \; \in \left\{ {0,\;1} \right\}\). The sum of A + B is stored as \(S = s_{n} s_{n - 1} s_{n - 2} \cdot \cdot \cdot s_{2} s_{1} s_{0} ,\;s_{i} \in \left\{ {0,\;1} \right\}\). Therein, the basic modules of CARRY and SUM (its quantum circuits are shown in Fig. 7a) are used to respectively calculate the carry of three binary bits and the sum of two binary bits.

Fig. 6
figure 6

Quantum effective circuits for ADDER

Full size image
Fig. 7
figure 7

a Quantum circuit for CARRY and SUM, (b) the simplified diagram of \({\text{ADDER } - \text{ MOD}}\;2^{n}\)

Full size image

According to the property of binary bits, quantum ADDER-MOD module to calculate the mod operation of \(\left( {A + B} \right)\bmod 2^{n}\) was proposed (Jiang and Wang, 2014), which can be easily realized through omitting the highest bit \(s_{n}\) of S. That is, \(\left( {A + B} \right)\bmod 2^{n} = s_{n - 1} s_{n - 2} \cdot \cdot \cdot s_{1} s_{0}\). For simplicity, Fig. 7b gives the simplified diagram of ADDER-MOD \(2^{n}\).

Noting that the positions of black boxes in the left and right within the CARRY module consists of all the same quantum gates but rearranged in a reverse order. In the following, we also adapt similar abbreviation notations to denote the quantum modules that include same quantum gates but rearrange in a reverse order.

Due to the reversibility of quantum gates, if we reverse the action of the plain adder network with the initial two inputs \(\left| A \right\rangle\) and \(\left| B \right\rangle\), the output will produce \(\left( {\left| A \right\rangle ,\left| {A - B} \right\rangle } \right)\) when A > B. When A < B, the output is \(\left( {\left| A \right\rangle ,\left| {2^{n} - \left( {B - A} \right)} \right\rangle } \right)\), where (n + 1) is the size of the second register \(\left| B \right\rangle\) with the most significant qubit (bn) will always contain 1 (Vedral et al. 1996). Therefore, the quantum circuit realization of \(\left( {A - B} \right)\;\bmod 2^{n}\) is similar to the ADDER-MOD, which is realized by sequencing all of the quantum gates within ADDER in a reverse order directly and with the most significant bit bn = 1 of the second register \(\left| B \right\rangle\). The proof verifies this can be seen in Appendix 1. Figure 8 gives the simplified diagram of quantum circuit module of \(\left( {A - B} \right)\;\bmod 2^{n}\).

Fig. 8
figure 8

Simplified diagram of quantum circuit module \(\left( {A - B} \right)\;\bmod 2^{n}\) equation

Full size image

2.5.2 Perfect shuffle permutation

The perfect shuffle permutation can be used to cyclic shift qubit sequence (Li et al. 2019a, b, c). For n-qubit sequence, it has two different forms of \(P_{{2^{n - 1} ,2}}\) and \(P_{{2,\;2^{n - 1} }}\) recursively defined as:

$$\begin{gathered} P_{{2^{n - 1} ,\;2}} = \left( {P_{{2^{n - 2} ,\;2}} \otimes I_{2} } \right)\left( {I_{{2^{n - 2} }} \otimes P_{2,\;2} } \right), \hfill \\ P_{{2,\;2^{n - 1} }} = \left( {P_{2,2} \otimes I_{{2^{n - 2} }} } \right)\left( {I_{2} \otimes P_{{2,\;2^{n - 2} }} } \right), \hfill \\ \end{gathered}$$
(16)

where \(P_{2,\;2}\) is the Swap gate as shown in Fig. 2.

Thus \(P_{{2^{n - 1} ,2}}\) and \(P_{{2,\;2^{n - 1} }}\) respectively transform the n-qubit \(\left| X \right\rangle = \left| {x_{n - 1} x_{n - 2} \cdot \cdot \cdot x_{1} x_{0} } \right\rangle\) into following forms:

$$\begin{gathered} P_{{2^{n - 1} ,2}} \left| X \right\rangle = \left| {x_{0} x_{n - 1} x_{n - 2} \cdot \cdot \cdot x_{1} } \right\rangle , \hfill \\ P_{{2,\;2^{n - 1} }} \left| X \right\rangle = \left| {x_{n - 2} \cdot \cdot \cdot x_{1} x_{0} x_{n - 1} } \right\rangle . \hfill \\ \end{gathered}$$
(17)

Figure 9 illustrates the quantum circuits for \(P_{{2^{n - 1} ,2}}\) and \(P_{{2,\;2^{n - 1} }}\), and their corresponding abbreviation notations are shown on the right.

Fig. 9
figure 9

Quantum circuits for \(P_{{2^{n - 1} ,2}}\) and \(P_{{2,\;2^{n - 1} }}\)

Full size image

2.5.3 Quantum equal

Quantum Equal module introduced in (Zhou et al. 2107) is used to compare two bit sequences whether they are equal or not. The quantum circuit for Quantum Equal and its simplified module are illustrated in Fig. 10, where \(\left| Y \right\rangle = \left| {y_{n - 1} \cdot \cdot \cdot y_{1} y_{0} } \right\rangle\), \(\left| X \right\rangle = \left| {x_{n - 1} \cdot \cdot \cdot x_{1} x_{0} } \right\rangle\), \(x_{i} ,y_{i} \in \{ 0,\;1\}\). The output C represents the relationship between Y and X, i.e., if C = 1, then Y = X; otherwise, \(Y \ne X\) when C = 0.

Fig. 10
figure 10

Circuit design for Quantum Equal

Full size image

3 Quantum image encryption and decryption

On the basis of generalized Arnold transform and Logistic map, our investigated quantum image encryption and decryption algorithms as well as the intact quantum implementation circuits are described in detail within this section.

3.1 Encryption and decryption processes

Figure 11 gives the whole procedure of our investigated quantum image encryption and decryption schemes. As shown in Fig. 11a, the encryption process mainly divides into two stages, i.e., twice scrambling and pixel encryption. Due to the decryption is exact the inverse operation of encryption, which also contains two stages, i.e., pixel decryption and inverse twice scrambling (as shown in Fig. 11b).

Fig. 11
figure 11

Quantum image encryption and decryption processes: (a) encryption, (b) decryption

Full size image

As illustrated in Fig. 11a, to encrypt a quantum plain image \(\left| I \right\rangle\) or \(\left| G \right\rangle\) (respectively expressed as Eqs. (5) and (7)), a secret quantum image \(\left| K \right\rangle\) with size of \(2^{n} \times 2^{n}\) is needed to be prepared first. Herein, K is a classical grayscale image generated based on Logistic map first, and then encoded into a quantum image \(\left| K \right\rangle\) based on NEQR model (Zhang et al. 2013a, b), which can be expressed as:

$$\begin{gathered} \left| K \right\rangle = \frac{1}{{2^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {K_{YX} } \right\rangle } } \left| Y \right\rangle \left| X \right\rangle \hfill \\ \;\;\;\;\; = \frac{1}{{2^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{7} \left| {K_{YX}^{T} } \right\rangle } } \left| Y \right\rangle \left| X \right\rangle , \hfill \\ \end{gathered}$$
(18)

where \(K_{YX} = K_{YX}^{0} K_{YX}^{1} \cdots K_{YX}^{6} K_{YX}^{7} = \sum\limits_{i = 0}^{7} {K_{YX}^{i} \times 2^{7 - i} } ,\;K_{YX}^{i} \in \left\{ {0,1} \right\}\;\) are generated by Logistic map under the initial values \(x_{0} ,\;\mu\) with iteration times \(t = 2^{2n}\). The relationship of \(K_{YX}\), \(x_{t}\), Y, X, t can be described:

$$\begin{gathered} K_{YX} = floor\left[ {\bmod \left( {\left( {x_{t} \times 256} \right),256} \right)} \right],\;t \in \left\{ {1,\;2,\; \cdots ,\;2^{2n} } \right\}, \hfill \\ Y = y_{n - 1} y_{n - 2} \cdot \cdot \cdot y_{1} y_{0} ,\;X = x_{n - 1} x_{n - 2} \cdot \cdot \cdot x_{1} x_{0} ,\;y_{i} ,\;x_{i} \in \{ 0,\;1\} , \hfill \\ t = Y \times 2^{n} + X + 1, \hfill \\ \end{gathered}$$
(19)

where floor and mod respectively stand for round down and modulus operations.

3.2 Quantum image encryption

The quantum image encryption is composed of two stages as illustrated in Fig. 11a. It can be described in detail as follows:

Stage 1 twice scrambling.

Suppose the final encrypted image \(\left| A \right\rangle\) in first stage can be written as:

$$\left| A \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {A_{YX} } \right\rangle \left| {YX} \right\rangle } } = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{q - 1} } } \left| {A_{YX}^{T} } \right\rangle \left| Y \right\rangle \left| X \right\rangle .$$
(20)

According to Eq. (10), the coordinate of encrypted image \(\left| A \right\rangle\) is defined as:

$$\begin{gathered} \left| {X_{A} } \right\rangle = \left| {\left( {X_{I} + t \cdot Y_{I} } \right)\bmod 2^{n} } \right\rangle , \hfill \\ \left| {Y_{A} } \right\rangle = \left| {\left[ {m \cdot X_{I} + \left( {t \cdot m + 1} \right)Y_{I} } \right]\bmod 2^{n} } \right\rangle , \hfill \\ \end{gathered}$$
(21)

where \(\left| {Y_{I} } \right\rangle\) and \(\left| {X_{I} } \right\rangle\) are the coordinates information of quantum image \(\left| I \right\rangle\), \(\left| {Y_{A} } \right\rangle\) and \(\left| {X_{A} } \right\rangle\) denote the coordinates information of quantum image \(\left| A \right\rangle\).

Due to the nature of modulo operation, we have:

$$\left( {X + 2 \cdot Y} \right)\bmod 2^{n} = \left[ {\left( {X + Y} \right)\bmod 2^{n} + Y} \right]\bmod 2^{n} .$$
(22)

Thus \(\left| Y \right\rangle_{A}\) and \(\left| X \right\rangle_{A}\) can be calculated in following forms:

$$\begin{gathered} \left( {Y_{I} ,X_{I} } \right) \to \left( {Y_{I} ,\left( {X_{I} + Y_{I} } \right)\bmod 2^{n} } \right) \to \left( {Y_{I} ,\left( {X_{I} + 2 \cdot Y_{I} } \right)\bmod 2^{n} } \right) \to \hfill \\ \cdots \to \left( {Y_{I} ,\left( {X_{I} + \left( {t - 1} \right) \cdot Y_{I} } \right)\bmod 2^{n} } \right) \to \left( {Y_{I} ,\underbrace {{\left( {X_{I} + t \cdot Y_{I} } \right)\bmod 2^{n} }}_{{X_{A} }}} \right). \hfill \\ \end{gathered}$$
(23)
$$\begin{gathered} \left( {X_{I} ,X_{I} } \right) \to \left( {X_{I} ,2 \cdot X_{I} \bmod 2^{n} } \right) \to \cdots \to \left( {X_{I} ,m \cdot X_{I} \bmod 2^{n} } \right) \hfill \\ \left( {Y_{I} ,m \cdot X_{I} \bmod 2^{n} } \right) \to \left( {Y_{I} ,\left( {m \cdot X_{I} + Y_{I} } \right)\bmod 2^{n} } \right) \hfill \\ \to \left( {Y_{I} ,\left( {m \cdot X_{I} + 2 \cdot Y_{I} } \right)\bmod 2^{n} } \right) \to \cdots \to \left( {Y_{I} ,\left( {m \cdot X_{I} + t \cdot Y_{I} } \right)\bmod 2^{n} } \right) \hfill \\ \to \left( {Y_{I} ,\underbrace {{\left( {m \cdot X_{I} + \left( {t + 1} \right) \cdot Y_{I} } \right)\bmod 2^{n} }}_{{Y_{A} }}} \right). \hfill \\ \end{gathered}$$
(24)

Based on quantum ADDER MOD 2n shown in Fig. 7(b), Fig. 12 illustrates the integrated quantum circuit implementation for calculating the coordinate information of the encrypted image \(\left| A \right\rangle\), in which the detailed quantum circuit for Box 1 is shown in Fig. 13.

Fig. 12
figure 12

Quantum circuits for encrypting the coordinate information

Full size image
Fig. 13
figure 13

Quantum circuit for box 1

Full size image

Based on generalized Arnold transform, the pixel’s color information of quantum encrypted image \(\left| A \right\rangle\) is defined as:

$$\begin{gathered} \left| {A1_{YX} } \right\rangle = \left| {\left( {I1_{YX} + t \cdot I2_{YX} } \right)\bmod 2^{n} } \right\rangle , \hfill \\ \left| {A2_{YX} } \right\rangle = \left| {\left[ {m \cdot I1_{YX} + \left( {t \cdot m + 1} \right)I2_{YX} } \right]\bmod 2^{n} } \right\rangle , \hfill \\ I1_{YX} = I_{YX}^{0} I_{YX}^{1} I_{YX}^{2} I_{YX}^{3} ,\;I2_{YX} = I_{YX}^{4} I_{YX}^{5} I_{YX}^{6} I_{YX}^{7} , \hfill \\ A1_{YX} = A_{YX}^{0} A_{YX}^{1} A_{YX}^{2} A_{YX}^{3} ,\;A2_{YX} = A_{YX}^{4} A_{YX}^{5} A_{YX}^{6} A_{YX}^{7} , \hfill \\ \end{gathered}$$
(25)

where \(I_{YX} = \left( {I1_{YX} ,I2_{YX} } \right)\) is the pixel color information of plain image \(\left| I \right\rangle\).\(A_{YX} = \left( {A1_{YX} ,A2_{YX} } \right)\) is the pixel color information of encrypted image \(\left| A \right\rangle\). Figure 14 illustrates the intact quantum circuit implementation for encrypting pixel color information based on generalized Arnold transform.

Fig. 14
figure 14

Quantum circuits for encrypting the pixel color information

Full size image

Stage 2 pixel encryption.

Herein, suppose that the final encrypted image \(\left| E \right\rangle\) in stage 2 is written as:

$$\left| E \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {E_{YX} } \right\rangle \left| {YX} \right\rangle } } = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{q - 1} } } \left| {E_{YX}^{T} } \right\rangle \left| Y \right\rangle \left| X \right\rangle .$$
(26)

The aim of current stage is to encrypt the pixel’s color information of image \(\left| A \right\rangle\) in first stage. The integrated quantum circuit for pixel information encryption is demonstrated in Fig. 15, which can be described as follows.

Fig. 15
figure 15

Quantum circuit for pixel encryption

Full size image

First, quantum Equal module is employed to compare the coordinate information of the two quantum images \(\left| K \right\rangle\) and \(\left| A \right\rangle\). The comparison results are denoted by the single output qubit \(\left| C \right\rangle\) defined as:

$$\left\{ \begin{gathered} \left| {YX} \right\rangle_{K} = \left| {YX} \right\rangle_{A} ,\;\;\;\left| C \right\rangle = \left| 1 \right\rangle , \hfill \\ \left| {YX} \right\rangle_{K} \ne \left| {YX} \right\rangle_{A} ,\;\;\;\left| C \right\rangle = \left| 0 \right\rangle , \hfill \\ \end{gathered} \right.$$
(27)

where \(\left| {YX} \right\rangle_{K}\) and \(\left| {YX} \right\rangle_{A}\) respectively denote the pixel’s location information of quantum images \(\left| K \right\rangle\) and \(\left| A \right\rangle\).

Second, quantum Pixel Encryption module is used to encrypt the pixel’s color information of image \(\left| A \right\rangle\) when the coordinate information of two images \(\left| K \right\rangle\) and \(\left| A \right\rangle\) are equal. That is, the output qubit \(\left| C \right\rangle\) in state of \(\left| 1 \right\rangle\) is utilized to act as a controlled qubit for Pixel Encryption module. The intact quantum circuit implementation for Pixel Encryption module is illustrated in Fig. 16, which consists of three steps described as follows.

Fig. 16
figure 16

Quantum circuit for Pixel Encryption module

Full size image

Step 1 encrypt the pixel’s color information of image \(\left| A \right\rangle\) through CNOT gates, where the qubit \(\left| {K_{YX}^{i} } \right\rangle\) is the control qubit while qubit \(\left| {A_{YX}^{i} } \right\rangle\) is the target qubit, \(i = 0,1,\; \cdots ,7\). Assume that the encrypted image is \(\left| {AX} \right\rangle\), then it can be defined as:

$$\begin{gathered} \left| {AX} \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\left| {A_{YX} \oplus K_{YX} } \right\rangle \left| {YX} \right\rangle } } \hfill \\ \;\;\;\;\;\;\; = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{q - 1} } } \left| {A_{YX}^{T} \oplus K_{YX}^{T} } \right\rangle \left| Y \right\rangle \left| X \right\rangle \hfill \\ \;\;\;\;\;\;\; = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{q - 1} } } \left| {AX_{YX}^{T} } \right\rangle \left| Y \right\rangle \left| X \right\rangle . \hfill \\ \end{gathered}$$
(28)

Step 2 current step consists of two substeps described as follows:

Substep 2.1 perform the bit-plane scrambling operation on image \(\left| {AX} \right\rangle\), then the obtained encrypted image \(\left| {AB} \right\rangle\) can be defined as:

$$\begin{gathered} \left| {AB} \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 7}^{4} } } \left| {AX_{YX}^{T} } \right\rangle \left| {AX_{YX}^{7} \oplus AX_{YX}^{3} } \right\rangle \left| {\overline{{AX_{YX}^{6} }} \oplus AX_{YX}^{2} } \right\rangle \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \otimes \left| {AX_{YX}^{5} \oplus AX_{YX}^{1} } \right\rangle \left| {\overline{{AX_{YX}^{4} }} \oplus AX_{YX}^{0} } \right\rangle \left| Y \right\rangle \left| X \right\rangle \hfill \\ = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 7}^{4} \left| {K_{YX}^{T} \oplus A_{YX}^{T} } \right\rangle \otimes } } \left| {K_{YX}^{7} \oplus A_{YX}^{7} \oplus K_{YX}^{3} \oplus A_{YX}^{3} } \right\rangle \hfill \\ \;\;\;\;\;\;\;\;\; \otimes \left| {\overline{{K_{YX}^{6} \oplus A_{YX}^{6} }} \oplus K_{YX}^{2} \oplus A_{YX}^{2} } \right\rangle \otimes \left| {K_{YX}^{5} \oplus A_{YX}^{5} \oplus K_{YX}^{1} \oplus A_{YX}^{1} } \right\rangle \hfill \\ \;\;\;\;\;\;\;\;\; \otimes \left| {\overline{{K_{YX}^{4} \oplus A_{YX}^{4} }} \oplus K_{YX}^{0} \oplus A_{YX}^{0} } \right\rangle \left| Y \right\rangle \left| X \right\rangle \hfill \\ = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{q - 1} } } \left| {AB_{YX}^{T} } \right\rangle \left| Y \right\rangle \left| X \right\rangle . \hfill \\ \end{gathered}$$
(29)

Substep 2.2 implement the CNOT gates on image \(\left| K \right\rangle\). Then the obtained image \(\left| {KX} \right\rangle\) is defined as:

$$\begin{gathered} \left| {KX} \right\rangle = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{3} } } \left| {K_{YX}^{T} \oplus K_{YX}^{7 - T} } \right\rangle \left| {K_{YX}^{4} K_{YX}^{5} K_{YX}^{6} K_{YX}^{7} } \right\rangle \left| Y \right\rangle \left| X \right\rangle \hfill \\ \;\;\;\;\;\;\;\; = \frac{{1}}{{{2}^{n} }}\sum\limits_{Y = 0}^{{2^{n} - 1}} {\sum\limits_{X = 0}^{{2^{n} - 1}} {\mathop \otimes \limits_{T = 0}^{7} } } \left| {KX_{YX}^{T} } \right\rangle \left| Y \right\rangle \left| X \right\rangle . \hfill \\ \end{gathered}$$
(30)

Step 3 under the control of qubits \(K_{YX}^{0} ,\;K_{YX}^{1} ,\;K_{YX}^{2} ,\;K_{YX}^{3}\), implement the controlled perfect shuffle permutation \(P_{{2^{7} ,\;2}}\) or \(P_{{2^{3} ,\;2}}\) on image \(\left| {AB} \right\rangle\). Since it is hard to describe the encryption process of this step in formula form, we omit it from here for simplicity. Assume that the image \(\left| {AB} \right\rangle\) after perfect shuffle permutation operations is final encrypted image \(\left| E \right\rangle\) written as Eq. (26).

Figure 17 gives the complete quantum circuit implementation for the proposed quantum image encryption process. Herein, the simplified diagram of “Generalized Arnold” means the twice scrambling based on generalized Arnold transform in stage 1, and the simplified diagram of “Pixel Encryption Based on Key Image” means the pixel encryption process in stage 2. Figures 17a, b respectively denote the encryption for the quantum grayscale and color images.

Fig. 17
figure 17

Quantum circuit modules for quantum image encryption process: (a) quantum grayscale image; (b) quantum color image

Full size image

3.3 Quantum image decryption

Quantum image decryption is the inverse process of encryption as illustrated in Fig. 11b. Based on quantum key image \(\left| K \right\rangle\) and quantum encrypted image \(\left| E \right\rangle\), the decryption process that recovering the quantum plain image \(\left| I \right\rangle\) can be described within following two stages.

Stage 1 pixel decryption.

The quantum circuit module for pixel decryption operation in this stage is shown in Fig. 18. The process can be explained as follows.

Fig. 18
figure 18

Quantum circuit module for Pixel Decryption operation

Full size image

First, the Quantum Equal module is employed to compare whether the coordinate information of two images \(\left| K \right\rangle\) and \(\left| E \right\rangle\) are equal or not.

Second, the output qubit \(\left| C \right\rangle\) of Quantum Equal module is used to act as the control qubit for quantum Pixel Decryption module. Figure 19 illustrates the detailed quantum circuit implementation for Pixel Decryption module, which consists of following three steps.

Fig. 19
figure 19

Quantum circuit for Pixel Decryption module

Full size image

Step 1 current step consists of two substeps described as follows:

Substep 1.1 implement the CNOT operations within image \(\left| K \right\rangle\), and then obtain the image \(\left| {KX} \right\rangle\) described as Eq. (30).

Substep 1.2 under the control of qubits \(K_{YX}^{0} ,\;K_{YX}^{1} ,\;K_{YX}^{2} ,\;K_{YX}^{3}\), implement the controlled perfect shuffle permutation \(P_{{2^{7} ,\;2}}\) or \(P_{{2^{3} ,\;2}}\) on image \(\left| E \right\rangle\). Then, we can decrypt the quantum image \(\left| E \right\rangle\) into \(\left| {AB} \right\rangle\) written as Eq. (29).

Step 2 current step includes following two substeps described as:

Susbstep 2.1 implement the CNOT operations on quantum image \(\left| {KX} \right\rangle\), which can transform image \(\left| {KX} \right\rangle\) into image \(\left| K \right\rangle\).

Substep 2.2 implement the inverse bit-plane scrambling operation for quantum image \(\left| {AB} \right\rangle\). Then we can obtain image \(\left| {AX} \right\rangle\) written as Eq. (28).

Step 3 implement the CNOT operations between images \(\left| K \right\rangle\) and \(\left| {AX} \right\rangle\), then \(\left| {AX} \right\rangle\) is transformed into the \(\left| A \right\rangle\) written as Eq. (20).

Stage 2 inverse twice scrambling.

Based on Eq. (12), the coordinate information based on inverse generalized Arnold transform can be defined as:

$$\begin{gathered} \left| {X_{I} } \right\rangle = \left| {\left[ {\left( {t \cdot m + 1} \right) \cdot X_{A} - t \cdot Y_{A} } \right]\bmod 2^{n} } \right\rangle , \hfill \\ \left| {Y_{I} } \right\rangle = \left| {\left( {Y_{A} - m \cdot X_{A} } \right)\bmod 2^{n} } \right\rangle . \hfill \\ \end{gathered}$$
(31)

Similarly, due to the nature of mod operation, we can deduce the following relationship:

$$\begin{gathered} \;\;\;\left( {t \cdot X - m \cdot Y} \right)\bmod 2^{n} \hfill \\ = \left( {t \cdot X\bmod 2^{n} - m \cdot Y\bmod 2^{n} } \right)\bmod 2^{n} \hfill \\ = \left\{ \begin{gathered} \left[ {\left( {t - 1} \right) \cdot X\bmod 2^{n} + X} \right]\bmod 2^{n} \hfill \\ - \left[ {\left( {m - 1} \right) \cdot Y\bmod 2^{n} + Y} \right]\bmod 2^{n} \hfill \\ \end{gathered} \right\}\bmod 2^{n} . \hfill \\ \end{gathered}$$
(32)

Thus, based on the quantum module \({\text{ADDER } - \text{ MOD}}\;2^{n}\) (shown in Fig. 7(b)) and its inverse module \({\text{ADDER } - \text{ MOD}}\;2^{n}\) (shown in Fig. 8), the coordinate information \(\left| {Y_{I} } \right\rangle\) and \(\left| {X_{I} } \right\rangle\) can be calculated as follows:

$$\begin{gathered} \left\{ \begin{gathered} \left( {X_{A} ,X_{A} } \right) \to \left( {X_{A} ,2 \cdot X_{A} \bmod 2^{n} } \right) \to \cdots \to \left( {X_{A} ,tm \cdot X_{A} \bmod 2^{n} } \right) \hfill \\ \to \left[ {X_{A} ,\left( {tm + 1} \right) \cdot X_{A} \bmod 2^{n} } \right] \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} \left( {Y_{A} ,Y_{A} } \right) \to \left( {Y_{A} ,2 \cdot Y_{A} \bmod 2^{n} } \right) \to \hfill \\ \cdots \to \left( {Y_{A} ,t \cdot Y_{A} \bmod 2^{n} } \right) \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} \left[ {\left( {tm + 1} \right) \cdot X_{A} \bmod 2^{n} ,t \cdot Y_{A} \bmod 2^{n} } \right] \hfill \\ \to \left\{ {\left( {tm + 1} \right) \cdot X_{A} \bmod 2^{n} ,\underbrace {{\left[ {\left( {tm + 1} \right) \cdot X_{A} - t \cdot Y_{A} } \right]\bmod 2^{n} }}_{{X_{I} }}} \right\}. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(33)
$$\begin{gathered} \left( {X_{A} ,X_{A} } \right) \to \left( {X_{A} ,2 \cdot X_{A} \bmod 2^{n} } \right) \to \cdots \to \left( {X_{A} ,m \cdot X_{A} \bmod 2^{n} } \right) \hfill \\ \left( {Y_{A} ,m \cdot X_{A} \bmod 2^{n} } \right) \to \left[ {Y_{A} ,\underbrace {{\left( {Y_{A} - m \cdot X_{A} } \right)\bmod 2^{n} }}_{{Y_{I} }}} \right]. \hfill \\ \end{gathered}$$
(34)

On the basis of Eqs. (33) and (34), Fig. 20 illustrates the integrated quantum circuit for calculating the coordinate information of the plain image \(\left| I \right\rangle\).

Fig. 20
figure 20

Quantum implementation circuits of the inverse generalized Arnold transform for coordinate information

Full size image

Based on Eq. (14), the pixel’s color information of plain image \(\left| I \right\rangle\) can be defined as:

$$\begin{gathered} \left| {I1_{YX} } \right\rangle = \left| {\left[ {\left( {t \cdot m + 1} \right) \cdot A1_{YX} - t \cdot A2_{YX} } \right]\bmod 2^{n} } \right\rangle , \hfill \\ \left| {I2_{YX} } \right\rangle = \left| {\left( {A2_{YX} - m \cdot A1_{YX} } \right)\bmod 2^{n} } \right\rangle . \hfill \\ \end{gathered}$$
(35)

According to Eq. (35), Fig. 21 illustrates the intact quantum circuit implementation for recovering pixel’s color information of image \(\left| I \right\rangle\).

Fig. 21
figure 21

Quantum circuits of inverse generalized Arnold transform for the pixel information

Full size image

Based on above-mentioned two stages operation, Fig. 22 illustrates the whole quantum circuit implementation module for proposed quantum image decryption scheme. Wherein, Figs. 22a, b respectively denote the decryption for the quantum grayscale and color images. The simplified diagram of “Pixel Decryption Based on Key Image” means the decryption process within stage 1, and the simplified diagram of “Inverse Generalized Arnold” means the inverse twice scrambling operation within stage 2.

Fig. 22
figure 22

Quantum circuit module for quantum image decryption: (a) quantum grayscale image; (b) quantum color image

Full size image

4 Complexity analyses

To give a detailed analysis about the computational complexity, the quantum cost and time complexity of a quantum circuit defined in (Li et al. 2018a, b, c) are adopted, which are defined as:

(1) The quantum cost of a quantum circuit can be regarded as the total number of basic operations which simulate the circuit.

(2) The time complexity of a quantum circuit is defined by the total number of time steps. In a time step, only one basic operation is executed or multiple ones can be performed in parallel.

4.1 Quantum cost

The complex quantum circuit on many qubits n can be decomposed into a sequence of one-qubit and two-qubit quantum gates compositions (Michael and Isaac 2000; Barenco 1995). Herein, the quantum cost of one-qubit and two-qubit quantum gates are taken as unit. Furthermore, it pointed out that a quantum \(C^{n} (X)\) gate can be decomposed into 2(n-1) Toffoli gates and a CNOT gate with n-1 ancillary qubits (Michael and Isaac 2000), in which n (\(n \ge 3\)) is the number of control qubits and X is NOT gate (as illustrated in Fig. 23), and one Toffoli gate (i.e., \(C^{2} (X)\)) can be simulated by five two-qubit quantum gates illustrated in Fig. 24 (Michael and Isaac 2000). Thus the quantum cost of a \(C^{n} (X)\) gate is deduced as \(2(n - 1) \times 5 + 1 = 10n - 9\).

Fig. 23
figure 23

The decomposition of \(C^{n} (X)\) gate via Toffoli gates and CNOT gate

Full size image
Fig. 24
figure 24

The decomposition of Toffoli gate via five two-qubit quantum gates

Full size image

Since the investigated quantum image encryption process mainly consists of two stages, i.e., twice scrambling within stage 1 and pixel encryption within stage 2, the quantum cost of intact quantum circuit for image encryption can be discussed as follows:

Stage 1 twice scrambling.

The quantum cost in current stage is dependent on the number of quantum ADDER-MOD module used. The quantum circuit implementations are illustrated in Figs. 12 and 14. For the coordinate information encryption shown in Fig. 12, the number of \({\text{ADDER } - \text{ MOD}}\;2^{n}\) module is \(t \cdot m + t + m - 1\), and as well as 2n additional CNOT gates. For pixel’s gray value encryption shown in Fig. 14, the number of \({\text{ADDER } - \text{ MOD}}\;2^{4}\) module also is \(t \cdot m + t + m - 1\), and as well as additional 8 CNOT gates. The detailed quantum circuit for ADDER is shown in Fig. 6, which contains (2n-1) CARRY modules (a CARRY module consists of 2 Toffoli and 1 CNOT gates), n SUM modules (a SUM module consists of 2 CNOT gates), and an additional CNOT gate. Thus, the quantum cost of \({\text{ADDER } - \text{ MOD}}\;2^{n}\) is calculated as:

$$\left( {2n - 1} \right) \times \left( {2 \times 5 + 1} \right) + 2n + 1 = 24n - 10.$$
(36)

Thus, the quantum cost of twice scrambling in stage 1 can be deduced as:

$$\begin{gathered} \;\;\;k_{1} \times \left[ {\left( {24n - 10} \right) \times \left( {t \cdot m + t + m - 1} \right) + 2n} \right] \hfill \\ + k_{2} \times \left[ {\left( {24 \cdot 4 - 10} \right) \times \left( {t \cdot m + t + m - 1} \right) + 8} \right] \hfill \\ = {\rm O}\left( n \right), \hfill \\ \end{gathered}$$
(37)

where two positive integers \(k_{1}\) and \(k_{2}\) are constants denote the iteration times of generalized Arnold transforms implemented on pixel’s coordinate and color information, respectively.

Stage 2 pixel encryption.

The quantum circuit within current stage 2 mainly consists of two modules: Quantum Equal and Pixel Encryption. According to effective circuit of Quantum Equal shown in Fig. 10, we can infer that the Quantum Equal module within current stage contains 4n CNOT gates and an additional \(C^{2n} \left( X \right)\) gate. Thus, the quantum cost of Quantum Equal module is \(24n - 9\). For the Pixel Encryption module shown in Fig. 16, it contains 16 CNOT gates, 4 Swap gates, 2 controlled \(P_{{2^{7} ,\;2}}\) modules and 4 controlled \(P_{{2^{3} ,\;2}}\) modules. Noting that Swap gate can be decomposed into three CNOT gates (shown in Fig. 2), then the controlled Swap gate (with one control qubit) can be regarded as consisting of three Toffoli gates. Then the quantum cost of Pixel Encryption module is calculated as: \(16 + 4 + \left( {2 \times 7 + 4 \times 3} \right) \times 3 \times 5 = 410\). Thus, the quantum cost in stage 2 is calculated as:

$$24n - 9 + 410 = 24n + 401 = {\rm O}\left( n \right).$$
(38)

Based on above two stage analysis, the quantum cost of presented quantum image encryption process is calculated as \({\rm O}\left( n \right)\). Furthermore, due to the decryption is exactly the inverse process of encryption, we can infer that the quantum cost of image decryption process is also \({\rm O}\left( n \right)\).

4.2 Time complexity

Similar to quantum cost analysis, the time complexity of quantum image encryption process is divided into following two stages.

Stage 1 twice scrambling.

Noting that the CARRY and SUM modules within ADDER are executed in sequence (shown in Fig. 6), and the quantum gates (i.e., Toffoli and CNOT gates) within these modules are also executed in sequence (shown in Fig. 7a). Thus, the time complexity of single ADDER module is 24n-10. For the quantum circuit of Box 1 shown in Fig. 12, it can be designed in parallel within two steps. Because the generalized Arnold transform implemented on pixel’s coordinate and color information are independent (i.e., these two processes can be executed in parallel), the time complexity of twice scrambling in stage 1 can be deduced as:

$$max\left\{ \begin{gathered} k_{1} \times \left[ {\left( {24n - 10} \right) \times \left( {t \cdot m + t + m - 1} \right) + 2} \right], \hfill \\ k_{2} \times \left[ {\left( {24 \cdot 4 - 10} \right) \times \left( {t \cdot m + t + m - 1} \right) + 2} \right] \hfill \\ \end{gathered} \right\},$$
(39)

where max means taking the maximum.

Stage 2 pixel encryption.

For the Quantum Equal module shown in Fig. 15, the 4n CNOT gates can be executed in parallel with 2 steps, and the \(C^{2n} \left( X \right)\) gate can be decomposed into (2n-1) Toffoli gates and 1 CNOT gate executed in sequence. Thus, the time complexity of Quantum Equal module calculated as \(2 + \left( {2n - 1} \right) \times 5 + 1 = 10n - 2\). For the Pixel Encryption module, it is divided into three steps: (1) the CNOT operations of step 1 can be executed in parallel with one step; (2) the Swap operations and CNOT operations of step 2 can be executed in parallel with two steps; (3) the controlled perfect shuffle permutations in step 3 contains 26 controlled Swap gates, where a controlled Swap gate can be regarded as three Toffoli gates. Thus, the time complexity step 3 is \(26 \times 3 \times 5 = 390\). Therefore, the time complexity of stage 2 is calculated as:

$$10n - 2 + 1 + 2 + 390 = 10n + 391.$$
(40)

From above two stages analyses, it is easily to infer that the time complexity for our investigated quantum image encryption and decryption schemes are both \({\rm O}\left( n \right)\). Noting that in classical image processing algorithms, the pixels needs to be processed one-by-one, it requires a computational complexity of at least \({\rm O}\left( {2^{2n} } \right)\) for a \(2^{n} \times 2^{n}\) digital image. Thus the presented quantum image encryption and decryption schemes have achieved an exponential speedup than the classical algorithms.

4.3 Comparisons

Compared to classical image processing algorithm that process the pixel’s information pixel-by-pixel, our presented quantum image encryption algorithm obviously has a lower complexity. Therefore, we only compare our presented quantum scheme with others existing quantum schemes to evaluate the performance in terms of quantum cost. Table 1 gives the comparisons in terms of quantum cost with existing researches, from which we can conclude that our investigated quantum scheme has the same or lower quantum cost than existing works.

Table 1 Comparisons in terms of quantum cost
Full size table

5 Experimental results and numerical analysis

Due to the absence of a practical and functional quantum computer, our experimental results are simulated under the classical computers equipped with the MATLAB environment. I.e., in a classical version (no quantum version) with an ideal environment without considering the effects of quantum noise introduced when implements the quantum gate and quantum measurement operations. MATLAB is a good tool that facilitates the representation and manipulation of large arrays of vectors and matrices, which makes it simulate quantum states and operators effectively, such as the superposition states of quantum images and the quantum unitary operations.

To evaluate the performance of our presented quantum encryption scheme, two grayscale images (Lena and Cameraman) and two color images (Lena and Airplane) with size of \(256 \times 256\) are used as the tested images illustrated in Fig. 25.

Fig. 25
figure 25

Tested images used in our simulation

Full size image

5.1 Experimental results

For simplicity, Figs. 26 and 27 only demonstrate several cases of the encrypted images based on our investigated quantum encryption algorithm. Figure 26 illustrates the visual effects of the encrypted grayscale images Lena and Cameraman. Herein, the iteration times of generalized Arnold transform with initial values t = m = 2 implemented in pixel’s coordinate and color information are 4 times and 2 times, respectively. Figure 27 illustrates the visual effects of the encrypted color images Lena and Airplane under the same conditions as Fig. 26 does. Herein, the text below encrypted image with four initial values (from left to right) respectively represent iteration times of generally Arnold transform implemented on pixel’s coordinate and color information, and two initial values \(x_{0} ,\;\mu\) of Logistic map.

Fig. 26
figure 26

Visual effects of the encrypted grayscale images: (a) Encrypted Lena, (b) Encrypted Cameraman

Full size image
Fig. 27
figure 27

Visual effects of the encrypted color images: (a) Encrypted Lena, (b) Encrypted Airplane

Full size image

5.2 Statistical analysis

5.2.1 Mean square error

A perfect encrypted image should significantly differ with the original one. The mean square error (MSE) is an effective merit that characterizes the difference between encrypted images and original versions. For two grayscale images with size of \(2^{n} \times 2^{n}\), MSE is defined as:

$$MSE = \frac{1}{{2{}^{n} \times 2^{n} }}\sum\limits_{i = 0}^{{2^{n} - 1}} {\sum\limits_{j = 0}^{{2^{n} - 1}} {\left[ {I\left( {i,j} \right) - E\left( {i,j} \right)} \right]^{2} } } ,$$
(41)

where \(I\left( {i,j} \right)\) and \(E\left( {i,j} \right)\) are the pixel gray value of original and encrypted images in position (i,j), respectively. Similarly, for two color images, MSE is defined via three channels red, green and blue as:

$$\begin{gathered} MSE_{R} = \frac{1}{{2{}^{n} \times 2^{n} }}\sum\limits_{i = 0}^{{2^{n} - 1}} {\sum\limits_{j = 0}^{{2^{n} - 1}} {\left[ {I_{R} \left( {i,j} \right) - E_{R} \left( {i,j} \right)} \right]^{2} } } , \hfill \\ MSE_{G} = \frac{1}{{2{}^{n} \times 2^{n} }}\sum\limits_{i = 0}^{{2^{n} - 1}} {\sum\limits_{j = 0}^{{2^{n} - 1}} {\left[ {I_{G} \left( {i,j} \right) - E_{G} \left( {i,j} \right)} \right]^{2} } } , \hfill \\ MSE_{B} = \frac{1}{{2{}^{n} \times 2^{n} }}\sum\limits_{i = 0}^{{2^{n} - 1}} {\sum\limits_{j = 0}^{{2^{n} - 1}} {\left[ {I_{B} \left( {i,j} \right) - E_{B} \left( {i,j} \right)} \right]^{2} } } , \hfill \\ \end{gathered}$$
(42)

where \(I_{K} \left( {i,j} \right)\) and \(E_{K} \left( {i,j} \right)\) are pixel gray value of original and encrypted images in position (i,j), respectively. \(K = R,\;G,\;B\) respectively denote the red, green and blue channels of RGB color image.

Obviously, the larger the MSE value is, the better the encryption effects is. For the four plain images shown in Fig. 25, the MSE values of the encrypted images shown in Fig. 26 based on our presented scheme are calculated as shown in Table 2. The MSE values of color image in three channels Red, Green and Blue for the encrypted color images Lena and Airplane shown in Fig. 27 are demonstrated in Table 3. Apparently, the numerical values in Tables 2 and 3 with high MSE values indicate that the images encrypted by using our proposed scheme are quite differ with the original images. Thus, our investigated image encryption algorithm has good encryption effects. Furthermore, to test the chance of a successful attack when decrypts an encrypted image using two very close initial values of Logistic map, the MSE of two encrypted grayscale images Lena and Cameraman are shown in Table 4 as examples. Obviously, the MSE values of two encrypted grayscale images under very two close initial values of Logistic map are larger than 1.08e + 04. Thus we can infer that the similarity of these two encrypted images is very small.

Table 2 MSE values of the encrypted grayscale images with original version
Full size table
Table 3 MSE values of the encrypted color images with original version
Full size table
Table 4 MSE values of two encrypted grayscale images
Full size table

To compare the performance of our presented scheme with existing references, Table 5 illustrates the MSE values of encrypted color image Lena in Li and Zhao 2017, Ran et al. 2018 and our scheme. The MSEs of our proposed encrypted image is a little small than the MSEs of schemes in Li and Zhao 2017, Ran et al. 2018.

Table 5 Comparisons with other existing works
Full size table

5.2.2 Correlation between adjacent pixels

Correlation Coefficient (CC) reflects the degree of similarity between two variables. Suppose that x, y are the grayscale values of adjacent pixels set. Then, the correlation coefficient between x and y is defined as:

$$CC_{XY} = \frac{{{\text{cov}} (x,y)}}{{\sqrt {D(x)D(y)\;} }} = \frac{{\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left[ {\left( {x_{i} - E(x)} \right)\left( {y_{i} - E(y)} \right)} \right]} }}{{\sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - E(x)} \right)^{2} \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {y_{i} - E(y)} \right)^{2} } } } }}$$
(43)

where \(E(x) = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}\sum\nolimits_{i = 1}^{n} {x_{i} }\) and \(E(y) = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}\sum\nolimits_{i = 1}^{n} {y_{i} }\) are the mean of two variables x and y, respectively. cov(x,y) is called the covariance of two variables x and y, and D(x) and D(y) are the variance of two variables x and y, respectively.

An effective image encryption algorithm should produce the encrypted image with sufficiently low correlation in horizontal, vertical and diagonal directions. Generally, the CC of original image in three directions (i.e., vertical, horizontal and diagonal) is close to 1 because each two pixels within image are highly correlated to each other. On the contrary, the CC of an encrypted image should be close to 0. To calculate the CC of original image and corresponding encrypted image, 8000 pairs of two adjacent pixels from horizontal, vertical and diagonal directions, are randomly choose, respectively. Table 6 illustrates the CCs of original images Lena and Cameraman in three directions, which is all close to 1. Table 7 gives the CCs of encrypted grayscale images under different initial values in three directions which are all close to zero. Apparently, on the basis of specific values shown in Tables 6 and 7, it is easily to find that the correlation between the adjacent pixels in original image is very strong while in encrypted image are almost irrelevant. So that there is no information obtained about the original image by analysis the correlations of neighborhood pixels in encrypted image.

Table 6 Correlation coefficients of the original grayscale images
Full size table
Table 7 Correlation coefficients of the encrypted color images
Full size table

To present the intuitive visual effects, Figs. 28 and 29 show the comparison of correlation distributions of two adjacent pixels in three directions between the original grayscale images and encrypted versions. Herein, images are encrypted under four initial values [4, 2, 0.65, 3.85]. Obviously, it is also clear from Figs. 28 and 29 that the correlation between the adjacent pixels in the original image is very strong and adjacent pixels in the encrypted image are almost irrelevant.

Fig. 28
figure 28

Correlation distributions between two adjacent pixels in three directions: (a) image Lena and (b) encrypted image Lena

Full size image
Fig. 29
figure 29

Correlation distributions between two adjacent pixels in three directions: (a) image Cameraman and (b) encrypted image Cameraman

Full size image

5.2.3 Information entropy

Information Entropy (IE) is a statistical measure of uncertainty feature of the image. The computing formula of information entropy \(H\left( s \right)\) for message source is defined as:

$$H\left( s \right) = - \sum\limits_{i = 0}^{{2^{n} - 1}} {p\left( {s_{i} } \right)\log_{2} p\left( {s_{i} } \right)}$$
(44)

where \(p\left( {s_{i} } \right)\) represents the probability of the occurrence of symbol \(s_{i}\), and the ideal entropy value for an encrypted grayscale image should be 8 bits in ideal conditions. In another words, if the gray values of an image are distributed more even, and then the entropy value is closer to the ideal value 8 to resist the entropy attacks.

The information entropy of original grayscale images Lena, Cameraman and their corresponding encrypted versions is listed in Table 8. From the results of statistics, the loss in the processing of information encryption is completely weak. Thus, the proposed scheme is stable and secure against entropy attack.

Table 8 Information entropy of the original and encrypted images (bit)
Full size table

5.3 Security analysis

5.3.1 Histogram

Image histogram reflects the distribution of an image’s pixel gray value, which is an essential merit to assess the performance of any image encryption algorithm. A good secure encryption algorithm should guarantee that the histograms of encrypted images are completely different to histograms of original versions. Figure 30 illustrates the histogram of original plain images, i.e., grayscale images Lena and Cameraman in first row, and color images Lena and Airplane in three channels (Red, Green and Blue) in second row.

Fig. 30
figure 30

Histograms of tested images shown in Fig. 25

Full size image

Figures 31 and 32 respectively demonstrate the histograms of encrypted images based on our presented scheme. Obviously, the histogram of the encrypted grayscale images Lena and Cameraman (shown in Fig. 31) are totally a different distribution forms compared to the original versions as well as the histogram of encrypted color images Lena and Airplane (shown in Fig. 32). Furthermore, under different initial values of Logistic map for generating the secret key image, the histogram graphs are also very similar to each other. Therefore, we can conclude that there is no similarity in terms of histograms between the plain images and the encrypted versions.

Fig. 31
figure 31

Histograms of encrypted grayscale images under the specific keys

Full size image
Fig. 32
figure 32

Histograms of encrypted color images under specific keys

Full size image

5.3.2 Key analysis

Key space is the number of different keys can be used to encrypt the plain image. Key sensitivity is known as the sensitivity of the secret key to decrypt effect, which ensures that one cannot obtain any useful information from the decrypted image when a tiny change occurs to the keys. Large key space plus sensitive key are the essential property for good image encryption algorithm, which can stand up to the brute-force attack.

The proposed quantum scheme has four initial values: k1, k2,\(x_{0}\) and \(\mu\). Wherein, positive integer k1 and k2 respectively denote the iteration times of generally Arnold transform implemented on plain image pixel’s coordinate and color information. Keys \(x_{0}\) and \(\mu\) are real numbers that belong to the initial values of Logistic map under condition of \(0 < x_{0} < 1,\;\;3.56 < \mu \le 4\). Thus the total key space can be deduced as:

$$k_{1} \times k_{2} \times c_{1} \times c_{2} \to \propto$$
(45)

where positive integers \(c_{1}\) and \(c_{2}\) respectively represent the number of real numbers \(x_{0}\) and \(\mu\) can be chose in interval of \((0,\;1)\) and \((3.65,\;4]\).

To verify our presented quantum scheme has a sensitive key, an example is tested as illustrated in Fig. 33. Herein, the visual effects and corresponding histogram graphs for the encrypted grayscale image Lena under the initial value [4, 2, 0.65, 3.75] are decrypted with the correct key and three different wrong keys [4, 2, 0.65, 3.85], [4, 2, 0.70, 3.75], [4, 2, 0.70, 3.85] demonstrated in Fig. 32. Apparently, the decrypted image with wrong initial keys are total disordered or meaningless, and the corresponding histogram graphs are quite different from its original versions and similar to each other. Thus, it can infer that our presented quantum scheme has a very sensitive key and the plain image can only be decrypted via correct keys.

Fig. 33
figure 33

Visual effects of decrypted images under correct and wrong initial values: (a) is the encrypted grayscale image Lena; (b) is the decrypted image under the correct initial values; (c, d) and (f) are the decrypted Lena images with wrong initial values as text shown; (f, g) and (h) are the corresponding histogram graphs of decrypted Lena images (c, d) and (e), respectively

Full size image

6 Conclusions

Based on chaos theory of the generalized Arnold transform and Logistic map, a two-stage quantum image encryption algorithm is investigated in this paper. In stage 1, twice scrambling operation based on generalized Arnold transform is proposed. Following that, according to the quantum key image generated and prepared via Logistic map, the CNOT operations, bit-plane scrambling and controlled perfect shuffle permutations are executed in orderly to encrypt the pixel gray value of the scrambled image. Both quantum cost and time complexity of the quantum implementation circuits are \({\rm O}\left( n \right)\) for a \(2^{n} \times 2^{n}\) quantum grayscale or color images. Thus, we can infer that the investigated quantum encryption algorithm has an exponential speedup in contrast of classical counterparts with complexity no less than \({\rm O}\left( {2^{2n} } \right)\) for a \(2^{n} \times 2^{n}\) digital image. Experiments are simulated on the classical computers with MATLAB environment, in which statistical and security analyses indicate that the encrypted images possess good visual effects and high security.