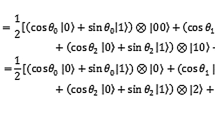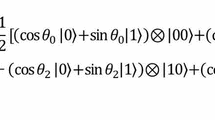NEQR: a novel enhanced quantum representation of digital images

Abstract

Quantum computation is becoming an important and effective tool to overcome the high real-time computational requirements of classical digital image processing. In this paper, based on analysis of existing quantum image representations, a novel enhanced quantum representation (NEQR) for digital images is proposed, which improves the latest flexible representation of quantum images (FRQI). The newly proposed quantum image representation uses the basis state of a qubit sequence to store the gray-scale value of each pixel in the image for the first time, instead of the probability amplitude of a qubit, as in FRQI. Because different basis states of qubit sequence are orthogonal, different gray scales in the NEQR quantum image can be distinguished. Performance comparisons with FRQI reveal that NEQR can achieve a quadratic speedup in quantum image preparation, increase the compression ratio of quantum images by approximately 1.5X, and retrieve digital images from quantum images accurately. Meanwhile, more quantum image operations related to gray-scale information in the image can be performed conveniently based on NEQR, for example partial color operations and statistical color operations. Therefore, the proposed NEQR quantum image model is more flexible and better suited for quantum image representation than other models in the literature.

1 Introduction

As a novel computing model, quantum computation can store, process and transport information using the peculiar properties of quantum mechanics [1] such as the superposition and the entangled state. Starting with Feynman who first proposed this concept in 1982 [2], quantum computation has become a hot topic. More recent years have witnessed a series of significant theoretical improvements and some encouraging experimental results in this field. In particular, in 1994, Shor designed a quantum integer factoring algorithm [3] to find secret key encryption of the RSA algorithm (Rivest, Shamiv, and Adleman) in polynomial time. In 1996, Grover explored a quantum search algorithm [4] for databases which could achieve quadratic speedup. After these two most representative quantum algorithms, the excellent properties of quantum computation have motivated more researchers to explore the quantum world. Quantum computation is considered to be a promising candidate to overcome the limitations of classical computing.

Digital image processing [5] is an important branch of information science and is the core procedure in many applications, including satellite sensing, weapon navigation, medical care and Web retrieval, to name a few. With recent dramatic developments in image sensors, the number of images has become huge and the image size large, which results in the often overwhelming time requirements of classical image-processing algorithms. Therefore, it is necessary to find high-performance ways to store and process digital images for these current applications.

To cope with this problem in classical image processing, the combination of quantum computation with digital image processing has been extensively investigated in recent decades. Various quantum image-representation models have been proposed to utilize quantum mechanics to store and process image information, such as Qubit Lattice [6], Entangled Image [7], Real Ket [8], and flexible representation of quantum images (FRQI) [9]. Some simple image-processing algorithms [10, 11] have been developed based on these. FRQI is the latest representation among the existing models. FRQI uses a normalized superposition to store all the pixels in an image, the same operations can be performed simultaneously on all pixels, and therefore FRQI can resolve the real-time computation problem of image-processing applications. However, because FRQI uses only a single qubit to store the gray-scale information for each pixel in an image, some digital image-processing operations, for example certain complex color operations, cannot be done on the basis of FRQI. This is the main reason why there have been few studies on complex FRQI-based image-processing algorithms.

In this paper, NEQR, a novel enhanced quantum representation for digital images, is proposed to improve the FRQI model. The new model uses the basis state of a qubit sequence to store the gray-scale value of every pixel for the first time. Therefore, to store the digital image using quantum mechanics, two entangled qubit sequences are used in NEQR to store the whole image, which represent the gray-scale and positional information of all the pixels. Through analyses and comparisons with FRQI, the following advantages of NEQR have been demonstrated:

• 1. The time complexity of preparing the NEQR quantum image exhibits an approximately quadratic decrease compared to FRQI.

• 2. For image compression based on minimization of Boolean expressions, the compression ratio of NEQR can be increased to 1.5X that of FRQI.

• 3. Through quantum measurements, the original classical image can be retrieved accurately from the NEQR quantum image, not probabilistically as with FRQI.

• 4. More image operations can be performed conveniently based on NEQR than on FRQI, especially some complex color operations such as partial color operations and statistical color operations which are described in Sect. 4.2.

Because of these advantages, the newly proposed model for quantum image processing is more flexible and better suited to be the fundamental model for quantum image processing than all other existing quantum image representations.

The rest of this paper is organized as follows: Sect. 2 discusses the related work. Section  3 describes the newly proposed NEQR image-representation model, gives the procedures of quantum image preparation and discusses image compression. Accurately image retrieving and image operations based on NEQR are presented in Sect. 4 in detail. Finally, we draw conclusions and outline possible future research tracks in Sect. 5.

2 Related work

Recently, the merging of quantum computation and digital image processing has proven to be a very fruitful approach to deal with the performance challenges of current image-processing applications.

To date, four quantum image-representation models have been proposed to store and process images, including Qubit Lattice, Entangled Image, Real Ket, and flexible representation of quantum images (FRQI). In the Qubit Lattice model [6], every pixel is stored in a single qubit, and all pixel operations are changed into their quantum counterpart operations on single qubit. Every quantum image is represented as a qubit matrix. Entangled Image [7] is similar to Qubit Lattice but uses the entangled state of quantum mechanics to represent relationships between image pixels. The Real Ket model [8] performs image quartering iteratively and builds a balanced quadtree index. Every pixel is mapped into a basis state of a four-dimensional qubit sequence. FRQI was proposed by Le [9]. This quantum image-representation model can be expressed as in (1) for a ${2^n}\times {2^n}$ image. In FRQI, the position information of every pixel is stored in a basis state of a two-dimensional qubit sequence, and the gray-scale information is stored as the probability amplitude of a single qubit which is entangled with the qubit sequence. Figure 1 shows a $4 \times 4$ FRQI quantum image.

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left( {\cos {\theta _{YX}}\left| 0 \right\rangle + \sin {\theta _{YX}}\left| 1 \right\rangle } \right) \left| {YX} \right\rangle } } \end{aligned}$$

(1)

Qubit Lattice and Entangled Image are similar to classical digital image processing, and therefore it is easy to find the quantum equivalents for classical image-processing operations, yet without much performance improvement. The Real Ket and FRQI models use the superposition of a qubit sequence to store images, and therefore they can process information for all pixels simultaneously. Compared with Real Ket, FRQI maintains a 2D pixel matrix, and therefore it is the most suitable and flexible model for designing quantum image-processing algorithms among all the existing quantum image representations.

Fig. 1

A $4\times 4$ FRQI quantum image. ${\theta _{YX}}$ is the phase of the color qubit which denotes the gray-scale value of pixel $(Y,X)$

Many studies on quantum image processing have been carried out based on FRQI [12, 13] discussed simple geometric and color operations based on FRQI and proved the great performance improvement of these quantum operations compared with classical image operations [14] expanded FRQI using three color qubits to store the full-color information of an RGB$\alpha$ image [15, 16] designed quantum watermarking algorithms based on FRQI, obtaining good performance. In general, all previous studies based on FRQI have focused on certain simple operations and algorithms in digital image processing. The main reason for this is that the FRQI model has some drawbacks:

• 1. The time complexity of quantum image preparation for FRQI is too high. For a ${2^n}\times {2^n}$ image, the procedure costs $O({2^{4n}})$, which is quadratic in the image size.

• 2. To simplify preparation of an FRQI quantum image, the Boolean expression minimization method is used to perform image compression. However, it has been found that the FRQI compression ratio depends on the gray-scale distribution of the digital image; especially when the image is highly disordered, the FRQI compression ratio is very low, even approaching zero.

• 3. Because FRQI stores the gray-scale information of the image pixels as the probability amplitude of a single qubit, it is impossible to obtain accurate probability amplitude for this qubit through finite quantum measurements. In other words, accurate image retrieval is an impossible task for the FRQI model.

• 4. FRQI stores the digital image into the superposition of a qubit sequence according to the position information of different pixels. Therefore, all operations which are suitable for FRQI should perform the same operations for pixels at different positions. Other operations cannot be accommodated.

These disadvantages of FRQI have become limitations on the exploration of complex quantum image-processing algorithms. Hence, it is of significant importance to improve existing quantum image models and to find better ways to represent quantum images for the future development of quantum image processing.

3 Quantum image representation, preparation and compression

To overcome the drawbacks of the FRQI image model, a novel enhanced quantum representation (NEQR) for digital images is proposed in this paper. In this section, the new representation model will be described in detail as well as the procedure for preparing NEQR image from a classical image. And then image compression is discussed to simplify the preparation.

3.1 NEQR

Through analysis of the FRQI quantum image model as described in Sect. 2, it is known that the advantages of FRQI result from using the superposition of a qubit sequence to store the position information of all the pixels, so that all can be operated on simultaneously. However, the main reason for the drawbacks of this model is that FRQI uses only a single qubit to store the gray-scale information for each pixel. To improve FRQI, the newly proposed NEQR model uses two entangled qubit sequences to store the gray-scale and position information, and stores the whole image in the superposition of the two qubit sequences.

Suppose the gray range of image is ${2^q}$, binary sequence $C_{YX}^0C_{YX}^1 \ldots C_{YX}^{q-2}C_{YX}^{q-1}$ encodes the gray-scale value $f(Y,X)$ of the corresponding pixel $(Y,X)$ as in (2):

$$\begin{aligned} f(Y,X) = C_{YX}^0C_{YX}^1 \ldots C_{YX}^{q - 2}C_{YX}^{q - 1},C_{YX}^k \in [0,1],\quad f(Y,X) \in [0,{2^q} - 1] \end{aligned}$$

(2)

The representative expression of a quantum image for a ${2^n}\times {2^n}$ image can be written as in (3):

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {f(Y,X)} \right\rangle \left| {YX} \right\rangle } } = \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{YX}^i} \right\rangle \left| {YX} \right\rangle } } \end{aligned}$$

(3)

Figure 2 shows a $4\times 4$ NEQR image example. Compared with the example of FRQI in Fig. 1, the obvious difference is that NEQR utilizes the basis state of qubit sequence to represent the gray scale of pixels instead of probability amplitude of a single qubit in FRQI. Different gray scales can be distinguished in NEQR because different basis states of qubit sequence are orthogonal. All the drastic improvements of NEQR in the following discussion are depended on this peculiar change.

Fig. 2

A $4\times 4$ NEQR quantum image. $f(Y,X)$ denotes the gray-scale value of pixel $(Y,X)$, which is stored as the basis state $\left| {f(Y,X)} \right\rangle$ of a qubit sequence

Figure 3 illustrates a $2\times 2$ gray-scale image and its representative expression in NEQR. In this figure, because the gray scale ranges between 0 and 255, eight qubits are needed in NEQR to store the gray-scale information for the pixels. Therefore, NEQR needs $q + 2n$ qubits to represent a ${2^n} \times {2^n}$ image with gray range ${2^q}$.

Fig. 3

A $2 \times 2$ example image and its representative expression in NEQR

3.2 Quantum image preparation

To use quantum mechanics to process an image, the image information should first be stored in a quantum state. The preparation procedure for NEQR will now be described.

From the representation of NEQR, $q + 2n$ qubits are needed to construct the quantum image model for a ${2^n} \times {2^n}$ image with gray range ${2^q}$.

The first step is to prepare $q + 2n$ qubits and to set all of them to $\left| 0 \right\rangle$. The initial state can be expressed as in (4):

$$\begin{aligned} {\left| \varPsi \right\rangle _0} = {\left| 0 \right\rangle ^{ \otimes 2n + q}} \end{aligned}$$

(4)

Figure 4 depicts the workflow of preparing the new quantum image model from the classical image representation. In this figure, the preparation is divided into two steps.

Fig. 4

Workflow of preparing the quantum image model for NEQR. The initial state ${\left| \varPsi \right\rangle _0}$ is transformed into the NEQR model through two steps

Step 1: this step is similar to the first step in the preparation for FRQI [9]. The single-qubit gates, I and H (5), are used to transform the initial state ${\left| \varPsi \right\rangle _0}$ to the intermediate state ${\left| \varPsi \right\rangle _1}$, which is the superposition of all the pixels of an empty image.

$$\begin{aligned} I = \left[ {\begin{array}{l@{\quad }l} 1 &{} 0 \\ 0 &{} 1 \\ \end{array}} \right] ,\quad H = \frac{1}{{\sqrt{2} }}\left[ {\begin{array}{l@{\quad }l} 1 &{} 1 \\ 1 &{} { - 1} \\ \end{array}} \right] \end{aligned}$$

(5)

The whole quantum operation in Step 1 can be expressed as ${U_1}$ in (6):

$$\begin{aligned} {U_1} = {I^{ \otimes q}} \otimes {H^{ \otimes 2n}} \end{aligned}$$

(6)

(7) interprets the transformation from the initial state ${\left| \varPsi \right\rangle _0}$ to the intermediate state ${\left| \varPsi \right\rangle _1}$. After this step, the position information for all the pixels is stored in the NEQR quantum model.

$$\begin{aligned} {U_1}({\left| \varPsi \right\rangle _0})&= {(I\left| 0 \right\rangle )^{ \otimes q}} \otimes {(H\left| 0 \right\rangle )^{ \otimes 2n}}\nonumber \\&= \frac{1}{{{2^n}}}{\left| 0 \right\rangle ^{ \otimes q}} \otimes \sum \limits _{i = 0}^{{2^{2n}} - 1} {\left| i \right\rangle }\nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {YX} \right\rangle } }\nonumber \\&= {\left| \varPsi \right\rangle _1} \end{aligned}$$

(7)

Step 2: To prepare the quantum image, it remains to set the gray-scale value for every pixel. In the intermediate state ${\left| \varPsi \right\rangle _1}$, all the pixels have been stored into the superposition of a qubit sequence in the NEQR model. In effect, Step 2 must be divided into ${2^{2n}}$ sub-operations to store the gray-scale information for every pixel. For pixel $(Y,X)$, the quantum sub-operation ${U_{YX}}$ is shown as (8):

$$\begin{aligned} {U_{YX}} = \left( {I \otimes \sum \limits _{j = 0}^{{2^n} - 1} {\sum \limits _{i = 0,ji \ne YX}^{{2^n} - 1} {\left| {ji} \right\rangle \left\langle {ji} \right| } } } \right) + {\varOmega _{YX}} \otimes \left| {YX} \right\rangle \left\langle {YX} \right| \end{aligned}$$

(8)

where ${\varOmega _{YX}}$ is a quantum operation as shown in (9), which is the value-setting operation for pixel $(Y,X)$:

$$\begin{aligned} {\varOmega _{YX}} = \mathop {\otimes }\limits _{i = 0}^{q - 1} \varOmega _{YX}^i \end{aligned}$$

(9)

Because $q$ qubits represent the gray-scale value in NEQR, ${\varOmega _{YX}}$ is consisted of $q$ quantum oracles as shown in (10):

$$\begin{aligned} \varOmega _{YX}^i:\left| 0 \right\rangle \rightarrow \left| {0 \oplus C_{YX}^i} \right\rangle \end{aligned}$$

(10)

From (10), if $C_{YX}^i=1, \varOmega _{YX}^i$ is a $2n-CNOT$ gate. Otherwise, it is a quantum identity gate which will do nothing on the quantum state. Therefore, the quantum transformation of ${\varOmega _{YX}}$ to set gray scale for the pixel is shown in (11):

$$\begin{aligned} {\varOmega _{YX}}{\left| 0 \right\rangle ^{ \otimes q}} = \mathop \otimes \limits _{i = 0}^{q - 1} (\varOmega _{YX}^i\left| 0 \right\rangle ) = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {0 \oplus C_{YX}^i} \right\rangle = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{YX}^i} \right\rangle = \left| {f(Y,X)} \right\rangle \end{aligned}$$

(11)

After ${U_{YX}}$, the intermediate state ${\left| \varPsi \right\rangle _1}$ is transformed as in (12):

$$\begin{aligned} {U_{YX}}\left( {{{\left| \varPsi \right\rangle }_1}} \right)&= {U_{YX}}\left( {\frac{1}{{{2^n}}}\sum \limits _{j = 0}^{{2^n} - 1} {\sum \limits _{i = 0}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } } } \right) \nonumber \\&= \frac{1}{{{2^n}}}{U_{YX}}\left( {\sum \limits _{j = 0}^{{2^n} - 1} {\sum \limits _{i = 0,ji \ne YX}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } + {{\left| 0 \right\rangle }^{ \otimes q}}\left| {YX} \right\rangle } } \right) \nonumber \\&= \frac{1}{{{2^n}}}\left( {\sum \limits _{j = 0}^{{2^n} - 1} {\sum \limits _{i = 0,ji \ne YX}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } + {\varOmega _{YX}}{{\left| 0 \right\rangle }^{ \otimes q}}\left| {YX} \right\rangle } } \right) \nonumber \\&= \frac{1}{{{2^n}}}\left( {\sum \limits _{j = 0}^{{2^n} - 1} {\sum \limits _{i = 0,ji \ne YX}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } + \left| {f(Y,X)} \right\rangle \left| {YX} \right\rangle } } \right) \end{aligned}$$

(12)

From (12), it is obvious that every sub-operation ${U_{YX}}$ only sets the gray-scale value of its corresponding pixel. Therefore, the whole work ${U_2}$ of Step 2 consists of all the sub-operations shown in (13). Through the quantum operation ${U_2}$, the intermediate state ${\left| \varPsi \right\rangle _1}$ is transformed into the final state ${\left| \varPsi \right\rangle _2}$, which is simply the quantum image of NEQR.

$$\begin{aligned} {U_2}&= \prod \limits _{Y = 0}^{{2^n} - 1} {\prod \limits _{X = 0}^{{2^n} - 1} {{U_{YX}}} }\end{aligned}$$

(13)

$$\begin{aligned} {U_2}\left( {{{\left| \varPsi \right\rangle }_1}} \right)&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {{\varOmega _{YX}}{{\left| 0 \right\rangle }^{ \otimes q}}\left| {YX} \right\rangle } }\nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {f(Y,X)} \right\rangle \left| {YX} \right\rangle } = {{\left| \varPsi \right\rangle }_2}} \end{aligned}$$

(14)

After the two steps described above, the entire preparation is done. Next, the time complexity of quantum image preparation will be discussed.

To begin with, the quantum operation of Step 1 is ${U_1}$, and it is known that the time complexity of Step 1 is $O(q + 2n)$ from (6). However, the work of Step 2 is more complex than that of Step 1. Because the whole operation of Step 2 is divided into ${2^{2n}}$ sub-operations to store the gray-scale information for every pixel, this discussion will focus on the time complexity of a single sub-operation ${U_{YX}}$.

Theorem 1

The quantum operation ${U_{YX}}$, which sets the gray-scale value for its corresponding pixel, costs no more than $O(qn)$ with the assistance of enough ancillary qubits.

Proof

The main work of ${U_{YX}}$ is ${\varOmega _{YX}}$, the quantum circuit of which is shown in Fig. 5. This circuit performs $q$ certain operations $\varOmega _{YX}^i$ for every qubit of the color qubit sequence in the NEQR model according to the gray-scale value of the corresponding pixel. When $C_{YX}^i=1, \varOmega _{YX}^i$ uses a $2n-CNOT$ qubit gate to invert the ${i{\text{ th }}}$ qubit of the color qubit sequence. Therefore, for every operation $\varOmega _{YX}^i$, no more than $q$ (the gray-scale range is ${2^q}$) $2n-CNOT$ gates are needed.

Fig. 5

The black-box circuit of quantum operation ${\varOmega _{YX}}$, which transforms the quantum state as in (11)

In [17], it is known that every $k-CNOT$ gate can be decomposed into ($4k - 8$) $2-CNOT$ gates (which are called Toffoli gates [18], a simple and common quantum gate) when $k-2$ ancillary qubits are present. In other words, the time complexity of $k-CNOT$ gate is no more than $O(k)$. Figure 6 shows an example of decomposing a $4-CNOT$ gate with the assistance of two ancillary qubits. Therefore, the time complexity of the sub-operation ${U_{YX}}$ is no more than $O(qn)$ with the assistance of enough ancillary qubits. $\square$

Lemma 1

The time complexity of Step 2 is $O(qn{2^{2n}})$ if enough ancillary qubits are available for the preparation of NEQR.

Fig. 6

The decomposed quantum circuit of a $4-CNOT$ gate; ${q_0}$-${q_4}$ are the operating qubits, while ${a_1}$ and ${a_2}$ are the ancillary qubits

Proof

From Theorem 1, every sub-operation ${U_{YX}}$ in Step 2 will cost no more than $O(qn)$ with enough ancillary qubits. In the whole step, the gray-scale value of every pixel is set individually. Therefore, the time complexity of Step 2 is $O(qn{2^{2n}})$ if enough ancillary qubits are available. $\square$

Theorem 2

The whole preparation of NEQR costs no more than $O(qn{2^{2n}})$ for a ${2^n} \times {2^n}$ image with gray range ${2^q}$. This is equivalent to an approximately quadratic decrease compared to FRQI.

Proof

From Lemma 1 and the discussion of the complexity of Step 1, the time complexity of the whole preparation of NEQR is no more than $O(qn{2^{2n}})$. Compared with the preparation complexity $O({2^{4n}})$ for FRQI, the time complexity of constructing the quantum image for NEQR has experienced an approximately quadratic decrease. $\square$

Figure 7 shows the detailed quantum circuit for NEQR preparation for the example image shown in Fig. 3. It is obvious that the whole operation of Step 2 consists of only 14 $2-CNOT$ gates. Because when $C_{YX}^i=0, \varOmega _{YX}^i$ is a quantum identity gate which can be ignored in the quantum circuit, the actual operations needed for preparation are fewer than the theoretical complexity.

Fig. 7

Quantum circuit for NEQR preparation for the image in Fig. 3. 14 $2-CNOT$ gates are needed to construct the quantum image

3.3 Image compression

Although the time complexity of the quantum image preparation of NEQR in Sect. 3.2 has a significant decrease than that of FRQI, the cost has still an approximately linear relationship with the image size. It means when the image size is large, the whole preparation will still take unacceptable time consumption. Therefore, in this subsection, image compression is discussed. It is a classical procedure which uses the classical algorithm of minimization of Boolean expressions to simplify the quantum circuit of quantum image preparation of NEQR. The substance of image compression is to utilize a new unitary transformation with fewer quantum logic gates to replace the original one for the quantum image preparation.

The time consumption in quantum image preparation is mainly concentrated in Step 2. The time complexity of the whole procedure depends on the number of controlled-not gates utilized in Step 2. Therefore, we will focus on how to compress these controlled-not gates to simplify the preparation.

Firstly, an operation set $\varPhi$ consists of all the quantum operations in Step 2 of quantum image preparation expressed as (15).

$$\begin{aligned} \varPhi = \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0}^{{2^n} - 1} {\bigcup \limits _{i = 0}^{q - 1} {\phi _{YX}^i} } } ,\quad \phi _{YX}^i \in \left\{ {I,2n - CNOT} \right\} \end{aligned}$$

(15)

where $\phi _{YX}^i$ represents the quantum operation for the ${i{\text{ th }}}$ qubit in the color qubit sequence of pixel $(Y,X)$.

From (15), for every pixel, $q$ quantum operations will be performed for all the qubits in the color qubit sequence. The whole operation set $\varPhi$ can also be divided into $q$ groups of quantum operations as shown in (16). And each group includes all the quantum operations for the same qubit in the color qubit sequence.

$$\begin{aligned} \varPhi = \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0}^{{2^n} - 1} {\bigcup \limits _{i = 0}^{q - 1} {\phi _{YX}^i} } } = \bigcup \limits _{i = 0}^{q - 1} {\left( \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0}^{{2^n} - 1} {\phi _{YX}^i} }\right) } = \bigcup \limits _{i = 0}^{q - 1} {{\varPhi _i}} \end{aligned}$$

(16)

Then $q$ groups will be compressed individually. The style of the quantum operation $\phi _{YX}^i$ depends on the value of $C_{YX}^i$. If $C_{YX}^i=0, \phi _{YX}^i$ is a quantum identity gate $I$. Otherwise, $\phi _{YX}^i$ is a $2n-CNOT$ qubit gate which will invert the ${i{\text{ th }}}$ qubits in the color qubit sequence when the pixel position is $(Y,X)$. According to the different styles of quantum operations, the ${i{\text{ th }}}$ group ${\varPhi _i}$ can be divided into two parts as (17).

$$\begin{aligned} {\varPhi _i}&= \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0}^{{2^n} - 1} {\phi _{YX}^i} } \nonumber \\&= \left( \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0,C_{YX}^i = 0}^{{2^n} - 1} I }\right) \cup \left( \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0,C_{YX}^i = 1}^{{2^n} - 1} {{{(2n - CNOT)}_{YX}}} } \right) \end{aligned}$$

(17)

Because quantum identity operations will not affect the quantum state, the first part in the ${i{\text{ th }}}$ group of quantum operations can be ignored. In the second part of ${{{\varPhi }_i}}$, every quantum logic gate is a controlled-not gate which contains two parts of information: the control information and the target information. Then Espresso algorithm [19] is utilized to compress the control information of all the quantum controlled-not gates in the second part in order to get a minimum set of quantum logic gates to do the same task. From (18), it is clear that we will take the control information $\bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0,C_{YX}^i = 1}^{{2^n} - 1} {YX} }$ of the quantum controlled-not gates as the input of Espresso algorithm. The algorithm can provide the equivalent and compact control information sets $\bigcup \limits _{{K_i}} {{K_i}}$ to build the new unitary quantum controlled-not gates $\bigcup \limits _{{K_i}} {{K_i} - CNOT}$ for the new ${i{\text{ th }}}$ group ${{{\varPhi ^{\prime }}_i}}$.

$$\begin{aligned} \bigcup \limits _{Y = 0}^{{2^n} - 1} {\bigcup \limits _{X = 0,C_{YX}^i = 1}^{{2^n} - 1} {YX} } \mathop \rightarrow \limits ^{\mathrm{{Espresso}}} \bigcup \limits _{{K_i}} {{K_i}} \end{aligned}$$

(18)

At last, according to all the results of minimizations of Boolean expressions for all the groups, we can reconstruct the new and simple quantum circuit $\varPhi ^{\prime }$ for the quantum image preparation as in (19):

$$\begin{aligned} \varPhi ^{\prime } = \bigcup \limits _{i = 0}^{q - 1} {{{\varPhi ^{\prime }}_i}} = \bigcup \limits _{i = 0}^{q - 1} {\bigcup \limits _{{K_i}} {{K_i} - CNOT} } \end{aligned}$$

(19)

The detailed workflow of image compression on the NEQR model is shown in Fig. 8. Beside the steps of this procedure, an example is given to explain the detailed compression method. In the example, $q=8$ ($q$ qubits are utilized to represent the gray-scale value). The ${i{\text{ th }}}$ group ${\varPhi _i}$ is shown and divided into two parts: the red (left) and blue (right) parts which denote the subset of the quantum identity operations and the subset of the controlled-not gates respectively. There are 8 $4-CNOT$ gates in the blue part. Then we utilize Espresso algorithm to compress the quantum controlled-not gates in the blue part for ${\varPhi _i}$. When the input of Espresso algorithm is all the control information $\bigcup \limits _{Y = 00}^{11} {\bigcup \limits _{X = 10}^{11} {YX} }$ of these quantum logic gates, the output is ${X_0}$, which means that we can only utilize one controlled-not gate $CNO{T_{{X_0}}}$ to replace the 8 $4-CNOT$ gates as shown in (20). Hence the compression for the preparation of quantum image is achieved.

$$\begin{aligned} \bigcup \limits _{Y = 00}^{11} {\bigcup \limits _{X = 10}^{11} {YX} } = \left\{ {\begin{array}{c} {{{\bar{Y}}_0}{{\bar{Y}}_1}{X_0}{{\bar{X}}_1}} \\ {{{\bar{Y}}_0}{{\bar{Y}}_1}{X_0}{X_1}} \\ \vdots \\ {{Y_0}{Y_1}{X_0}{{\bar{X}}_1}} \\ {{Y_0}{Y_1}{X_0}{X_1}} \\ \end{array}} \right. \mathop {\rightarrow }\limits ^{Espresso} {X_0} \end{aligned}$$

(20)

Fig. 8

Detailed workflow of image compression for the NEQR model. In addition to the workflow chart, an example is given to explain the detailed compression steps

In Fig. 9, we use image compression to construct the new quantum image preparation for the quantum image in Fig. 3. Compared with the quantum circuit in Fig. 7, there are only 8 controlled-not gates utilized in the new circuit.

Fig. 9

New quantum circuit for NEQR preparation for the image in Fig. 3 through image compression. Only 8 controlled-not quantum gates are utilized

Image compression for NEQR is more effective than for FRQI. The FRQI quantum image can be compressed by minimization of Boolean expressions only when the adjacent pixels in a certain area have the same gray-scale value, because FRQI uses only a single qubit to store the gray-scale information for each pixel in an image. However, in the new NEQR model, the gray-scale information is stored in the basis state of a qubit sequence. Every qubit in the sequence is independent, and the preparation for each can be simplified by the method of minimization of Boolean expressions. Therefore, qualitatively speaking, compared with the compression ratio for FRQI, NEQR can use the method of minimization of Boolean expressions to obtain a better compression ratio for a quantum image.

A case will be given to show the comparison between the quantum image compressions of FRQI and NEQR. Figure 10a shows an $8\times 8$ image and the gray range is 256. It is obvious that the gray distribution of this image is very regular: the pixels in every column have the same gray scale. Figure 10b gives the detailed gray scales of all the pixels. If FRQI is used to store the image, the preparation includes 64 controlled-rotation operations for all the pixels before compression. Since the regular gray scale distribution, the amount of rotation operations for FRQI will decrease to 5 in (21).

$$\begin{aligned} \begin{array}{l} Column0:\left| {{X_0}{X_1}{X_2}} \right\rangle = \left| {000} \right\rangle ,{R_{102}} \\ Column2:\left| {{X_0}{X_1}{X_2}} \right\rangle = \left| {010} \right\rangle ,{R_{170}} \\ Column4:\left| {{X_0}{X_1}{X_2}} \right\rangle = \left| {100} \right\rangle ,{R_{204}} \\ Column6:\left| {{X_0}{X_1}{X_2}} \right\rangle = \left| {110} \right\rangle ,{R_{238}} \\ Column1,3,5,7:\left| {{X_2}} \right\rangle = \left| 1 \right\rangle ,{R_{255}} \\ \end{array} \end{aligned}$$

(21)

where ${R_x}$ denotes the rotation operation to set the gray-scale value $x$.

Fig. 10

a An example of an $8 \times 8$ gray image; b gray-scale values of all the pixels in the image; c the eight groups of quantum operation sets for the quantum image preparation of image (a)

Because the gray-scale range is 256, when NEQR is used to store the image, eight qubits are needed to represent the gray-scale information for the pixels in the image. Figure 10c demonstrates all the information of the eight groups of the quantum operations in quantum image preparation. It can be determined that 400 controlled not gates are needed to prepare the quantum image before compression. The method of minimization of Boolean expressions can be used to simplify the quantum operations for every color qubit. After compression, the numbers of controlled not gates required for preparation of the eight groups are 3, 3, 3, 1, 3, 3, 3 and 1 respectively. The reconstructed quantum operations for the first group ${\varPhi ^{\prime }_0}$ are shown as (22):

$$\begin{aligned} \begin{array}{l} Column2,6:\left| {{X_1}{X_2}} \right\rangle = \left| {10} \right\rangle ,2-CNOT \\ Column4:\left| {{X_0}{X_1}{X_2}} \right\rangle = \left| {100} \right\rangle ,3-CNOT \\ Column1,3,5,7:\left| {{X_2}} \right\rangle = \left| 1 \right\rangle ,CNOT \\ \end{array} \end{aligned}$$

(22)

According to (23), the compression ratio of NEQR is 95 %, while that of FRQI is approximately 92.19 %.

$$\begin{aligned} Compression\_Ratio = \left( 1 - \frac{{Ops\_After\_Compression}}{{Ops\_Before\_Compression}}\right) \times 100 \,\% \end{aligned}$$

(23)

The calculation of the compression ratio in (33) is approximate because it depends only on the number of operations before and after image compression. It has been found that the number of operations required for NEQR is $6-CNOT$ gates before compression for the image in Fig.10, while the operations after compression become simple gates including the $CNOT$ gate, the $2-CNOT$ gate, and the $3-CNOT$ gate. The time requirements of these operations are different. However, the simplification does not affect the qualitative result of the comparison between FRQI and NEQR.

To compare the different performance of image compression in NEQR and FRQI, six test images are shown in Fig.11. In these images, the gray-scale distributions of the first four images are to some extent regular, while the last two were obtained in a random manner.

Fig. 11

Six examples of $8 \times 8$ images. The detailed gray-scale values are shown. The gray-scale distributions of a–d are to some extent regular, while e and f were obtained in a random manner

Table 1 gives the different compression ratios for the six images using the two quantum image models. The average compression ratio achieved by NEQR for the six images was approximately 74.11 %, which represents a 1.5X improvement over the ratio achieved by FRQI (50 %). It was found that both models have good compression ratios when the gray-scale distribution of the images is regular, such as in images A and B. As the gray-scale information in the image becomes more irregular, the advantage of NEQR in compression ratio becomes more obvious. In particular, when the image is random, that is to say, almost all adjacent pixels have different gray-scale values, the method of minimization of Boolean expressions can do nothing for FRQI compression. However, NEQR can still attain compression ratio of 40–50 % for these random images. These results support the analytical conclusion that NEQR can use the method of minimization of Boolean expressions to achieve better compression for a quantum image than FRQI.

Table 1 Compression ratios of the two quantum image models for the six images

4 Quantum image processing based on NEQR

This section will discuss how to use the newly proposed NEQR quantum image representation to do quantum image processing, including image retrieval and certain color operations on the quantum image.

4.1 Image retrieving

An essential requirement for quantum representation of digital images is to retrieve the classical image efficiently because this is the only information that people can recognize.

Quantum measurement is a unique way to recover classical information from a quantum state. However, none of the existing quantum representations can retrieve the classical image accurately through finite quantum measurements. Because all of them store the gray-scale information as the probability amplitude of a single qubit, quantum measurements of a single qubit $\left| C \right\rangle$ as in (14) yield a result of 0 or 1 and leave the qubit in the corresponding state $\left| 0 \right\rangle$ or $\left| 1 \right\rangle$ with respective probabilities ${\left| \alpha \right| ^2}$ and ${\left| \beta \right| ^2}$. Finite quantum measurements are nowhere near enough to recover $\alpha$ and $\beta$, the accurate information for an unknown qubit, unless it is known that $\alpha = 0$ or $\beta \mathrm{{ = 0}}$.

$$\begin{aligned} \left| C \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle \end{aligned}$$

(24)

The inaccuracies of image retrieval in existing quantum image models are the main reason that all these models are currently unsuitable for storing or transporting image information. In NEQR, the gray-scale information of all the pixels is stored in the basis state of a qubit sequence for the first time, so that the information can be accurately recovered.

During image retrieval from the quantum image, every pixel should be recovered individually. The following operations have been devised to retrieve pixel from a ${2^n} \times {2^n}$ quantum image.

Firstly, the quantum measurement $\varGamma$ for the position qubit sequence as shown in (25) extracts the corresponding information of pixel $(Y,X)$ as $\left| {{P_{YX}}} \right\rangle$, as shown in (26).

$$\begin{aligned} \varGamma&= \sum \limits _{YX = 0}^{{2^{2n}} - 1} {{I^{ \otimes q}} \otimes \left| {YX} \right\rangle \left\langle {YX} \right| }\end{aligned}$$

(25)

$$\begin{aligned} \left| {{P_{YX}}} \right\rangle&= \left| {f(Y,X)} \right\rangle \left| {YX} \right\rangle \end{aligned}$$

(26)

It has been mentioned that the gray-scale information is stored in the first qubit sequence in $\left| {{P_{YX}}} \right\rangle$. Then projective measurements, as in (27), are used to recover the gray-scale values from the quantum state.

$$\begin{aligned} M&= \sum \limits _{m = 0}^{{2^q} - 1} {m\left| m \right\rangle \left\langle m \right| }\end{aligned}$$

(27)

$$\begin{aligned} \left\langle {f(Y,X)} \right| M\left| {f(Y,X)} \right\rangle&= \left\langle {f(Y,X)} \right| \left( \sum \limits _{m = 0}^{{2^q} - 1} {m\left| m \right\rangle \left\langle m \right| }\right) \left| {f(Y,X)} \right\rangle \nonumber \\&= \sum \limits _{m = 0}^{{2^q} - 1} {m\left\langle {f(Y,X)} \right| \left| m \right\rangle \left\langle m \right| \left| {f(Y,X)} \right\rangle } = f(Y,X) \end{aligned}$$

(28)

Through the operations described above, the accurate classical gray-scale value of pixel $(Y,X)$ can be recovered. In other words, after all the pixels have been recovered, the accurate classical image has been retrieved from the NEQR quantum image model. This is an impossible task in all existing quantum image representations.

4.2 Color operations of quantum image

In image processing, operations to process gray-scale information play an important role in many complex image algorithms. Especially when the image is complex or blurry, certain color operations can make the image features more obvious or the objects in the image clearer.

FRQI uses only a single qubit to store the gray-scale information for each pixel. This becomes a limitation on complex color operations in FRQI. In [9, 13], only some simple color operations can be performed using the FRQI model.

All image operations relating to gray-scale information in digital images can be classified into three categories:

• 1. Complete Color Operations (CC): These operations deal with all the pixels in the whole image or a certain area of the image without being controlled by the gray-scale information in these pixels.

• 2. Partial Color Operations (PC): Unlike CC, these operations are controlled by the gray-scale values of the pixels being processed. Each PC can deal only with pixels which have certain gray-scale values or fall into certain ranges.

• 3. Color Statistical Operation (CS): These operations perform certain statistical computations according to the gray-scale information in the whole image, such as drawing a gray-scale histogram or finding the pixels with maximum or minimum gray-scale values.

In FRQI, only CC operations can be performed by designing quantum circuits. Because only one qubit is used to represent the gray-scale information, it is difficult to separate pixels with different gray-scale values to perform different quantum operations in FRQI. However, in the new NEQR quantum image-representation model, because a qubit sequence is used instead of one qubit in FRQI to store the gray-scale information, each color qubit in this sequence can function as a controller of color operations, so that all three kinds of color operations can be performed conveniently in the NEQR model.

Then some examples of common image operations will be used to illustrate the three kinds of color operations in NEQR. Noted that these image color operations are not the complete quantum algorithm, but they are important modules for most complex image processing algorithms. The study on the quantum image color operations in this subsection is fundamental for the future quantum image processing algorithms based on NEQR.

4.2.1 Complete color operation

In this subsection, two examples of CC color operations based on the NEQR quantum image-representation model are discussed.

The first CC operation, ${U_C}$, is defined in (29):

$$\begin{aligned} U_C = {X^{ \otimes q}} \otimes {I^{ \otimes 2n}} \end{aligned}$$

(29)

where $X$ denotes the quantum not gate as (30) and $I$ represents the quantum identity gate as shown in (5).

$$\begin{aligned} X = \left[ {\begin{array}{l@{\quad }l} 0 &{} 1 \\ 1 &{} 0 \\ \end{array}} \right] = \left| 0 \right\rangle \left\langle 1 \right| + \left| 1 \right\rangle \left\langle 0 \right| \end{aligned}$$

(30)

For a quantum image $\left| I \right\rangle , {U_C}$ takes $q$ quantum not gates for every qubit of the color qubit sequence and $2n$ quantum identity gates for others. Therefore, this operation inverts all the qubits in the color qubit sequence in NEQR and change the gray-scale value of every pixel in the image to its opposite value. (31) produces the result of the operation of ${U_C}$ on the quantum image $\left| I \right\rangle$.

$$\begin{aligned} {U_C}(\left| I \right\rangle )&= {U_C}\left( \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {f(Y,X)} \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \right) \nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} \sum \limits _{X = 0}^{{2^n} - 1} \left( \mathop \otimes \limits _{i = 0}^{q - 1} \left( X\left| {C_{YX}^i} \right\rangle \right) \left| Y \right\rangle \left| X\right\rangle \right) \nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1}\sum \limits _{X = 0}^{{2^n} - 1} \left( \mathop \otimes \limits _{i = 0}^{q - 1} \left| {\bar{C}_{YX}^i} \right\rangle \left| Y \right\rangle \left| X \right\rangle \right) \nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {{2^q} - 1 - f(Y,X)} \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \end{aligned}$$

(31)

Figure 12 shows the quantum circuit of ${U_C}$ in the NEQR model, with the Lena image used as an example. This CC operation makes the target in the image clearer and easier to observe, especially for some medical images.

Fig. 12

a Quantum circuit of ${U_C}$ in the NEQR model. $\oplus$ Denotes the inversion operation for a single qubit. b Lena image. c The result of image (b) through the CC operation ${U_C}$

The second CC operation, ${U_H}$, is depicted in (32).

$$\begin{aligned} U_H = X \otimes {I^{ \otimes q - 1 + 2n}} \end{aligned}$$

(32)

The operation ${U_H}$ is consisted of one quantum not gate and $q-1+2n$ quantum identity gates. The quantum not gate inverts the highest qubit $\left| {C_{YX}^0} \right\rangle$ in the color qubit sequence in NEQR. This operation changes the gray-scale values of all the pixels in the image into their complementary colors. (33) produces the result of ${U_H}$ on the quantum image $\left| I \right\rangle$.

$$\begin{aligned} {U_H}(\left| I \right\rangle )&= {U_H}\left( \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left( \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{YX}^i} \right\rangle \right) \left| Y \right\rangle } } \left| X \right\rangle \right) \nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} \sum \limits _{X = 0}^{{2^n} - 1} \left( X\left| {C_{YX}^0} \right\rangle \right) \left( \mathop \otimes \limits _{i = 1}^{q - 1} \left| {C_{YX}^i} \right\rangle \left| Y \right\rangle \left| X \right\rangle \right) \nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} \sum \limits _{X = 0}^{{2^n} - 1} \left| {\bar{C}_{YX}^0} \right\rangle \left( \mathop \otimes \limits _{i = 1}^{q - 1} \left| {C_{YX}^i} \right\rangle \left| Y \right\rangle \left| X \right\rangle \right) \nonumber \\&= \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {(f(Y,X) + {2^{q - 1}})\,\,\text{ mod }\, {2^q}} \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \end{aligned}$$

(33)

Figure 13 gives the quantum circuit of ${U_H}$ in the NEQR model, with the Lena image used as an example. This CC operation is also convenient and helpful for observing the image in certain applications.

Fig. 13

a Quantum circuit of ${U_H}$ in the NEQR model. In ${U_H}$, only the highest qubit of the color qubit sequence is inverted. b Lena image. c The result of image (b) through the CC operation ${U_H}$

Next, the time complexity of the CC operations in the novel NEQR quantum image representation will be discussed. In the NEQR quantum image, all the pixels are stored in a superposition of a $2n + q$ qubit sequence. This means that all the color transformations for all the pixels can be performed simultaneously. Hence, the quantum CC operations have a time complexity of no more than $O(2n + q)$, for example ${U_C}$ in (29) and ${U_H}$ in (32).

It should be pointed out that the time complexity discussed above only includes the time consumption of the image color transformations. The costs of the quantum image preparation and the measurements for the transformed quantum image are not included here. Since the quantum color operations should be considered as one step (i.e. image pre-processing) of most quantum image processing algorithms, the time complexity discussed here can be utilized directly to analyze the cost of complex quantum image processing algorithms.

4.2.2 Partial color operation

Two example NEQR PC operations will be demonstrated in this subsection.

Firstly, we will discuss how to design quantum $\cap$ gate and quantum $\cup$ gate. Because the classical $\cap$ gate and $\cup$ gate are inreversible, there not exist two-qubit quantum gates which are the quantum counterparts of the two common classical gates. Here we utilize two common quantum gates (Toffoli gate and Swap gate) and an ancillary qubit to construct quantum $\cap$ gate and quantum $\cup$ gate.

In Fig. 14a and b shows the quantum circuit of Toffoli gate and Swap gate. We utilize an ancillary qubit initialized as $\left| 0 \right\rangle$ to construct the quantum circuit of quantum $\cap$ gate as Fig. 14c. The quantum transform is shown as (24).

$$\begin{aligned} \cap :\left| a \right\rangle \left| b \right\rangle \left| 0 \right\rangle \rightarrow \left| a \right\rangle \left| {a \cap b} \right\rangle \left| b \right\rangle \end{aligned}$$

(34)

Similarly, we can construct the quantum $\cup$ gate with an ancillary qubit initialized as $\left| 1 \right\rangle$ as Fig. 14d. And (35) shows the quantum transform of quantum $\cup$ gate.

$$\begin{aligned} \cup :\left| a \right\rangle \left| b \right\rangle \left| 1 \right\rangle \rightarrow \left| a \right\rangle \left| {a \cup b} \right\rangle \left| b \right\rangle \end{aligned}$$

(35)

Then we will utilize the quantum $\cap$ gate and $\cup$ gate to design the quantum PC operations.

Fig. 14

a Toffoli gate. b Swap gate. c Quantum $\cap$ gate. d Quantum $\cup$ gate

The first PC operation is ${U_S}$ defined in (36).

$$\begin{aligned} {U_S}:\left| {C_{YX}^0} \right\rangle \left| {C_{YX}^{q - 1}} \right\rangle \left| 0 \right\rangle \rightarrow \left| {C_{YX}^0} \right\rangle \left| {C_{YX}^0 \cap C_{YX}^{q - 1}} \right\rangle \left| {C_{YX}^{q - 1}} \right\rangle \end{aligned}$$

(36)

This operation ${U_S}$ is a quantum $\cap$ gate, the input of which is the highest qubit $\left| {C_{YX}^0} \right\rangle$ and the lowest qubit $\left| {C_{YX}^{q - 1}} \right\rangle$ in the color qubit sequence while the output will be stored into $\left| {C_{YX}^{q - 1}} \right\rangle$. For NEQR, this quantum operation stores $\left| 0 \right\rangle$ in the qubit $\left| {C_{YX}^{q - 1}} \right\rangle$ if the qubit $\left| {C_{YX}^0} \right\rangle$ of the pixel is $\left| 0 \right\rangle$. (37) shows the quantum transform of ${U_S}$ for a quantum image $\left| I \right\rangle$. And the quantum circuit of ${U_S}$ is shown as Fig. 15.

$$\begin{aligned}&{U_S}:\left| I \right\rangle \left| 0 \right\rangle \rightarrow \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left( \mathop \otimes \limits _{i = 0}^{q - 2} \left| {C_{YX}^i} \right\rangle \right) \left| {C_{YX}^0 \cap C_{YX}^{q - 1}} \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \left| {C_{YX}^{q - 1}} \right\rangle \nonumber \\&\quad = \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0,C_{YX}^0 = 1}^{{2^n} - 1} {\left| 1 \right\rangle \left( \mathop \otimes \limits _{i = 1}^{q - 2} \left| {C_{YX}^i} \right\rangle \right) \left| {C_{YX}^{q - 1}} \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \left| {C_{YX}^{q - 1}} \right\rangle \nonumber \\&\quad + \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0,C_{YX}^0 = 0}^{{2^n} - 1} {\left| 0 \right\rangle \left( \mathop \otimes \limits _{i = 1}^{q - 2} \left| {C_{YX}^i} \right\rangle \right) \left| 0 \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \left| {C_{YX}^{q - 1}} \right\rangle \end{aligned}$$

(37)

The quantum operation ${U_S}$ halves the gray-scale range for the pixels with gray-scale values 0–127. After this operation, the number of gray-scale values in this image will decrease from 256 to 192. Figure 15 shows comparative examples of the Lena image. This kind of operation is often applied in image adaptive quantization [20]. When the gray-scale values of most pixels in the image are concentrated in a certain range, this PC operation can be used to decrease the gray-scale values of the remaining pixels, so that the storage requirements for the image decline sharply with little loss of image quality.

Fig. 15

a Quantum circuit of the gray-range halving operation ${U_S}$. A quantum $\cap$ gate will be taken on the qubit $\left| {C_{YX}^0} \right\rangle , \left| {C_{YX}^{q - 1}} \right\rangle$ and an ancillary qubit. b The original Lena image. c The result of image (b) through the gray-range halving operation ${U_S}$

The second PC operation ${U_B}$ is the bi-valuing operation for an image. The operation is defined in (38).

$$\begin{aligned} {U_B}:\mathrm{{ }}\mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{YX}^i} \right\rangle \left| a \right\rangle \rightarrow \left| {C_{YX}^0} \right\rangle \mathop \otimes \limits _{i = 1}^{q - 1} \left| {C_{YX}^0 \cup (C_{YX}^0 \cap C_{YX}^i)} \right\rangle \left| {a^{\prime }} \right\rangle \end{aligned}$$

(38)

where $\left| a \right\rangle$ denotes some ancillary qubits. There are $2(q-1)$ ancillary qubits for this operation because it is consisted of $q-1$ quantum $\cap$ gates and $q-1$ quantum $\cup$ gates in this operation. $\left| {a^{\prime }} \right\rangle$ is the final state of these ancillary qubits.

After this operation, all the qubits in the color qubit sequence will be set $\left| 0 \right\rangle$ if $\left| {C_{YX}^0} \right\rangle = \left| 0 \right\rangle$; otherwise, all of them will be set $\left| 1 \right\rangle$. (39) shows the quantum transform of ${U_B}$ for a quantum image $\left| I \right\rangle$.

$$\begin{aligned}&{U_B}:\left| I \right\rangle \left| a \right\rangle \rightarrow \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left( \left| {C_{YX}^0} \right\rangle \mathop \otimes \limits _{i = 1}^{q - 1} \left| {C_{YX}^0 \cup (C_{YX}^0 \cap C_{YX}^i)} \right\rangle \right) } } \left| {a^{\prime }} \right\rangle \nonumber \\&\quad = \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0,C_{YX}^0 = 1}^{{2^n} - 1} {\mathop \otimes \limits _{i = 0}^{q - 1} \left| 1 \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \left| {a^{\prime }} \right\rangle \nonumber \\&\quad + \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0,C_{YX}^0 = 0}^{{2^n} - 1} {\mathop \otimes \limits _{i = 0}^{q - 1} \left| 0 \right\rangle \left| Y \right\rangle } } \left| X \right\rangle \left| {a^{\prime }} \right\rangle \end{aligned}$$

(39)

Figure 16 gives the quantum circuit of the PC operation ${U_B}$ in the NEQR model. This PC operation sets all the pixels with gray-scale values of 0–127 to black and the others to white. The result for the Rice image is shown in Fig. 16. After this operation, the targets in the image are clearer and easier to analyze and to recognize.

Fig. 16

a Quantum circuit of the bi-valuing operation ${U_B}$. 7 quantum $\cap$ gates and 7 Quantum $\cup$ gates will be taken on the different qubits in the color qubit sequence. 14 Ancillary qubits are needed in this operation. b The original Rice image. c The result of (b) after the bi-valuing operation ${U_B}$

Similarly to the discussion of the time complexity of the CC operations, for the NEQR quantum image, it has been found that the time complexity of PC operations such as the quantum PC operations described in (36) and (38) is no more than approximately $O(q)$.

4.2.3 Color statistical operation

The third kind of image color operation is the CS operation. A CS operation uses the gray-scale information of the whole image to perform some statistical computation, such as constructing a gray-scale histogram by counting the numbers of pixels with the same gray-scale values, or finding the maximum and minimum gray-scale values to change the gray-scale contrast. In the classical image context, CS operations cost not less than $O({2^{2n}})$ for a ${2^n} \times {2^n}$ image. In the FRQI quantum image model, because the gray-scale information is stored as the probability amplitude of a single qubit, it is impossible to separate pixels with different gray-scale values, CS operations cannot be done in FRQI.

Through analysis of the expression for NEQR in (3), it can be determined that when the quantum image has been prepared, the whole quantum image can be considered as a data set of size ${2^{2n}}$, as shown in (40). In NEQR, the position sequence $\left| {YX} \right\rangle$ gives the order $\left| x \right\rangle$ of each element, while the entangled color qubit sequence $\left| {f(Y,X)} \right\rangle$ gives the value $\left| {f(x)} \right\rangle$ of the corresponding element. Moreover, the quantum image becomes the equiprobable superposition of all the elements of a data set. Therefore, CS operations for a NEQR quantum image are equivalent to statistical operations on a data set.

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{{2^n}}}\sum \limits _{x = 0}^{{2^{2n}} - 1} {\left| {f(x)} \right\rangle \left| x \right\rangle } \end{aligned}$$

(40)

Next, a quantum algorithm for finding minimum pixels will be presented as one example of a quantum CS operation. [21] proposed a quantum algorithm for finding the minimum element of an unsorted data set. Based on this quantum algorithm, a detailed quantum algorithm for finding the minimum pixels in a quantum image can be stated as shown in Fig. 17.

Fig. 17

Quantum algorithm of finding the minimum pixel

From the complexity discussion in [21], it is known that this quantum algorithm can obtain the minimum pixel in the image with probability at least 0.5 and with a running time of $O(\sqrt{{2^{2n}}} ) = O({2^n})$, which amounts to a quadratic speedup compared to the same operation for classical images.

5 Conclusion and future work

Combining quantum mechanics with image processing is an important and effective approach to address the high real-time computational requirements of classical image processing. In this paper, through analyzing the state of the art of quantum image representation, the drawbacks of these existing quantum image models have been identified. Then a novel enhanced quantum representation (NEQR) for digital images has been proposed to improve FRQI, which is the latest and best existing quantum image model. The NEQR model uses a qubit sequence to store the gray-scale information of all the pixels in the image for the first time, instead of the probability amplitude of a single qubit, as in FRQI. Therefore, NEQR can enhance FRQI in the following ways:

• 1. When preparing the quantum image, NEQR avoids complex quantum rotation operations, and the whole preparation costs no more than $O(qn{2^{2n}})$. Compared with FRQI, NEQR exhibits an approximately quadratic decrease in the time complexity for image preparation.

• 2. By using the compression method of minimization of Boolean expressions, the image compression ratio of NEQR was found to be 74.11 %, which was 1.5$\times$ better than the ratio obtained from FRQI (50 %). In particular, when the gray-scale distribution of the image is irregular and complex, the compression ratio of FRQI is nearly 0, while NEQR can still obtain 40–50 % compression for irregular images.

• 3. Through quantum measurements, the original digital image can be accurately retrieved from the NEQR quantum image, not probabilistically as in FRQI.

• 4. All three kinds of color operation described in Sect. 4.2 can be performed conveniently in the NEQR quantum model. However, FRQI can perform CC operations only.

Because NEQR uses a qubit sequence to store gray-scale information, NEQR needs an extra $q-1$ qubits (${2^q}$ being the number of gray-scale values in the image) for storage compared to FRQI. However, it is very valuable for NEQR to make this tradeoff between a little extra quantum storage and a significant performance improvement in quantum image processing.

Quantum image processing is still in its infancy, most studies based on the existing quantum image models can focus only on certain simple geometric and color operations. The new NEQR quantum image-representation model proposed in this paper constitutes a significant improvement in some aspects over existing quantum image models, and this will motivate the authors to explore further this novel quantum image model. Whether it is suitable to use NEQR to perform complex image processing such as quantum pattern recognition and quantum image matching will be the topic of future research on quantum image processing.