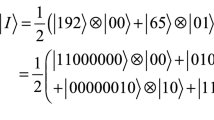1 Introduction

With the rapid development of multimedia technology, more and more important information is embodied in images and videos and the security of private images becomes a serious issue. For private images in conventional computers, there have been many good image encryption algorithms [1–20]. Double random-phase encoding is a classical method of optical encryption [2]. The phase encoding has been developed and employed in some encryption schemes [3–8]. An image encryption method based on compressive sensing and double random-phase encoding was proposed, and the data volume for encryption was lowered due to the dimensional decrease properties of compressive sensing [7]. Zhang et al. proposed an image encryption algorithm by combining fractional Fourier transform with pixel scrambling operation based on double random-phase encoding [8]. However, some studies have shown that the double random-phase encoding scheme is vulnerable to various attacks including known-plaintext attack [9, 10], chosen-ciphertext attack [11] and chosen-plaintext attack [12]. Image scrambling, as a common way to encrypt image data, is to hide image content from illegal user. Arnold transform is an effective image pixel scrambling tool called as the “cat’s mapping” [13]. Arnold transform can scramble the matrix-pixel sequence by encoding a single parameter and reduce the length of the key. A novel image scrambling and watermarking scheme based on the orbits of Arnold transform were proposed, where Arnold transform disordered the pixel positions to obtain a totally visual difference from the original images [14]. An efficient image encryption algorithm with the generalized Arnold map was proposed, which can resist statistical analyses, chosen-plaintext attacks and known-plaintext attacks [15]. Arnold transform is applied widely in digital image scramble. To enhance security of the encryption algorithm, some encryption schemes have been designed by combining Arnold transform with other transforms [16–20]. Liu et al. [16] designed a double image encryption algorithm based on Arnold transform and discrete fractional angular transform. A novel color image encryption method by combining discrete fractional random transform with Arnold transform in the intensity–hue–saturation color space was proposed, where Arnold transform yields good scrambling results and its periodicity ensures the implementation of decryption is accurate and easy [20].

Quantum computation has been applied in many fields of information sciences [21]. The rapid development of quantum computation and quantum computer attracts people to investigate quantum data security. The quantum images as an important part of quantum information will make the applications of quantum computers more widely and comprehensively in the future. A series of methods to represent quantum images were proposed [22–27]. Moreover, a novel enhanced quantum representation (NEQR) for digital images was proposed, which improves the flexible representation of quantum images (FRQI) [28]. Consequently, some new quantum algorithms were developed to secure quantum images [29–37]. For example, Yang et al. [36] proposed a novel gray image encryption scheme based on quantum Fourier transform (QFT) and double random-phase encoding technique, which is heuristic to introduce more optical information processing techniques into quantum scenarios. Jiang et al. [38] proposed the Arnold and Fibonacci scrambling quantum circuits based on FRQI, which does not take advantage of the particularities of “\(\hbox {mod } 2^{n}\),” multiply by 2 and subtraction in binary arithmetic. Later, a simplified scheme was presented in [39] to cut down the network complexity apparently. However, there are no quantum versions of some basic classical image transforms, such as generalized Arnold transform, fractional Fourier transform, fractional Mellin transform and so on.

We will design a quantum version of the generalized Arnold transform and will propose a quantum image encryption algorithm by combining generalized Arnold transform with double random-phase encoding technology. The algorithm is composed of two stages, i.e., diffusion and confusion. In the diffusion stage, the random-phase operations are controlled by the classical binary sequence, which can change different angles of the color information for different positions. However, in Yang et al’s scheme [36], the angle of every positions in quantum image is changed with a same angle with the phase operation, which cannot guarantee the changes for different positions. In the confusion stage, the generalized Arnold transform is applied to shuffle the positions of image pixels. It changes not only the gray values of pixels but also the locations of pixels. Unlike Yang et al’s scheme, the proposed quantum image encryption algorithm is expected with good diffusion and confusion performances. Moreover, the generalized Arnold transform is introduced into the encryption algorithm to increase the number of keys and then enhances the security. Numerical simulations and theoretical analysis are presented to illustrate the feasibility and effectiveness of the proposed algorithm.

The rest of this paper is organized as follows. In Sect. 2, the flexible representation for quantum images and the double random- phase encoding are reviewed. The quantum realization of the generalized Arnold image scrambling is designed in Sect. 3. The proposed quantum image encryption and decryption algorithm is given in Sect. 4. Section 5 is devoted to classical simulation analysis and performance comparison. Finally, a conclusion is drawn in Sect. 6.

2 Flexible representation for quantum images and double random-phase encoding technique

2.1 Flexible representation for quantum images

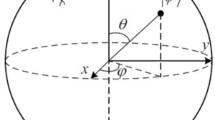
Classical image is represented by a matrix with the same size of the image, i.e., the number of pixels. In a classical gray image, each pixel consists of the grayscale value and the position information. Inspired by the pixel representation for images in classical computers, a flexible representation for quantum images on quantum computers was proposed [23]. For a quantum image, the color information and the corresponding position information of every pixels are stored into the corresponding quantum states, respectively. According to the flexible representation for quantum images, suppose \(M\) is a classical image of size \(2^{n}\times 2^{n}\), \(\left| M \right\rangle \) is the storage of the whole quantum states for a grayscale image, the quantum image representation can be expressed as:

$$\begin{aligned} \left| M \right\rangle&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } \left| {yx} \right\rangle \nonumber \\ \left| {g\left( {y,x} \right) } \right\rangle&= \cos \theta _i \left| 0 \right\rangle +\sin \theta _i \left| 1 \right\rangle ,\theta _i \in \left[ {0,\frac{\pi }{2}} \right] ,i=yx=0,1,\ldots ,2^{2n}-1 \end{aligned}$$
(1)

where \(\theta \hbox {=}\left( {\theta _0 ,\theta _1 ,\ldots ,\theta _{2^{2n}-1} } \right) \) is the vector of angles encoding colors, \(\left| {g\left( {y,x} \right) } \right\rangle \) encodes the color information of quantum image, \(\left| i \right\rangle =\left| {yx} \right\rangle =\left| y \right\rangle \left| x \right\rangle =\left| {y_{n-1} y_{n-2} \ldots y_0 } \right\rangle \left| {x_{n-1} x_{n-2} \ldots x_0 } \right\rangle \) encodes the corresponding positions of the quantum image, \(\left| {y_{n-1} y_{n-2} \ldots y_0 } \right\rangle \) encodes the first \(n\)-qubit along the vertical location information while \(\left| {x_{n-1} x_{n-2} \ldots x_0 } \right\rangle \) encodes the second \(n\)-qubit along the horizontal location information and \(n\) is the number of quantum bits required for encoding.

2.2 Double random-phase encoding technique

The double random-phase encoding technique was proposed by Refregier and Javidi in 1995 [2]. The technique can encrypt an original image by using two statistically independent random-phase masks in the input and Fourier planes, respectively. If two random-phase masks are used to encrypt the image in the input and Fourier planes, respectively, the encrypted image would be generalized to a stationary white noise of statistical properties with time shift invariant. If only the random-phase mask is used to encrypt the original image in the input plane, the encrypted image would be a non-stationary white noise of statistical properties changing over time. If one only uses the random-phase mask to encrypt image in the Fourier plane, the encrypted image can easily be deciphered.

Assume \(f\left( {x,y} \right) \) is the plaintext image, while \(g\left( {x,y} \right) \) is the cipher one. Let \(\left( {x,y} \right) \) and \(\left( {\mu ,v} \right) \) denote the spatial plane and the Fourier plane coordinates, respectively, \(\phi \left( {x,y} \right) \) and \(\varphi \left( {u,v} \right) \) denote two white noise sequences in input phase and Fourier phase, which are uniformly distributed from 0 to 1. The random-phase masks \(\exp \left[ {j2\pi \phi \left( {x,y} \right) } \right] \) and \(\exp \left[ {j2\pi \varphi \left( {u,v} \right) } \right] \) as the keys are generated by two white noise sequences. The encoding and decoding procedures are shown as follows.

$$\begin{aligned} g\left( {x,y} \right)&= \hbox {FFT}^{-1}\left\{ {\hbox {FFT}\left\{ {f\left( {x,y} \right) \exp \left[ {j2\pi \phi \left( {x,y} \right) } \right] } \right\} \exp \left[ {j2\pi \varphi \left( {u,v} \right) } \right] } \right\} \end{aligned}$$
(2)
$$\begin{aligned} f\left( {x,y} \right)&= \hbox {FFT}^{-1}\left\{ {\hbox {FFT}\left\{ {g\left( {x,y} \right) } \right\} \exp \left[ {-j2\pi \varphi \left( {u,v} \right) } \right] } \right\} \exp \left[ - {j2\pi \phi \left( {x,y} \right) } \right] \end{aligned}$$
(3)

where \(\hbox {FFT}\) and \(\hbox {FFT}^{-1}\) represent the Fourier transform and inverse Fourier transform, respectively.

3 Realization of generalized Arnold transform

3.1 Quantum representation of generalized Arnold transform

Arnold transform was proposed by Arnold [13] in the research of ergodic theory, it was also called cat map. Dyson et al. [40] quoted the transform as an image scrambling method in 1992. The two-dimensional generalized Arnold transform in the form of matrix is defined as

$$\begin{aligned} \left[ \begin{array}{l} x'\\ y'\\ \end{array}\right] =\left[ \begin{array}{ll} 1&{}t\\ m&{}tm+1\\ \end{array}\right] \left[ \begin{array}{l} x\\ y\\ \end{array}\right] \left( {\hbox {mod } N}\right) =C\left[ \begin{array}{l} x\\ y\\ \end{array}\right] \left( {\hbox {mod } N}\right) \end{aligned}$$
(4)

The inverse transformation is:

$$\begin{aligned} \left[ \begin{array}{l} x\\ y\\ \end{array}\right] =\left[ \begin{array}{ll} 1&{}t\\ m&{}tm+1\\ \end{array}\right] ^{-1}\left[ \begin{array}{l} x^\prime \\ y^\prime \\ \end{array}\right] \left( {\hbox {mod } N}\right) =\left[ \begin{array}{ll} tm+1&{}-t\\ -m&{}1\\ \end{array}\right] \left[ \begin{array}{l} x^\prime \\ y^\prime \\ \end{array}\right] \left( {\hbox {mod } N} \right) \end{aligned}$$
(5)

where \(x,y,{x}^\prime ,{y}^\prime \in \left\{ {0,1,\ldots ,N-1} \right\} \), \(t\) and \(m\) are positive integers, \(x\) and \(y\) are the pixel coordinates of the original image, \(N\) is the size of the square image, \({x}^\prime \) and \({y}^\prime \) are the pixel coordinates of the generalized Arnold scrambled image. The generalized Arnold transform in the form of coordinates can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} x'=\left( {x+ty} \right) \hbox {mod } N \\ y'=\left( {mx+\left( {tm+1} \right) y} \right) \hbox {mod } N\\ \end{array}\right. \end{aligned}$$
(6)

The generalized Arnold transform has the features of chaotic mapping, which changes the positions of two pixels. The generalized Arnold transform focuses on manipulating the information about the position of each pixel in the image. Corresponding to the classical image, the quantum representation of the generalized Arnold transform can be described as

$$\begin{aligned} \left\{ \begin{array}{l} \left| {{x}^\prime } \right\rangle =\left| {\left( {x+ty} \right) \hbox {mod } 2^{n}} \right\rangle \\ \left| {{y}^\prime } \right\rangle =\left| {\left( {mx+\left( {tm+1} \right) y} \right) \hbox {mod } 2^{n}} \right\rangle \\ \end{array}\right. \end{aligned}$$
(7)

3.2 Quantum circuit architecture of generalized Arnold transform

An explicit construction of several elementary quantum networks, i.e., plain adder, adder modulo \(N\), controlled multiplier modulo \(N\) and exponentiation modulo \(N\) are designed in [41]. The plain adder is a quantum network that can calculate the sum of two numbers. Inputs are encoded in a binary form in the computational basis of selected qubits usually called a quantum register. The addition of two quantum registers \(\left| a \right\rangle \) and \(\left| b \right\rangle \) can be written as \(\left| {a,b} \right\rangle \rightarrow \left| {a,a+b} \right\rangle \). The plain adder network is illustrated in Fig. 1a. The adder modulo \(N\) is a quantum network that can calculate the modular sum of two numbers. The modular addition of two quantum registers \(\left| a \right\rangle \) and \(\left| b \right\rangle \) can be expressed as \(\left| {a,b} \right\rangle \rightarrow \left| {a,\left( {a+b} \right) \hbox {mod } N} \right\rangle \). The adder modulo \(N\) network is demonstrated in Fig. 1b. However, the plain adder network and the adder modulo \(N\) network require the inputs are two \(n\) qubits binary numbers. A quantum circuit \(\hbox {ADDER-MOD}2^{n}\) defined in [39] can accomplish \(\left( {a+b} \right) \hbox {mod } 2^{n}\) simply by ignoring the carry bit from ADDER module. The \(\hbox {ADDER-MOD}2^{n}\) network is shown in Fig. 1c. In the generalized quantum Arnold transform, the states \(\left| {{x}^\prime } \right\rangle \) and \(\left| {{y}^\prime } \right\rangle \) are independent of each other, which can be realized by connecting several quantum circuit \(\hbox {ADDER-MOD}2^{n}\). Hence, the quantum \(\hbox {ADDER-MOD}2^{n}\) network is fundamental to realize the generalized Arnold transform in quantum computer.

Assuming that \(x\) and \(y\) are both \(n\) qubits binary numbers, \(x=x_{n-1} x_{n-2} \ldots x_0\), \(y=y_{n-1} y_{n-2} \ldots y_0\), \(x_i ,y_i \in \left\{ {0,1} \right\} \), \(i=n-1,n-2,\ldots ,0\). According to the nature of the modulo, \(\left( {x+y} \right) \hbox {mod } 2^{n}=\left( {x\hbox {mod } 2^{n}+y\hbox {mod } 2^{n}} \right) \hbox {mod} 2^{n}=\left( {x+y\hbox {mod } 2^{n}} \right) \hbox {mod } 2^{n}\), so \(\left( {x+2y} \right) \hbox {mod } 2^{n}=\left( {x+2y\hbox {mod } 2^{n}} \right) \hbox {mod } 2^{n}\). The realization of \(\left| {{x}^\prime } \right\rangle \) is divided into \(t\) steps, as shown in Fig. 2. The \(\hbox {ADDER-MOD}2^{n}\) network is used to obtain \(\left( {ty+x} \right) \hbox {mod } 2^{n}\) from the first step to the \(t\)-th step.

$$\begin{aligned}&\left| {y,x} \right\rangle \rightarrow \left| {y,\left( {y+x} \right) \hbox {mod } 2^{n}} \right\rangle \rightarrow \cdots \rightarrow \nonumber \\&\left| {y,\left( {\left( {t-1} \right) y+x} \right) \hbox {mod } 2^{n}} \right\rangle \rightarrow \left| {y,\left( {ty+x} \right) \hbox {mod } 2^{n}} \right\rangle \end{aligned}$$
(8)

The input is the position information \(\left| x \right\rangle \) and \(\left| y \right\rangle \) of original image, and the output is the position information \(\left| {{x}^\prime } \right\rangle \) of Arnold scrambled image.

The realization of \(\left| {{y}^\prime } \right\rangle \) is divided into \(tm+m+1\) steps, as shown in Fig. 3. From the first step to the \(\left( {m-1} \right) \)-th step, the \(\hbox {ADDER-MOD}2^{n}\) network is used to obtain \(mx\hbox {mod } 2^{n}\), in the \(m\)-th step, \(x\) is replaced by \(y\), from the \(\left( {m+1} \right) \)-th step to the last step, the \(\hbox {ADDER-MOD}2^{n}\) network is employed to obtain \(\left( {mx+\left( {tm+1} \right) y} \right) \hbox {mod } 2^{n}\).

$$\begin{aligned} \left| {x,x} \right\rangle&\rightarrow \left| {x,2x\hbox {mod } 2^{n}} \right\rangle \rightarrow \cdots \rightarrow \left| {x,mx\hbox {mod } 2^{n}} \right\rangle \rightarrow \left| {y,mx\hbox {mod } 2^{n}} \right\rangle \nonumber \\&\rightarrow \left| {y,\left( {y+mx} \right) \hbox {mod } 2^{n}} \right\rangle \rightarrow \cdots \rightarrow \left| {y,\left( {tmy+mx} \right) \hbox {mod } 2^{n}} \right\rangle \nonumber \\&\rightarrow \left| {y,\left( {\left( {tm+1} \right) y+mx} \right) \hbox {mod } 2^{n}} \right\rangle \end{aligned}$$
(9)

Thus, the \(\left| {{y}^\prime } \right\rangle \) network outputs the position information \(\left| {{y}^\prime } \right\rangle \) of Arnold scrambled image with inputs \(\left| x \right\rangle \) and \(\left| y \right\rangle \).

Fig. 1
figure 1

a Plain adder network, b adder modulo \(N\) network, c \(\hbox {ADDER-MOD}2^{n}\) network

Full size image
Fig. 2
figure 2

\(\left| {{x}^\prime } \right\rangle \) network

Full size image
Fig. 3
figure 3

\(\left| {{y}^\prime } \right\rangle \) network

Full size image

From Eq. (5), it is clear that the position information \(\left| x \right\rangle \) and \(\left| y \right\rangle \) is regained only depending on \(\left| {{x}^\prime } \right\rangle \) and \(\left| {{y}^\prime } \right\rangle \) of the scrambled image. Hence, the inverse scrambling circuits are necessary. The inverse scrambling networks are designed to regain \(\left| x \right\rangle \) and \(\left| y \right\rangle \). A theorem in [39] was related as follows.

$$\begin{aligned} \left( {x-y} \right) \hbox {mod } 2^{n}=\left( {x+\left( {\bar{{y}}+1} \right) } \right) \hbox {mod } 2^{n} \end{aligned}$$
(10)

where \(\bar{{y}}=\bar{{y}}_{n-1} \bar{{y}}_{n-2} \ldots \bar{{y}}_0\), \(\bar{{y}}_i =1-y_i\), \(i=n-1,n-2,\ldots ,0\). According to Eq. (10), we obtain \(\left( {\left( {tm+1} \right) {x}^\prime -t{y}^\prime } \right) \hbox {mod } 2^{n}=\left( {\left( {tm+1} \right) {x}^\prime +t\overline{{y}^\prime } +t} \right) \hbox {mod } 2^{n}\). So the realization of \(\left| x \right\rangle \) is divided into \(t+tm+3\) steps, as shown in Fig. 4. The \(\hbox {ADDER-MOD}2^{n}\) network is used to obtain \(\left( {\left( {tm+1} \right) {x}^\prime } \right) \hbox {mod } 2^{n}\) from the first step to the \(tm\)-th step, in the \(\left( {tm+1} \right) \)-th step, \({x}^\prime \) is replaced by \(\overline{{y}^\prime }\), the \(\hbox {ADDER-MOD}2^{n}\) network is used to retrieve \(\left( {\left( {tm+1} \right) {x}^\prime +t\overline{{y}^\prime } } \right) \hbox {mod } 2^{n}\) from the \(\left( {tm+2} \right) \)-th step to the \(\left( {tm+t+1} \right) \)-th step, in the \(\left( {tm+t+2} \right) \)-th step, \({x}^\prime \) is replaced by \(\overline{{y}^\prime }\), and in the last step, an \(\hbox {ADDER-MOD}2^{n}\) network is involved.

$$\begin{aligned} \left| {{x}^\prime ,{x}^\prime } \right\rangle&\rightarrow \cdots \rightarrow \left| {{x}^\prime ,\left( {tm+1} \right) {x}^\prime \hbox {mod } 2^{n}} \right\rangle \rightarrow \left| {\overline{{y}^\prime } ,\left( {tm+1} \right) {x}^\prime \hbox {mod } 2^{n}} \right\rangle \nonumber \\&\rightarrow \cdots \rightarrow \left| {\overline{{y}^\prime } ,\left( {\left( {tm+1} \right) {x}^\prime +t\overline{{y}^\prime } } \right) \hbox {mod } 2^{n}} \right\rangle \nonumber \\&\rightarrow \left| {t,\left( {\left( {tm+1} \right) {x}^\prime +t\overline{{y}^\prime } } \right) \hbox {mod } 2^{n}}\right\rangle \nonumber \\&\rightarrow \left| {t,\left( {\left( {tm+1} \right) {x}^\prime +t\overline{{y}^\prime } +t} \right) \hbox {mod } 2^{n}} \right\rangle \end{aligned}$$
(11)

Due to \(\left( {-m{x}^\prime +{y}^\prime } \right) \hbox {mod } 2^{n}=\left( {m\overline{{x}^\prime } +m+y} \right) \hbox {mod } 2^{n}\), the realization of \(\left| y \right\rangle \) is divided into \(m+2\) steps, as depicted in Fig. 5. From the first step to the \((m-1)\)-th step, the \(\hbox {ADDER-MOD}2^{n}\) network is exploited to obtain \(m\overline{{x}^\prime } \hbox {mod } 2^{n}\), in the \(m\)-th step, \({x}^\prime \) is replaced with \({y}^\prime \), the \(\hbox {ADDER-MOD}2^{n}\) operation is used to obtain \(\left( {m\overline{{x}^\prime } +{y}^\prime } \right) \hbox {mod } 2^{n}\) in the \((m+1)\)-th step, in the \((m+2)\)-th step, \({y}^\prime \) is replaced with \(m\), and in the last step, \(\hbox {ADDER-MOD}2^{n}\) network is necessary to obtain \(\left( {m\overline{{x}^\prime } +{y}^\prime +m} \right) \hbox {mod } 2^{n}\).

$$\begin{aligned} \left| {\!\overline{\!} {{x}^\prime } ,\!\overline{\!} {{x}^\prime } } \right\rangle&\rightarrow \cdots \rightarrow \left| {\overline{{x}^\prime } ,m\overline{{x}^\prime } \hbox {mod } 2^{n}} \right\rangle \rightarrow \left| {{y}^\prime ,m\overline{{x}^\prime } \hbox {mod } 2^{n}} \right\rangle \rightarrow \left| {{y}^\prime ,\left( {m\overline{{x}^\prime } +{y}^\prime } \right) \hbox {mod } 2^{n}} \right\rangle \nonumber \\&\rightarrow \left| {m,\left( {m\overline{{x}^\prime } +{y}^\prime } \right) \hbox {mod } 2^{n}} \right\rangle \rightarrow \left| {m,\left( {m\overline{{x}^\prime } +{y}^\prime +m} \right) \hbox {mod } 2^{n}} \right\rangle \end{aligned}$$
(12)
Fig. 4
figure 4

\(\left| x \right\rangle \) network

Full size image
Fig. 5
figure 5

\(\left| y \right\rangle \) network

Full size image

4 Quantum image encryption and decryption algorithm

4.1 Quantum image encryption algorithm

Assume that plaintext quantum image is \(\left| M \right\rangle \hbox {=}\frac{1}{2^{n}}\sum \limits _{y=0}^{2^{n}-1} {\sum \limits _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } \left| {yx} \right\rangle \), where \(\left| {g\left( {y,x} \right) } \right\rangle =\cos \theta _i \left| 0 \right\rangle +\sin \theta _i \left| 1 \right\rangle \), \(\theta _i \in \left[ {0,\frac{\pi }{2}} \right] \), \(i=yx=0,1,\ldots ,2^{2n}-1\). The proposed image encryption algorithm consists of the following steps:

Step 1. Perform generalized Arnold transform operation on \(\left| M \right\rangle \) for \(k\) times to obtain \(\left| {Q_1 } \right\rangle \), where \(\left| {x_A } \right\rangle \) and \(\left| {y_A } \right\rangle \) represent the horizontal and the vertical location information of the final scrambled quantum image \(\left| {Q_1 } \right\rangle \), respectively. \(A\) represents the generalized Arnold image scrambling, and \(\left| Q \right\rangle \) represents the scrambled quantum image for once. The quantum version of generalized Arnold transform is defined as

$$\begin{aligned} \left| Q \right\rangle&= A\left( {\left| M \right\rangle } \right) \hbox {=}\frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } A\left( {\left| {yx} \right\rangle } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } A\left( {\left| y \right\rangle } \right) A\left( {\left| x \right\rangle } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } \left| {{y}^\prime {x}^\prime } \right\rangle \end{aligned}$$
(13)

where

$$\begin{aligned} \left\{ {\begin{array}{l} \left| {{x}^\prime } \right\rangle =A\left( {\left| x \right\rangle } \right) =\left| {\left( {x+ty} \right) \hbox {mod } 2^{n}} \right\rangle \\ \left| {{y}^\prime } \right\rangle =A\left( {\left| y \right\rangle } \right) =\left| {\left[ {mx+\left( {tm+1} \right) y} \right] \hbox {mod } 2^{n}} \right\rangle \\ \end{array}} \right. \end{aligned}$$
(14)

Step 2. Perform quantum random-phase operation on \(\left| Q \right\rangle \) in the spatial domain to encode each color angle to a new angle. Random-phase gate \(U_i\) is controlled by a classical binary number \(k_i\), where \(k_i \in \left\{ {0,1} \right\} \), \(i=0,1,\ldots ,2^{2n}-1\). Binary sequence \(K=k_0 k_1 \ldots k_{2^{2n}-1}\) is the key.

$$\begin{aligned} T_i&= \left( {U_i}\right) ^{k_i }=\left\{ \begin{array}{l} {U_i,}\\ {I,}\\ \end{array}\right. {\begin{array}{l} \\ \\ \end{array} }{\begin{array}{l} {k_i =1;} \\ {k_i =0.} \\ \end{array} } i=0,1,\ldots ,2^{2n}-1.\end{aligned}$$
(15)
$$\begin{aligned} U_i&= \left[ \begin{array}{ll} 1&{}0\\ 0&{}e^{\mathrm{j}2\pi \varphi _i}\\ \end{array}\right] \end{aligned}$$
(16)

where \(\varphi _i\) is a real number and distributed uniformly between 0 and 1. Unitary transform \(T_i\) is used to construct a \(2n+1\) qubits-based unitary transform \(B_i\).

$$\begin{aligned} B_i =I\otimes \sum _{y=0}^{2^{n}-1} \mathop {\mathop {\sum }_{x=0}}_{yx \ne i}^{2^{n}-1} {\left| {yx} \right\rangle \left\langle {yx} \right| }+T_i \otimes \left| i \right\rangle \left\langle i \right| \end{aligned}$$
(17)

The controlled phase matrix \(B_i\) is a unitary matrix since \(B_i B_i^\dagger \hbox {=}I^{\otimes 2n+1}\). By applying a \(2n+1\) qubits unitary transform \(B\) on quantum image \(\left| {Q_1 } \right\rangle \), \(\left| {Q_2 } \right\rangle \) is obtained.

$$\begin{aligned} B\left( {\left| {Q_1 } \right\rangle } \right)&= \prod _{i=0}^{2^{2n}-1} {B_i } \left( {\left| {Q_1 } \right\rangle } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {T_{yx} \left( {\cos \theta _{yx} \left| 0 \right\rangle +\sin \theta _{yx} \left| 1 \right\rangle } \right) } } \left| {y_A x_A } \right\rangle \nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {f\left( {y,x} \right) } \right\rangle } } \left| {y_A x_A } \right\rangle =\left| {Q_2 } \right\rangle \end{aligned}$$
(18)

Step 3. Execute QFT on \(\left| {Q_2 } \right\rangle \), then perform quantum random-phase operation in the Fourier transform domain. Random-phase gate \(U_i ^{\prime }\) is controlled by a binary number \(d_i\), where \(d_i \in \left\{ {0,1} \right\} \), \(i=0,1,\ldots ,2^{2n}-1\). Binary sequence \(D=d_0 d_1 \ldots d_{2^{2n}-1}\) is another key.

$$\begin{aligned} H_i&= \left( {U_i ^{\prime }} \right) ^{d_i }=\left\{ \begin{array}{l} U_i ^{\prime },\\ I,\\ \end{array}\right. \begin{array}{l} \\ \\ \end{array}\begin{array}{l} d_i =1;\\ d_i =0.\\ \end{array}i=0,1,\ldots ,2^{2n}-1.\end{aligned}$$
(19)
$$\begin{aligned} U_i^{\prime }&= \left[ \begin{array}{ll} 1&{}0\\ 0&{}e^{j2\pi \psi _i}\\ \end{array}\right] \end{aligned}$$
(20)

where \(\psi _i\) is a real number and distributed uniformly between 0 and 1. Unitary transform \(H_i\) is used to construct a \(2n+1\) qubits-based unitary transform \(C_i\).

$$\begin{aligned} C_i =I\otimes \sum _{y=0}^{2^{n}-1} \mathop {\mathop {\sum }_{x=0}}_{yx\ne i}^{2^{n}-1} {\left| {yx} \right\rangle \left\langle {yx} \right| } +H_i \otimes \left| i \right\rangle \left\langle i \right| \end{aligned}$$
(21)

The controlled phase matrix \(C_i\) is a unitary matrix since \(C_i C_i^\dagger \hbox {=}I^{\otimes 2n+1}\). Apply a \(2n+1\) qubits unitary transform \(C\) on \(\hbox {QFT}\left( {\left| {Q_2 } \right\rangle } \right) \).

$$\begin{aligned} \left| {Q_3 } \right\rangle&= C\left( {\hbox {QFT}\left( {\left| {Q_2 } \right\rangle } \right) } \right) =\prod _{i=0}^{2^{2n}-1} {C_i } \left( {\hbox {QFT}\left( {\left| {Q_2 } \right\rangle } \right) } \right) \nonumber \\&= \prod _{i=0}^{2^{2n}-1} {C_i } \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\hbox {QFT}\left( {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } }\nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {H_{yx} \hbox {QFT}\left( {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } } \end{aligned}$$
(22)

Step 4. Perform the inverse quantum Fourier transform (IQFT) on \(\left| {Q_3 } \right\rangle \).

$$\begin{aligned} \left| {Q_4 } \right\rangle&= \hbox {IQFT}\left( {\left| {Q_3 } \right\rangle } \right) \nonumber \\&= \hbox {IQFT}\left( {\frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {H_{yx} \hbox {QFT}\left( {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } } } \right) \end{aligned}$$
(23)

4.2 Quantum image decryption algorithm

The key involved in the encryption process is composed of the independent parameters \(t\) and \(m\) of coefficients matrix, iterative times \(k\), the classical binary sequences \(K=k_0 k_1 \ldots k_{2^{2n}-1}\) and \(D=d_0 d_1 \ldots d_{2^{2n}-1}\). According to the encryption, the decryption process is as follows.

Step 1. Perform QFT on \(\left| {Q_4 } \right\rangle \).

$$\begin{aligned} \hbox {QFT}\left( {\left| {Q_4 } \right\rangle } \right) =\hbox {QFT}\left( {\hbox {IQFT}\left( {\left| {Q_3 } \right\rangle } \right) } \right) =\left| {Q_3 } \right\rangle \end{aligned}$$
(24)

Step 2. Perform the decryption operation on \(\left| {Q_3 } \right\rangle \) with the key \(D\).

$$\begin{aligned} C^{-1}\left( {\left| {Q_3 } \right\rangle } \right)&= \prod _{i=0}^{2^{2n}-1} {C_i^\mathbf{\dagger } } \left( {\left| {Q_3 } \right\rangle } \right) \nonumber \\&= \prod _{i=0}^{2^{2n}-1} {C_{_i }^\mathbf{\dagger } } \left( {\frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {H_{yx} \hbox {QFT}\left( {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } } } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{x=0}^{2^{n}-1} {\sum _{y=0}^{2^{n}-1} {H_{_{yx} }^{-1} H_{yx} \hbox {QFT}\left( {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } }\nonumber \\&= \frac{1}{2^{n}}\sum _{x=0}^{2^{n}-1} {\sum _{y=0}^{2^{n}-1} {\hbox {QFT}\left( {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } } =\hbox {QFT}\left( {\left| {Q_2 } \right\rangle } \right) \end{aligned}$$
(25)

where \(C_{_{yx} }^\dagger \) is the Hermitian conjugate of \(C_{yx}\).

Step 3. Execute the IQFT to obtain \(\left| {Q_2 } \right\rangle \) and then perform the decryption operation on \(\left| {Q_2 } \right\rangle \) with the key \(K\).

$$\begin{aligned} B^{-1}\left( {\left| {Q_2 } \right\rangle } \right)&= \prod _{i=0}^{2^{2n}-1} {B_i^\mathbf{\dagger } } \left( {\left| {Q_2 } \right\rangle } \right) \nonumber \\&= \prod _{i=0}^{2^{2n}-1} {B_i^\mathbf{\dagger } } \left( {\frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {f\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } } } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{x=0}^{2^{n}-1} {\sum _{y=0}^{2^{n}-1} {T_{_{yx} }^{-1} T_{yx} \left( {\left| {g\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } \right) } }\nonumber \\&= \frac{1}{2^{n}}\sum _{x=0}^{2^{n}-1} {\sum _{y=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle \left| {y_A x_A } \right\rangle } } =\left| {Q_1 } \right\rangle \end{aligned}$$
(26)

Step 4. Perform the inverse generalized Arnold transform operation \(A^{-1}\) on quantum image \(\left| {Q_1 } \right\rangle \) for \(k\) times. The quantum version of inverse generalized Arnold transform is defined as

$$\begin{aligned} \left| M \right\rangle&= A^{-1}\left( {\left| Q \right\rangle } \right) \hbox {=}\frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } A^{-1}\left( {\left| {{y}^\prime {x}^\prime } \right\rangle } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } A^{-1}\left( {\left| {{y}^\prime } \right\rangle } \right) A^{-1}\left( {\left| {{x}^\prime } \right\rangle } \right) \nonumber \\&= \frac{1}{2^{n}}\sum _{y=0}^{2^{n}-1} {\sum _{x=0}^{2^{n}-1} {\left| {g\left( {y,x} \right) } \right\rangle } } \left| {yx} \right\rangle \end{aligned}$$
(27)

where

$$\begin{aligned} \left\{ {\begin{array}{l} \left| x \right\rangle =A^{-1}\left( {\left| {{x}^\prime } \right\rangle } \right) =\left| {\left( {\left( {tm+1} \right) {x}^\prime -t{y}^\prime } \right) \hbox {mod } 2^{n}} \right\rangle \\ \left| y \right\rangle =A^{-1}\left( {\left| {{y}^\prime } \right\rangle } \right) =\left| {\left( {-m{x}^\prime +{y}^\prime } \right) \hbox {mod } 2^{n}} \right\rangle \\ \end{array}} \right. \end{aligned}$$
(28)

5 Numerical simulation and discussion

The experiments are limited to classical simulations on a classical computer with MATLAB, since the lack of quantum hardware. The simulations are based on linear algebraic constructions. The quantum states and the quantum operations are simulated by complex vectors and unitary matrices, respectively. The final step is the measurement in quantum computation, which converts the quantum information into the classical form as probability distribution. In a classical computer, the quantum images are transformed into large matrices, and the simulations of the transformation are implemented by using linear algebraic constructions equivalent to the quantum circuit elements.

To achieve classical numerical simulation, the simulations on encryption process are completed in two stages. In the confusion stage, the simulation is implemented by the corresponding classical generalized Arnold transform. In the diffusion stage, classical binary sequences are used to control the random-phase gates, which makes the angles of the color information different for different positions. Thus, the simulation is implemented differently from the corresponding classical double random-phase encoding. The binary sequences are represented by a matrix with the same size of the image on the software of MATLAB. All the elements of the matrix are only 0 and 1, and the matrix is used to control the random-phase mask (random-phase matrix). If the matrix element is 1 in one position, the random-phase matrix element is replaced by 1 in the corresponding position. Then, the random-phase encoding can be implemented by the random-phase matrix and the image matrix point multiplication.

According to the definition of the generalized Arnold transform, the independent parameters of coefficient matrices \(t\) and \(m\) are any positive integers, which makes the determinant of coefficient matrix to be 1. The period of the generalized Arnold transform is connected with image size. The pixel size of all the images is \(512\,\times \,512\). Thus, the period of the generalized Arnold transform can be computed as \(T=384\). If the iterative times is not exactly a multiple of the period, the generalized Arnold transform can scramble the positions of image pixels. Therefore, one has a chance to select these parameters randomly to some degree. The parameters in simulation are set as: \(t=600\), \(m=300\) and \(k=45\). The binary sequences and random-phase matrices are generated by the random number generation function in MATLAB R2012a (version 7.14.0.739). The plaintext image is Lena shown in Fig. 6a, and the corresponding cipher image is shown in Fig. 6b.

Fig. 6
figure 6

a Plaintext image Lena, b cipher image

Full size image
Fig. 7
figure 7

Correlation distributions of two horizontally adjacent pixels: a original image Lena and b encrypted image

Full size image

5.1 Statistical analysis

Statistical analysis has been performed with the proposed quantum image encryption algorithm to demonstrate its confusion and diffusion properties.

5.1.1 Correlation of adjacent pixels

Generally, each pixel in the plaintext image is highly correlated with its adjacent pixels in horizontal, vertical or diagonal directions. To test the correlations of adjacent pixels in Lena and encrypted Lena, 8,000 pairs of two adjacent pixels are randomly selected from horizontal, vertical and diagonal directions, respectively. The correlation coefficient can be calculated by

$$\begin{aligned} C_{xy} =\frac{\sum \limits _{i=1}^N {(x_i -\bar{{x}})(y_i -\bar{{y}})} }{\sqrt{\sum \limits _{i=1}^N {(x_i -\bar{{x}}} )^{2}\sum \limits _{i=1}^N {(y_i -\bar{{y}})^{2}} }} \end{aligned}$$
(29)
Fig. 8
figure 8

Correlation distributions of two vertically adjacent pixels: a original image Lena and b encrypted image

Full size image
Fig. 9
figure 9

Correlation distributions of two diagonally adjacent pixels: a original image Lena and b encrypted image

Full size image
Table 1 Correlation coefficients of adjacent pixels
Full size table
Fig. 10
figure 10

a Peppers; b encrypted Peppers; c histogram of Peppers; d histogram of Lena; e histogram of encrypted Peppers; and f histogram of encrypted Lena

Full size image

where \(\bar{{x}}=\frac{1}{N}\sum \limits _{i=1}^N {x_i}\) and \(\bar{{y}}=\frac{1}{N}\sum \limits _{i=1}^N {y_i}\). Figures 7,  8, 9 give the correlation distribution of horizontally, vertically and diagonally adjacent pixels in the plaintext image “Lena” and its corresponding cipher image. The results of correlation coefficients for the original images and their corresponding encrypted images are compiled in Table 1. The correlation of the plaintext is close to 1 in each direction of each component, while the correlation of the encrypted image is close to 0 in each direction. That is to say, the proposed algorithm removes the tight correlation among adjacent pixels of the original image successfully. The results demonstrate that the attackers cannot obtain useful information according to the statistical analysis.

5.1.2 Histogram analysis

The histogram is one of the most important statistical characteristics of an image and represents the frequency of all the gray-level values from all over the image. Figure 10a is the gray image Peppers which is obviously different from the image Lena shown in Fig. 6a, and it comes to the same conclusion by comparing their histograms shown in Fig. 10c, d, respectively. The two images are encrypted under the same conditions. The encrypted result of peppers is shown in Fig. 10b. Figure 10e, f are the histograms for encrypted Lena and encrypted Peppers, and they are quite similar. After a number of parallel experiments, it can be concluded that the ciphertext of different original images have similar histograms. Thus, the attackers cannot obtain useful information according to the statistical properties.

5.1.3 Information entropy

Entropy is a statistical measure of randomness to characterize the texture of an image. The entropy \(H\left( s \right) \) of a message source \(s\) can be calculated as

$$\begin{aligned} H\left( s \right) =-\sum _{i=0}^{2^{N}-1} {p\left( {s_i } \right) \log _2 p\left( {s_i } \right) } \end{aligned}$$
(30)

where \(p\left( {s_i } \right) \) represents the probability of symbol \(s_i\) and the entropy is expressed in bits. The ideal entropy value for an encrypted image should be 8 bits [42]. For a cryptosystem able to resist the entropy attacks, the entropy of the ciphertext should be close to the ideal value [43, 44]. The entropy of the six original images and their corresponding encrypted images are computed and listed in Table 2. From Table 2, one can see that the entropy of encrypted images is very close to the theoretical value. The increase in entropy reflects that the distribution of gray scale becomes more even. Therefore, the encryption algorithm is secure against the entropy attack.

Table 2 Information entropy of original and encrypted images
Full size table

5.2 Key space analysis

The key space of a good image encryption algorithm should be large enough to make brute-force attack invalid. In the proposed algorithm, assuming key space for generalized Arnold transform is \(S_1\) and key space for double random-phase encoding is \(S_2\) then the key space of the entire algorithm is \(S_1 \times S_2\). The keys are composed of the independent parameters \(t\) and \(m\) of coefficients matrix, iterative times \(k\), binary sequences \(K=k_0 k_1 \ldots k_{2^{2n}-1}\) and \(D=d_0 d_1 \ldots d_{2^{2n}-1}\). The key space for the generalized Arnold transform is estimated to be \(S_1 \approx 10^{8}\). The key space for the binary sequences is about \(S_2 =4^{512\times 512}\). The total key space is a very huge number, and thus, the proposed algorithm can resist the brute-force attack.

5.3 Key sensitivity analysis

Key sensitivity is an essential factor for any good cryptosystem, which ensures the security of the cryptosystem against the brute-force attack. According to the properties of the generalized Arnold transform, the parameters of coefficients matrix \(t\) and \(m\) are any positive integers, so we can select the parameters randomly to some extent. The period of the generalized Arnold transform is connected with image size. In the simulation, the iteration number in the encryption process is \(k=45\), and thus, the iteration number in the decryption process should be multiple of \(T-k=339\). The attacker cannot obtain the correct original image if he decrypts the image with the wrong iteration number of the generalized Arnold transform. To analyze the key sensitivity, six groups of keys are used to decrypt the cipher image. The simulation results are shown in Fig. 11a–f. Figure 11a is the decrypted image with the correct keys. Figure 11b gives the decrypted image with an incorrect independent parameter \(t\), while the other keys are all correct. Figure 11c shows the decrypted image with an incorrect independent parameter \(m\), while the other keys are all intact. Figure 11d shows the decrypted image with a wrong iterative times, while the other keys are all right. Figure 11e gives the decrypted image with an incorrect binary sequence \(K\), while the other keys are all correct. Figure 11f shows the decrypted image with an incorrect binary sequence \(D\), while the other keys are all intact. From the results, it is shown that the image can be reconstructed correctly iff the decryption keys are all right. For a large key space, it is difficult to reconstruct the plain image if the key distribution is unknown.

Fig. 11
figure 11

Decrypted images with: a correct keys; b incorrect independent parameter \(t=601\); c incorrect independent parameter \(m=301\); d wrong iterative times \(k=46\); e incorrect binary sequence \(K\); f incorrect binary sequence \(D\)

Full size image

5.4 Performance comparison

5.4.1 Diffusion and confusion

Since Yang et al. presented a novel gray-level image encryption scheme based on QFT and double random-phase encoding technique, it is meaningful to compare the proposed algorithm with Yang et al.’s scheme. This is the reason why we introduced the generalized Arnold transform into quantum image encryption. Moreover, we also compared the proposed algorithm with the method only utilizing the Arnold transform. The correlations for the proposed algorithm, Yang et al.’s scheme and the Arnold transform method are shown in Table 3. It can be seen that the correlation of the proposed quantum encryption algorithm is much weaker than the other two methods.

The security of the proposed encryption system depends on not only the number of keys, but also the cryptosystem structure. Generally, for a secure encryption algorithm, the cryptosystem structure meets the principle of confusion and diffusion in cryptography. The encryption algorithm based on QFT and double random-phase encoding can be considered as a kind of encryption of the gray-level information. It is well known that Arnold transform has the characteristics of chaotic mapping. However, it can only scramble the position information of quantum image. The proposed encryption algorithm implements quantum image encryption by combining generalized Arnold transform with double random-phase encoding technology, which helps to realize the diffusion and confusion of the image information. What’s more, the parameters and iteration times of generalized Arnold transform are the keys, which enlarges the key space and consequently enhances the security further.

Table 3 Correlation of three algorithms for encrypted Lena
Full size table

5.4.2 Computational complexity

Assume that \(M\) is a \(2^{n}\,\times \,2^{n}\) original image. There are \(2^{2n}\) pixels in the original image. The computational complexity of the proposed encryption algorithm depends very much on what is considered to be elementary gate. We choose the Control-NOT gate, NOT gate and phase gate to be basic units. The Toffoli gate can be realized by six Control-NOT gates [41]. The numbers of elementary gates in basic carry and sum operations are 13 and 2, respectively. The plain adder includes \(2n-1\) carry operations, \(n\) sum operations and one Control-NOT gate. Consequently, the elementary gates of the plain adder are \(28n-12\). Because the architecture of \(\hbox {ADDER-MOD}2^{n}\) is same as the plain adder, the elementary gates of \(\hbox {ADDER-MOD}2^{n}\) are \(28n-12\). So, the generalized Arnold transform needs \(\left( {tm+t+m} \right) \left( {28n-12} \right) \) basic gates. The QFT operation needs \(\frac{n\left( {n-1} \right) }{2}\) basic gates. The complexity of random-phase operation is \(O\left( n \right) \). Thus, the total computational complexity of the encryption algorithm is \(O\left( {n^{2}} \right) \). By analyzing the corresponding classical image encryption algorithm, the computational complexity of the generalized Arnold transform is \(O\left( {2^{2n}} \right) \). The classical random-phase encoding is realized by using \(2^{2n}\) multiplication operations. The computational complexity of the classical Fourier transform operation is \(O\left( {n2^{2n}} \right) \). Therefore, the total computational complexity is \(O\left( {n2^{2n}} \right) \). Therefore, the proposed encryption algorithm takes advantage over its classical counterparts in terms of computational complexity.

6 Conclusion

A quantum version of generalized Arnold transform is defined, and its quantum circuit is suggested. By combining generalized Arnold transform with double random-phase encoding, a quantum image encryption algorithm is proposed. The encryption process can be realized by performing generalized Arnold transform and double random-phase operations on positions information and gray-level information of the quantum image, respectively. The independent parameters, the iterative times of the generalized Arnold transform and the classical binary sequences are used as the keys, therefore, the key space of the proposed algorithm is very large. Simulation results show the validity and the reliability of the image encryption algorithm. Moreover, the proposed image encryption algorithm has lower computational complexity than its classical counterparts.