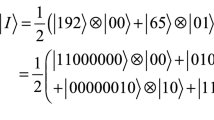1 Introduction

Feynman proposed the quantum computer model in 1982 [1]. The model uses the superposition and entanglement properties of quantum mechanics to store, process and transmit information. It has higher computing power compared to normal computers. Subsequently, Shor and Grover proposed quantum prime factorization algorithm [2] and quantum search algorithms [3] respectively. Therefore, the quantum computers began to appear in various fields of computer science. Such as quantum cryptography [4,5,6], quantum communication [7, 8], quantum image encryption and so on. Among them, quantum image encryption has become more and more important in recent years because it is more secure and efficient than traditional image encryption [9].

However, the digital image is converted into a quantum image before performing the quantum processing. Thus there are some quantum image representation methods are proposed. In 2003 Bose proposed the Qubit Lattice representation method [10]. The image is considered as a matrix and each qubit stores only one pixel. In 2010, a flexible representation of quantum images (FRQI) was proposed [11], an algorithm that represents color information as an angle. For an image of size 2n × 2n, its horizontal and vertical coordinates are expressed in n qubits. However, FRQI uses only one qubit to represent the color information, so it is not easy to perform some complex color manipulation. To address this problem, the novel enhanced quantum representation (NEQR) [12] was proposed in 2013. The total number of qubits required in NEQR is q + 2n for a gray range \(0\sim 2^{q}-1 \) image with size of 2n × 2n. Although it increases the use of qubits, it facilitates the handling of colors. It has also become a more widely used image representation model in quantum image processing. There are other quantum image representation models, such as the generalized quantum image representation (GNEQR) model [36], FRQIM [38] by slightly modifying FRQI, the normal arbitrary superposition state (NASS) model [13] and the multi-channel quantum image (MCQI) model [38], which improve the efficiency of specific applications.

According to the characteristics and convenience of various quantum image representation methods, NEQR and its improved method GNEQR are often used for time domain image encryption [15,16,17, 39], and FRQI and its improved method FRQIM are often used for frequency domain image encryption [19, 20, 40, 41]. Time-domain image encryption scheme generally encrypts images by scrambling pixel positions and changing pixel values. For example, in [15], a three-level quantum image encryption algorithm based on Arnold transform and logistic mapping is proposed, which performs block-level permutation, bit-level permutation and pixel-level diffusion respectively. The key space is increased by setting different block sizes as well as Arnold transform parameters. In 2019, Li et al. proposed a block image encryption algorithm based on GNEQR [16]. It is not only applicable to grey-scale and color images, but also can be used for rectangular images. The scheme uses both geometric and bit-plane transformations to change the position and pixel values of the image. Frequency-domain encryption are more complicated than the encryption algorithms over the time domain. Because they usually convert the image to the frequency domain for encryption while maintaining permutation and diffusion operations. There are some encryption schemes in frequency domain. For example, in [19], it proposes a quantum image encryption algorithm based on Arnold permutation and wavelet transform, which combines the time domain and frequency domain permutation to achieve good encryption results. The algorithm uses a modified FRQI model to represent the image. In [41], it uses Fibonacci transform and geometric transform to scramble the position and double random-phase encoding to encode the pixel information. There are some encryption schemes that only disturb the frequency domain characteristics of the image. For example, the algorithms in [18] use the double random phase encoding (DRPE) technique for quantum image encryption in the Fourier transform domain. Then the paper [18] is improved by Du, he makes the results of the double random phase coding as uniformly mixed as possible in [20].

In recent years, chaotic maps are often used to image encryption due to the features of sensitivity to initial values, a period and pseudo randomness [37]. Therefore, we propose a quantum image encryption method based on chaotic mapping and Fourier transform in time-frequency domain. Considering that most encryption operations are performed in the time domain, we choose NEQR as the representation method of quantum images. We incorporate the idea of selective encryption [24] into it to equalize histogram of cipher image. Selective encryption first to block the image. Then, different operations are performed on the image block according to whether the correlation coefficient in the block is greater than the threshold. The main advantages of this scheme as follows: (1) Associate the key with the plain image. It can effectively resist chosen-plaintext attack. (2) Equalize histogram of encrypted image. It can remarkably resist statistical attack. (3) The introduction of QFT increases the complexity of the encryption scheme.

The remainder of this paper is organised as follows. Section 2 presents some preliminary knowledges. The proposed encryption and decryption schemes are presented in Section 3. Section 4 presents simulations and security evaluations of the scheme. Finally, the conclusion is presented in Section 5.

2 Preliminary

Before introducing the background, we agree on some symbols in Table 1.

Table 1 Notation Convention
Full size table

2.1 NEQR representation and quantum computation model

In [28], Zhang et al. presented the NEQR representation of quantum image. The digital image I can be stored into a normalized superposition state |I〉, that is, the proposed NEQR model stores the gray-scale and position information of the image using the superposition of the qubit sequences.

The NEQR model of a quantum image |I〉 for a 2n × 2n image can be written as

$$ |I\rangle=\frac{1}{2^{n}}\sum\limits_{Y=0}^{2^{n}-1}\sum\limits_{X=0}^{2^{n}-1} |C_{YX}\rangle|YX\rangle, $$
(1)

where the gray-scale value of the corresponding pixel (Y, X) is

$$ |C_{YX}\rangle=|C_{YX}^{0}C_{YX}^{1}{\cdots} |C_{YX}^{q}\rangle\in [0, 2^{q}-1], C_{YX}^{i}\in \{0, 1\}. $$

While the vertical position Y and horizontal position X are represented with qubits |Y X〉. Thus, in the representation of NEQR, a quantum image with the gray-scale 2q and position information 2n × 2n consists of q + 2n qubits.

Next we introduce the quantum computation model. Quantum computation consists of a series of quantum logic gates and measurement results. It can accepts superposition states input and outputs corresponding superposition states. The special quantum computation model is as follow

$$ U_{f}:|x, 0\rangle \rightarrow |x, f(x)\oplus 0\rangle , $$
(2)

where f is any function and Uf is a unitary operator [31].

2.2 Discrete Baker map (DBM) and quantum DBM

Baker mapping is a block scrambling method, and at the same time, selecting encryption requires dividing the image into blocks. That’s why Baker mapping was chosen for scrambling. The classical Baker map B(x, y), which maps the unit square 0 ≤ x, y ≤ 1 onto itself, is a special chaotic map in [29]. Classical Baker map B(x, y) is described as follows

$$ B(x,y)=\begin{cases} (2x,\frac{y}{2}),\hfill0 \leq x<1/2\\ (2x-1,\frac{y+1}{2}),\hfill1/2\leq x\leq1, \end{cases} $$
(3)

where y ∈ [0,1]. In other words, as shown in Fig. 1, the classical Baker map maps the left rectangle of the square \([0, \frac {1}{2})\times [0,1)\) to rectangle \([0,1)\times [0, \frac {1}{2})\), and it transforms the right rectangle of the square \([\frac {1}{2},1)\times [0,1)\) to rectangle \([0,1)\times [\frac {1}{2},1)\).

Fig. 1
figure 1

Baker Map

Full size image

The Baker map used for image encryption needs to be discretized because each image is composed of discrete pixel values. The Baker map can be discretized in the following.

Assume ni|N(i = 1, ⋯ , k) and n1 + n2 + ... + nk = N, N ∈ Z+. The discrete Baker Map is defined as follows. Firstly, it divides the image BN×N into N blocks, i.e.

$$B_{11},\cdots,B_{1n_{1}},B_{21},\cdots,B_{2n_{2}},\cdots,B_{k1},\cdots,B_{kn_{k}} $$

where Bij is a matrix of \( \frac {N}{n_{i}} \) rows and ni columns, i = 1, ⋯ , k, j = 1, ⋯ , ni. Secondly, it performs matrix vec operator [30] on Bij to obtain B1N×N, i.e.

$$ B1_{N\times N}=\left[ \begin{array}{c} vec^{T}(B_{11}) \\ {\vdots} \\ vec^{T}(B_{ij}) \\ {\vdots} \\ vec^{T}(B_{kn_{k}}) \end{array} \right]=\left[ \begin{array}{c} B1_{11} \\ {\vdots} \\ B1_{ij} \\ {\vdots} \\ B1_{kn_{k}} \end{array} \right] $$
(4)

where B1ij is a matrix of 1 row and N columns. For example, let N = 4, n1 = 1, n2 = 2, n3 = 1, the discrete Baker Map is as shown in Fig. 2.

Fig. 2
figure 2

Discrete Baker Map

Full size image

For an example with N = 4 in Fig. 2, we give a concrete quantum circuit of the quantum Baker map. The quantum analogy of classical image BN×N is |I〉, and its NEQR representation is expressed as

$$ \begin{array}{@{}rcl@{}} |I\rangle&&=\frac{1}{4}\Big(|C_{0000}\rangle|0000\rangle+|C_{0100}\rangle|0100\rangle+|C_{1000}\rangle|1000\rangle+|C_{1100}\rangle|1100\rangle+\\ &&~~~~~~~~~~|C_{0001}\rangle|0001\rangle+|C_{0101}\rangle|0101\rangle+|C_{1001}\rangle|1001\rangle+|C_{1101}\rangle|1101\rangle+\\ &&~~~~~~~~~~|C_{0010}\rangle|0010\rangle+|C_{0110}\rangle|0110\rangle+|C_{1010}\rangle|1010\rangle+|C_{1110}\rangle|1110\rangle+\\ &&~~~~~~~~~~|C_{0011}\rangle|0011\rangle+|C_{0111}\rangle|0111\rangle+|C_{1011}\rangle|1011\rangle+|C_{1111}\rangle|1111\rangle\Big). \end{array} $$

Apply the quantum Baker map on quantum image |I〉, and we obtain the new quantum image \(|I^{\prime }\rangle \). That is,

$$ \begin{array}{@{}rcl@{}} |I^{\prime}\rangle&=& U_{QBM}|I\rangle=\frac{1}{4}\Big(|C_{0000}\rangle|0000\rangle+|C_{0001}\rangle|0100\rangle+|C_{0010}\rangle|1000\rangle+|C_{0011}\rangle|1100\rangle\\ &&+|C_{0100}\rangle|0001\rangle+|C_{0101}\rangle|0101\rangle+|C_{1000}\rangle|1001\rangle+|C_{1001}\rangle|1101\rangle\\ &&+|C_{0110}\rangle|0010\rangle+|C_{0111}\rangle|0110\rangle+|C_{1010}\rangle|1010\rangle+|C_{1011}\rangle|1110\rangle\\ &&+|C_{1100}\rangle|0011\rangle+|C_{1101}\rangle|0111\rangle+|C_{1110}\rangle|1011\rangle+|C_{1111}\rangle|1111\rangle\Big), \end{array} $$

and its quantum circuit is shown in Fig. 3.

Fig. 3
figure 3

Quantum circuit of QBM

Full size image

2.3 2D Logistic Map

The 2D Logistic Map [32] is defined as follows

$$ \begin{cases} x_{1}(n+1)=\mu_{1}x_{1}(n)(1-x_{1}(n))+\gamma_{1}{x_{2}^{2}}(n)\\ x_{2}(n+1)=\mu_{2}x_{2}(n)(1-x_{2}(n))+\gamma_{2}(x_{1}(n)+x_{1}(n)x_{2}(n)) \end{cases} $$
(5)

where x1(n), x2(n) ∈ (0,1) and 2.75 < μ1 ≤ 3.4, 2.7 < μ2 ≤ 3.45, 0.15 < γ1 ≤ 0.21, 0.13 < γ2 ≤ 0.15. The 2D Logistic Map can ensure the keyspace larger and the encryption system more complex since there are two quadratic terms in the 2D Logistic Map.

3 Quantum image encryption scheme

In this section, the quantum image encryption scheme based on Baker map, 2D logistic map and quantum Fourier transform is presented in detail. The whole quantum image scheme has three main parts including key generation, encryption process and decryption process. More details can be introduced in the following subsections.

3.1 Key generation

Let the original classical image with size 28 × 28 be denoted as I. We use 2D logistic map to generate pseudo-random numbers with good cryptographic characteristics as the key. The specific steps are as follows.

Step 1. Caculate offset

a) Apply the discrete Baker map B(x, y) on classical image I, then it obtains a new image \(I^{\prime }\) denoted as \(I^{\prime }=B1_{N\times N}\) through equation (4).

b) Let B111 = (b11, ⋯ , b1N) be a vector from B1N×N, where b1k ∈ [0,255], k = 1, ⋯ , N. Apply operation dec2bin(⋅) on b1k of B111, and it has dec2bin(b1k) = (b1k)2 = (ek1, ⋯ , ekl)T, where ekl ∈{0,1} and l = 1, ⋯ , 8. Thus we obtain a 8 × N binary matrix \( BM=((b_{11})_{2}^{T},\cdots ,(b_{1N})_{2}^{T}) \).

c) Perform bitwise XOR operation on each row of BM, i.e., \( \alpha _{l}=\bigoplus _{k=1}^{N}e_{kl}, \alpha _{l}\in {{0,1}}, l=1,\dots ,8 \). Then, it obtains E = (α1, ⋯ , α8)T.

d) Perform bin2dec(⋅) operation on E, and it obtains bin2dec(E) = E10 = α7 × 27 + ⋯ + α1 × 20 and denotes E10 as the offset ∈ [0,255].

For example, let N = 8, the above calculation process of offset is shown in Fig. 4.

Fig. 4
figure 4

Block binary XOR

Full size image

Step 2. Update the initial values of the 2D logistic map.

Suppose the initial values of the 2D logistic map are x1(0)′, x2(0)′. The offset that is obtain in Step 1 will be mapped to (0,1) by equation δ(s, offset). The δ(s, offset) is defined as follows

$$ \delta(s,\textit{offset})=\lfloor\frac{10^{s}\times\textit{offset}}{257}\rfloor\times10^{-s}, \textit{offset}\in[0,255] $$
(6)

where symbol ⌊⋅⌋ is a floor function and s is a given value. In this paper, we convention s = 4.

Add the result of δ(s, offset) to x1(0)′, x2(0)′, and obtain the modified initial values x1(0), x2(0) i.e.,

$$ \begin{cases} x_{1}(0)=\left\lbrace x_{1}(0)'+\delta(s,\textit{offset})\right\rbrace \\ x_{2}(0)=\left\lbrace x_{2}(0)'+\delta(s,\textit{offset})\right\rbrace \end{cases} $$
(7)

where x1(0)′, x2(0)′ are given initial values and \( \left \lbrace x\right \rbrace \) is the fractional part of x.

Step 3. Generate key

Modified initial values will be used to generate the key. Substituting x1(0), x2(0) into equation (5), the equation yields two chaotic sequences x1 = (x1(1), ⋯ , x1(N/2)) and x2 = (x2(1), ⋯ , x2(N/2)). The chaotic sequences x1, x2 are mapped to \( \left [ 1,255\right ] \) using the equation as follows

$$ g(u)=floor(255u)+1 $$
(8)

where u ∈ (x1(1), ⋯ , x1(N/2), x2(1), ⋯ , x2(N/2)).

The mapped values g(u) are considered as

$$ k=\Big(g(x_{1}(1)),\dots,g(x_{1}(N/2)),\cdots, g(x_{2}(1)),\dots,g(x_{2}(N/2))\Big). $$

It shorted by \( k=(k_{1},\dots ,k_{N}) \).

Finally, after performing the dec2bin(⋅) function on k, we obtain the classical information k2 = dec2bin(k1) ⊕⋯ ⊕ dec2bin(kN) as the encryption key.

3.2 Encryption process

Alice and Bob secretly transmit image information using quantum technology. The encryption process involves the following steps.

Step 1. Let \(C_{Y^{\prime }X^{\prime }}\) be the corresponding discrete pixel values of image \(I^{\prime }\). Alice calculates \(A=floor(\frac {1}{N^{2}}{\sum }_{Y^{\prime }, X^{\prime }}C_{Y^{\prime }X^{\prime }})\) from \(I^{\prime }\) and selects a random number T ∈ [0,255]. Alice sends the binary sequence (k2, dec2bin(A)) to Bob through quantum key distribution protocol such as BB84 protocol.

Step 2. Initialization of the quantum state.

After performing the quantum Baker map (QBM) on I, and Alice obtains quantum image with size 28 × 28 denoted as \(|I^{\prime }\rangle \), and its NEQR representation is expressed as

$$ \begin{array}{@{}rcl@{}} |I^{\prime}\rangle&&=|T\rangle U_{QBM}|I\rangle\\ &&=\frac{1}{2^{n}}\sum\limits_{Y^{\prime}=0}^{2^{n}-1}\sum\limits_{X^{\prime}=0}^{2^{n}-1} |C_{Y^{\prime}X^{\prime}}\rangle|Y^{\prime}X^{\prime}\rangle\\ &&=\frac{1}{2^{n}}\sum\limits_{Y=0}^{2^{n}-1}\sum\limits_{X=0}^{2^{n}-1} |C_{Y^{\prime}X^{\prime}}\rangle|y^{\prime}_{0}y^{\prime}_{1}\cdots y^{\prime}_{n-1}\rangle|x^{\prime}_{0}x^{\prime}_{1}{\cdots} x^{\prime}_{n-1}\rangle. \end{array} $$

Step 3. Alice computes \(C_{Y^{\prime } X^{\prime }}- T\) and stores the result on a auxiliary qubit |0〉a. If \(C_{Y^{\prime } X^{\prime }}\geq T (C_{Y^{\prime } X^{\prime }}<T)\), the auxiliary qubit |0〉a = |1〉(|0〉a = |0〉).

Step 4. If |0〉a = |1〉(|0〉a = |0〉), then Alice performs the unitary operation U⊕k(U⊕A) on quantum states \(|I^{\prime }\rangle \) and sequentially performs quantum Fourier transform (QFT) on it.

Step 5. Alice iterates the quantum Baker Map (QBM) nine times and obtains cipher image \(|C\rangle =|0\rangle _{a}|T\rangle |C^{\prime }_{YX}\rangle |YX\rangle \). After at least nine iterations, the original adjacent pixels will be distributed to the entire scrambled image [29]. That’s the reason for the nine iterations of QBM.

The flowchart of the proposed quantum image encryption is demonstrated in Fig. 5, and the corresponding quantum circuit in Fig. 6.

Fig. 5
figure 5

Encryption process

Full size image
Fig. 6
figure 6

Quantum circuit of encryption process

Full size image

Note that the unitary operation U denotes as an inverse quantum adder operation in Fig. 6.

3.3 Decryption process

Step 1. Iterate discrete inverse quantum Baker Map (IQBM) on the entire cipher image |C〉 ten times, and the transformed image is still denoted as |C〉.

Step 2. Bob performs the inverse quantum Fourier transform (IQFT) on |C〉.

Step 3. Bob applies the control unitary operation C − U on plain image. If the control qubit is |1〉(|0〉), then the C − U is equivalent to C − U⊕k(C − U⊕A).

Step 4. Bob performs the inverse quantum Baker Map (IQBM) and obtains plain image I.

The flowchart of quantum image decryption is demonstrated in Fig. 7, and the corresponding quantum circuit in Fig. 8.

Fig. 7
figure 7

Decryption process

Full size image
Fig. 8
figure 8

Quantum circuit of decryption process

Full size image

Note that the unitary operation U− 1 denotes as the quantum adder operation in Fig. 8.

4 Simulation Results

The experiments are performed on MATLAB R2018a. We use 256 × 256 images Cameraman, Peppers, Baboon, Lake and Lena to test the security performance of the encryption scheme. The security performance indicators include visual inspection, keyspace, entropy, encryption quality, histogram and differential analysis. The key of the encryption scheme is composed of (n1, ⋯ , nk;x1(0), x2(0), μ1, μ2, γ1, γ2). Set the key to (64, 32, 4, 8, 4, 16, 32, 64, 16, 16; 0.5, 0.5, 3, 3, 0.2, 0.14) during the experiment.

4.1 Visual Inspection

In evaluating the ciphered image, visual inspection is the easiest and most remarkable factor. The five original images and their corresponding encrypted images are shown in Fig. 9, there is a big difference between the original images and the ciphers. Thus the proposed scheme can hide the main information of the original images.

Fig. 9
figure 9

Encryption result. a: original Cameraman. b: original Peppers. c: original Baboon. d: cipher Lake. e: cipher Lena. f: cipher Cameraman. g: cipher Peppers. h:cipher Baboon. i:cipher Lake. j:cipher Lena

Full size image

4.2 Keyspace

In the permutation stage, the key relies on the width (height) of the image to be encrypted due to the scrambling phenomenon of the chaotic Baker map. Thus, the keyspace of size 256 × 256 is equal to 1063 [23]. In the substitution stage, every parameter of the logistic map is a double precision number [23]. Thus, the keyspace in this stage is 1014 × 1014 × 1014 × 1014 × 1014 × 1014 = 1084. Such a large keyspace is enough to resist brute-force attacks.

4.3 Entropy

Entropy is an unpredictability measurement of structural characteristics for a cipher image x. The formula is defined as [22]

$$ E(x)=-\sum\limits_{i=0}^{2^{N}-1}P(x_{i})\log_{2}P(x_{i}) $$
(9)

where N is the number of bits for the pixel value xi. In this paper, let N = 8. P(xi) is the proportion of pixel value xi ∈ [0,255] in the encrypted image x. To attach high-level security, the entropy E(x) should be close to 8. The entropy values of the cipher image corresponding to Cameraman, Peppers, Baboon, Lake and Lena are 7.983, 7.9854, 7.9812, 7.9888 and 7.9812 respectively as shown in Table 2. It shows that the proposed scheme has the unpredictability of structural characteristics.

Table 2 Entropy of encrypted images
Full size table

4.4 Encryption Quality

In this section, correlation coefficient(CC), histogram deviation(HD), and irregular deviation(ID) have been calculated to evaluate the encryption quality.

CC is used to evaluate the correlation between plain image and cipher image. The value of CC is \( \left [ -1,1\right ] \). If the absolute value of CC equals to 1 that means the two images are the same. Thus, the lower absolute value of CC is, the better. The CC is measured by [22]

$$ CC(x,y)=\frac{{\sum}_{i=1}^{N}(x_{i}-E(x))(y_{i}-E(y))}{\sqrt{{\sum}_{i=1}^{N}(x_{i}-E(x))^{2}}\sqrt{{\sum}_{i=1}^{N}(y_{i}-E(y))^{2}}} $$
(10)

where \( E(x)=\frac {1}{N}{\sum }_{i=1}^{N}x_{i} \), N defines the pixel count in the image, and x, y are the pixel values of the plain image and encrypted image respectively.

The histogram deviation(HD) calculates the gap between the histogram of the original image and the histogram of the encrypted image and it can be defined as [22]

$$ HD=\frac{{\sum}_{i=0}^{255}|h_{1}(i)-h_{2}(i)|}{W\times H} $$
(11)

where W(Width) and H(Height) are the size of the image, and h1(i), h2(i) define the histogram of original image and enciphered image at value i respectively. The higher the HD value is, the better.

The histogram of an ideal encrypted image should keep each pixel level containing the same pixels. For example, for a 512 × 512 encrypted image, each pixel level should contain 512 × 512/256 = 1024 pixels. The irregular deviation(ID) measures the gap between the histogram of the cipher image and the histogram of the ideal encrypted image. The equation is [22]

$$ ID=\frac{{\sum}_{i=0}^{255}(\left|h(i)-M \right| ) }{W\times H} $$
(12)

where h(i) is enciphered image histogram at value i, and M is the average of an ideal enciphered image histogram. Given an image of size 256 × 256, M is set to 256. The smaller the ID value, the histogram of the encrypted image is closer to the histogram of the ideal encrypted image. Thus, the target is to attach the lower value of ID.

As shown in Table 3, the CC value of the encrypted Cameramen, Peppers, Baboon, Lake, Lena are 0.0025, -0.0005, -0.0024, -0.002 and -0.0061 respectively. It shows that the plain images and cipher images with a low correlation. The mean of HD is 0.8175. It shows that the difference between plain images and cipher images encrypted by the proposed scheme is large. The histograms of the cipher images are close to ideal histogram due to the ID values of five encrypted images are near to 0.1.

Table 3 CC, HD and ID of encrypted images
Full size table

4.5 Histogram Analysis

The histograms of the plain images and cipher images are shown in Fig. 10. It proves that the histograms of the cipher images are different from the plain one. The cipher images have a uniformed histogram due to change the pixel value in time domain, which can resist statistical attacks better. The proposed scheme hides the histogram features well.

Fig. 10
figure 10

Histograms of original images and cipher images. a: original Cameraman. b: original Peppers. c: original Baboon. d: cipher Lake. e: cipher Lena. f: cipher Cameraman. g: cipher Peppers. h:cipher Baboon. i:cipher Lake. j:cipher Lena

Full size image

4.6 Differential Analysis

In order to resist differential attacks, a good encryption scheme should be sensitive to small changes in the key. There are two parameters used for differential analysis, namely Number of Pixel Change Rate (NPCR) and the Unified Averaged Changed Intensity (UACI), described as follows [22]

$$ NPCR=\frac{{\sum}_{i,j}D(i,j)}{W\times H}\times100\%, $$
(13)
$$ UACI=\frac{1}{W\times H}\left[ \sum\limits_{i,j}\frac{E_{1}(i,j)-E_{2}(i,j)}{255} \right]\times100\% $$
(14)

where E1 and E2 are two different cipher images of size W × H. If the pixel values of E1 and E2 at position (i, j) are different, that is, E1(i, j)≠E2(i, j), then D(i, j) = 1. There will be a big gap between E1 and E2 if the values of NPCR and UACI are big and it shows that the proposed scheme is sensitive to key. The original key is used to encrypt the original image to obtain cipher image E1. After that we exchange the position of the key n2 and n3, and keep other parameters unchanged. Then, the changed key is used to encrypt the original image to obtain cipher image E2.

The results of NPCR and UACI are shown in Table 4. We observe that the values of NPCR are above 90%. For a 256 gray level image, the expected UACI value is 33% and the UACI value of the Peppers is 33.17%. It means our scheme can resist differential attacks well.

Table 4 NPCR and UACI of encrypted images
Full size table

4.7 Comparative Analysis

To verify the safety of the proposed scheme, various experiments have been carried out to compare the security based on entropy, CC, NPCR and UACI.

The comparative study between the proposed quantum image encryption scheme and other similar quantum image encryption schemes is performed based on the image Peppers. The values of entropy, CC, NPCR and UACI are listed in Table 5 for the proposed and other schemes in [15, 33,34,35]. One can see that the image encrypted by the proposed scheme has the lowest CC value, that is, the correlation of the encrypted image is the lowest. In addition, the results of the experiment indicate that the other key indicators are approximately comparable to those of other scheme.

Table 5 The estimated entropy and others results of the proposed scheme and the related schemes in [15, 33,34,35]
Full size table

5 Conclusion

This paper proposed an image encryption scheme based on QFT and two chaotic maps. The proposed cryptographic system use the selecting encryption method to equalize histogram. If \(C^{\prime }_{YX}\geq T (C^{\prime }_{YX}< T)\), it performs U⊕k(U⊕A) transformation, where the k and A are associated with the plain image. Then use QFT to transform the image to the frequency domain. Finally, we use a QBM to scramble the entire image. From the simulation results, the keyspace of two chaotic maps is enough to resist brute-force attacks. The mean values of CC, HD and ID are 0.0027, 0.8175, 0,1189, which have been demonstrated the security of the proposed scheme. Change the pixel values in the time domain makes the histogram uniform. The key related to the plain image can effectively resist plaintext attacks. The values of NRCR are all above 90%, and the highest is 99.58%. The values of UACI are all around 30%, and the highest is 33.17%. That shows the proposed scheme is sensitive to key. However, this scheme still has some shortcomings, that is, the histogram of the encrypted image is not balanced enough. In the future, the encryption scheme can be optimized to obtain a more evenly distributed histogram.