1 Introduction

In everyday life, people transmit various images through networks. Sometimes, we want to encrypt them to protect important information carried by the images. In 1997, Fridrich proposed the chaos-based image encryption method for the first time [1]. This method can well complete the proliferation and confusion of the cryptosystem and has good security performance. Chaotic system is non-periodic, randomic, ergodic, deterministic and sensitive to initial conditions. Therefore, it is well suited for image encryption. The chaotic image encryption algorithm generates a pseudo-random sequence based on the nonlinear dynamics of the chaotic system, which is used to encrypt image data [2]. Due to the existence of quantum mechanical superposition, quantum computers are far more efficient than classical computers. Moreover, the non-cloned nature of quantum states ensures the security of quantum image encryption.

Quantum image encryption can be divided into three kinds: image encryption based on spatial domain, image encryption based on transform domain, and image encryption based on chaos. Researchers have developed image encryption based on spatial and transform domain in quantum computers. In 2012, Zhou et al. proposed a quantum image encryption algorithm based on quantum image geometric transformations [3]. In 2014, Song et al. raised quantum image encryption based on restricted geometric and color transformations [4]. In 2015, Zhou and Hua et al. introduced a quantum image encryption method based on Arnold transform [5]. Hua et al. proposed a quantum image encryption algorithm based on image correlation decomposition [6].

Besides, some researchers try to develop chaos based quantum image encryption algorithms. Ref. [7] noticed the advantanges of quantum chaos to encrypt classical images. In 2013, El-Latif et al. proposed a new approach to chaotic image encryption based on quantum chaotic system [8]. In 2014, Cao et al. proposed quantum chaotic image encryption with one time running key [9]. In 2015, Seyedzadeh et al. proposed a novel color image encryption algorithm based on spatial permutation and quantum chaotic map [10]. In 2016, Liang et al. gave a quantum image encryption algorithm based on generalized affine transformation and logistic mapping [11]. In the same year, Tan et al. proposed a quantum color image encryption algorithm based on a hyper-chaotic system and quantum Fourier transform [12]. In 2017, Wang et al. proposed a quantum image encryption based on iterative framework of frequency-spatial domain transforms [13]. Li et al. proposed a quantum color image encryption based on multiple discrete chaotic systems [14]. In 2018, Zhou et al. proposed bit-level quantum color image encryption scheme with quantum cross-exchange operation and hyper-chaotic system [15]. Recently, Wang et al. gave a quantum image encryption algorithm based on quantum key image [16, 17]. Although they all have a good encryption effect, the encryption sequences are generated on classical computers, which make them still depend on classical computers.

In this paper, Henon mapping is used to encrypt a quantum image, and it is generated in a quantum computer, which breaks away from the restriction of classical computers and increases the security and convenience. Henon mapping is a two-dimensional chaos map and it has better randomness and security than one-dimensional chaos. However, the sequence obtained from Henon mapping has the problem of uneven distribution, which makes it cannot be directly applied to image encryption. Referring to the improvement of the Henon mapping on traditional computers in Ref. [18], we improve the sequence on quantum computers. On the basis of binary storage, each data is shifted left by 13 digits, and the obtained sequence is ideal. Through a series of analysis, it is found that the Henon-based image encryption on quantum computers is feasible, safe and reliable.

2 Related Works

2.1 Henon Mapping

The commonly used chaotic systems include one-dimensional Logistic maps [19], two-dimensional Henon maps [20], and three-dimensional Lorenz maps [21].

One-dimensional Logistic mapping is too simple and easy to be cracked, and three-dimensional Lorenz is too complex to be realized in quantum computers. Hence, we use two-dimensional Henon mapping to do quantum image encryption.

Henon mapping is defined as shown in (1) [20].

$$ \left\{ \begin{array}{ll} x_{i + 1}= y_{i}+ 1-a{x_{i}^{2}} \\ y_{i + 1}= bx_{i} \end{array} \right. $$
(1)

It can be seen that the Henon mapping is a chaotic map consisted by two variables x and y, where a and b are control parameters. The Henon mapping is more complicated than the one-dimensional mapping. Hence, the generated encrypted image is less easily cracked, which makes it suitable for image encryption algorithms.

2.2 GQIR Representation of Quantum Images

GQIR can represent quantum images of any size H × W, which needs ⌈log2H⌉ + ⌈log2W⌉ + q qubits, where q is the image color depth, ⌈log2H⌉ is the size of the Y -axis coordinate information, and ⌈log2W⌉ is the size of the X-axis coordinate information [22].

An H × W quantum image I can be expressed as

$$ \begin{array}{ll} |I\rangle=\frac{1}{\sqrt{2}^{h+w}}{\sum}_{u = 0}^{H-1}{\sum}_{v = 0}^{W-1}\otimes_{i = 0}^{q-1}|C_{UV}^{i}\rangle|UV\rangle \\ |UV\rangle=|U\rangle|V\rangle=|u_{0}u_{1}{\cdots} u_{h-1}\rangle|v_{0}v_{1}{\cdots} v_{w-1}\rangle,u_{i}v_{i}\in \{0,1\} \\ |C_{UV}\rangle=|C_{UV}^{0}C_{UV}^{1}{\cdots} C_{UV}^{q-1}\rangle,C_{UV}^{i}\in \{0,1\} \end{array} $$
(2)

2.3 Quantum Adder and Quantum Multiplier

Our algorithm needs some quantum modules. Hence, we introduce them in this section.

A quantum adder is a quantum computation circuit that calculates the sum of the values stored in two quantum registers [23]. By assuming that the two quantum registers are a and b, the quantum adder performs the following function and is shown in Fig. 1.

$$|a,b\rangle \to |a,a+b\rangle$$
Fig. 1
figure 1

Quantum adder

Full size image

If the black bar in Fig. 1 is on the left side, its function becomes a subtractive device [23]. The subtractor performs the function and is shown in Fig. 2.

$$|a,b\rangle \to |a,a-b\rangle$$
Fig. 2
figure 2

Quantum subtractor

Full size image

In this paper, we also need an subtractor for output |a − b, a − b〉. Ref. [24] mentions how to get the output of two identical values. We call it as double-output adder (D-ADDER), which can be expressed in the following equation and is shown in Fig. 3.

$$|a,b\rangle \to |a-b,a-b\rangle$$
Fig. 3
figure 3

Quantum double-subtractor

Full size image

Saurabh Kotiyal et al. introduced the quantum multiplier [25]. The quantum multiplier is represented as the following equation and in Fig. 4.

$$|a,b,0\rangle \to |a,b,a \times b\rangle$$
Fig. 4
figure 4

Quantum multiplier

Full size image

3 Quantum Image Encryption Algorithm Based on Henon Mapping

3.1 Encryption

  1. Step 1.

    This step generates the Henon chaotic sequence in a quantum computer, which has the same size as the quantum image to be encrypted. By assuming the size of the original image is 2n × 2n, Eq. (1) is iterated \(\frac {2^{n}\times 2^{n}}{2}+k\) times to get the quantum chaotic sequence, where k is a positive integer. Due to each iteration generates two numbers x and y, \(\frac {2^{n}\times 2^{n}}{2}\) iteration will output 2n × 2n numbers, which has the same size as the image. There are extra k times because the randomness of the beginning part of the Henon chaotic sequence is not good enough. Hence, we take the chaotic sequence from the k + 1 iteration. In general, k = 2 × 104.

For each iteration, as shown in Fig. 5 and according to (1) \(x_{i + 1}=y_{i}+ 1-a{x_{i}^{2}}\), firstly, a D-ADDER is used to get two xi, a MULER is used to get \({x_{i}^{2}}\), and another MULER is used to get \(a{x_{i}^{2}}\). Then, an ADDER helps to get yi + 1. At last, the second and the third D-ADDERs help to get three \(y_{i}+ 1-a{x_{i}^{2}}\), i.e., three xi+ 1. We call it as “First Part”, which is used to generate xi+ 1 and whose inputs include xi, a and yi.

Fig. 5
figure 5

\(x_{i + 1}=y_{i}+ 1-a{x_{i}^{2}}\) quantum circuit diagram

Full size image

The “Second Part” module is for preparing Y sequence: yi+ 1 = bxi as shown in Fig. 6, which uses one MULER model and one D-ADDER to get two bxi, i.e., yi+ 1.

Fig. 6
figure 6

yi+ 1 = bxi quantum circuit diagram

Full size image

The whole circuit for Henon mapping is shown in Fig. 7. All the xi and yi are stored in 21-qubit binary storages. This figure also tells us the reason that “First Part” outputs three xi+ 1: two are used to generate the quantum Henon sequence and the other is reserved as the Henon sequence, i.e., the reserved one is the output of this step. The reason that “Second Part” outputs two yi+ 1 is the same.

  1. Step 2.

    The chaotic sequence \(\{x_{k + 1},y_{k + 1},x_{k + 2},y_{k + 2},\cdots ,x_{k + 2^{2n-1}},y_{k + 2^{2n-1}}\}\) obtained in Step 1 can not be directly used because it it not uniformly distributed. Hence, the idea in Ref. [18] is used to improve the sequence. In decimal system, xi = 10rxi − round(10rxi) is used to map xi to the range [− 0.5,0.5]. In general, r = 4. In this paper, 213 is used to replace 104 because 213 is the closest value to 104 in all 2i and multiplying 213 is easy to realize in quantum binary circuit: omitting the most significant 13 qubits and only reserving the least significant 8 qubits.

  2. Step 3.

    As Fig. 8 shows, the image is XORed with the chaotic sequence \(\{x_{k + 1},y_{k + 1},x_{k + 2},y_{k + 2},\cdots ,x_{k + 2^{2n-1}},y_{k + 2^{2n-1}}\}\) pixel by pixel. For the first pixel |C00〉, a (2n + 1)-CNOT gate (a CNOT gate with 2n + 1 control qubits) is used to do XOR, where 2n qubits (the location information |UV 〉 of the image) are 0-control to ensure that pixel (0,0) is selected and 1 qubit are 1-control to achieve XOR. For the second pixel, |UV 〉 = |00⋯001〉 to ensure that pixel (0,1) is selected. Similarly, the control qubits of the last (2n + 1)-CNOT gate are all 1-control to ensure that the last pixel (2n − 1,2n − 1) is selected.

Fig. 7
figure 7

The quantum circuit of Henon mapping process

Full size image
Fig. 8
figure 8

Comparators combine XOR operation circuits

Full size image

3.2 Decryption

The decryption circuit is exactly the same as the encryption circuit. Firstly, the same Henon chaotic sequence as used in encryption is generated by the circuit shown in Fig. 7. Then, as Fig. 8 shows, the encrypted image is XORed with the chaotic sequence to recover the plain image, because a ⊕ b ⊕ b = a, where a, b ∈{0,1} and ⊕ is the XOR operation.

4 Analysis of the Algorithm

4.1 Visual Effects

We simulate the above steps through Matlab, with initial value x0 = 0.2, y0 = 0.1, a = 1.4, b = 0.3. The experimental results are shown in Fig. 9. It can be seen obviously that the encrypted images seem meaningless, and we can’t see any information about the original images from them. That is to say, our scheme is good enough to protect the original image visually.

Fig. 9
figure 9

Encryption effect: the column on the left shows the original images: a Lena, b Cameraman, c Peppers and d Boats; the column on the right shows the corresponding encrypted images

Full size image

4.2 Statistical Analysis

The ability to resist statistical analysis attacks is an important criterion for judging the advantages and disadvantages of image encryption algorithms. Here, histogram and correlation of adjacent pixels are used.

4.2.1 Histogram

Histogram analysis is performed on the original grayscale image and the encrypted image, the result is shown in Fig. 10. In this figure, “Lena” and “Cameraman” are two examples. (a1) and (b1) are the histograms of the original images, and (a2) and (b2) are the histograms of the encrypted images. Figure 10 tells us that the histogram of the original grayscale image has a large fluctuation and uneven distribution of pixels, while the encrypted image is more evenly distributed. That is to say, after encryption, the numbers of all the 256 colors are almost the same, which makes the entropy approaches the maximum value, i.e., the difficulty of cracking is almost the greatest.

Fig. 10
figure 10

Original image histogram and encrypted image histogram for Lena and Cameraman

Full size image

4.2.2 Correlation of Adjacent Pixels

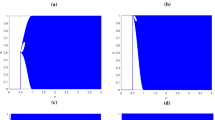
Since a natural image is an information source with memory, it has a high correlation between adjacent pixels. For example, if the current pixel is red, its 8 adjacent pixels are usually red, with very very little difference from the current pixel value. In a Cartesian system, if let I(u, v) as the X-coordinate and I(u, v + 1) as the Y -coordinate, all the pixel-pairs (i.e., a point in the Cartesian system) (I(u, v),I(u, v + 1)) will appear in the vicinity of the 45-degree slash, because I(u, v) ≈ I(u, v + 1). Figure 11(c1) and (d1) take “Peppers” and “Boats” as examples to show their adjacent pixel correlation. All the dots roughly compose a 45-degree slash.

Fig. 11
figure 11

Adjacent pixel correlation analysis of original image and encrypted image

Full size image

However, a good encrypted image is similar to a random number whose adjacent elements have no correlation. Hence, in the (I(u, v),I(u, v + 1))-coordinate, all dots should be evenly distributed throughout the space. Figure 11(c2) and (d2) give the adjacent pixel correlation of the encrypted image. All the dots are actually evenly spread across the space. That is to say, the encrypted image has no correlation, which indicates that Henon encryption is a good image encryption algorithm.

The correlation coefficients of the adjacent pixels is another index for security. The definition of correlation coefficient R is shown in the following equation.

$$ R_{\alpha\beta}=\frac{cov(\alpha,\beta)}{{\sqrt{D(\alpha)}\sqrt{D(\beta)}}} $$
(3)

where, α = (α1,α2,⋯ ,αL) and β = (β1,β2,⋯ ,βL) are two sequences of length L, and

$$ \begin{array}{ll} &E(\alpha)=\frac{1}{L}{\sum}_{i = 1}^{L}\alpha_{i}\\ &D(\alpha)=\frac{1}{L}{\sum}_{i = 1}^{L}{(\alpha_{i}-E(\alpha))}^{2}\\ &cov(\alpha,\beta)=\frac{1}{L}{\sum}_{i = 1}^{L}{(\alpha_{i}-E(\alpha))(\beta_{i}-E(\beta))} \end{array} $$
(4)

That is to say, E(α), D(α) and cov(α, β) are mean, variance and covariance respectively.

If α = {I(u, v)} and β = {I(u, v + 1)}, β = {I(u + 1,v)} or β = {I(u + 1,v + 1)}, Rαβ is defined as the correlation coefficient of an image in horizontal, vertical or diagonal directions respectively. Tables 1 and 2 give the experimental data. It is obviously that the correlation coefficients of original images is high (near 1 which is the biggest value), and the correlation coefficients of encrypted images is almost 0.

Table 1 Correlation coefficients of adjacent pixels about original images
Full size table
Table 2 Correlation coefficients of adjacent pixels about encrypted images
Full size table

4.3 Key Sensitivity Test

The results of the cryptographic key sensitivity test are shown in Fig. 12. In the figure, (a) is the original image; (b) is the decrypted image with an encryption key of x0 = 0.2, y0 = 0.1, a = 1.4, b = 0.3; (c) is the decrypted image with an encrypted key of x0 = 0.2 + 1 × 10− 15, y0 = 0.1, a = 1.4, b = 0.3; (d) is the decrypted image with an encrypted key of x0 = 0.2, y0 = 0.1 + 1 × 10− 15, a = 1.4, b = 0.3; (e) is the decrypted image with an encrypted key of x0 = 0.2, y0 = 0.1, a = 1.4 + 1 × 10− 15, b = 0.3; and (f) is the decrypted image with an encrypted key of x0 = 0.2, y0 = 0.1, a = 1.4, b = 0.3 + 1 × 10− 15. The test results of the encryption key and decryption key sensitivity test show that when the encryption key is slightly changed in the range of less than 10− 15, the decrypted image changes obviously . The decryption key in the same range of small changes will lead to the decryption failure. Therefore, this algorithm is sensitive to the key.

Fig. 12
figure 12

Key sensitivity

Full size image

5 Conclusion

This paper gives a quantum image encryption algorithm based on quantum Henon mapping. The main contribution is that it generates the chaos sequence in quantum computers, which is the biggest difference from previous works and breaks away from the restriction of classical computers. Experiments show that Henon map can encrypt the image on quantum computers well. The algorithm has strong key sensitivity and good statistical properties, and has low correlation of encrypted image pixels and uniform pixel value. Hence, quantum image encryption based on Henon mapping is secure.

The next step is to explore a better way to improve the Henon mapping algorithm, so that it can run more efficiently and safely on the quantum computer.