A novel quantum representation for log-polar images

Abstract

The power of quantum mechanics has been extensively exploited to meet the high computational requirement of classical image processing. However, existing quantum image models can only represent the images sampled in Cartesian coordinates. In this paper, quantum log-polar image (QUALPI), a novel quantum image representation is proposed for the storage and processing of images sampled in log-polar coordinates. In QUALPI, all the pixels of a QUALPI are stored in a normalized superposition and can be operated on simultaneously. A QUALPI can be constructed from a classical image via a preparation whose complexity is approximately linear in the image size. Some common geometric transformations, such as symmetry transformation, rotation, etc., can be performed conveniently with QUALPI. Based on these geometric transformations, a fast rotation-invariant quantum image registration algorithm is designed for log-polar images. Performance comparison with classical brute-force image registration method reveals that our quantum algorithm can achieve a quartic speedup.

1 Introduction

As a novel topic in recent information science, quantum computation is considered to be a promising candidate to overcome the limitations of classical computation. By exploiting the inherent properties of quantum mechanics [1], a quantum computation can find solutions of certain problems more efficiently than can a classical computation. Recent decades have witnessed a series of significant theoretical progresses in quantum information processing, such as Shor’s integer factoring algorithm [2] and Grover’s search algorithm [3] and some others [4]. The excellent properties of quantum computation have motivated extensive research on quantum information processing.

Digital image processing [5] is important in many practical applications. However, the explosive increase of image data calls for efficient classical image processing algorithms. To address this challenge, quantum image processing has been extensively investigated in the last decade. To utilize quantum states to store image information, four quantum image representation models, i.e., Qubit Lattice [6], Entangled Image [7], Real Ket [8] and Flexible Representation of Quantum Images (FRQI) [9], have been proposed. However, these existing quantum image models can only represent images sampled in Cartesian coordinates so that complex affine transformations such as rotation and scaling cannot be performed based on these models. Therefore, many complex quantum image processing algorithms cannot be designed based on the existing models.

In this paper, quantum log-polar image (QUALPI), a novel quantum image representation is proposed for storing and processing images sampled in log-polar coordinates for the first time. In QUALPI, three entangled qubit (2-dimensional quantum bit) sequences are utilized to store the gray scale information, the log-radius position and the angular position information of each pixel in a log-polar image. Every pixel will be stored into a basis state of a normalized superposition consisting of these qubit sequences, so they can be operated on simultaneously.

A QUALPI can be constructed from a classical image via a preparation whose complexity is approximately linear in the image size. Compared with the existing quantum image models, more geometric transformations can be performed easily based on QUALPI, including those complex ones such as symmetry transformation and rotation.

Image registration is the process of obtaining the correspondence between two images of the same scene or object but acquired with different sensors, times, or viewpoints. It is widely used in computer vision, medical imaging, automatic target recognition, and remote sensing image analysis [10]. Based on the rotation transformation of QUALPI, a fast quantum image registration algorithm is designed which can achieve a quartic speedup over the classical image registration method. Therefore, QUALPI might be more flexible and suitable for complex quantum image processing than other state-of-the-art quantum image representations.

The remainder of the paper is organized as follows. Section 2 discusses related works. Section 3 describes the proposed quantum image representation model QUALPI as well as its preparation procedure. Two types of quantum geometry transformations based on QUALPI, i.e., symmetry transformation and rotation, are presented in Sect. 4 in detail. Then a fast quantum image registration algorithm is designed in Sect. 5 based on the rotation transformation of QUALPI. Finally, conclusion and possible future work are provided in Sect. 6.

2 Related work

The utilization of quantum information processing in digital image processing has been quite successful in terms of performance improvement. So far, four quantum image models for storing and processing images have been proposed, i.e., Qubit Lattice [6], Entangled Image [7], Real Ket [8] and FRQI [9].

Qubit Lattice [6] maps every pixel to a single qubit. Entangled Image [7] is similar to Qubit Lattice except that it utilizes the entangled state to express the relation of some certain pixels. Both of them are similar to classical digital images so it is easy to find quantum counterparts of classical image processing. However, they cannot provide any performance improvement.

Real Ket [8] utilizes the coefficients of a basis state of a qudit (4-dimensional quantum bit) sequence to represent the gray-scale of every pixel and stores an image into a quantum superposition.

The state-of-the-art model of FRQI [9] for a ${2^n} \times {2^n}$ image is expressed as seen in the following equation:

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{{2^n}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left( {\cos {\theta _{YX}}\left| 0 \right\rangle + \sin {\theta _{YX}}\left| 1 \right\rangle } \right) \left| {YX} \right\rangle } } \end{aligned}$$

(1)

where ${\theta _{YX}}$ is the phase of the color qubit which denotes the gray-scale value of pixel $(Y,X)$.

In FRQI, the position information of every pixel is mapped to a basis state of a 2-dimensional qubit sequence, while the gray scale information is stored in the probability amplitude of a single qubit. Since these two models utilize the superposition of qubit sequence to store image, they can process the information of all pixels simultaneously.

Many researches on quantum image processing have been explored based on the existing quantum image models. The works in [11, 12] discussed some simple image geometric transformations and color transformations respectively; significant performance improvement of these quantum operations has been made compared with the classical image operations. Sun et al. [13] extended FRQI and utilized 3 qubits to represent the full color information for an RGB$\alpha$ image. Zhang et al. [14] improved FRQI and more complex color transformations could be performed based on the enhanced model. Iliyasu et al. [15], Zhang et al. [16] designed the quantum watermarking algorithms and obtained good performance. However, existing models can only store and process image sampled in Cartesian coordinates. Many complex affine transformations such as rotation and scaling cannot be performed with these models because a lot of irreversible interpolations are needed. Restricted quantum image transformations have limited the development of complex quantum image processing algorithms. This motivates us to find a better way of quantum image representation to overcome the above limits.

Log-polar coordinates is a well-known sampling method in the field of image processing. Many image processing algorithms have been studied based on log-polar sampling. Araujo and Dias [17] introduced the fundamental theory of log-polar sampling and analyzed two important properties, i.e., rotation and scale invariances. Based on log-polar sampling, Zokai and Wolberg [18], Matungka et al. [19], Pun and Lee [20] designed novel algorithms for image registration, target recognition and image classification respectively. Matungka [21] pointed out that log-polar sampling is nonlinear and non-uniform, so adaptive polar sampling and logarithmic spiral sampling were designed to address the problem. For the peculiar properties, we see that log-polar sampling is more suitable for some complex image transformations such as rotation and scaling. However, as far as we know, there is no research on utilizing quantum mechanics to store and process images sampled in log-polar coordinates.

3 Quantum representation for log-polar images

To overcome the drawbacks of the existing quantum image models, a novel quantum representation model QUALPI is proposed for the log-polar images in this paper. In this section, the new model will be described in detail as well as the preparation procedure of QUALPI.

3.1 Quantum image representation

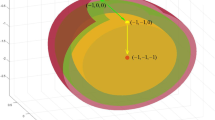
Both Cartesian sampling and log-polar sampling are important 2-dimensional sampling methods. Figure 1a, b show a comparison between the two sampling methods. In Cartesian coordinates, every pixel $(X,Y)$ is indexed in the horizontal and vertical orientations. $X$ and $Y$ denote the positions in the two axes. While in log-polar coordinates, every pixel is sampled as $(\rho ,\theta )$ where $\rho$ denotes the log-radius and $\theta$ the angular position. Figure 1c depicts the sampling distribution of log-polar image in the angular and log-radius directions. From this aspect, the log-polar image can also be considered as a 2-dimensional pixel matrix.

Fig. 1

a A $4 \times 4$ image example sampled in Cartesian coordinates. b A $4 \times 8$ image example sampled in log-polar coordinates. $base = 2$. c The sampling distribution of b in the angular and log-radius directions

The relationship between these two kinds of 2-dimensional image sampling methods is as follows:

$$\begin{aligned} \rho&= {\log _{base}}\sqrt{{{(x - {x_c})}^2} + {{(y - {y_c})}^2}},\end{aligned}$$

(2)

$$\begin{aligned} \theta&= {\tan ^{ - 1}}\frac{{y - {y_c}}}{{x - {x_c}}} , \end{aligned}$$

(3)

where $({x_c},{y_c})$ denotes the center pixel of log-polar sampling in Cartesian coordinates and $base$ is the logarithmic base.

Inspired by the FRQI quantum image model [9], we propose a novel quantum representation QUALPI to store and process the log-polar images. The sampling resolutions of the log-radius and the angular orientations of a log-polar image are assumed to be ${2^m}$ and ${2^n}$ respectively. For this image, the quantum image representation can be expressed as seen in the following equation:

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } }) \end{aligned}$$

(4)

where $g(\rho ,\theta )$ represents the gray scale of the corresponding pixel. The gray range of the image is assumed to be ${2^q}$. Thus the gray scale can be encoded by binary sequence $C_{0}C_{1} \ldots C_{q-2}C_{q-1}$ as seen in the following equation:

$$\begin{aligned} g(\rho ,\theta ) = C_{0}C_{1} \ldots C_{q-2}C_{q-1},\mathrm{{ }}g(\rho ,\theta ) \in [0,{2^q} - 1] \end{aligned}$$

(5)

Equation (4) shows that the whole QUALPI quantum image is stored in a normalized and equiprobable quantum superposition, in which each basis state represents one pixel. The basis state is consisted of the tensor product of three qubit sequences, where all the information of a pixel, i.e., the gray scale, the log-radius position and the angular position, are stored in.

Figure 2 demonstrates an example of a $2 \times 8$ log-polar image with gray range 256, i.e., $m = 1$, $n = 3$ and $q = 8$. It is obvious that the pixels in different quadrants have different gray scales. Meanwhile, in Fig. 2, the quantum representation of the log-polar image is expressed and all pixels are stored in a normalized quantum superposition $\left| I \right\rangle$.

From (4), $m + n + q$ qubits are utilized to store image information into a QUALPI state for a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$.

Fig. 2

A $2 \times 8$ log-polar image and its quantum representation expression of QUALPI

3.2 Quantum image preparation of QUALPI

In order to utilize quantum mechanics in image processing, image information will be stored into quantum state firstly. Here how to prepare QUALPI quantum image from classical log-polar image will be discussed.

Figure 3 shows the workflow of the quantum image preparation of the QUALPI model. The whole procedure is divided into two steps. Firstly, for a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$, a quantum register with $m + n + q$ qubits needs to be initialized as seen in the following equation:

$$\begin{aligned} {\left| I \right\rangle _0} = {\left| 0 \right\rangle ^{ \otimes m + n + q}} \end{aligned}$$

(6)

Step 1: At first, we will construct an empty QUALPI with size ${2^m} \times {2^n}$ from the initial state ${\left| I \right\rangle _0}$.

Fig. 3

The workflow of preparing the QUALPI quantum image model. The initial state will be transformed into the QUALPI model through two steps

Two common single quantum gates are shown in (7), which will be utilized to build the quantum operation ${U_1}$ of this step as in (8).

$$\begin{aligned} I&= \left[ {\begin{array}{*{20}{c}} 1 &{} 0 \\ 0 &{} 1 \\ \end{array}} \right] \,,H = \frac{1}{{\sqrt{2}}}\left[ {\begin{array}{*{20}{c}} 1 &{} 1 \\ 1 &{} { - 1} \\ \end{array}} \right] \end{aligned}$$

(7)

$$\begin{aligned} {U_1}&= {I^{ \otimes q}} \otimes {H^{ \otimes m + n}} \end{aligned}$$

(8)

Equation (9) represents the quantum transformation from the initial state ${\left| I \right\rangle _0}$ to the middle state ${\left| I \right\rangle _1}$ via using the quantum operation ${U_1}$.

$$\begin{aligned} {U_1}({\left| I \right\rangle _0})&= {\left| 0 \right\rangle ^{ \otimes q}} \otimes \left( {\frac{1}{{\sqrt{{2^m}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\left| \rho \right\rangle } } \right) \otimes \left( {\frac{1}{{\sqrt{{2^n}} }}\sum \limits _{\theta = 0}^{{2^n} - 1} {\left| \theta \right\rangle } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {\rho \theta } \right\rangle } } = {\left| I \right\rangle _1} \end{aligned}$$

(9)

The middle state ${\left| I \right\rangle _1}$ is an empty quantum image with size ${2^m} \times {2^n}$, every pixel in which is stored in a normalized quantum superposition and the gray scale is 0.

Step 2: Next we should set the gray scales of all pixels in the middle state ${\left| I \right\rangle _1}$. Because the log-polar image resolution is ${2^m} \times {2^n}$, ${2^{m + n}}$ sub-operations are needed to set gray scale for every pixel individually in this procedure.

For pixel $(\rho ,\theta )$, the quantum operation for gray scale setting is ${\varOmega _{\rho \theta }}$ as (10). In this operation, every qubit in the gray scale qubit sequence is processed according to the binary code of the gray scale value $g(\rho ,\theta )$ in (5). When ${C_i} = 1$, the $i$th qubit will be operated on by a controlled gate $(m + n) - CNot$. Otherwise, nothing will be done for the qubit.

$$\begin{aligned} {\varOmega _{\rho \theta }}:{\left| 0 \right\rangle ^{ \otimes q}}&\rightarrow {\mathop {\otimes }\limits _{i = 0}}^{q - 1} \left| {0 \oplus C_i} \right\rangle \nonumber \\ {\mathop {\otimes }\limits _{i = 0}}^{q - 1} \left| {0 \oplus C_i} \right\rangle&= {\mathop {\otimes }\limits _{i = 0}}^{q - 1} \left| {C_i} \right\rangle = \left| {g(\rho ,\theta )} \right\rangle \end{aligned}$$

(10)

The sub-operation to set gray scale for pixel $(\rho ,\theta )$ will not affect other pixels. Therefore for every sub-operation in Step 2, the normalized quantum operation is expressed as ${U_{\rho \theta }}$ in the following equation:

$$\begin{aligned} {U_{\rho \theta }} = \left( {{I^{ \otimes q}} \otimes \sum \limits _{j = 0}^{{2^m} - 1} {\sum \limits _{i = 0,ji \ne \rho \theta }^{{2^n} - 1} {\left| {ji} \right\rangle \left\langle {ji} \right| } } } \right) + {\varOmega _{\rho \theta }} \otimes \left| {\rho \theta } \right\rangle \left\langle {\rho \theta } \right| \end{aligned}$$

(11)

Equation (12) denotes the quantum transformation of applying every sub-operation on the middle state ${\left| I \right\rangle _1}$.

$$\begin{aligned} {U_{\rho \theta }}\left( {{{\left| I \right\rangle }_1}} \right)&= {U_{\rho \theta }}\left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {\rho \theta } \right\rangle } } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}{U_{\rho \theta }}\left( {\sum \limits _{j = 0}^{{2^m} - 1} {\sum \limits _{i = 0,ji \ne \rho \theta }^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } + {{\left| 0 \right\rangle }^{ \otimes q}}\left| {\rho \theta } \right\rangle } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\left( {\sum \limits _{j = 0}^{{2^m} - 1} {\sum \limits _{i = 0,ji \ne \rho \theta }^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } + {\varOmega _{\rho \theta }}{{\left| 0 \right\rangle }^{ \otimes q}}\left| {\rho \theta } \right\rangle } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\left( {\sum \limits _{j = 0}^{{2^m} - 1} {\sum \limits _{i = 0,ji \ne \rho \theta }^{{2^n} - 1} {{{\left| 0 \right\rangle }^{ \otimes q}}\left| {ji} \right\rangle } + \left| {g(\rho ,\theta )} \right\rangle \left| {\rho \theta } \right\rangle } } \right) \end{aligned}$$

(12)

From (12), every sub-operation can set the gray scale for the corresponding pixel. Therefore, the whole operation ${U_2}$ shown in (13) is consisted of all the aforementioned sub-operations.

$$\begin{aligned} {U_2} = \prod \limits _{\rho = 0}^{{2^m} - 1} {\prod \limits _{\theta = 0}^{{2^n} - 1} {{U_{\rho \theta }}} } \end{aligned}$$

(13)

Through the quantum operation ${U_2}$, all pixels have been set gray scales and the quantum state ${\left| I \right\rangle _2}$ is the final quantum image.

$$\begin{aligned} {U_2}\left( {{{\left| I \right\rangle }_1}} \right)&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {{\varOmega _{\rho \theta }}{{\left| 0 \right\rangle }^{ \otimes q}}\left| {\rho \theta } \right\rangle } } \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left| {g(\rho ,\theta )} \right\rangle \left| {\rho \theta } \right\rangle } = {{\left| I \right\rangle }_2}} \end{aligned}$$

(14)

After these two steps, the whole quantum image preparation has been finished. Then we will discuss the time complexity of this preparation procedure.

Theorem 1

In order to store a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$ into the QUALPI quantum image model, the whole quantum image preparation will cost no more than $O(q(m + n) \cdot {2^{m + n}})$.

Proof

The whole preparation is divided into two steps. The time complexities of each step will be analyzed as follows.

Firstly, the quantum operation of Step 1 is ${U_1}$. From (8), it is known that ${U_1}$ will cost $O(q + m + n)$ because it is consisted of $q + m + n$ single quantum gates.

Secondly, the main work ${U_2}$ of Step 2 is to set gray scale for all the pixels in the quantum image. The whole operation is consisted of ${2^{m + n}}$ sub-operations shown in (13).

Every sub-operation ${U_{\rho \theta }}$ will perform the quantum operation ${\varOmega _{\rho \theta }}$ for the corresponding pixel. In this quantum transformation, the $i$th qubit in the gray scale qubit sequence of QUALPI will be operated on by a controlled quantum gate if the corresponding binary bit ${C_i}$ of $g(\rho ,\theta )$ is equal to 1. Note that all the controlled quantum gates are $(m + n) - CNot$ (this quantum gate can be decomposed to no more than $O(m + n)$ Toffoli gates [22]). Therefore, the time complexity of the quantum operation ${U_{\rho \theta }}$ is no more than $O(q(m + n))$. And the whole operation of Step 2 will cost no more than $O(q(m + n) \cdot {2^{m + n}})$.

Based on the aforementioned analyses, for a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$, the time complexity of the whole quantum image preparation of QUALPI is no more than $O(q(m + n) \cdot {2^{m + n}})$, which is approximately linear to the resolution of the log-polar image. $\square$

According to the Holevo Bound Theorem [25], when an exponential amount of the classical image information is encoded into the QUALPI state via quantum image preparation, we will not be able to retrieve the whole image information perfectly via quantum measurements. Therefore the proposed quantum image model and algorithms cannot be used in image-showing tasks.

In general, the aim of many image processing tasks is not to show the whole image, but to extract a little of more important information through analyzing the image data (for example, these image processing tasks always need to solve some problems like “whether or not the image contains a target of interest”,“which pixel in the image has the minimum gray-scale” and “how many targets the image has” and so on. The commonness of these tasks is that the output is a Boolean or Integer which is no more than Holevo’s bound). QUALPI is designed for these kinds of image processing tasks. It utilizes a quantum superposition to encode the image information so that the quantum image processing algorithm based on QUALPI which will be discussed later can achieve an amazing speedup compared with the classical counterpart. That is the reason why we discuss the quantum image processing and design the quantum image representation QUALPI.

4 Geometric transformations on QUALPI quantum image

In this section, we will discuss how to utilize the QUALPI quantum image model to perform geometric transformations. Because of the peculiar properties of the log-polar images, two kinds of geometric transformations of the QUALPI images, i.e., symmetry transformation and rotation, can be performed flexibly and quickly.

4.1 Quantum symmetry transformation

Symmetry transformation is a kind of important geometric transformation, including centrosymmetry and axisymmetry. For the classical images, the position information of all pixels needs to be modified during symmetry transformations. Therefore, when the sampling resolution is large, the time requirements of these image operations are unacceptable. In the QUALPI quantum image model, all the pixels are stored in a quantum superposition and can be operated on simultaneously during transforming. Three kinds of symmetry transformations are discussed, including quantum centrosymmetry, quantum horizontal axisymmetry and quantum vertical axisymmetry.

4.1.1 Quantum centrosymmetry

Centrosymmetry is a geometric transformation that all pixels will be rotated half a circumference around the image center. Assume that the angular resolution of the image is ${2^n}$, the angular positions of all pixels should be shifted counter-clockwise by ${2^{n - 1}}$. For the QUALPI quantum image model, centrosymmetry can be performed only by overturning the highest qubit $\left| {{\theta _0}} \right\rangle$ in the angular sequence $\left| \theta \right\rangle$ of the quantum image $\left| I \right\rangle$.

For a ${2^m} \times {2^n}$ QUALPI quantum image with gray range ${2^q}$, ${U_C}$ is the quantum centrosymmetry operation as seen in the following equation:

$$\begin{aligned} {U_C} = {I^{ \otimes q + m}} \otimes X \otimes {I^{ \otimes n - 1}} \end{aligned}$$

(15)

where $X$ denotes the quantum Not gate as seen in the following equation:

$$\begin{aligned} X = \left[ {\begin{array}{*{20}{c}} 0 &{} 1 \\ 1 &{} 0 \\ \end{array}} \right] = \left| 0 \right\rangle \left\langle 1 \right| + \left| 1 \right\rangle \left\langle 0 \right| \end{aligned}$$

(16)

Equation (17) represents the quantum transformation of the quantum centrosymmetry for the quantum image $\left| I \right\rangle$.

$$\begin{aligned} {U_C}\left| I \right\rangle&= {U_C}\left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } \right) } } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {\overline{{\theta _0}} } \right\rangle \otimes \left( {{\mathop {\otimes }\limits _{i = 1}}^{n - 1} \left| {{\theta _i}} \right\rangle } \right) } \right) } } \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {(\theta + {2^{n - 1}})\,{\mathrm{mod}}\, {2^n}} \right\rangle } \right) } } \end{aligned}$$

(17)

If $\theta ^{\prime } = \overline{{\theta _0}} {\theta _1} \ldots {\theta _{n - 2}}{\theta _{n - 1}}$, the quantum image will be transformed as (18) after quantum centrosymmetry.

$$\begin{aligned} {U_C}\left| I \right\rangle = \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta ^{\prime })} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } }) \end{aligned}$$

(18)

Figure 4 gives the quantum circuit of ${U_C}$ in the model QUALPI and toy image [24] is used as a log-polar image example. This quantum operation would make quantum image rotate half a circumference.

Fig. 4

a Quantum circuit of ${U_C}$. $\oplus$ denotes the quantum Not gate. Since the quantum identity gate $I$ will not modify the quantum state, we do not draw it in the quantum circuit. b The log-polar toy image. c The result of image b through the quantum centrosymmetry ${U_C}$

4.1.2 Quantum axisymmetry

Axisymmetry is a kind of geometric transformation that all pixels will be overturned around a certain axis. We only focus on two kinds of common axisymmetries, i.e. horizontal axisymmetry and vertical axisymmetry. When the image resolution of the angular orientation is ${2^n}$, they will make different operations for the QUALPI quantum image.

For horizontal axisymmetry, the angular positions of all pixels should be changed to the angle difference between ${2^n}$ and the current position $\theta$. For the QUALPI quantum image model, horizontal axisymmetry will overturn all the qubits in the angular qubit sequence $\left| \theta \right\rangle$ in $\left| I \right\rangle$.

The quantum operation of horizontal axisymmetry for a QUALPI quantum image is ${U_{HA}}$ as seen in the following equation:

$$\begin{aligned} {U_{HA}} = {I^{ \otimes q + m}} \otimes {X^{ \otimes n}} \end{aligned}$$

(19)

Equation (20) represents the quantum transformation of the quantum horizontal axisymmetry for the quantum image $\left| I \right\rangle$.

$$\begin{aligned} {U_{HA}}\left| I \right\rangle&= {U_{HA}}\left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } \right) } } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left( {{\mathop {\otimes }\limits _{i = 0}}^{n - 1} \left| {\overline{{\theta _i}} } \right\rangle } \right) } \right) } } \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {{2^n} - \theta } \right\rangle } \right) } } \end{aligned}$$

(20)

If $\theta ^{\prime \prime } = \overline{{\theta _0}} \overline{{\theta _1}} \ldots \overline{{\theta _{n - 2}}} \overline{{\theta _{n - 1}}}$, the QUALPI quantum image will be transformed as (21) after quantum horizontal axisymmetry.

$$\begin{aligned} {U_{HA}}\left| I \right\rangle = \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta ^{\prime \prime })} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } }) \end{aligned}$$

(21)

Figure 5 gives the quantum circuit of ${U_{HA}}$ in the QUALPI model and the example of toy image. This quantum operation would make quantum image overturn based on the horizontal axis.

For quantum vertical axisymmetry, the angular positions of all pixels should be changed into the angle difference between ${2^{n - 1}}$ and the current position $\theta$ (mod ${2^n}$). The operation will overturn all the qubits of the angular sequence $\left| \theta \right\rangle$ except the highest qubit $\left| {{\theta _0}} \right\rangle$ for the QUALPI quantum image $\left| I \right\rangle$.

Fig. 5

a Quantum circuit of ${U_{HA}}$. In ${U_{HA}}$, all the qubits in the angular sequence $\left| \theta \right\rangle$ are overturned. b The log-polar toy image. c The result of image b through the quantum horizontal axisymmetry ${U_{HA}}$

The quantum operation of vertical axisymmetry for a QUALPI quantum image is ${U_{VA}}$ as seen in the following equation:

$$\begin{aligned} {U_{VA}} = {I^{ \otimes q + m + 1}} \otimes {X^{ \otimes n - 1}} \end{aligned}$$

(22)

Equation (23) represents the quantum transformation of the quantum vertical axisymmetry for the quantum image $\left| I \right\rangle$.

$$\begin{aligned} {U_{VA}}\left| I \right\rangle&= {U_{VA}}\left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } \right) } } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {{\theta _0}} \right\rangle \otimes \left( {{\mathop {\otimes }\limits _{i = 1}}^{n - 1} \left| {\overline{{\theta _i}} }\right\rangle } \right) } \right) } } \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {({2^{n - 1}} - \theta )\,{\mathrm{mod}}\, {2^n}} \right\rangle } \right) } } \end{aligned}$$

(23)

If $\theta ^{\prime \prime \prime } = {\theta _0}\overline{{\theta _1}} \ldots \overline{{\theta _{n - 2}}} \overline{{\theta _{n - 1}}}$, the quantum image will be transformed as (24) after quantum vertical axisymmetry ${U_{VA}}$.

$$\begin{aligned} {U_{VA}}\left| I \right\rangle = \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta ^{\prime \prime \prime })} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } }) \end{aligned}$$

(24)

Figure 6 gives the quantum circuit of ${U_{VA}}$ in the QUALPI model and the example of toy image. This quantum operation would make quantum image overturn based on the vertical axis.

Fig. 6

a Quantum circuit of ${U_{VA}}$. All the qubits in the angular sequence $\left| \theta \right\rangle$ are overturned except $\left| {{\theta _0}} \right\rangle$. b The log-polar toy image. c The result of image b through the quantum vertical axisymmetry ${U_{VA}}$

From (15), (19) and (22), it is obvious that for all three kinds of quantum symmetry transformations, every qubit is operated by only one single qubit gate. It means the time complexities of these quantum operations are $O(q + m + n)$.

4.2 Quantum rotation transformation

Rotation is a common geometric transformation of images sampled in the log-polar coordinates. Different from the images sampled in Cartesian coordinates, rotation transformation of a log-polar image is lossless and reversible because there is no interpolation operation. Meanwhile, many features of a log-polar image are invariant to arbitrary rotation transformation. Therefore, it is obvious that log-polar image has rotation-invariance [17]. The special properties result from a rotation of a log-polar image is just the shift operation in angular directions.

Here we discuss the quantum rotation transformation of the QUALPI quantum image model. Because all the pixels in the quantum image can be rotated simultaneously, the quantum rotation will be more flexible and faster.

4.2.1 Unit rotation transformation

Firstly, we focus on the quantum unit rotation. For this transformation, all the pixels of a log-polar image will rotate counter-clockwise by one unit. For the QUALPI quantum image model, it will add the angular positions of every pixel by 1 (mod ${2^n}$).

The quantum unit rotation operation is defined as ${R_1}$ in the following equation:

$$\begin{aligned} {R_1}\left| I \right\rangle&= {R_1}\left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } } )} \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {(\theta + 1)\,{\mathrm{mod}}\, {2^n}} \right\rangle } \right) } } \end{aligned}$$

(25)

From (25), it is obvious that the angular positions of all pixels will be shifted by one unit. Through the discussion about the shift operation of quantum image in [11], it is known that we can build the quantum circuit of the quantum operation ${R_1}$ as Fig. 7. For a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$, ${R_1}$ can be decomposed to $n$ controlled-not gates.

Fig. 7

The quantum circuit of ${R_1}$ for a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$. The qubit $\left| {{\theta _i}} \right\rangle$ will be overturned only when $\left| {{\theta _{i + 1}}{\theta _{i + 2}} \ldots {\theta _{n - 1}}} \right\rangle = \left| {11 \ldots 1} \right\rangle$

Through the analysis of the shift operation in [11], it is known that the time complexity of the quantum operation ${R_1}$ is no more than $O({n^2})$ for a ${2^m} \times {2^n}$ log-polar image.

4.2.2 Arbitrary rotation transformation

For arbitrary rotation, we can utilize some unit rotations to finish it naively. However, when the rotation angle is large, the procedure will cost much time. For example, the worst case happens if the rotation angle is ${2^n} - 1$, the time complexity of ${2^n} - 1$ units rotation will be approximately $O({n^2}{2^n})$. Then a fast quantum rotation method for arbitrary rotation is designed to simplify the naive procedure.

Assume that we will make a rotation transformation ${R_x}$ for the quantum image and the rotation angle can be encoded by binary sequence ${r_0}{r_1} \ldots {r_{n - 2}}{r_{n - 1}}$ in the following equation:

$$\begin{aligned} {R_x} = {r_0}{r_1} \ldots {r_{n - 2}}{r_{n - 1}},{r_i} \in \{ 0,1\} ,{R_x} \in [0,{2^n} - 1]\nonumber \\ \end{aligned}$$

(26)

Then ${R_x}$ can be represented as seen in the following equation:

$$\begin{aligned} {R_x} = \sum \limits _{i = 0}^{n - 1} {{r_i} \times {2^{n - 1 - i}}} \end{aligned}$$

(27)

Therefore, when ${R_x}$ rotation is performed, the procedure can be divided into $n$ sub-operations. If ${r_i} = 0$, none operation will be done for the $i$th sub-operation. Otherwise we need to do a ${2^{n - 1 - i}}$ rotation ${R_{{2^{n - 1 - i}}}}$ for the quantum image.

Next, we will discuss the quantum ${2^k}$ rotation transformation ${R_{{2^k}}}$. Similar to the quantum unit rotation ${R_1}$, quantum ${2^k}$ rotation ${R_{{2^k}}}$ will add the angular positions of every pixel by ${2^k}$ (mod ${2^n}$). And this operation means to make a unit shift for the highest $n - k$ qubits of the angular sequence $\left| \theta \right\rangle$ in the QUALPI quantum image.

The quantum rotation operation ${R_{{2^k}}}$ is defined as seen in the following equation:

$$\begin{aligned} {R_{{2^k}}}\left| I \right\rangle&= {R_{{2^k}}}\left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } \right) } } } \right) \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {(\theta + {2^k})\,{\mathrm{mod}}\, {2^n}} \right\rangle } \right) } } \nonumber \\&= \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle } } \nonumber \\&\quad \otimes \left| {({\theta _0}{\theta _1} \ldots {\theta _{n - k - 1}} + 1)\,{\mathrm{mod}}\, {2^{n - k}}} \right\rangle \otimes \left| {{\theta _{n - k}}{\theta _{n - k + 1}} \ldots {\theta _{n - 1}}} \right\rangle ) \end{aligned}$$

(28)

The quantum circuit of this operation ${R_{{2^k}}}$ is shown in Fig. 8. Similar to the discussion of ${R_1}$, the time complexity of ${R_{{2^k}}}$ is approximately $O({(n - k)^2})$. Therefore, an arbitrary rotation will be decomposed into $n$ rotation operations at most and the total time complexity of the arbitrary rotation transformation is no more than $O({n^3})$. Compared with the naive method, an approximately exponential speedup can be achieved by using the fast quantum rotation.

Fig. 8

The quantum circuit of ${R_{{2^k}}}$ for a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$. The lowest $k$ qubits in the angular sequence $\left| \theta \right\rangle$ will not be modified in this quantum operation

5 Quantum image registration based on QUALPI

Image registration is one of the most important topics in image processing which can obtain the correspondence of two different images for a same scene or object from different circumstances.

In this section, a fast quantum image registration algorithm is proposed based on the QUALPI quantum image model. Using this quantum algorithm, the exact rotation difference between two quantum images can be found out. Figure 9 shows an example of image-pair. Our task is to find the unknown rotation difference between the two log-polar images.

Fig. 9

An example of image registration for two toy log-polar images. The observed image is transformed by the reference image via an unknown rotation

5.1 Classical brute-force image registration algorithm

In order to obtain the rotation difference between the reference image and the observed image, a classical image registration algorithm is brute-force image matching. It continues trying every rotation angle for the reference image and comparing the transformed image with the observed image until a matching is reached. The pseudo code of this classical algorithm is shown in Algorithm 1. Assume that the resolution of the log-polar image is ${2^m} \times {2^n}$.

Firstly, since the rotation is unknown, all the possible rotations have to be tried. Thus the whole procedure will make $O({2^n})$ tries averagely.

Secondly, every classical rotation operation will cost approximately $O({2^{m + n}})$ because the positions of all pixels will be changed in log-polar coordinates.

Thirdly, the pixel pairs in all the positions between the two images will be compared in the similarity comparison stage. Therefore, every image comparison will cost $O({2^{m + n}})$.

From the analyses, the time complexity of the whole algorithm is approximately $O({2^{m + 2n}})$ for a ${2^m} \times {2^n}$ log-polar image pair.

Recently, feature-based image registration algorithms are also widely explored in the practical image processing since they usually cost less time. However, as an original method, brute-force algorithm is simpler, and it is preferred when the transformation between two images is single such as the example in Fig. 9. Therefore, it is prone to design the quantum counterpart of brute-force image registration algorithm.

5.2 Quantum image registration algorithm

In this section, a fast quantum image registration algorithm is designed to obtain the rotation difference between the two log-polar images based on the QUALPI quantum image model. The whole workflow of the quantum image registration algorithm is given as follows:

Step 1: Quantum Image Preparation. During this step, the reference image and the observed image will be stored into the QUALPI states. The details of quantum image preparation have been introduced in Sect. 3.2.

Step 2: Quantum Image Expanding. In this procedure, the quantum state of the reference image is expanded to an image set in which each element represents a transformed result of the reference image with a specific rotation angle. Section 5.2.1 introduces the details of this quantum procedure.

Step 3: Quantum Image Searching. Based on Grover’s Search Algorithm, the observed image will be found out in the image set produced in Step 2. Section 5.2.2 depicts this quantum search procedure.

Step 4: Quantum Measurement. After Grover iterations in Step 3, the quantum measurement is applied to the final quantum state, and the output is the index of the observed image in the image set. The accuracy of the output is nearly 100 %. And the value of the index is just the angle of the rotation difference between the reference image and the observed image. Section 5.2.3 gives the description in detail.

The time complexity of the quantum image registration algorithm is discussed in Sect. 5.2.4. The proposed algorithm can achieve an approximately quartic speedup in time complexity compared with that of the classical counterpart in Sect. 5.1.

5.2.1 Quantum image expanding

To find out the rotation difference between the reference image and observed image, the first step is to expand the reference image into an image set in which all the images are transformed from the reference image with difference rotations. Therefore, a fast quantum image expanding procedure is designed to fulfill this task.

For a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$, we need another quantum register with $n$ qubits to represent the order of every expanded image. The order denotes the angle of the rotation difference between the original reference image and the expanded image.

Before the expanding procedure, we should initialize the order register as ${\left| 0 \right\rangle ^{ \otimes n}}$ and make tensor product between the order register and the reference quantum image $\left| I \right\rangle$. The whole quantum state is $\left| {{I_0}} \right\rangle$ is shown as follows,

$$\begin{aligned} \left| {{I_0}} \right\rangle = {\left| 0 \right\rangle ^{ \otimes n}}\left| I \right\rangle = {\left| 0 \right\rangle ^{ \otimes n}} \otimes \frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {(\left| {g(\rho ,\theta )} \right\rangle \otimes \left| \rho \right\rangle \otimes \left| \theta \right\rangle } } ) \end{aligned}$$

(29)

The workflow of the quantum image expanding procedure is shown as follow which will make the full expanding for the reference image in the angular orientation.

The whole procedure of quantum image expanding will iterate $n$ times. For the $i$th iteration, two steps will be performed.

Step 1: Make quantum operation ${E_i}$ as (30). It will make a hadamard gate on the $i$th qubit in the order register.

$$\begin{aligned} {E_i} = {I^{ \otimes i - 1}} \otimes H \otimes {I^{n - i + q + m + n}} \end{aligned}$$

(30)

To be convenient, we define that $\left| + \right\rangle = \frac{1}{{\sqrt{2} }}\left| 0 \right\rangle + \frac{1}{{\sqrt{2} }}\left| 1 \right\rangle$.

When $i = 0$, Equation (31) shows the quantum transformation of the quantum operation ${E_0}$.

$$\begin{aligned} \left| {{I_1}} \right\rangle = {E_0}\left| {{I_0}} \right\rangle = \left| + \right\rangle {\left| 0 \right\rangle ^{ \otimes n - 1}} \otimes \left| I \right\rangle \end{aligned}$$

(31)

When $i > 0$, the quantum transformation is represented as seen in the following equation:

$$\begin{aligned} \left| {{I_i}} \right\rangle = {E_i}\left| {{I_{i - 1}}} \right\rangle = {\left| + \right\rangle ^{ \otimes i + 1}}{\left| 0 \right\rangle ^{ \otimes n - i - 1}} \otimes \left| I \right\rangle \end{aligned}$$

(32)

Through Step 1, the whole quantum state will be divided into two parts on the $i$th qubit in the order register.

Step 2: According to the value of the $i$th qubit in the order register, make different operations for the different basis states of the whole superposition. Only when the $i$th qubit in the order register is $\left| 1 \right\rangle$, the corresponding basis states will be rotated counter-clockwise by ${2^{n - 1 - i}}$. This quantum operation is denoted as ${T_i}$ in the following equation:

$$\begin{aligned} {T_i} = {I^{ \otimes i - 1}} \otimes \left| 0 \right\rangle \left\langle 0 \right| \otimes {I^{ \otimes n - i + q + m + n}} + {I^{ \otimes i - 1}} \otimes \left| 1 \right\rangle \left\langle 1 \right| \otimes {I^{ \otimes n - i}} \otimes {R_{{2^{n - 1 - i}}}}\nonumber \\ \end{aligned}$$

(33)

Equation (34) represents the quantum transformation of the operation ${T_i}$.

$$\begin{aligned} {T_i}\left| {{I_i}} \right\rangle&= {T_i}\left( {\frac{1}{{\sqrt{2} }}{{\left| + \right\rangle }^{ \otimes i}}\left| 0 \right\rangle {{\left| 0 \right\rangle }^{ \otimes n - i - 1}} \otimes \left| I \right\rangle \mathrm{{ + }}\frac{1}{{\sqrt{2} }}{{\left| + \right\rangle }^{ \otimes i}}\left| 1 \right\rangle {{\left| 0 \right\rangle }^{ \otimes n - i - 1}} \otimes \left| I \right\rangle } \right) \nonumber \\&= \frac{1}{{\sqrt{2} }}{\left| + \right\rangle ^{ \otimes i}}\left| 0 \right\rangle {\left| 0 \right\rangle ^{ \otimes n - i - 1}} \otimes \left| I \right\rangle \mathrm{{ + }}\frac{1}{{\sqrt{2} }}{\left| + \right\rangle ^{ \otimes i}}\left| 1 \right\rangle {\left| 0 \right\rangle ^{ \otimes n - i - 1}} \otimes {R_{{2^{n - 1 - i}}}}\left| I \right\rangle \nonumber \\ \end{aligned}$$

(34)

After the $n$ iterations, the whole state will be transformed to the result state $\left| {{I_n}} \right\rangle$.

Figure 10 depicts the procedure of the quantum image expanding procedure for a quantum image with angular resolution ${2^3}$. Through $n$ iterations ($n = 3$ in Fig. 10), the quantum procedure will change the initial state $\left| {{I_0}} \right\rangle$ into the final result state as (35). Because every rotation operation will be performed simultaneously for half of all the basis states in the quantum superposition, the whole procedure can be decomposed into only $n$ controlled rotation operations.

$$\begin{aligned} \left| {{I_n}} \right\rangle&= \frac{1}{{\sqrt{{2^n}} }}\sum \limits _{i = 0}^{{2^n} - 1} {\left| i \right\rangle {R_i}\left| I \right\rangle } \nonumber \\&= \frac{1}{{\sqrt{{2^n}} }}\sum \limits _{i = 0}^{{2^n} - 1} {\left| i \right\rangle } \left( {\frac{1}{{\sqrt{{2^{m + n}}} }}\sum \limits _{\rho = 0}^{{2^m} - 1} {\sum \limits _{\theta = 0}^{{2^n} - 1} {\left( {\left| {g(\rho ,\theta } \right\rangle \otimes \left| \rho \right\rangle \otimes \left| {(\theta + i)\,{\mathrm{mod}}\, {2^n}} \right\rangle } \right) } } } \right) \nonumber \\ \end{aligned}$$

(35)

From (35), the order register is entangled with the quantum image state. For every basis state in the superposition $\left| {{I_{n}}} \right\rangle$, the quantum image state represents the expanded image resulted from the reference image through a certain rotation which is stored in the order register. ${2^n}$ expanded images are stored in an equiprobable and normalized superposition and they can be operated on simultaneously.

Figure 11 gives the quantum circuit of the quantum image expanding procedure for a ${2^m} \times {2^n}$ log-polar image. From the circuit, the whole procedure is consisted of $n$ hadamard gates and $n$ controlled rotation gates. Since every controlled rotation operation in the circuit will cost no more than $O({n^2})$ as discussed in Sect. 4.2.2, the time complexity of the whole procedure is approximately $O({n^3})$.

Fig. 10

The workflow of the quantum image expanding procedure when the angular resolution is ${2^3}$. $\odot$ denotes a basis state which is an expanded image with order X. The whole algorithm includes 3 iterations. And the last quantum state $\left| {{I_3}} \right\rangle$ is the superposition of all the possible expanded images

Fig. 11

The quantum circuit of the quantum image expanding procedure for a ${2^m} \times {2^n}$ log-polar image with gray range ${2^q}$. The detailed quantum rotation operation of ${R_{{2^k}}}$ is shown in Fig. 8

5.2.2 Quantum image searching

After image expanding, the reference image is transformed into a quantum image database. In the final quantum state $\left| {{I_{n}}} \right\rangle$, the order register can be considered as the image index while every basis state represents an expanded image as an element in the image database. According to the image registration problem, it is known that there is at least one record in the database which is the same with the observed image. Then we will utilize Grover’s search algorithm [3] to do the image retrieving in the database.

Firstly, we need another ancillary qubit to be set as seen in the following equation:

$$\begin{aligned} \left| - \right\rangle = \frac{1}{{\sqrt{2} }}(\left| 0 \right\rangle - \left| 1 \right\rangle ) \end{aligned}$$

(36)

Equation (37) represents the tensor product between the image database and the ancillary qubit.

$$\begin{aligned} \left| {{I_{n}}} \right\rangle \left| - \right\rangle = \frac{1}{{\sqrt{{2^n}} }}\sum \limits _{i = 0}^{{2^n} - 1} {\left| i \right\rangle {R_i}\left| I \right\rangle } \otimes \left| - \right\rangle \end{aligned}$$

(37)

Then we design new quantum oracle ${U_f}$ for the image database as seen in the following equation:

$$\begin{aligned} {U_f}(\left| i \right\rangle {R_i}\left| I \right\rangle \left| j \right\rangle ) = \left| i \right\rangle {R_i}\left| I \right\rangle \left| {j \oplus f({R_i}\left| I \right\rangle )} \right\rangle \end{aligned}$$

(38)

where $f({R_i}\left| I \right\rangle )$ is shown as (39) and it can assess the similarity between the expanded image ${R_i}\left| I \right\rangle$ and the observed image $\left| {I^{\prime }} \right\rangle$ which is designed in a similar way of [23].

$$\begin{aligned} f({R_i}\left| I \right\rangle ) = \left\{ {\begin{array}{ll} 1,&{}\mathrm{if}\, \mathrm{sim}({R_i}\left| I \right\rangle ,\left| {I^{\prime }} \right\rangle ) = 1 \\ 0,&{}\mathrm{else} \\ \end{array}} \right. \end{aligned}$$

(39)

Through the new quantum oracle, the whole quantum state will be transformed as seen in the following equation:

$$\begin{aligned} \left| \varPsi \right\rangle = \frac{1}{{\sqrt{{2^n}} }}\left( {\sum \limits _{i = 0,i \ne j}^{{2^n} - 1} {\left| i \right\rangle {R_i}\left| I \right\rangle } + ( - 1)\left| j \right\rangle {R_j}\left| I \right\rangle } \right) \end{aligned}$$

(40)

Through this oracle and the ancillary qubit, the whole quantum state $\left| \varPsi \right\rangle$ will be divided into two parts:

$$\begin{aligned} \left| \varPsi \right\rangle = \frac{1}{{\sqrt{{2^n}} }}\left( {\sum \limits _{i = 0,i \ne j}^{{2^n} - 1} {\left| i \right\rangle {R_i}\left| I \right\rangle } + ( - 1)\left| j \right\rangle {R_j}\left| I \right\rangle } \right) \end{aligned}$$

(41)

where $j$ is just the index of the observed image in the image set.

From the well-known Grover Iteration [3], the number $k$ of the iterations for the whole procedure is $\left[ {\frac{\pi }{4}\sqrt{{2^n}} } \right]$. After these iterations, the final quantum state $\left| \varPsi \right\rangle$ will be transformed as seen in the following equation:

$$\begin{aligned} \left| \varPsi \right\rangle \!=\! \cos \left( {\frac{{2k \!+\! 1}}{2}\theta } \right) \left( {\frac{1}{{\sqrt{{2^n} \!- \!1} }}\sum \limits _{i \!=\! 0,i \ne j}^{{2^n} \!-\! 1} {\left| i \right\rangle {R_i}\left| I \right\rangle } } \right) \!+\! \sin \left( {\frac{{2k \!+\! 1}}{2}\theta } \right) \left| j \right\rangle {R_j}\left| I \right\rangle \qquad \quad \end{aligned}$$

(42)

where $\theta = 2\arccos \sqrt{1 - \frac{1}{{{2^n}}}}$.

5.2.3 Quantum measurement

In the last stage, the quantum measurement for the order register in the final quantum state [shown in (42)] is applied using the computational basis $\{ \left| 0 \right\rangle ,\left| 1 \right\rangle \cdots \left| {{2^n} - 1} \right\rangle \}$.

Because $k = \left[ {\frac{\pi }{4}\sqrt{{2^n}} } \right]$ and $\theta = 2\arccos \sqrt{1 - \frac{1}{{{2^n}}}}$, we know that $\frac{{2k + 1}}{2}\theta \approx \frac{\pi }{2}$ and ${\left| {\sin (\frac{{2k + 1}}{2}\theta )} \right| ^2} \approx 1$. It means that via the quantum measurement for the order register, the probability of the output index $j$ is approximately 100 %.

The result $j$ of the proposed algorithm is an $n$-bit integer while the final quantum state is consisted of $2n+m+q$ qubits [from (42)], so the proposed quantum image registration algorithm obeys the Holevo Bound Theorem [25].

5.2.4 Asymptotic complexity

In general, the time cost of the quantum state preparation usually does not include the time complexity of quantum algorithm. Meanwhile the cost of quantum measurement can be ignored, so we will mainly focus on the other two steps in the whole algorithm.

Firstly, we utilize the quantum image expanding algorithm for the reference image and obtain a quantum image database. The time complexity is approximately $O({n^3})$.

Then, we design a new quantum oracle for the quantum image database and utilize Grover’s search algorithm to search the observed image in the database. Through quantum measurement, the algorithm can obtain the value of the rotation difference between the reference image and observed image. Since the number of basis states in the database is ${2^n}$, approximately $O(\sqrt{{2^n}} )$ quantum Grover iterations are operated on in the procedure.

Therefore, the time complexity of the quantum image registration is no greater than $O(\sqrt{{2^n}} )$ which has an approximately quartic decrease compared with that of the classical image registration algorithm.

6 Conclusion and future work

Quantum computation has become a novel and important tool in the field of image processing. In this paper, a novel quantum image model QUALPI is proposed. Different from the existing quantum image models, QUALPI is, for the first time, designed for the images sampled in log-polar coordinates.

Since all the pixels of a log-polar image can be stored and operated on simultaneously in the QUALPI model, some complex geometric transformations, such as quantum symmetry transformation and quantum rotation transformation, can be performed. Based on a fast quantum image expanding algorithm and quantum image searching, a quantum image registration algorithm is proposed to obtain the rotation difference between two quantum images. Compared with the classical brute-force image registration method, the new quantum image registration algorithm can achieve a quartic speedup. Therefore, QUALPI is more suitable for complex image processing than the existing quantum image models in the literature.

In the QUALPI model, for each radius, the circumference is sampled with the same number of sample pixels. Hence, image pixels close to the center are oversampled while those which are far away from the center are under-sampled, which is a drawback of the sampling method of the log-polar image. In [21], adaptive log-polar and logarithmic spiral are proposed to address the non-uniform sampling problem. Designing proper quantum image models for these enhanced log-polar images will be one of our future researches. In addition, since rotation is only one kind of the affine transformations, the proposed quantum image registration algorithm is still preliminary for practical applications. How to utilize quantum mechanics to design a more powerful quantum image registration algorithm accounting for real affine transformations is also worth investigating in the future work.