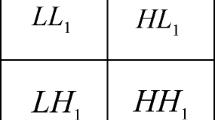The quantum realization of Arnold and Fibonacci image scrambling

Abstract

The quantum Fourier transform, the quantum wavelet transform, etc., have been shown to be a powerful tool in developing quantum algorithms. However, in classical computing, there is another kind of transforms, image scrambling, which are as useful as Fourier transform, wavelet transform, etc. The main aim of image scrambling, which is generally used as the preprocessing or postprocessing in the confidentiality storage and transmission, and image information hiding, was to transform a meaningful image into a meaningless or disordered image in order to enhance the image security. In classical image processing, Arnold and Fibonacci image scrambling are often used. In order to realize these two image scrambling in quantum computers, this paper proposes the scrambling quantum circuits based on the flexible representation for quantum images. The circuits take advantage of the plain adder and adder modulo $N$ to factor the classical transformations into basic unitary operators such as Control-NOT gates and Toffoli gates. Theoretical analysis indicates that the network complexity grows linearly with the size of the number to be operated.

1 Introduction

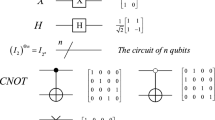
In 1982, Feynman [1] proposed a novel computation model, named quantum computers. A quantum computer is a physical machine that can accept input states which represent a coherent superposition of many different possible inputs and subsequently evolve them into a corresponding superposition of outputs. Computation, i.e., a sequence of unitary transformations, affects simultaneously each element of the superposition, generating a massive parallel data processing albeit within one piece of quantum hardware. By this way, quantum computers can efficiently solve some problems which are believed to be intractable on any classical computer. A quantum computer will be viewed as a quantum network (or a quantum circuit) composed of quantum logic gates, each gate performing an elementary unitary operation on one, two, or more two-state quantum systems called qubits [2].

The developing of quantum computer causes people’s interest to study quantum image processing (QIP), which is still in its infancy [3–5]. At present, QIP has three main directions: (1) representing quantum images; (2) expanding basic classical image transformation into quantum computers; (3) watermarking quantum images.

• 1. Representing quantum images. Research in the field of quantum image processing started with proposals on quantum image representations such as qubit lattice [6], real ket [7], and FRQI [8] and also a method for storing and representing binary geometrical forms [9]. The quantum images are two-dimensional arrays of qubits in [6] and a quantum state in [7]. FRQI method that our circuits are based on captures information about colors and their corresponding positions in an image into a normalized quantum state.

• 2. Expanding basic classical image transformation into quantum computers. It has also been proven that there are quantum processing transformations more efficient than their classical versions: quantum Fourier transform [3], quantum wavelet transform [10], the quantum discrete cosine transform [11, 12], and the geometric transformations on quantum images (GTQI) [26]. In fact, since all irreversible operations have a reversible counterpart, convolution, and correlation, typically defined in computer science as irreversible operations, can be applied on quantum images only if reversible versions of those operations are used instead.

• 3. Watermarking quantum images. Watermarking is different from cryptography. It aims at guard against image abuse by embedding invisible signal (watermark) carrying information about the copyright owner into multimedia data (carrier, such as audio, video, and image). The watermarked carriers are still readable. Several quantum images watermarking methods have been proposed [14–16] which are all based on the quantum transformations such as quantum Fourier transform (QFT) and GTQI.

In this paper, we address the second problem. The basic transformation we focused on is image scrambling. We provide quantum circuits to realize the Arnold and the Fibonacci image scrambling, respectively. As we know, this work has not been studied yet.

Image scrambling as an encryption technology is a good tool to make the scrambled image visually unrecognizable. It has become an important means of the digital image transmission, the confidentiality storage, and digital image watermarking [17–22]. Throughout all the image scrambling methods, such as Hilbert [23], magic cube [24], cat chaotic mapping [25], and so on, Arnold and Fibonacci transform algorithms are commonly used [17, 18]. All the experiences in classical computers indicate that Arnold and Fibonacci image scrambling belongs to basic transformations in image processing. They are often used in many image processing algorithms. So, we use quantum circuits to realize these two transformations to promote QIP.

The rest of the paper is organized as follows. A brief background on the FRQI representation, Arnold and Fibonacci image scrambling, and quantum adder networks is presented in Sect. 2. The quantum circuit architecture of Arnold image scrambling and Fibonacci image scrambling is discussed in Sect. 3. This is followed in Sect. 4 by the theoretical analysis of network complexity. Finally, a conclusion is given in Sect. 5.

2 Preliminaries

2.1 The flexible representation for quantum images (FRQI)

In order to represent images on quantum computers, the flexible representation for quantum images (FRQI) was proposed in [8, 26] which contents the color information and corresponding position information of every pixel in image. According to the FRQI, a quantum image can be written as the form shown below.

$$\begin{aligned} I(\theta )&= \frac{1}{2^{n}}\sum \limits _{i=0}^{2^{2n}-1}|c_{i}\rangle \otimes |i\rangle ,\\ |c_{i}\rangle&= \cos \theta _{i}|0\rangle +\sin \theta _{i}|1\rangle , \theta _{i}\in [0,\frac{\pi }{2}], i=0,1,\ldots ,2^{2n}-1. \end{aligned}$$

where $|0\rangle , |1\rangle$ are two-dimensional computational basis quantum states, $(\theta _{0},\theta _{1},\ldots ,\theta _{2^{2n}-1})$ is the vector of angles encoding colors, $|i\rangle$, for $i=0,1,\ldots ,2^{2n}-1$, are $2^{2n}$-dimensional computational basis quantum states, and $\otimes$ denote the Kronecker product. There are two parts in the FRQI of an image: $|c_{i}\rangle$ and $|i\rangle$, which encode information about the colors and their corresponding positions in the image, respectively. The size of the quantum image is $2^{n}\times 2^{n}$.

For two-dimensional images, the location information encoded in the position qubit $|i\rangle$ includes two parts: the vertical and horizontal coordinates. Considering quantum images in 2n-qubit systems, or n-sized images, the vector

$$\begin{aligned} |i\rangle =|y\rangle |x\rangle =|y_{n-1}y_{n-2}\ldots y_{0}\rangle |x_{n-1}x_{n-2}\ldots x_{0}\rangle , |y_{i}\rangle |x_{i}\rangle \in \{0,1\}, i=0,1,\ldots ,n.\nonumber \\ \end{aligned}$$

(1)

For every $i=0,1,\ldots ,n$, encodes the first n-qubit $y_{n-1},y_{n-2},\ldots ,y_{0}$ along the vertical location and the second n-qubit $x_{n-1},x_{n-2},\ldots ,x_{0}$ along the horizontal axis. An example of a $2\times 2$ FRQI image is shown in Fig. 1. Its FRQI representation is shown below. In this example, n=1.

$$\begin{aligned} |I\rangle =\frac{1}{2}\Big [(\cos \theta _{0}|0\rangle +\sin \theta _{0}|1\rangle )\otimes |00\rangle +(\cos \theta _{1}|0\rangle +\sin \theta _{1}|1\rangle )\otimes |01\rangle \\ +\,(\cos \theta _{2}|0\rangle +\sin \theta _{2}|1\rangle )\otimes |10\rangle +(\cos \theta _{3}|0\rangle +\sin \theta _{3}|1\rangle )\otimes |11\rangle \Big ] \end{aligned}$$

Fig. 1

A simple image and its FRQI state

2.2 Arnold and Fibonacci image scrambling

The Arnold transform, or Arnold’s cat map, was set up during the research of ergodic theory by V.I. Arnold [27]. Dyson et al. [28] quoted the transform as an image scrambling method in 1992. Since then, it has been widely used in image processing.

Assume $I(x,y)$ is the original image, where $(x,y)$ is the pixel coordinates, $x,y=0,1,\ldots ,N-1$. $N$ is the size of the image (that is, the image is generally considered a square image). The two-dimensional Arnold scrambling is defined as follows:

$$\begin{aligned} \left( \begin{array}{c} x_{A}\\ y_{A} \end{array} \right) = \left( \begin{array}{c@{\quad }c} 1&{}1\\ 1&{}2 \end{array} \right) \left( \begin{array}{c} x\\ y \end{array} \right) (\hbox {mod} N) \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{aligned} x_{A}&=(x+y)\mathrm{mod}N \\ y_{A}&=(x+2y)\mathrm{mod}N \end{aligned} \end{aligned}$$

(2)

$(x_{A},y_{A})$ is the pixel coordinates in the Arnold transformed image. The inverse transformation is:

$$\begin{aligned} \left( \begin{array}{c} x\\ y \end{array} \right) = \left( \begin{array}{c@{\quad }c} 1&{}1\\ 1&{}2 \end{array} \right) ^{-1} \left( \begin{array}{c} x_{A}\\ y_{A} \end{array} \right) (\hbox {mod} N) = \left( \begin{array}{c@{\quad }c} 2&{}-1\\ -1&{}1 \end{array} \right) \left( \begin{array}{c} x_{A}\\ y_{A} \end{array} \right) (\hbox {mod} N) \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{aligned} x&=(2x_{A}-y_{A})\hbox {mod} N \\ y&=(-x_{A}+y_{A})\hbox {mod} N \end{aligned} \end{aligned}$$

(3)

For example, a simple “image” has nine pixels. $N=3$, $x,y=0,1,2$. The Arnold scrambling of this image is shown in Fig. 2.

Fig. 2

A simple example for Arnold image scrambling

Arnold transformation is not a “pure” two-dimensional affine transformation because it has a “mod” operator. It can be seen as a process of cutting and splicing.

The two-dimensional Fibonacci scrambling is defined as follows:

$$\begin{aligned} \left( \begin{array}{c} x_{F}\\ y_{F} \end{array} \right) = \left( \begin{array}{c@{\quad }c} 1&{}1\\ 1&{}0 \end{array} \right) \left( \begin{array}{c} x\\ y \end{array} \right) (\hbox {mod} N) \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{aligned} x_{F}&=(x+y)\hbox {mod} N\\ y_{F}&=x \end{aligned} \end{aligned}$$

(4)

$(x_{F},y_{F})$ is the pixel coordinates in the Fibonacci transformed image. The inverse transformation is as follows:

$$\begin{aligned} \left( \begin{array}{c} x\\ y \end{array} \right) = \left( \begin{array}{c@{\quad }c} 1&{}1\\ 1&{}0 \end{array} \right) ^{-1} \left( \begin{array}{c} x_{F}\\ y_{F} \end{array} \right) (\hbox {mod} N) = \left( \begin{array}{c@{\quad }c} 0&{}1\\ 1&{}-1 \end{array} \right) \left( \begin{array}{c} x_{F}\\ y_{F} \end{array} \right) (\hbox {mod} N) \end{aligned}$$

i.e.,

$$\begin{aligned} \begin{aligned} x&=y_{F}\\ y&=(x_{F}-y_{F})\hbox {mod} N \end{aligned} \end{aligned}$$

(5)

It is similar with Arnold image scrambling.

The two transformations all have period, i.e., when repeating Arnold/Fibonacci transform to a certain iteration step, it will surely resume the image. In [28], Dyson researched the period. Generally speaking, the explicit value of the period cannot be calculated. Dyson gave the upper bounds and the lower bounds for the period, and gave explicit values for particular cases as shown in Table 1. We can see that the period is connected with image size $N$.

Table 1 The period of Arnold and Fibonacci transform

For real images, we can see the scrambling results and the period from Fig. 3.

Fig. 3

The results and period of Arnold and Fibonacci image scrambling. The original image is $128\times 128$ “Lena.” a–e Arnold transformation. f–j Fibonacci transformation. The subcaptions are the iteration times

For a more comprehensive survey of the state-of-the-art of this topic, readers can referred to [27, 28].

2.3 Adder modulo $N$

From Eqs. (2) and (4), we can see that Arnold and Fibonacci image scrambling mainly use additions modulo $2^{n}$ operation. Hence, the quantum adder modulo $N$ network is fundamental for realizing these two scramblings in quantum computer. In, Vedral et al. [2] have already given such network based on the plain adder.

2.3.1 Plain adder

The plain adder is a quantum network that can calculate the sum of two numbers which are stored in two quantum registers $|a\rangle$ and $|b\rangle$.

The addition is probably the most basic operation, in the simplest form it can be written as

$$\begin{aligned} |a,b,0\rangle \rightarrow |a,b,a+b\rangle \end{aligned}$$

Rewrite the result of the computation into the one of the input registers, which is the usual way additions are performed in conventional irreversible hardware; i.e.,

$$\begin{aligned} |a,b\rangle \rightarrow |a,a+b\rangle \end{aligned}$$

(6)

As one can reconstruct the input $(a,b)$ out of the output $(a, a+b)$, there is no loss of information, and the calculation can be implemented reversibly. The operation of the full addition network is illustrated in Fig. 4, where the basic carry and sum operations for the plain addition network are shown in Fig. 5.

Fig. 4

Plain adder network

Fig. 5

Basic sum and carry operations

Note that, there was a thick black bar on the right- or left-hand side of basic carry and sum networks. A network with a bar on the left side represents the reversed sequence of elementary gates embedded in the same network with the bar on the right side.

In fact, operations such as addition, multiplication, and exponentiation cannot be directly deduced from their classical Boolean counterparts because they are irreversible. For example, reading three at the output of the addition does not provide enough information to determine the input which could be $(0,3), (1,2), (-1,4)$, or others. Quantum arithmetic must be built from reversible logical components. It has been shown that reversible networks require some additional memory for storing intermediate results [2].

If the action of the network is reversed with the input $(a,b)$, the output will produce $(a,b-a)$ when $b\geqslant a$. When $b<a$, the output is $(a,2^{n}-(a-b))$.

2.3.2 Adder modulo $N$

The adder modulo $N$ is a quantum network that can calculate the modulo sum of two numbers.

A slight complication occurs when one attempts to build a network that effects

$$\begin{aligned} |a,b\rangle \rightarrow |a,(a+b) \hbox {mod} N\rangle \end{aligned}$$

(7)

where $0\leqslant a,b<N$, because if we just omit the highest carry $b_{n+1}$ from Fig. 4 to gain adder modulo $N$ as in classical computers, there will be a violation of unitarity (a loss of information) since the input $(a,b)$ cannot be reconstructed from the output $(a,(a+b) \hbox {mod} N)$. The approach used by Vedral is based on taking the output of the plain adder network, and subtracting $N$, depending on whether the value $a+b$ is bigger or smaller than $N$. Figure 6 illustrates the various steps needed to implement modular addition.

Fig. 6

Adder modulo $N$

The plain adder and the adder modulo $N$ are all unitary operators. Readers can find more information of this topic from [2].

3 Quantum circuit architecture of Arnold and Fibonacci image scrambling

3.1 Arnold and Fibonacci image scrambling’s FRQI representation

In this paper, we use FRQI to represent quantum images. Because Arnold image scrambling is the operation which focuses on manipulating the information about the position of every pixel in the images, we only need to change the position information $|i\rangle$ in Eq. (1). We define Arnold image scrambling as A, the original quantum image as I, and the scrambled quantum image as $I_{A}$. The operation A which on FRQI quantum images can be defined as

$$\begin{aligned} I_{A}(\theta )=A\Big (I(\theta )\Big )=\frac{1}{2^{n}}\sum \limits _{i=0}^{2^{2n}-1}|c_{i}\rangle \otimes A(|i\rangle ) \end{aligned}$$

According to Eq. (2), we define $A(|i\rangle )$ as

$$\begin{aligned} A(|i\rangle )=A(|y\rangle |x\rangle )=A(|y\rangle )A(|x\rangle ) \end{aligned}$$

where

$$\begin{aligned} |x_{A}\rangle&= A(|x\rangle )=|x+y\rangle \hbox {mod} 2^{n} \end{aligned}$$

(8)

$$\begin{aligned} |y_{A}\rangle&= A(|y\rangle )=|x+2y\rangle \hbox {mod} 2^{n} \end{aligned}$$

(9)

Likewise, Fibonacci image scrambling F can be described as

$$\begin{aligned} I_{F}(\theta )&= F(I(\theta ))=\frac{1}{2^{n}}\sum \limits _{i=0}^{2^{2n}-1}|c_{i}\rangle \otimes F(|i\rangle )\\ F(|i\rangle )&= F(|y\rangle |x\rangle )=F(|y\rangle )F(|x\rangle ) \end{aligned}$$

$$\begin{aligned} |x_{F}\rangle&= F(|x\rangle )=|x+y\rangle \hbox {mod} 2^{n} \end{aligned}$$

(10)

$$\begin{aligned} |y_{F}\rangle&= F(|y\rangle )=|x\rangle \end{aligned}$$

(11)

Equations (8, 9) and (10, 11) give the quantum representations of Arnold and Fibonacci image scrambling, respectively. In the following, the circuits we gave are based on them.

3.2 Quantum circuit architecture of Arnold and Fibonacci image scrambling

3.2.1 The scrambling networks

Because the operators $|x_{A}\rangle$, $|y_{A}\rangle$, $|x_{F}\rangle$, and $|y_{F}\rangle$ are independent of each other as shown in Eqs. (8–11), we can give several circuits to realize them, respectively.

• 1. The scrambling network that realize $|x_{A}\rangle$ and $|x_{F}\rangle$. Eqs. (8) and (10) indicate that $|x_{A}\rangle$ is the same as $|x_{F}\rangle$. By contrasting Eqs. (8)/(10) with (7), we only need to replace $a,b,N$ in (7) with $x,y,2^{n}$, respectively, to construct $|x_{A}\rangle$ and $|x_{F}\rangle$ networks.

  $$\begin{aligned} |x,y\rangle \rightarrow |x,(x+y)\hbox {mod} 2^{n}\rangle \end{aligned}$$

  (12)

  The adder modulo $2^{n}$ network is shown in Fig. 7. The input is the position information $|x\rangle$ and $|y\rangle$ of original images, and the output is the position information $|x_{A}\rangle$/$|x_{F}\rangle$ of Arnold/Fibonacci scrambled images.

  Fig. 7

  

  $|x_{A}\rangle$ and $|x_{F}\rangle$ network

• 2. The scrambling network that realize $|y_{A}\rangle$. According to Eq. (8), because

  $$\begin{aligned} (x+2y) \hbox {mod} 2^{n}=(y+(y+x)) \hbox {mod} 2^{n}, \end{aligned}$$

  we can divide the realization of $|y_{A}\rangle$ into two steps.

  $$\begin{aligned} |y,x\rangle \rightarrow |y,y+x\rangle \rightarrow |y,(y+(y+x)) \hbox {mod} 2^{n}\rangle \end{aligned}$$

  (13)

  The first step corresponds to the plain adder and the second one corresponds to adder modulo $2^{n}$. We can cascade them to realize $|y_{A}\rangle$ as shown in Fig. 8. The output of the whole network, $(y+(y+x)) \hbox {mod} 2^{n}$, which is the same as $(x+2y) \hbox {mod} 2^{n}$, is the position information $|y_{A}\rangle$ of Arnold scrambled images.

• 3. For $|y_{F}\rangle$,

  $$\begin{aligned} |y_{F}\rangle =|x\rangle \end{aligned}$$

  (14)

  It needs no circuit.

Fig. 8

$|y_{A}\rangle$ network

The reversibility of the two networks showed in Figs. 7 and 8 roots in the unitarity of the plain adder and the adder modulo $N$ proposed in [2].

If we reverse the action of the above networks (i.e., if we input a scrambled image from the right), we will get the original image from the left. However, the reversed networks also need the original coordinate $|y\rangle$ as their inputs. It is unrealistic. Applications require that the original image is regained only depending on the scrambled image. Hence, the special inverse scrambling circuits are necessary.

3.2.2 The inverse circuits

From Eqs. (3) and (5), we can see that the inverse transformations use subtraction. It can be realized by reversing the inputs and the outputs of adders as described in the last paragraph of Sect. 2.3.1.

• 1. Inverse Arnold: $|x\rangle$:

  $$\begin{aligned} |x_{A},x_{A}\rangle \rightarrow |x_{A},2x_{A}\rangle \rightarrow |y_{A},2x_{A}\rangle \rightarrow |y_{A},(2x_{A}-y_{A}) \hbox {mod} 2^{n}\rangle \end{aligned}$$

  The first step uses a plain adder to double $x_{A}$; the second step replaces $x_{A}$ with $y_{A}$; and the third step uses an inverse adder modulo $2^{n}$ to gain $(2x_{A}-y_{A}) \hbox {mod} 2^{n}$. $|y\rangle$:

  $$\begin{aligned} |x_{A},y_{A}\rangle \rightarrow |x_{A},(y_{A}-x_{A}) \hbox {mod} 2^{n}\rangle \end{aligned}$$

  It is corresponding to an inverse adder modulo $2^{n}$.

• 2. Inverse Fibonacci: $|x\rangle$:

  $$\begin{aligned} |x\rangle =|y_{F}\rangle \end{aligned}$$

  $|y\rangle$:

  $$\begin{aligned} |y_{F},x_{F}\rangle \rightarrow |y_{F},(x_{F}-y_{F}) \hbox {mod} 2^{n}\rangle \end{aligned}$$

  It is corresponding to an inverse adder modulo $2^{n}$.

Thus, the inverse circuits can be seen in Fig. 9.

Fig. 9

The inverse circuits. a $|(2x_{A}-y_{A})\hbox {mod} 2^{n}\rangle$. b $|(y_{A}-x_{A})\hbox {mod} 2^{n}\rangle$. c $|(x_{F}-y_{F})\hbox {mod} 2^{n}\rangle$

3.2.3 A simple example

Let us consider the simple $4\times 4$ image shown in Fig. 10a as an example. Here, $n=2$.

Fig. 10

Arnold and Fibonacci image scrambling results on a quantum image sized $4\times 4$. a The original image. b The Arnold scrambled image. c The Fibonacci scrambled image

According to the circuits, the truth table of the quantum circuits is shown in Table 2.

Table 2 The truth table

According to the truth table, the results of Arnold and Fibonacci image scrambling results are shown in Fig. 10b and c, respectively.

4 Network complexity

The network complexity depends very much on what is considered to be an elementary gate. In this section, we choose the Control-NOT to be our basic unit; then, the Toffoli gate can be simulated by six Control-NOT gates [2].

The numbers of elementary gates in basic carry and sum operations are 13 and 2, respectively. Consequently, the network complexity of the plain adder is $28n-12$ as it contains $2n-1$ carries, $n$ sums, and one Control-NOT gate. It scales linearly with the size of the circuit’s input $n$. Because the adder modulo $N$ contains five plain adders plus several Control-NOT gates and NOT gates, the network complexity of it, approximately $140n$, also is linear.

Therefore, the complexities of the scrambling networks and the inverse circuits are all linear because they contain only one or two plain adder or adder modulo $N$.

Although the slope of $140n$ is high, its value will not exceed 2,000 in general because the size of an image is less than 10,000 $\times$ 10,000 according to the empirical value in classical computer. That is to say, $n<14$ because $2^{14}=16,384$.

5 Conclusion

In this paper, Arnold and Fibonacci image scrambling circuits based on FRQI are proposed. Arnold and Fibonacci image scrambling are fundamental image transformations as useful as discrete Fourier transform, discrete cosine transform, discrete wavelet transform, and so on. The realization of them in quantum computers can promote QIP. The quantum circuits take advantage of the plain adder and adder modulo $N$ to scramble the quantum images. The complexity of the networks is linear.

The future work includes the following:

• 1. Give the Hilbert image scrambling circuit because Hilbert transformation is a more commonly used image scrambling algorithm. It cannot be simply boiled down to the addition or other simple operations.

• 2. Give the affine transformation quantum circuit. Affine transformation is a collection of transformations. Arnold and Fibonacci image scrambling belong to it. Affine transformation can be defined as follows:

  $$\begin{aligned} \left( \begin{array}{c} x'\\ y' \end{array} \right) = \left( \begin{array}{c@{\quad }c} a&{}b\\ c&{}d \end{array} \right) \left( \begin{array}{c} x\\ y \end{array} \right) (\hbox {mod} N) \end{aligned}$$

  where $ad=bc\pm 1$, $a,b,c,d\in Z$, Z is the integer set.

• 3. Apply these circuits to quantum watermarking.