Introduction

Due to their highly appealing properties, practical applications of polymer-based composite materials in various engineering and science fields are rapidly increasing. Among the different areas of activity involved in this technology of composite materials, can be mentioned as good practices: automotive, aerospace, civil, electronic, thermal, energy, biomedical fields, and much more [1, 2]. Most recently, a new generation of composites, namely nanocomposite materials, has emerged as an advanced multifunctional, lightweight and high-strength material [3,4,5,6,7]. This type of composite material differs from other types of conventional materials by the constitution of nano-scale reinforcements. Among these nano-reinforcements, it can be mentioned Boron-Nitride nanotubes (BNNTs) and carbon-based nanomaterials such as carbon nanotubes (CNTs) and graphene (Gr). In this subject matter, the reported results in Refs [8, 9] found that polymer-based nanocomposites that are reinforced with carbon-based reinforcements (such as CNTs) could be four to five times lighter and several times stronger than metallic materials for the same cross-section. BNNTs reinforced composite materials also shows outstanding performances, Guan et al. [10] found that adding 5 weight fraction (wt) % of functionalized BNNT to epoxy resin resulted in a significant 21% increase in Young's modulus. Moreover, they observed 12%, 21%, and 49% increases in tensile strength, failure strain, and toughness, respectively, when 2 wt% of functionalized BNNT was added. Additionally, a notable 34% enhancement in fracture toughness was observed by adding 3 wt% of functionalized BNNT. Although BNNTs and CNTs offer similar mechanical properties (e.g. Young’s modulus of 1.3 TPa for CNTs vs. 1.2 TPa for BNNTs) [11, 12] and similar integration challenges when used as reinforcement for nanocomposite materials, BNNTs offer various functional properties such as a wide band gap of approximately 6 eV, excellent thermal stability, high electrical resistivity, transparency in the visible light region, and high neutron absorption capability. These properties provide distinct advantages for specific applications, such as aircraft windows, transparent armor, and electrical insulation [10]. Although the excellent abilities offered in terms of mechanical, thermal and electrical properties of CNTs and BNNTs graphene and its derivatives have recently attracted the attention of many researchers in various disciplines, because CNTs and BNNTs are (i) highly agglomerative (due to the van der Waals interactions between nanotubes), have (ii) low interfacial interactions, have (iii) highly anisotropic properties, have (iv) high manufacturing costs, and have (v) high difficulties in obtaining appropriate uniform dispersions [10, 13]. It should be noted that graphene has a unique two-dimensional hexagonal network geometry [14], which results in a larger surface area and lower manufacturing cost compared to carbon nanotubes [15]. As a result, graphene has gained increasing attention and research interest in recent years, as many studies focusing on its superior properties [16,17,18]. Graphene is nowadays proposed as one of the most ideal nano-reinforcements for nanocomposite materials. In this area of research, Rafiee et al. [19] confirmed the superiority of graphene nano-platelets (GPLs) over CNTs reinforcements through an investigation conducted with his fellow researchers. They compared the effective mechanical properties of composite polymer reinforced with GPLs and SWCNT fillers. Rafiee and his coauthors concluded that by adding a low content of GPL (0.1wt%) to an epoxy matrix, Young’s moduli of the GPLs reinforced composite increased by 31% when compared with the pristine epoxy, while it increased by only 3% for the SWCNT reinforced composite.

While remaining in this context, it is worth mentioning that over the last decades, advanced composite materials, such as functionally graded materials (FGMs), have emerged since then. This class of materials are known for their high thermomechanical properties, where they are notably characterized by the continuous gradual variation of their constituent materials from one structure interface to another. An FGM is often made of metal and ceramic so that the mixture is protected against high-temperature gradients. However, due to its poor thermal conductivity, the ceramic material provides high-temperature opposition, while the metal material provides high strength because of its higher toughness [20,21,22]. A significant amount of publications have been reported on the mechanical and thermomechanical behavior of different FGM structures, including plates [23], beams [24], and shells [25]. To further enhance the efficiency of reinforcing polymer-based composites, the distribution of nano-reinforcements such as CNTs and graphene can be modeled using the FGM concept. In the research work conducted by Shen [26], who first implemented the FGM concept on CNT-reinforced composite plates, for which the distribution of CNT volume fraction varies linearly across the plate thickness direction. Since then, the mechanical behavior of FG-CNT-reinforced nanocomposite structures has been an increasingly hot topic of discussion. The effects of many influencing parameters, such as CNT volume fraction and distribution patterns on the post-buckling analysis [27], buckling analysis [28], vibrational analysis [29, 30], and static analysis [31] have been reported for various plate types, including sandwich plates [32], elliptical plates [33], circular plates [34], skew plates [35], shell structures [36], arbitrarily shaped plates [37], laminated plates [38], trapezoidal plates [39], and quadrilateral plates [40].

With the highly valued involvement of many researchers from academia and industry in recent years, the concept of FGMs has also been implemented in polymeric composite reinforced with graphene-based nano-materials. Reddy et al. [41] analyzed the free vibration characteristics of FG graphene nano-platelet reinforced composite (GNPL-RC) plates and FG ceramic/metal plates under the effect of different types of boundary conditions. Reddy and his co-authors used the commercial numerical software STRAND7, which is based on the FSDT. However, Song et al. [42] conducted an investigation on the free and forced vibrations of FG GNPLs composite plates using FSDT and Navier-type solutions. Furthermore, Arefi et al. [43] utilized a two-variable sinusoidal shear deformation theory incorporated with nonlocal elasticity theory to examine the linear free vibrational characteristics of FG polymer composite plates reinforced with GNPLs. Based on the Non-Uniform Rational B-Splines (NURBS) formulation and the four-variable refined plate theory, Thai et al. [44] investigated the free vibration, buckling, and bending behavior of multilayer FG GNPL reinforced composite plates. In another attempt, using a modified strain gradient theory, Thai and his co-authors [45] studied the size-dependent free vibration characteristics of multilayer FG GNPL-RC square and circular microplates. According to their findings, the authors concluded that adding GNPLs to polymer-based composite can lead to a notable drop in the structure deflection. Another effort was made by Chiker et al. [46], whose aim was focused on the investigation of free vibration characteristics of FG polymeric composite plates reinforced with carbon-based nano-fillers using FSDT assumptions. In this study, both linear and non-linear forms of the distributed nano-reinforcements were considered. In another research work, Garcia et al. [47] compared the bending and free vibration behavior of functionally graded GNPL and CNT-reinforced composite nano-plates under the effect of nano-reinforcements agglomeration using the FSDT coupled with the finite element method (FEM). Furthermore, Anamagh and Bediz [48] utilized the spectral Chebyshev approach to study the free vibration and buckling behaviors of FG porous plates reinforced with GNPLs; the governing boundary value problem was derived using the FSDT assumptions and the energy-based approach. However, the free vibration behavior of post-buckled arbitrarily shaped FG-GNPL reinforced porous composite plates was performed by Ansari et al. [49] using the third-order shear deformation theory (TSDT) and the FEM approach coupled with the variational differential quadrature (VDQ) method. Moreover, Qin et al. [50] studied the vibrational characteristics of FG shallow shells reinforced with GNPLs under arbitrary boundary conditions using a developed unified solution method; the general equations were obtained using the FSDT assumptions combined together with the artificial spring technique.

It should be noted that, more recently, the FGM concept was also implemented in the mono-layer graphene-reinforced polymer-based composite, where several investigations have been conducted on the vibrational behavior of plate structures. Consequently, Wang et al. [51] studied the buckling and free vibration behavior of shear deformable functionally graded graphene-reinforced nanocomposite (GRNC) laminated plates using FSDT frameworks and the multi-term Kantorovich Galerkin method. Additionally, the free vibration analysis of polymeric laminated plates containing piece-wise GRNC plies was conducted by Saiah et al. [52]; theoretical assumptions were based on the FSDT, while Lagrange's equation and the FEM were used to derive the natural frequencies. Another investigation in this field of interest was carried out by Yang et al. [53], carrying out the buckling and free vibration characteristics of FG graphene nano-platelets reinforced porous polymeric composite plates; the governing equations of the structure were derived and solved according to the FSDT and Chebyshev-Ritz method. In addition, the thermo-elastic vibration analysis of GRNC stiffened plate with general boundary conditions was performed by Maji et al. [54] using the FSDT and finite element method. However, thickness stretching effects were considered by Wang and Ma [55] when analyzing the bending and free vibration characteristics of FG-GRNC plates; Hamilton's principle and Navier solution method was used to conduct the governing equations. Additionally, a molecular dynamics (MD)-based multiscale analysis was employed by Wang et al. [56] to study the free vibration behavior of FG-GRNC quadrilateral plates; the plate governing equation was derived based on the FSDT coupled with a meshless method.

Since the mechanical behavior of mono-layer graphene-reinforced polymer-based composites are highly sensitive to the thermal environmental conditions in which they operate, the thermomechanical analysis conducted by Lin et al. [57] has been a hot research subject, in which several research works have been reported in the open literature. For instance, Shen et al. [58] studied the nonlinear vibration of functionally graded GRNC laminated plates in thermal environments, where a higher-order shear deformation theory (HSDT) with the framework of von Kármán strains was used to develop the motion equations of the plates. The authors concluded that the plate nonlinear to linear frequency ratios increase, but the natural frequencies are reduced when the temperature rises. In addition, Shen et al. [59] studied the vibration of FG-GRNC laminated plates resting on elastic foundations. In their study, the authors assumed that the laminated plate is thermally post-buckled. Based on their results, the authors concluded that the FG reinforcement patterns significantly influence the nonlinear vibration behavior of thermally post-buckled GRNC laminated plates. In further research, Kiani [60] used the non-uniform rational basis spline (NURBS) formulation to investigate the effect of thermal environments on the isogeometric large amplitude free vibration of FG-GRNC plates. The authors found that the laminated plates nonlinear to linear frequency ratios increase as the temperature increases. In another attempt, Kiani and Mirzaei [61] studied the thermal post-buckling characteristics of piecewise temperature-dependent FG-GRNC laminated beams. The system total strain energy was developed based on nonlinearly geometrical von Karman type and the first-order shear deformation beam theory. The problem of nonlinear forced vibration responses of FG-GRNC laminated plates resting on visco-Pasternak foundations in thermal environments was solved by Fan et al. [62] based on Reddy’s HSDT assumptions, where the effects of the initial loading and the von Karman geometric nonlinearity were included in the derivation of the motion equations. According to their analytical results, the authors concluded that (i) the FG distribution patterns of graphene, (ii) the foundation stiffness, (iii) the temperature variation, and (iv) the damping factor have remarkable influences on the dynamic characteristics of FG-GRNC laminated plates. Furthermore, Kiani [63] analyzed the thermal post-buckling of temperature-dependent FG-GRNC laminated plates using a NURBS-based isogeometric finite element method. It was concluded that the post-buckling deflection of graphene-reinforced composite laminated plates might be largely reduced by introducing the FG distribution of graphene. Regarding the nonlinearity effects, Shen et al. [64] conducted another attempt to study the bending of FG-GRNC laminated plates resting on elastic foundations under the effect of different thermal environments. The governing equations for the bending of the laminated plates were based on HSDT assumptions, while the load-bending moment and load–deflection curves were determined according to the two-step perturbation technique. The authors found that the temperature rise, foundation stiffness, character of the in-plane boundary conditions, and the initial compressive load significantly influence the nonlinear bending behaviors of FG-GRNC laminated plates. Moreover, Shen et al. [65] highlighted the effect of elastic foundations on the nonlinear dynamic instability of GRNC laminated plates under different thermal environments, employing the HSDT assumptions. Shen and his co-workers concluded that the variation in the (i) nano-reinforcement distribution types, (ii) temperature, plate side-to-thickness ratio, and (iii) foundation stiffness considerably influence the nonlinear dynamic instability of GRNC laminated plates.

After reviewing the research works cited above, the following observations can be revealed:

  • Having exceptional physical, mechanical, chemical, and optical properties, composite and nanocomposite materials are considered to be the most promising alternatives to conventional materials [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

  • Most research works have been focused on investigating the mechanical behavior of carbon-based nanocomposite materials (i.e., carbon nanotubes-reinforced composite materials) [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. On the other hand, research on the mechanical behavior of graphene-based nanocomposite materials, including GRNC and graphene platelets reinforced composite (GNPL-RC) materials, has only recently become a popular topic [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65].

  • Most works dealing with the mechanical behavior of GNPL-RC materials have used the Halpin–Tsai micromechanical model to estimate their mechanical properties [41,42,43,44,45,46,47,48,49,50]; while, the mechanical properties of GRNC materials were determined according to the so-called Extended Halpin–Tsai model [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65].

  • Numerous studies have been reported in the literature regarding the free vibration analysis of GRNC laminated structures at ambient temperature [51,52,53,54,55,56].

  • Little studies have been published on the free vibration behavior of functionally graded GRNC laminated plates in thermal environments. Most of reported works have focused on investigating other mechanical behaviors [57,58,59,60,61,62,63,64,65].

In addition to the above observations, it is worth noting that only limited parametric studies have been conducted in most reported publications when examining the performance of functionally graded GRNC laminated structures in thermal environments [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. Therefore, to better understand how this type of nanocomposite material behaves under such conditions of thermal environments, it is essential to investigate the impact of other parameters that also affect their mechanical behavior. To address this gap and further enrich the database of functionally graded nanocomposite structures, the present paper aims to provide results of parametric studies on the free vibration characteristics of temperature-dependent laminated nanocomposite plates reinforced with functionally graded mono-layer graphene, taking into account the effect of several influencing parameters that we believe have not been so far considered in other open literature publications. In this context, for the first time, the present paper aims to explore the impact of (i) dependence of mechanical properties on temperature, (ii) lay-up arrangement of plies, (iii) plate number of plies, (iv) linear and non-linear distributions of graphene, and (v) lamination angles of the plies on the free vibration behavior and the mode shapes of GRNC laminated plates in thermal environments.

In the present work, a numerical investigation will be undertaken to determine the natural frequencies and associated mode shapes of functionally graded GRNC laminated plates in different thermal environments. Four non-uniform distribution patterns of the graphene are considered in this paper. The FG patterns are modeled according to the piece-wise technique. The so-called extended Halpin–Tsai method is used to estimate the GRNC mechanical properties. The laminated plate governing equations are obtained based on the first-order shear deformation theory (FSDT). Then, adequate solutions to the problem posed are carried out numerically via a computer program developed internally using the finite element method (FEM). After verifying the accuracy of the used solving method, various illustrative analyses are provided to investigate the effects of several parameters, namely: (i) graphene distribution pattern and graphene weight fraction, (ii) geometric parameters (including the number of plies, lay-up arrangement of plies, lamination angles of the plies, boundary conditions, length/thickness, and width/length ratios), and (iii) external effects (e.g., various thermal environments) on the dimensionless natural frequencies of FG-GRNC laminated plates.

Mathematical Formulations and Field Equations

Formulations of Effective Mechanical Properties

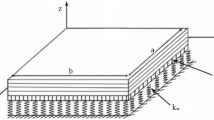
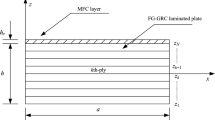
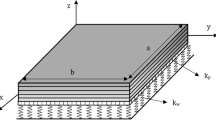
Let us consider a perfectly bonded graphene-reinforced nanocomposite (GRNC) laminated plate. As can be seen from Fig. 1, the plate length, width, and thickness are denoted by a, b, and h, respectively. Represented by its principle directions (x, y, and z), the plate is located in the standard Cartesian coordinate system (see Fig. 1). It is assumed that the GRNC laminated plates contain NP plies of zigzag graphene fillers (referred to as 0-ply) imbedded in an isotropic polymer matrix. Constituent plies of GRNC laminated plates may have an unequal concentration of graphene volume fraction, if so, this may lead to the construction of a piece-wise functionally graded nanocomposite structure (referred to as FG-GRNC) with different patterns (i.e., FG-X, FG-Λ, UD, FG-V, and FG-O). UD denotes the uniform distribution of graphene nano-reinforcement across the plate thickness direction, while each of FG-X, FG-Λ, UD, FG-V, and FG-O refer to plates with non-uniform distribution patterns as shown in Fig. 2.

Fig. 1
figure 1

Geometric features coordinate system of a piece-wise GRNC laminated plate

Full size image
Fig. 2
figure 2

Different distribution types of the piece-wise functionally graded graphene nano-reinforcements

Full size image

Values of the graphene volume fraction (\(f_{G}^{(k)}\)) and matrix volume fraction (\(f_{m}^{(k)}\)) of the plate k-th ply are given as [57]:

$$ f_{G}^{(k)} = \frac{{w_{f} }}{{w_{f} + \left( {{{\rho^{G} } \mathord{\left/ {\vphantom {{\rho^{G} } {\rho^{m} }}} \right. \kern-0pt} {\rho^{m} }}} \right) - \left( {{{\rho^{G} } \mathord{\left/ {\vphantom {{\rho^{G} } {\rho^{m} }}} \right. \kern-0pt} {\rho^{m} }}} \right)w_{f} }} $$
(1)

and

$$ f_{m}^{(k)} = 1 - f_{G}^{(k)} $$
(2)

in which k = 1, 2, 3, … NP; and \(w_{f}\) is the mass fraction of graphene; \(\rho^{G}\) and \(\rho^{m}\) refer to the graphene and matrix densities, respectively.

Prediction of elastic properties of various composite materials can be handled using different micromechanical approaches. Among them, we can mention the rule of mixture approach [66], Mori–Tanaka approach [47], and Halpin–Tsai approach [67]. Generally, these approaches depend on the engineering constants of the materials constituting the mixture; among them, we can mention: Young’s (E) and shear moduli (G), and Poisson’s ratio (v). Comparisons of the mechanical properties obtained from the mathematical modeling and experimental examination showed that the micromechanical approaches mentioned above could be sufficiently accurate for certain composite materials and not for others. Thus, it has been agreed that the Mori–Tanaka, rule of mixture, and Halpin–Tsai’s micromechanical models are more applicable to micro-particles, fiber fillers, and two-dimensional aligned anisotropic fillers, respectively. It has been reported in the open literature [68,69,70] that the mechanical properties of composites that contain nanoscale reinforcement (e.g., carbon nanotubes or graphene) cannot be simply estimated using the bare form of the micromechanics mentioned above. Nevertheless, by introducing some parameters (later referred to as efficiency parameters) in the initial form of the models perversely mentioned, they can provide predictions that agree very well with those of molecular dynamic (MD) simulation. It has been found that adding efficient parameters to the original form of the rule of mixture to become “extended rule of mixture” and “Halpin–Tsai” nomination to become the “extended Halpin–Tsai” can lead to estimate the accurate material properties of carbon nanotubes and graphene-reinforced composites as reported in Refs [26] and [71], respectively. It can be said that the main way to differentiate the rule of mixture from the extended rule of mixture approaches and Halpin–Tsai from extended Halpin–Tsai approaches is by the presence or absence of efficiency parameters within these approaches.

Since this paper deal with nanocomposites with 2D aligned anisotropic fillers as reinforcements (i.e., graphene fillers), the material properties of the GRNC plies are predicted according to Extended Halpin– Tsai model. In the following, the mathematical expressions of the Extended Halpin–Tsai approach will be presented.

Based on the extended Halpin–Tsai model, the effective Young's modulus and shear modulus of the k-th ply of the GRNC laminated plates can be obtained as follows [71]:

$$ E_{11}^{(k)} = \eta_{1} \left( {\frac{{1 + \xi_{L} \gamma_{11} f_{G} }}{{1 - \gamma_{11} f_{G} }}} \right)E^{m} $$
(3a)
$$ E_{22}^{(k)} = \eta_{2} \left( {\frac{{1 + \xi_{W} \gamma_{22} f_{G} }}{{1 - \gamma_{22} f_{G} }}} \right)E^{m} $$
(3b)
$$ G_{12}^{(k)} = \eta_{3} \left( {\frac{1}{{1 - \gamma_{12} f_{G} }}} \right)G^{m} $$
(3c)

where

$$ \gamma_{11} = \frac{{\left( {{{E_{11}^{G} } \mathord{\left/ {\vphantom {{E_{11}^{G} } {E^{m} }}} \right. \kern-0pt} {E^{m} }}} \right) - 1}}{{\xi_{L} + \left( {{{E_{11}^{G} } \mathord{\left/ {\vphantom {{E_{11}^{G} } {E^{m} }}} \right. \kern-0pt} {E^{m} }}} \right)}} $$
(4a)
$$ \gamma_{22} = \frac{{\left( {{{E_{22}^{G} } \mathord{\left/ {\vphantom {{E_{22}^{G} } {E^{m} }}} \right. \kern-0pt} {E^{m} }}} \right) - 1}}{{\xi_{W} + \left( {{{E_{22}^{G} } \mathord{\left/ {\vphantom {{E_{22}^{G} } {E^{m} }}} \right. \kern-0pt} {E^{m} }}} \right)}} $$
(4b)
$$ \gamma_{12} = \frac{{\left( {{{G_{12}^{G} } \mathord{\left/ {\vphantom {{G_{12}^{G} } {G^{m} }}} \right. \kern-0pt} {G^{m} }}} \right) - 1}}{{\left( {{{G_{12}^{G} } \mathord{\left/ {\vphantom {{G_{12}^{G} } {G^{m} }}} \right. \kern-0pt} {G^{m} }}} \right)}} $$
(4c)

and

$$ \xi_{L} = 2\left( {\frac{{l_{G} }}{{h_{G} }}} \right)\;{\text{and}}\;\xi_{W} = 2\left( {\frac{{w_{G} }}{{h_{G} }}} \right) $$
(5)

Herein, \(\xi_{L}\) and \(\xi_{W}\) denote the graphene geometry and size, respectively. \(E^{m}\) refer to the Young’s modulus of the matrix, while \(E_{11}^{G}\) and \(E_{22}^{G}\) are the longitudinal and transversal Young’s moduli, respectively. \(h_{G}\), \(l_{G}\), and \(w_{G}\) are average thickness, length, and width of monolayer graphene, respectively. \(G_{12}^{G}\) is the graphene shear modulus.

G and m subscripts refer to graphene filler and matrix, respectively. The Greek letters \(\eta_{1}\), \(\eta_{2}\), and \(\eta_{3}\) are the graphene/matrix efficiency parameters. These parameters are added to the original Halpin–Tsai model to eliminate the small-scale effects. They are calculated by matching the composite material properties obtained by the Halpin–Tsai model with those obtained by MD simulations.

The thermal expansion coefficients (i.e., \(\alpha_{11}^{(k)}\) and \(\alpha_{22}^{(k)}\)) are determined based on the Schapery’s model; according to this model, the two coefficients of a GRNC ply are expressed as [58, 60]:

$$ \alpha_{11}^{(k)} = \left( {\frac{{f_{G} E_{11}^{G} \alpha_{11}^{G} + f_{m} E^{m} \alpha^{m} }}{{f_{G} E_{11}^{G} + f_{m} E^{m} }}} \right) $$
(6)
$$ \alpha_{22}^{(k)} = (1 + \nu_{12}^{G} )f_{G} \alpha_{22}^{G} + (1 + \nu^{m} )f_{m} \alpha^{m} - \nu_{12} \alpha_{11} $$
(7)

where \(\alpha_{11}^{G}\), \(\alpha_{22}^{G}\), and \(\alpha^{m}\) are the graphene and matrix thermal expansion coefficients, respectively. While \(\nu_{12}^{G}\) and \(\nu^{m}\) refer to the graphene and matrix Poisson ratio, respectively.

Based on the rule of mixture, the mass density and Poisson ratio of a GRNC ply are expressed as [47]:

$$ \rho^{(k)} = \rho^{G} f_{G} + \rho^{m} f_{m} $$
(8)
$$ \nu_{12}^{(k)} = \nu_{12}^{G} f_{G} + \nu^{m} f_{m} $$
(9)

In which, \(\rho^{G}\) and \(\rho^{m}\) are the graphene and matrix mass density, respectively.

Since both the mass density and Poisson’s ratio are weakly dependent on temperature change, only shear modulus (\(G_{12}^{(k)}\)), Young’s moduli (\(E_{11}^{(k)}\) and \(E_{22}^{(k)}\)), and thermal expressions (\(\alpha_{11}^{(k)}\) and \(\alpha_{22}^{(k)}\)) are taken to be temperature-dependent.

Governing Equations

The displacement components of the GRNC laminated plates in the directions: x-, y-, and z- are determined using the FSDT [72]:

$$ \left\{ {\begin{array}{*{20}c} {u(x,y,z)} \\ {v(x,y,z)} \\ {w(x,y,z)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{0} (x,y)} \\ {v_{0} (x,y)} \\ {w_{0} (x,y)} \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\theta_{x} (x,y)} \\ {\theta_{y} (x,y)} \\ 0 \\ \end{array} } \right\} $$
(10)

in which \(u_{0}\), \(v_{0}\), and \(w_{0}\) are the displacement components of the mid-plane of the laminated plates in the directions: x-, y-, and z-. Whereas \(\theta_{y}\) and \(\theta_{x}\) stand for transverse normal rotations around the x- and y- axes, respectively.

Based on the same theory (i.e., FSDT), the components of the in-plane and transverse shear strain of the GRNC laminated plates are expressed as follows [72]:

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ \end{array} } \right\} = \varepsilon_{0}^{{}} + z\kappa ,\;\left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} $$
(11)

where,

$$ \varepsilon_{0}^{{}} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ {\frac{{\partial v_{0} }}{\partial y}} \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \\ \end{array} } \right\},\;\kappa = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \theta_{x} }}{\partial x}} \\ {\frac{{\partial \theta_{y} }}{\partial y}} \\ {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \\ \end{array} } \right\},\;{\text{and}}\;\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\theta_{y} + \frac{{\partial w_{0} }}{\partial y}} \\ {\theta_{x} + \frac{{\partial w_{0} }}{\partial x}} \\ \end{array} } \right\} $$
(12)

The constitutive equation that relates stress and strain of the k-th ply of the GRNC laminated plate can be expressed as follows [73]:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ \end{array} } \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]^{(k)} \left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ {\varepsilon_{yz} } \\ {\varepsilon_{xz} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\alpha_{11} } \\ {\alpha_{22} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}\Delta T} \right)^{(k)} $$
(13)

where,

$$ Q_{11}^{(k)} = \frac{{E_{11}^{(k)} }}{{1 - \nu_{12}^{(k)} \nu_{21}^{(k)} }},\;Q_{22}^{(k)} = \frac{{E_{22}^{(k)} }}{{1 - \nu_{12}^{(k)} \nu_{21}^{(k)} }},\;Q_{12}^{(k)} = \frac{{\nu_{21}^{(k)} E_{11}^{(k)} }}{{1 - \nu_{12}^{(k)} \nu_{21}^{(k)} }},\;Q_{66}^{(k)} = G_{12}^{(k)} ,\;Q_{44}^{(k)} = G_{23}^{(k)} ,\;Q_{55}^{(k)} = G_{13}^{(k)} $$
(14)

and

\(\Delta T\) is the variation of temperature (\(\Delta T = T - T_{0}\)) with respect to the reference temperature ( \(T_{0}\)).

The components of total axial force (N), total moment resultants (M), and total shear forces (Q) are related to the components of strain by the following expressions [73]:

$$ \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \left( {\left[ {A_{ij} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} } \\ {\varepsilon_{xy}^{0} } \\ \end{array} } \right\} + \left[ {B_{ij} } \right]\kappa } \right) - \left\{ {\begin{array}{*{20}c} {N_{xx}^{N} } \\ {N_{yy}^{N} } \\ {N_{xy}^{N} } \\ \end{array} } \right\} $$
(15a)
$$ \left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \left( {\left[ {B_{ij} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} } \\ {\varepsilon_{xy}^{0} } \\ \end{array} } \right\} + \left[ {D_{ij} } \right]\kappa } \right) - \left\{ {\begin{array}{*{20}c} {M_{xx}^{N} } \\ {M_{yy}^{N} } \\ {M_{xy}^{N} } \\ \end{array} } \right\} $$
(15b)
$$ \left\{ {\begin{array}{*{20}c} {Q_{yy} } \\ {Q_{xx} } \\ \end{array} } \right\} = k_{s} \left[ {F_{ij} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{yz}^{0} } \\ {\gamma_{xz}^{0} } \\ \end{array} } \right\} $$
(15c)

where \(k_{s}\) refers to the transverse shear correction factor, given by [72]:

$$ k_{s} = \frac{5}{6} $$
(16)

The stiffness components \(A_{ij}\), \(B_{ij}\), \(D_{ij}\), and \(F_{ij}\) can be expressed in the following reduced forms:

$$ (A_{ij} ,B_{ij} ,D_{ij} ) = \sum\limits_{k = 1}^{{N_{p} }} {\int\limits_{{Z_{k} }}^{{Z_{k + 1} }} {[\overline{Q}_{ij} ]^{(k)} } } (1,z,z^{2} )dz,\;\left( {i,j\, = \,1,2,6} \right) $$
(17)

and,

$$ F_{ij} = \sum\limits_{k = 1}^{{N_{p} }} {\int\limits_{{Z_{k} }}^{{Z_{k + 1} }} {[\overline{Q}_{ij} ]^{(k)} } } dz,\;\left( {i,j\, = \,4,\;5} \right) $$
(18)

whereas the components of non-mechanical force resultants (\(N^{N}\)) and moment resultants ( \(M^{N}\)) are defined as follows:

$$ \left\{ {\begin{array}{*{20}c} {N_{xx}^{N} } \\ {N_{yy}^{N} } \\ {N_{xy}^{N} } \\ \end{array} } \right\} = \sum\limits_{k = 1}^{{N_{p} }} {\int\limits_{{Z_{k} }}^{{Z_{k + 1} }} {[\overline{Q}_{ij} ]^{(k)} \{ e\}^{(k)} } } dz,\;\left( {i,j\, = \,1,\;2,\;6} \right) $$
(19)
$$ \left\{ {\begin{array}{*{20}c} {M_{xx}^{N} } \\ {M_{yy}^{N} } \\ {M_{xy}^{N} } \\ \end{array} } \right\} = \sum\limits_{k = 1}^{{N_{p} }} {\int\limits_{{Z_{k} }}^{{Z_{k + 1} }} {[\overline{Q}_{ij} ]^{(k)} \{ e\}^{(k)} Z_{{}} } } dz,\;\left( {i,j\, = \,{1},\;{2},\;{6}} \right) $$
(20)

where,

$$ \begin{gathered} \overline{Q}_{11} = Q_{11} \cos^{4} \theta + 2(Q_{12} + 2Q_{66} )\sin^{2} \theta \cos^{2} \theta + Q_{22} \sin^{4} \theta \hfill \\ \overline{Q}_{12} = Q_{12} (\cos^{4} \theta + \sin^{4} \theta ) + (Q_{11} + Q_{22} - 4Q_{66} )\sin^{2} \theta \cos^{2} \theta \hfill \\ \overline{Q}_{16} = (Q_{11} - Q_{12} - 2Q_{66} )\cos^{3} \theta \sin \theta + (Q_{12} - Q_{22} + 2Q_{66} )\sin^{3} \theta \cos \theta \hfill \\ \overline{Q}_{22} = Q_{11} \sin^{4} \theta + Q_{22} \cos^{4} \theta + (2Q_{11} + 4Q_{66} )\sin^{2} \theta \cos^{2} \theta \hfill \\ \overline{Q}_{26} = (Q_{11} - Q_{12} - 2Q_{66} )\sin^{3} \theta \cos \theta + (Q_{12} - Q_{22} + 2Q_{66} )\cos^{3} \theta \sin \theta \hfill \\ \overline{Q}_{66} = (Q_{11} - 2Q_{12} + Q_{22} - 2Q_{66} )\sin^{2} \theta \cos^{2} \theta + Q_{66} (\cos^{4} \theta + \sin^{4} \theta ) \hfill \\ \overline{Q}_{44} = Q_{44} \cos^{2} \theta + Q_{55} \sin^{2} \theta \hfill \\ \overline{Q}_{45} = (Q_{55} - Q_{44} )\cos \theta \sin \theta \hfill \\ \overline{Q}_{55} = Q_{44} \sin^{2} \theta + Q_{55} \cos^{2} \theta \hfill \\ \end{gathered} $$
(21)

and,

$$ \{ e\}^{(k)} = \left\{ {\begin{array}{*{20}c} {e_{xx} } \\ {e_{yy} } \\ {e_{xy} } \\ \end{array} } \right\} = [Tr]\left\{ {\begin{array}{*{20}c} {\alpha_{11} } \\ {\alpha_{22} } \\ \end{array} } \right\}^{(k)} (T - T_{0} ) $$
(22)

in which

$$ [Tr] = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & {\sin^{2} \theta } \\ {\sin^{2} \theta } & {\cos^{2} \theta } \\ {\sin 2\theta } & { - \sin 2\theta } \\ \end{array} } \right] $$
(23)

Herein, θ is the lamination angle.

When combined, Eqs. (15a–c) can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} N \\ M \\ Q \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} A & B & 0 \\ B & D & 0 \\ 0 & 0 & F \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon^{0} } \\ \kappa \\ {\gamma^{0} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {N^{N} } \\ {M^{N} } \\ 0 \\ \end{array} } \right\} $$
(24)

Finite Element Approach

The free vibration problem of the GRNC laminated plates is solved using a finite element method. In this work, a nine-node quadratic element with five degrees of freedom is selected. The generalized elementary displacements can be approximated as follows:

$$ \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ {\theta_{x} } \\ {\theta_{y} } \\ \end{array} } \right\} = \sum\limits_{i = 1}^{9} {\left[ {\begin{array}{*{20}c} {N_{i} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i} } & 0 & 0 & 0 \\ 0 & 0 & {N_{i} } & 0 & 0 \\ 0 & 0 & 0 & {N_{i} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i} } \\ \end{array} } \right]} \left\{ {\begin{array}{*{20}c} {u_{0i} } \\ {v_{0i} } \\ {w_{0i} } \\ {\theta_{xi} } \\ {\theta_{yi} } \\ \end{array} } \right\} $$
(25a)

or in reduced matrix form:

$$ \{ \delta \} = [N]\{ \delta_{e} \} $$
(25b)

in which, \(N_{i}\) stand for the shape functions.

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{0x} } \\ {\varepsilon_{0y} } \\ {\gamma_{0xy} } \\ {\kappa_{x} } \\ {\kappa y} \\ {\kappa_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \sum\limits_{i = 1}^{9} {\left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i,y} } & 0 & 0 & 0 \\ {N_{i,y} } & {N_{i,x} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {N_{i,x} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i,y} } \\ 0 & 0 & 0 & {N_{i,y} } & {N_{i,x} } \\ 0 & 0 & {N_{i,x} } & {N_{i} } & 0 \\ 0 & 0 & {N_{i,y} } & 0 & {N_{i} } \\ \end{array} } \right]} \left\{ {\begin{array}{*{20}c} {u_{0i} } \\ {v_{0i} } \\ {w_{0i} } \\ {\theta_{xi} } \\ {\theta_{yi} } \\ \end{array} } \right\} $$
(26a)

where,

$$ N_{i,x} = \frac{{\partial N_{i} }}{\partial x}\;{\text{and}}\;N_{i,y} = \frac{{\partial N_{i} }}{\partial y}. $$

Equation (26a) can be written as:

$$ \{ \varepsilon \} = [B]\{ \delta_{e} \} $$
(26b)

The computation of the frequencies \(\omega\) and mode shapes \(\delta\) of the laminated nanocomposite plates under different thermal environments are obtained by solving the following governing equation of motion:

$$ ([K] - [K_{th} ] - \omega^{2} [M])\{ \delta \} = \{ 0\} $$
(27)

where, {\(\delta\)} refers to the nodal displacement vector, \([K]\) refers to the stiffness matrix; \([K_{th} ]\) stands for the thermal-stress stiffness matrix; and \([M]\) stands for the mass matrix.

The matrices related to the elementary stiffness \([K_{e} ]\), thermal-stress stiffness \(\left[ {K_{th\;\;e} } \right]\), and mass \([M_{e} ]\) can be expressed as follows:

$$ [K_{e} ] = \int\limits_{\Lambda e} {[B]^{T} [C][B]} \;d\Lambda_{e} $$
(28)
$$ \left[ {K_{th\;\;e} } \right] = \int\limits_{\Lambda e} {[G]^{T} [S][G]} \;d\Lambda_{e} $$
(29)
$$ [M_{e} ] = \int\limits_{\Lambda e} {[N]^{T} [\overline{m}][N]} \;d\Lambda_{e} $$
(30)

in which, \(\Lambda_{e}\) refers to the elementary surface,and,

$$ \overline{m} = \left[ {\begin{array}{*{20}c} {I_{0} } & 0 & 0 & {I_{0} } & 0 \\ 0 & {I_{0} } & 0 & 0 & {I_{1} } \\ 0 & 0 & {I_{0} } & 0 & 0 \\ {I_{1} } & 0 & 0 & {I_{2} } & 0 \\ 0 & {I_{1} } & 0 & 0 & {I_{2} } \\ \end{array} } \right],\;C = \left[ {\begin{array}{*{20}c} A & B & 0 \\ B & D & 0 \\ 0 & 0 & F \\ \end{array} } \right] $$
(31)
$$ [G] = \sum\limits_{i = 1}^{9} {\left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & 0 & 0 \\ {N_{i,y} } & 0 & 0 & 0 & 0 \\ 0 & {N_{i,x} } & 0 & 0 & 0 \\ 0 & {N_{i,y} } & 0 & 0 & 0 \\ 0 & 0 & {N_{i,x} } & 0 & 0 \\ 0 & 0 & {N_{i,y} } & 0 & 0 \\ 0 & 0 & 0 & {N_{i,x} } & 0 \\ 0 & 0 & 0 & {N_{i,y} } & 0 \\ 0 & 0 & 0 & 0 & {N_{i,x} } \\ 0 & 0 & 0 & 0 & {N_{i,y} } \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]} $$
(32)
$$ [S] = \left[ {\begin{array}{*{20}c} {S_{11} } & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ {S_{21} } & {S_{22} } & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ 0 & 0 & {S_{33} } & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ 0 & 0 & {S_{43} } & {S_{44} } & {} & {} & {} & {sym} & {} & {} & {} & {} \\ 0 & 0 & 0 & 0 & {S_{55} } & {} & {} & {} & {} & {} & {} & {} \\ 0 & 0 & 0 & 0 & {S_{65} } & {S_{66} } & {} & {} & {} & {} & {} & {} \\ 0 & 0 & {S_{73} } & {S_{74} } & 0 & 0 & {S_{77} } & {} & {} & {} & {} & {} \\ 0 & 0 & {S_{83} } & {S_{84} } & 0 & 0 & {S_{87} } & {S_{88} } & {} & {} & {} & {} \\ {S_{91} } & {S_{92} } & 0 & 0 & 0 & 0 & 0 & 0 & {S_{99} } & {} & {} & {} \\ {S_{101} } & {S_{102} } & 0 & 0 & 0 & 0 & 0 & 0 & {S_{109} } & {S_{1010} } & {} & {} \\ 0 & 0 & {S_{113} } & {S_{114} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {} \\ {S_{121} } & {S_{122} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
(33)

in which,

$$ S_{33} = S_{11} = S_{55} = N_{x}^{i} ,\;S_{44} = S_{22} = S_{66} = N_{y}^{i} ,\;S_{43} = S_{21} = S_{65} = N_{xy}^{i} , $$
$$ S_{99} = S_{77} = {{N_{x}^{i} h^{2} } \mathord{\left/ {\vphantom {{N_{x}^{i} h^{2} } {12}}} \right. \kern-0pt} {12}},\;S_{1010} = S_{88} = {{N_{y}^{i} h^{2} } \mathord{\left/ {\vphantom {{N_{y}^{i} h^{2} } {12}}} \right. \kern-0pt} {12}},\;S_{109} = S_{87} = {{N_{xy}^{i} h^{2} } \mathord{\left/ {\vphantom {{N_{xy}^{i} h^{2} } {12}}} \right. \kern-0pt} {12}}, $$
$$ S_{91} = - S_{73} = M_{x}^{i} ,\;S_{102} = - S_{84} = M_{y}^{i} ,\;S_{92} = S_{101} = - S_{83} = - S_{74} = M_{xy}^{i} , $$
$$ S_{121} = - S_{113} = Q_{x}^{i} ,\;S_{122} = - S_{114} = Q_{y}^{i} . $$

Results and Discussions

A series of parametric studies has been undertaken in this section with the effect of an extensive range of influencing variants, including: (i) temperature dependency of the composite constituent materials, (ii) graphene distribution patterns, (iii) ply lay-up, (iv) geometric parameters, (v) lamination sequences, (vi) plate mode shapes, and (vii) plate boundary conditions on the free vibration characteristics of temperature-dependent FG-GRNC laminated plates. The reinforcing and matrix phases of the mixture selected are zigzag graphene sheets and polymethyl methacrylate (PMMA), respectively. The graphene mechanical properties are listed in Table 1 with different temperature environments, while those of the PMMA matrix are taken as follows: \(E^{m} = (3.52 - 0.0034T)_{{}} GPa\), \(\nu^{m} = 0.34\), \(\alpha^{m} = 45(1 + 0.0005\Delta T) \times 10^{ - 6} /K\),\(\rho^{m} = 1150_{{}} Kg/m^{3}\), where \(\Delta T = T - T_{0}\) in which T0 is the reference temperature (T0 = 300 K). Also, it should be noted that in this work, it is assumed that G23 = G13 = 0.5G12 [58, 60]. Table 2 lists the efficiency parameters of the graphene/PMMA nanocomposite for five levels of graphene volume fractions and different temperature conditions. Whereas, Table 3 presents the estimation values of GRNC material properties using the Halpin–Tsai and extended Halpin–Tsai approaches. The values presented in Table 3 reveal significant differences between the Yong’s and shear moduli of the GRNC calculated using the extended Halpin–Tsai approach compared to those calculated using the conventional Halpin–Tsai approach. This discrepancy arises from the fact that the extended Halpin–Tsai approach incorporates efficiency parameters, which the Halpin–Tsai approach does not include. According to Lin et al. [57], the most accurate prediction of mechanical properties of GRNC can be achieved by introducing \({\text{CIW}}{\mkern 1mu} { = }{\mkern 1mu} \left[ {\left( {{\text{Al}}_{{2}} {\text{O}}_{{3}} } \right){/}\left( {{\text{Al}}_{{2}} {\text{O}}_{{3}} {\mkern 1mu} { + }{\mkern 1mu} {\text{CaO*}}{\mkern 1mu} { + }{\mkern 1mu} {\text{Na}}_{{2}} {\text{O}}} \right)} \right] \, \times { 100}\), \(\eta_{2}\), and \(\eta_{3}\) into the Halpin–Tsai approach, i.e., using the extended Halpin–Tsai approach.

Table 1 Material properties of zigzag graphene nanosheet with \(w_{G} = 14.77_{{}} nm\), \(h_{G} = 0.188_{{}} nm\), and \(l_{G} = 14.76_{{}} nm\) [58]
Full size table
Table 2 Efficiency parameters \(\eta_{i}\)(i = 1, 2, 3) of GRNC for different thermal environments and graphene volume fractions [58]
Full size table
Table 3 Estimating shear and Young’s moduli of the GRNC using both extended Halpin–Tsai and Halpin–Tsai models for different levels of graphene volume fractions (\(f_{G}\)) (T = 300 K)
Full size table

Different patterns of the FG-GRNC laminated plates are considered. They can be achieved by arranging the volume fraction of nano-reinforcements in the GRNC plies according to specific distribution patterns. Among these patterns, we can mention the following: (i) uniform distribution (UD), (ii) distribution type Λ (FG-Λ), (iii) distribution type V (FG-V), (iv) distribution type O (FG-O), and (v) distribution type X (FG-X). An example of the graphene concentration percentage in each individual ply of laminated plates with 10 plies of GRNC is given as follows:

  • - For the UD pattern, the graphene volume fractions are distributed across the thickness of the laminated plate according to the following sequence: [0.07/0.07/0.07/0.07/0.07]S,

  • - For FG-Λ and FG-V patterns, the graphene volume fractions are distributed across the thickness of the laminated plate according to the following lamination sequences: [(0.03)2/(0.05)2/(0.07)2/(0.09)2/(0.11)2] for FG-Λ laminated plates and [(0.11)2/(0.09)2/(0.07)2/(0.05)2/(0.03)2] for FG-V laminated plates,

  • - For the remaining plate types (i.e., FG-X and FG-O), the graphene volume fractions are distributed across the thickness of the laminated plate according to the following lamination sequences: [0.03/0.05/0.07/0.09/0.11]S in the case of FG-O and as [0.11/0.09/0.07/0.05/0.03]S in the case of FG-X.

  • The different distribution patterns of the graphene nanosheets along the laminated plate thickness, as well as their corresponding configurations (lay-up arrangements), are listed in Table 4 for different numbers of plies (NP = 5, 10, 15, and 20). It should be noted that the total volume fraction of the considered lay-up arrangements is kept identical, whatever the value taken for the NP.

Table 4 Arrangements of GRNC plies with various distribution patterns of nano-reinforcement volume fraction (\(f_{G}\)) and plies number (NP) [52]
Full size table

The boundary conditions of the GRNC laminated plates are given as follows:

  • Fully clamped sides (CCCC):

at y = 0, b and x = 0, a, \(u_{0} = v_{0} = w_{0} = \theta_{x} = \theta_{y} = 0\)

  • Fully simply-supported sides (SSSS):at y = 0 and y = b, \(u_{0} = w_{0} = \theta_{x} = 0\), at x = 0 and x = a, \(v_{0} = w_{0} = \theta_{y} = 0\).

Unless otherwise noted, the mathematical expression that corresponds to the i-th non-dimensional frequency parameter is given as follows:

$$ \overline{\omega } = \omega \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-0pt} h}} \right)\sqrt {{{\rho^{m} } \mathord{\left/ {\vphantom {{\rho^{m} } {E_{m} }}} \right. \kern-0pt} {E_{m} }}} $$
(34)

Code validation and Results Comparison

This section aims to give an idea of the accuracy and reliability of the obtained results using our self-developed code by comparing them with the results reported in the published papers. Comparison studies are conducted on three types of composite plates (i.e., graphite/epoxy composite, FG ceramic/metal composite, and FG graphene-reinforced composite).

First Comparison Study

The first comparison example analyzes the effects of different width-to-thickness (b/h) ratios and thermal conditions on the first non-dimensional frequency (\(\overline{\omega } = \omega \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-0pt} h}} \right)\sqrt {{{\rho^{{}} } \mathord{\left/ {\vphantom {{\rho^{{}} } {E_{2} }}} \right. \kern-0pt} {E_{2} }}}\)) of fully clamped cross-ply (00/900/900/00) and angle-ply (450/−450/450/−450) graphite/epoxy composite laminated plates. Figure 3 presents the obtained results versus those reported by Ram and Sinha [73] for different values of b/h and variable temperatures, T. In the numerical modeling, the elastic properties of the lamina at different temperatures are those reported in Ref [73].

Fig. 3
figure 3

Comparison examination of the fundamental non-dimensional frequency \(\overline{\omega }\) for CCCC graphite/epoxy laminated plates with different (i) staking sequences, (ii) width-to-thickness ratios and (iii) thermal environments (a/b = 1)

Full size image

Second Comparison Study

The first dimensionless natural frequency (\(\overline{\omega } = \omega \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-0pt} h}} \right)\sqrt {{{\rho^{b} (1 - \nu^{2} )} \mathord{\left/ {\vphantom {{\rho^{b} (1 - \nu^{2} )} {E_{m} }}} \right. \kern-0pt} {E_{m} }}}\)) of functionally graded simply-supported (SSSS) ceramic/metal plates are compared in Table 5 with those reported by: (i) Shahrjerdi et al. [74] using a SSDT, (ii) Attia et al. [75] using a TSDT, (iii) Huang and Shen [76] using a TSDT, and (vi) Zaoui et al. [77] using a HSDT. The analysis was performed with different upper surface temperatures (Tt = 300, 400, and 600 K) and different values of the parameter which controls how the constituent materials are dispersed across the plate thickness (Pin = 0, 0.5, 1, 2, and 200).

Table 5 Comparative examination of the fundamental dimensionless frequency \(\overline{\omega }\) for simply-supported FG Si3N4/SUS304 plates with different power-low indexes and thermal environments (h = 0.025 m; a = b = 0.2 m; Tb = 300 K)
Full size table

For the case of FG plates made of Si3N4/SUS304 mixture, the temperature of the bottom surface of the plate (Tb) is set to 300 K, while the geometric characteristics of the plate are taken to be equal to 0.025 m, 0.2 m, and 0.2 m, for h, b and a, respectively. The mechanical properties of the FG Si3N4/SUS304 plate under different thermal environments are the same to those reported in Refs [70,71,72,73]. The plate mechanical properties are calculated based on the rule of the mixture as follows:

$$ \Gamma (k,T) = P_{m} (T) + \, (P_{{SI_{3} N_{4} }} (T) - \, P_{SUS304} (T)) \times V_{{SI_{3} N_{4} }} (k) $$
(35)

where,

$$ V_{{SI_{3} N_{4} }} (k) = \left( {\frac{k - 0.5}{{N_{L} }}} \right)^{{P_{in} }} ,\;k\, = \,1, \, 2, \, 3 \ldots N_{L} $$
(36)

in which \(\Gamma\) refers to the effective elastic properties of the FG plates i.e., E, ρ, ν, and thermal expansion coefficient α. \(P_{{SI_{3} N_{4} }}\) and \(P_{SUS304}\) refer to the elastic properties of the Si3N4 and SUS304, respectively, which are given by the following function:

$$ {\text{P(T) = (P}}_{{ - 1}} {\text{T}}^{{ - 1}} {\text{ + 1 + P}}_{{1}} {\text{T + P}}_{{2}} {\text{T}}^{{2}} {\text{ + P}}_{{3}} {\text{T}}^{{3}} {\text{)P}}_{{0}} $$
(37)

where T is the temperature change. P-1, P0, P1, P2, and P3 denote the temperature-dependent coefficients of the constituent materials (i.e., Si3N4 and SUS304).

Third Comparison Study

The third comparison study considers laminated composite plates reinforced with graphene monolayer. The validity of the first six obtained dimensionless natural frequencies \(\overline{\omega }{ = }\omega \left( {{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-0pt} h}} \right)\sqrt {{{\rho^{m} } \mathord{\left/ {\vphantom {{\rho^{m} } {E_{m} }}} \right. \kern-0pt} {E_{m} }}}\) are presented in Table 6 and compared with those of Shen et al. [58] using a HSDT, and Kiani [60] using a TSDT. The effects of different thermal environments on the UD, FG-V, FG-A, FG-O, and FG-X laminated plates are analyzed; however only laminated plates with ten plies are considered in this analysis. The corresponding lay-up arrangements of the volume fraction of the graphene fillers are given in Table 4. The a/b, b/h, and h parameters are taken to be equal to 1, 10, and 0.002 m, respectively. Elastic properties and efficiency parameters of the matrix/graphene used in this example are given in Tables 1 and 2, respectively.

Table 6 omparative examination of the first six non-dimensional natural frequencies \(\overline{\omega }\) of SSSS GRNC laminated plates with: b/h = 10; a/b = 1; h = 0.002 mT0 = 300 K
Full size table

As it can be observed from Fig. 3 and Tables 5 and 6, the results provided by our self-developed computer code agree well with those available in the literature. This confirms that our approach provides good precision and accuracy of the obtained results.

Parametric Studies

In this section, all of the numerical results will be thoroughly interpreted to identify the impact of different temperature environments on the vibrational behavior of piece-wise GRNC laminated plates with consideration of the effects of: graphene distribution patterns, lay-up of the GRNC plies, geometric parameters, lamination sequences, number of plies, and boundary conditions.

Effects of Plate Width-to-Thickness Ratio in Thermal Environments and Distribution Patterns of Graphene

Table 7 provides the numerical results corresponding to the fundamental non-dimensional frequency of clamped (CCCC) GRNC square laminated plates with consideration of the effects of width-to-thickness ratios (b/h), thermal environments (T), and distribution patterns of graphene. In this study, the plate aspect (length-to-width) ratio is taken to be equal to 1(a/b = 1). It is to discern from Table 7 that under the same characteristics (same distribution pattern and same thermal environment), and when the width-to-thickness ratio increases from 5 to 12, the fundamental frequency also increases for all graphene distribution patterns. The results also show that the distribution types of the graphene nano-reinforcements have a remarkable influence on the behavior of the GRNC laminated plates. It is observed that the plates that are arranged according to the X pattern (i.e., FG-X) gain the highest non-dimensional frequency (\(\overline{\omega }\)); In contrast, plates that are arranged according to the O patterns (i.e., FG-O) yield the lowest frequency. The main reason for this disparity in the results is believed to be related to the fact that the nano-reinforcements are highly concentrated in the upper and lower plies of the FG-X laminated plates and highly concentrated in the mid-plane plies of the FG-O laminated plates. Hence, it is evident that the mechanical behavior of FG-GRNC laminated plates depends strongly on the b/h parameter, as well as on the distribution patterns of the graphene reinforcement. Further examination of the results shows that the FG-Λ and FG-V distribution types have the same natural frequencies for all width-to-thickness ratios and thermal environments.

Table 7 Non-dimensional fundamental frequency (\(\overline{\omega }\)) of clamped GRNC square laminated plates under the effects of different (i) thermal environments, (ii) width-to-thickness ratios, and (iii) graphene distribution patterns (with a/b = 1; (0)10)
Full size table

Effects of Plate Length-to-Width Ratio in Uniform Thermal Environments and Distribution Patterns of Graphene

Table 8 investigates the simultaneous influences of thermal boundaries, plate aspect ratios (a/b), and distribution types of graphene on the fundamental \(\overline{\omega }\) of clamped GRNC laminated plates. The b/h ratio of the plate is taken to be equal to 10. Results presented in Table 8 show that the \(\overline{\omega }\) of the nanocomposite plates decreases as the a/b ratio rises from 1 to 2. This observation is sensed for all the considered distribution types of graphene (i.e., FG-V, FG-Λ, UD, FG-O, and FG-X) and thermal boundaries (T = 300 k, 400 k, and 500 k). This is due to the fact that as the plate surface becomes larger, its bending stiffness decreases. Among the five studied cases of nano-reinforcements dispersion types, one can see that the FG-X laminated plates provide maximum non-dimensional frequency, whereas the FG-O distribution type yields a minimum frequency. This confirms that FG-X laminated plates offer superior mechanical performance (i.e., greater bending stiffness). In contrast, the FG-O laminated plates exhibit the worst mechanical performance with the lowest bending stiffness. Thus, one can conclude that the physical behavior of FG-GRNC laminated plates is noticeably affected by both the a/b ratio and distribution patterns of graphene across the laminated plates thickness.

Table 8 Non-dimensional fundamental frequency (\(\overline{\omega }\)) of clamped GRNC square laminated plates under the effects of different (i) thermal environments, (ii) length-to-width ratios, and (iii) graphene distribution patterns (with b/h = 10; (0)10)
Full size table

Effects of Boundary Conditions in Thermal Environments and Graphene Distribution Patterns

The influences of various combinations of boundary conditions and distribution types of graphene nano-reinforcements on the fundamental \(\overline{\omega }\) of clamped GRNC square laminated plates are presented in Table 9. In the numerical study, the b/h and a/b ratios are taken to be equal to 10 and 1, respectively. A four-letter notation is used to identify the different combinations of the boundary conditions. For instance, the combination CSCS indicates that the GRNC laminated plate is clamped (i.e., C) at the sides y = 0 and x = 0, and simply-supported (i.e., S) at the sides y = b and x = a. Furthermore, it should be noted that the letter (F) represents the fully free side. The fundamental non-dimensional frequencies of the GRNC laminated plates are listed in Table 9 from the largest to the smallest ones, and vary gradually in between. Results show that for clamped and combined boundary conditions, the fundamental \(\overline{\omega }\) of the nanocomposite plate decreases as the T increases from the reference temperature (i.e., T = 300 K to 500 K). It is noted that when the material properties of the plates are temperature-dependent, the natural frequencies reach lower values. Also, it is observed that the FG-X laminated plates yield the largest fundamental frequencies, while the FG-O distribution pattern provides the smallest for the different boundary condition combinations. Hence, it can be considered that FG-X laminated plates combined with clamped sides would ensure more remarkable mechanical behavior improvement than with other combinations of boundary conditions.

Table 9 Non-dimensional fundamental frequency (\(\overline{\omega }\)) of GRNC square laminated plates under the effects of different (i) thermal environments, (ii) boundary conditions, and (iii) graphene distribution patterns (with b/h = 10; a/b = 1; (0)10)
Full size table

Effects of Plate Lamination Angle in Thermal Environments and Graphene Distribution Patterns

Table 10 investigates the combined effects of the lamination angle, thermal environment, and distribution patterns of graphene on the first natural frequency \(\overline{\omega }\) of CCCC GRNC square laminated plates. In this analysis, a/b and b/h are taken to be equal to 1 and 10, respectively. The results listed in Table 10 show that when the lamination angles (0/90/0/90/0)S, (0)10, or (0/90)5 T are selected, the fundamental frequency remains the same while it decreases slightly for the lamination angle (45/-45)5 T. Thus, it can be concluded that laminated plates with (45/-45) lamination sequence slightly waken the effective stiffness of GRNC laminated plates. This observation shows that the laminated plates will be described by higher stiffness when the lamination angle (0/90) is chosen. The variation of the fundamental frequency \(\overline{\omega }\) shows a similar trend for different thermal environments. Moreover, one can see that the first frequency of the GRNC laminated plates is almost constant for the different lamination angles. The leading cause for this phenomenon is believed to be related to the GRNC plies’ elastic properties (Young’s moduli of the nanocomposite plies are the same in both transverse and longitudinal directions).

Table 10 Non-dimensional fundamental frequency (\(\overline{\omega }\)) of clamped GRNC square laminated plates under the effects of different (i) thermal environments, (ii) lamination angles, and (iii) graphene distribution patterns (with b/h = 10; a/b = 1)
Full size table

Effects of Plate Number of Plies in Thermal Environments and Graphene Distribution Patterns

This section investigates the effects of the number of plies (Np), distribution patterns of graphene, and thermal environments on the first natural frequency \({\overline{\omega }}\) of clamped (CCCC) GRNC laminated plates. In the modeling, b/h and a/b are taken to be equal to 10 and 1, respectively. The results presented in Table 11 show that the fundamental frequency of the UD laminated plates is not affected by increasing the number of plies (Np). In fact, this result is expected because the graphene volume fraction in each individual ply of the laminated plate is kept the same regardless of the selected Np. However, for the non-uniform distribution patterns, the results reveal two distinct trends: (i) the first trend shows that for all thermal environments considered, the first frequency \(\overline{\omega }\) of the FG-Λ and FG-V laminated plates is not affected by increasing Np; (ii) the second trend reveals that the first frequency \(\overline{\omega }\) of the FG-O and FG-X laminated plates changes slightly as the Np increases from 5 to 20 under the same variants. The leading reason for these results is possibly related to the distribution of volume fractions of graphene fillers which are distributed across the laminated plates in linear form for FG-Λ and FG-V laminated plates while distributed in non-linear form for FG-O and FG-X laminated plates for all considered ply numbers (Np = 5, 10, 15, 20). Overall, it can be considered that the use of lower number of plies (Np = 5 for instance) may be recommended to enhance the mechanical performance of functionally graded GRNC structures.

Table 11 Non-dimensional fundamental frequency (\(\overline{\omega }\)) of clamped GRNC square laminated plates under the effects of different (i) thermal environments, (ii) number of plies, and (iii) graphene distribution patterns (with b/h = 10; a/b = 1; (0)10)
Full size table

Effect of Lay-up Arrangement and Number of Plies in Thermal Environments and Graphene Distribution Patterns

Table 12 presents the variation of the fundamental non-dimensional frequency (\(\overline{\omega }\)) of CCCC GRNC laminated plates under the effects of different (i) lay-up arrangements, (ii) graphene desperation types, and (iii) number of plies. In this analysis, the b/h and a/b are taken to be equal to 10 and 1, respectively. In order to give a meaningful comparison of the plate fundamental frequencies for a given ply number value, the total amounts of graphene in the laminated plates are kept the same regardless of the type of ply lay-up arrangement and the graphene distribution pattern. Based on the results presented in Table 12, it can be seen that the fundamental frequency \(\overline{\omega }\) associated to FG-Λ, FG-V, and FG-O laminated plates that are composed of 5 plies (i.e., FG-Λ(5), FG-V(5), and FG-O(5)) and 10 plies (i.e., FG-Λ(10) FG-V(10) and FG-O(10)) results in higher values as NP varies from 5 to 20 and from 10 to 20, respectively. Numerical results also reveal that when Np is set to 15 or 20 plies, the first natural frequency \({\overline{\omega }}\) of the [Λ(5)/X(5)/V(5)] and [Λ(5)/ Λ(5)/V(5)/V(5)] laminated plates reaches larger values than the [X(5)/X(5)/X(5)] and [X(5)/X(5)/X(5)/X(5)] laminated plates. These results indicate that the arrangement of the upper and lower surfaces of the laminated plates according to the FG-V and FG-Λ patterns can lead the structure to achieve better performance which can exceed that of the FG-X laminated plates. Hence, one can conclude that the effective stiffness of graphene-reinforced nanocomposite laminated plates is notably affected by the following parameters: (i) the number of plies (Np), (ii) the distribution patterns of graphene, as well as (iii) the arrangement of the GRNC plies.

Table 12 Non-dimensional fundamental frequency (\(\overline{\omega }\)) of clamped GRNC square laminated plates under the effects of different (i) thermal environments, (ii) plate lay-up arrangements, and (iii) graphene distribution patterns (with b/h = 10; a/b = 1; (0)10)
Full size table

Effect of Temperature Environment

Regarding the effect of temperature environments on the frequency characteristics of GRNC laminated plate structures, the results presented in Tables 7–12 indicate that the effective stiffness of FG-Λ, FG-V, FG-O, UD, and FG-X laminated plates are strongly dependent on thermal conditions. The results show that the evolution of fundamental frequencies of the laminated plates decreases as the temperature increases, whatever the different cases discussed, including the geometric parameters, the lamination angles, the number of plies, the boundary conditions, and the lamination lay-up. In fact, this phenomenon is expected because it is known that when the temperature rises from the temperature reference to a higher degree, e.g., from T = 300 K to T = 450 K, the thermally induced compressive forces of the composite are generated, which leads to a considerable decrease in the overall plate effective stiffness. This phenomenon is more obvious for plates with temperature-dependent material properties. One can conclude that the increase in temperature environment for nanocomposites that contain graphene as reinforcements can lead to the decrease of their vibrational frequencies, which causes in turn a decrease in their effective stiffness.

Effect of Temperature Environment on the First Eight Non-dimensional Frequencies

Figure 4 investigates the effects of graphene distribution types and thermal environments on the first eight non-dimensional frequencies of fully clamped GRNC square laminated plates. In the present analysis, the b/h and a/b are taken to be equal to 10 and 1, respectively. The comparison of results reveals that the first eight natural frequencies decrease each time the temperature T increases for all types of graphene distribution considered. However, it can be concluded that when the material properties of the GRNC plates are temperature-dependent, their overall stiffness is more affected by the temperature rise since their first eight natural frequencies yield smaller values than plates with temperature-independent material properties. The graphene distribution types play an important role in the reinforcement effect of nanofillers, as shown by the large gain achieved in the first eight natural frequencies when dispersing graphene according to the FG-X pattern, followed by FG-Λ & V patterns than the FG-O pattern. Therefore, it can be concluded that suggesting a nanocomposite plate with a higher concentration of graphene in its upper and lower surfaces (i.e., FG-X distribution type) can lead the plate to reach its optimum performance.

Fig. 4
figure 4

First eight non-dimensional natural frequencies (\(\overline{\omega }\)) of clamped GRNC square laminated plates under the effects of different (i) thermal environments, (ii) graphene distribution patterns (with b/h = 10; a/b = 1; (0)10)

Full size image

Mode Shapes

The final study considers the effects of temperature rises and ply lamination angle on the first six natural mode shapes of fully clamped FG-X GRNC square laminated plates. For this purpose, the first six contours corresponding to the first six shapes of eigenmodes of the nanocomposite laminated plates are displayed in Table 13 according to different thermal environments (T = 300, 400, and 500 K) and lamination angles [(0/90)5 T, (0)10, and (45/−45)5 T). In the computational analysis, the b/h and a/b are taken to be equal to 10 and 1, respectively. Table 13 indicates that the mode shapes of the (0)10 GRNC laminated plates are slightly influenced by changes in temperature. Specifically, the 5th and 6th mode shapes of the (0)10 nanocomposite plates shift to a higher mode as the temperature increases from 300 to 400 K and 500 K. In contrast, the mode shapes of laminated plates with (45/−45)5 T and (0/90)5 T lamination sequences remain unchanged with temperature variation, where the contour curves of the GRNC laminated plates maintain the same form across different temperatures. Moreover, by comparing the rows that have the same temperature environments and different staking sequences, for instance: row (a), row (d) and row (g), one can see that the contour curves of the nanocomposite plates are slightly affected by the staking sequence variation. This phenomenon can be observed by comparing the second and third contour curves of the (0/90)5 T laminated plate with those of (0)10 and (45/−45)5 T.

Table 13 First six mode shapes corresponding to clamped square FG-X GRNC laminated plates under the effects of different (i) lamination angles and (ii) thermal environments (with b/h = 10; a/b = 1; (0)10)
Full size table

Conclusion

The present research paper has addressed the issue of free vibration characteristics of polymeric nanocomposite piece-wise laminated plates in thermal environments. The materials constituting the nanocomposite plate are graphene nanosheets and PMMA matrix. The mechanical properties of the graphene-reinforced nanocomposite (GRNC) laminated plate are calculated under different thermal environments. The distributions of graphene volume fraction across the plate thickness follow two major types of distribution, namely: uniform (UD) and non-uniform. This latter type of functionally graded (FG) distribution follows four distribution patterns, namely FG-X, FG-Λ, FG-V, and FG-O. The laminated plate governing equations are obtained according to the FSDT principles. While the problem solution method is obtained based on Lagrange's equation and isogeometric finite element formulation. A linear eigenproblem is derived through a self-developed code, which yields the plate natural frequencies and the associated mode shapes. The output numerical results generated by the self-developed code showed excellent agreement with the results published in the open literature. Detailed parametric analyses have been performed to underline and highlight the significant influence of thermal environments on the GRNC laminated plates and the consequences on the problem of their eigenvalues. The overall revelations of the present work are summarized as follows:

  • Results reveal that the efficiency of the reinforcing effect of graphene depends strongly on the temperature environments in which it evolves. It has been observed that the temperature rise causes a diminution in the natural frequencies of the GRNC plates, which causes a decrease in their overall stiffness.

  • Results demonstrate that the most efficient way to enhance the performance of GRNC laminated plates is by making their top and bottom plies rich in graphene: disperse for instance the nano-reinforcements according to FG-X pattern.

  • Results indicate that GRNC laminated plates with fewer plies have higher natural frequencies and it was found that the optimal effective stiffness can be achieved when the number of plies is set to five.

  • A relatively negligible effect of the lamination angle on the stiffness of the GRNC laminated plates was found. The results show that composite plates with lamination angles (0/90/0/90/0)S, (0)10, (45/-45)5 T, and (0/90)5 T have almost equal natural frequencies.

  • Results indicate that the stacking sequence and temperature environments weakly affect the mode shapes of the GRNC laminated plate.