An Analytical Investigation on Linear and Nonlinear Vibrational Behavior of Stiffened Functionally Graded Shell Panels Under Thermal Environment

Abstract

Purpose

In this paper, an analytical investigation of the nonlinear dynamic response and vibrational behavior of stiffened and unstiffened FGM shell panels of different geometries under thermo-mechanical loading is presented.

Methods

The kinematic relations considered for shell panels are in accordance with the first-order shear deformation theory along with von Kármán geometrical nonlinearities, and the contribution of stiffeners is considered based on smeared stiffener technique. The nonlinear governing equations of motion for eccentrically stiffened FGM shell panels are derived using Hamilton’s principle. Navier’s functions are assumed to satisfy the prescribed boundary conditions, whereas Galerkin and fourth-order Runge–Kutta methods are employed to attain nonlinear dynamic responses.

Results

After establishing the accuracy of the present analytical formulation by comparing the results with the existing literature, various numerical studies are conducted to divulge the impact of parameters such as shell geometries, stiffeners, material inhomogeneity, and temperature difference on the nonlinear dynamic response and vibrational behavior of simply-supported FGM shell panels.

Conclusions

It is revealed that among the un-stiffened as well as stiffened FGM shell panels, the spherical shell panel exhibits the highest natural frequency with the lowest vibration amplitude, whereas the lowest natural frequency with the highest amplitude is depicted by the hyperbolic-paraboloidal shell panel. Moreover, the effects of the increase in the temperature difference across the thickness and the power law index are to reduce the natural frequency and to increase the amplitude of dynamic response, irrespective of the geometry of shell panels. Further, the effect of damping on the dynamic behavior of the FGM shell panel is initially indistinguishable; however, after a few time periods the damping is found to have a considerable effect on its dynamic response.

Introduction

Out of the many basic structural elements like beam, plate, and shell, thin-walled curved shells are being used in many engineering applications in mechanical, civil, marine, and aeronautical fields because of their many advantages such as high strength-to-weight ratio, high stiffness, high efficiency of load-carrying behavior, structural integrity, high reserved strength, and aesthetic look [1]. Moreover, to further enhance their performance, these thin-walled shells have been reinforced with stiffeners/ribs. The assimilation of the stiffeners provides a promising advantage of controlling the vibration response by altering the natural frequencies of these shell structures with the enhanced stiffness, without increasing the shell thickness. Nevertheless, the dynamic behavior of these structures is quite complex due to which there is an overwhelming research interest pertaining to the linear and nonlinear vibration analysis of stiffened shell structures. In the early exploratory attempts, Miller [2] used the energy method to calculate natural frequencies and mode shapes of a circular cylindrical shell uniformly stiffened with closely spaced stiffeners and frames, and Hoppmann [3] described the experimental method and verified the existing theoretical results experimentally for orthogonally stiffened cylindrical shells. The free vibration of ring stiffened conical shell based on linear shell theory was presented by Weingarten [4].

The effects of eccentrically placed stiffeners over the dynamic response of plate and shell structures were investigated by McElman et al. [5]. In all these studies [2,3,4,5], and reviewed in [6], on free vibration response of isotropic shells, equidistant closely spaced stiffeners were simplified by uniformly averaging the effect of stiffeners over the entire shell surface. Thereafter, the effects of shell geometry, the position of multi-directional stiffeners, and the boundary conditions on the free vibration behavior of stiffened isotropic shells were also revealed in many subsequent studies [6]. Later on, Nayak and Bandyopadhyay [7]analyzed the free vibration of doubly curved shallow shells using a finite element method with the eight-/nine-node doubly curved iso-parametric thin shallow shell element and the three-node curved iso-parametric beam element. Free vibration of various types of shallow and deep stiffened shell structures was studied using a new stiffened shell element by Samanta et al. [8], and thereafter, Qu et al. [9] presented a modified variational approach to analyse vibration of ring-stiffened conical–cylindrical shells with different boundary conditions.

In addition to the aforementioned studies on isotropic shells, the increased uses of composite materials in many engineering applications generated the interest of researchers in composite structures, including composite shells. Attributable to the wide applicability, free vibration and dynamic behavior of composite shells have drawn overwhelming research interest of researchers over the last four decades[10, 11]. Very recently, Tran et al. [12] implemented FSDT for the static and free vibration analysis of stiffened cross-ply laminated composite doubly-curved shallow shells. TSDT based finite element analysis of free vibration of doubly curved laminated composite shells with cutout was presented by Chaubey et al. [13]. Guo et al. [14] performed free and forced vibration analysis of composite laminated doubly-curved shells, based on FSDT using a domain decomposition method. Ni et al. [15] proposed FSDT based semi-analytical approach to investigate free vibration of stiffened composite laminated shells of revolution with classical and elastic boundaries. In the study, of the nonlinear vibration of fiber-reinforced polymer composite cylindrical shells Li et al. [16] employed Love’s shell theory including geometric nonlinearities and thermal effect.

Despite the many preferable properties of laminated composites, the abrupt change in material composition at the interface provoke high interfacial stresses leading delamination, matrix cracking, and adhesive bond separation failure, under critical loading conditions at elevated temperature. While looking to overcome the limitations of traditional composite materials, a new class of composites, namely Functionally Graded Materials (FGMs) were developed by the Japanese material Scientists in 1984 [17]. FGMs are inhomogeneous composite materials with the composition of constituting materials varying smoothly and continuously in one or more spatial directions according to some mathematical function, and hence, eliminating any problem at interface caused by properties mismatch. Usually, FGMs have ceramic and metal constituents, and the preferable material properties at a particular location is tailored and achieved by controlling the volume fractions of these constituent materials. It is found in many investigations that functionally graded structures show much better structural performance as compared to homogenous materials under thermo-mechanical loading conditions [17,18,19]. Further, the FGMs shells are most suitable for important engineering structures such as thermal protection systems in space vehicles, thrust chamber of aero-structures, rocket engine components, turbine blades, etc. [20,21,22]. As reported by Punera and Kant [23] in their recently published review article that in the last 2–3 decades, many investigations have been carried out to study vibration and dynamics responses of FGM shells (i.e., plate, circular/elliptical cylindrical, spherical, hyperbolic-paraboloidal) without and with stiffeners using different shell theories (i.e., Love shell theory/CST, shear deformation theories, normal/higher-order theories) with different analytical and numerical techniques.

It is noteworthy that in the classical shell theories, rotary inertia and transverse shear effects are disregarded as a consequence of which these theories overestimate the natural frequencies for moderately thick shells, therefore the results from CST can’t be relied on much, especially for thick shells. Thereby to consider the transverse shear effects and to predict the free vibration response of moderately thick FGM shell structures, many researchers adopted FSDT (first-order shear deformation theory). Kim [24] analyzed free vibration characteristics of oblique-edged FGM cylindrical shell using the Rayleigh–Ritz method. Khayat et al. [25] used the semi-analytical finite strip method along with different shell theories to examine the free vibration response of stiffened FGM cylindrical shells. Free vibration characteristics of FG porous spherical shell were determined by Li et al. [26] using the energy method utilizing FSDT. Kumar et al. [27] presented a mathematical model based on FSDT to investigate the free vibration of eccentrically stiffened doubly curved functionally graded shallow shells with simply supported boundary conditions and subjected to the thermo-mechanical loading.

It is well known that the linear free vibration analysis is restricted to the small displacements and just provides a first approximation of the actual behavior; however, the thin FGM structures with material complexity may exhibit large amplitude vibration response especially under the effects of external excitations. Therefore it becomes imperative to incorporate the nonlinearity in the dynamic analysis of FGM structures and being reflected in a number of studies, for instance, Alijani et al. [28] presented primary and sub-harmonic responses of FGM doubly curved thin shallow-shells using Donnell’s nonlinear kinematic relationships. A perturbation-based solution methodology was presented to investigate the nonlinear thermos-mechanical vibration response of FGM shell structures by Shen et al. [29, 30]. In addition to the analytical methodology, FEM is also applied by Kar and Pandya [31, 32] to compute nonlinear free mechanical and thermal vibration responses of doubly curved shallow shells. Recently, Hashemi et al. [33]implemented the Lindstedt-Poincare technique to obtain an analytical solution for nonlinear vibrations of the functionally graded plate.

It is observed that the works pertaining to the nonlinear vibration of stiffened FGM shells are comparatively less [34,35,36,37]. Further, it is also revealed that the nonlinear dynamic analysis of stiffened FGM shells is mostly carried out by using Volmir’s assumption and the rotary inertia effects are ignored. However, the present analysis is carried out by solving all five simultaneous equations, while considering the effects of both rotary inertia and transverse shear deformations. Hence, the present method can provide more accurate results as compared to the aforementioned studies. A further advantage of the present generalized method is its simplicity that can be adopted to analyze thin to moderately thick shell panels of different geometries.

Contemplating the aforementioned facts, the present work is intended to explore analytically the free and forced vibration characteristics of FGM shell panels to divulge the impact of geometrical nonlinearity, rotary inertia, shell geometries, stiffeners orientation, thermal environment, temperature-dependent material properties, and other geometrical as well as material parameters on the natural frequency, frequency-amplitude relations, and force-amplitude curves.

Analytical Formulation

Nomenclatures

$x,{\text{ }}y\;{\text{and}}\;z$ :

Cartesian co-ordinate axes.

$t$ :

Time

$a,b{\text{ and }}h$ :

Length, width and thickness of the shell, respectively

$R_{x} ,R_{y}$ :

Radius of principal curvatures in xz and yz planes, respectively

$h_{x} ,h_{y}$ :

Height of stiffeners along x and y directions, respectively

$b_{x} ,b_{y}$ :

Width of stiffeners along x and y directions, respectively

$n_{x} ,\;n_{y}$ :

Number of stiffeners along x and y directions, respectively

$A_{x} ,A_{y}$ :

Area of cross-sections of stiffeners along x and y directions, respectively

$e_{x} ,e_{y}$ :

Eccentricity of stiffeners along x and y directions, respectively

$I_{{xx}} ,{\text{ }}I_{{yy}}$ :

Area moment of inertia of stiffeners along x and y direction, respectively

$T$ :

Temperature in K

$E_{{\text{c}}} ,E_{{\text{m}}} ,{\text{ and}}\;E_{0}$ :

Young’s moduli of ceramic, metal and stiffeners materials, respectively

$\rho _{{\text{c}}} ,\rho _{{\text{m}}} ,{\text{ and}}\;\rho _{0}$ :

Mass densities of ceramic, metal and stiffeners materials, respectively

$\alpha _{{\text{c}}} ,{\text{ }}\alpha _{{\text{m}}}$ :

Thermal expansion coefficients of ceramic and metal, respectively

$\kappa _{{\text{c}}} ,\kappa _{{\text{m}}}$ :

Thermal conductivity of ceramic and metal, respectively

$\nu$ :

Poisson ratio

$V_{{\text{c}}} ,V_{{\text{m}}}$ :

Volume fractions of ceramic and metal, respectively

$k$ :

Power law index

$u,v,{\text{ and}}\;w$ :

Displacements corresponding to x, y and z directions, respectively

$\phi _{x} ,\phi _{y}$ :

Rotations with respect to y and x axes, respectively

$m,n$ :

Half wave number

$\varepsilon _{{xx}} ,\varepsilon _{{yy}}$ :

Normal strain components in shell in x and y directions, respectively

$\gamma _{{xy}} ,\gamma _{{xz}} ,{\text{ and}}\;\gamma _{{yz}}$ :

Shear strain components in shell in xy, xz and yz planes, respectively

$\sigma _{{xx}}^{{\rm shell}} ,\,\sigma _{{yy}}^{{\rm shell}}$ :

Normal stress components in shell in x and y directions, respectively

$\begin{gathered} \tau _{{xy}}^{{\rm shell}} ,\,\,\tau _{{xz}}^{{\rm shell}} \,\,\text{and} \hfill \\ \,\tau _{{yz}}^{{\rm shell}} \hfill \\ \end{gathered}$ :

Shear stress components in shell in xy, xz and yz planes, respectively

$\sigma _{{xx}}^{{stx}} ,\,\sigma _{{yy}}^{{sty}}$ :

Normal stress components in stiffeners along x and y directions, respectively

$N_{{xx}} ,N_{{yy}}$ :

Normal force resultants in x and y directions, respectively

$N_{{xy}} ,Q_{{xz}} ,{\text{ and}}\;Q_{{yz}}$ :

Shear force resultants in xy, xz and yz planes, respectively

$M_{{xx}} ,M_{{yy}}$ :

Normal moment resultants in x and y directions, respectively.

$M_{{xy}}$ :

Moment resultant in xy plane

$\omega$ :

Natural frequency

$\omega _{{{\text{nl}}}}$ :

Nonlinear natural frequency

$q$ :

Intensity of uniformly distributed pressure

$\Omega$ :

Angular frequency of distributed pressure

Temperature-Dependent Material Properties of FGM

In the present study, any thermo-elastic material properties P (i.e., the modulus of elasticity E and the thermal expansion coefficient α) of the constituting materials (i.e., ceramic and metal)of the FGM are considered to be temperature-dependent and are evaluated by cubic fit equation of the form [38]:

$$P\left( T \right) = P_{0} \left( {P_{{ - 1}} T^{{ - 1}} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right),\,\,\,\,T \ge 300\,\text{K} ,$$

(1)

where P₀, P₋₁, P₁, P₂ and P₃are material-specific constants and their values, given in Table 1, are evaluated experimentally [39].

Table 1 Material coefficients to evaluate temperature-dependent material properties of the constituents of FGM [38]

It is assumed that the doubly-curved shallow shell is made up of FGM, a non-homogeneous combination of metal and ceramic, and the gradient of material properties is taken only in the thickness direction (i.e., $z$-direction). It is assumed that the top surface (z = h/2) is ceramic and the bottom one (z = − h/2) is metal surface.

It is to mention here that in the present study the Young’s Modulus and thermal expansion coefficient of FGM shell are assumed to be temperature-dependent and calculated using the rule of the mixture as follows:

$$\begin{aligned} E_{{{\text{eff}}}} \left( {z,T} \right) & = E_{{\text{c}}} \left( T \right)V_{{\text{c}}} \left( z \right) + E_{{\text{m}}} \left( T \right)V_{{\text{m}}} \left( z \right), \\ \alpha _{{{\text{eff}}}} \left( {z,T} \right) & = \alpha _{{\text{c}}} \left( T \right)V_{{\text{c}}} \left( z \right) + \alpha _{{\text{m}}} \left( T \right)V_{{\text{m}}} \left( z \right). \\ \end{aligned}$$

(2)

The material coefficients to evaluate these temperature-dependent material properties of the constituents of FGM i.e., E_c(T), E_m(T), α_c(T) and α_m(T) are given in Table 1.

The thermal conductivity $\kappa$(z) and material density $\rho$(z) of FGM are assumed to be temperature-independent and are calculated using:

$$\begin{gathered} \kappa \left( z \right) = \kappa _{{\text{c}}} V_{{\text{c}}} \left( z \right) + \kappa _{{\text{m}}} V_{{\text{m}}} \left( z \right), \hfill \\ \rho \left( z \right) = \rho _{{\text{c}}} V_{{\text{c}}} \left( z \right) + \rho _{{\text{m}}} V_{{\text{m}}} \left( z \right). \hfill \\ \end{gathered}$$

(3)

The respective values of thermal conductivity of ceramic and metal are taken as $\kappa$_c = 1.0 W/mK and $\kappa$_m = 1.7 W/mK, respectively; whereas, the material density of ceramic and metal constituents are considered to be $\rho$_c = 3000 kg/m³ and $\rho$_m = 4429 kg/m³, respectively.

Further, in the Eqs. (2) and (3), V_c and V_m represent the volume fractions of ceramic and metal constituents of FGM shell, respectively, and are calculated across the shell-thickness as per the following power law:

$$V_{{\text{c}}} \left( z \right) = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} ,V_{{\text{m}}} \left( z \right) = 1 - V_{{\text{c}}} \left( z \right)\,\,{\text{where}}\,\, - h/2 \le z \le h/2.$$

(4)

where k is power law index which is used to control the FGM gradation profile and the subscripts ‘c’ and ‘m’ refer to the metallic and ceramic constituents of the FGM, respectively.

Based on the very small difference in the values of Poisson’s ratio of the FGM constituents (i.e., ceramic and metal), the Poisson’s ratio of the FGM is assumed to be the same as that of the constituents (i.e., 0.28) and it is taken to be constant across the thickness of FGM shell.

It is assumed that the temperature varies nonlinearly in the thickness direction, and its distribution is obtained by solving the following steady-state heat transfer equation:

$$- \frac{{\text{d}}}{{{\text{d}}z}}\left[ {\kappa \left( z \right)\frac{{{\text{d}}T}}{{{\text{d}}z}}} \right] = 0,\,\,\,T = T_{{\text{m}}} \,\,\,at\,\,z = - {h \mathord{\left/ {\vphantom {h {2,\,\,\,}}} \right. \kern-\nulldelimiterspace} {2,\,\,\,}}T = T_{{\text{c}}} \,\,\,{\text{at}}\,\,z = {h \mathord{\left/ {\vphantom {h {2.\,\,\,}}} \right. \kern-\nulldelimiterspace} {2.\,\,\,}}$$

(5)

The aforementioned equation along with the boundary conditions can be solved by means of power series as [40]

$$T\left( z \right) = T_{{\text{m}}} + \left( {T_{{\text{c}}} - T_{{\text{m}}} } \right)\lambda \left( z \right),$$

(6)

where,

$$\begin{aligned} \lambda \left( z \right) & = \frac{1}{H}\left[ {\left( {\frac{{2z + h}}{{2h}}} \right) - \frac{{\kappa _{{{\text{cm}}}} }}{{\left( {k + 1} \right)\kappa _{{\text{m}}} }}\left( {\frac{{2z + h}}{{2h}}} \right)^{{k + 1}} + \frac{{\kappa _{{{\text{cm}}}}^{2} }}{{\left( {2k + 1} \right)\kappa _{{\text{m}}}^{2} }}\left( {\frac{{2z + h}}{{2h}}} \right)^{{2k + 1}} } \right. \\ & - \left. {\frac{{\kappa _{{{\text{cm}}}}^{3} }}{{\left( {3k + 1} \right)\kappa _{{\text{m}}}^{3} }}\left( {\frac{{2z + h}}{{2h}}} \right)^{{3k + 1}} + \frac{{\kappa _{{{\text{cm}}}}^{4} }}{{\left( {4k + 1} \right)\kappa _{{\text{m}}}^{4} }}\left( {\frac{{2z + h}}{{2h}}} \right)^{{4k + 1}} - \frac{{\kappa _{{{\text{cm}}}}^{5} }}{{\left( {5k + 1} \right)\kappa _{{\text{m}}}^{5} }}\left( {\frac{{2z + h}}{{2h}}} \right)^{{5k + 1}} } \right] \\ \end{aligned}$$

(7)

where, H and $\kappa$_cm are

$$H = 1 - \frac{{\kappa _{{{\text{cm}}}} }}{{\left( {k + 1} \right)\kappa _{{\text{m}}} }} + \frac{{\kappa _{{{\text{cm}}}}^{2} }}{{\left( {2k + 1} \right)\kappa _{{\text{m}}}^{2} }} - \frac{{\kappa _{{{\text{cm}}}}^{3} }}{{\left( {3k + 1} \right)\kappa _{{\text{m}}}^{3} }} + \frac{{\kappa _{{{\text{cm}}}}^{4} }}{{\left( {4k + 1} \right)\kappa _{{\text{m}}}^{4} }} - \frac{{\kappa _{{{\text{cm}}}}^{5} }}{{\left( {5k + 1} \right)\kappa _{{\text{m}}}^{5} }},\,\,\,\text{and} \,\,\,\kappa _{{{\text{cm}}}} = \kappa _{{\text{c}}} - \kappa _{{\text{m}}} .$$

Geometrical Model

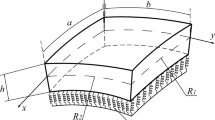
A doubly curved shallow FGM shell possessing length, width and thickness as a, b and h, respectively, and having radii of curvature R_x and R_y along x-and y-directions is considered, as shown in Fig. 1. The Cartesian coordinate system, as shown in Fig. 1, is fixed at the mid-plane i.e., at z = 0 of the shell. In the present analysis, generalized formulation is proposed for different types of shell geometries by setting the different combinations of curvatures as given in Table 2.

Fig. 1

a Doubly curved shallow shell with stiffeners, and b geometry of FGM shallow shell with stiffeners in x–z plane

Table 2 Different curvatures to obtain different geometries of doubly-curved shell

Stiffeners, as shown in Fig. 1, are used, along x and y direction, to reinforce the skin of the shell and are assumed to be made of the same isotropic and homogeneous material (ceramic or metal, as determined at $z~ = ~ - h/2$ by the power law defined in Eq. 4) as that of the shell surface to avoid the material discontinuity. Geometrical parameters as presented in Fig. 1 for the stiffeners are defined as follows.

l_x and l_y are equal spacing between the stiffeners along x and y directions, respectively; e_x and e_y represent eccentricity of stiffeners along x and y directions, respectively, and they are defined as: e_x = (h + h_x)/2 and e_y = (h + h_y)/2, wherein h_x and h_y are the height of stiffeners in x and y directions, respectively; b_x and b_y denote the breadth of stiffeners along x and y directions, respectively, and; A_x and A_y stand for areas of cross section of stiffeners along x and y direction, respectively.

First-Order Shear Deformation Theory (FSDT)

According to the FSDT, the displacement components u, v, and w along x, y and z-direction, respectively, of an arbitrary point in the FGM shell can be evaluated using the corresponding displacement components u₀, v₀, w₀ at mid-surface of the shell (i.e., at z = 0) and the slopes (ϕ_x, ϕ_y) of the transverse normal about the $x$- and $y$-axes, respectively, as follows [41]:

$$\left[ {\begin{array}{*{20}c} {u\left( {x,y,z,t} \right)} \\ {v\left( {x,y,z,t} \right)} \\ {w\left( {x,y,z,t} \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u_{0} \left( {x,y,t} \right)} \\ {v_{0} \left( {x,y,t} \right)} \\ {w_{0} \left( {x,y,t} \right)} \\ \end{array} } \right] + z\left[ {\begin{array}{*{20}c} {\phi _{x} } \\ {\phi _{y} } \\ 0 \\ \end{array} } \right].$$

(8)

Incorporating the geometrical nonlinearity in von Karman’s sense (i.e., small strains and moderate rotations) in the FSDT, the strain components for doubly curved shallow shell can be written in the following form:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {\varepsilon _{{xx}} } \\ {\varepsilon _{{yy}} } \\ {\gamma _{{xy}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{{\partial x}} + C_{1} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \\ {\frac{{\partial v_{0} }}{{\partial y}} + C_{2} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \\ {\frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \\ \end{array} } \right] + z\left[ {\begin{array}{*{20}c} {\frac{{\partial \phi _{x} }}{{\partial x}}} \\ {\frac{{\partial \phi _{y} }}{{\partial y}}} \\ {\frac{{\partial \phi _{x} }}{{\partial y}} + \frac{{\partial \phi _{y} }}{{\partial x}}} \\ \end{array} } \right] \hfill \\ {\rm and} \,\,\,\left[ {\begin{array}{*{20}c} {\gamma _{{xz}} } \\ {\gamma _{{yz}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - C_{1} u_{0} } \\ {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - C_{2} v_{0} } \\ \end{array} } \right]. \hfill \\ \end{gathered}$$

(9)

Here, C₁ and C₂ are principal curvatures of the shell, as defined in Table 2.

The thermo-mechanical constitutive relations within the skin of the doubly-curved shallow shell can be expressed as:

$$\,\left\{ {\begin{array}{*{20}c} {\sigma _{{xx}}^{{{\text{shell}}}} } \\ {\sigma _{{yy}}^{{{\text{shell}}}} } \\ {\tau _{{yz}}^{{{\text{shell}}}} } \\ {\tau _{{xz}}^{{{\text{shell}}}} } \\ {\tau _{{xy}}^{{{\text{shell}}}} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{{11}} } & {Q_{{12}} } & 0 & 0 & 0 \\ {Q_{{21}} } & {Q_{{22}} } & 0 & 0 & 0 \\ 0 & 0 & {K_{s} Q_{{44}} } & 0 & 0 \\ 0 & 0 & 0 & {K_{s} Q_{{55}} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{{66}} } \\ \end{array} } \right]\left[ {\left\{ {\begin{array}{*{20}c} {\varepsilon _{{xx}} } \\ {\varepsilon _{{yy}} } \\ {\gamma _{{yz}} } \\ {\gamma _{{xz}} } \\ {\gamma _{{xy}} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}\alpha \left( {z,\,T} \right)\Delta T\left( {z,\,T} \right)} \right],$$

(10)

where, $\,Q_{{11}} = Q_{{22}} = \frac{{E_{{{\text{eff}}}} (z,T)}}{{1 - \nu ^{2} }},\,\,Q_{{12}} = Q_{{21}} = \nu Q_{{11}} ,\,\;{\text{and}}\;\,Q_{{44}} = Q_{{55}} = Q_{{66}} = \frac{{E_{{{\text{eff}}}} (z,T)}}{{2\left( {1 + \nu } \right)}}$, K_s is the shear correction factor and its value is taken equal to 5/6 [42].

It is to mention that to consider the effect of temperature on the dynamic response of stiffened FGM shell, the top of FGM shell (i.e., ceramic side) is retained at elevated temperature whereas ambient temperature is assumed at the bottom of FGM shell (i.e., metallic side). The non-uniform temperature difference across the thickness is obtained using Eq. (6).

In the present study, the FGM shell is reinforced by rectangular stiffeners along both x and y directions and the contribution of stiffeners is considered based on smeared stiffener technique. As per this technique, if the stiffeners are placed closely and equally-spaced then the skin-stiffener interaction effect can be treated adequately by averaging the stiffening effects over the shell surface [43]. Moreover, it is assumed that the stiffeners are stressed uni-axially along their length only and hence, do not provide any shear resistance because of a large length-to-depth ratio. Further, the stiffeners are assumed to be perfectly connected to the shell and the normal strain components of stiffeners are similar to those of the shell. Based on the above assumptions, the relations between stress–strain for the stiffeners can be expressed as:

$$\left[ {\begin{array}{*{20}c} {\sigma _{{xx}}^{{stx}} } & {\sigma _{{yy}}^{{sty}} } \\ \end{array} } \right] = E_{0} \left[ {\begin{array}{*{20}c} {\varepsilon _{{xx}} } & {\varepsilon _{{yy}} } \\ \end{array} } \right]$$

(11)

E₀ is the modulus of elasticity of material of the shell skin on which stiffeners are attached. The superscripts ‘stx’ and ‘sty’ are referring to the stiffeners in x and y directions, respectively.

The stress (both normal and shear) and moment resultants of the eccentrically stiffened shell can be expressed as:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {N_{{xx}} } \\ {N_{{yy}} } \\ {N_{{yy}} } \\ {M_{{xx}} } \\ {M_{{yy}} } \\ {M_{{xy}} } \\ \end{array} } \right] = \int\limits_{{ - {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\left[ {\begin{array}{*{20}c} {\sigma _{{xx}}^{{{\text{shell}}}} } \\ {\sigma _{{yy}}^{{{\text{shell}}}} } \\ {\tau _{{xy}}^{{{\text{shell}}}} } \\ {z\sigma _{{xx}}^{{{\text{shell}}}} } \\ {z\sigma _{{yy}}^{{{\text{shell}}}} } \\ {z\tau _{{xy}}^{{{\text{shell}}}} } \\ \end{array} } \right]} \,\text{d} z + \left[ {\begin{array}{*{20}c} {\frac{{b_{x} }}{{l_{x} }}\int\limits_{{e_{x} - {{h_{x} } \mathord{\left/ {\vphantom {{h_{x} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{e_{x} + {{h_{x} } \mathord{\left/ {\vphantom {{h_{x} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {\sigma _{{xx}}^{{stx}} {\text{d}}z} } \\ {\frac{{b_{y} }}{{l_{y} }}\int\limits_{{e_{y} - {{h_{y} } \mathord{\left/ {\vphantom {{h_{y} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{e_{y} + {{h_{y} } \mathord{\left/ {\vphantom {{h_{y} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {\sigma _{{yy}}^{{sty}} {\text{d}}z} } \\ 0 \\ {\frac{{b_{x} }}{{l_{x} }}\int\limits_{{e_{x} - {{h_{x} } \mathord{\left/ {\vphantom {{h_{x} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{e_{x} + {{h_{x} } \mathord{\left/ {\vphantom {{h_{x} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {z\sigma _{{xx}}^{{stx}} {\text{d}}z} } \\ {\frac{{b_{y} }}{{l_{y} }}\int\limits_{{e_{y} - {{h_{y} } \mathord{\left/ {\vphantom {{h_{y} } 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{e_{y} + {{h_{y} } \mathord{\left/ {\vphantom {{h_{y} } 2}} \right. \kern-\nulldelimiterspace} 2}}} {z\sigma _{{yy}}^{{sty}} {\text{d}}z} } \\ 0 \\ \end{array} } \right]\,\,\,\,{\text{and}}\,\,\left[ {\begin{array}{*{20}c} {Q_{{xz}} } \\ {Q_{{yz}} } \\ \end{array} } \right] = \int\limits_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left[ {\begin{array}{*{20}c} {\tau _{{xz}} } \\ {\tau _{{yz}} } \\ \end{array} } \right]} {\text{d}}z \hfill \\ \hfill \\ \end{gathered}$$

(12)

From Eqs. (9)–(12), the expressions for stress resultants in expanded forms can be written as:

$$\begin{aligned} N_{{xx}} & = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\left\{ {\frac{{\partial u_{0} }}{{\partial x}} + C_{1} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right\} + \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\frac{{\partial \phi _{x} }}{{\partial x}} \\ & + A_{{12}} \left\{ {\frac{{\partial v_{0} }}{{\partial y}} + C_{2} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right\} + B_{{12}} \frac{{\partial \phi _{y} }}{{\partial y}}, \\ \end{aligned}$$

(13a)

$$\begin{aligned} N_{{yy}} & = \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)\left\{ {\frac{{\partial v_{0} }}{{\partial y}} + C_{2} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right\} + \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\frac{{\partial \phi _{y} }}{{\partial y}} \\ & + A_{{12}} \left\{ {\frac{{\partial u_{0} }}{{\partial x}} + C_{1} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right\} + B_{{12}} \frac{{\partial \phi _{x} }}{{\partial x}} - N_{y}^{T} , \\ \end{aligned}$$

(13b)

$$N_{{xy}} = A_{{66}} \left( {\frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{66}} \left( {\frac{{\partial \phi _{x} }}{{\partial y}} + \frac{{\partial \phi _{y} }}{{\partial x}}} \right),$$

(13c)

$$\begin{aligned} M_{{xx}} & = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\left\{ {\frac{{\partial u_{0} }}{{\partial x}} + C_{1} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right\} + \left( {D_{{11}} + \frac{{E_{0} I_{{xx}} }}{{l_{x} }} + \frac{{E_{0} A_{x} e_{x}^{2} }}{{l_{x} }}} \right)\frac{{\partial \phi _{x} }}{{\partial x}} \\ & + B_{{12}} \left\{ {\frac{{\partial v_{0} }}{{\partial y}} + C_{2} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right\} + D_{{12}} \frac{{\partial \phi _{y} }}{{\partial y}} - M_{x}^{T} , \\ \end{aligned}$$

(13d)

$$\begin{aligned} M_{{yy}} & = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\left\{ {\frac{{\partial v_{0} }}{{\partial y}} + C_{2} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right\} + \left( {D_{{22}} + \frac{{E_{0} I_{{yy}} }}{{l_{y} }} + \frac{{E_{0} A_{y} e_{y}^{2} }}{{l_{y} }}} \right)\frac{{\partial \phi _{y} }}{{\partial y}} \\ & + B_{{12}} \left\{ {\frac{{\partial u_{0} }}{{\partial x}} + C_{1} w_{0} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right\} + D_{{12}} \frac{{\partial \phi _{x} }}{{\partial x}} - M_{y}^{T} , \\ \end{aligned}$$

(13e)

$$M_{{xy}} = B_{{66}} \left( {\frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + D_{{66}} \left( {\frac{{\partial \phi _{x} }}{{\partial y}} + \frac{{\partial \phi _{y} }}{{\partial x}}} \right),$$

(13f)

$$Q_{{xz}} = K_{s} A_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - C_{1} u_{0} } \right)\,\,\,\,\text{and} \,\,\,Q_{{yz}} = K_{s} A_{{44}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - C_{2} v_{0} } \right).$$

(13g)

where I_xx and I_yy are the area moment of inertia of stiffeners along x and y direction, respectively, and $\left\{ {A_{{ij}} ,\,B_{{ij}} ,\,D_{{ij}} } \right\} = \int\limits_{{ - {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\left\{ {1,\,z,\,z^{2} } \right\}Q_{{ij}} \,{\text{d}}z}$ are the extensional, coupling and bending stiffnesses, respectively; and the thermal stress and moment resultants are defined as:

$$\left[ {\begin{array}{*{20}c} {N_{{xx}}^{T} } \\ {N_{{yy}}^{T} } \\ \end{array} } \right] = \int\limits_{{ - {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\left[ {\begin{array}{*{20}c} {\frac{{E_{{{\text{eff}}}} \left( {z,T} \right)}}{{1 - \upsilon }}\alpha _{{{\text{eff}}}} \left( {z,\,T} \right)\Delta T\left( z \right)} \\ {\frac{{E_{{{\text{eff}}}} \left( {z,T} \right)}}{{1 - \upsilon }}\alpha _{{{\text{eff}}}} \left( {z,\,T} \right)\Delta T\left( z \right)} \\ \end{array} } \right]\,{\text{d}}z} ;\,\,{\text{and}}\,\,\left[ {\begin{array}{*{20}c} {M_{{xx}}^{T} } \\ {M_{{yy}}^{T} } \\ \end{array} } \right] = \int\limits_{{ - {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\left[ {\begin{array}{*{20}c} {z\frac{{E_{{{\text{eff}}}} \left( {z,T} \right)}}{{1 - \upsilon }}\alpha _{{{\text{eff}}}} \left( {z,\,T} \right)\Delta T\left( z \right)} \\ {z\frac{{E_{{{\text{eff}}}} \left( {z,T} \right)}}{{1 - \upsilon }}\alpha _{{{\text{eff}}}} \left( {z,\,T} \right)\Delta T\left( z \right)} \\ \end{array} } \right]\,{\text{d}}z} .$$

(14)

To obtain the governing equations for vibration analysis of the FGM shell panels carrying stiffeners using variational approach under thermal environment, the total strain energy (U_total) and kinetic energy (K_total) of the system are written as:

$$\begin{aligned} U_{{{\text{total}}}} & = \frac{1}{2}\int\limits_{V} {\left[ {\left( {\sigma _{{xx}}^{{\left( {{\text{shell}}} \right)}} + \sigma _{{xx}}^{{stx}} } \right)\varepsilon _{{xx}} + \left( {\sigma _{{yy}}^{{\left( {{\text{shell}}} \right)}} + \sigma _{{yy}}^{{sty}} } \right)\varepsilon _{{yy}} + \tau _{{xy}} \gamma _{{xy}} + \tau _{{xz}} \gamma _{{xz}} + \tau _{{yz}} \gamma _{{yz}} } \right.} \\ & - \left. {\left( {\sigma _{{xx}}^{{\left( {{\text{shell}}} \right)}} + \sigma _{{yy}}^{{\left( {{\text{shell}}} \right)}} } \right)\alpha _{{eff}} \left( {z,T} \right)\Delta T\left( {z,T} \right)} \right]\,{\text{d}}V \\ & = \frac{1}{2}\int\limits_{A} {\left[ {\left( {N_{{xx}} - N_{x}^{T} } \right)\left( {u_{{0,x}} + C_{1} w_{0} + \frac{1}{2}w_{{0,x}}^{2} } \right) + \left( {N_{{yy}} - N_{y}^{T} } \right)\left( {v_{{0,y}} + C_{2} w_{0} + \frac{1}{2}w_{{0,y}}^{2} } \right)} \right.} \\ & + N_{{xy}} \left( {u_{{0,y}} + v_{{0,x}} + w_{{0,x}} w_{{0,y}} } \right) + \left( {M_{{xx}} - M_{x}^{T} } \right)\phi _{{x,x}} + \left( {M_{{yy}} - M_{y}^{T} } \right)\phi _{{y,y}} \\ & + \left. {M_{{xy}} \left( {\phi _{{x,y}} + \phi _{{y,x}} } \right) + Q_{{yz}} \left( {\phi _{y} + w_{{0,y}} - C_{2} v_{0} } \right) + Q_{{yz}} \left( {\phi _{x} + w_{{0,x}} - C_{1} u_{0} } \right) + N^{*} } \right]\,\,{\text{d}}A \\ \end{aligned}$$

(15)

where, $N^{*} = \int\limits_{{ - {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\frac{{E_{{\rm eff}} \left( z \right)}}{{\left( {1 - \upsilon } \right)}}\alpha _{{eff}}^{2} \left( {z,T} \right)\Delta T^{2} \left( z \right)\,\text{d} z}$.

For the total kinetic energy,

$$K_{{{\text{total}}}} = \frac{1}{2}\int\limits_{V} {\rho _{{{\text{eq}}}} \left( z \right)\left( {\dot{u}^{2} + \dot{v}^{2} + \dot{w}^{2} } \right)} {\text{d}}V = \frac{1}{2}\int\limits_{A} {\left[ {I_{0} \left( {\dot{u}_{0}^{2} + \dot{v}_{0}^{2} + \dot{w}_{0}^{2} } \right) + I_{1} \left( {\dot{u}_{0} \dot{\phi }_{x} + \dot{v}_{0} \dot{\phi }_{y} } \right) + I_{2} \left( {\dot{\phi }_{x}^{2} + \dot{\phi }_{y}^{2} } \right)} \right]} {\text{d}}A,$$

(16)

where, ($\cdot$ ) indicates partial differentiation with respect to time (i.e., ∂()/∂t).

$$\rho _{{{\text{eq}}}} = \rho \left( z \right) + \rho _{0} \left( {\frac{{A_{x} }}{{l_{x} h}} + \frac{{A_{y} }}{{l_{y} h}}} \right),$$

(17)

where $\rho$₀ = the mass density of the material of stiffeners;

$${\text{and}},\,\,\,I_{i} = \int\limits_{{ - {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\rho _{{{\text{eq}}}} \left( z \right)z^{i} {\text{d}}z,\,\,\,\,\,\,\left( {i = 0,\,\,1,\,\,2} \right).}$$

(18)

In the present work, it is considered that the FGM shell is subjected to transverse harmonic distributed pressure (i.e., q), and the work done by this distributed pressure is written as:

$$W_{q} = \int\limits_{A} {qw_{0} } \,{\text{d}}A\,,$$

(19)

where q = Q sin Ωt, and Ω is the angular frequency of harmonic distributed pressure.

In the present study, the internal damping is assumed only in the transverse direction and the energy dissipated due to damping is given as [44]:

$$D = I_{0} \zeta \int\limits_{A} {w_{0} \dot{w}_{0} \,} {\text{d}}A\,,$$

(20)

where is damping coefficient.

Governing Differential Equations

For nonlinear vibration analysis, the governing differential equations for FGM doubly curved shallow shell, with stiffeners and temperature gradient across the thickness, are derived by employing the extended Hamilton’s principle for the non-conservative system with the following variational principle:

$$\int\limits_{0}^{t} {\left( {\delta K_{{{\text{total}}}} - \delta U_{{{\text{total}}}} - \delta W_{q} - \delta D} \right)\,{\text{d}}t} = 0.$$

(21)

Use integration-by-parts after inserting for U_total, K_total, W_q, and D from Eqs. (15), (16), (19), and (20), in Eq. (21), respectively; and then, collecting the coefficients of $\delta u_{0} ,\,\delta v_{0} ,\,\delta w_{0} ,\,\delta \phi _{x} \,\text{and} \,\delta \phi _{y}$ leads, respectively, to the following governing differential equations.

$$N_{{x,x}} + N_{{xy,y}} + C_{1} Q_{{xz}} = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} ,$$

(22a)

$$N_{{y,y}} + N_{{xy,x}} + C_{2} Q_{{yz}} = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{y} ,$$

(22b)

$$\begin{gathered} Q_{{xz,x}} + Q_{{yz,y}} - C_{1} N_{x} - C_{2} N_{y} + N_{x} w_{{0,xx}} + N_{{x,x}} w_{{0,x}} + N_{y} w_{{0,yy}} + N_{{y,y}} w_{{0,y}} + 2N_{{xy}} w_{{0,xy}} \hfill \\ + N_{{xy,x}} w_{{0,y}} + N_{{xy,y}} w_{{0,x}} + C_{1} N_{x}^{T} + C_{2} N_{y}^{T} - N_{x}^{T} w_{{0,xx}} - N_{y}^{T} w_{{0,yy}} + q = I_{0} \ddot{w}_{0} + 2\varsigma I_{0} \dot{w}_{0} , \hfill \\ \end{gathered}$$

(22c)

$$M_{{x,x}} + M_{{xy,y}} - Q_{{xz}} = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x} ,$$

(22d)

$${\text{and}}\,\,M_{{y,y}} + M_{{xy,x}} - Q_{{yz}} = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{y} .$$

(22e)

Further, using Eqs. 13(a)–(g), Eqs. 22(a)–(e) are expanded in the following forms:

$$l_{{11}} \left( {u_{0} } \right) + l_{{12}} \left( {v_{0} } \right) + l_{{13}} \left( {w_{0} } \right) + l_{{14}} \left( {\phi _{x} } \right) + l_{{15}} \left( {\phi _{y} } \right) + n_{1} \left( {w_{0}^{2} } \right) = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} ,$$

(23a)

$$l_{{21}} \left( {u_{0} } \right) + l_{{22}} \left( {v_{0} } \right) + l_{{23}} \left( {w_{0} } \right) + l_{{24}} \left( {\phi _{x} } \right) + l_{{25}} \left( {\phi _{y} } \right) + n_{2} \left( {w_{0}^{2} } \right) = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{y} ,$$

(23b)

$$\begin{gathered} l_{{31}} \left( {u_{0} } \right) + l_{{32}} \left( {v_{0} } \right) + l_{{33}} \left( {w_{0} } \right) + l_{{34}} \left( {\phi _{x} } \right) + l_{{35}} \left( {\phi _{y} } \right) + n_{3} \left( {w_{0}^{2} } \right) + n_{4} \left( {w_{0}^{3} } \right) + n_{5} \left( {u_{0} w_{0} } \right) \hfill \\ + n_{6} \left( {v_{0} w_{0} } \right) + n_{7} \left( {w_{0} \phi _{x} } \right) + n_{8} \left( {w_{0} \phi _{y} } \right) - q = I_{0} \ddot{w}_{0} + 2\zeta I_{0} \dot{w}_{0} , \hfill \\ \end{gathered}$$

(23c)

$$l_{{41}} \left( {u_{0} } \right) + l_{{42}} \left( {v_{0} } \right) + l_{{43}} \left( {w_{0} } \right) + l_{{44}} \left( {\phi _{x} } \right) + l_{{45}} \left( {\phi _{y} } \right) + n_{9} \left( {w_{0}^{2} } \right) = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x} ,$$

(23d)

$$l_{{51}} \left( {u_{0} } \right) + l_{{52}} \left( {v_{0} } \right) + l_{{53}} \left( {w_{0} } \right) + l_{{54}} \left( {\phi _{x} } \right) + l_{{55}} \left( {\phi _{y} } \right) + n_{{10}} \left( {w_{0}^{2} } \right) = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{y} ,$$

(23e)

where, all linear and nonlinear operators in the set of governing differential equations Eq. (21) are represented, respectively, by l_ij () and n_i () symbols and, are presented in expanded form in “Appendix A”.

Solution Methodology

The present study explores the nonlinear dynamic behavior of simply-supported FGM shallow shell, the boundary conditions at different edges of the shell are defined as:

$$\begin{gathered} v_{0} = w_{0} = \phi _{y} = 0,\,\,\,M_{x} = \,\,N_{x} = N_{{xy}} = 0\,\,\,\text{at} \,\,\,x = 0\,\,\text{and} \,\,x = a, \hfill \\ u_{0} = w_{0} = \phi _{x} = 0,\,\,\,M_{y} = \,\,N_{y} = N_{{xy}} = 0\,\,\,\text{at} \,\,\,y = 0\,\,\text{and} \,\,y = b. \hfill \\ \end{gathered}$$

(24)

Assuming the Navier solutions for the simply-supported FGM shell, the following admissible trigonometric displacement and rotation functions, satisfying the above-mentioned boundary conditions in Eq. (22), are introduced in the aforementioned set of governing differential equations [i.e., Eqs. 21(a)-(e)].

$$\begin{aligned} u_{0} & = U\left( t \right)\cos \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b},\,\,\,v_{0} = V\left( t \right)\sin \frac{{m\pi x}}{a}\cos \frac{{n\pi y}}{b},w_{0} = W\left( t \right)\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b},\, \\ \,\phi _{x} & = X\left( t \right)\cos \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b},\,\,\,\phi _{y} = Y\left( t \right)sin\frac{{m\pi x}}{a}\cos \frac{{n\pi y}}{b}. \\ \end{aligned}$$

(25)

It is to mention that U, V, W, X, and Y are the vibration amplitudes in the corresponding directions, whereas m and n are half wave numbers along x and y directions, respectively.

By substituting the assumed admissible displacement and rotation functions from Eq. (25) into Eqs. 23(a)–(e), and applying the Galerkin method over the shell domain, the partial differential equations [i.e., Eqs. 23(a)–(e)] are converted into the following nonlinear governing equations.

$$C_{{11}} U + C_{{12}} V + C_{{13}} W + C_{{14}} X + C_{{15}} Y + N_{1} W^{2} = I_{0} \ddot{U} + I_{1} \ddot{X},$$

(26a)

$$C_{{21}} U + C_{{22}} V + C_{{23}} W + C_{{24}} X + C_{{25}} Y + N_{2} W^{2} = I_{0} \ddot{V} + I_{1} \ddot{Y},$$

(26b)

$$\begin{gathered} C_{{31}} U + C_{{32}} V + C_{{33}} W + C_{{34}} X + C_{{35}} Y + N_{3} W^{2} + N_{4} W^{3} + N_{5} UW + N_{6} VW \hfill \\ \, + N_{7} WX + N_{8} WY - \frac{{16q}}{{\pi ^{2} mn}} = I_{0} \ddot{W} + 2\zeta I_{0} \dot{W}, \hfill \\ \end{gathered}$$

(26c)

$$C_{{41}} U + C_{{42}} V + C_{{43}} W + C_{{44}} X + C_{{45}} Y + N_{9} \,W^{2} = I_{1} \ddot{U} + I_{2} \ddot{X},$$

(26d)

$$C_{{51}} U + C_{{52}} V + C_{{53}} W + C_{{54}} X + C_{{55}} Y + N_{{10}} W^{2} = I_{1} \ddot{V} + I_{2} \ddot{Y},$$

(26e)

In the Eqs. 26(a)–(e), the C_ij (i, j = 1, 2,…5) and N_i (i = 1, 2, …10) represent the coefficients of linear and nonlinear terms, respectively, and the same are specified in “Appendix B”.

The natural frequencies are calculated by solving the standard eigen value problem formulated by ignoring the nonlinear and damping terms and setting q = 0 in the Eqs. 226(a)–(e). Thereafter, the dynamic response of doubly-curved shallow FGM shells reinforced with stiffeners can be determined by solving time-dependent nonlinear governing equations Eqs. 26(a)–(e) using the fourth order Runge–Kutta method, along with the initial conditions:

$$U\left( 0 \right) = V\left( 0 \right) = W\left( 0 \right) = X\left( 0 \right) = Y\left( 0 \right) = 0\,;$$

and

$$\dot{U}\left( 0 \right) = \dot{V}\left( 0 \right) = \dot{W}\left( 0 \right) = \dot{X}\left( 0 \right) = \dot{Y}\left( 0 \right) = 0.$$

(27)

Numerical Studies and Discussion

To carry out the present research work, a MATLAB code based on the generalized analytical formulation for different shell configurations was developed for conducting linear and nonlinear vibration analysis of unstiffened- and stiffened- FGM doubly-curved shallow shells. The accuracy of developed code is established through various verification studies conducted by comparing the results obtained with those reported in the literature. After the verification studies, a parametric study was conducted to investigate the linear and nonlinear dynamic behavior of un-stiffened and stiffened doubly-curved shallow Ti–6Al–4V/ZrO₂ FGM shells with temperature-dependent material properties, as given in Table 1. Numerical results are presented for free and forced vibration analysis of different shell geometries obtained by setting the different combinations of curvatures, as given in Table 2.

Verification Studies

In the first verification study, non-dimensional natural frequencies ($\bar{\omega } = \omega h\sqrt {{{\rho _{{\text{c}}} } \mathord{\left/ {\vphantom {{\rho _{{\text{c}}} } {E_{{\text{c}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{c}}} }}}$ of un-stiffened, doubly-curved FGM shallow shells (with a/b = 1, a/h = 10) of different geometrical configurations (i.e., plate, cylindrical, spherical, and hyperbolic-paraboloidal) and different power law index (i.e., 0, 1, 4, 10) are compared with the results reported in the literature by Wattanasakulpong and Chaikittiratana [22], Alijani et al. [28], and Matsunaga [45]. The FGM shell panels were assumed to be simply-supported and made up of Al/Al₂O₃ with temperature-independent material properties (i.e., E_m = 70 × 10⁹ N/m², ρ_m = 2702 kg/m³, E_c = 380 × 10⁹ N/m² and ρ_c = 3800 kg/m³). Table 3 shows the comparison of results, and it can be observed from this table that the results obtained from the present formulation are in good concurrence with the results published in the literature.

Table 3 Verification of non-dimensional natural frequency $\bar{\omega } = \omega h\sqrt {{{\rho _{\rm c} } \mathord{\left/ {\vphantom {{\rho _{\rm c} } {E_{\rm c} }}} \right. \kern-\nulldelimiterspace} {E_{\rm c} }}}$_.

In the second verification study, the non-dimensional natural frequency $\bar{\omega } = \left( {{{\omega a^{2} } \mathord{\left/ {\vphantom {{\omega a^{2} } h}} \right. \kern-\nulldelimiterspace} h}} \right)\sqrt {{{\left( {1 - \nu ^{2} } \right)\rho _{{\text{m}}} } \mathord{\left/ {\vphantom {{\left( {1 - \nu ^{2} } \right)\rho _{{\text{m}}} } {E_{{\text{m}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{m}}} }}}$ of an unstiffened SUS304/Si₃N₄ FGM plate (i.e., $(C_{1} = C_{2} = 0)$) with simply-supported boundary condition is compared with that reported by Alijani [46] and Huang and Shen [47], for different power law index (i.e., 0, 0.5, 1, 2) and for different values of temperature differences (i.e., ΔT = 0 K, 100 K, 300 K). The material properties were considered to be temperature-dependent. The results are tabulated in Table 4. It can be ascertained from Table 4 that the present results are in good compliance with the published results by Alijani [46] and Huang and Shen [47].

Table 4 Verification of non-dimensional natural frequency $\bar{\omega } = \left( {{{\omega a^{2} } \mathord{\left/ {\vphantom {{\omega a^{2} } h}} \right. \kern-\nulldelimiterspace} h}} \right)\sqrt {{{\left( {1 - \nu ^{2} } \right)\rho _{{\text{m}}} } \mathord{\left/ {\vphantom {{\left( {1 - \nu ^{2} } \right)\rho _{{\text{m}}} } {E_{{\text{m}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{m}}} }}}$ of square FGM plate with h/a = 0.125 and a/b = 1 under thermal environment

In addition, the non-dimensional natural frequency $\left( {\bar{\omega } = 10^{2} \omega h\sqrt {{{\rho _{{0{\text{c}}}} } \mathord{\left/ {\vphantom {{\rho _{{0{\text{c}}}} } {E_{{0{\text{c}}}} }}} \right. \kern-\nulldelimiterspace} {E_{{0{\text{c}}}} }}} } \right)$ of Al₂O₃/Al and Si₃N₄/SUS304 FGM spherical shell panels containing 10 stiffeners in x and y directions both were compared with the values presented by Wattanasakulpong and Chaikittiratana [22]. The results of comparison for spherical shell panels made of Al₂O₃/Al are shown in Table 5 for different power law index; whereas, for Si₃N₄/SUS304 FGM with temperature-dependent material properties under thermal environment (i.e., ΔT = 100 K), the results are presented in Table 6 for different values of side-to-radius of curvature ratio (i.e., $a/{R}_{x}$). An acceptable agreement between the results of current study and the literature can be seen in Table 5 and Table 6.

Table 5 Comparison of non-dimensional natural frequency of Al₂O₃/Al FGM spherical shell panels with a/b = 1.0, a/h = 20, h_x = h_y = 3 h, and h_x/b_x = h_y/b_y = 5.0

Table 6 Comparison of non-dimensional natural frequency of Si₃N₄/SUS304 FGM spherical shell panels under thermal environment with a/b = 1.0; a/h = 20, k = 0.5, h_x = h_y = 3 h, h_x/b_x = h_y/b_y = 5.0

Furthermore, to verify the nonlinear formulation, the nonlinear frequency ratio $\omega _{{nl}} /\omega$ for a simply-supported Si₃N₄/SUS304 FGM cylindrical shell panel obtained using the present formulation is compared with the results reported by Shen and Wang [30]. As evident from Table 7, the results of the present formulation are in good accordance with the literature [30]. However, a little difference in the values in Table 7 can be ascribed to the use of different deformation theories- higher-order shear deformation theory by Shen and Wang [30], and first-order shear deformation theory in the present work.

Table 7 Comparison of nonlinear-linear frequency ratios (ω_nl/ω) of simply-supported cylindrical shell panel of FGM Si₃N₄/SUS304 (for k = 2 and a/h = 20)

Additionally, the accuracy of the present formulation in predicting the nonlinear vibration response of stiffened FGM structures is established by comparing the nonlinear vibration response of Al/Al₂O₃ FGM stiffened spherical shell panel subjected to uniformly distributed pressure with Bich et al. [48], as shown in Fig. 2a. While Fig. 2b depicts a similar comparison of nonlinear vibration response of Al/Al₂O₃ FGM stiffened plate under thermal environment (i.e., ΔT = 105⁰ K) with Duc et al. [49]. The comparisons shown in Fig. 2a, b assure the reliability of the present formulation in predicting the nonlinear vibration response of FGM stiffened shell panels under mechanical as well as thermal loadings.

Fig. 2

Comparison of nonlinear vibration response of a stiffened FGM spherical panel for k = 1,a/b = 1, a/h = 30, m = n = 1, R_x = R_y = 6 m, =$\xi$  0.1, q = 5000 sin (500t), and b FGM plate for k = 1, a/b = 1, a/h = 20, m = n = 1, = 0.1,q = 1500 sin (600t) and T = 105 K

Parametric Investigation and Discussion

After verification of the present formulation, a parametric study is conducted to explore the linear and nonlinear dynamic behavior of un-stiffened and stiffened doubly curved shallow Ti–6Al–4V/ZrO₂ FGM shells with temperature-dependent material properties, as given in Table 1. It is important to mention here that all the numerical studies are conducted by considering: half-wave numbers m = n = 1, aspect ratio, a/b = 1, and a/h = 20 with different shell geometries obtained by setting C₁ = C₂ = 0 for plate, C₁ = 1/5, C₂ = 0 for cylindrical, C₁ = C₂ = 1/5 for spherical, and C₁ = 1/5, C₂ = -1/5 for hyperbolic-paraboloidal shell panels, as mentioned in Table 2. Moreover, for stiffened shell panels the heights (i.e., h_x = h_y) and widths (i.e., b_x = b_y) of the stiffeners are taken as 3 h and 3 h/10 respectively, where h being the thickness of the shell. In addition, the natural frequency is presented in the non-dimensional form as: $\bar{\omega } = 10^{2} \omega h\sqrt {{{\rho _{{\text{m}}} \left( {1 - \upsilon ^{2} } \right)} \mathord{\left/ {\vphantom {{\rho _{{\text{m}}} \left( {1 - \upsilon ^{2} } \right)} {E_{{\text{m}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{m}}} }}}$.

In order to fix the number of stiffeners (i.e., n_x, n_y), the effect of number of stiffeners (with n_x = n_y) on non-dimensional natural frequency (i.e., $\bar{\omega } = 10^{2} \omega h\sqrt {{{\rho {\text{s}}\left( {1 - \upsilon ^{2} } \right)} \mathord{\left/ {\vphantom {{\rho {\text{s}}\left( {1 - \upsilon ^{2} } \right)} {E_{{\text{m}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{m}}} }}}$) of the FGM plate and three different FGM (with $k$ = 1) stiffened shell geometries was studied and the plots obtained are shown in Fig. 3. It is found that initially with the increase in the number of stiffeners, the natural frequency increases up to 15 stiffeners and thereafter, the natural frequency decreases. This is true for the plate as well as for other considered shell geometries. It can also be observed from Fig. 3 that irrespective of the number of equal stiffeners in $x$ and $y$ directions, spherical shell has the highest natural frequency, whereas the hyperbolic-paraboloidal shell is found to have a lowest natural frequency. Based on the finding that the effect of 15 stiffeners (n_x = n_y = 15) is most significant on the natural frequency, it is to mention here that in any of the subsequent investigations on stiffened shell panels, the number of stiffeners in x- and y-directions both is taken equal to 15.

Fig. 3

Effect of the number of stiffeners on non-dimensional natural frequency $\left( {\bar{\omega }} \right)$ of stiffened FGM (ZrO₂/Ti–6Al–4V) shell panels with different geometries (k = 1)

Table 8 shows the effect of stiffeners on the non-dimensional natural frequencies $\left( {\bar{\omega }} \right)$ of free vibration of FGM shell panels of different geometries, for different values of power law index. It can be seen that the non-dimensional natural frequency $\left( {\bar{\omega }} \right)$ of stiffened shell panels are significantly greater than that of unstiffened ones. It can also be observed that natural frequency decreases with the increase of power law index, k and the effect of stiffeners is more prominent for power law index, k = 0 (i.e., ceramic) than other values of $k$. This is because of the reason that for $k$ = 0, the whole panel, including the stiffeners, would be made of ceramic material.

Table 8 Non-dimensional natural frequency $\left( {\bar{\omega }} \right)$ of un-stiffened and stiffened FGM (ZrO₂/Ti–6Al–4V) doubly-curved shallow shells (n_x = n_y = 15, and $\Delta$T = 0 K)

Table 9 illustrates the effect of the temperature difference (i.e., $\Delta$T = 0 K, 100 K, 300 K) across the thickness of stiffened FGM shell panels of different geometries on the non-dimensional natural frequency, for different values of power law index, k. It can be clearly seen from Table 9 that a higher temperature difference will lower the non-dimensional natural frequency remarkably. In addition, it can also be observed from Tables 8 and 9 that the natural frequencies of spherical and hyperbolic-paraboloidal shell panels are highest and lowest, respectively, among all the shell geometries considered in the present work.

Table 9 Effect of the temperature difference across thickness on the non-dimensional natural frequency $\left( {\bar{\omega }} \right)$ of FGM (ZrO₂/Ti–6Al–4V) doubly-curved shallow shells (n_x = n_y = 15)

Figure 4a–d present comparisons of the amplitude of nonlinear dynamic response of un-stiffened and stiffened (i.e., uni-directional stiffened and orthogonally stiffened) shell panels of different shell geometries. It is quite evident from these Figs that irrespective of shell geometry, shell panels without stiffeners show a considerably large amplitude of nonlinear forced vibration in comparison to uni-directional stiffened and orthogonally stiffened shell panels. This is attributed to the reason that shell panels without stiffeners have lower stiffness.

Fig. 4

Nonlinear vibration response of FGM a plate b cylindrical, c spherical, and d hyperbolic-paraboloidal shell panels with and without stiffeners (for k = 1 and q = 1500sin(600t))

Figure 5 (a-d) depicts the effect of FGM power law index on the nonlinear dynamic response of the stiffened shells panels of different geometries under a harmonic force of constant amplitude. A similar study is shown in Fig. 6a–d at resonance condition (i.e., Ω/ω = 1). It can be clearly seen in Figs. 5a–d and 6a–d that with the increase of power law index, value of the maximum amplitude of nonlinear vibration of stiffened shell panels increases. This can be attributed to the fact that with the increase of power law index, metal (having lower stiffness than ceramic) proportion is increased in FGM causing a decrease in the overall stiffness of the FGM panel, and hence, the amplitude of vibration increases. It is justifiable to mention that with the increase in power law index natural frequency decreases and it can be seen clearly in the case of resonance in Figs. 6 (a-d) that the time period of vibration response increases significantly.

Fig. 5

Nonlinear vibration response of FGM a plate b cylindrical, c spherical, and d hyperbolic -paraboloidal shell panels (for n_x = n_y = 15 and q = 1500sin(600t))

Fig. 6

Nonlinear vibration response of FGM (a plate b cylindrical, c spherical, and d hyperbolic -paraboloidal shell panels at different values of power law index k (for q = 1500sin(Ωt) with Ω/ $\omega$ = 1, $\xi$ = 0, and n_x = n_y = 15)

Effect of the temperature difference on nonlinear dynamic responses of the stiffened shell panels at different excitation frequencies (${\text{i}}.{\text{e}}.,~~\Omega = 600\;~{\text{and}}~\;\Omega /\omega ~ = ~0.95$) is shown, respectively, in Figs. 7a–d and 8a–d. To achieve the temperature difference, the metal surface is kept at a temperature (T_m) of 300 K while the ceramic surface temperature (T_c) is taken as 300 K, 400 K and 600 K. As observed from Fig. 7a–d that temperature difference rise results in the increase of vibration amplitude, for all geometries of shell panels. Further, as demonstrated in Fig. 8a–d, the rise in temperature difference across the thickness of FGM shell panels also results in an increase in the time period of the beat phenomenon, a vibrational behaviour of engineering structures observed when the excitation frequency is close to the natural frequency. These observations are customary because an increase in the temperature difference across the thickness reduces the stiffness of the shell panels.

Fig. 7

Nonlinear vibration response of FGM a plate, b cylindrical, c spherical, and d hyperbolic-paraboloidal shell panels under different temperature differences $\Delta$T across thickness (for k = 1, n_x = n_y = 15, and q = 1500sin(600t))

Fig. 8

Nonlinear vibration response (i.e., beat phenomenon) of FGM a plate, b cylindrical, c spherical, and d hyperbolic -paraboloidal shell panels under different temperature differences $\Delta$T across thickness (for q = 1500sin(Ωt) with $\Omega ~/~\omega ~~ = ~0.95$,  $\xi$ =  0, k = 1, and n_x = n_y = 15)

The effect of damping on the nonlinear vibration response of a typical stiffened spherical FGM shell panel is studied here. Figure 9 shows the effect of damping on nonlinear vibration response the spherical FGM shell panel but in the absence of excitation force. The initial conditions were taken as: W = 10⁻⁷ m and $\dot{W} = 0$. It can be observed that the amplitude of vibration reduces exponentially with time. Further, the effect of damping under the condition of resonance (i.e., Ω/ω = 1) shown in Fig. 10 demonstrates that initially the impact of damping is indistinguishable and thereafter, a substantial difference in the amplitude caused by damping can be observed after a few initial periods of vibration. It is also observed from Fig. 10 that the amplitude of undamped nonlinear vibration response increases linearly in an unbounded manner with time, whereas the amplitude of damped nonlinear vibration response is bounded and it reduces considerably in comparison to undamped nonlinear vibration response. Further, Fig. 11 shows that the effect of damping is not clearly observable during the time periods of the first few beats, but the effect in terms of reduction in the amplitude is apparent thereafter in successive time periods.

Fig. 9

Exponential decay of amplitude of nonlinear vibration of stiffened spherical panel (for k = 1, q = 0, $\xi$ =  0.5, T = 100 K, and n_x = n_y = 15)

Fig. 10

Effect of damping on nonlinear vibration response of stiffened spherical panel (for k = 1, q = 1500sin(Ωt) with $/$ = 1, T = 100 K, and n_x = n_y = 15)

Fig. 11

Effect of damping on nonlinear vibration response (i.e., beat phenomenon) of stiffened spherical panel (for k = 1, q = 1500 sin (Ωt) with Ω/ω = 0.95, T = 100 K, and n_x = n_y = 15)

Conclusion

In the present paper, an analytical formulation based on the first-order shear deformation theory in conjunction with von Karman geometric nonlinearity is utilized for the dynamic analysis of eccentrically stiffened, simply-supported doubly-curved FGM shallow shell panels under thermo-mechanical loading. After ascertaining the accuracy of the formulation by comparing the results obtained, for FGM (with temperature-dependent and –independent material properties) shell panels of different geometries, in the present study with the published results in the literature, a parametric study is conducted to investigate the effect of shell geometries, stiffeners, material inhomogeneity, different temperature differences across the thickness, and material parameters on the natural frequency, and nonlinear dynamic response. Natural frequencies are obtained by solving a linear standard eigenvalue problem. Galerkin method is used to obtain the coupled differential equations of motion with cubic and quadratic nonlinearity, and thereafter, the dynamic response is obtained by solving simultaneous nonlinear differential equations of motion using the fourth-order Runge–Kutta method. Based on the present study following important observations are revealed:

• Shell geometry is found to affect the vibration behavior prominently. Among the un-stiffened as well as stiffened FGM shell panels, the spherical shell panel exhibits the highest natural frequency with the lowest vibration amplitude, whereas lowest natural frequency with the highest amplitude is depicted by hyperbolic-paraboloidal shell.

• Irrespective of shell geometry, the natural frequencies of FGM shell panels are affected by the number of stiffeners significantly, whereas the inclusion of stiffeners reduces the amplitude of vibration considerably.

• Natural frequencies and dynamic response of un-stiffened and stiffened FGM shell panels are found to be greatly affected by material gradation profile, and at resonance conditions, higher amplitude of vibration is noticed for the increased power law index.

• An increase of temperature difference across the thickness of the shell panel reduces the natural frequency as well as increases the amplitude of vibration for all FGM shell geometries. It is attributed to the reduction of stiffness of FGM shell panels with an increase in temperature difference across the thickness of shell panel.

• Damping causes an exponential decay with time in the amplitude of unexcited vibration of stiffened FGM spherical shell panel. Further, at the resonance condition, damping causes a bound on the increase in the amplitude of stiffened FGM spherical shell panel.

Appendices

Appendix

Appendix A

$$l_{{11}} \left( {u_{0} } \right) = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)u_{{0,xx}} + A_{{66}} u_{{0,yy}} - K_{s} A_{{55}} C_{1}^{2} u_{0} ;$$

$$l_{{12}} \left( {v_{0} } \right) = \left( {A_{{12}} + A_{{66}} } \right)v_{{0,xy}} ;\,\,l_{{13}} \left( {w_{0} } \right) = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} w_{{0,x}} + \left( {A_{{12}} C_{2} + K_{s} A_{{55}} C_{1} } \right)w_{{0,x}} ;$$

$$l_{{14}} \left( {\phi _{x} } \right) = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\phi _{{x,xx}} + B_{{66}} \phi _{{x,yy}} + K_{s} A_{{55}} C_{1} \phi _{x} ,\,\,l_{{15}} \left( {\phi _{y} } \right) = \left( {B_{{12}} + B_{{66}} } \right)\phi _{{y,xy}} ;$$

$$n_{1} \left( {w_{0}^{2} } \right) = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)w_{{0,x}} w_{{0,xx}} + \left( {A_{{12}} + A_{{66}} } \right)w_{{0,y}} w_{{0,xy}} + A_{{66}} w_{{0,x}} w_{{0,yy}} ;$$

$$l_{{21}} \left( {u_{0} } \right) = \left( {A_{{12}} + A_{{66}} } \right)u_{{0,xy}} ;\,\,\,l_{{22}} \left( {v_{0} } \right) = \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)v_{{0,yy}} + A_{{66}} v_{{0,xx}} - K_{s} A_{{44}} C_{2}^{2} v_{0} ;$$

$$l_{{23}} \left( {w_{0} } \right) = \left[ {\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} + A_{{12}} C_{1} + K_{s} A_{{44}} C_{2} } \right]w_{{0,y}} ;\,\,\,l_{{24}} \left( {\phi _{x} } \right) = \left( {B_{{12}} + B_{{66}} } \right)\phi _{{x,xy}} ;$$

$$l_{{25}} \left( {\phi _{y} } \right) = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\phi _{{y,yy}} + B_{{66}} \phi _{{y,xx}} + K_{s} A_{{44}} C_{2} \phi _{y} ;$$

$$n_{2} \left( {w_{0}^{2} } \right) = \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)w_{{0,y}} w_{{0,yy}} + A_{{66}} w_{{0,xx}} w_{{0,y}} + \left( {A_{{12}} + A_{{66}} } \right)w_{{0,x}} w_{{0,xy}} ;$$

$$l_{{31}} \left( {u_{0} } \right) = - \left[ {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} + A_{{12}} C_{2} + K_{s} A_{{55}} C_{1} } \right]u_{{0,x}} ;\,$$

$$l_{{32}} \left( {v_{0} } \right) = - \left[ {\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} + A_{{12}} C_{1} + K_{s} A_{{44}} C_{2} } \right]v_{{0,y}} ;$$

$$\begin{gathered} l_{{33}} \left( {w_{0} } \right) = - \left[ {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1}^{2} + 2A_{{12}} C_{1} C_{2} - \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2}^{2} } \right]w_{0} + K_{s} A_{{55}} w_{{0,xx}} + K_{s} A_{{44}} w_{{0,yy}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - N_{{xx}}^{T} w_{{0,xx}} - N_{{yy}}^{T} w_{{0,yy}} ; \hfill \\ \end{gathered}$$

$$l_{{34}} \left( {\phi _{x} } \right) = - \left[ {\left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)C_{1} + B_{{12}} C_{2} - K_{s} A_{{55}} } \right]\phi _{{x,x}} ;$$

$$l_{{35}} \left( {\phi _{y} } \right) = - \left[ {\left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)C_{2} + B_{{12}} C_{1} - K_{s} A_{{44}} } \right]\phi _{{y,y}} ;$$

$$\begin{gathered} n_{3} \left( {w_{0}^{2} } \right) = \frac{1}{2}\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} w_{{0,x}}^{2} + \frac{1}{2}\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} w_{{0,y}}^{2} + \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} w_{0} w_{{0,xx}} + \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} w_{0} w_{{0,yy}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{2}A_{{12}} C_{1} w_{{0,y}}^{2} + \frac{1}{2}A_{{12}} C_{2} w_{{0,x}}^{2} + A_{{12}} C_{2} w_{0} w_{{0,xx}} + A_{{12}} C_{1} w_{0} w_{{0,yy}} ; \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered}$$

$$\begin{gathered} n_{4} \left( {w_{0}^{3} } \right) = \frac{3}{2}\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)w_{{0,x}}^{2} w_{{0,xx}} + \frac{3}{2}\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)w_{{0,y}}^{2} w_{{0,yy}} + \frac{1}{2}A_{{12}} w_{{0,x}}^{2} w_{{0,yy}} + \frac{1}{2}A_{{12}} w_{{0,y}}^{2} w_{{0,xx}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\left( {A_{{12}} + 2A_{{66}} } \right)w_{{0,x}} w_{{0,y}} w_{{0,xy}} + A_{{66}} w_{{0,x}}^{2} w_{{0,yy}} + A_{{66}} w_{{0,y}}^{2} w_{{0,xx}} ; \hfill \\ \end{gathered}$$

$$\begin{gathered} n_{5} \left( {u_{0} w_{0} } \right) = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\left( {u_{{0,xx}} w_{{0,x}} + u_{{0,x}} w_{{0,xx}} } \right) + \left( {A_{{12}} + A_{{66}} } \right)u_{{0,xy}} w_{{0,y}} + A_{{12}} u_{{0,x}} w_{{0,yy}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + A_{{66}} u_{{0,yy}} w_{{0,x}} + 2A_{{66}} u_{{0,y}} w_{{0,xy}} ; \hfill \\ \end{gathered}$$

$$\begin{gathered} n_{6} \left( {v_{0} w_{0} } \right) = \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)\left( {v_{{0,yy}} w_{{0,y}} + u_{{0,y}} w_{{0,yy}} } \right) + \left( {A_{{12}} + A_{{66}} } \right)v_{{0,xy}} w_{{0,y}} + A_{{12}} v_{{0,y}} w_{{0,xx}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + A_{{66}} v_{{0,xx}} w_{{0,y}} + 2A_{{66}} v_{{0,x}} w_{{0,xy}} ; \hfill \\ \end{gathered}$$

$$\begin{gathered} n_{7} \left( {w_{0} \phi _{x} } \right) = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\left( {w_{{0,x}} \phi _{{x,xx}} + w_{{0,xx}} \phi _{{x,x}} } \right) + \left( {B_{{12}} + B_{{66}} } \right)w_{{0,y}} \phi _{{x,xy}} + B_{{12}} w_{{0,yy}} \phi _{{x,x}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + B_{{66}} w_{{0,x}} \phi _{{x,yy}} + 2B_{{66}} w_{{0,xy}} \phi _{{x,y}} ; \hfill \\ \end{gathered}$$

$$\begin{gathered} n_{8} \left( {w_{0} \phi _{y} } \right) = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\left( {w_{{0,y}} \phi _{{y,yy}} + w_{{0,yy}} \phi _{{y,y}} } \right) + \left( {B_{{12}} + B_{{66}} } \right)w_{{0,x}} \phi _{{y,xy}} + B_{{12}} w_{{0,xx}} \phi _{{y,y}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + B_{{66}} w_{{0,y}} \phi _{{y,xx}} + 2B_{{66}} w_{{0,xy}} \phi _{{y,x}} ; \hfill \\ \end{gathered}$$

$$l_{{41}} \left( {u_{0} } \right) = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)u_{{0,xx}} + B_{{66}} u_{{0,yy}} + K_{s} A_{{55}} C_{1} u_{0} ;$$

$$l_{{42}} \left( {v_{0} } \right) = \left( {B_{{12}} + B_{{66}} } \right)v_{{0,xy}} ;\,\,\,l_{{42}} \left( {w_{0} } \right) = \left[ {\left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)C_{1} + B_{{12}} C_{2} - K_{s} A_{{55}} } \right]w_{{0,x}} ;$$

$$l_{{44}} \left( {\phi _{x} } \right) = \left( {D_{{11}} + \frac{{E_{0} I_{{xx}} }}{{l_{x} }} + \frac{{E_{0} A_{x} e_{x}^{2} }}{{l_{x} }}} \right)\phi _{{x,xx}} + D_{{66}} \phi _{{x,yy}} - K_{s} A_{{55}} \phi _{x} ;$$

$$l_{{45}} \left( {\phi _{y} } \right) = \left( {D_{{12}} + D_{{66}} } \right)\phi _{{y,xy}} ;$$

$$n_{9} \left( {w_{0}^{2} } \right) = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)w_{{0,x}} w_{{0,xx}} + \left( {B_{{12}} + B_{{66}} } \right)w_{{0,y}} w_{{0,xy}} + B_{{66}} w_{{0,x}} w_{{0,yy}} ;$$

$$l_{{51}} \left( {u_{0} } \right) = \left( {B_{{12}} + B_{{66}} } \right)u_{{0,xy}} ;\,\,\,l_{{52}} \left( {v_{0} } \right) = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)v_{{0,yy}} + B_{{66}} v_{{0,xx}} + K_{s} A_{{44}} C_{2} v_{0} ;$$

$$\,l_{{53}} \left( {w_{0} } \right) = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)C_{2} w_{{0,y}} + B_{{12}} C_{1} w_{{0,y}} - K_{s} A_{{44}} w_{{0,y}} ;$$

$$\,l_{{54}} \left( {\phi _{x} } \right) = \left( {D_{{12}} + D_{{66}} } \right)\phi _{{x,xy}} ;\,\,\,\,l_{{55}} \left( {\phi _{y} } \right) = \left( {D_{{22}} + \frac{{E_{0} I_{{yy}} }}{{l_{y} }} + \frac{{E_{0} A_{y} e_{y}^{2} }}{{l_{y} }}} \right)\phi _{{y,yy}} + D_{{22}} \phi _{{y,xx}} - K_{s} A_{{44}} \phi _{y} ;$$

$$n_{{10}} \left( {w_{0}^{2} } \right) = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)w_{{0,y}} w_{{0,yy}} + \left( {B_{{12}} + B_{{66}} } \right)w_{{0,x}} w_{{0,xy}} + B_{{66}} w_{{0,y}} w_{{0,xx}} .$$

Appendix B

$$C_{{11}} = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi ^{2} }}{{a^{2} }} + A_{{66}} \frac{{n^{2} \pi ^{2} }}{{b^{2} }} + K_{s} A_{{66}} C_{1}^{2} {\text{ ,}}$$

$$C_{{12}} = \left( {A_{{12}} + A_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,\,\,\,C_{{13}} = - \left( {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} + A_{{12}} C_{2} + K_{s} A_{{66}} C_{1} } \right)\frac{{m\pi }}{a},$$

$$C_{{14}} = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi ^{2} }}{{a^{2} }} + \,B_{{66}} \frac{{n^{2} \pi ^{2} }}{{b^{2} }} - K_{s} A_{{66}} C_{1} \,,\,\,\,C_{{15}} = \left( {B_{{12}} + B_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},$$

$$N_{1} = - \frac{{16}}{9}\left[ {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi }}{{na^{3} }}\, + \,\left( {A_{{12}} - A_{{66}} } \right)\frac{{n\pi }}{{ab^{2} }}} \right]\,,$$

$$C_{{21}} = \,\left( {A_{{12}} + A_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,\,\,C_{{22}} = \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\frac{{n^{2} \pi ^{2} }}{{b^{2} }} + A_{{66}} \frac{{m^{2} \pi ^{2} }}{{a^{2} }} + K_{s} A_{{66}} C_{2}^{2} {\text{,}}$$

$$C_{{23}} = - \left( {\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} + A_{{12}} C_{1} + K_{s} A_{{66}} C_{2} } \right)\frac{{n\pi }}{b},\,\,\,\,C_{{24}} = \left( {B_{{12}} + B_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,$$

$$C_{{25}} = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\frac{{n^{2} \pi ^{2} }}{{b^{2} }} + \,B_{{66}} \frac{{m^{2} \pi ^{2} }}{{a^{2} }} - K_{s} A_{{66}} C_{2} \,,{\text{ }}\,\,\,$$

$$N_{2} = - \frac{{16}}{9}\left[ {\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)\frac{{n^{2} \pi }}{{mb^{3} }}\, + \,\left( {A_{{12}} - A_{{66}} } \right)\frac{{m\pi }}{{a^{2} b}}} \right]\,,\,\,\,$$

$$C_{{31}} = - \left( {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} + A_{{12}} C_{2} + K_{s} A_{{66}} C_{1} } \right)\frac{{m\pi }}{a},\,\,\,$$

$$C_{{32}} = - \left( {\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} + A_{{12}} C_{1} + K_{s} A_{{66}} C_{2} } \right)\frac{{n\pi }}{b},$$

$$C_{{33}} = \left( {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1}^{2} + \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2}^{2} + 2A_{{12}} C_{1} C_{2} } \right) + K_{s} A_{{66}} \left( {\frac{{m^{2} \pi ^{2} }}{{a^{2} }} + \frac{{n^{2} \pi ^{2} }}{{b^{2} }}} \right)$$

$$C_{{34}} = - \left( {\left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)C_{1} + B_{{12}} C_{2} - K_{s} A_{{66}} } \right)\frac{{m\pi }}{a},\,\,\,$$

$$C_{{35}} = - \left( {\left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)C_{2} + B_{{12}} C_{1} - K_{s} A_{{66}} } \right)\frac{{n\pi }}{b},$$

$$N_{3} = \frac{{16}}{3}\left( {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)C_{1} + A_{{12}} C_{2} } \right)\frac{m}{{na^{2} }} + \frac{{16}}{3}\left( {\left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)C_{2} + A_{{12}} C_{1} } \right)\frac{n}{{mb^{2} }},$$

$$N_{4} = \frac{9}{{32}}\left( {\left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\frac{{m^{4} \pi ^{4} }}{{a^{4} }} + \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)\frac{{n^{4} \pi ^{4} }}{{b^{4} }}} \right) + \left( {A_{{12}} + 2A_{{66}} } \right)\frac{{m^{2} n^{2} \pi ^{4} }}{{16a^{2} b^{2} }},$$

$$N_{5} = \frac{{32}}{9}\left( {A_{{66}} \frac{{n\pi }}{{ab^{2} }} - \left( {A_{{11}} + \frac{{E_{0} A_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi }}{{na^{3} }} - A_{{12}} \frac{{n\pi }}{{ab^{2} }}} \right),\,\,\,\,$$

$$N_{6} = \frac{{32}}{9}\left( {A_{{66}} \frac{{m\pi }}{{a^{2} b}} - \left( {A_{{22}} + \frac{{E_{0} A_{y} }}{{l_{y} }}} \right)\frac{{n^{2} \pi }}{{mb^{3} }} - A_{{12}} \frac{{m\pi }}{{a^{2} b}}} \right),$$

$$N_{7} = \frac{{32}}{9}\left( {B_{{66}} \frac{{n\pi }}{{ab^{2} }} - \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi }}{{na^{3} }} - B_{{12}} \frac{{n\pi }}{{ab^{2} }}} \right),\,\,\,$$

$$N_{8} = \frac{{32}}{9}\left( {B_{{66}} \frac{{m\pi }}{{a^{2} b}} - \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\frac{{n^{2} \pi }}{{mb^{3} }} - B_{{12}} \frac{{m\pi }}{{a^{2} b}}} \right),$$

$$C_{{41}} = \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi ^{2} }}{{a^{2} }} + \,B_{{66}} \frac{{n^{2} \pi ^{2} }}{{b^{2} }} - K_{s} A_{{66}} C_{1} ,\,\,\,C_{{42}} = \left( {B_{{12}} + B_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,$$

$$C_{{43}} = - \left( {\left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)C_{1} + B_{{12}} C_{2} - K_{s} A_{{66}} } \right)\frac{{m\pi }}{a},\,\,$$

$$C_{{44}} = \left( {D_{{11}} + \frac{{E_{0} I_{{xx}} }}{{l_{x} }} + \frac{{E_{0} A_{x} e_{x}^{2} }}{{l_{x} }}} \right)\frac{{m^{2} \pi ^{2} }}{{a^{2} }} + D_{{66}} \frac{{n^{2} \pi ^{2} }}{{b^{2} }} + K_{s} A_{{66}} ,$$

$$C_{{45}} = \left( {D_{{12}} + D_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,\,\,\,\,N_{4} = \frac{{16}}{9}\left( {B_{{66}} \frac{{n\pi }}{{ab^{2} }} - \left( {B_{{11}} + \frac{{E_{0} A_{x} e_{x} }}{{l_{x} }}} \right)\frac{{m^{2} \pi }}{{na^{3} }} - B_{{12}} \frac{{n\pi }}{{ab^{2} }}} \right),$$

$$C_{{51}} = \left( {B_{{12}} + B_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,\,\,C_{{52}} = \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\frac{{n^{2} \pi ^{2} }}{{b^{2} }} + \,B_{{66}} \frac{{m^{2} \pi ^{2} }}{{a^{2} }} - K_{s} A_{{66}} C_{2} ,$$

$$C_{{53}} = - \left( {\left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)C_{2} + B_{{12}} C_{1} - K_{s} A_{{66}} } \right)\frac{{n\pi }}{b},\,\,\,C_{{54}} = \left( {D_{{12}} + D_{{66}} } \right)\frac{{mn\pi ^{2} }}{{ab}},\,$$

$$C_{{55}} = \left( {D_{{22}} + \frac{{E_{0} I_{{yy}} }}{{l_{y} }} + \frac{{E_{0} A_{y} e_{y}^{2} }}{{l_{y} }}} \right)\frac{{n^{2} \pi ^{2} }}{{b^{2} }} + D_{{66}} \frac{{m^{2} \pi ^{2} }}{{a^{2} }} + K_{s} A_{{66}} ,$$

$$N_{5} = \frac{{16}}{9}\left( {B_{{66}} \frac{{m\pi }}{{a^{2} b}} - \left( {B_{{22}} + \frac{{E_{0} A_{y} e_{y} }}{{l_{y} }}} \right)\frac{{n^{2} \pi a}}{{mb^{3} }} - B_{{12}} \frac{{m\pi }}{{a^{2} b}}} \right).$$