Effect of Thermal Environment and Peripheral Loading on Axisymmetric Vibrations of Non-uniform FG Circular Plates via Generalized Differential Quadrature Method

Abstract

In this article, axisymmetric vibrations of a non-uniform functionally graded circular plate subjected to uniform in-plane peripheral loading and non-linear temperature rise across the thickness have been analyzed on the basis of classical theory of plates. The thickness of the plate is assumed to vary exponentially along the radial direction. The plate material is graded in thickness direction using a power-law model and its mechanical properties are temperature-dependent. Keeping the uniform thermal environment over the top and bottom surfaces, the equations for thermoelastic equilibrium and axisymmetric motion for such a plate model have been derived by Hamilton’s energy principle. Employing generalized differential quadrature method, the frequency equations for clamped and simply supported plates have been obtained and solved numerically using MATLAB. The lowest three roots have been retained as the frequencies for the first three modes of vibration. The influence of various parameters, such as power-law index, in-plane force parameter and temperature difference with varying values of thickness parameter, has been analyzed on the vibration characteristics of the plate. By allowing the frequency to approach zero, the critical buckling loads with varying values of other parameters have been computed. The benchmark results for linear as well as uniform temperature rise have also been computed. The validity of the present technique is verified by comparing the results with the published work.

Introduction

In recent years, the study on fundamental characteristics of functionally graded materials (FGMs) has attracted the attention of engineers and industrialists due to their wide applications in modern science and technology, particularly, in energy conservation devices, spacecraft heat shields, power transmission shafts, nuclear energy rectors, plasma facing for fusion reactors, oil sucker rods used in lifting underground oil, high-power electrical components, sensors, biomaterial electronics, robotics, armor protection for military applications [1, 2], to mention a few. Usually, FGMs are tailored by mixing two or more materials in a systematic manner to achieve the desired mechanical properties in one or more directions. Beyond this, they also provide the attractive features of light weight, high strength, and low thermal conductivity. These advancements in properties of FGMs help the designer in improving the performance of a structure. The classic ceramic/metal FGMs are prepared by mixing ceramics and metals using Powder metallurgy technique. In the literature, either Power-law function/Mori–Tanaka scheme/Sigmoidal function/Exponential function [3,4,5,6] is being used to examine their mechanical properties. Among these homogenization schemes, the Power-law model has been extensively used to analyze the mechanical/thermal behavior of functionally graded (FG) plate type structural elements in a variety of experimental and theoretical problems of practical importance [7,8,9,10]. The appropriate variations in their thickness further enhance significantly greater efficiency for vibration as compared to the uniform thickness. This consideration fulfils the requirement of desired shapes as per physical situations together with additional advantage of material saving, weight reduction, stiffness enhancing, and high strength in various technological situations, particularly, in space and missile technology. In view of this, a significant number of investigations dealing with different types of thickness variations, such as linear [11, 12], bi-linear [13], double linear [14], nonlinear [11, 12, 15], exponential [16], stepped [17], arbitrary [18], polynomial [19], general [20], etc., have been reported in the literature. In many engineering and industrial applications, such as in photographic facilities, driven plate of friction clutch, hydraulic structures, bridges, satellite thermal shields, thermal barrier coatings used in gas turbines blades and rocket nozzles, heat exchanger tubes, etc. [21], these plates may be subjected to a variety of mechanical or / and thermal stresses. A review of recent researchers since 1998–2012, dealing with thermoelastic effect on static, vibration and stability analysis of such plates has been presented by Jha et al. [22]. The later work up to 2016 on developments, applications, various mathematical idealization of materials, temperature profiles, modelling techniques and solution methods for the thermal analysis has been compiled by Swaminathan and Sangeetha [6]. Recently, Nikbakht et al. [7] presented a comprehensive review for the majority of publications on optimal design of FG structures, such as beams, plates, shells, tubes, implants, rotating disks, sports instruments, etc. with key outputs of each article in 2018.

In the literature, the studies on FGM plates have been carried out with the two suppositions: whether the mechanical properties are temperature-independent (TI) or temperature-dependent (TD). Confining the present discussion on static / dynamic behavior of circular / annular FG plates with TI mechanical properties, the recent researches have been reported in references [5, 6, 9,10,11, 17,18,19,20,21,22,23,24], to mention a few. Out of these, Hosseini-Hashemi et al. [17] used separation of variables method and Bessel functions approach for the free vibration analysis of circular and annular FG plates on the basis of first-order shear deformation theory (FSDT). Shariyat and Alipour [23] employed differential transform method (DTM) to study the free vibrational behavior of FG circular plates on the basis of FSDT while Lal and Ahlawat [24] used classical plate theory for the buckling analysis. The spectral Ritz method has been presented by Hyderi et al. [11] for the buckling analysis of elastically supported FG plates subjected to unifrom radial compression. The thermoelastic solution for elastically supported FG circular plates has been obtained by Behravan [15, 16] employing state-space and differential quadrature (DQ) method in transverse and radial directions, respectively. Using FSDT and Laplace transformation together with Galerkin finite element method, the thermoelastic response of FG annular plate has been presented by Jafarinezhad and Eslami [25]. An improved Fourier series method in conjunction with Rayleigh–Ritz approach has been used by Lyu et al. [26] to study the free in-plane vibrations of elastically restrained FG plate. Very recently, the radial vibration analysis of FG discs has been presented by Yildirim and Tutuncu [12] employing fifth-order Runge–Kutta method, and complementary functions method. Finite annular prism method-based Reissner’s mixed variational theorem has been developed by Wu and Yu [27] for the static analysis of two-directional FG circular plates. The axisymmetric vibrations of FG circular plates have been analyzed by Zur employing quasi-Green’s function method [28] and Neumann series method [29] on the basis of classical theory of plates. Using harmonic differential quadrature (HDQ) and discrete singular convolution method, the free vibration analysis of FGM annular sector plates has been presented by Civalek and Baltacioglu [30] using FSDT. For TD mechanical properties, the available articles on FG circular plates are listed in references [25,26,27,28,29,30,31], to mention a few. In these references, the static / dynamic behavior of FG circular / annular plates has been presented using DQ method by Malekzadeh and his co-workers [31, 32], conventional multi-term Ritz-method together with hybrid iterative Newton–Raphson–Newmark scheme by Kiani and Eslami [33], and Fourier expansion through the circumferential direction and generalized differential quadrature (GDQ) method through radial direction by Bagheri et al. [34], on the basis of FSDT. The effect of thermal environment on the free vibration behavior of FG sector plates has been analyzed by Mirtalaie [35] on the basis of classical plate theory. Very recently, Javani et al. [36] analyzed the thermally induced vibrations of annular FG plate using GDQ method on the basis of von Karman assumptions and FSDT, and Saini and Lal [37,38,39,40,41,42,43] presented the vibration analysis of thin and thick circular plates without and with hydrostatic peripheral loading employing quadrature method.

The work reported in this paper comprises the derivation of the frequency equations for clamped and simply supported functionally graded circular plates of variable thickness subjected to uniform in-plane peripheral loading and non-linear temperature rise in the thickness direction using GDQ [44] method. The mechanical properties of the plate materials are taken temperature-dependent and vary as a power-law function across the thickness. In the analysis, Hamilton’s energy principle has been used to obtain the equations for thermoelastic equilibrium and axisymmetric motion for a plate of exponentially varying thickness in the radial direction using classical plate theory. The frequency equations have been solved for their roots using MATLAB and the lowest three are retained as the frequencies for the first three modes of vibration. The parametric varying studies are performed to analyze the effect of taper parameter, power-law index, in-plane force parameter and temperature difference on the non-dimensional frequencies and critical buckling load. A study for the plates with temperature-independent material properties has also been performed. The results have been compared with published literature. Three-dimensional plate configurations have been shown.

Geometrical Description and Formulation

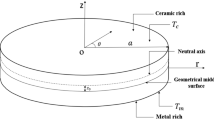
Consider an FG circular plate of radius $a$, variable thickness $h\left( R \right)$, density $\rho$, subjected to uniform tensile in-plane force $N_{0}$ and referred to a cylindrical co-ordinate system $\left( {R, \theta , z} \right)$, $z = 0$ being the middle plane. The line $R = 0$ is the axis of the plate. The top surface $z = + h/2$ is taken as ceramic-rich while the bottom $z = - h/2$ as metal-rich. The plate is subjected to the variable temperature $T\left( z \right)$ distributed across the thickness (Fig. 1).

Fig. 1

3D geometry, top view and cross section of the tapered circular FG plate;

The typical effective material properties $P\left( {z, T} \right)$ of fabricated FG plate are related with the material properties of metal $P_{m} \left( T \right)$ and ceramic $P_{c} \left( T \right)$ according to a Power-law model [31], i.e.,

$$P\left( {z,T} \right) = P_{m} \left( T \right) + \left[ {P_{c} \left( T \right) - P_{m} \left( T \right)} \right] V_{c} \left( z \right),$$

(1)

where, $V_{c} \left( z \right)$ describes the volume fraction of ceramic at any point $z$ and defined as,

$$V_{c} \left( z \right) = \left( {\frac{2z + h}{{2h}}} \right)^{g} ,$$

the power-law index $g\left( { \ge 0} \right)$ represents the shape of the volume fraction $V_{c} \left( z \right)$. For better understanding of the distribution, the graphs for plate thickness versus volume fraction of ceramic for different values of power-law index $g$ are shown in Fig. 2. The portion below to each line represents the amount of ceramic in FG plate while above portion for the metal component. Figure 2a, b and c represent the distribution at the center of the plate, thicker towards the boundary $\left( {\gamma = 0.5} \right)$ and thinner towards the boundary $\left( {\gamma = - 0.5} \right)$ of the plate, respectively.

Fig. 2

Variation of the volume fraction of ceramic through the thickness for various values of g and (a) at the center of the plate $\left( {r = 0} \right)$; b the boundary of the plate $\left( {r = 1} \right)$, for ${\upgamma } =$ 0.5; c the boundary of the plate $\left( {r = 1} \right)$, for ${\upgamma } =$ − 0.5

The material properties $P_{m}$ and $P_{c}$ for the constituents of the FG plate are assumed to be temperature-dependent [31] as follows:

$$P_{b} \left( T \right) = P_{0} (P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} ) , b = m, c$$

(2)

where subscripts $m$ and $c$ refer to metal and ceramic, respectively, and $T\left( { = T\left( z \right)} \right)$ be the temperature at any point of the plate. The constituent materials of the plate are taken as Titanium alloy $\left( {TC4:rTi - 6Al - 4V} \right)$ for metal and Zirconia $\left( {ZrO_{2} } \right)$ for ceramic. The experimental values of the coefficients $P_{i} \left( {i = - 1, 0 , 1 , 2 , 3} \right)$ are taken from the reference [31]. The symbol ‘$P$’ has been used for the material properties, such as Young’s modulus $E$, Poisson’s ratio $\nu$, mass density $\rho$, thermal expansion coefficient $\alpha$ and thermal conductivity$k$.

Thermal Stress Analysis

Following [3], most of the two-dimensional thermoelastic studies have been carried out using one-dimensional heat conduction equation [9, 25,26,27,28,29,30,31], to mention a few. This is due to the assumption of material homogeneity in the plane of the plate and varies only in the thickness direction. Accordingly, the effect of non-linear variation of temperature which arises from the solution of static one-dimensional heat equation with zero heat flux [40],

$$\frac{d}{dz}\left( {k\left( z \right)\frac{dT}{{dz}}} \right) = 0,$$

(3)

subject to the boundary conditions: $T = T_{m}$ at $z = - h/2$ and $T = T_{c}$ at $z = + h/2$.

Following [40], the solution of Eq. (3) is:

$$T\left( z \right) = T_{m} + \frac{\Delta T}{{C^{*} }}\mathop \sum \limits_{i = 0}^{N} \left( { - 1} \right)^{i} \frac{{k_{cm}^{i} }}{{\left( {ig + 1} \right)k_{m}^{i} }}\left( {\frac{2z + h}{{2h}}} \right)^{ig + 1} ,$$

(4)

where $k_{cm} = k_{c} - k_{m} , \Delta T = T_{c} - T_{m} , C^{*} = \mathop \sum \limits_{i = 0}^{N} \left( { - 1} \right)^{i} \frac{{k_{cm}^{i} }}{{\left( {ig + 1} \right)k_{m}^{i} }},$ and N represents the number of terms in the binomial expansion occurring in the integral during the integration of Eq. (3) for $T(z)$.

The thermal strains and stresses at an arbitrary point $\left(R, \theta , z\right)$ on the mid-plane of the plate are as follows [40]:

$$\begin{gathered} e_{TRR} = - z\frac{{d^{2} w_{T} }}{{dR^{2} }} , e_{T\theta \theta } = - \frac{z}{R}\frac{{dw_{T} }}{dR}, e_{TR\theta } = e_{Tzz} = e_{T\theta z} = e_{TRz} = 0, \hfill \\ \left. \begin{gathered} \sigma_{TRR} = - \overline{E}\left( {z,T} \right)\left\{ {z\left( {\frac{{d^{2} w_{T} }}{{dR^{2} }} + \frac{\nu }{R}\frac{{dw_{T} }}{dR}} \right) + T_{E} } \right\}, \hfill \\ \sigma_{T\theta \theta } = - \overline{E}\left( {z,T} \right)\left\{ {z\left( {\nu \frac{{d^{2} w_{T} }}{{dR^{2} }} + \frac{1}{R}\frac{{dw_{T} }}{dR}} \right) + T_{E} } \right\}, \hfill \\ \sigma_{TR\theta } = \sigma_{Tzz} = \sigma_{T\theta z} = \sigma_{TRz} = 0 , \hfill \\ \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered}$$

(5)

where $\overline{E}\left( {z,T} \right) = \frac{{E\left( {z,T} \right)}}{{\left( {1 - \nu^{2} } \right)}}$, $T_{E} = \alpha \left( {z,T} \right) \Delta T\left( z \right) \left( {1 + \nu } \right)$, $\Delta T\left( z \right) = T\left( z \right) - T_{0}$, $T_{0}$ being the reference temperature at which the plate is stress-free and $w_{T} \left( R \right)$ is the transverse displacement arisen due to the axisymmetric temperature distribution over the surfaces of the plate.

Following [40], the thermoelastic equilibrium equation is obtained by Hamilton’s energy principle and given by

$$\begin{gathered} D_{1} \frac{{d^{4} w_{T} }}{{dR^{4} }} + \frac{2}{R}\left( {D_{1} + R\frac{{dD_{1} }}{dR}} \right)\frac{{d^{3} w_{T} }}{{dR^{3} }} - \frac{1}{{R^{2} }}\left\{ {D_{1} - 2R\left( {\frac{{dD_{1} }}{dR} + \frac{{dD_{2} }}{dR}} \right) - R^{2} \frac{{d^{2} D_{1} }}{{dR^{2} }} + R^{2} N_{0} } \right\}\frac{{d^{2} w_{T} }}{{dR^{2} }} + \hfill \\ \frac{1}{{R^{3} }}\left( {D_{1} - R\frac{{dD_{1} }}{dR} + R^{2} \frac{{d^{2} D_{2} }}{{dR^{2} }} - R^{2} N_{0} } \right)\frac{{dw_{T} }}{dR} + \frac{1}{R}\left( {\frac{{dm_{T} }}{dR} + R\frac{{d^{2} m_{T} }}{{dR^{2} }}} \right) = 0 , \hfill \\ \end{gathered}$$

(6)

together with the boundary conditions:

• (i) ${\text{Clamped }}\left( C \right){\text{ plate}}: \left\{ {w_{T} } \right\}_{R = a } = 0 , \left\{ {\frac{{dw_{T} }}{dR}} \right\}_{R = a} = 0 ,$

• (ii) ${\text{Simply Supported }}\left( S \right){\text{ plate}}: \{ w_{T} \}_{R = a} = 0 , \left\{ {D_{1} \frac{{d^{2} w_{T} }}{{dR^{2} }} + m_{T} + \frac{{D_{2} }}{R}\frac{{dw_{T} }}{dR}} \right\}_{R = a} = 0,$

where, $\left[ {D_{1} , D_{2} } \right] = \mathop \smallint \limits_{ - h/2}^{h/2} z^{2} \overline{E}\left( {z,T} \right)\left[ { 1 , \nu } \right]dz$ are the flexural rigidities of the plate and $m_{T} = \mathop \smallint \limits_{ - h/2}^{h/2} \left\{ {z T_{E} \overline{E}\left( {z,T} \right)} \right\}dz.$

Introducing the non-dimensional variables $W_{T} = w_{T} /a, Z = z/a$, $r = R/a$ and $\overline{h} = h/a$, together with the exponential thickness variation $\overline{h} = h_{0} exp\left( {\gamma r} \right)$, where $\gamma$ is the taper constant and $h_{0} = \left\{ h \right\}_{r = 0}$ is the non-dimensional thickness, Eq. (6) and the boundary conditions reduce to

$$\mathop \sum \limits_{i = 1}^{4} Q_{i} \frac{{d^{i} W_{T} }}{{dr^{i} }} = - \frac{1}{r}\left( {\frac{{dm_{T}^{*} }}{dr} + r\frac{{d^{2} m_{T}^{*} }}{{dr^{2} }}} \right),$$

(7)

$$\left\{ {W_{T} } \right\}_{r = 1} = \left\{ {\frac{{dW_{T} }}{dr}} \right\}_{r = 1} = 0 , \left\{ {W_{T} } \right\}_{r = 1} = \frac{1}{r} \left\{ {r\left( {Q_{4} \frac{{d^{2} W_{T} }}{{dr^{2} }} + m_{T}^{*} } \right) + D_{2}^{*} \frac{{dW_{T} }}{dr}} \right\}_{r = 1} = 0,$$

(8a, b)

where $Q_{1} = \frac{1}{{r^{3} }}\left( {Q_{4} - r\frac{{dQ_{4} }}{dr} + r^{2} \frac{{d^{2} D_{2}^{*} }}{{dr^{2} }} - r^{2} N^{*} } \right) , Q_{2} = - \frac{1}{{r^{2} }}\left\{ {Q_{4} - r\left( {2\frac{{dQ_{4} }}{dr} + \frac{{dD_{2}^{*} }}{dr}} \right) - r^{2} \frac{{d^{2} Q_{4} }}{{dr^{2} }} + r^{2} N^{*} } \right\} ,$$Q_{3} = \frac{2}{r}\left( {Q_{4} + r\frac{{dQ_{4} }}{dr}} \right) , Q_{4} = D_{1}^{*} , D_{1} = D^{*} D_{1}^{*} , D_{2} = D^{*} D_{2}^{*} , m_{T}^{*} = \frac{{am_{T} }}{{D^{*} }} , N^{*} = \frac{{a^{2} N_{0} }}{{D^{*} }}, D^{*} = \frac{{E_{0} h_{0}^{3} }}{{12\left( {1 - \nu^{2} } \right)}}$

$$\left[ {D_{1} , D_{2} } \right] = \mathop \smallint \limits_{{ - ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}}^{{ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}} z^{2} \overline{E}\left( {z,T} \right)\left[ { 1 , \nu } \right]dz, m_{T} = \mathop \smallint \limits_{{ - ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}}^{{ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}} \left\{ {z T_{E} \overline{E}\left( {z,T} \right)} \right\}dz ,$$

and $E_{0} = E_{c}$ at $T = 0$ from Eq. (2).

Vibration Analysis

Following [40], the non-dimensional form of the equation of motion and the boundary conditions for the plate with exponentially varying thickness are as follows:

$$\mathop \sum \limits_{i = 0}^{4} S_{i} \frac{{d^{i} W}}{{dr^{i} }} = 0,$$

(9)

$$\left\{ W \right\}_{r = 1} = \left\{ {\frac{dW}{{dr}}} \right\}_{r = 1} = 0 , \left\{ W \right\}_{r = 1} = \left\{ {D_{1}^{*} \frac{{d^{2} W}}{{dr^{2} }} + \frac{{D_{2}^{*} }}{r} \frac{dW}{{dr}}} \right\}_{r = 1} = 0 ,$$

(10a, b)

where $S_{0} = - S{\Omega }^{2} , S_{1} = \frac{1}{{r^{3} D^{*} }}\left\{ {S_{T\theta \theta } - r\frac{{dS_{T\theta \theta } }}{dr} - \left( {a .r} \right)^{2} N_{T\theta \theta } + D^{*} \left( {Q_{4} - r\frac{{dQ_{4} }}{dr} + r^{2} \frac{{d^{2} D_{2}^{*} }}{{dr^{2} }}} \right) - r^{2} N^{*} } \right\},$

$$S_{2} = \frac{ - 1}{{r^{2} D^{*} }}\left[ {S_{T\theta \theta } - r\frac{{dS_{T\theta \theta } }}{dr} + \left( {a .r} \right)^{2} N_{TRR} + D^{*} \left\{ {Q_{4} - r\left( {2\frac{{dQ_{4} }}{dr} + \frac{{dD_{2}^{*} }}{dr}} \right) - r^{2} \frac{{d^{2} Q_{4} }}{{dr^{2} }}} \right\} + r^{2} N^{*} } \right],$$

$$S_{3} = \frac{2}{r}\left( {Q_{4} + \frac{{S_{T\theta \theta } }}{{D^{*} }} + r\frac{{dQ_{4} }}{dr}} \right), S_{4} = Q_{4} + \frac{{S_{TRR} }}{{D^{*} }}, S = \frac{{A_{1} }}{{h_{0} \rho_{0} }}, A_{1} = \mathop \smallint \limits_{{ - ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}}^{{ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}} \rho \left( {z,T} \right)dz, {\Omega }^{2} = \frac{{\rho_{0} a^{4} h_{0} }}{{D^{*} }}\omega^{2} ,$$

$$\left[ {S_{{TRR}} ,\,~S_{{T\theta \theta }} } \right]{\text{~ = }}\mathop \smallint \limits_{{ - ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}}^{{ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}} z^{2} [\sigma _{{TRR}} ~,~~\sigma _{{T\theta \theta }} ]dz,~~[N_{{TRR}} ~,~~N_{{T\theta \theta }} = \mathop \smallint \limits_{{ - ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}}^{{ah_{0} {\text{exp}}\left( {\gamma r} \right)/2}} \left[ {\sigma _{{TRR}} ,~\sigma _{{T\theta \theta }} } \right]dz,$$

$w/a = W\left( r \right) exp\left( {i\omega t} \right)$ for harmonic solution, $W\left( r \right)$ is the non-dimensional transverse deflection, $\omega$ is the radian frequency and $\rho_{0} = \rho_{c}$ at $T = 0$ from Eq. (2). Being the variable coefficients in governing differential Eqs. (7) and (9), their closed-form solutions are not possible, except for certain values of various parameters. Hence, the approximate solution has been obtained using GDQ method.

Solution Procedure

Thermal Stress Analysis

Using GDQ method, discretizing Eq. (7) rat ith internal nodal point $r_{i} , i = 2, 3, \ldots$, $\left( {n - 2} \right)$, rafter substituting the values for derivatives of $W_{T}$, by putting $W_{T}$ for $W$, one gets

$$\left[ {\mathop \sum \limits_{j = 1}^{n} \left\{ {\left( {Q_{4} } \right)_{{r_{i} }} E_{ij}^{4} + \left( {Q_{3} } \right)_{{r_{i} }} E_{ij}^{3} + \left( {Q_{2} } \right)_{{r_{i} }} E_{ij}^{2} + \left( {Q_{1} } \right)_{{r_{i} }} E_{ij}^{1} } \right\} W_{j}^{T} } \right] = - \left\{ {\frac{1}{r}\left( {\frac{{dm_{T}^{*} }}{dr} + r\frac{{d^{2} m_{T}^{*} }}{{dr^{2} }}} \right)} \right\}_{{r_{i} }}$$

(11)

where the superscript $T$ rover $W_{j}$ i.e. $W_{j}^{T}$ represents the independent variables $W_{1} ,W_{2} , \ldots , W_{n - 1} ,W_{n}$ for thermal displacements as $W_{1}^{T} ,W_{2}^{T} , \ldots , W_{n - 1}^{T} ,W_{n}^{T}$.

The satisfaction of Eq. (11) at internal nodal points together with regularity condition $\left\{ {dW_{T} /dr} \right\}_{r = 0} = 0$ and two boundary conditions (8a, b) provides a set of $n$ equations in $n$ unknowns $W_{j}^{T} , j = 1, 2, 3, \ldots ,n$. For a $C$-plate (8a), the matrix form of the resulting non-homogeneous equations is given by:

$$\left[ {\begin{array}{*{20}c} A \\ {A^{C} } \\ \end{array} } \right] \left[ X \right] = \left[ {\begin{array}{*{20}c} F \\ {F^{C} } \\ \end{array} } \right],$$

(12a)

where $A, A^{c}$ are matrices of order $\left( {n - 3} \right) \times n$, $3 \times n$, and $F, F^{C}$ are column vectors of order $\left( {n - 3} \right) \times 1, 3 \times 1$, respectively, while $X = \left\{ {W_{1}^{T} , W_{2}^{T} , \ldots ,W_{n}^{T} } \right\}^{^{\prime}}$.

Similarly, for $S$-plate (8b), the matrix form of the system of equations can be written as

$$\left[ {\begin{array}{*{20}c} A \\ {A^{S} } \\ \end{array} } \right] \left[ X \right] = \left[ {\begin{array}{*{20}c} F \\ {F^{S} } \\ \end{array} } \right].$$

(12b)

Equations (12a, b) have been solved for $W_{1}^{T} ,W_{2}^{T} , \ldots , W_{n - 1}^{T} ,W_{n}^{T}$ using the computer software MATLAB.

The thermal stresses raised in the plate due to temperature field have been obtained as follows:

Step 1: Equation (5) has been discretized using equation GDQ method,

$$\left. \begin{gathered} \sigma_{TRR} = - \overline{E}\left( {z,T} \right)\left[ {z\left( {\mathop \sum \limits_{j = 1}^{n} \left( {E_{ij}^{\left( 2 \right)} + \frac{\nu }{{r_{i} }}E_{ij}^{\left( 1 \right)} } \right)W_{j}^{T} } \right) + T_{E} } \right] , \hfill \\ \sigma_{T\theta \theta } = - \overline{E}\left( {z,T} \right)\left[ {z\left( {\mathop \sum \limits_{j = 1}^{n} \left( {\nu E_{ij}^{\left( 2 \right)} + \frac{1}{{r_{i} }}E_{ij}^{\left( 1 \right)} } \right)W_{j}^{T} } \right) + T_{E} } \right], \hfill \\ \sigma_{TRz} = \sigma_{TR\theta } = \sigma_{T\theta z} = \sigma_{TRz} = 0 , \hfill \\ \end{gathered} \right\}$$

(13)

Step 2. Substitution of the numerical values for $W_{1}^{T} ,W_{2}^{T} , \ldots , W_{n - 1}^{T} ,W_{n}^{T}$ (obtained from solving Eqs. (12a, b) in Eq. (13) provide the thermal stresses for $C$ and $S$-plates, respectively.

Vibration Analysis

For the vibration analysis, Eq. (9) has been discretized using GDQ method for various order derivatives of $W$ at ith internal nodal point $r_{i}$, it leads to

$$\left[ {\mathop \sum \limits_{j = 1}^{n} \left\{ {\left( {S_{4} } \right)_{{r_{i} }} E_{ij}^{4} + \left( {S_{3} } \right)_{{r_{i} }} E_{ij}^{3} + \left( {S_{2} } \right)_{{r_{i} }} E_{ij}^{2} + \left( {S_{1} } \right)_{{r_{i} }} E_{ij}^{1} } \right\}W_{j} } \right] + \left( {S_{0} } \right)_{{r_{i} }} W_{i} = 0.$$

(14)

Now, the satisfaction of Eq. (14) at internal nodal points together with regularity condition and two boundary conditions (10a, b), gives a complete set of $n$ equations in $n$ unknowns. For a $C$-plate (10a), the matrix form of these $n$ homogeneous equations is given by

$$\left[ {\begin{array}{*{20}c} B \\ {B^{C} } \\ \end{array} } \right]\left[ Y \right] = \left[ 0 \right],$$

(15)

where $B$, $B^{C}$ are the matrices of order $\left( {n - 3} \right) \times n$, $3 \times n$, respectively, and $Y = \left\{ {W_{1} , W_{2} , \ldots ,W_{n} } \right\}^{^{\prime}}$.

The non-trivial solution of Eq. (15) exists if the determinant vanishes and hence

$$\left| {\begin{array}{*{20}c} B \\ {B^{C} } \\ \end{array} } \right| = 0.$$

(16a)

Similarly, for a $S$-plate (10b), the determinant can be written as

$$\left| {\begin{array}{*{20}c} B \\ {B^{S} } \\ \end{array} } \right| = 0.$$

(16b)

Numerical Results

The frequency Eqs. (16 a, b) have been solved using MATLAB and the lowest three roots of these equations have been retained as the frequency parameter Ω for the first three modes of vibration. The values for critical buckling load $N_{cr}^{*}$ have been obtained by Bisection method. The influence of thickness variation, in-plane force and thermal environment together with power-law index has been analyzed on Ω for $C$ and $S$-plates. The values of various parameters are taken as:

${\text{taper parameter}}\,\gamma = - 0.5,~ - 0.3,~ - 0.1,~0,~0.1,~0.3,~0.5,\,{\text{power}} - {\text{law index}}\,g = 0,1,~2,~3,~4,~5,$

in-plane force parameter $N^{*} = - 10, 0,10,20,30,$

temperature $T_{0} = 300 {\text{kelvin}}\left( K \right), T_{m} = 300\,{\text{K}}, 300\,{\text{K}} \le T_{c} \le 700\,{\text{K}}$.

The value of Poisson’s ratio is assumed to remain almost same all over the plate and taken as 0.3 while $h_{0}$ as 0.1.

Convergence and Comparison Study

To choose an appropriate value of the grid points, a computer program developed to evaluate the frequency parameter Ω was run for varying values of $g$, $\gamma$ and $T_{c}$ keeping $T_{m} = 300 K$ taking $n = 8, 9, 10, \ldots , 20$, nd observe that $\left| {{\Omega }_{n + 1}^{i} - {\Omega }_{n}^{i} } \right| \le 0.00005$, for all the three modes $i = 1, 2, 3$. In the present study, the number of grid points $n$ has been fixed as 18. Figure 3 shows the percentage error $\left| {1 - {\Omega }_{n} /{\Omega }_{18} } \right| \times 100$ with varying values of $n$, for the first three modes of a specific plate $g = 5$, $\gamma = - 0.5$, $T_{0} = T_{m} = 300K$, and $T_{c} = 700K$, as maximum deviations were obtained for this data. The rate of convergence with number of nodal points $n$ was comparatively slow for $S$-plate as compared to the $C$-plate. For the accuracy of four decimals, the number of terms $N$ in the Eq. (4) has been taken as 20.

Fig. 3

Percentage error vs number of nodal points n

A comparison of non-dimensional frequencies for FG plates of uniform thickness $\left( {\gamma = 0} \right)$ has been presented in Tables 1 and 2. Table 1 presents the values in absence of thermal environment i.e., $\alpha = 0$, $T = 0$, with those obtained by DTM [24], Quasi-Green’s function approach [28], Neumann series method [29], and Rayleigh–Ritz method [45] while Table 2 in presence of thermal environment with only available by GDQ rule [40]. By allowing the frequency to approach zero, the value of critical buckling load $N_{cr}^{*}$ has been compared with DTM [24] and GDQ rule [40] in Table 3 for both the cases. A close agreement of results shows the versatility of the present technique.

Table 1 Comparison of frequency parameter Ω in the absence of thermal environment

Table 2 Comparison of frequency parameter Ω in the presence of thermal environment, $\Delta {\text{T}} = 400\,{\text{K}}$

Table 3 Comparison of critical buckling load ${N}_{cr}^{*}$ in the absence / presence of thermal environment

Parametric Discussion

For the parametric study of various parameters, a huge amount of results was obtained. For selected data, these are presented in Figs. 4, 5, 6, 7, 8, 9, 10 and Table 4. The results show that the values of frequency parameter Ω for $C$-plate are higher than those for the corresponding $S$-plate. Further, the value of Ω is found to decrease with the increase in the value of temperature difference $\Delta T$.

Fig. 4

Frequency parameter Ω vs power-law index g, for $N^{*} = 0$, $\Delta T = 0$, 400 ${\text{K}}$, ${\upgamma } =$ − 0.5, 0, 0.5;

Fig. 5

Ω vs taper parameter ${\upgamma }$ for $N^{*} =$ 0, 10, ${\text{g}} =$ 0, 1, 5, $\Delta T =$ 400 ${\text{K}}$

Fig. 6

Ω vs in-plane force $N^{*}$, ${\upgamma } =$ -0.5, 0, 0.5, ${\text{g}} =$ 0, 5, ${\Delta T} =$ 400 ${\text{K}}$

Fig. 7

a ${\text{N}}_{{{\text{cr}}}}^{*}$ for C-plate,$\gamma =$ − 0.5, 0, 0.5, g = 0, 5, $\Delta T =$ 400 ${\text{K}}$. b ${\text{N}}_{{{\text{cr}}}}^{*}$ for S-plate, ${\upgamma } =$ − 0.5, 0, 0.5, ${\text{g}} =$ 0, 5, $\Delta T =$ 400

Fig. 8

Ω vs temperature difference ${\Delta T}$ for UTR, LTR and NTR, ${\upgamma } =$ − 0.5, 0, 0.5, $N^{*} =$ 10, ${\text{g}} =$ 5

Fig. 9

Ω vs. ΔT for TI and TD material properties; ${\upgamma } =$ − 0.5, 0, 0.5, $N^{*} =$ 10, ${\text{g}} =$ 5

Fig. 10

Three-dimensional mode shapes for ${\upgamma } =$ − 0.5, ${\text{g}} =$ 5, $N^{*} =$ 10, $\Delta T =$ 400 K

Table 4 Values of ${N}_{cr}^{*}$ with varying values of $g$ for both the plates and $\gamma =$ − 0.5, 0.5, $\Delta T=$ 0, 400 K

In Fig. 4, the behavior of Ω with varying values of power-law index $g$ for $\gamma = - 0.5, 0, 0.5$, $\Delta T = 0, \,400\,{\text{K}}$, and $N^{*} = 0$, has been presented. The value of Ω decreases with the increasing values of g  for both the plates in all the three modes except for $S$-plate vibrating in the first mode when the thickness of the plate is either uniform or decreases towards the boundary of the plate and $\Delta T = 400\,{\text{K}}$. In this case, there is a point of maxima in the vicinity of $g = 0.2$ and shifts towards to $g = 0.4$ as $\gamma$ changes from 0 to 0.5. The rate of change for $g \le 1$ is much higher as compared to $g > 1$ whatever be the values of ther parameters.

Figure 5 describes the effect of taper parameter $\gamma$ on Ω for $g = 0, 1, 5$, $N^{*} = 0, 10$, $\Delta T = 400\,{\text{K}}$ and all the three modes. The value of Ω is found to increase with the increasing values of $\gamma$ for both the plates except for $S$-plate vibrating in the first mode when $N^{*} = 10$. In this case, there exist a point of minima in the neighborhood of $\gamma = 0.1$ for $g = 0, 1, 5$. It is also found that when $\gamma \le - 0.2$ for $S$-plate the value of Ω is higher for $g = 1$ as compared to $g = 0$. The rate of change in the value of Ω is higher for $C$-plate as compared to $S$-plate and increases with the increase in the number of modes.

The graphs of Ω versus in-plane force parameter $N^{*}$ for different values of $\gamma = - 0.5, 0, 0.5$, and $\Delta T = 400\, {\text{K}}$ for fully ceramic $\left( {g = 0} \right)$ and FG $\left( {g = 5} \right)$ plates are shown in Fig. 6. It is found that the value of Ω increases with the increase in the values of $N^{*}$, keeping other parameters fixed. The rate of increase for fully ceramic plate is higher than that for FG ones. From the graphs, it is evident that the effect of $N^{*}$ decreases as the thickness of the plate increases towards the boundary of the plate. This effect increases with the increase in the number of modes.

Figure 7a, b depicts the behavior of critical buckling load $N_{cr}^{*}$ for $C$, $S$-plate, respectively, for $g = 0, 1, 5$, $\gamma = - 0.5, 0, 0.5$, and $\Delta T = 400K$ when the plate is vibrating in first mode. For a $C$-plate, the values of $N_{cr}^{*}$ for $g = 1$ are less than those for $g = 0$ but greater than those for $g = 5$, i.e., while this order becomes $N_{cr}^{*} \left( {g = 1} \right) > N_{cr}^{*} \left( {g = 0} \right) > N_{cr}^{*} \left( {g = 5} \right)$, for $S$-plate, keeping other parameters fixed.

A study for uniform temperature rise (UTR): $T\left( z \right) = T_{m} + \Delta T$, linear temperature rise (LTR): $T\left( z \right) = T_{m} + \left( {\Delta T\left( {2z + h} \right)/2hC^{*} } \right)$ and non-linear temperature rise (NTR) in equation $N_{cr}^{*} \left( {g = 0} \right) > N_{cr}^{*} \left( {g = 1} \right) > N_{cr}^{*} \left( {g = 5} \right)$(5) has been made and the corresponding numerical results with varying values of $\Delta T$ have been plotted in Fig. 8, for $\gamma = - 0.5, 0, 0.5$, $g = 5$, and $N^{*} = 10$. It has been noticed that Ω decreases with the increase in the values of $\Delta T$ for all the three types of temperature distributions. The rate of decay for UTR is much higher as compared to LTR as well as NTR for the same set of the values of other parameters. With respect to taper parameter $\gamma$, this rate of decay decreases as the plate becomes thicker and thicker towards the center of the plate and more pronounced in case of $C$-plate as compared to $S$-plate, keeping other parameters fixed.

Further, the effect of $\Delta T$ on Ω for TI and TD plate materials for $\gamma = - 0.5, 0, 0.5$, $N^{*} = 10$, $g = 5$, and NTR has been shown in Fig. 9. It can be seen that the values of Ω for TD materials are less than those for corresponding TI materials. This effect is more pronounced for $C$-plate as compared to $S$-plate and increases with the increase in the number of modes. It has been noticed that the rate of decay in the value of Ω increases as the plate becomes thicker and thicker towards the boundary of the plate for TI materials while decreases for TD materials for the fixed values of other parameters. This rate of decay increases with the increase in the number of modes.

Three-dimensional mode shapes for FG $\left( {g = 5,\gamma = - 0.5, \Delta T = 400\,{\text{K}}, N^{*} = 10} \right)$ circular plates have been shown in Fig. 10.

Conclusion

The conclusions are as follows:

• The frequency of the plate increases as the contribution of metallic constituent in the plate increases. When $g$ changes from 0 to 5 for $N^{*} = 0$, and $\Delta T = 400\,{\text{K}}$, the percentage variations in Ω for a $C$-plate vibrating in the first mode are -12.24, -11.22 and − 10.83, for $\gamma = - 0.5, 0$, and 0.5, respectively. The corresponding values for $S$-plate are − 37.09, − 14.50 and -12.07. This effect decreases with the increase in the number of modes.

• The value of Ω increases with the increase in the values of $\gamma$ except for the first mode of $S$-plate when $N^{*} = 10$, there is a point of minima in the vicinity of $\gamma = 0.1$ for $g = 0, 1, 5$. Further, for the $S$-plate, values of Ω are found in the order of ${\Omega }_{g = 1} > {\Omega }_{g = 0} > {\Omega }_{g = 5}$, for $\gamma \le - 0.2$, $N^{*} = 0$, which becomes ${\Omega }_{g = 0} > {\Omega }_{g = 1} > {\Omega }_{g = 5}$, for $\gamma > - 0.2$. The corresponding percentage increase in the values of Ω for the first mode is reported in Table 5.

• The values of frequency parameter Ω for a $C$-plate are found in the order of ${\Omega }_{g = 0} > {\Omega }_{g = 1} > {\Omega }_{g = 5}$ with varying values of $N^{*}$ for $\gamma = - 0.5, 0, 0.5$, and $\Delta T = 400\,{\text{K}}$. For $S$-plate, this order becomes ${\Omega }_{g = 1} > {\Omega }_{g = 0} > {\Omega }_{g = 5}$, when $N^{*} < \left( {1.0, - 0.5, - 4.6} \right)$, for $\gamma = \left( { - \,0.5, 0, 0.5} \right)$, respectively, and ${\Omega }_{g = 0} > {\Omega }_{g = 1} > {\Omega }_{g = 5}$ for the other values of $N^{*}$.

• With the increase in the values of $\Delta T$, value of Ω decreases. The order of values for Ω with UTR, LTR and NTR is ${\Omega }_{NTR} \ge {\Omega }_{LTR} \ge {\Omega }_{UTR}$, keeping other parameters fixed. The percentage decrease in Ω for $g = 5$, $\gamma = - 0.5, 0, 0.5$ with varying value of $\Delta T$ from 0 to $400K$ are given in Table 6 and found in the order UTR > LTR > NTR.

• During a comparison made with TI materials (Table 7), it has been noticed that the percentage decrease in Ω for $\gamma = - 0.5, 0, 0.5$, $g = 5$, is higher for TD as compared to TI when $\Delta T$ varies from 0 to $400K$. This may be attributed to the dependency of material properties under thermal environment which contributes in the thermally induced stresses, moments and gives more accurate results as compared to TI materials.

• The percentage variations studied under points 5 and 6, decrease with the increase in the number of modes.

Table 5 Percentage decrease in the values of Ω

Table 6 Percentage decrease in the values of Ω

Table 7 Percentage decrease in the values of Ω

A design engineer dealing with circular FG plates can use these results in obtaining the desired frequency by controlling one or more parameters involved in the present study.