Nonlinear Damped Transient Vibrations of Carbon Nanotube-Reinforced Magneto-Electro-Elastic Shells with Different Electromagnetic Circuits

Abstract

Purpose

In this research work, the nonlinear damped transient response of functionally graded carbon nanotube (CNT)-reinforced magneto-electro-elastic (FG-CNTMEE) shells are investigated using finite element methods.

Method

The controlled response is obtained through active constrained layer damping (ACLD) treatment composed of a 1–3 piezoelectric (PZC) patch and the viscoelastic layer. The FG-CNTMEE shell subjected to different forms of load cases including mechanical and electro-magnetic loads are considered for evaluation. In addition, the influence of open circuit and closed circuit electro-magnetic boundary conditions on the damped transient response of the FG-CNTMEE shell is investigated for the first time in the literature. The equations of motion are derived using the principle of virtual work. The solutions are obtained through the condensation approach and the direct-iterative method.

Results

Several numerical examples are presented to assess the influence of parameters such as shell geometries, CNT distribution pattern, CNT volume fraction, and boundary conditions. Special attention has been paid to understand the effect of coupling fields on the damped response of the FG-CNTMEE shell.

Introduction

The discovery of CNTs by Iijima in the year 1991 revolutionised the approach of designing engineering structures [1]. The superior material properties along with the multifunctionality exhibited by CNTs made them the potential candidates for aerospace, automotive, energy harvesters, marine, medical, power plant applications. At the early stages, due to a lack of knowledge on fabricating CNT-based composites, the accurate distribution of CNTs reinforcements could not be achieved. Hence, the required superior properties were not met. However, with the tremendous improvement in manufacturing technologies, it is now possible to achieve any desired pattern of CNT distribution. One such category of CNTs based composites is functionally graded CNT-reinforced composites (FG-CNTRC). It ensures smooth and continuous material properties across the thickness of the structures which in turn reduces the problem of delamination, which is commonly noticed in layered structures. Among the many prominent works on structural analysis of FG-CNTRC, few are discussed here. Van Do et al. [2] evaluated the static behaviour of FG-CNTRC plates in the framework of higher-order shear deformation theory (HSDT) and isogeometric finite element (FE) analysis. Ritz element free method was adopted by Xiang et al. [3] to probe the free vibration characteristics of FG-CNTRC conical shell panels. Qin et al. [4] proposed a Fourier series solution to investigate the natural frequencies of FG-CNTRC structures subjected to arbitrary conditions. Yang et al. [5] examined the effect of temperature on the nonlinear vibrations of FG-CNTRC auxetic plates and extended their study for the nonlinear flexural response of auxetic beams [6]. Similarly, Foroutan et al. [7] investigated the effect of temperature associated with the external pressure on the nonlinear frequencies of FG-CNTRC panels. Mellouli et al. [8] adopted mesh-free radial interpolation method and improved first-order shear deformation theory (FSDT) to assess the free vibration response of FG-CNTRC shells. Making use of FSDT, Fu et al. [9] studied the effect of elastic foundations on the dynamic instability behaviour of FG-CNTRC shells. Ansari et al. [10] proposed a novel solution technique through FE methods and variational differential quadrature method to understand the effect of temperature on the post-buckling characteristics of arbitrary shaped FG-CNTRC plates. To this end, they made use of HSDT in their analysis. Jiao et al. [11] implemented a differential quadrature method (DQM) to study the influence of edge compression loads on the stability response of FG-CNTRC plates. Analogously, Nguyen et al. [12] exploited the benefits of the isogeometric analysis approach to understand the post-buckling behaviour of imperfect FG-CNTRC shells. Through an analytical approach within the framework of FSDT, Sofiyev et al. [13] examined the stability response of FG-CNTRC conical shells subjected to external pressure.

Meanwhile, the transient and damped vibration study of FG-CNTRC structures becomes prominent as it depends on the time factor as well. Yadav et al. [14] developed semi-analytical solutions to investigate the large damped vibrations of FG-CNTRC cylindrical shells. Through the FE method, Patnaik and Roy [15] assessed the influence of the hygrothermal environment on the damped response of FG-CNTRC shells with geometrical skewness. Lee and Hwang [16] developed a FE formulation and studied the effect of cut-outs on the nonlinear transient behaviour of FG-CNTRC shells. Considering internal and external damping, the transient response of CNTs was examined by Malikan et al. [17]. They applied refined Timoshenko beam theory in their study. Based on the isogeometric analysis, Phung-van [18] probed the effect of thermal fields on the nonlinear transient response of FG-CNTRC nanoplates. Thanh et al. [19] researched the nonlinear damped response of FG-CNTRC microplates. Thomas and Roy [20] worked on addressing the damped problem of FG-CNTRC shells using FE methods.

The triple energy interaction displayed by the magneto-electro-elastic (MEE) materials has grasped the attention of the engineers to implement it for various smart structure applications. Different numerical approaches have been proposed by various researchers to investigate the variety of structural responses such as free vibration [21,22,23,24,25,26,27], static [28,29,30,31,32], and buckling [33,34,35,36,37,38] analysis. In addition to this, very recently mathematical models of smart structures with CNTs embedded as reinforcements in the MEE matrix have been discussed by a few researchers. Mohammadimehr et al. [39] made use of FSDT and proposed an analytical solution to investigate the natural frequencies of FG-CNTMEE shells. Vinyas [40] exploited the benefits of HSDT along with FE methods and probed on the natural frequency response of FG-CNTMEE plates. It was further extended to investigate the influence of electromagnetic boundary conditions and geometrical skewness on the coupled frequency of FG-CNTMEE plates by Vinyas et al. [41]. Very recently, the nonlinear free vibration [42, 43] and deflection analysis [44] of FG-CNTMEE shells and plates were studied by Mahesh and Harursampath. Meanwhile, the effect of pyrocoupling on the nonlinear deflection of multiphase MEE plates was probed by Mahesh [45] through the FE approach. Using layer-wise shear deformation theory (LSDT), Kattimani [46] evaluated the influence of interphase thickness on the nonlinear characteristics of multiphase MEE plate.

On the other hand, the control strategies [47,48,49] for hazardous vibrations are considered to be one of the hot topics in structural analysis. In this regard, two prominent strategies such as passive control and active control have emerged. The damped transient response of actively controlled, blast impacted sandwich beams was studied by Damanpack et al. [50] using FSDT. Gao and Shen [51] proposed a mathematical model and investigated the damped nonlinear transient response of composite plates embedded with piezoelectric actuators. Baz [52] proposed a unique way of associating the inherent vibration control capabilities of piezoelectric (PE) material and viscoelastic (VE) material in the form of active constrained layer damping (ACLD). Here, PE and VE layers play the role of constraining and constrained layer, respectively. Several works incorporated this technique and assessed the damping characteristics of different host structures. Sarangi and Ray [53, 54] developed a FE formulation to interpret the damped nonlinear vibrations of laminated composite plates and beams subjected to ACLD treatment, which was later extended to laminated cylindrical panels by Shivakumar et al. [55]. Panda and Ray [56] examined the controllability of FG composite plates through ACLD treatment. Based on layerwise shear deformation theory, Kattimani and Ray [57] investigated the effect of ACLD treatment on the nonlinear vibrations of MEE plates. Mahesh and co-researchers [58,59,60,61] investigated the influence of geometrical skewness on the vibration attenuation of ACLD treated laminated, fiber reinforced and three-phase MEE plates.

From the exhaustive literature survey carried out, it was revealed that there has been no work reported on assessing the influence of ACLD treatment on the nonlinear damped transient response of FG-CNTMEE structures. Also, since the external electro-magnetic (EM) constraints applied on the smart structures varies its vibration response, it is much necessary to understand the influence of EM boundary condition on the damped characteristics of ACLD-treated FG-CNTMEE shells. Hence, this work makes the first attempt through the FE method, to investigate the effect of active controlling on the attenuated transient response of FG-CNTMEE shells subjected to open and closed EM circuits. Alongside, parametric studies dealing with the shell geometries, load cases, CNT distribution, CNT volume fraction has been discussed in detail. In addition, a special emphasis is placed on examining the influence of coupled fields and EM loads associated with EM circuit condition on the damped transient response of FG-CNTMEE shells which will be discussed in the subsequent sections.

Problem Statement

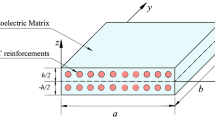
The influence of ACLD treatment on the controlled nonlinear transient response of FG-CNTMEE shells has been studied using the framework of FE methods. The geometric representation of the shell considered for evaluation is shown in Fig. 1). The length, width and thickness of the shell has been denoted through the notations a, b and h, respectively. The radius of curvature from the mid surface along x- and y-directions is denoted by R₁ and R₂, respectively. Meanwhile, the thicknesses of the constraining piezoelectric layer and constrained viscoelastic layer of the ACLD patch is represented by h_p and h_v, respectively. The FG-CNTMEE shell is assumed to be subjected to different loads including mechanical and electromagnetic loads.

Fig. 1

Schematic representation of FG-CNTMEE shell with ACLD patch

Materials and Constitutive Relations

The effective material properties of CNTMEE material is estimated with the aid of extended mixture rule as follows [62]:

$$\begin{aligned} E_{11} & = \eta_{11} V_{{{\text{CNT}}}} E_{11}^{{{\text{CNT}}}} + V_{{\text{m}}} E^{{\text{m}}} \\ \frac{{\eta_{2} }}{{E_{22} }} & = \frac{{V_{{{\text{CNT}}}} }}{{E_{22}^{{{\text{CNT}}}} }} + \frac{{V_{{\text{m}}} }}{{E^{{\text{m}}} }} \\ \frac{{\eta_{3} }}{{G_{12} }} & = \frac{{V_{{{\text{CNT}}}} }}{{G_{12}^{{{\text{CNT}}}} }} + \frac{{V_{{\text{m}}} }}{{G^{{\text{m}}} }} \\ \upsilon_{12} & = V_{{{\text{CNT}}}} \upsilon_{12}^{{{\text{CNT}}}} + V_{{\text{m}}} \upsilon_{{\text{m}}} , \\ \end{aligned}$$

(1)

in which, $E_{11}^{{{\text{CNT}}}}$, $E_{22}^{{{\text{CNT}}}}$, $G_{12}^{{{\text{CNT}}}}$ and $V_{{{\text{CNT}}}}$ are the longitudinal and transverse elastic modulus, shear modulus and CNT volume fraction, respectively. Meanwhile, $E^{{\text{m}}}$, $G^{{\text{m}}}$ and $V_{{\text{m}}}$ represent the matrix material properties.$\upsilon_{12}^{{{\text{CNT}}}}$ and $\upsilon_{{\text{m}}}$ corresponds to the CNT and matrix Poisson’s ratio, respectively. Further, $\eta_{1} , \eta_{2}$ and $\eta_{3}$ are CNT/matrix efficiency parameters which are determined by molecular dynamics simulation [62].

The present work considers FG-CNTMEE material whose material properties can be expressed through constitutive relations as follows [41]:

$$\begin{aligned} \left\{ \sigma \right\} & = \left[ C \right]\{ \varepsilon \} - \left[ e \right]\left\{ E \right\} - \left[ q \right]\left\{ H \right\} \\ \left\{ D \right\} & = \left[ e \right]^{{\text{T}}} \{ \varepsilon \} + \left[ \eta \right]\left\{ E \right\} + \left[ m \right]\left\{ H \right\} \\ \left\{ B \right\} & = \left[ q \right]^{{\text{T}}} \{ \varepsilon \} + \left[ m \right]\left\{ E \right\} + \left[ \mu \right]\left\{ H \right\}, \\ \end{aligned}$$

(2.a)

in which

$$\begin{gathered} \left[ C \right] = V_{{{\text{CNT}}}} \left[ {C^{{{\text{CNT}}}} } \right] + V_{{\text{m}}} \left[ {C^{{\text{m}}} } \right]; \hfill \\ \left[ e \right] = V_{{{\text{CNT}}}} \left[ {e^{{{\text{CNT}}}} } \right] + V_{{\text{m}}} \left[ {e^{{\text{m}}} } \right]; \hfill \\ \left[ q \right] = V_{{{\text{CNT}}}} \left[ {q^{{{\text{CN}}T}} } \right] + V_{{\text{m}}} \left[ {q^{{\text{m}}} } \right]; \hfill \\ \left[ m \right] = V_{{{\text{CNT}}}} \left[ {m^{{{\text{CNT}}}} } \right] + V_{{\text{m}}} \left[ {m^{{\text{m}}} } \right]; \hfill \\ \left[ \eta \right] = V_{{{\text{CNT}}}} \left[ {\eta^{{{\text{CNT}}}} } \right] + V_{{\text{m}}} \left[ {\eta^{{\text{m}}} } \right]; \hfill \\ \left[ \mu \right] = V_{{{\text{CNT}}}} \left[ {\mu^{{{\text{CNT}}}} } \right] + V_{{\text{m}}} \left[ {\mu^{{\text{m}}} } \right]; \hfill \\ \rho = V_{{{\text{CNT}}}} \rho^{{{\text{CNT}}}} + V_{{\text{m}}} \rho^{{\text{m}}} \hfill \\ \end{gathered}$$

(2.b)

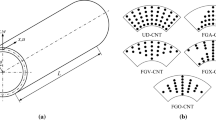
The detailed explanation of the terminologies appearing in Eqs. (2.a) and (2.b) and subsequent equations are shown in the nomenclature at the very beginning of this article. The different FG patterns of CNTs adopted in this work are mathematically expressed in Table 1).

Table 1 CNT distribution with a corresponding mathematical expression

The constraining 1–3 PZC piezoelectric layer of the ACLD patch can be represented through the constitutive equation as follows [57]:

$$\begin{aligned} \left\{ {\sigma_{b}^{p} } \right\} & = \left[ {\overline{C}_{b}^{p} } \right]\left\{ {\varepsilon_{b}^{p} } \right\} - \left[ {\overline{C}_{bs}^{p} } \right]\left\{ {\varepsilon_{s}^{p} } \right\} - \left\{ {\overline{e}_{b}^{p} } \right\}E_{z} \\ \left\{ {\sigma_{s}^{p} } \right\} & = \left[ {\overline{C}_{bs}^{p} } \right]^{{\text{T}}} \left\{ {\varepsilon_{b}^{p} } \right\} + \left[ {\overline{C}_{s}^{p} } \right]\left\{ {\varepsilon_{s}^{p} } \right\} - \left\{ {\overline{e}_{b}^{p} } \right\}E_{z} \\ D_{z}^{p} & = \left\{ {\overline{e}_{b}^{p} } \right\}^{{\text{T}}} \left\{ {\varepsilon_{b}^{p} } \right\} + \left\{ {\overline{e}_{s}^{p} } \right\}^{{\text{T}}} \left\{ {\varepsilon_{s}^{p} } \right\} + \overline{ \in }_{33}^{p} E_{z}^{p} , \\ \end{aligned}$$

(3)

here the superscript ‘p’ denoted piezoelectric layer of ACLD patch. The expanded form of the material property matrices of Eqs. (2) and (3) are illustrated in Appendix-A (Eqs. (27)–(28)) .

The visco-elastic layer of the ACLD patch is modelled in the time domain via Golla–Hughes–McTavish (GHM) method whose constitutive equation can be denoted as follows [57]:

$$\left( {\sigma_{s} } \right)_{v} = \int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left( {\varepsilon_{s}^{k} } \right)}}{\partial \tau }\partial \tau .$$

(4)

The electric and magnetic potentials are assumed to vary linearly across the thickness of the shell according to

$$\phi = \frac{{z - h_{1} }}{h}\overline{\phi };\,\;\psi = \frac{{z - h_{1} }}{h}\overline{\psi }.$$

(5)

In addition, as per Maxwell's law, the electromagnetic equations that depict the variation of transverse electric and magnetic field can be represented in relation with the potentials as follows [22]:

$$E_{z} = - \frac{\partial \phi }{{\partial z}};\;H_{z} = - \frac{\partial \psi }{{\partial z}}.$$

(6)

Kinematics of Shell Deformation

To assess the nonlinear transient response of FG-CNTMEE shells, the kinematics are assumed to follow layerwise shear deformation theory (LSDT), in which the displacement components are represented as follows [57]:

$$\begin{aligned} u & = u_{0} + \left( {z - \left\langle {z - \frac{h}{2}} \right\rangle } \right)\theta_{x} + \left( {\left\langle {z - \frac{h}{2}} \right\rangle - \left\langle {z - h_{{\text{N + 2}}} } \right\rangle } \right)\kappa_{x} + \left\langle {z - h_{{\text{N + 2}}} } \right\rangle \gamma_{x} , \\ v & = v_{0} + \left( {z - \left\langle {z - \frac{h}{2}} \right\rangle } \right)\theta_{y} + \left( {\left\langle {z - \frac{h}{2}} \right\rangle - \left\langle {z - h_{{\text{N + 2}}} } \right\rangle } \right)\kappa_{y} + \left\langle {z - h_{{\text{N + 2}}} } \right\rangle \gamma_{y} . \\ \end{aligned}$$

(7)

Meanwhile, several higher order terms are implemented in the equation of transverse displacement to facilitate accurate vertical actuation of ACLD treatment. It can be shown as follows:

$$w = w_{0} + z\theta_{z} + z^{2} \kappa_{z} .$$

(8)

Based on the Eqs. (7) and (8), the bending and shear strains can be expressed as follows:

$$\begin{aligned} \left\{ {\varepsilon_{b}^{{}} } \right\} & = \left\{ {\varepsilon_{bt} } \right\} + \left[ {Z_{1} } \right]\left\{ {\varepsilon_{rb} } \right\} + \left\{ {\varepsilon_{{bt\_{\text{NL}}}} } \right\}, \\ \left\{ {\varepsilon_{b}^{P} } \right\} & = \left\{ {\varepsilon_{bt} } \right\} + \left[ {Z_{2} } \right]\left\{ {\varepsilon_{rb} } \right\} + \left\{ {\varepsilon_{{bt\_{\text{NL}}}} } \right\}, \\ \left\{ {\varepsilon_{s}^{{}} } \right\} & = \left\{ {\varepsilon_{ts} } \right\} + \left[ {Z_{3} } \right]\left\{ {\varepsilon_{rs} } \right\}, \\ \left\{ {\varepsilon_{s}^{Vis} } \right\} & = \left\{ {\varepsilon_{ts} } \right\} + \left[ {Z_{4} } \right]\left\{ {\varepsilon_{rs} } \right\}, \\ \left\{ {\varepsilon_{s}^{P} } \right\} & = \left\{ {\varepsilon_{ts} } \right\} + \left[ {Z_{5} } \right]\left\{ {\varepsilon_{rs} } \right\}, \\ \end{aligned}$$

(9)

where the different strain components can be shown as follows:

$$\begin{aligned} \left\{ {\varepsilon _{{bt}} } \right\} & = \left\{ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{${\partial u_{0} }$} \!\mathord{\left/ {\vphantom {{\partial u_{0} } {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}} + {\raise0.7ex\hbox{$w$} \!\mathord{\left/ {\vphantom {w {R_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{1} }$}}} \\ {{\raise0.7ex\hbox{${\partial v_{0} }$} \!\mathord{\left/ {\vphantom {{\partial v_{0} } {\partial y}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial y}$}} + {\raise0.7ex\hbox{$w$} \!\mathord{\left/ {\vphantom {w {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}} \\ 0 \\ {{\raise0.7ex\hbox{${\partial u_{0} }$} \!\mathord{\left/ {\vphantom {{\partial u_{0} } {\partial y}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial y}$}} + {\raise0.7ex\hbox{${\partial v_{0} }$} \!\mathord{\left/ {\vphantom {{\partial v_{0} } {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \\ \end{array} } \right\};{\text{ }}\left\{ {\varepsilon _{{ts}} } \right\} = \left\{ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{${\partial w_{0} }$} \!\mathord{\left/ {\vphantom {{\partial w_{0} } {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}} - {\raise0.7ex\hbox{${u_{0} }$} \!\mathord{\left/ {\vphantom {{u_{0} } {R_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{1} }$}}} \\ {{\raise0.7ex\hbox{${\partial w_{0} }$} \!\mathord{\left/ {\vphantom {{\partial w_{0} } {\partial y}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial y}$}} - {\raise0.7ex\hbox{${v_{0} }$} \!\mathord{\left/ {\vphantom {{v_{0} } {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}} \\ \end{array} } \right\};\left\{ {\varepsilon _{{bt\_{\text{N}}L}} } \right\} = \frac{1}{2}\left\{ {\begin{array}{*{20}c} {\left( {\frac{{{\text{d}}w_{0} }}{{dx}}} \right)^{2} } \\ {\left( {\frac{{{\text{d}}w_{0} }}{{{\text{d}}y}}} \right)^{2} } \\ 0 \\ {2\left( {\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right)\left( {\frac{{{\text{d}}w_{0} }}{{{\text{d}}y}}} \right)} \\ \end{array} } \right\}; \\ \left\{ {\varepsilon _{{rs}} } \right\} & = \left\{ {\begin{array}{*{20}c} {\theta _{x} } \\ {\theta _{y} } \\ {\kappa _{x} } \\ {\kappa _{y} } \\ {\gamma _{x} } \\ {\gamma _{y} } \\ {{\raise0.7ex\hbox{${\partial \theta _{z} }$} \!\mathord{\left/ {\vphantom {{\partial \theta _{z} } {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \\ {{\raise0.7ex\hbox{${\partial \theta _{z} }$} \!\mathord{\left/ {\vphantom {{\partial \theta _{z} } {\partial y}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial y}$}}} \\ {{\raise0.7ex\hbox{${\partial \kappa _{z} }$} \!\mathord{\left/ {\vphantom {{\partial \kappa _{z} } {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \\ {{\raise0.7ex\hbox{${\partial \kappa _{z} }$} \!\mathord{\left/ {\vphantom {{\partial \kappa _{z} } {\partial y}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial y}$}}} \\ \end{array} } \right\};\left\{ {\varepsilon _{{rb}} } \right\} = \left\{ {\begin{array}{*{20}c} {{{\partial \theta _{x} } \mathord{\left/ {\vphantom {{\partial \theta _{x} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial \theta _{y} } \mathord{\left/ {\vphantom {{\partial \theta _{y} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ {{{\partial \theta _{x} } \mathord{\left/ {\vphantom {{\partial \theta _{x} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} + {{\partial \theta _{y} } \mathord{\left/ {\vphantom {{\partial \theta _{y} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {\theta _{z} } \\ {\kappa _{z} } \\ {{{\partial \kappa _{x} } \mathord{\left/ {\vphantom {{\partial \kappa _{x} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial \kappa _{y} } \mathord{\left/ {\vphantom {{\partial \kappa _{y} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ {{{\partial \kappa _{x} } \mathord{\left/ {\vphantom {{\partial \kappa _{x} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} + {{\partial \kappa _{y} } \mathord{\left/ {\vphantom {{\partial \kappa _{y} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial \gamma _{x} } \mathord{\left/ {\vphantom {{\partial \gamma _{x} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial \gamma _{y} } \mathord{\left/ {\vphantom {{\partial \gamma _{y} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ {{{\partial \gamma _{x} } \mathord{\left/ {\vphantom {{\partial \gamma _{x} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} + {{\partial \gamma _{y} } \mathord{\left/ {\vphantom {{\partial \gamma _{y} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ \end{array} } \right\}. \\ \end{aligned}$$

(10)

The different transformation matrices [Z₁]–[Z₅] can be elaborated and expressed as follows:

$$\begin{aligned} \left[ {Z_{1} } \right] & = \left[ {\begin{array}{*{20}c} z & 0 & 0 & {{z \mathord{\left/ {\vphantom {z {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & {{{z^{2} } \mathord{\left/ {\vphantom {{z^{2} } {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & z & 0 & {{z \mathord{\left/ {\vphantom {z {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & {{{z^{2} } \mathord{\left/ {\vphantom {{z^{2} } {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & {2z} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & z & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ \left[ {Z_{2} } \right] & = \left[ {\begin{array}{*{20}c} {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & {{z \mathord{\left/ {\vphantom {z {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & {{{z^{2} } \mathord{\left/ {\vphantom {{z^{2} } {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & {h_{{\text{v}}} } & 0 & 0 & {\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} & 0 & 0 \\ 0 & {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & {{z \mathord{\left/ {\vphantom {z {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & {{{z^{2} } \mathord{\left/ {\vphantom {{z^{2} } {R_{1} }}} \right. \kern-\nulldelimiterspace} {R_{1} }}} & 0 & {h_{{\text{v}}} } & 0 & 0 & {\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} & 0 \\ 0 & 0 & 0 & 1 & {2z} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 & 0 & 0 & 0 & {h_{{\text{v}}} } & 0 & 0 & {\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \\ \end{array} } \right] \\ \left[ {Z_{3} } \right] & = \left[ {\begin{array}{*{20}c} {(1 - {z \mathord{\left/ {\vphantom {z {R_{1} )}}} \right. \kern-\nulldelimiterspace} {R_{1} )}}} & 0 & 0 & 0 & 0 & 0 & z & 0 & {z^{2} } & 0 \\ 0 & {(1 - {z \mathord{\left/ {\vphantom {z {R_{1} )}}} \right. \kern-\nulldelimiterspace} {R_{1} )}}} & 0 & 0 & 0 & 0 & 0 & z & 0 & {z^{2} } \\ \end{array} } \right]; \\ \left[ {Z_{4} } \right] & = \left[ {\begin{array}{*{20}c} {{{ - h} \mathord{\left/ {\vphantom {{ - h} {2R_{1} }}} \right. \kern-\nulldelimiterspace} {2R_{1} }}} & 0 & {1 - \left( {{\raise0.7ex\hbox{${\left( {z - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {z - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} {R_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{1} }$}}} \right)} & 0 & 0 & 0 & z & 0 & {z^{2} } & 0 \\ 0 & {{{ - h} \mathord{\left/ {\vphantom {{ - h} {2R_{2} }}} \right. \kern-\nulldelimiterspace} {2R_{2} }}} & 0 & {1 - \left( {{\raise0.7ex\hbox{${\left( {z - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {z - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}} \right)} & 0 & 0 & 0 & z & 0 & {z^{2} } \\ \end{array} } \right] \\ \left[ {Z_{5} } \right] & = \left[ {\begin{array}{*{20}c} {{{ - h} \mathord{\left/ {\vphantom {{ - h} {2R_{1} }}} \right. \kern-\nulldelimiterspace} {2R_{1} }}} & 0 & {{{ - h_{{\text{v}}} } \mathord{\left/ {\vphantom {{ - h_{{\text{v}}} } {2R_{1} }}} \right. \kern-\nulldelimiterspace} {2R_{1} }}} & 0 & {\left( {1 - {\raise0.7ex\hbox{${\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} {R_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{1} }$}}} \right)} & 0 & z & 0 & {z^{2} } & 0 \\ 0 & {{{ - h} \mathord{\left/ {\vphantom {{ - h} {2R_{2} }}} \right. \kern-\nulldelimiterspace} {2R_{2} }}} & 0 & {{{ - h_{{\text{v}}} } \mathord{\left/ {\vphantom {{ - h_{{\text{v}}} } {2R_{2} }}} \right. \kern-\nulldelimiterspace} {2R_{2} }}} & 0 & {\left( {1 - {\raise0.7ex\hbox{${\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {z - h_{{\text{v}}} - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}} \right)} & 0 & z & 0 & z \\ \end{array} } \right]. \\ \end{aligned}$$

(11)

Finite Element Formulation

The FG-CNTMEE shell is modelled through eight-noded isoparametric element whose nodal displacement degrees of freedom can be explicitly represented as follows:

$$\left\{ {d_{ti} } \right\} = \left[ {\begin{array}{*{20}c} {u_{0i} } & {v_{0i} } & {w_{0i} } \\ \end{array} } \right]^{{\text{T}}} ;\left\{ {d_{ri} } \right\} = \left[ {\begin{array}{*{20}c} {\theta_{xi} } & {\theta_{yi} } & {\theta_{zi} } & {\kappa_{zi} } & {\kappa_{xi} } & {\kappa_{yi} } & {\gamma_{xi} } & \gamma \\ \end{array}_{yi} } \right]^{{\text{T}}} \, (i = 1,2 \ldots 8).$$

(12)

Further, the generalised displacement vectors of an element can be represented using the nodal d.o.f and shape functions as follows:

$$\left\{ {d_{t} } \right\} = \left[ {N_{t} } \right]\left\{ {d_{t}^{e} } \right\};\;\left\{ {d_{r} } \right\} = \left[ {N_{r} } \right]\left\{ {d_{r}^{e} } \right\};\;\phi = \left[ {N_{\phi } } \right]\left\{ {\phi^{e} } \right\};\psi = \left[ {N_{\psi } } \right]\left\{ {\psi^{e} } \right\}.$$

(13)

Also, the electromagnetic fields can be rewritten in terms of FE quantities as follows:

$$E_{z}^{{}} = - \frac{1}{h}\left[ {N_{\phi } } \right]\left\{ {\phi^{e} } \right\};\,H_{z} = - \frac{1}{h}\left[ {N_{\psi } } \right]\left\{ {\psi^{e} } \right\}.$$

(14)

The strains represented by Eq. (9) can be expressed in terms of FE parameters in the following manner:

$$\begin{aligned} \left\{ {\varepsilon_{b}^{h} } \right\} & = \left[ {B_{tb} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{1} } \right]\left[ {B_{rb} } \right]\left\{ {d_{r}^{e} } \right\} + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}; \\ \left\{ {\varepsilon_{b}^{p} } \right\} & = \left[ {B_{tb} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{2} } \right]\left[ {B_{rb} } \right]\left\{ {d_{r}^{e} } \right\} + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}; \\ \left\{ {\varepsilon_{s}^{h} } \right\} & = \left[ {B_{ts} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{3} } \right]\left[ {B_{rs} } \right]\left\{ {d_{r}^{e} } \right\}; \\ \left\{ {\varepsilon_{s}^{v} } \right\} & = \left[ {B_{ts} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{4} } \right]\left[ {B_{rs} } \right]\left\{ {d_{r}^{e} } \right\} \\ \left\{ {\varepsilon_{s}^{p} } \right\} & = \left[ {B_{ts} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{5} } \right]\left[ {B_{rs} } \right]\left\{ {d_{r}^{e} } \right\}, \\ \end{aligned}$$

(15)

where the strain displacement matrices can be expressed as follows:

$$\begin{aligned} \left[ {B_{tb} } \right] & = \left[ {\begin{array}{*{20}c} {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {R_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{1} }$}}} \\ 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}} \\ 0 & 0 & 0 \\ {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 \\ \end{array} } \right];\;\left[ {B_{ts} } \right] = \left[ {\begin{array}{*{20}c} {{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} {R_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{1} }$}}} & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ 0 & {{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}} & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ \end{array} } \right] \\ \left[ {B_{rb} } \right] & = \left[ {\begin{array}{*{20}c} {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & 0 & 0 & 0 & 0 & 0 & 0 \\ {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ 0 & 0 & 0 & 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ \end{array} } \right],\;\left[ {B_{rs} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & 0 & 0 & 0 & 0 \\ \end{array} } \right]. \\ \end{aligned}$$

(16)

Governing Equations

The equations of motion of the FG-CNTMEE shell embedded with the ACLD patch can be derived through the principle of virtual work, which can be expressed as follows [57]:

$$\begin{gathered} \int\limits_{{\Omega^{h} }} {\delta \left\{ {\varepsilon_{b}^{h} } \right\}^{{\text{T}}} \left\{ {\sigma_{b}^{h} } \right\}{\text{d}}\Omega^{h} + } \int\limits_{{\Omega^{h} }} {\delta \left\{ {\varepsilon_{s}^{h} } \right\}^{{\text{T}}} \left\{ {\sigma_{s}^{h} } \right\}{\text{d}}\Omega^{h} + } \int\limits_{{\Omega^{V} }} {\delta \left\{ {\varepsilon_{s}^{v} } \right\}^{{\text{T}}} \left\{ {\sigma_{s}^{v} } \right\}{\text{d}}\Omega^{v} } + \int\limits_{{\Omega^{P} }} {\delta \left\{ {\varepsilon_{b}^{p} } \right\}^{{\text{T}}} \left\{ {\sigma_{b}^{p} } \right\}{\text{d}}\Omega^{p} } \hfill \\ + \int\limits_{{\Omega^{p} }} {\delta \left\{ {\varepsilon_{s}^{p} } \right\}^{{\text{T}}} \left\{ {\sigma_{s}^{p} } \right\}{\text{d}}\Omega^{p} - } \int\limits_{{\Omega^{p} }} {\delta E_{z} D_{z} {\text{d}}\Omega^{p} } + \int\limits_{A} {Q^{\phi } } \delta \phi {\text{d}}A + \int\limits_{A} {Q^{\psi } } \delta \psi {\text{d}}A - \int\limits_{{\Omega^{h} }} {\delta E_{z} } D_{z} (z){\text{d}}\Omega^{h} \hfill \\ - \int\limits_{{\Omega^{h} }} {\delta H_{z} } B_{z} (z){\text{d}}\Omega^{h} - \int\limits_{A} \delta \left\{ {d_{t} } \right\}^{{\text{T}}} \left\{ f \right\}{\text{d}}A \hfill \\ + \frac{1}{2}\int\limits_{{\Omega^{h} }} {\delta \left\{ {d_{t} } \right\}^{{\text{T}}} \rho_{h} (z)\left\{ {\ddot{d}_{t} } \right\}{\text{d}}\Omega^{h} + } \frac{1}{2}\int\limits_{{\Omega^{v} }} {\delta \left\{ {d_{t} } \right\}^{{\text{T}}} \rho_{v} (z)\left\{ {\ddot{d}_{t} } \right\}{\text{d}}\Omega^{v} + } \frac{1}{2}\int\limits_{{\Omega^{p} }} {\delta \left\{ {d_{t} } \right\}^{{\text{T}}} \rho_{p} (z)\left\{ {\ddot{d}_{t} } \right\}{\text{d}}\Omega^{p} = 0} . \hfill \\ \end{gathered}$$

(17)

The superscripts ‘h’, ‘p’ and ‘v’ denote host structure (FG-CNTMEE shell), the piezoelectric layer of ACLD treatment and the viscoelastic layer of ACLD treatment, respectively. By substituting the constitutive equations (Eqs. (1)–(6)) and other FE equations (Eqs. (12)–(16)) in Eq. (17), followed by a grouping of the matrices in a straight forward manner, it can be re-written as follows:

$$\begin{aligned} \left[ {M^{e} } \right]\left\{ {\ddot{d}_{t}^{e} } \right\} & + \left[ {K_{T15}^{e} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {K_{T16}^{e} } \right]\left\{ {d_{r}^{e} } \right\} \\ & + \left[ {K_{31}^{e} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {d_{t}^{e} } \right\}}}{\partial \tau }{\text{d}}\tau + \left[ {K_{32}^{e} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {d_{r}^{e} } \right\}}}{\partial \tau }{\text{d}}\tau \\ & + \left[ {K_{T3}^{e} } \right]\left\{ {\phi^{e} } \right\} + \left[ {K_{T4}^{e} } \right]\left\{ {\psi^{e} } \right\} = \left\{ {F^{e} } \right\} - \left\{ {F_{{_{{{\text{tp}}1}} }}^{e} } \right\}V - \left\{ {F_{{_{{{\text{tpn}}1}} }}^{e} } \right\}V \\ & \times \left[ {K_{T17}^{e} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {K_{T18}^{e} } \right]\left\{ {d_{r}^{e} } \right\} + \left[ {K_{32}^{e} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {d_{t}^{e} } \right\}}}{\partial \tau }{\text{d}}\tau \\ & + \left[ {K_{30}^{e} } \right]\int\limits_{0}^{t} {G\left( {t - \tau } \right)} \frac{{\partial \left\{ {d_{r}^{e} } \right\}}}{\partial \tau }{\text{d}}\tau + \left[ {K_{3}^{e} } \right]\left\{ {\phi^{e} } \right\} + \left[ {K_{4}^{e} } \right]\left\{ {\psi^{e} } \right\} = - \left( {\left\{ {F_{{{\text{rp}}1}}^{e} } \right\} + \left\{ {F_{{{\text{rp}}2}}^{e} } \right\}} \right)V \\ & \times \left[ {K_{33}^{e} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {K_{{_{34} }}^{e} } \right]^{{\text{T}}} \left\{ {d_{r}^{e} } \right\} - \left[ {K_{{_{35} }}^{e} } \right]\left\{ {\phi^{e} } \right\} - \left[ {K_{{_{36} }}^{e} } \right]\left\{ {\psi^{e} } \right\} = 0 \\ & \times \left[ {K_{37}^{e} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {K_{{_{38} }}^{e} } \right]\left\{ {d_{r}^{e} } \right\} - \left[ {K_{{_{39} }}^{e} } \right]^{{\text{T}}} \left\{ {\phi^{e} } \right\} - \left[ {K_{{_{40} }}^{e} } \right]\left\{ {\psi^{e} } \right\} = 0. \\ \end{aligned}$$

(18)

The various stiffness matrices, rigidity matrices and force vectors appearing in Eq. (18) are explicitly denoted in the Appendix. Further, Eq. (18) is applied with the boundary conditions and globalised in a straight-forward manner. The resulting equation is enforced with the Laplace transform to get

$$\begin{aligned} s^{2} \left[ M \right]\left\{ {\tilde{X}_{t} } \right\} & + L\left( {\left[ {K_{C12} } \right]\left\{ {X_{t} } \right\} + \left[ {K_{C13} } \right]\left\{ {X_{r} } \right\}} \right) \\ & + \left[ {K_{{{\text{tsv}}}} } \right]s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{t} } \right\} + \left[ {K_{{{\text{trsv}}}} } \right]s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{r} } \right\} = \left\{ {\tilde{F}} \right\} - \left\{ {F_{{{\text{tp}}}} } \right\}\tilde{V} - L\left\{ {F_{{{\text{tpn}}}} } \right\}\tilde{V} \\ & \times L\left( {\left[ {K_{C17} } \right]\left\{ {X_{t} } \right\} + \left[ {K_{C18} } \right]\left\{ {X_{r} } \right\}} \right) \\ & + \left[ {K_{{{\text{trsv}}}} } \right]^{{\text{T}}} s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{t} } \right\} + \left[ {K_{{{\text{rrsv}}}} } \right]s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{r} } \right\} = - \left\{ {F_{{{\text{rp}}}} } \right\}\tilde{V}. \\ \end{aligned}$$

(19)

In the time domain, by expressing the material modulus function as a single mini oscillator term using the GHM model for viscoelastic material, it can be shown that

$$s\tilde{G}\left( s \right) = G^{\infty } \left[ {1 + \alpha \frac{{s^{2} + 2\hat{\xi }\hat{\omega }s}}{{s^{2} + 2\hat{\xi }\hat{\omega }s + \hat{\omega }^{2} }}} \right].$$

(20)

By introducing Z and Z_r as the auxiliary dissipation coordinates and taking its Laplace transform, several equations can be obtained as

$$\begin{aligned} s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{t} } \right\} & = G^{\infty } \left[ {\left( {1 + \alpha } \right)} \right]\left\{ {\tilde{X}_{t} } \right\} - \alpha \tilde{Z}\left( s \right), \\ s\tilde{G}\left( s \right)\left\{ {\tilde{X}_{r} } \right\} & = G^{\infty } \left[ {\left( {1 + \alpha } \right)} \right]\left\{ {\tilde{X}_{r} } \right\} - \alpha \tilde{Z}_{r} \left( s \right), \\ \tilde{Z}\left( s \right) & = \frac{{\hat{\omega }^{2} }}{{s^{2} + 2\hat{\xi }\hat{\omega }s + \hat{\omega }^{2} }}\left\{ {X_{t} } \right\}, \\ \tilde{Z}_{r} \left( s \right) & = \frac{{\hat{\omega }^{2} }}{{s^{2} + 2\hat{\xi }\hat{\omega }s + \hat{\omega }^{2} }}\left\{ {X_{r} } \right\}. \\ \end{aligned}$$

Meanwhile, by incorporating inverse Laplace transformations and closed-loop model as depicted in the Ref. [57], the final equations of motion can be expressed after condensation as follows:

$$\left[ {M^{*} } \right]\left\{ {\ddot{X}_{t} } \right\} + \left[ {C_{{\text{d}}}^{*} } \right]\left\{ {\dot{X}_{t} } \right\}\left[ {K^{*} } \right]\left\{ {X_{{\text{t}}} } \right\} = \left\{ {F^{*} } \right\}$$

(22)

The proposed model is computationally effective in a manner that the structural variables are independent of the number of layers. Hence, a proper coupling between three fields can be established with ease. Also, unlike the other LSDT, the proposed kinematic model ensures the continuity of the transverse displacement field and its derivative with respect to the thickness coordinate by implementing the higher order terms. However, the major limitation is that the computational cost may slightly improve with more number of layers.

Results and Discussion

This section deals with the numerical examples to demonstrate the effectiveness of the proposed FE formulation to predict the nonlinear transient response of ACLD-treated FG-CNTMEE shell. The geometrical dimensions considered in this study are a = b = 1.0 m; and a/h = 100. Further, the h_v and h_p are chosen to be 50.8 μm and 250 μm, respectively. The material properties depicted in Table 2 are used for the current study. A converged mesh size of 10 × 10 is used in the current study. Also, from the outcomes of the authors’ previous work [61], the optimum values of ACLD parameters are selected for this entire study which can be mentioned as follows:

$${\text{Control gain}}\;K_{{\text{d}}} = { 6}00;{\text{ piezoelectric fiber angle }} = \, 0^{{\text{o}}} ,{\text{ centre patch}}$$

(23)

Table 2 Material properties corresponding to CNTMEE and 1–3 PZC patch [39, 62, 63]

At first, the formulated mathematical model is verified against the published results. To this end, the deflection problem of the MEE flat panel as considered by Sladek et al. [31] is resolved using the current method, by nullifying the effect of the ACLD patch. From Fig. 2a, b it is clear that the proposed formulation yields accurate results for both clamped and simply supported conditions. In addition, the validation is extended for the free vibration characteristics of CNT reinforced plates, to verify proper incorporation of material and stiffness properties. From Table 3), it can be clearly seen that the results are matching with those reported by Kiani [62]. Therefore, it can be extended to assess the nonlinear transient response as well.

Fig. 2

Validation of the FE formulation with Sladek et al. [31] for the case of layered MEE flat panels

Table 3 Validation for FG-CNT plate ($V_{{{\text{CNT}}}}^{*} = 0.17$; CCCC boundary condition; a/b = 1; a/h = 100)

Based on the preliminary studies performed, the pulse load $q_{0} = 2\;{\text{kN}}/{\text{m}}^{2}$ is considered in order to ensure non-linearity in the response. The present study considers three different transient load cases which can be mathematically expressed as follows:

Load Case-I: Finite duration step load

$$\begin{gathered} q = q_{0} , t \le 1s, \hfill \\ q = 0, t \ge 1s. \hfill \\ \end{gathered}$$

(24.a)

Load Case-II: Infinite duration step load

$$q = q_{0} .$$

(24.b)

Load Case-III: Finite duration half-sine load

$$q = q_{0} \sin \pi t, t \le 1s.$$

(24.c)

The mechanical boundary conditions enforced on the structure can be represented as follows:

Simply supported:

$$\begin{gathered} v_{0}^{{}} = w_{0}^{{}} = \theta_{y}^{{}} = \kappa_{y}^{{}} = \gamma_{y}^{{}} = \theta_{z}^{{}} = \kappa_{z}^{{}} = 0 \;at\; x = \left( {0, a} \right), \hfill \\ u_{0} = w_{0} = \theta_{x} = \kappa_{x} = \gamma_{x} = \theta_{z} = \kappa_{z} = 0\;at\;y = \left( {0, b} \right). \hfill \\ \end{gathered}$$

(25.a)

Clamped:

$$u_{0} = v_{0} = w_{0} = \theta_{x} = \theta_{y} = \theta_{z} = \kappa_{x} = \kappa_{y } = \kappa_{z} = \gamma_{x} = \gamma_{y} = \gamma_{z} = 0\;{\text{at}}\;x = \left( {0, a} \right)\;{\text{and}}\;y = \left( {0, b} \right).$$

(25.b)

The electromagnetic boundary conditions adopted in this work can be shown as

$$\begin{gathered} {\text{Closed-circuit}}:\phi = \psi = 0 \left( {z = \pm \frac{h}{2}} \right), \hfill \\ {\text{Open-circuit}}:D_{z} = B_{z} = 0 \left( {z = \pm \frac{h}{2}} \right). \hfill \\ \end{gathered}$$

(26)

The influence of various shell geometries on the damped transient response of FG-CNTMEE shells subjected to the mechanical loading is depicted in Fig. 3. As noticed from this plot, the efficiency of ACLD treatment in reducing the amplitude of vibration and damping characteristics are more on spherical shells, followed by cylindrical, ellipsoid and hyperboloid shells. The anticlastic behaviour of FG-CNTMEE hyperboloid shells makes it difficult to attenuate the geometrically nonlinear vibrations quickly in contrast to other shell geometries.

Fig. 3

Effect of shell geometry on the damped transient response of CNTMEE shells

The investigation is extended to assess the effect of different load cases on the damped nonlinear transient response of FG-CNTMEE shells. The results plotted in Fig. 4a, b suggest that the damping characteristics are predominantly influenced by the load cases for both CCCC and SSSS boundary conditions. A higher damped response can be noticed for Load Case-III while the ACLD treatment has a minimal effect on the FG-CNTMEE shells when subjected to the load case-II. Meanwhile, Fig. 5 shows the effect of CNTs functional gradation pattern on the coupled nonlinear transient response of sandwich shells, Due to superior flexural rigidity offered by the FG-X pattern, quick control of vibration is possible in this case. Also, the lower controllability is witnessed for the FG-O pattern of CNTs in the shell structure.

Fig. 4

Effect of load cases on the damped transient response of CNTMEE spherical shells

Fig. 5

Effect of CNT distributions on the damped transient response of CNTMEE spherical shell

The control voltage required to attenuate the amplitude to 50% of the maximum amplitude is shown in Table 4 for all the shell geometries and load cases considered for evaluation. For a given load case, the required control voltage is the maximum for the hyperboloid shells compared to other shell geometries. This holds good for all three load cases. Analogously, for a given geometry, Load case-II requires a higher control voltage to bring the amplitude of vibration to 50% of the original amplitude. In comparison with the CCCC condition, a higher magnitude of control voltage is needed for the SSSS condition to attenuate the vibrations of the shells.

Table 4 Maximum control voltage for various CNTMEE shell geometries subjected to different load cases and boundary conditions (FG-X; closed-circuit)

The volume fraction of CNTs plays a prominent role in damped transient response. To this end, Fig. 6 makes an attempt to investigate the damped characteristics of FG-CNTMEE spherical shell with different CNTs volume fraction. For the specified control voltage, the higher volume fraction of CNTs makes it easier to control the amplitude of vibrations. This may be due to the fact that the stiffness of the shell enhances with more volume fraction of CNTs.

Fig. 6

Effect of CNT volume fraction on the damped transient response of CNTMEE spherical shell

The CNTs are very much responsive to both electric and magnetic forces. The sensing and actuating behaviour of CNT structures vary uniquely when operated with EM loads. In this regard, the study also makes an attempt to evaluate the damped transient response of FG-CNTMEE shells subjected to the different magnitude of EM loads. From Fig. 7, it is evident that with higher values of positive EM loads the shell becomes more vulnerable for deflections and the controllability of vibrations reduces as the stiffness of the shell reduces. On the other hand, with the application of negative EM loads, it can be seen that the damping characteristics magnifies and the ease of attenuation improves. The reason may be due to the fact that the application of negative EM loads adds up to the stiffness and makes the structure more rigid against the deflections. In addition, the control voltage required to attenuate the vibrations of different FG-CNTMEE shells from the original amplitude to 50% of its value is shown in Table 5. A higher control voltage is necessary for positive EM loads whereas the required voltage reduces with the increase in the negative values of EM loads.

Fig. 7

Effect of electro-magnetic loads on the damped transient response of CNTMEE spherical shell

Table 5 Effect of electro-magnetic loads on the control voltage for various CNTMEE shell geometries (Load case-II; CCCC; FG-X; closed circuit)

The effect of various coupling fields on the nonlinear damped transient response of CNTMEE spherical shell with FG-X type of CNTs distribution is shown in Fig. 8. It can be witnessed that the complete coupling between magnetic, electric and elastic fields makes the attenuation easier through ACLD treatment. Further, the pure elastic field results in a higher amplitude of vibration, at a given point of time. The variation in the required control voltage of the completely coupled and elastic FG-CNTMEE shell to attenuate the original amplitude to 50% of its value is shown in Table 6. The effect of coupling is noticed to be significant for FG-X distribution.

Fig. 8

Effect of coupling on the damped transient response of CNTMEE spherical shell

Table 6 Effect of coupling on the control voltage for various CNTMEE shell geometries

The application of different electro-magnetic (EM) circuits such as open circuit and closed circuits alters the overall stiffness of the structure, which in turn drastically affects the coupled response of smart structures. Therefore, it is very much crucial to assess the influence of EM circuits on the damped transient response of FG-CNTMEE shells. Figure 9a–d shows the variation of the non-dimensional damped transient response of various shell geometries subjected to different EM circuits. For all the shell geometries, a higher vibration controlling capability is witnessed for open circuit condition as opposed to closed-circuit condition. In addition, at any point of time, higher discrepancies between the non-dimensional transient deflection corresponding to open and closed circuit are seen for the spherical shell, whereas hyperboloid shells exhibit minimum EM circuit effect.

Fig. 9

Effect of electro-magnetic circuits associated with different shell geometries on the damped transient response of CNTMEE shells

Similarly, the effect of CNT distributions associated with the EM circuits on the damped transient response of FG-CNTMEE spherical shell is shown in Fig. 10a–d. The predominant influence of EM circuits is noticed on the FG-X distribution whereas the minimum effect is witnessed for FG-O distribution. The control voltage required to attenuate the damped vibration amplitude to 50% of its original amplitude for various CNT distribution and EM circuits is shown in Table 7. It can be seen from the encapsulated results that when the FG-CNTMEE shell is subjected to closed-circuit EM condition, it demands a higher control voltage to achieve efficient damping. Also, the effect of EM circuits associated with the control voltage is predominant on spherical shell geometry and FG-X distribution, similar to the trend of non-dimensional deflection. From Table 8, an attempt has been made to assess the influence of CNTs volume fraction on the % difference between the vibration amplitude of FG-CNTMEE spherical shell with open and closed circuit conditions. The results reveal that with the increase in the volume fraction of CNTs, the EM circuits’ effect enlarges.

Fig. 10

Effect of electro-magnetic circuits associated with different CNT distributions on the damped transient response of CNTMEE spherical shells

Table 7 Effect of CNT distribution and electro-magnetic circuits on the control voltage for various CNTMEE shell geometries (Load case-II; CCCC)

Table 8 Effect of CNT volume fractions associated with the electro-magnetic circuits on the percentage difference in w* of various shell geometries with different CNT distributions (Load case-II)

The effect of EM circuits associated with different mechanical load cases on the transient behaviour of FG-CNTMEE spherical shell is studied in Fig. 11 and extended for other shell geometries in Table 9. It can be witnessed from the figure that the influence of EM circuits is predominant on the mechanical load case-II while the minimal effect is noticed when the FG-CNTMEE shell is subjected to load case-III. Alongside, from Table 9, it is evident that the discrepancies between the vibration amplitude corresponding to open and closed circuit is minimum for hyperboloid shell. Meanwhile, FG-O distribution exhibits a negligible effect of EM circuit conditions. Similarly, from Fig. 12, it can be seen that when FG-CNTMEE spherical shell with FG-X distribution is subjected to positive EM loads the reduced effect of EM circuits prevails as opposed to pure mechanical loading. However, the EM circuits’ effect has a significant influence when the sign of the EM loads changes from positive to negative. For the rest of the shell geometries and CNTs distribution, the effect of EM circuits can be seen in Table 10.

Fig. 11

Effect of electro-magnetic circuits associated with different load cases on the damped transient response of CNTMEE spherical shell

Table 9 Effect of electro-magnetic circuits on the percentage difference in w* of various shell geometries with different CNT distributions and load cases ($V_{{{\text{CNT}}}}^{*} = 0.12$)

Fig. 12

Effect of electro-magnetic circuits on the damped transient response of CNTMEE spherical shell subjected to different electro-magnetic loads

Table 10 Effect of electro-magnetic circuits on the percentage difference in w* of various shell geometries with different CNT distributions and electro-magnetic loads ($V_{{{\text{CNT}}}}^{*} = 0.28$; load case-II)

The effect of coupling on the nonlinear transient response of the various FG-CNTMEE shells with different EM circuits is shown in Table 11. All three forms of load cases are considered. It can be seen from the results that the coupling fields play a significant role for spherical shell geometry with FG-X distribution. Further, the coupling effects are higher for the open circuit condition. Meanwhile, among all the load cases considered, the predominant coupling effect is seen when the shell is loaded with the load case-III. On the same ground, the study is extended to assess the influence of coupling on FG-CNTMEE shells subjected to EM loads (Table 12). In contrast to the coupling effect noticed when FG-CNTMEE shells are subjected to mechanical loading alone, a reduced effect is seen for positive EM loads. On the other hand, the negative EM loads show a magnified effect of coupling.

Table 11 Comparison of the coupling effect in terms of % difference of w* for various CNTMEE shell geometries

Table 12 Comparison of the coupling effect in terms of % difference of w* for various CNTMEE shell geometries

Conclusions

This article mainly focuses on evaluating the damped transient response of FG-CNTMEE shells embedded with the ACLD patch through a finite element approach. A special emphasis has been made on investigating the influence of different electromagnetic circuits and load cases on the damped response of the FG-CNTMEE shell. Also, the effect of coupling associated with these parameters is evaluated for accurate design and operation of these structures for sensors and actuators application. The equations of motion are derived using the principle of minimum potential energy through the condensation approach and solved via the direct iterative method. The outcomes of various numerical examples considered in this study can be encapsulated as follows:

• 1. Among the various shell geometries considered, damping can be effectively achieved for spherical shell geometry

• 2. The controlling ability of the ACLD patch enhances when the FG-CNTMEE is subjected to load case-III.

• 3. Hyperboloid shells and load case-II require a higher control voltage in contrast to the other shell geometries and load cases, respectively.

• 4. The improved volume fraction of CNTs and FG-X distribution help to dampen the vibrations with a minimal time.

• 5. The amplitude of vibrations of FG-CNTMEE shells subjected to negative electromagnetic loads reduces drastically over a period of time when compared with that of positive electromagnetic loads.

• 6. The effect of open circuit condition is predominant on the damped response of FG-CNTMEE shells as opposed to the closed circuits

• 7. The coupling between the fields has a significant role to play in the damped response of FG-CNTMEE shells. Further, the effect of coupling enhances with the open circuit electromagnetic condition and negative electromagnetic load.

Appendices

Appendix A

The expanded representation of various material property matrices of Eq. (2.a) can be shown as follows:

$$\begin{aligned} \left[ {\overline{C}_{b}^{h} } \right] & = \left[ {\begin{array}{*{20}c} {\overline{C}_{11}^{h} } & {\overline{C}_{12}^{h} } & {\overline{C}_{13}^{h} } & {\overline{C}_{16}^{h} } \\ {\overline{C}_{12}^{h} } & {\overline{C}_{22}^{h} } & {\overline{C}_{23}^{h} } & {\overline{C}_{26}^{h} } \\ {\overline{C}_{13}^{h} } & {\overline{C}_{32}^{h} } & {\overline{C}_{33}^{h} } & {\overline{C}_{36}^{h} } \\ {\overline{C}_{16}^{h} } & {\overline{C}_{26}^{h} } & {\overline{C}_{36}^{h} } & {\overline{C}_{66}^{h} } \\ \end{array} } \right];\;\left[ {\overline{C}_{s}^{h} } \right] = \left[ {\begin{array}{*{20}c} {\overline{C}_{55}^{h} } & {\overline{C}_{45}^{h} } \\ {\overline{C}_{45}^{h} } & {\overline{C}_{66}^{h} } \\ \end{array} } \right]; \, \\ \left\{ {\overline{e}^{h} } \right\} & = \left\{ {\begin{array}{*{20}c} {\overline{e}_{31}^{h} } \\ {\overline{e}_{32}^{h} } \\ {\overline{e}_{33}^{h} } \\ {\overline{e}_{36}^{h} } \\ \end{array} } \right\};\left\{ {\overline{q}^{h} } \right\} = \left\{ {\begin{array}{*{20}c} {\overline{q}_{31}^{h} } \\ {\overline{q}_{32}^{h} } \\ {\overline{q}_{33}^{h} } \\ {\overline{q}_{36}^{h} } \\ \end{array} } \right\}. \\ \end{aligned}$$

(27)

Also, the elastic stiffness coefficient matrices, piezoelectric coefficient matrices of 1–3 PZC (Eq. 3) can be given as follows:

$$\begin{aligned} \left[ {\overline{C}_{b}^{p} } \right] & = \left[ {\begin{array}{*{20}c} {\overline{C}_{11}^{p} } & {\overline{C}_{12}^{p} } & {\overline{C}_{13}^{p} } & {\overline{C}_{16}^{p} } \\ {\overline{C}_{12}^{p} } & {\overline{C}_{22}^{p} } & {\overline{C}_{23}^{p} } & {\overline{C}_{26}^{p} } \\ {\overline{C}_{13}^{p} } & {\overline{C}_{32}^{p} } & {\overline{C}_{33}^{p} } & {\overline{C}_{36}^{p} } \\ {\overline{C}_{16}^{p} } & {\overline{C}_{26}^{p} } & {\overline{C}_{36}^{p} } & {\overline{C}_{66}^{p} } \\ \end{array} } \right];\left[ {\overline{C}_{s}^{p} } \right] = \left[ {\begin{array}{*{20}c} {\overline{C}_{55}^{p} } & {\overline{C}_{45}^{p} } \\ {\overline{C}_{45}^{p} } & {\overline{C}_{66}^{p} } \\ \end{array} } \right];\;\left[ {\overline{C}_{bs}^{p} } \right] = \left[ {\begin{array}{*{20}c} {\overline{C}^{p}_{15} } & {\overline{C}^{p}_{25} } & {\overline{C}^{p}_{35} } & 0 \\ 0 & 0 & 0 & {\overline{C}^{p}_{46} } \\ \end{array} } \right]^{{\text{T}}} ; \\ \left[ {\overline{C}_{bs}^{p} } \right] & = \left[ {\begin{array}{*{20}c} {\overline{C}^{p}_{15} } & {\overline{C}^{p}_{25} } & {\overline{C}^{p}_{35} } & 0 \\ 0 & 0 & 0 & {\overline{C}^{p}_{46} } \\ \end{array} } \right]^{{\text{T}}} ; \\ \left\{ {\overline{e}_{b}^{p} } \right\} & = \left\{ {\begin{array}{*{20}c} {\overline{e}_{31}^{p} } \\ {\overline{e}_{32}^{p} } \\ {\overline{e}_{33}^{p} } \\ {\overline{e}_{36}^{p} } \\ \end{array} } \right\};\left\{ {\overline{e}_{s}^{p} } \right\} = \left\{ {\begin{array}{*{20}c} {\overline{e}_{35}^{p} } \\ {\overline{e}_{34}^{p} } \\ \end{array} } \right\}. \\ \end{aligned}$$

Appendix B

Equation (17) can be expanded using the FE parameters and can be re-written as follows:

$$\begin{gathered} \int\limits_{{\Omega ^{h} }} {\delta \left( {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{1} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\} + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}} \right)^{{\text{T}}} \times \left[ {\left[ {\bar{C}_{b}^{h} } \right] \times \left[ {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{1} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\}} \right.} \right.} \hfill \\ \left. { + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}} \right] + \left. {\left\{ {e_{b}^{h} } \right\}\frac{1}{h}\left[ {N_{\phi } } \right]\left\{ \phi \right\} + \left\{ {q_{b}^{h} } \right\}\frac{1}{H}\left[ {N_{\psi } } \right]\left\{ \psi \right\}} \right]{\text{d}}\Omega ^{h} \hfill \\ + \int\limits_{{\Omega ^{h} }} {\delta \left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{3} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)^{{\text{T}}} \times \left[ {\left[ {\bar{C}_{s}^{h} } \right]\left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{3} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)} \right]{\text{d}}\Omega ^{h} } \hfill \\ + \int\limits_{{\Omega ^{h} }} {\delta \left[ {\frac{1}{h}\left\{ {\phi ^{e} } \right\}^{{\text{T}}} \left[ {N_{\phi } } \right]^{{\text{T}}} } \right] \times \left[ {\left\{ {e_{b}^{h} } \right\}^{{\text{T}}} \left( {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{1} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)} \right.} - \left. { \in _{{33}}^{h} \left( {\frac{1}{h}\left[ {N_{\phi } } \right]\left\{ {\phi ^{e} } \right\}} \right) - d_{{33}}^{h} \left( {\frac{1}{h}\left[ {N_{\psi } } \right]\left\{ {\psi ^{e} } \right\}} \right)} \right]{\text{d}}\Omega ^{h} \hfill \\ + \int\limits_{{\Omega ^{h} }} {\delta \left[ {\frac{1}{h}\left\{ {\psi ^{e} } \right\}^{{\text{T}}} \left[ {N_{\psi } } \right]^{{\text{T}}} } \right]} \times \left[ {\left\{ {q_{b}^{h} } \right\}^{{\text{T}}} \left( {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{1} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)} \right. - \left. {d_{{33}}^{h} \left( {\frac{1}{h}\left[ {N_{\phi } } \right]\left\{ {\phi ^{e} } \right\}} \right) - \mu _{{33}}^{h} \left( {\frac{1}{h}\left[ {N_{\psi } } \right]\left\{ {\psi ^{e} } \right\}} \right)} \right]{\text{d}}\Omega ^{h} {\text{ }} \hfill \\ + \int\limits_{{\Omega ^{p} }} {\delta \left( {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{2} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\} + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}} \right)^{{\text{T}}} \times \left[ {\left[ {\bar{C}_{b}^{p} } \right] \times \left[ {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{2} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\}} \right.} \right.} \hfill \\ \left. {\left. { + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}} \right] + \left[ {\bar{C}_{{bs}}^{p} } \right]\left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{5} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right) + \frac{1}{{h_{p} }}\left\{ {e_{b}^{p} } \right\}V} \right]{\text{d}}\Omega ^{p} \hfill \\ \int\limits_{{\Omega ^{p} }} {\delta \left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{5} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)^{{\text{T}}} \times \left[ {\left[ {\bar{C}_{{bs}}^{p} } \right]^{{\text{T}}} \times \left[ {\left[ {B_{{tb}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{2} } \right]\left[ {B_{{rb}} } \right]\left\{ {d_{r}^{e} } \right\}} \right.} \right.} \hfill \\ \left. {\left. { + \frac{1}{2}\left[ {B_{1} } \right]\left[ {B_{2} } \right]\left\{ {d_{t}^{e} } \right\}} \right] + \left[ {\bar{C}_{s}^{p} } \right]\left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{5} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right) + \frac{1}{{h_{p} }}\left\{ {e_{s}^{p} } \right\}V} \right]{\text{d}}\Omega ^{p} \hfill \\ + \int\limits_{{\Omega ^{v} }} {\delta \left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{4} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)^{{\text{T}}} \left[ {\left[ {\overline{C} _{s}^{v} } \right]\left( {\left[ {B_{{ts}} } \right]\left\{ {d_{t}^{e} } \right\} + \left[ {Z_{4} } \right]\left[ {B_{{rs}} } \right]\left\{ {d_{r}^{e} } \right\}} \right)} \right]{\text{d}}\Omega ^{v} } \hfill \\ - \int\limits_{A} \delta \left\{ {d_{t} } \right\}^{{\text{T}}} \left\{ f \right\}dA + \int\limits_{A} {Q^{\phi } } \delta \left[ {N_{\phi } } \right]\left\{ \phi \right\}dA + \int\limits_{A} {Q^{\psi } } \delta \left[ {N_{\psi } } \right]\left\{ \psi \right\}{\text{d}}A \hfill \\ + \frac{1}{2}\left\{ {d_{t}^{e} } \right\}^{{\text{T}}} \left[ {M^{e} } \right]\left\{ {\ddot{d}_{t}^{e} } \right\}. \hfill \\ \end{gathered}$$

(29)

The different nonlinear and linear stiffness matrices, force vectors leading to Eq. (22) can be represented as follows:

$$\begin{aligned} \left[ {K_{{{\text{NL}}1}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{1} } \right]\left[ {B_{{tb}} } \right]} } {\text{ d}}x{\text{d}}y;\;\;\left[ {K_{{{\text{NL}}2}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{2} } \right]\left[ {B_{{rb}} } \right]} } {\text{ d}}xdy; \\ \left[ {K_{{{\text{NL}}3}}^{e} } \right] & = \frac{1}{4}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{1} } \right]\left[ {B_{1} } \right]} } \left[ {B_{2} } \right]{\text{ d}}x{\text{d}}y;\;\left[ {K_{{{\text{NL}}4}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{3} } \right]} } {\text{ }}\left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y; \\ \left[ {K_{{{\text{NL}}5}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{4} } \right]} } {\text{ }}\left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;\;\left[ {K_{{{\text{NL}}6}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{T} \left[ {D_{5} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y; \\ \left[ {K_{{{\text{NL}}7}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{1} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y;\left[ {K_{{{\text{NL}}8}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{T} \left[ {B_{1} } \right]^{T} \left[ {D_{{13}} } \right]} } {\text{ }}\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y; \\ \left[ {K_{{{\text{NL}}9}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{{14}} } \right]} } {\text{ }}\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;\left[ {K_{{{\text{NL}}10}}^{e} } \right] = \frac{1}{4}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{T} \left[ {B_{1} } \right]^{T} \left[ {D_{{13}} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y; \\ \left[ {K_{{{\text{NL}}11}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{{\text{T}}} \left[ {B_{1} } \right]^{{\text{T}}} \left[ {D_{{14}} } \right]} } {\text{ }}\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;\left[ {K_{{{\text{NL}}12}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{2} } \right]^{T} \left[ {B_{1} } \right]^{T} \left[ {D_{{15}} } \right]} } {\text{ }}\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y; \\ \left[ {K_{{{\text{NL}}13}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{{17}} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y;\left[ {K_{{{\text{NL}}14}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{T} \left[ {D_{{13}} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y; \\ \left[ {K_{{{\text{NL}}15}}^{e} } \right] & = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{24}} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y;\left[ {K_{{{\text{NL}}16}}^{e} } \right] = \frac{1}{2}\int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{T} \left[ {D_{{24}} } \right]} } {\text{ }}\left[ {B_{1} } \right]\left[ {B_{2} } \right]{\text{d}}x{\text{d}}y; \\ \end{aligned}$$

$$\begin{aligned} \left[ {K_{1}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{5} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} \;} \left[ {K_{2}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{6} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \;\left[ {K_{3}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{7} } \right]\left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;} } \;\left[ {K_{4}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{8} } \right]\left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{5}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{1} } \right]} \left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} \;\left[ {K_{6}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{2} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{7}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{3} } \right]\left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{8}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{4} } \right]\left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{9}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{9} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{10}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{T} \left[ {D_{{10}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{11}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{11}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{12}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{12}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{13}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{{17}} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{14}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{{18}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{15}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{{17s}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{16}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{{19}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{17}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{{13}} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{18}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{{14}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{19}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{{21}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{18}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{{14}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{21}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{24}} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{22}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{25}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{23}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{25}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{24}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{26}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{25}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{24}} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{26}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{28}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{27}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{29}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{28}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{30}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{29}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{31}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{30}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{32}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{31}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{33}} } \right]\left[ {B_{{ts}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{32}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{34}} } \right]\left[ {B_{{rs}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{33}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{{\text{T}}} \left[ {D_{{35}} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{34}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{{\text{T}}} \left[ {D_{{36}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{35}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{{\text{T}}} \left[ {D_{{37}} } \right]\left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{36}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\phi } } \right]^{{\text{T}}} \left[ {D_{{38}} } \right]\left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{37}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{{\text{T}}} \left[ {D_{{39}} } \right]\left[ {B_{{tb}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{38}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{{\text{T}}} \left[ {D_{{40}} } \right]\left[ {B_{{rb}} } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {K_{{39}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{{\text{T}}} \left[ {D_{{41}} } \right]\left[ {N_{\phi } } \right]{\text{d}}x{\text{d}}y;} } \left[ {K_{{40}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {N_{\psi } } \right]^{T} \left[ {D_{{42}} } \right]\left[ {N_{\psi } } \right]{\text{d}}x{\text{d}}y;} } \\ \left[ {F_{{{\text{tp}}N1}}^{e} } \right] & = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{1} } \right]^{{\text{T}}} \left[ {B_{2} } \right]\left[ {D_{{16}} } \right]{\text{d}}x{\text{d}}y;} } {\text{ }}\left[ {F_{{tp1}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{tb}} } \right]^{{\text{T}}} \left[ {D_{{23}} } \right]{\text{d}}x{\text{d}}y;} } \left[ {F_{{tp2}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{ts}} } \right]^{{\text{T}}} \left[ {D_{{27}} } \right]{\text{d}}x{\text{d}}y;} } {\text{ }}\left[ {F_{{rp1}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rb}} } \right]^{{\text{T}}} \left[ {D_{{20}} } \right]{\text{d}}x{\text{d}}y;} } {\text{ }}\left[ {F_{{rp2}}^{e} } \right] = \int\limits_{0}^{{a_{e} }} {\int\limits_{0}^{{b_{e} }} {\left[ {B_{{rs}} } \right]^{{\text{T}}} \left[ {D_{{27}} } \right]{\text{d}}x{\text{d}}y;} } \\ \end{aligned}$$

$$\begin{gathered} \left[ {K_{T1}^{e} } \right] = \left[ {K_{NL1} } \right] + \left[ {K_{NL3} } \right] + \left[ {K_{5} } \right] + \left[ {K_{NL17} } \right] + \left[ {K_{11} } \right];\left[ {K_{T2}^{e} } \right] = \left[ {K_{NL2} } \right] + \left[ {K_{6} } \right] + \left[ {K_{12} } \right]; \hfill \\ \left[ {K_{T3}^{e} } \right] = \left[ {K_{NL14} } \right] + \left[ {K_{7} } \right];\left[ {K_{T4}^{e} } \right] = \left[ {K_{NL15} } \right] + \left[ {K_{8} } \right];\left[ {K_{T5}^{e} } \right] = \left[ {K_{NL6} } \right] + \left[ {K_{1} } \right] + \left[ {K_{9} } \right]; \hfill \\ \left[ {K_{T6}^{e} } \right] = \left[ {K_{2} } \right] + \left[ {K_{10} } \right];\left[ {K_{T7}^{e} } \right] = \left[ {K_{NL8} } \right] + \left[ {K_{NL10} } \right] + \left[ {K_{17} } \right] + \left[ {K_{NL11} } \right] + \left[ {K_{19} } \right] + \left[ {K_{NL14} } \right]; \hfill \\ \left[ {K_{T8}^{e} } \right] = \left[ {K_{NL19} } \right] + \left[ {K_{NL12} } \right] + \left[ {K_{18} } \right] + \left[ {K_{20} } \right];\left[ {K_{T9}^{e} } \right] = \left[ {K_{NL13} } \right] + \left[ {K_{13} } \right] + \left[ {K_{15} } \right];\left[ {K_{T10}^{e} } \right] = \left[ {K_{14} } \right] + \left[ {K_{16} } \right];\left[ {K_{T11}^{e} } \right] = \left[ {K_{NL15} } \right] + \left[ {K_{21} } \right] + \left[ {K_{23} } \right];\left[ {K_{T12}^{e} } \right] = \left[ {K_{22} } \right] + \left[ {K_{24} } \right]; \hfill \\ \left[ {K_{T13}^{e} } \right] = \left[ {K_{NL16} } \right] + \left[ {K_{25} } \right] + \left[ {K_{27} } \right];\left[ {K_{T14}^{e} } \right] = \left[ {K_{26} } \right] + \left[ {K_{28} } \right] + \left[ {K_{32} } \right];\left[ {K_{T15}^{e} } \right] = \left[ {K_{T1} } \right] + \left[ {K_{T7} } \right] + \left[ {K_{T13} } \right];\left[ {K_{T16}^{e} } \right] = \left[ {K_{T2} } \right] + \left[ {K_{T8} } \right] + \left[ {K_{T14} } \right];\left[ {K_{T17}^{e} } \right] = \left[ {K_{T5} } \right] + \left[ {K_{T9} } \right] + \left[ {K_{T11} } \right] + \left[ {K_{T29} } \right]; \hfill \\ \left[ {K_{T18}^{e} } \right] = \left[ {K_{T6} } \right] + \left[ {K_{T10} } \right] + \left[ {K_{T12} } \right] + \left[ {K_{30} } \right]; \hfill \\ \left[ {K_{C1}^{{}} } \right] = - \left[ {K_{40} } \right]^{ - 1} \left[ {K_{37} } \right];\left[ {K_{C2}^{{}} } \right] = - \left[ {K_{40} } \right]^{ - 1} \left[ {K_{38} } \right];\left[ {K_{C3}^{{}} } \right] = - \left[ {K_{40} } \right]^{ - 1} \left[ {K_{39} } \right]; \hfill \\ \left[ {K_{C4}^{{}} } \right] = \left[ {K_{33} } \right] - \left[ {K_{36} } \right]\left[ {K_{C1} } \right];\left[ {K_{C5}^{{}} } \right] = \left[ {K_{34} } \right] - \left[ {K_{36} } \right]\left[ {K_{C2} } \right]; \hfill \\ \left[ {K_{C6}^{{}} } \right] = \left[ {K_{35} } \right] - \left[ {K_{36} } \right]\left[ {K_{C3} } \right];\left[ {K_{C7}^{{}} } \right] = - \left[ {K_{C6} } \right]^{ - 1} \left[ {K_{C4} } \right];\left[ {K_{C8}^{{}} } \right] = - \left[ {K_{C6} } \right]^{ - 1} \left[ {K_{C5} } \right]; \hfill \\ \left[ {K_{C9}^{{}} } \right] = \left[ {K_{T17} } \right] - \left[ {K_{4} } \right]\left[ {K_{C1} } \right];\left[ {K_{C10}^{{}} } \right] = \left[ {K_{T18} } \right] - \left[ {K_{4} } \right]\left[ {K_{C2} } \right];\left[ {K_{C11}^{{}} } \right] = \left[ {K_{3} } \right] - \left[ {K_{4} } \right]\left[ {K_{C3} } \right]; \hfill \\ \left[ {K_{C12}^{{}} } \right] = \left[ {K_{C9} } \right] - \left[ {K_{C11} } \right]\left[ {K_{C7} } \right];\left[ {K_{C13}^{{}} } \right] = \left[ {K_{C10} } \right] - \left[ {K_{C11} } \right]\left[ {K_{C8} } \right]; \hfill \\ \left[ {K_{C14}^{{}} } \right] = \left[ {K_{T15} } \right] - \left[ {K_{T4} } \right]\left[ {K_{C1} } \right];\left[ {K_{C15}^{{}} } \right] = \left[ {K_{T16} } \right] - \left[ {K_{T4} } \right]\left[ {K_{C2} } \right];\left[ {K_{C16}^{{}} } \right] = \left[ {K_{T3} } \right] - \left[ {K_{T4} } \right]\left[ {K_{C3} } \right]; \hfill \\ \left[ {K_{C17}^{{}} } \right] = \left[ {K_{C14} } \right] - \left[ {K_{C16} } \right]\left[ {K_{C7} } \right];\left[ {K_{C18}^{{}} } \right] = \left[ {K_{C15} } \right] - \left[ {K_{C16} } \right]\left[ {K_{C8} } \right]; \hfill \\ \left[ {K_{{}}^{*} } \right] = \left[ {K_{C17} } \right] - \left[ {K_{C18} } \right]\left[ {K_{C13} } \right]^{ - 1} \left[ {K_{C12} } \right]; \hfill \\ \left\{ {F_{{}}^{*} } \right\} = \left\{ F \right\} - \left( {\left\{ {F_{tp1} } \right\} + \left\{ {F_{tp2} } \right\} + \left\{ {F_{tpN1} } \right\}} \right)V + \left[ {K_{C18} } \right]\left[ {K_{C13} } \right]\left( {\left\{ {F_{rp1} } \right\} + \left\{ {F_{rp2} } \right\}} \right)V. \hfill \\ \end{gathered}$$

(30)

The various rigidity matrices contributing to the stiffness matrices and force vectors of Eq. (30) are shown as follows:

$$\begin{gathered} \left[ {D_{1} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {\bar{C}_{b}^{h} } \right]} {\text{ }}{\rm d}z;\left[ {D_{2} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {\bar{C}_{b}^{h} } \right]} \left[ {Z_{1} } \right]{\text{ }}{\rm d}z;\left[ {D_{3} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left\{ {\overline{e} _{b}^{h} } \right\}\frac{1}{h}} {\text{ }}{\rm d}z;\left[ {D_{4} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left\{ {\overline{q} _{b}^{h} } \right\}\frac{1}{h}{\text{ }}} {\rm d}z; \hfill \\ \left[ {D_{5} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{1} } \right]^{{\rm T}} \left[ {\bar{C}_{b}^{h} } \right]} {\text{ }}{\rm d}z;\left[ {D_{6} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{1} } \right]^{{\rm T}} \left[ {\bar{C}_{b}^{h} } \right]} \left[ {Z_{1} } \right]{\text{ }}{\rm d}z;\left[ {D_{7} } \right] = \int\limits_{{h1}}^{{h_{2} }} {\left[ {z_{1} } \right]^{{\rm T}} \left\{ {\overline{e} _{b}^{h} } \right\}\frac{1}{h}} {\text{ }}{\rm d}z; \hfill \\ \left[ {D_{8} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{1} } \right]^{{\rm T}} \left\{ {\overline{q} _{b}^{h} } \right\}} \frac{1}{h}{\rm d}z;\left[ {D_{9} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{3} } \right]^{{\rm T}} \left[ {\bar{C}_{s}^{h} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{10}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {Z_{3} } \right]^{{\rm T}} \left[ {\bar{C}_{s}^{h} } \right]} \left[ {Z_{3} } \right]{\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{11}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {\bar{C}_{s}^{h} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{12}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left[ {\bar{C}_{s}^{h} } \right]} \left[ {Z_{3} } \right]{\rm d}z;\left[ {D_{{13}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {\bar{C}_{b}^{p} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{14}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {\bar{C}_{b}^{p} } \right]} \left[ {Z_{2} } \right]{\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{14}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {\bar{C}_{{bs}}^{p} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{15}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {\bar{C}_{{bs}}^{p} } \right]} \left[ {Z_{5} } \right]{\text{ }}{\rm d}z;\left[ {D_{{16}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left\{ {e_{b}^{p} } \right\}\frac{1}{{h_{p} }}} {\text{ }}{\rm d}z;\left[ {D_{{17}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{2} } \right]^{{\rm T}} {\text{ }}\left[ {\bar{C}_{b}^{p} } \right]} {\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{17}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{2} } \right]^{{\rm T}} {\text{ }}\left[ {\bar{C}_{{bs}}^{p} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{18}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{2} } \right]^{{\rm T}} {\text{ }}\left[ {\bar{C}_{b}^{p} } \right]} \left[ {Z_{2} } \right]{\text{ }}{\rm d}z;\left[ {D_{{19}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{2} } \right]^{{\rm T}} {\text{ }}\left[ {\bar{C}_{{bs}}^{p} } \right]} \left[ {Z_{5} } \right]{\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{20}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {Z_{2} } \right]^{{\rm T}} \left\{ {e_{b}^{p} } \right\}\frac{1}{{h_{p} }}} {\text{ }}{\rm d}z;\left[ {D_{{21}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {\bar{C}_{{bs}}^{p} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{22}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {\bar{C}_{{bs}}^{p} } \right]} \left[ {Z_{5} } \right]{\text{ }}{\rm d}z;\left[ {D_{{23}} } \right] = \left[ {D_{{16}} } \right]; \hfill \\ \left[ {D_{{24}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {Z_{5} } \right]^{{\rm T}} \left[ {\bar{C}_{{bs}}^{p} } \right]^{{\rm T}} } {\rm d}z;\left[ {D_{{25}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {Z_{5} } \right]^{{\rm T}} \left[ {\bar{C}_{{bs}}^{p} } \right]^{{\rm T}} } \left[ {Z_{2} } \right]{\rm d}z;\left[ {D_{{25\_s}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {Z_{5} } \right]^{{\rm T}} \left[ {\bar{C}_{s}^{p} } \right]} {\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{26}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {Z_{5} } \right]^{{\rm T}} \left[ {\bar{C}_{s}^{p} } \right]^{{\rm T}} } \left[ {Z_{5} } \right]{\rm d}z;\left[ {D_{{27}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {\left[ {z_{5} } \right]^{{\rm T}} \left\{ {e_{s}^{p} } \right\}\frac{1}{{h_{p} }}} {\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{28}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {\bar{C}_{{bs}}^{p} } \right]^{{\rm T}} } \left[ {Z_{2} } \right]{\rm d}z;\left[ {D_{{29}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {\bar{C}_{s}^{p} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{30}} } \right] = \int\limits_{{h_{3} }}^{{h_{4} }} {{\text{ }}\left[ {\bar{C}_{s}^{p} } \right]} \left[ {Z_{5} } \right]{\rm d}z; \hfill \\ \left[ {D_{{31}} } \right] = \int\limits_{{h_{2} }}^{{h_{3} }} {{\text{ }}\left[ {Z_{4} } \right]^{{\rm T}} \left[ {\bar{C}_{s}^{v} } \right]{\text{ }}} {\rm d}z;\left[ {D_{{32}} } \right] = \int\limits_{{h_{2} }}^{{h_{3} }} {{\text{ }}\left[ {Z_{4} } \right]^{{\rm T}} \left[ {\bar{C}_{s}^{v} } \right]\left[ {Z_{4} } \right]{\text{ }}} {\rm d}z;\left[ {D_{{33}} } \right] = \int\limits_{{h_{2} }}^{{h_{3} }} {{\text{ }}\left[ {\bar{C}_{s}^{v} } \right]{\text{ }}} {\rm d}z; \hfill \\ \left[ {D_{{34}} } \right] = \int\limits_{{h_{2} }}^{{h_{3} }} {{\text{ }}\left[ {\bar{C}_{s}^{v} } \right]\left[ {Z_{4} } \right]{\text{ }}} {\rm d}z;\left[ {D_{{35}} } \right] = \left[ {D_{3} } \right]^{{\rm T}} ;\left[ {D_{{36}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left\{ {e_{b}^{h} } \right\}\frac{1}{h}\left[ {Z_{1} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{37}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\frac{{\overline{ \in } _{{33}}^{h} }}{h}} {\text{ }}{\rm d}z; \hfill \\ \left[ {D_{{38}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\frac{{\overline{d} _{{33}}^{h} }}{h}} {\text{ }}{\rm d}z;\left[ {D_{{39}} } \right] = \left[ {D_{4} } \right]^{{\rm T}} ;\left[ {D_{{40}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\left\{ {q_{b}^{h} } \right\}\frac{1}{h}\left[ {Z_{1} } \right]} {\text{ }}{\rm d}z;\left[ {D_{{41}} } \right] = \left[ {D_{{38}} } \right]; \hfill \\ \left[ {D_{{42}} } \right] = \int\limits_{{h_{1} }}^{{h_{2} }} {\frac{{\overline{\mu } _{{33}}^{h} }}{h}{\text{ }}} {\rm d}z. \hfill \\ \end{gathered}$$

(31)