Thermal vibration analysis of embedded graphene oxide powder-reinforced nanocomposite plates

Abstract

In this research, thermal vibration analysis of a graphene oxide powder-reinforced (GOPR) nanocomposite embedded plate is carried out once the plate is exposed to different types of thermal loading. The plate is reinforced with various functionally graded (FG) distributions through the thickness, namely uniform, X, V, and O in a comparative way to find out the most efficient model of GOPs’ distribution for the purpose of improving vibrational behaviors of the structure. Also, the Halpin–Tsai micromechanical model is employed to describe the material properties of an FG nanocomposite plate. The shear deformation effects are taken into account using a refined higher order shear deformation plate theory. Moreover, the governing equations of the structure have been derived using Hamilton’s principle and then solved analytically for a simply supported GOPR nanocomposite plate. Besides, detailed parametric studies are procured to show the influences of different variants on the natural frequency of the nanocomposite plates. Presented results reveal that the frequency responses of the nanocomposite plates in a thermal environment dramatically depend on the distribution pattern of the GOPs.

1 Introduction

Nowadays in the modern engineering systems, one can rarely find industries free from the utilization of the composite materials due to their distinctive properties that cannot be achieved by any of the constituents alone. The primary reason that composites are chosen for components is their remarkable weight saving as well as their relative stiffness and strength. In common, composites are composed of at least two materials, combined to enrich material properties superior to those of the individuals. Also, they are typically categorized with respect to their matrix constituent and their reinforcements. Fiber-reinforced and -laminated composites are the two groups of composites with outstanding properties such as high strength, specific stiffness, high resistance to fatigue failure and a large coefficient of thermal expansion which can provide the required engineering properties for the structural purposes. According to the mentioned properties of these groups of composites and their potential to be used in evolving applications, scientists have tried to analyze these materials as more as possible for different mechanical purposes. For example, Kant and Babu [31] surveyed the thermo-mechanical stability problem of fiber-reinforced composite (FRC) skew plates using a shear deformable theorem coupled with the finite element method (FEM). Anlas and Göker [4] investigated the vibration analysis of a laminated composite structure in which each layer was in a shape of a skew plate and reinforced with fibers to find out how skew angle can affect the natural frequency of this structure. In other researches, a combination of both analytical and experimental methods is utilized to study the buckling behavior of both cantilever I and open channel beams by considering shear effects [41, 42]. Also, many of the authors allocated their studies to the field of analyzing the mechanical characteristics of laminated composites (LCs). Liu et al. [34] presented an investigation of the buckling analysis of LC plates via an element-free method to show the efficiency of this method in such a stability problem. A global higher order plate theory was presented by Zhen and Wanji [68] to probe the free vibration problem of LCs. Urthaler and Reddy [55] investigated the bending response of LC plates to find out an accurate prediction of the global bending response of the plates subjected to large rotation. Shariyat [43] introduced a new theory for analyzing the thermally affected bending and vibration problems of sandwich plates to cover the continuity conditions between layers. Also, some investigations have been performed on LCs via non-uniform rational B-spline (NURBS) method [48, 53]. Carrera unified formulation (CUF) was employed by Tornabene et al. [54] to analyze the stability problem of doubly curved shells in the framework of numerical solutions. Demir et al. [18] studied the buckling behavior of the LC conical panels based on Donnell’s shell theory to show some geometrical effects on the critical buckling loads of the structure. The Fourier–Ritz method was applied by Wang et al. [57] with the aim of analyzing the vibrational behavior of LC shells and panels by considering various boundary conditions (BCs). Sobhani et al. [49] solved the stability problem of an LC with respect to the delamination effects in the framework of acoustic emission and signal processing techniques.

Furthermore, once elements with at least one dimension in nanoscale are selected as reinforcements, the composite has named a nanocomposite. Indeed, the outstanding mechanical properties of nanoparticles were appealing enough in the engineers’ opinion to be employed as reinforcement in composites. One of the most famous nanosize reinforcing elements is carbon nanotube (CNT) which is an important new class of technological materials that possess numerous novel and useful properties. Therefore, it is of high importance to analyze the mechanical behaviors of CNT-reinforced (CNTR) nanocomposites. In a remarkable endeavor, the Eshelby–Mori–Tanaka homogenization model was employed by Formica et al. [27] to investigate the vibration behavior of CNTR nanocomposites via FEM. Single-walled CNTs (SWCNTs) have attracted the attention of the researchers recently with their evolving applications such as reinforcements in composites, additives in polymers, catalysts and so on. For example, Shen and Zhang [47] investigated both thermo-elastic pre- and post-buckling responses of nanocomposite plates reinforced with SWCNTs to show how the nanofillers’ distribution type can improve the stability limits of nanocomposite plates. Also, Arani et al. [5] employed both FE and analytical methods to investigate effects of some variants such as aspect ratio, BCs and CNTs’ orientation on the buckling loads of SWCNTR multi-layered plates. Wang and Shen [58] presented a thermal analysis of the nonlinear vibrational behaviors of nanocomposite plates reinforced with SWCNTs via a higher order plate theory. Both static and dynamic FEM analyses of SWCNTR nanocomposite plates have been performed by Zhu et al. [69] by considering different types of reinforcements’ distributions. In addition, Shen and Xiang [44] probed the nonlinear thermo-elastic vibration behaviors of CNTR nanocomposite shells with respect to various distribution patterns of nanofillers. Yas and Samadi [62] solved the vibration and buckling problems of the CNTR nanocomposite beams numerically by considering the influences of the elastic foundation. Moreover, Wattanasakulpong and Ungbhakorn [59] surveyed static and dynamic behaviors of the embedded nanocomposite beams reinforced with SWCNTs by the means of Navier method. Lei et al. [32] implemented the Eshelby–Mori–Tanaka homogenization technique to account for the nanotubes’ aggregation while investigating the buckling behaviors of CNTR nanocomposite plates via an FE-based element-free method. In another research, Liew et al. [33] introduced a meshless approach for the purpose of studying the post-buckling responses of axially compressed CNTR nanocomposite panels. Also, Zhang et al. [65] employed first-order shear deformation plate theory incorporated with Ritz method to analyze the vibrational behaviors of CNTR skew nanocomposites. Wu et al. [60] found it significant to account for the geometrical imperfections once examining the nonlinear vibration behaviors of FG-CNTR nanocomposite beams. Civalek [17] considered five types of CNTs’ distribution for reinforcing the composite cylindrical shells and annular plates with the purpose of analyzing the vibrational responses of these structures. He also derived the governing equations of the motion based on transverse shear deformation theory via discrete singular convolution method. Ebrahimi and Farazmandnia [23] employed a higher order shear deformation beam theory to analyze the thermo-mechanical vibrational characteristics of sandwich beams with FG-CNTR nanocomposite face sheets. Ebrahimi and Rostami [25] have just analyzed the wave propagation problem of CNTR nanocomposite beams via different shear deformation theories. Also, Bakhadda et al. [6] carried out the dynamic and bending analyses of the CNTR nanocomposites. On the other hand, CNTs are not the only nanosize reinforcement which is used in the nanocomposites. Boron nitride nanotube (BNNT) and silicon carbide nanotubes (SiCNTs) are two kinds of nanotubes with superior mechanical properties. The buckling analysis of these nanotube materials was investigated by some of the researchers to show the static stability of these materials [36, 37]. Nanofillers are consisted of other carbon-based materials utilized in nanocomposites, too. For instance, graphene platelets (GPLs) and graphene oxide powders (GOPs) are recently employed by researchers to design and analyze novel nanocomposites. Suk et al. [52] investigated the mechanical properties of the GO by combining the AFM measurement with the FEM in a new approach for evaluating the mechanical properties of ultrathin membranes. The Halpin–Tsai model was employed by Shen et al. [45] for homogenization of the nanocomposites to investigate the effects of using GPLs, as reinforcements in a nanocomposite, on the nonlinear bending responses of a beam. Also, a higher order plate model is incorporated with the nonlinear theory of von-Kármán by some of the authors to consider for the impacts of thermal environment and elastic medium on the nonlinear bending and vibration characteristics of functionally graded graphene-reinforced composite (FG-GRC)-laminated plates [45, 46]. Also, the issue of the post-buckling problem of a porous GPL-reinforced (GPLR) nanocomposite beam is undertaken and studied by Barati and Zenkour [8] with respect to the influences of geometrical imperfection. Yang et al. [61] carried out an analysis of the stability of FG nanocomposite beams reinforced with GPLs. Also, Zhao et al. [67] studied the bending and vibration behaviors of an FG trapezoidal plate reinforced with GPLs by employing the modified Halpin–Tsai model and the rule of the mixture to predict the effective material properties. In addition, some mechanical analyses such as damping vibration and wave propagation of the embedded graphene sheets have been recently conducted by authors [20, 21] in thermal environments. Besides, researchers have also probed the vibration, bending and compressive buckling of the GPLR polymeric nanocomposite plates via Mindlin–Reissner theory [50, 51]. Bouadi et al. [11] and Mokhtar et al. [39] both analyzed the static stability of the single-layer graphene sheet based on novel higher order shear deformation theories. Also, the wave propagation analysis of GPLR nanocomposite structures with different shapes such as plates and shells have been performed in the recent years [22, 24]. Also, the GO is a novel nanofiller with astounding thermal [7, 16], mechanical and optical [63] properties. In the recent years, it is found that GO can be an excellent reinforcement for the plates with the polymer matrix to enhance the mechanical and functional properties of the polymer materials due to its remarkable compatibility with polymers [40]. The experiments on this novel nanofiller show that monolayer GO has the Young modulus of 0.25 ± 0.25 TPa [29]. Due to this fact, nanocomposites reinforced with GO have extraordinary tensile strength in addition to their low cost. GO has been also used in fabricating flexible displays and transparent conducting films, accumulators, and supercapacitors [38]. Moreover, owing to the GOs’ hierarchical structure, it can be utilized as an adsorbent material. Most recently, Zhang et al. [66] surveyed the buckling, bending and vibration problems of the GOP-reinforced (GOPR) nanocomposite beams via Timoshenko theory. To the best of the authors’ knowledge, the thermal vibration problem of an embedded FG-GOPR nanocomposite plate, subjected to different types of temperature rise, has never been studied up to now.

The present paper contains a free vibration analysis of GOPR nanocomposite plates under three types of thermal loadings and two different kinds of elastic foundations. The GOP nanoparticles are distributed through the thickness of the plates with various FG patterns according to the Halpin–Tsai scheme. The governing equations of the problem are obtained via Hamilton’s principle on the basis of refined higher order plate theory. Afterward, the achieved differential equations are solved analytically via Navier method. Various illustrative results are provided to investigate the effects of geometric parameters (including aspect ratio and length-to-thickness ratio), material parameters (such as GOPs’ weight fraction and GOPs’ distribution type) and external effects (such as various thermal loadings and different substrates) on the dimensionless natural frequency of the structure.

2 Theory and formulations

2.1 Material homogenization

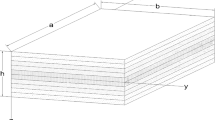
The studied structure, which is shown in Fig. 1, is consisted of an initial polymer matrix that is strengthened via a group of GOPs. The reinforcements are dispersed in the primary material via different patterns. These patterns can be generated by putting the nanofillers in a series of specified positions which can be calculated by following simple modeling:

Fig. 1

The geometry of a nanocomposite plate rested on a Winkler–Pasternak substrate

$$\left\{ \begin{gathered} {V_{{\text{GOP}}}}=V_{{{\text{GOP}}}}^{*}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{GOPR-U}} \hfill \\ {V_{{\text{GOP}}}}=\left( {2 - 4\frac{{|z|}}{h}} \right)V_{{{\text{GOP}}}}^{*}\,\,\,\,{\text{GOPR-O}} \hfill \\ {V_{{\text{GOP}}}}=4\frac{{|z|}}{h}V_{{{\text{GOP}}}}^{*}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{GOPR-X}} \hfill \\ {V_{{\text{GOP}}}}=\left( {1+2\frac{z}{h}} \right)V_{{{\text{GOP}}}}^{*}\,\,\,\,\,\,\,\,\,{\text{ }}\,{\text{GOPR-V}} \hfill \\ \end{gathered} \right.,$$

(1)

in which $V_{{{\text{GOP}}}}^{*}$ stands for the total volume fraction of GOPs and can be formulated as

$$V_{{{\text{GOP}}}}^{*}=\frac{{{W_{{\text{GOP}}}}}}{{{W_{{\text{GOP}}}}+\left( {{{{\rho _{{\text{GOP}}}}} \mathord{\left/ {\vphantom {{{\rho _{{\text{GOP}}}}} {{\rho _{\text{M}}}}}} \right. \kern-0pt} {{\rho _{\text{M}}}}}} \right)\left( {1 - {W_{{\text{GOP}}}}} \right)}},$$

(2)

where GOP and M subscripts are related to GOP reinforcements and the matrix, respectively. In addition, ρ stands for mass density and W_GOP denotes GOP weight fraction. Afterward, it is necessary to earn the effective Young’s modulus and the effective Poisson’s ratio of the nanocomposite. Herein, the Halpin–Tsai homogenization technique is extended for the derivation of the material properties [56, 66]. Now, Young’s modulus can be written as

$${E_{{\text{eff}}}}=0.49{E_{\text{l}}}+0.51{E_{\text{t}}},$$

(3)

where E_l and E_t account for longitudinal and transverse Young’s modulus of the composite, respectively. These elastic parameters can be calculated as [66]

$${E_{\text{l}}}=\frac{{1+{\xi _{\text{l}}}{\eta _{\text{l}}}{V_{{\text{GOP}}}}}}{{1 - {\eta _{\text{l}}}{V_{{\text{GOP}}}}}} \times {E_{\text{M}}},\,\,\,\,\,{E_{\text{t}}}=\frac{{1+{\xi _{\text{t}}}{\eta _{\text{t}}}{V_{{\text{GOP}}}}}}{{1 - {\eta _{\text{t}}}{V_{{\text{GOP}}}}}} \times {E_{\text{M}}},$$

(4)

where

$${\eta _{\text{l}}}=\frac{{\left( {{{{E_{{\text{GOP}}}}} \mathord{\left/ {\vphantom {{{E_{{\text{GOP}}}}} {{E_{\text{M}}}}}} \right. \kern-0pt} {{E_{\text{M}}}}}} \right) - 1}}{{\left( {{{{E_{{\text{GOP}}}}} \mathord{\left/ {\vphantom {{{E_{{\text{GOP}}}}} {{E_{\text{M}}}}}} \right. \kern-0pt} {{E_{\text{M}}}}}} \right)+{\xi _{\text{l}}}}}\,,\,\,\,\,\,{\eta _t}=\frac{{\left( {{{{E_{{\text{GOP}}}}} \mathord{\left/ {\vphantom {{{E_{{\text{GOP}}}}} {{E_{\text{M}}}}}} \right. \kern-0pt} {{E_{\text{M}}}}}} \right) - 1}}{{\left( {{{{E_{{\text{GOP}}}}} \mathord{\left/ {\vphantom {{{E_{{\text{GOP}}}}} {{E_{\text{M}}}}}} \right. \kern-0pt} {{E_{\text{M}}}}}} \right)+{\xi _{\text{t}}}}},$$

(5)

in which E_GOP and E_M stand for GOPs and matrix Young modulus, respectively. Also, the geometry factors (${\xi _{\text{l}}},\,\,{\xi _{\text{t}}}$) can be computed in the following form [66]:

$${\xi _{\text{l}}}={\xi _{\text{t}}}=\frac{{2\,{d_{{\text{GOP}}}}}}{{{h_{{\text{GOP}}}}}},$$

(6)

in which d_GOP and h_GOP are related to the diameter and thickness of GOPs, respectively. Now, the effective Poisson’s ratio of the composite can be achieved using the rule of the mixture in the following form:

$${\nu _{{\text{eff}}}}={\nu _{{\text{GOP}}}}{V_{{\text{GOP}}}}+{\nu _{\text{M}}}{V_{\text{M}}},$$

(7)

where V_GOP and V_M correspond with the volume fractions of GOPs and matrix, respectively. It is worth mentioning that the effective mass density can be computed in the same form as Poisson’s ratio is achieved in Eq. (7). The volume fractions are related to each other as

$${V_{{\text{GOP}}}}+{V_{\text{M}}}=1.$$

(8)

Now, it is time to calculate the coefficient of thermal expansion (CTE) for the GOPR nanocomposite in the following form of Van Es [56]:

$${\alpha _{{\text{eff}}}}={\alpha _{\text{M}}}+\frac{{{\alpha _{\text{M}}}+{\alpha _{{\text{GOP}}}}}}{{\tfrac{1}{{{K_{\text{M}}}}}+\tfrac{1}{{{K_{{\text{GOP}}}}}}}}\left[ {\tfrac{1}{{{K_{{\text{eff}}}}}}+\tfrac{1}{{{K_{\text{M}}}}}} \right],$$

(9)

in which K is the bulk moduli and α is the CTE. Also, the M and GOP subscripts are referred to the matrix and graphene oxide powder, respectively.

2.2 Refined higher order plate theory

The classical theory of plates possesses some simplifying assumptions which lead to some limitations in modeling. For example, this theory cannot present reliable results whenever the length-to-thickness ratio is inside 10. Due to this fact, the researchers have introduced some mathematical modeling which is able to estimate the shear stress and strain of the plate [1, 14]. In addition, Belkorissat et al. [10] studied the free vibration behavior of nanoplates using refined four variable plate theory. Also, Ahouel et al. [3] developed a new method for capturing both small scale and transverse shear deformation effect on the basis of shear deformation theory for the vibration, bending and buckling analysis of beams. In comparison with the other works in which the thickness stretching effect is taken into account [2, 13, 64], the very small difference was seen on the vibrational behavior of FG plates which could be negligible for the sake of simplicity. On the other hand, in some other researches, other versions of the classical kinematic theories are presented which are modified to be applicable in the cases that influences of the shear deformation cannot be ignored [9, 30]. For the purpose of capturing the shear effect in the higher order theorems, a shape function is presented in each theory. In this paper, the refined form of sinusoidal plate theory is utilized to achieve the kinematic relations of the plate. According to this theory, the displacement field of a plate can be written as

$${u_x}(x,y,z)=u(x,y) - z\frac{{\partial {w_{\text{b}}}}}{{\partial x}} - f(z)\frac{{\partial {w_{\text{s}}}}}{{\partial x}},$$

(10)

$${u_y}(x,y,z)=v(x,y) - z\frac{{\partial {w_{\text{b}}}}}{{\partial y}} - f(z)\frac{{\partial {w_{\text{s}}}}}{{\partial y}},$$

(11)

$${u_z}(x,y,z)={w_{\text{b}}}(x,y)+{w_{\text{s}}}(x,y),$$

(12)

where u is longitudinal displacement, and w_b and w_s are bending and shear deflections, respectively. The corresponding shape function of the employed theory can be expressed as

$$f(z)=z - \frac{h}{\pi }\sin \left( {\tfrac{{\pi z}}{h}} \right).$$

(13)

The non-zero strains of the plate can be expressed by the following equations:

$$\left\{ \begin{gathered} {\varepsilon _x} \hfill \\ {\varepsilon _y} \hfill \\ {\gamma _{xy}} \hfill \\ \end{gathered} \right\}=\left\{ \begin{gathered} \varepsilon _{x}^{0} \hfill \\ \varepsilon _{y}^{0} \hfill \\ \gamma _{{xy}}^{0} \hfill \\ \end{gathered} \right\}+z\left\{ \begin{gathered} k_{x}^{b} \hfill \\ k_{y}^{b} \hfill \\ k_{{xy}}^{b} \hfill \\ \end{gathered} \right\}+f(z)\left\{ \begin{gathered} k_{x}^{s} \hfill \\ k_{y}^{s} \hfill \\ k_{{xy}}^{s} \hfill \\ \end{gathered} \right\},{\text{ }}\left\{ \begin{gathered} {\gamma _{yz}} \hfill \\ {\gamma _{xz}} \hfill \\ \end{gathered} \right\}=g\left\{ \begin{gathered} \gamma _{{yz}}^{s} \hfill \\ \gamma _{{xz}}^{s} \hfill \\ \end{gathered} \right\},$$

(14)

where

$$\begin{gathered} \left\{ \begin{gathered} \varepsilon _{x}^{0} \hfill \\ \hfill \\ \varepsilon _{y}^{0} \hfill \\ \hfill \\ \gamma _{{xy}}^{0} \hfill \\ \end{gathered} \right\}\,=\,\left\{ \begin{gathered} {\text{ }}\frac{{\partial u}}{{\partial x}} \hfill \\ {\text{ }}\frac{{\partial v}}{{\partial y}} \hfill \\ \frac{{\partial u}}{{\partial y}}+\frac{{\partial v}}{{\partial x}} \hfill \\ \end{gathered} \right\}{\text{, }}\left\{ \begin{gathered} k_{x}^{b} \hfill \\ \hfill \\ k_{y}^{b} \hfill \\ \hfill \\ k_{{xy}}^{b} \hfill \\ \end{gathered} \right\}{\text{=}}\left\{ \begin{gathered} \frac{{ - {\partial ^2}{w_b}}}{{\partial {x^2}}} \hfill \\ \frac{{ - {\partial ^2}{w_b}}}{{\partial {y^2}}} \hfill \\ - 2\frac{{{\partial ^2}{w_b}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\}{\text{, }}\left\{ \begin{gathered} k_{x}^{s} \hfill \\ \hfill \\ k_{y}^{s} \hfill \\ \hfill \\ k_{{xy}}^{s} \hfill \\ \end{gathered} \right\}{\text{=}}\left\{ \begin{gathered} \frac{{ - {\partial ^2}{w_s}}}{{\partial {x^2}}} \hfill \\ \frac{{ - {\partial ^2}{w_s}}}{{\partial {y^2}}} \hfill \\ - 2\frac{{{\partial ^2}{w_s}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\}{\text{,}} \hfill \\ \left\{ \begin{gathered} \gamma _{{yz}}^{s} \hfill \\ \hfill \\ \gamma _{{xz}}^{s} \hfill \\ \end{gathered} \right\}=\left\{ \begin{gathered} \frac{{\partial {w_s}}}{{\partial y}} \hfill \\ \frac{{\partial {w_s}}}{{\partial x}} \hfill \\ \end{gathered} \right\},{\text{ }}g(z)=1 - \frac{{{\text{d}}f(z)}}{{{\text{d}}z}}. \hfill \\ \end{gathered}$$

(15)

2.3 Hamilton’s principle

Now, to derive the Euler–Lagrange equation, Hamilton’s principle can be defined as

$$\int\limits_{0}^{t} {\delta (U+V+K){\text{d}}t} =0.$$

(16)

Here, U is the strain energy, V work done by external forces and K is the kinetic energy. The variation of strain energy is written as

$$\delta U=\int\limits_{V} {{\sigma _{ij}}\delta {\varepsilon _{ij}}{\text{d}}V} =\int\limits_{V} {\left( {{\sigma _x}\delta {\varepsilon _x}+{\sigma _y}\delta {\varepsilon _y}+{\sigma _{xy}}\delta {\gamma _{xy}}+{\sigma _{yz}}\delta {\gamma _{yz}}+{\sigma _{xz}}\delta {\gamma _{xz}}} \right){\text{d}}V} .$$

(17)

Substituting Eqs. (10)–(15) in Eq. (17) yields:

$$\delta U=\int\limits_{0}^{L} {\left( \begin{gathered} {N_x}\frac{{\partial \delta u}}{{\partial x}} - M_{x}^{b}\frac{{{\partial ^2}\delta {w_b}}}{{\partial {x^2}}} - M_{x}^{s}\frac{{{\partial ^2}\delta {w_s}}}{{\partial {x^2}}}+Q\frac{{\partial {w_s}}}{{\partial x}}+{N_y}\frac{{\partial \delta v}}{{\partial y}} \hfill \\ - M_{y}^{b}\frac{{{\partial ^2}\delta {w_b}}}{{\partial {y^2}}} - M_{y}^{s}\frac{{{\partial ^2}\delta {w_s}}}{{\partial {y^2}}}+{N_{xy}}\left( {\frac{{\partial \delta u}}{{\partial y}}+\frac{{\partial \delta v}}{{\partial x}}} \right) - 2M_{{xy}}^{b}\frac{{{\partial ^2}\delta {w_b}}}{{\partial x\partial y}} \hfill \\ - 2M_{{xy}}^{s}\frac{{{\partial ^2}\delta {w_s}}}{{\partial x\partial y}}+{Q_{yz}}\frac{{\partial \delta {w_s}}}{{\partial y}}+{Q_{xz}}\frac{{\partial \delta {w_s}}}{{\partial x}} \hfill \\ \end{gathered} \right){\text{d}}x} ,$$

(18)

In which the variables introduced in arriving at the last expression are defined as follows:

$$\left[ {{N_i},M_{i}^{b},M_{i}^{b}} \right]=\int\limits_{A} {\left[ {1,z,f(z)} \right]{\sigma _i}{\text{d}}A} ,{\text{ }}i=(x,y,xy),$$

(19)

$${Q_i}=\int\limits_{A} {g(z){\sigma _i}{\text{d}}A} ,{\text{ }}i=(xz,yz).$$

(20)

Now, the first variation of work done by applied forces can be stated as

$$\delta V=\int\limits_{0}^{L} {\left( \begin{gathered} (N_{x}^{T})\frac{{\partial \delta \left( {{w_b}+{w_s}} \right)}}{{\partial x}}\frac{{\partial \left( {{w_b}+{w_s}} \right)}}{{\partial x}} - {k_w}\delta ({w_b}+{w_s})+{k_p}+\frac{{{\partial ^2}\delta \left( {{w_b}+{w_s}} \right)}}{{\partial {x^2}}} \hfill \\ +\,(N_{y}^{T})\frac{{\partial \delta \left( {{w_b}+{w_s}} \right)}}{{\partial y}}\frac{{\partial \left( {{w_b}+{w_s}} \right)}}{{\partial y}}+2\delta N_{{xy}}^{0}\frac{{\partial \left( {{w_b}+{w_s}} \right)}}{{\partial x}}\frac{{\partial \left( {{w_b}+{w_s}} \right)}}{{\partial y}} \hfill \\ \end{gathered} \right){\text{d}}x} .$$

(21)

In above relations, ${k_w}$ and ${k_p}$ are elastic foundation parameters and also it is assumed that the nanocomposite plate is under a biaxial thermal loading ($N_{x}^{T}=N_{y}^{T}={N^T}$); also, the shear loading is ignored ($N_{{xy}}^{0}=0)$. The thermal loading (${N^T})$ can be defined as

$${N^T}=\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\frac{{{E_{{\text{eff}}}}}}{{1 - {\nu _{{\text{eff}}}}}}{\alpha _{{\text{eff}}}}\Delta T} \right)} {\text{ d}}z.$$

(22)

The variation of the Kinetic energy can be expressed as

$$\delta K=\int\limits_{0}^{a} {\int\limits_{0}^{b} {\left( \begin{gathered} {I_0}\left( {\frac{{\partial u}}{{\partial t}}\frac{{\partial \delta u}}{{\partial t}}+\frac{{\partial v}}{{\partial t}}\frac{{\partial \delta v}}{{\partial t}}+\frac{{\partial ({w_b}+{w_s})}}{{\partial t}}\frac{{\partial \delta ({w_b}+{w_s})}}{{\partial t}}} \right) \hfill \\ - \,{I_1}\left( {\frac{{\partial u}}{{\partial t}}\frac{{\partial \delta {w_b}}}{{\partial x\partial t}}+\frac{{\partial {w_b}}}{{\partial x\partial t}}\frac{{\partial \delta u}}{{\partial t}}+\frac{{\partial v}}{{\partial t}}\frac{{\partial \delta {w_b}}}{{\partial y\partial t}}+\frac{{\partial {w_b}}}{{\partial y\partial t}}\frac{{\partial \delta v}}{{\partial t}}} \right)+{I_2}\left( {\frac{{\partial {w_b}}}{{\partial x\partial t}}\frac{{\partial \delta {w_b}}}{{\partial x\partial t}}+\frac{{\partial {w_b}}}{{\partial y\partial t}}\frac{{\partial \delta {w_b}}}{{\partial y\partial t}}} \right) \hfill \\ - \,{J_1}\left( {\frac{{\partial u}}{{\partial t}}\frac{{\partial \delta {w_s}}}{{\partial x\partial t}}+\frac{{\partial {w_b}}}{{\partial x\partial t}}\frac{{\partial \delta u}}{{\partial t}}+\frac{{\partial v}}{{\partial t}}\frac{{\partial \delta {w_s}}}{{\partial y\partial t}}+\frac{{\partial {w_s}}}{{\partial y\partial t}}\frac{{\partial \delta v}}{{\partial t}}} \right)+{K_2}\left( {\frac{{\partial {w_s}}}{{\partial x\partial t}}\frac{{\partial \delta {w_s}}}{{\partial x\partial t}}+\frac{{\partial {w_s}}}{{\partial y\partial t}}\frac{{\partial \delta {w_s}}}{{\partial y\partial t}}} \right) \hfill \\ {J_2}\left( {\frac{{\partial {w_b}}}{{\partial x\partial t}}\frac{{\partial \delta {w_s}}}{{\partial x\partial t}}+\frac{{\partial {w_s}}}{{\partial x\partial t}}\frac{{\partial \delta {w_b}}}{{\partial x\partial t}}+\frac{{\partial {w_b}}}{{\partial y\partial t}}\frac{{\partial \delta {w_s}}}{{\partial y\partial t}}+\frac{{\partial {w_s}}}{{\partial y\partial t}}\frac{{\partial \delta {w_b}}}{{\partial y\partial t}}} \right) \hfill \\ \end{gathered} \right)} } {\text{d}}x{\text{d}}y,$$

(23)

where

$$\left[ {{I_0},{I_1},{J_1},{I_2},{J_2},{K_2}} \right]=\int_{{ - h/2}}^{{h/2}} {\left( {1,z,f,{z^2},zf,{f^2}} \right)} \rho {\text{d}}z.$$

(24)

By Substituting Eqs. (18), (21) and (23) into Eq. (16) and setting the coefficients of$\delta u$, $\delta v$, δ${w}_{b}$, and δ${w}_{s}$ to zero, the following Euler–Lagrange equation can be obtained:

$$\frac{{\partial {N_x}}}{{\partial x}}+\frac{{\partial {N_{xy}}}}{{\partial y}}={I_0}\frac{{{\partial ^2}u}}{{\partial {t^2}}} - {I_1}\frac{{{\partial ^3}{w_b}}}{{\partial x\partial {t^2}}} - {J_1}\frac{{{\partial ^3}{w_s}}}{{\partial x\partial {t^2}}},$$

(25)

$$\frac{{\partial {N_{xy}}}}{{\partial x}}+\frac{{\partial {N_y}}}{{\partial y}}={I_0}\frac{{{\partial ^2}v}}{{\partial {t^2}}} - {I_1}\frac{{{\partial ^3}{w_b}}}{{\partial y\partial {t^2}}} - {J_1}\frac{{{\partial ^3}{w_s}}}{{\partial y\partial {t^2}}},$$

(26)

$$\begin{aligned} \frac{{{\partial ^2}M_{x}^{b}}}{{\partial {x^2}}} & +2\frac{{{\partial ^2}M_{{xy}}^{b}}}{{\partial x\partial y}}+\frac{{{\partial ^2}M_{y}^{b}}}{{\partial {y^2}}}+\frac{{\partial Q}}{{\partial x}} - {N^T}{\nabla ^2}({w_b}+{w_s}) - {k_w}({w_b}+{w_s}) \\ \quad & +{k_p}{\nabla ^2}({w_b}+{w_s})={I_0}\frac{{{\partial ^2}({w_b}+{w_s})}}{{\partial {t^2}}}+{I_1}\left( {\frac{{{\partial ^3}u}}{{\partial x\partial {t^2}}}+\frac{{{\partial ^3}v}}{{\partial y\partial {t^2}}}} \right) \\ \quad & - {I_2}{\nabla ^2}\left( {\frac{{{\partial ^2}{w_b}}}{{\partial {t^2}}}} \right) - {J_2}{\nabla ^2}\left( {\frac{{{\partial ^2}{w_s}}}{{\partial {t^2}}}} \right), \\ \end{aligned}$$

(27)

$$\begin{aligned} \frac{{{\partial ^2}M_{x}^{s}}}{{\partial {x^2}}}+ & 2\frac{{{\partial ^2}M_{{xy}}^{s}}}{{\partial x\partial y}}+\frac{{{\partial ^2}M_{y}^{s}}}{{\partial {y^2}}}+\frac{{\partial {Q_{xy}}}}{{\partial x}}+\frac{{\partial {Q_{yz}}}}{{\partial y}} - {N^T}{\nabla ^2}({w_b}+{w_s}) - {k_w}({w_b}+{w_s}) \\ \quad - & {k_p}{\nabla ^2}({w_b}+{w_s})={I_0}\frac{{{\partial ^2}({w_b}+{w_s})}}{{\partial {t^2}}}+{J_1}\left( {\frac{{{\partial ^3}u}}{{\partial x\partial {t^2}}}+\frac{{{\partial ^3}v}}{{\partial y\partial {t^2}}}} \right) \\ \quad - & {J_2}{\nabla ^2}\left( {\frac{{{\partial ^2}{w_b}}}{{\partial {t^2}}}} \right) - {K_2}{\nabla ^2}\left( {\frac{{{\partial ^2}{w_s}}}{{\partial {t^2}}}} \right), \\ \end{aligned}$$

(28)

in which ${\nabla }^{2}$ is the Laplacian operator.

2.4 Constitutive equations

The constitutive equations of the nanocomposite structure including the stress–strain relations of isotropic materials are expressed as follows to obtain the fundamental elastic equations of solids:

$${\sigma _{ij}}={C_{ijkl}}{\varepsilon _{kl}},$$

(29)

where σ_ij and ε_kl are the components of second-order stress and strain tensors, respectively; whereas, C_ijkl corresponds with the components of the fourth-order elasticity tensor. Whenever extending the aforementioned equation for a shear deformable plate, the following relations can be reached:

$$\left[ \begin{gathered} {\sigma _{xx}} \hfill \\ {\sigma _{yy}} \hfill \\ {\sigma _{yz}} \hfill \\ {\sigma _{xz}} \hfill \\ {\sigma _{xy}} \hfill \\ \end{gathered} \right]=\left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}&0&0&0 \\ {{Q_{12}}}&{{Q_{22}}}&0&0&0 \\ 0&0&{{Q_{44}}}&0&0 \\ 0&0&0&{{Q_{55}}}&0 \\ 0&0&0&0&{{Q_{66}}} \end{array}} \right]\left[ \begin{gathered} {\varepsilon _{xx}} \hfill \\ {\varepsilon _{yy}} \hfill \\ {\varepsilon _{yz}} \hfill \\ {\varepsilon _{xz}} \hfill \\ {\varepsilon _{xy}} \hfill \\ \end{gathered} \right],$$

(30)

where

$$\begin{aligned} {Q_{11}}= & \frac{{{E_{{\text{eff}}}}}}{{1 - {\nu _{{\text{eff}}}}^{2}}},\,\,\,\,\,{Q_{12}}={\nu _{{\text{eff}}}}{Q_{11}},\,\,\,\,\,{Q_{22}}={Q_{11}}, \\ {Q_{44}}= & {Q_{55}}={Q_{66}}={G_{{\text{eff}}}}, \\ \end{aligned}$$

(31)

in which E_eff and G_eff denote the Young and shear moduli of the nanocomposite, respectively. Integrating from Eqs. (25)–(28) over the cross-section area of the plate, the following equations can be written for the stress resultants:

$$\begin{aligned} \left\{ \begin{gathered} {N_X} \hfill \\ {N_y} \hfill \\ {N_{Xy}} \hfill \\ \end{gathered} \right\}=\, & \left( \begin{gathered} {A_{11}}{\text{ }}{A_{12}}{\text{ 0}} \hfill \\ {A_{21}}{\text{ }}{A_{22}}{\text{ 0}} \hfill \\ 0{\text{ 0 }}{A_{66}} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }}\frac{{\partial u}}{{\partial x}} \hfill \\ {\text{ }}\frac{{\partial v}}{{\partial y}} \hfill \\ \frac{{\partial u}}{{\partial y}}+\frac{{\partial v}}{{\partial x}} \hfill \\ \end{gathered} \right\}+\left( \begin{gathered} {B_{11}}{\text{ }}{B_{12}}{\text{ 0}} \hfill \\ {B_{21}}{\text{ }}{B_{22}}{\text{ 0}} \hfill \\ 0{\text{ 0 }}{B_{66}} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }} - \frac{{{\partial ^2}{w_b}}}{{\partial {u^2}}} \hfill \\ {\text{ }} - \frac{{{\partial ^2}{w_b}}}{{\partial {y^2}}}{\text{ }} \hfill \\ - 2\frac{{{\partial ^2}{w_b}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\} \\ & {\text{+}}\left( \begin{gathered} B_{{11}}^{s}{\text{ }}B_{{12}}^{s}{\text{ 0}} \hfill \\ B_{{21}}^{s}{\text{ }}B_{{22}}^{s}{\text{ 0}} \hfill \\ 0{\text{ 0 }}B_{{66}}^{s} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }} - \frac{{{\partial ^2}{w_s}}}{{\partial {u^2}}} \hfill \\ {\text{ }} - \frac{{{\partial ^2}{w_s}}}{{\partial {y^2}}}{\text{ }} \hfill \\ - 2\frac{{{\partial ^2}{w_s}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

(32)

$$\begin{aligned} \left\{ \begin{gathered} M_{x}^{b} \hfill \\ M_{y}^{b} \hfill \\ M_{{xy}}^{b} \hfill \\ \end{gathered} \right\}= \,& \left( \begin{gathered} {B_{11}}{\text{ }}{B_{12}}{\text{ 0}} \hfill \\ {B_{21}}{\text{ }}{B_{22}}{\text{ 0}} \hfill \\ 0{\text{ 0 }}{B_{66}} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }}\frac{{\partial u}}{{\partial x}} \hfill \\ {\text{ }}\frac{{\partial v}}{{\partial y}} \hfill \\ \frac{{\partial u}}{{\partial y}}+\frac{{\partial v}}{{\partial x}} \hfill \\ \end{gathered} \right\}+\left( \begin{gathered} {D_{11}}{\text{ }}{D_{12}}{\text{ 0}} \hfill \\ {D_{21}}{\text{ }}{D_{22}}{\text{ 0}} \hfill \\ 0{\text{ 0 }}{D_{66}} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }} - \frac{{{\partial ^2}{w_b}}}{{\partial {u^2}}} \hfill \\ {\text{ }} - \frac{{{\partial ^2}{w_b}}}{{\partial {y^2}}}{\text{ }} \hfill \\ - 2\frac{{{\partial ^2}{w_b}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\} \\ & {\text{+}}\left( \begin{gathered} D_{{11}}^{s}{\text{ }}D_{{12}}^{s}{\text{ 0}} \hfill \\ D_{{21}}^{s}{\text{ }}D_{{22}}^{s}{\text{ 0}} \hfill \\ 0{\text{ 0 }}D_{{66}}^{s} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }} - \frac{{{\partial ^2}{w_s}}}{{\partial {u^2}}} \hfill \\ {\text{ }} - \frac{{{\partial ^2}{w_s}}}{{\partial {y^2}}}{\text{ }} \hfill \\ - 2\frac{{{\partial ^2}{w_s}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

(33)

$$\begin{aligned} \left\{ \begin{gathered} M_{x}^{s} \hfill \\ M_{y}^{s} \hfill \\ M_{{xy}}^{s} \hfill \\ \end{gathered} \right\}= \,& \left( \begin{gathered} B_{{11}}^{s}{\text{ }}B_{{12}}^{s}{\text{ 0}} \hfill \\ B_{{21}}^{s}{\text{ }}B_{{22}}^{s}{\text{ 0}} \hfill \\ 0{\text{ 0 }}B_{{66}}^{s} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }}\frac{{\partial u}}{{\partial x}} \hfill \\ {\text{ }}\frac{{\partial v}}{{\partial y}} \hfill \\ \frac{{\partial u}}{{\partial y}}+\frac{{\partial v}}{{\partial x}} \hfill \\ \end{gathered} \right\}+\left( \begin{gathered} D_{{11}}^{s}{\text{ }}D_{{12}}^{s}{\text{ 0}} \hfill \\ D_{{21}}^{s}{\text{ }}D_{{22}}^{s}{\text{ 0}} \hfill \\ 0{\text{ 0 }}D_{{66}}^{s} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }} - \frac{{{\partial ^2}{w_b}}}{{\partial {u^2}}} \hfill \\ {\text{ }} - \frac{{{\partial ^2}{w_b}}}{{\partial {y^2}}}{\text{ }} \hfill \\ - 2\frac{{{\partial ^2}{w_b}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\} \\ & {\text{+}}\left( \begin{gathered} H_{{11}}^{s}{\text{ }}H_{{12}}^{s}{\text{ 0}} \hfill \\ H_{{21}}^{s}{\text{ }}H_{{22}}^{s}{\text{ 0}} \hfill \\ 0{\text{ 0 }}H_{{66}}^{s} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} {\text{ }} - \frac{{{\partial ^2}{w_s}}}{{\partial {u^2}}} \hfill \\ {\text{ }} - \frac{{{\partial ^2}{w_s}}}{{\partial {y^2}}}{\text{ }} \hfill \\ - 2\frac{{{\partial ^2}{w_s}}}{{\partial x\partial y}} \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

(34)

$$\left\{ \begin{gathered} {Q_x} \hfill \\ {Q_y} \hfill \\ \end{gathered} \right\}=\left( \begin{gathered} A_{{44}}^{s}{\text{ 0}} \hfill \\ 0{\text{ }}A_{{55}}^{s} \hfill \\ \end{gathered} \right)\left\{ \begin{gathered} \frac{{\partial {w_s}}}{{\partial x}} \hfill \\ \frac{{\partial {w_s}}}{{\partial y}} \hfill \\ \end{gathered} \right\}.$$

(35)

In Eqs. (32)–(35), the cross-sectional rigidities are given by following relations:

$$\left\{ \begin{gathered} {A_{11}}{\text{ }}{B_{11}}{\text{ }}{D_{11}}{\text{ }}B_{{11}}^{s}{\text{ }}D_{{11}}^{s}{\text{ }}H_{{11}}^{s} \hfill \\ {A_{12}}{\text{ }}{B_{12}}{\text{ }}{D_{12}}{\text{ }}B_{{12}}^{s}{\text{ }}D_{{12}}^{s}{\text{ }}H_{{12}}^{s} \hfill \\ {A_{66}}{\text{ }}{B_{66}}{\text{ }}{D_{66}}{\text{ }}B_{{66}}^{s}{\text{ }}D_{{66}}^{s}{\text{ }}H_{{66}}^{s} \hfill \\ \end{gathered} \right\}=\int_{\begin{subarray}{l} \\ - \frac{h}{2} \end{subarray} }^{\begin{subarray}{l} \frac{h}{2} \\ \end{subarray} } {\frac{{{E_{{\text{eff}}}}}}{{1 - \nu _{{{\text{eff}}}}^{2}}}\left( {1,z,{z^2},f(z),zf(z),{f^2}(z)} \right)} \left\{ \begin{gathered} {\text{ }}1 \hfill \\ {\text{ }}{\nu _{{\text{eff}}}} \hfill \\ \frac{{1 - {\nu _{{\text{eff}}}}}}{2} \hfill \\ \end{gathered} \right\}{\text{d}}z,$$

(36)

$$({A_{22}},{B_{22}},{D_{22}},B_{{22}}^{s},D_{{22}}^{s},H_{{22}}^{s})=({A_{11}},{B_{11}},{D_{11}},B_{{11}}^{s},D_{{11}}^{s},H_{{11}}^{s}),$$

(37)

$$A_{{44}}^{s}=A_{{55}}^{s}=\int_{\begin{subarray}{l} \\ - \frac{h}{2} \end{subarray} }^{\begin{subarray}{l} \frac{h}{2} \\ \end{subarray} } {{\text{ }}\frac{{{E_{{\text{eff}}}}}}{{2(1+{\nu _{{\text{eff}}}})}}({g^2}(z)} ){\text{ d}}z.$$

(38)

By substituting Eqs. (32)–(35) into Eqs. (25)–(28), the governing equations of nanocomposite plate can be directly written in terms of displacements (u, v, ${w}_{b}$, and ${w}_{s}$) as

$$\begin{aligned} & {A_{11}}\frac{{{\partial ^2}u}}{{\partial {x^2}}}+({A_{12}}+{A_{66}})\frac{{{\partial ^2}v}}{{\partial x\partial y}}+{A_{66}}\frac{{{\partial ^2}u}}{{\partial {y^2}}} - {B_{11}}\frac{{{\partial ^3}{w_b}}}{{\partial {x^3}}} \\ & \quad - ({B_{12}}+2{B_{66}})\frac{{{\partial ^3}{w_b}}}{{\partial x\partial {y^2}}} - B_{s}^{{11}}\frac{{{\partial ^3}{w_s}}}{{\partial {x^3}}} \\ & \quad - (B_{{12}}^{s}+2B_{{66}}^{s})\frac{{{\partial ^3}{w_s}}}{{\partial x\partial {y^2}}} - {I_0}\frac{{{\partial ^2}u}}{{\partial {t^2}}}+{I_1}\frac{{{\partial ^2}{w_b}}}{{\partial x\partial {t^2}}}+{J_1}\frac{{{\partial ^2}{w_s}}}{{\partial x\partial {t^2}}}=0, \\ \end{aligned}$$

(39)

$$\begin{aligned} & {A_{22}}\frac{{{\partial ^2}v}}{{\partial {y^2}}}+({A_{12}}+{A_{66}})\frac{{{\partial ^2}u}}{{\partial x\partial y}}+{A_{66}}\frac{{{\partial ^2}v}}{{\partial {x^2}}} \\ & \quad - {B_{11}}\frac{{{\partial ^3}{w_b}}}{{\partial {x^3}}} - {B_{22}}\frac{{{\partial ^3}{w_b}}}{{\partial {y^3}}} - ({B_{12}}+2{B_{66}})\frac{{{\partial ^2}{w_b}}}{{\partial {x^2}\partial y}} - B_{s}^{{22}}\frac{{{\partial ^3}{w_s}}}{{\partial {y^3}}} \\ & \quad - (B_{{12}}^{s}+2B_{{66}}^{s})\frac{{{\partial ^3}{w_s}}}{{\partial {x^2}\partial y}} - {I_0}\frac{{{\partial ^2}v}}{{\partial {t^2}}}+{I_1}\frac{{{\partial ^2}{w_b}}}{{\partial y\partial {t^2}}}+{J_1}\frac{{{\partial ^2}{w_s}}}{{\partial y\partial {t^2}}}=0, \\ \end{aligned}$$

(40)

$$\begin{aligned} & {B_{11}}\frac{{{\partial ^3}u}}{{\partial {x^3}}}+({B_{12}}+2{B_{66}})\frac{{{\partial ^3}u}}{{\partial x\partial {y^2}}}+{B_{22}}\frac{{{\partial ^3}v}}{{\partial {y^3}}} \\ & \quad - ({B_{12}}+2{B_{66}})\frac{{{\partial ^3}v}}{{\partial {x^2}\partial y}} - {D_{11}}\frac{{{\partial ^4}{w_b}}}{{\partial {x^4}}} \\ & \quad - 2({D_{12}}+2{D_{66}})\frac{{{\partial ^4}{w_b}}}{{\partial {x^2}\partial {y^2}}} - {D_{22}}\frac{{{\partial ^4}{w_b}}}{{\partial {y^4}}} \\ & \quad - D_{{11}}^{s}\frac{{{\partial ^4}{w_s}}}{{\partial {x^4}}} - 2(D_{{12}}^{s}+2D_{{66}}^{s})\frac{{{\partial ^4}{w_s}}}{{\partial {x^2}\partial {y^2}}} \\ & \quad - D_{{22}}^{s}\frac{{{\partial ^4}{w_s}}}{{\partial {y^4}}} - {I_0}\frac{{{\partial ^2}({w_b}+{w_s})}}{{\partial {t^2}}} \\ & \quad - {I_1}\left( {\frac{{{\partial ^2}u}}{{\partial x\partial {t^2}}}+\frac{{{\partial ^2}v}}{{\partial y\partial {t^2}}}} \right)+{I_2}{\nabla ^2}\frac{{{\partial ^2}{w_b}}}{{\partial {t^2}}}+{J_2}{\nabla ^2}\frac{{{\partial ^2}{w_s}}}{{\partial {t^2}}} \\ & \quad +({k_p} - {N^T}){\nabla ^2}({w_b}+{w_s}) - {k_w}({w_b}+{w_s})=0, \\ \end{aligned}$$

(41)

$$\begin{aligned} & B_{{11}}^{s}\frac{{{\partial ^3}u}}{{\partial {x^3}}}+(B_{{12}}^{s}+2B_{{66}}^{s})\frac{{{\partial ^3}u}}{{\partial x\partial {y^2}}}+B_{{22}}^{s}\frac{{{\partial ^3}v}}{{\partial {y^3}}} \\ & \quad - (B_{{12}}^{s}+2B_{{66}}^{s})\frac{{{\partial ^3}v}}{{\partial {x^2}\partial y}} - D_{{11}}^{s}\frac{{{\partial ^4}{w_b}}}{{\partial {x^4}}} \\ & \quad - 2(D_{{12}}^{s}+2D_{{66}}^{s})\frac{{{\partial ^4}{w_b}}}{{\partial {x^2}\partial {y^2}}} - D_{{22}}^{s}\frac{{{\partial ^4}{w_b}}}{{\partial {y^4}}} \\ & \quad - H_{{11}}^{s}\frac{{{\partial ^4}{w_s}}}{{\partial {x^4}}} - 2(H_{{12}}^{s}+2H_{{66}}^{s})\frac{{{\partial ^4}{w_s}}}{{\partial {x^2}\partial {y^2}}} \\ & \quad - H_{{22}}^{s}\frac{{{\partial ^4}{w_s}}}{{\partial {y^4}}}+A_{{44}}^{s}{\nabla ^2}{w_s} - {I_0}\frac{{{\partial ^2}({w_b}+{w_s})}}{{\partial {t^2}}} - {J_1}\left( {\frac{{{\partial ^2}u}}{{\partial x\partial {t^2}}}+\frac{{{\partial ^2}v}}{{\partial y\partial {t^2}}}} \right)+{J_2}{\nabla ^2}\frac{{{\partial ^2}{w_b}}}{{\partial {t^2}}} \\ & \quad +{K_2}{\nabla ^2}\frac{{{\partial ^2}{w_s}}}{{\partial {t^2}}}+({k_p} - {N^T}){\nabla ^2}({w_b}+{w_s}) - {k_w}({w_b}+{w_s})=0. \\ \end{aligned}$$

(42)

3 Solution procedure

Here, on the basis of the Navier method, an analytical solution of the governing equations for free vibration of a simply supported FG-GOPR nanocomposite plate is presented. To satisfy the simply supported boundary condition, the displacement fields are in the following form:

$$u=\sum\limits_{{m=1}}^{\infty } {\sum\limits_{{n=1}}^{\infty } {{U_{mn}}\cos (\alpha x)\sin (\beta y){\text{ }}{{\text{e}}^{i{\omega _n}t}}} } ,$$

(43)

$$v=\sum\limits_{{m=1}}^{\infty } {\sum\limits_{{n=1}}^{\infty } {{V_{mn}}\sin (\alpha x)\cos (\beta y){\text{ }}{{\text{e}}^{i{\omega _n}t}}} } ,$$

(44)

$${w_b}=\sum\limits_{{m=1}}^{\infty } {\sum\limits_{{n=1}}^{\infty } {{W_{bmn}}\sin (\alpha x)\sin (\beta y){\text{ }}{{\text{e}}^{i{\omega _n}t}}} } ,$$

(45)

$${w_s}=\sum\limits_{{m=1}}^{\infty } {\sum\limits_{{n=1}}^{\infty } {{W_{smn}}\sin (\alpha x)\sin (\beta y){\text{ }}{{\text{e}}^{i{\omega _n}t}}} } ,$$

(46)

where ${U_{mn}}$, ${V_{mn}}$, ${W_{bmn}}$, and ${W_{smn}}$ are the unknown Fourier coefficients, $\alpha =\frac{{m\pi }}{a}$, and $\beta =\frac{{n\pi }}{b}$. Once Eqs. (43)–(46) are inserted in Eqs. (39)–(44) respectively, the following relation can be obtained:

$$\left\{ {\left( {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}&{{k_{14}}} \\ {{k_{21}}}&{{k_{22}}}&{{k_{23}}}&{{k_{24}}} \\ {{k_{31}}}&{{k_{32}}}&{{k_{33}}}&{{k_{34}}} \\ {{k_{41}}}&{{k_{42}}}&{{k_{43}}}&{{k_{44}}} \end{array}} \right) - {\omega ^2}\left( {\begin{array}{*{20}{c}} {{m_{11}}}&{{m_{12}}}&{{m_{13}}}&{{m_{14}}} \\ {{m_{21}}}&{{m_{22}}}&{{m_{23}}}&{{m_{24}}} \\ {{m_{31}}}&{{m_{32}}}&{{m_{33}}}&{{m_{34}}} \\ {{m_{41}}}&{{m_{42}}}&{{m_{43}}}&{{m_{44}}} \end{array}} \right)} \right\}\left\{ \begin{gathered} {U_{mn}} \hfill \\ {V_{mn}} \hfill \\ {W_{bmn}} \hfill \\ {W_{smn}} \hfill \\ \end{gathered} \right\}=0,$$

(47)

in which K and M are the stiffness and mass matrix, respectively. The k_ij and m_ij arrays can be calculated in the following form:

$$\begin{aligned} {k_{11}}= & - ({A_{11}}{\alpha ^2}+{A_{66}}{\beta ^2}),{\text{ }}{k_{12}}= - \alpha \beta ({A_{12}}+{A_{66}}),{\text{ }}{k_{13}}={\alpha ^3}{B_{11}}+\alpha {\beta ^2}({B_{12}}+2{B_{66}}),{\text{ }} \\ {k_{14}}= & B_{{11}}^{s}{\alpha ^3}+\alpha {\beta ^2}(B_{{12}}^{s}+2B_{{66}}^{s}),{\text{ }}{k_{21}}={k_{12}},{\text{ }}{k_{22}}= - ({\beta ^2}{A_{22}}+{\alpha ^2}{A_{66}}), \\ {k_{23}}= & {\beta ^3}{B_{22}}+\beta {\alpha ^2}({B_{12}}+2{B_{66}}),{\text{ }}{k_{24}}={\beta ^3}B_{{22}}^{s}+\beta {\alpha ^2}(B_{{12}}^{s}+2B_{{66}}^{s}),{\text{ }}{k_{31}}={k_{13}}, \\ {k_{32}}= & {k_{23}},{\text{ }}{k_{33}}= - ({\alpha ^4}{D_{11}}+2{\alpha ^2}{\beta ^2}({D_{12}}+2{D_{66}})+{\beta ^4}{D_{22}}+{k_w}+({\alpha ^2}+{\beta ^2})({k_p} - {N^T}), \\ {k_{34}}= & - ({\alpha ^4}D_{{11}}^{s}+2{\alpha ^2}{\beta ^2}(D_{{12}}^{s}+2D_{{66}}^{s})+{\beta ^4}D_{{22}}^{s}+{k_w}+({\alpha ^2}+{\beta ^2})({k_p} - {N^T}),{\text{ }} \\ {k_{42}}= & {k_{24}},{\text{ }}{k_{43}}={k_{34}}{\text{, }}{k_{41}}={k_{14}}{\text{, }} \\ {k_{44}}= & - ({\alpha ^4}H_{{11}}^{s}+2{\alpha ^2}{\beta ^2}(H_{{12}}^{s}+2H_{{66}}^{s})+{\beta ^4}H_{{22}}^{s}+{k_w}+({\alpha ^2}+{\beta ^2})({A^s}+{k_p} - {N^T}), \\ {m_{11}}= & {I_0},{\text{ }}{m_{12}}=0,{\text{ }}{m_{13}}= - {I_1}\alpha ,{\text{ }}{m_{14}}= - {J_1}\alpha , \\ {m_{21}}= & 0,{\text{ }}{m_{22}}={I_0},{\text{ }}{m_{23}}= - {I_1}\beta ,{\text{ }}{m_{24}}{\text{=}} - {J_1}\beta , \\ {m_{31}}= & {m_{13}}{\text{, }}{m_{32}}{\text{=}}{m_{23}}{\text{, }}{m_{33}}{\text{=}}{I_0}+{I_2}{\text{(}}{\alpha ^2}+{\beta ^2}{\text{), }}{m_{34}}{\text{=}}{I_0}+{J_2}{\text{(}}{\alpha ^2}+{\beta ^2}{\text{),}} \\ {m_{41}}= & {m_{14}}{\text{, }}{m_{42}}{\text{=}}{m_{24}}{\text{, }}{m_{43}}{\text{=}}{m_{34}}{\text{, }}{m_{44}}{\text{=}}{I_0}+{K_2}{\text{(}}{\alpha ^2}+{\beta ^2}{\text{)}}. \\ \end{aligned}$$

4 Thermal loadings

Applying the thermal effects to the structure is procured through considering the temperature rise as a function of thickness according to the previous works in the open literature [12, 15, 19, 26, 35].

4.1 Uniform temperature rise (UTR)

By assuming an FG-GOPR nanocomposite plate at reference temperature ${T_0}=300\;{\text{K}}$ (room temperature) and final temperature $T$, the uniform temperature change can be defined as $\Delta T=T - {T_0}$.

4.2 Linear temperature rise (LTR)

The temperature of an FG-GOPR nanocomposite plate can be raised linearly through the thickness through the following formulation by considering the plate to be thin enough:

$$T={T_0}+~\Delta T\left( {\frac{1}{2}+\frac{z}{h}} \right),$$

where $T$ is the final temperature and ${T_0}$ is the reference temperature of the plate.

4.3 Sinusoidal temperature rise (STR)

When the plate is subjected to sinusoidal temperature rise, the temperature distribution throughout the thickness can be expressed as

$$T={T_0}+~\Delta T\left( {1 - \cos \frac{\pi }{2}\left( {\frac{1}{2}+\frac{z}{h}} \right)} \right),$$

where $\Delta T=T - {T_0}$ is the temperature change.

5 Numerical results and discussion

Through this section, the effects of various parameters such as three kinds of thermal loading, GOPs’ weight fraction, aspect ratio, length to thickness ratio, two kinds of elastic foundation and different types of GOPs’ distribution on the critical buckling loads of GOPR nanocomposite plates will be figured out by interpreting the numerical results stated in the following. For the sake of simplicity, the dimensionless form of the natural frequency, Winkler and Pasternak parameters are defined in the following form:

$${K_w}={k_w}\frac{{{a^4}}}{{{D_C}}},~~~~~~{K_p}={k_p}\frac{{{a^2}}}{{{D_C}}},~~~~~~~{\Omega _{mn}}={\omega _{mn}}\frac{{{a^2}}}{h}\sqrt {\frac{{{\rho _m}}}{{{E_m}}}} ,~~~~~~{D_C}=\frac{{{E_{\text{M}}}{h^3}}}{{12(1 - \nu _{{\text{M}}}^{2})}},$$

where ${\omega _{mn}}$ is the natural frequency of the nanocomposite plate and m and n refers to the mode numbers in x and y directions, respectively. The material properties of the constituent materials are chosen as same as those presented by Zhang et al. [66]. Figure 1 shows the geometry parameter of the plate embedded on a Winkler–Pasternak foundation. The validity of the presented results can be realized from Table 1, where a reliable agreement can be observed between the results of our modeling with those reported by García-Macías et al. [28] and Song et al. [50].

Table 1 Comparison of the dimensionless fundamental frequency of SSSS GPLR nanocomposite square plates for various distribution patterns of nanofillers

The effect of different types of thermal loading on the frequency responses can be figured out from Fig. 2 in which the dimensionless natural frequency of the nanocomposite plate is plotted against temperature rise for each type of GOP distribution. It can be seen that during the increment of the temperature change, the value of natural frequency will be decreased owing to the fact that the stiffness of the constituent material will be reduced in thermal environments. However, this negative effect can be reduced by changing the way that the thermal loadings are applied. As shown in this figure, the STR is a better alternative because the natural frequency of the plate decreases under this type of thermal loading lesser followed by LTR and UTR. This trend is due to the function of the temperature distribution for each type of thermal loading. For the UTR, the thermal loading will be applied all over the structure uniformly with the same intensity which can affect the structure more. However, for the LTR and STR, the temperature will be raised through the thickness via linear and sinusoidal functions, respectively. These kinds of applying thermal loadings to the structure can remarkably decrease the influence of the thermal effects. Through perusing the values of frequency for each pattern of GOP distribution in Fig. 2a–d, it can be found that the X distribution has the highest values of natural frequency followed by UD, V and O distribution type. This is due to the fact that the maximum moments of the forces which are applied to the structure around the neutral surface of the plate occur at the places which have the most distances from the neutral surface. Hence, the edges of the plate are the places in which the moments possess their maximum value. These moments can significantly intensify the stiffness of the structure. So, it is concluded that the existence of the nanofillers at the edges of the plate through the thickness will lead to a better reinforcement. From this sense, it can be figured out that why the structure with X distribution of GOPs has the highest values of natural frequency followed by UD, V and O distribution types.

Fig. 2

Variation of the dimensionless natural frequency of a GOPR nanocomposite plate versus temperature rise for a X, b U, c V and d O distribution types with respect to various types of thermal loading through the thickness

Figures 3 and 4 show the variations of dimensionless natural frequency against Winkler and Pasternak coefficients, respectively, for each GOP distribution pattern by considering three types of temperature rise. As can be seen in these figures, for all types of temperature rise, an increase in the foundation parameters’ stiffness will improve the dimensionless natural frequency of the nanocomposite plate gradually. Moreover, comparing these figures, it can be also concluded that the Pasternak parameter can affect the structure fantastically more than Winkler parameter due to the fact that Winkler foundation interacts with the nanocomposite plate in a discontinuous way, whereas Pasternak foundation interacts with the plate continuously. From this sense, it can be found that Pasternak parameter can improve the vibrational behavior of the GOPR nanocomposite plates in a more efficient manner than Winkler parameter. Also, it is interesting to note that applying an STR lessens the flexibility of the structure; hence, the natural frequency of the plates under this type of thermal loading possesses a higher range in comparison with other types of thermal loading. Also, as same as Fig. 2, the nanocomposite plate with X distribution has the greatest natural frequency.

Fig. 3

Variation of dimensionless natural frequency versus Pasternak coefficient of elastic foundation for a X, b U, c V and d O distribution types through the thickness with respect to various types of thermal loading

Fig. 4

Variation of dimensionless natural frequency versus Winkler coefficient of elastic foundation for a X, b U, c V and d O distribution types through the thickness with respect to various types of thermal loading

Furthermore, Fig. 5 is allocated to study the influence of aspect ratio on the dimensionless natural frequency of the nanocomposite plate by considering different types of GOPs’ distribution to compare the vibrational behavior of the structure with and without thermal effects. In this figure, the decreasing effect of natural frequency can be seen as a result of increment in amounts of plate’s aspect ratio for each type of GOPs’ distribution and thermal loadings. The reason for this trend is that the structural stiffness of the structure decreases when the plate gets out from the square model and one of its dimensions becomes larger than the other one. It is obvious that without regarding thermal effects, the structure will have a higher range of natural frequency related to the stiffness-softening effect of thermal loadings. Although the differences between the natural frequency under sinusoidal and linear temperature changes are small, STR is still the most efficient one. Also, by comparing the four plots of Fig. 5 together, it can be clearly observed that reinforcing the plate with O distribution type of GOPs will result in the lowest range of natural frequency while the X distribution type has the highest range of natural frequency.

Fig. 5

Variation of dimensionless natural frequency versus plate’s aspect ratio for a X, b U, c V and d O distribution types through the thickness with respect to various types of thermal loading

Also, the simultaneous effects of GOPs’ weight fraction, different types of temperature rise and elastic foundation on the dimensionless natural frequency of the plate are covered in detail in Fig. 6. As expected, the stiffness of the structure will be improved by adding the GOPs’ weight fraction which causes the natural frequency to be increased. This is because of the high strength of the GOPs’ nanoparticle that improved the structures’ stiffness as a novel reinforcement. This trend will be seen in all subfigures of this figure except Fig. 6d with O-type distribution. According to this figure, the plate with elastic foundation subjected to UTR has a lower range of natural frequency compared to the plate without elastic foundation subjected to either LTR or STR, which means the thermal loading with UTR prevails over the elastic foundation’s effects. According to this diagram, for the O-type distribution, it can be figured out that an increase in the amount of weight fraction generates a decrease in the dimensionless natural frequency of the plate under UTR. This trend reveals that in such cases the softening influence of negative thermal expansion of the nanoparticles defeats the stiffness enhancement which is generated from dispersing nanoparticles in the media. Also, it is worth mentioning that in all subfigures whenever the weight fraction of the GOPs is around 5%, the embedded plate under LTR type of thermal loading behaves approximately the same with the plate without elastic foundation under STR type of thermal loading; means, the effect of the embedding the plate in elastic foundation is approximately equal to the effect of changing the type of thermal loading from LTR to STR.

Fig. 6

Variation of the dimensionless natural frequency of a GOPR nanocomposite plate versus weight fraction of GOPs for a X, b U, c V and d O distribution types through the thickness with respect to various types of thermal loading as well as the influence of elastic foundation

Figure 7 indicates the influences of length-to-thickness ratio on the dimensionless natural frequency of the FG-GOPR nanocomposite plates with respect to various types of GOPs’ distribution. The figure is included from four parts devoted to various types of thermal loading. By taking a brief look at this figure, it can be deduced from first three plots that for all types of GOPs’ distribution, the reduction range of the natural frequency under UTR is remarkably greater than other types of thermal loading followed by LTR and STR. In other words, the structure can be exposed to higher frequencies in an equal length-to-thickness ratio by applying the STR. Also, by neglecting the thermal effects as shown in Fig. 7d, the influence of the length-to-thickness ratio on the natural frequency of the plate would be negligible.

Fig. 7

Variation of dimensionless natural frequency versus plate’s length-to-thickness ratio for a UTR, b LTR, cSTR thermal loading and d without thermal effect with respect to various types of GOPs’ distribution

Finally, it is time to investigate how the GOPs’ negative coefficient of thermal expansion affects the structure. For this purpose, the variation of the dimensionless natural frequency of the plate is plotted versus length-to-thickness ratio in Fig. 8 with respect to different values of GOPs’ weight fraction and various types of thermal loadings. Through a rational trend, as illustrated in Fig. 8, the stiffness-hardening effect is occurred via increasing the amount of GOPs’ weight fraction which can improve the vibrational behavior of the structure. As seen in all subfigures, the plates with more amounts of GOPs’ weight fraction have a higher range of natural frequencies except Fig. 8d. By comparing this subfigure to the other sub figures of Fig. 8, it was expected that in the highest rate of length-to-thickness ratio (a/h = 30), the plate with 4% of GOPs’ weight fraction under UTR type of thermal loading should possess greater dimensionless natural frequency than the plate with 1% of GOPs’ weight fraction under STR type of thermal loading, but as seen, it does not happen in this figure and an addition in the amount of GOPs’ weight fraction causes a reduction in the value of dimensionless natural frequency. It can be inferred from this sense that the GOPs’ negative CTE is the reason for this reverse trend. It means that the GOPs’ negative CTE defeats the stiffness enhancement which is generated from dispersing nanoparticles in the media. Also, as it was mentioned in the previous figures, the UTR causes a significant reduction in the stiffness of the structure.

Fig. 8

Variation of the dimensionless natural frequency of a GOPR nanocomposite plate versus plate’s length-to-thickness ratio for a X, b U, c V and d O distribution types through the thickness with respect to various types of thermal loading as well as the influence of GOPs’ weight fraction

6 Conclusion

This paper was concerned with the free vibration analysis of the GOPR nanocomposite embedded plates under three types of thermal loadings. Different types of temperature rises including uniform, linear and sinusoidal were captured. The governing equations of the plate were achieved through the incorporation of Hamilton’s principle with a refined higher order shear deformation theory. By implementing Navier’s method, the governing equations were solved analytically. Now, the outcomes of this vibrational investigation are going to be reviewed as follows:

• It was discovered that UTR was the most powerful type in stiffness softening and consequently caused the structure to have a lower range of natural frequencies.

• It was observed that embedding the structure on an elastic foundation is able to dramatically improve the vibrational behavior of the nanocomposite plate. Moreover, it was understood that the Pasternak parameter can affect the structure fantastically more than Winkler parameter.

• It was found that the nanocomposite plate under STR has a higher range of dimensionless natural frequencies followed by LTR and UTR, respectively.

• It was also revealed that natural frequencies decrease gradually as aspect ratio grows which is meant that the more the plate is got out from the square model, the plate gets lower values of dimensionless natural frequencies.

• It was deduced that reinforcing the plate with X-type distribution leads to a higher range of the dimensionless natural frequencies followed by U, V and O types.

• It was inferred that the natural frequency of the plate with O distribution will be unexpectedly decreased through the increment of the GOPs’ weight fraction under uniform thermal loading according to the GOPs’ negative coefficient of thermal expansion.