1 Introduction

Due to their superior mechanical, thermal and electrical properties, CNTs can be utilized in many applications including the reinforcement of polymer composites, such as CNTRC beams, plates and shells. So, since the discovery of CNTs by Ijima [1] in 1991, many researchers have investigated their unique capabilities as reinforcements in composite structures. On the other hand, trapezoidal plates are widely used in mechanical, civil and aeronautical engineering applications such as bridges, wings, tails and fins of aircrafts. However, due to the mathematical difficulties and complexities involved in formulation, mechanical analysis of CNTRC trapezoidal plates is poorly investigated in comparison with those of rectangular, skew and circular plates [2,3,4,5,6,7].

In recent years, some authors focused on the bending, buckling and vibration analyses of CNTRC rectangular and skew plates. Based on FSDT, Zhu et al. [8] presented an element for bending and free vibration analyses of CNTRC moderately thick rectangular plates. They investigated influences of distribution and volume fractions of CNTs, boundary conditions and edge-to-thickness ratio on the bending characteristics, natural frequencies and mode shapes of the plate. Zhang et al. [9, 10] used FSDT and element-free IMLS-Ritz method and focused on the free flexural vibration analysis of FG-CNTR triangular and skew plates. They presented new sets of natural frequencies and mode shapes for various FG-CNTRC triangular and skew plates and studied effect of volume fraction and distribution of CNTs, plate thickness-to-width ratio, plate aspect ratio and boundary condition on the natural frequencies of plates. In a similar work, Zhang et al. [11] studied free vibration analysis of triangular plates subjected to in-plane stresses. In this case, they studied effect of in-plane stress on the natural frequencies of the plate. Again with similar theory for modeling of plate and method of solution, Lei et al. [12] focused on free flexural vibration analysis of FG-CNTRC quadrilateral plates resting on Pasternak foundations. For different boundary conditions, they presented a parametric study on natural frequencies for various types of CNTs distributions, volume fraction of CNTs and geometries parameters of the plate.

Based on FSDT, García-Macías et al. [13] presented an element for static and dynamic simulations of moderately thick FG-CNTRC skew plates with arbitrary-oriented reinforcements. They investigated a parametric study to investigate influences of skew angle, fiber orientation, distribution and volume fraction of CNTs, thickness-to-width ratio, aspect ratio and boundary conditions on deflection and natural frequencies of FG-CNTRC skew plates. Lei et al. [14] employed FSDT and kp-Ritz method and studied free vibration analysis of laminated FG-CNTRC rectangular plates. They focused on the effects of lamination angle, number of layers, distributions and volume fractions of CNTs, plate width-to-thickness ratio and plate aspect ratio on the natural frequencies of laminated FG-CNTRC rectangular plates with various boundary conditions. Using third-order shear deformation theory (TSDT), Mori–Tanaka method and method of calculating the average stress of composite materials, Guo and Zhang [15] studied nonlinear vibration behaviors of CNTRC rectangular plates under combined dynamic axial and transverse excitations. They investigated effects of the forcing excitations on the different kinds of the periodic and chaotic motions of the CNTRC plates through a comprehensive parametric study.

Based on a higher-order shear deformation theory (HSDT) and using element-free kp-Ritz method, Selim et al. [16] studied free vibration analysis of CNTRC rectangular plates in a thermal environment. They studied effects of volume fraction and distribution of CNTs, boundary conditions, plate aspect ratio, plate thickness-to-width ratio and CNT volume fraction on the natural frequencies and sequence of first six mode shapes. Using FSDT and element-free improved moving least-squares Ritz (IMLS-Ritz) method, Zhang et al. [17] studied free vibration analysis of FG-CNTRC moderately thick rectangular plates with edges elastically restrained against transverse displacements and rotation. Besides volume fraction and distribution of CNTs and also geometrical parameters, they focused on the effect of elastically restrained edges on the natural frequencies of the plate. Zhang and Selim [18] employed an HSDT along with element-free IMLS-Ritz method and focused on free vibration behavior of FG-CNTRC thick laminated composite plates. For various CNT orientation angles and boundary conditions, they presented a parametric study to show effects of CNT volume fraction, plate aspect ratio, plate width-to-thickness ratio and number of plate’s layers on natural frequencies of the plate. Employing FSDT along with Ritz method, Kiani et al. [19] focused on the free vibration analysis of FG-CNTRC skew plates. For various types of boundary conditions, he studied effect of aspect ratio, thickness-to-width ratio, skew angle and also volume fraction and distribution of CNTs on the natural frequencies of the FG-CNTRC skew plates. Again using FSDT along with Ritz method, he focused on the free vibration analysis of FG-CNTRC rectangular plates integrated with piezoelectric layers at the bottom and top surfaces [20]. He showed that fundamental frequency of a closed circuit plate is always higher than corresponding value of a plate with open-circuit boundary conditions.

Memar et al. [21] employed TSDT and presented an isogeometric analysis for bending and free vibration analysis of CNTRC skew plates with arbitrary-oriented CNTs. They studied effect of CNT orientation on deflection and natural frequencies of the plate and found the orientation which leads to minimum or maximum values in maximum deflection and fundamental frequency of the skew plates. Employing a refined TSDT and using GDQM, Nejati et al. [22] focused on the static bending and free vibration analyses of rotating FG-CNTRC truncated conical shells. They studied effect of volume fraction, agglomeration and geometry of CNTs on the natural frequencies and static deflection of the conical shells. Fantuzzi et al. [23] used non-uniform rational B-splines (NURBS) curves and studied free vibration analysis of arbitrarily shaped FG-CNTRC plates. They focused on the influence of agglomeration on the natural frequencies. A semi-analytical solution was presented by Wang et al. [24] for free vibration analysis of FG-CNTRC doubly curved panels and shells of revolution with arbitrary boundary conditions. They studied effect of the geometrical parameters, CNTs distributions, volume fraction of CNTs as well as boundary restraint parameters on the natural frequencies. Wang et al. [25] employed FSDT and focused on the free vibration analysis of the FG-CNTRC shallow shells with arbitrary boundary conditions. They presented a comprehensive parametric investigation on the influence of elastic restraint parameters, shear deformation and rotary inertia, shallowness and material properties on the vibration characteristics of the shell. A meshless discretization technique is used by Ansari et al. [26] to present a numerical solution for free vibration analysis of FG-CNTRC elliptical plates. They modeled the plate based on the FSDT and presented various numerical results to explore the effects of concerned parameters on the natural frequencies.

Using multi-term Kantorovich–Galerkin method (MTKGM), Wang et al. [27] presented a semi-analytical solution for free vibration of symmetric sandwich plates resting on elastic foundation. They considered plate to be composed of two thin CNTRC face sheets and a thick homogenous core. They studied influence of sandwich configurations, volume fractions of CNTs, plate aspect ratio, core-to-skin thickness ratio and foundation stiffness on the natural frequencies. Zhong et al. [28] employed FSDT and presented a semi-analytical solution for free vibration analysis of FG-CNTRC circular, annular and sector plates. They presented some crucial parametric studies covering the effect of the geometrical parameters, CNTs distributions, volume fraction of CNTs and boundary conditions on the natural frequencies. Ansari et al. [29] used finite element method (FEM) and presented a numerical solution for bending and free vibration analyses of FG-CNTRC rectangular plates carrying a concentrated mass. They studied effect of boundary conditions, volume fraction and distribution of CNTs on the deflection, stress distribution and natural frequencies of the plate and effect of translational inertia of the concentrated mass on the natural frequencies of the plate. Using GDQM, Ansari et al. [30] studied free vibration analysis of arbitrary-shaped thick FG-CNTRC plates. They modeled plate based on an HSDT and reported natural frequencies for FG-CNTRC skew, quadrilateral, triangular, circular, sector and elliptical plates. Ghorbanpour Arani et al. [31, 32] used TSDT along with GDQM and studied free vibration and supersonic flutter analyses of laminated FG-CNTRC cylindrical panels. For various combinations of clamped and simple boundary conditions, they studied effects of lamination angle, number of layers, volume fractions and distributions of CNTs and geometrical parameters of the panel on the natural frequencies and critical speed of laminated FG-CNTRC panels. Using the Ritz method, Zhao et al. [33] obtained approximate values for natural frequencies of FG-CNTRC truncated conical panels with general boundary conditions. They presented a parametric study on the influence of the volume fractions of CNTs, distribution type of CNTs, boundary restraint parameters and geometrical parameters on the natural frequencies. Through a nonlinear analysis, Nguyen et al. [34] employed FSDT and presented an NURBS-based analysis for postbuckling behavior of FG-CNTRC shells. They presented some complex and useful postbuckling curves of FG-CNTRC panels and cylinders that could be useful for future references.

It can be seen that vibration analysis of CNTRC trapezoidal plates is poorly studied, especially the cantilever one which is more similar to the conditions of wings, tails and fins of aircrafts. It is due to the mathematical complexities involved in geometry of trapezoidal plates and difficulties involved in free edges. So, in this paper, free vibration analysis of cantilever FG-CNTRC trapezoidal plates are studied. The plate is modeled based on FSDT, and the set of governing equations and boundary conditions are mapped from the trapezoidal area into a rectangular one. GDQM is employed as a numerical approaches, and natural frequencies and corresponding mode shapes are reported for various cases.

2 Governing equations

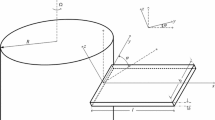
As depicted in Fig. 1, an FG-CNTRC cantilever trapezoidal plate clamped at y = 0 and free at other edges is considered. The plate is of dimensions a and b and angles α and β and is reinforced by CNTs arranged in y direction. As Fig. 2 shows, four standard patterns of distribution of CNTs are considered including UD, FG-V, FG-O and FG-X. For these types of distribution, volume fraction of CNTs is given as [35]

$$ \begin{array}{*{20}c} {{\text{UD}}:} & {V_{\text{CNT}} \left( z \right) = V_{\text{CNT}}^{*} } \\ {{\text{FG}} - V:} & {V_{\text{CNT}} \left( z \right) = \left( {1 + \frac{2z}{h}} \right)V_{\text{CNT}}^{*} } \\ {{\text{FG}} - O:} & {V_{\text{CNT}} \left( z \right) = 2\left( {1 - \frac{2\left| z \right|}{h}} \right)V_{\text{CNT}}^{*} } \\ {{\text{FG}} - X:} & {V_{\text{CNT}} \left( z \right) = 4\frac{\left| z \right|}{h}V_{\text{CNT}}^{*} } \\ \end{array} $$
(1)

where h is thickness of the plate and \( V_{\text{CNT}}^{*} \) is total volume fraction of CNTs which is same in all types of distribution. Also, volume fraction of isotropic matrix can be calculated as Vm = 1 − VCNT. Based on the extended rule of mixture, the elastic moduli (E11 and E22) and shear modulus (G12) can be expressed as follows [36]:

$$ \begin{array}{*{20}c} {E_{11} \left( z \right) = \eta_{1} V_{\text{CNT}} \left( z \right)E_{11}^{\text{CNT}} + V_{\text{m}} \left( z \right)E^{\text{m}} } & {\frac{{\eta_{2} }}{{E_{22} \left( z \right)}} = \frac{{V_{\text{CNT}} \left( z \right)}}{{E_{22}^{\text{CNT}} }} + \frac{{V_{\text{m}} \left( z \right)}}{{E^{\text{m}} }}\,} & {\frac{{\eta_{3} }}{{G_{12} \left( z \right)}} = \frac{{V_{\text{CNT}} \left( z \right)}}{{G_{12}^{\text{CNT}} }} + \frac{{V_{\text{m}} \left( z \right)}}{{G^{\text{m}} }}} \\ \end{array} $$
(2)

in which ECNT11, ECNT22 are elastic moduli of CNTs, GCNT12 is shear modulus of CNT and Gm, and Em indicate shear modulus and elastic modulus of isotropic matrix, respectively. Also, η1, η2 and η3 are CNT efficiency parameters which can be calculated by matching the modulus of CNTs from the molecular dynamics (MD) results with those obtained from the rule of mixture.

Fig. 1
figure 1

Cantilever CNTRC trapezoidal plate

Full size image
Fig. 2
figure 2

Distribution patterns of CNTs

Full size image

Using the rule of mixture, density (ρ) and the Poisson’s ratio (ν12) can be calculated as [36]

$$ \begin{array}{*{20}c} {\rho \left( z \right) = V_{\text{CNT}} \left( z \right)\rho^{\text{CNT}} + V_{\text{m}} \left( z \right)\rho^{\text{m}} } & {\upsilon_{12} = V_{\text{CNT}}^{*} \upsilon_{12}^{\text{CNT}} + \left( {1 - V_{\text{CNT}}^{*} } \right)\upsilon^{\text{m}} } \\ \end{array} $$
(3)

where νCNT12 and ρCNT are Poisson’s ratio and density of CNT, respectively, and νm and ρm are Poisson’s ratio and density of matrix, respectively.

According to FSDT, the displacement field in the plate can be considered as [37, 38]

$$ \begin{aligned}&{u_{z} \left( {x,y,z} \right) = u\left( {x,y} \right) + z\psi_{x} \left( {x,y} \right)}\quad\\&{v_{z} \left( {x,y,z} \right) = v\left( {x,y} \right) + z\psi_{y} \left( {x,y} \right)} \hfill \\ &{w_{z} \left( {x,y,z} \right) = w\left( {x,y} \right)} \end{aligned} $$
(4)

in which uz, vz and wz are components of displacement in any desired position of the plate and u, v and w are corresponding ones at z = 0. Also, ψx and ψy are rotation about y and x axes, respectively. Normal (εij) and shear (γij) components of strain can be calculated as [3]

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left( {} \right)_{,x} } & 0 & 0 & {z\left( {} \right)_{,x} } & 0 \\ 0 & {\left( {} \right)_{,y} } & 0 & 0 & {z\left( {} \right)_{,y} } \\ 0 & 0 & {\left( {} \right)_{,y} } & 0 & 1 \\ 0 & 0 & {\left( {} \right)_{,x} } & 1 & 0 \\ {\left( {} \right)_{,y} } & {\left( {} \right)_{,x} } & 0 & {z\left( {} \right)_{,y} } & {z\left( {} \right)_{,x} } \\ \end{array} } \right]\left\{ p \right\}} & {\varepsilon_{zz} = 0} \\ \end{array} $$
(5)

in which

$$ \begin{array}{*{20}c} {\left\{ p \right\} = \left\{ {\begin{array}{*{20}c} u & v & w & {\psi_{x} } & {\psi_{y} } \\ \end{array} } \right\}^{T} } & {\left( {} \right)_{,x} = \frac{\partial }{\partial x}} & {\left( {} \right)_{,y} = \frac{\partial }{\partial y}} \\ \end{array} $$
(6)

where superscript T indicates to transpose operator and corresponding components of stress (σij) can be stated as follows [39]:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {kQ_{44} } & 0 & 0 \\ 0 & 0 & 0 & {kQ_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\} $$
(7)

where k is shear correction factor and due to the direction of CNTs, following relation should be considered for Qij [39]:

$$ \begin{aligned}& {Q_{11} = \frac{{E_{22} }}{{1 - \upsilon_{12} \upsilon_{21} }}}\; {Q_{22} = \frac{{E_{11} }}{{1 - \upsilon_{12} \upsilon_{21} }}} \;{Q_{12} = \frac{{\upsilon_{12} E_{22} }}{{1 - \upsilon_{12} \upsilon_{21} }}} \\&{Q_{44} = G_{13} } \;\; {Q_{55} = G_{23} } \;\; {Q_{66} = G_{12} } \end{aligned} $$
(8)

in which G13 and G23 are shear moduli and \( \upsilon_{21} = {{\upsilon_{12} E_{22} } \mathord{\left/ {\vphantom {{\upsilon_{12} E_{22} } {E_{11} }}} \right. \kern-0pt} {E_{11} }} \) is the Poisson’s ratio.

Substituting Eq. (5) into Eq. (7), following relation can be achieved:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} \left( {} \right)_{,x} } & {Q_{12} \left( {} \right)_{,y} } & 0 & {zQ_{11} \left( {} \right)_{,x} } & {zQ_{12} \left( {} \right)_{,y} } \\ {Q_{12} \left( {} \right)_{,x} } & {Q_{22} \left( {} \right)_{,y} } & 0 & {zQ_{12} \left( {} \right)_{,x} } & {zQ_{22} \left( {} \right)_{,y} } \\ 0 & 0 & {kQ_{44} \left( {} \right)_{,y} } & 0 & {kQ_{44} } \\ 0 & 0 & {kQ_{55} \left( {} \right)_{,x} } & {kQ_{55} } & 0 \\ {Q_{66} \left( {} \right)_{,y} } & {Q_{66} \left( {} \right)_{,x} } & 0 & {zQ_{66} \left( {} \right)_{,y} } & {zQ_{66} \left( {} \right)_{,x} } \\ \end{array} } \right]\left\{ p \right\} $$
(9)

The set of governing equations and boundary conditions can be derived using Hamilton’s principle as [40]

$$ \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U + \delta W_{\text{ext}} } \right){\text{d}}t} = 0 $$
(10)

in which δ is variational operator, [t1,t2] is a desired time interval and T, U and Wext are kinetic energy, potential energy and work done by external loads calculated as [31, 32]

$$ \begin{aligned} U & = \frac{1}{2}\iiint\limits_{V} {\left( {\sigma_{xx} \varepsilon_{xx} + \sigma_{yy} \varepsilon_{yy} + \sigma_{zz} \varepsilon_{zz} + \sigma_{xy} \gamma_{xy} + \sigma_{xz} \gamma_{xz} + \sigma_{yz} \gamma_{yz} } \right){\text{d}}V} \\ T & = \frac{1}{2}\iiint\limits_{V} {\rho \left[ {\left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v_{z} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w_{z} }}{\partial t}} \right)^{2} } \right]{\text{d}}V} \\ W_{ext} & = \iint\limits_{S} {q\left( {x,y,t} \right)w\left( {x,y,t} \right){\text{d}}S} \\ \end{aligned} $$
(11)

where V and S are volume and surface of the plate and q is the external load per unit area. Substituting Eqs. (4), (5), (7) and (11) into Eq. (10), the set of governing equations can be derived as

$$ \begin{aligned} & \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} = 0 \\ & \frac{{\partial N_{yy} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} - I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }} = 0 \\ & \frac{{\partial Q_{xz} }}{\partial x} + \frac{{\partial Q_{yz} }}{\partial y} + q - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} = 0 \\ & \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{xz} - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }} = 0 \\ & \frac{{\partial M_{yy} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x} - Q_{yz} - I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \psi_{y} }}{{\partial t^{2} }} = 0 \\ \end{aligned} $$
(12)

and external boundary conditions can be written as

$$ \begin{array}{*{20}c} {N_{nn} \delta u_{n} = 0} & {N_{ns} \delta u_{s} = 0} & {Q_{nz} \delta w = 0} & {M_{nn} \delta \psi_{n} = 0} & {M_{ns} \delta \psi_{s} = 0} \\ \end{array} $$
(13)

in which

$$ \begin{array}{*{20}l} {\begin{array}{*{20}c} {N_{nn} = N_{xx} n_{x}^{2} + 2N_{xy} n_{x} n_{y} + N_{yy} n_{y}^{2} } & {N_{ns} = \left( {N_{yy} - N_{xx} } \right)n_{x} n_{y} + N_{xy} \left( {n_{x}^{2} - n_{y}^{2} } \right)} \\ {M_{nn} = M_{xx} n_{x}^{2} + 2M_{xy} n_{x} n_{y} + M_{yy} n_{y}^{2} } & {M_{ns} = \left( {M_{yy} - M_{xx} } \right)n_{x} n_{y} + M_{xy} \left( {n_{x}^{2} - n_{y}^{2} } \right)} \\ \end{array} } \hfill & {Q_{nz} = Q_{xz} n_{x} + Q_{yz} n_{y} } \hfill \\ \end{array} $$
(14)

where nx = cosθ and ny = sinθθ are components of the normal unit vector (see Fig. 3) and components of stress resultant and inertia are defined as follows:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}{\text{d}}z} } & {\left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}z{\text{d}}z} } & {\left\{ {\begin{array}{*{20}c} {Q_{xz} } \\ {Q_{yz} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\}dz} } & {\left\{ {\begin{array}{*{20}c} {I_{0} } \\ {I_{1} } \\ {I_{2} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left\{ {\begin{array}{*{20}c} 1 \\ z \\ {z^{2} } \\ \end{array} } \right\}{\text{d}}z} } \\ \end{array} $$
(15)
Fig. 3
figure 3

n–s coordinate against Cartesian coordinate [6]

Full size image

Substituting Eq. (9) into Eq. (15) leads to the following relation

$$ \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ {Q_{yz} } \\ {Q_{xz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} \left( {} \right)_{,x} } & {A_{12} \left( {} \right)_{,y} } & 0 & {B_{11} \left( {} \right)_{,x} } & {B_{12} \left( {} \right)_{,y} } \\ {A_{12} \left( {} \right)_{,x} } & {A_{22} \left( {} \right)_{,y} } & 0 & {B_{12} \left( {} \right)_{,x} } & {B_{22} \left( {} \right)_{,y} } \\ {A_{66} \left( {} \right)_{,y} } & {A_{66} \left( {} \right)_{,x} } & 0 & {B_{66} \left( {} \right)_{,y} } & {B_{66} \left( {} \right)_{,x} } \\ {B_{11} \left( {} \right)_{,x} } & {B_{12} \left( {} \right)_{,y} } & 0 & {D_{11} \left( {} \right)_{,x} } & {D_{12} \left( {} \right)_{,y} } \\ {B_{12} \left( {} \right)_{,x} } & {B_{22} \left( {} \right)_{,y} } & 0 & {D_{12} \left( {} \right)_{,x} } & {D_{22} \left( {} \right)_{,y} } \\ {B_{66} \left( {} \right)_{,y} } & {B_{66} \left( {} \right)_{,x} } & 0 & {D_{66} \left( {} \right)_{,y} } & {D_{66} \left( {} \right)_{,x} } \\ 0 & 0 & {A_{44} \left( {} \right)_{,y} } & 0 & {A_{44} } \\ 0 & 0 & {A_{55} \left( {} \right)_{,x} } & {A_{55} } & 0 \\ \end{array} } \right]\left\{ p \right\} $$
(16)

in which

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {A_{11} } \\ {A_{12} } \\ {A_{22} } \\ {A_{66} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {Q_{11} } \\ {Q_{12} } \\ {Q_{22} } \\ {Q_{66} } \\ \end{array} } \right\}{\text{d}}z} } & {\left\{ {\begin{array}{*{20}c} {B_{11} } \\ {B_{12} } \\ {B_{22} } \\ {B_{66} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {Q_{11} } \\ {Q_{12} } \\ {Q_{22} } \\ {Q_{66} } \\ \end{array} } \right\}z{\text{d}}z} } & {\left\{ {\begin{array}{*{20}c} {D_{11} } \\ {D_{12} } \\ {D_{22} } \\ {D_{66} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {Q_{11} } \\ {Q_{12} } \\ {Q_{22} } \\ {Q_{66} } \\ \end{array} } \right\}z^{2} {\text{d}}z} } & {\left\{ {\begin{array}{*{20}c} {A_{44} } \\ {A_{55} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {k\left\{ {\begin{array}{*{20}c} {Q_{44} } \\ {Q_{55} } \\ \end{array} } \right\}{\text{d}}z} } \\ \end{array} $$
(17)

Substituting Eq. (16) into Eq. (12) and considering q = 0 for free vibration analysis leads to the following set of governing equations:

$$ \left[ S \right]\left\{ p \right\} = \left\{ 0 \right\}_{5 \times 1} $$
(18)

in which Sij = Sji are presented in “Appendix 1”.

Also, using Eqs. (13), (14) and (16), following relations can be written for boundary conditions:

Clamped edge (y = 0):

$$ \begin{array}{*{20}c} {u = 0} & {v = 0} & {w = 0} & {\psi_{x} = 0} & {\psi_{y} = 0} \\ \end{array} $$
(19)

Free edges:

$$ \left\{ {\begin{array}{*{20}c} {N_{nn} } \\ {N_{ns} } \\ {M_{nn} } \\ {M_{ns} } \\ {Q_{nz} } \\ \end{array} } \right\} = \left[ P \right]\left\{ p \right\} = \left\{ 0 \right\}_{5 \times 1} $$
(20)

where [P] can be found in “Appendix 2”

The analysis of the non-rectangular plates uses a local parameter coordinate system rather than a Cartesian one. As shown in Fig. 4, the original trapezoidal shape of the plate in the x–y coordinates system can be mapped into a square in the ζ–η coordinates, using the following transformation [4]:

$$ \begin{array}{*{20}c} {x = a\zeta + L\eta \left( {\tan \alpha - G\zeta } \right)} & {y = L\eta } \\ \end{array} $$
(21)

in which

$$ \begin{array}{*{20}c} {L = b\cos \alpha } & {G = \tan \alpha - \tan \beta } \\ \end{array} $$
(22)
Fig. 4
figure 4

Original and computational coordinates [4]

Full size image

Applying Eq. (21) in Eq. (18) and using the method of separation of variables as

$$ \left\{ {\begin{array}{*{20}c} {u\left( {\zeta ,\eta ,t} \right)} \\ {v\left( {\zeta ,\eta ,t} \right)} \\ {w\left( {\zeta ,\eta ,t} \right)} \\ {\psi_{x} \left( {\zeta ,\eta ,t} \right)} \\ {\psi_{y} \left( {\zeta ,\eta ,t} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {U\left( {\zeta ,\eta } \right)} \\ {V\left( {\zeta ,\eta } \right)} \\ {W\left( {\zeta ,\eta } \right)} \\ {X\left( {\zeta ,\eta } \right)} \\ {Y\left( {\zeta ,\eta } \right)} \\ \end{array} } \right\}e^{i\,\varOmega \,t} $$
(23)

in which i2 = − 1 and Ω is the natural frequency, the set of equations can be rewritten as

$$ \left[ R \right]\left\{ q \right\} = \left\{ 0 \right\} $$
(24)

in which Rij = Rji can be found in “Appendix 3” and

$$ \begin{array}{*{20}c} {\left\{ q \right\} = \left\{ {\begin{array}{*{20}c} U & V & W & X & Y \\ \end{array} } \right\}^{T} } & {E = E\left( \eta \right) = \frac{1}{\phi \sec \alpha - G\eta }} & {F = F\left( \zeta \right) = G\zeta - \tan \alpha } & {\phi = \frac{a}{b}} \\ \end{array} $$
(25)

Also, in a similar manner, boundary conditions can be written as

Clamped edge (η = 0):

$$ \begin{array}{*{20}c} {U = 0} & {V = 0} & {W = 0} & {X = 0} & {Y = 0} \\ \end{array} $$
(26)

Free edges (η = 1, ζ = 0,1)

$$ \left[ J \right]\left\{ q \right\} = \left\{ 0 \right\} $$
(27)

where [J] is presented in “Appendix 4”

3 Differential quadrature method

Differential quadrature method (DQM) is one of the most popular numerical approaches which was first presented by Bellman et al. [41] in 1971. This method has been applied by many authors to present numerical solution for one-dimensional and two-dimensional problems [42,43,44,45]. Values of a two-dimensional function like F(ζ,η) can be expressed in a matrix form as

$$ \begin{array}{*{20}c} {F_{ij} = F\left( {\zeta_{i} ,\eta_{j} } \right)} & {i = 1,2, \ldots ,N} & {j = 1,2, \ldots ,M} \\ \end{array} $$
(28)

where N and M are number of grid points in ζ and η directions, respectively. According to the differential quadrature rules, all derivatives of the function can be approximated by means of weighted linear sum of the function values at the pre-selected grid of points as [46]

$$ \left[ {\frac{{\partial^{r + s} F}}{{\partial \zeta^{r} \partial \eta^{s} }}} \right] = \left[ {A_{\zeta }^{\left( r \right)} } \right]\left[ F \right]\left[ {A_{\eta }^{\left( s \right)} } \right]^{T} $$
(29)

in which superscripts (r) and (s) indicate to order of derivation, subscripts ζ and η show derivative with respect to ζ or η, respectively. These matrices for the first-order derivatives are given as [46]:

$$ \begin{array}{*{20}c} {\left[ {A_{\zeta }^{\left( 1 \right)} } \right]_{in} = \left\{ \begin{aligned} \frac{{\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne i,n \end{subarray} }^{N} {\left( {\zeta_{i} - \zeta_{k} } \right)} }}{{\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne n \end{subarray} }^{N} {\left( {\zeta_{n} - \zeta_{k} } \right)} }}\quad i,n = 1,2,3, \ldots ,N;\,i \ne n \hfill \\ \sum\limits_{\begin{subarray}{l} k = 1 \\ k \ne i \end{subarray} }^{N} {\frac{1}{{\zeta_{i} - \zeta_{k} }}\quad i = n = 1,2,3, \ldots ,N} \hfill \\ \end{aligned} \right.} & {\left[ {A_{\eta }^{\left( 1 \right)} } \right]_{jm} = \left\{ \begin{aligned} \frac{{\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne j,m \end{subarray} }^{\text{m}} {\left( {\eta_{j} - \eta_{k} } \right)} }}{{\prod\limits_{\begin{subarray}{l} k = 1 \\ k \ne m \end{subarray} }^{\text{m}} {\left( {\eta_{\text{m}} - \eta_{k} } \right)} }}\quad j,m = 1,2,3, \ldots ,M;\,j \ne m \hfill \\ \sum\limits_{\begin{subarray}{l} k = 1 \\ k \ne j \end{subarray} }^{\text{m}} {\frac{1}{{\eta_{j} - \eta_{k} }}\quad j = m = 1,2,3, \ldots ,M} \hfill \\ \end{aligned} \right.} \\ \end{array} $$
(30)

and of higher-order derivatives are calculated as:

$$ \begin{array}{*{20}c} {\left[ {A_{\zeta }^{\left( r \right)} } \right] = \left[ {A_{\zeta }^{\left( 1 \right)} } \right]\left[ {A_{\zeta }^{{\left( {r - 1} \right)}} } \right]} & {\left[ {A_{\eta }^{\left( s \right)} } \right] = \left[ {A_{\eta }^{\left( 1 \right)} } \right]\left[ {A_{\eta }^{{\left( {s - 1} \right)}} } \right]} & {r,s = 2,3,4, \ldots } \\ \end{array} $$
(31)

For matrix [F]N×M, an equivalent column vector \( \left\{ {\hat{F}} \right\}_{NM \times 1} \) can be defined as [3]:

$$ \begin{array}{*{20}c} {\hat{F}_{v} = F_{ij} } & {v = \left( {j - 1} \right)N + i} \\ \end{array} $$
(32)

and multiple of three matrices as [a][F][b] can be replaced by \( \left( {\left[ b \right]^{T} \otimes \left[ a \right]} \right)\left\{ {\hat{F}} \right\} \), in which \( \otimes \) indicates the Kronecker product [3]. Thus, Eq. (29) can be rewritten as

$$ \left\{ {\frac{{\partial^{r + s} \hat{F}}}{{\partial \zeta^{r} \partial \eta^{s} }}} \right\} = \left( {\left[ {A_{\eta }^{\left( s \right)} } \right] \otimes \left[ {A_{\zeta }^{\left( r \right)} } \right]} \right)\left\{ {\hat{F}} \right\} $$
(33)

In addition to number of grid points, distribution of them affects convergence of the solution. A well-accepted set of the grid points is the Gauss–Lobatto–Chebyshev points given for interval [0,1] as [46]:

$$ \begin{array}{*{20}c} {\zeta_{i} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\left( {i - 1} \right)\pi }}{N - 1}} \right]} \right\}} & {\eta_{j} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\left( {j - 1} \right)\pi }}{M - 1}} \right]} \right\}} \\ \end{array} $$
(34)

4 DQ analog

Using DQ rules, the set of governing equation (24) can be written in the following algebraic form:

$$ \left[ K \right]\left\{ s \right\} = \varOmega^{2} \left[ M \right]\left\{ s \right\} $$
(35)

in which [K] and [M] are stiffness and mass matrices and

$$ \left\{ s \right\}_{5NM \times 1} = \left\{ {\begin{array}{*{20}c} {\left\{ {\hat{U}} \right\}} \\ {\left\{ {\hat{V}} \right\}} \\ {\left\{ {\hat{W}} \right\}} \\ {\left\{ {\hat{X}} \right\}} \\ {\left\{ {\hat{Y}} \right\}} \\ \end{array} } \right\} $$
(36)

Also, external boundary conditions (26) and (27) can be written using DQ rules as

$$ \left[ T \right]\left\{ s \right\} = \left\{ 0 \right\} $$
(37)

The grid points can be separated into two sets: boundary points which are located at the four edges of the plate and domain ones which are other interior points. By neglecting satisfying Eq. (35) at the boundary points, this equation can be written as [47]

$$ \left[ {\bar{K}} \right]\left\{ s \right\} = \varOmega^{2} \left[ {\bar{M}} \right]\left\{ s \right\} $$
(38)

in which bar sign implies corresponding non-square matrix. Equations (37) and (38) may be rearranged and partitioned in order to separate boundary (b) and domain (d) points as

$$ \left[ {\bar{K}} \right]_{d} \left\{ s \right\}_{d} + \left[ {\bar{K}} \right]_{b} \left\{ s \right\}_{b} = \varOmega^{2} \left( {\left[ {\bar{M}} \right]_{d} \left\{ s \right\}_{d} + \left[ {\bar{M}} \right]_{b} \left\{ s \right\}_{b} } \right) $$
(39.a)
$$ \left[ T \right]_{d} \left\{ s \right\}_{d} + \left[ T \right]_{b} \left\{ s \right\}_{b} = \left\{ 0 \right\} $$
(39.b)

Substituting Eq. (39.b) into Eq. (39.a) leads to the following eigen value equation:

$$ \left[ {K^{*} } \right]\left\{ s \right\}_{d} = \varOmega^{2} \left[ {M^{*} } \right]\left\{ s \right\}_{d} $$
(40)

in which

$$ \begin{array}{*{20}c} {\left[ {M^{*} } \right] = \left[ {\bar{M}} \right]_{d} + \left[ {\bar{M}} \right]_{b} \left[ p \right]} & {\left[ {K^{*} } \right] = \left[ {\bar{K}} \right]_{d} + \left[ {\bar{K}} \right]_{b} \left[ p \right]} \\ \end{array} $$
(41)

Solving Eq. (40), values of the natural frequencies and mode shapes can be calculated as eigen values and eigen vectors, respectively. Also, mode shapes can be completed using Eq. (39.b).

5 Numerical results

In the previous section, a numerical solution was presented for free vibration analysis of FG-CNTRC cantilever trapezoidal plates. In this section, numerical results are proposed for the presented numerical solution. Unless otherwise stated, results are presented for a plate made of poly-co-vinylene (PmPV), as matrix with material properties Em = 2.1 GPa, νm = 0.34 and ρm = 1150 kg/m3 [36] and (10,10) armchair single wall CNTs (L = 9.26 nm, R = 0.68 nm, h = 0.067 nm) as the reinforcements. Elasticity moduli, shear modulus, Poisson’s ratio and density of CNT at reference temperature are ECNT11 = 5.6466 TPa, ECNT22 = 7.08 TPa, GCNT12 = 1.9447 TPa, νCNT12 = 0.175 and ρCNT = 1400 kg/m3 [36]. The shear moduli G13 and G23 are taken equal to G12 [36] and corresponding efficiency parameters are presented in Table 1 for some selected values of the total volume fraction of CNT. Also, shear correction factor is considered as k = 5/6 [48].

Table 1 Efficiency parameters [36]
Full size table

First of all, convergence of the presented solution must be examined. For this purpose, consider an FG-X CNTRC trapezoidal plate of b = 1 m, a/b = 0.75, h/b = 0.01, α = 15°, β = − 5° and \( V_{\text{CNT}}^{*} \) = 0.14. Effect of number of grid points (Nx = Ny) on the values of the first six natural frequencies of the plate is presented in Table 2. This table confirms convergence of the presented solution, and Nx = Ny = 19 is considered in all of the following examples.

Table 2 Convergence of the presented numerical solution (b = 1 m, a/b = 0.75, h/b = 0.01, α = 15°, β = − 5°, \( V_{\text{CNT}}^{*} \) = 0.14)
Full size table

In order to confirm accuracy of the presented solution, a homogenous trapezoidal plate of E11 = E22 = 68.2 GPa, ν12 = ν21 = 0.35, ρ = 2860 kg/m3, a = 8.8 cm, b = 10.35 cm, h = 0.98 mm, α = 27° and β = − 13° is considered. Table 3 shows values of the first six natural frequencies of the plate and corresponding ones presented by other researchers. A comparison between results confirms high accuracy of the presented solution. Also corresponding mode shapes are depicted in Fig. 5 which show accuracy of the presented solution.

Table 3 Natural frequencies of a homogenous trapezoidal plate (E11 = E22 = 68.2 Gpa, ν12 = ν21 = 0.35, ρ = 2860 kg/m3, a = 8.8 cm, b = 10.35 cm, h = 0.98 mm, α = 27°, β = − 13°)
Full size table
Fig. 5
figure 5

First six mode shapes of a homogenous trapezoidal plate (E = 68.2 Gpa, ν = 0.35, ρ = 2860 kg/m3, a = 8.8 cm, b = 10.35 cm, h = 0.98 mm, α = 27°, β = − 13°)

Full size image

An UD CNTRC square plate of h/b = 0.02 and \( V_{\text{CNT}}^{*} \) = 0.14 is considered. In Table 4, dimensionless values (\( \lambda = {{\varOmega b^{2} \sqrt {{{\rho^{\text{m}} } \mathord{\left/ {\vphantom {{\rho^{\text{m}} } {E^{\text{m}} }}} \right. \kern-0pt} {E^{\text{m}} }}} } \mathord{\left/ {\vphantom {{\varOmega b^{2} \sqrt {{{\rho^{\text{m}} } \mathord{\left/ {\vphantom {{\rho^{\text{m}} } {E^{\text{m}} }}} \right. \kern-0pt} {E^{\text{m}} }}} } h}} \right. \kern-0pt} h} \)) of the first eight natural frequencies are reported and are compared with numerical ones reported by Memar et al. [21]. As this table shows, results are in good agreement and the small difference can be explained by difference in employed theories which is FSDT in the presented paper and TSDT in Ref. [21]. Also, in Fig. 6, corresponding mode shapes are depicted against corresponding ones reported by Memar et al. [21] which reveals high accuracy of the presented numerical solution.

Table 4 Dimensionless natural frequencies of an UD CNTRC square plate (h/b = 0.02, \( V_{\text{CNT}}^{*} \) = 0.14)
Full size table
Fig. 6
figure 6

First eight mode shapes of an UD CNTRC square plate (h/b = 0.02, \( V_{\text{CNT}}^{*} \) = 0.14)

Full size image

Consider an FG-CNTRC trapezoidal plate of b = 1 m, a/b = 0.7, h/b = 0.02, α = 15° and β = − 15°. For various values of volume fraction of CNTs and different types of distribution, Table 5 presents values of the first six natural frequencies in Hz. This table shows that using CNTs leads to considerable increase in all natural frequencies and increase in value of the volume fraction of CNTs increases all natural frequencies as well. It can be explained by high values of elastic and shear moduli of CNTs. Table 5 also shows that types of distribution of CNTs can be sorted in order of increase in natural frequencies as FG-X, UD, FG-V and FG-O which is in agreement with those reported by other authors for free vibration analysis of FG-CNTRC plates and shells [19, 31]. It is worth mentioning that results of Table 5 may serve as benchmarks for future studies.

Table 5 Effect of distribution and volume fraction of CNTs on the natural frequencies of an FG-CNTRC trapezoidal plate (b = 1 m, a/b = 0.7, h/b = 0.02, α = 15°, β = − 15°)
Full size table

An FG-X CNTRC trapezoidal plate of \( V_{\text{CNT}}^{*} \) = 0.11, b = 1 m, a/b = 0.75 and h/b = 0.02 is chosen. Effect of angles α and β on the natural frequencies of the first six modes are depicted in Fig. 7. As shown in this figure, increase in values of α increases all natural frequencies and in order to achieve higher natural frequencies it is better to use negative value of β. Big positive values of α and big negative values of β decreases width (mass) of the plate at unsupported areas and makes the plate more similar to a triangle which leads to rise in all natural frequencies.

Fig. 7
figure 7

Effect of angles α and β of CNTs on the natural frequencies of an FG-CNTRC trapezoidal plate (FG-X, \( V_{\text{CNT}}^{*} \) = 0.11, b = 1 m, a/b = 0.75, h/b = 0.02)

Full size image

Because of opposite effects of α and positive values of β on values of the natural frequencies of trapezoidal plates, it can be interesting to study effect of skew angles on natural frequencies of FG-CNTRC skew plates. For this purpose, consider an FG-X CNTRC skew plate (α = β) of b = 1 m, a/b = 0.25 and h/b = 0.01. For various values of α = β and volume fraction of CNTs, Table 6 presents values of the first six natural frequencies. This table shows that no specified trend can be detected for effect of skew angle on value of natural frequencies of the plate which can be explained by confrontation between effects of α and β.

Table 6 Effect of skew angle on the natural frequencies of an FG-CNTRC skew plate for various values of volume fraction (FG-X, b = 1 m, a/b = 0.25, h/b = 0.01)
Full size table

Consider a UD CNTRC trapezoidal plate of \( V_{\text{CNT}}^{*} \) = 0.17, b = 1 m, α = 15° and β = − 5°. Effect of thickness ratio (h/b) and aspect ratio (a/b) on the first six natural frequencies of the plate are depicted in Fig. 8. As shown in this figure, increase in thickness of the plate leads to rise in all natural frequencies of the plate which shows more increase in stiffness of the plate in comparison with its inertia. This figure also shows that increase in width of the plate decreases all natural frequencies intensively. Increase in width of the plate increases inertia and decreases stiffness of the plate which decreases all natural frequencies.

Fig. 8
figure 8

Effect of thickness and aspect ratio on the natural frequencies of an FG-CNTRC trapezoidal plate (UD, \( V_{\text{CNT}}^{*} \) = 0.17, b = 1 m, α = 15° and β = − 5°)

Full size image

As depicted in Fig. 8, smooth decrease can be seen for variation of the first three modes of the plate versus variation of aspect ratio; but for specified values of aspect ratio (a/b = 0.87 and a/b = 1.136), some sudden changes can be seen in fourth, fifth and sixth modes. Figure 9 shows variation of natural frequencies of modes 4–6 simultaneously. This figure reveals that for a/b = 0.87 and a/b = 1.136, sequence of mode changes and it is the main reason of those sudden changes.

Fig. 9
figure 9

Effect of aspect ratio on sequence of modes

Full size image

6 Conclusions

Using GDQM, a numerical solution was presented for free vibration analysis of cantilever FG-CNTRC trapezoidal plates. The plate was modeled based on FSDT, and effective mechanical properties were calculated using extended rule of mixture. Convergence and accuracy of the presented numerical solution were confirmed, and effect of geometrical parameters and volume fraction and distribution of CNTs on the natural frequencies of the plate were studied through numerical examples. Numerical results showed that adding CNTs to cantilever trapezoidal plates leads to considerable rise in all natural frequencies and in order to increase natural frequencies it is better to increase volume fraction of CNTs and using FG-X pattern for distribution of CNTs. Numerical examples showed that increase in thickness of the plate leads to increase in natural frequencies but increase in width of the plate decreases all natural frequencies and may change sequence of modes. It was shown by numerical results that all natural frequencies increases by decreasing width of the plate at the unsupported parts of the plate located near the outer free edge.