Effects of geometric nonlinearities on the coupled dynamics of CNT strengthened composite beams with porosity, mass and geometric imperfections

Abstract

This study investigates the effects of geometric nonlinearities on the dynamical behaviour of carbon nanotube (CNT) strengthened imperfect composite beams by considering both axial and transverse motions. For the given general model of the beam, the system modelling has been adopted from the literature and the nonlinear dynamic response in presence of an external harmonic load is examined for the first time in the case of axially functionally graded (AFG) CNT fibre, which is used for strengthening the structure. Porosity imperfection with the ability to vary though the thickness is modelled using simple, closed and open-cell models; the porosity variation is formulated using uniform, linear, symmetric and un-symmetric models. The geometrical imperfection is considered by allowing the beam to have an initial curved longitudinal axis and the mass imperfection is modelled by introducing a concentrated mass at a certain point of the beam. Using a combination of the Galerkin scheme together with dynamic equilibrium technique, the influence of different imperfections and porosities on the frequency response of the system is examined. It is shown that, for the case of AFG CNT strengthened beam, geometrical imperfection can change the nonlinear response from a hardening to a softening behaviour. Besides, the importance of considering the interaction between axial and transverse motion is examined in detail. The influence of lumped mass imperfection and its position is also studied showing that this type of imperfection can change the nonlinear behaviour of the system significantly. Moreover, the influence of increasing the CNT volume fraction and functionally spreading the CNTs through the length is discussed. The results are useful for analysing the resonance phenomena in strengthened structures facing various imperfections.

Graphic abstract

1 Introduction

With recent developments in various cross-disciplinary engineering fields, the importance of having optimum structures with higher durability-to-weight, stiffness-to-weight and strength-to-weight is visible in engineering horizon. Accordingly, numerous studies concentrated on strengthening conventional structures using different algorithms. Carbon-fibre, aramid-fibre and glass-fibre strengthened structures are some of the well-known outcomes of the research studies in this field [1,2,3,4,5,6]. Meanwhile, improvements in nano/micro-scale technologies made it possible to introduce carbon nanotubes (CNTs) as a reliable new reinforcement fibre [7,8,9,10,11]. CNTs are well-known for their spectacular mechanical, thermal, and electrical properties which made them an important element in different areas of science. Due to their ultra-small scale, size-dependent effects and molecular interactions have been observed where modelled for different small-scale structures using nonlocal elasticity theories [12,13,14,15,16,17,18,19,20,21,22,23,24].

Moreover, the possibility to arrange the layout of fibres in CNT strengthened structures could make it flexible for designers to obtain different desirable mechanical behaviours in various applications of such structures. This importance could be achieved by functionally grading the fibres inside the matrix; however, to reach an efficient CNT distribution model for different purposes, it is necessary to comprehend the physical and mechanical properties of strengthened beams.

In the past few years, the mechanical response of CNT strengthened structures has been investigated by arranging the fibres through the thickness direction. For linear analysis, Lin and Xiang [25] investigated the free oscillation behaviour of functionally graded (FG) CNT strengthened beams. Shear deformable beam theories were used to model the beam and differences between the computed natural frequency terms were presented showing that by decreasing the CNT volume fraction, natural frequency terms decrease significantly compared to increasing the volume fraction. Shi et al. [26] analysed the effects of different types of boundary conditions on the linear oscillation of FG CNT reinforced beams; it was shown that the CNT distribution could affect the natural frequency terms significantly. Joshi et al. [27] analysed the strength and elasticity of CNT strengthened hexagonal section beams using finite-element simulation. Randomly dispersed and aligned CNTs were studied and it was shown that the effective elastic reinforcement is a function of CNT length and accordingly increasing the length of CNT fibres will increase the relative modulus term.

For large deformations and nonlinear analysis, Ke et al. [28] examined the nonlinear vibration behaviour of composite beams reinforced with single-walled carbon nanotubes (SWCNTs); the beam was modelled using Timoshenko beam theory and von Kármán geometry nonlinearity was taken into account—it was shown that the volume fraction and distribution of SWCNTs in the matrix could change the frequency ratio and mode shapes significantly. In another study, Pourasghar and Chen [29] investigated the effects of hyperbolic heat conduction on displacements and vibration response of CNT strengthened FG microbeams using Timoshenko beam theory and von Kármán geometry nonlinearity. It was concluded that linear and nonlinear frequencies decrease by increasing the thermal conductivity of the beam.

For analysing geometrical imperfection in CNT strengthened beams varying through the thickness, Wu et al. [30] studied the nonlinear oscillation response of composite beams strengthened with CNT; it was concluded that the nonlinear vibrations in the system is very sensitive to the initial imperfections.

Stability and buckling behaviour of strengthen beams with thickness FG CNT fibres have been examined by many researchers. Ke et al. [31] studied the dynamic stability of FG CNT strengthened beams by the means of differential quadrature method and Bolotin’s technique highlighting that symmetric functionally graded CNT strengthened beams have higher excitation frequencies compared to the uniformly distributed model. In another study, Fattahi and Safaei [32] studied the buckling of functionally graded SWCNT strengthened beams with different boundary conditions where it was shown that decreasing the volume fraction of SWCNT causes smaller stiffness in the system.

Main concentration in the previous studies is on grading the CNTs through the thickness direction [25, 33, 34]. There have been few studies on analysing the influence of grading the CNTs along the length (AFG CNT strengthened beams) which focuses on the linear vibrations of the structure. In Ref. [35], authors analysed the linear vibration response of CNT strengthened beams. The beam was modelled by considering the influence of an elastic Winkler-Pasternak foundation and the linear natural frequencies were obtained using a generalised differential quadrature method (GDQM). Results were compared with literature and finite-element simulation for simplified models shown a great accuracy. In another study, the influence of imperfection on the linear vibrations of the beam was examined [36]. Different types of imperfections were considered and the results were obtained using a generalised decomposition technique. It was shown that the linear frequencies of the beam are sensitive to the distribution of CNTs and imperfections.

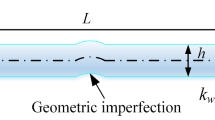
In this study, the effects of geometric nonlinearities on the coupled forced vibrations of AFG CNT reinforced beams are investigated in the presence of an external time-dependent transverse load with not neglecting axial motion (Fig. 1); this is for the first time. The coupled equation of motion is adopted from Ref. [36] and the non-dimensional form and the solution procedure are presented in details. General forms of functionally graded CNT distributions are presented for modelling the reinforcement in the structure. The governing equations are solved using a combination of Galerkin scheme and dynamic equilibrium technique, and a comprehensive parametric study on the nonlinear vibrations of the structure is conducted by considering different types of porosities and imperfections.

Fig. 1

Schematic representation of porous axially functionally graded CNT strengthened beams with geometric and mass imperfections

2 Problem definition and solution procedure

2.1 Model description

The coupled equations of motion of geometrical/mass imperfect porous CNT strengthened beams have previously been obtained in Ref. [36], by the same authors which by adding the presence of an external harmonic load, is briefly described here. For a hollow beam model, by having a geometrical imperfection and neglecting the shear deformation, variations of potential and kinetic energy terms are written as

$$\begin{gathered} \delta U = \mathop \int \limits_{0}^{L} \mathop \int\limits_{A}^{ } \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} \left( x \right)}} \left[ \begin{gathered} \frac{\partial u(x,t)}{{\partial x}} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} \hfill \\ + \frac{\partial w(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx} \hfill \\ \end{gathered} \right]\delta \left( {\frac{\partial u(x,t)}{{\partial x}}} \right)dAdx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - \mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } z\frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} \left( x \right)}} \left[ \begin{gathered} \frac{\partial u(x,t)}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} \hfill \\ + \frac{\partial w(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx} \hfill \\ \end{gathered} \right]\delta \left( {\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right)dAdx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + \mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} \left( x \right)}}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right) \left[ \begin{gathered} \frac{\partial u(x,t)}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} \hfill \\ + \frac{\partial w(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx} \hfill \\ \end{gathered} \right]\delta \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)dAdx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + \mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} \left( x \right)}}\left( {\frac{{dw_{0} (x)}}{dx}} \right) \left[ \begin{gathered} \frac{\partial u(x,t)}{{\partial x}} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} \hfill \\ + \frac{\partial w(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx} \hfill \\ \end{gathered} \right]\delta \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)dAdx \hfill \\ \end{gathered}$$

(1)

$$\begin{gathered} \delta K = M\mathop \int\limits_{0}^{L} \left[ {\frac{\partial u(x,t)}{{\partial t}}\delta \left( {\frac{\partial u(x,t)}{{\partial t}}} \right) + \frac{\partial w(x,t)}{{\partial t}}\delta \left( {\frac{\partial w(x,t)}{{\partial t}}} \right)} \right]\delta_{d} \left( {x - x_{0} } \right)dx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - \,\mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \rho \left( {x,z} \right)z\left[ {\left( {\frac{\partial u(x,t)}{{\partial t}} - z\frac{{\partial^{2} w(x,t)}}{\partial x\partial t}} \right)\delta \left( {\frac{{\partial^{2} w(x,t)}}{\partial x\partial t}} \right)} \right]dAdx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \,\mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \rho \left( {x,z} \right)\left[ {\left( {\frac{\partial u(x,t)}{{\partial t}} - z\frac{{\partial^{2} w(x,t)}}{\partial x\partial t}} \right)\delta \left( {\frac{\partial u(x,t)}{{\partial t}}} \right)} \right]dAdx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \,\mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \rho \left( {x,z} \right)\left[ {\frac{\partial w(x,t)}{{\partial t}}\delta \left( {\frac{\partial w(x,t)}{{\partial t}}} \right)} \right]dAdx, \hfill \\ \end{gathered}$$

(2)

where E is the Young’s modulus (function of x and z), v is the Poisson ratio (function of x), ρ is the density (function of x and z), w and u are the transverse and axial displacements in z and x directions, respectively, w₀ is the geometrical imperfection, M is the lumped mass imperfection, x₀ is the axial position of the mass imperfection, A is the cross section, t is time, L is the length of the beam, δ_d is the Dirac delta, and δ is the variation symbol. For the sake of brevity, the procedure for obtaining Eqs. (1) and (2) is shown in Appendix A. The variation of the external work (W_F) due to a transverse external harmonic excitation force is

$$\delta W_{F} = \mathop \int\limits_{0}^{L} F\cos \left( {\omega t} \right)\delta wdx,$$

(3)

where F is the external force magnitude and ω is the frequency of the harmonic excitation. Employing the coupled equations of motion, Hamilton’s principle gives [36]

$$\begin{gathered} \frac{\partial }{\partial x} \left[ {A_{11} \left( x \right)\frac{\partial u(x,t)}{{\partial x}}} \right] - M\left[ {\frac{{\partial^{2} u(x,t)}}{{\partial t^{2} }}} \right]\delta \left( {x - x_{0} } \right) - \frac{\partial }{\partial x}\left[ {B_{11} \left( x \right)\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{2}\frac{\partial }{\partial x}\left[ {A_{11} \left( x \right)\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} } \right] + \frac{\partial }{\partial x}\left[ {A_{11} \left( x \right)\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)\left( {\frac{{dw_{0} (x)}}{dx}} \right)} \right]\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = I_{0} \left( x \right)\left( {\frac{{\partial u^{2} (x,t)}}{{\partial t^{2} }}} \right) - I_{1} \left( x \right)\left( {\frac{{\partial^{3} w(x,t)}}{{\partial x\partial t^{2} }}} \right), \hfill \\ \end{gathered}$$

(4)

$$\begin{gathered} - \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {D_{11} \left( x \right)\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right] - \frac{\partial }{\partial x}\left[ {B_{11} \left( x \right) \frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}\frac{\partial w(x,t)}{{\partial x}}} \right] - \frac{\partial }{\partial x}\left[ {B_{11} \left( x \right)\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}\frac{{dw_{0} (x)}}{dx}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {B_{11} \left( x \right)\frac{\partial u(x,t)}{{\partial x}}} \right] + \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {B_{11} \left( x \right) \frac{{dw_{0} (x)}}{dx} \frac{\partial w(x,t)}{{\partial x}}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{\partial }{\partial x}\left[ {A_{11} \left( x \right)\frac{\partial u(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx}} \right] + \frac{1}{2}\frac{\partial }{\partial x}\left[ {A_{11} \left( x \right)\frac{\partial w(x,t)}{{\partial x}}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{\partial }{\partial x}\left[ {A_{11} \left( x \right) \frac{\partial w(x,t)}{{\partial x}}\frac{\partial u(x,t)}{{\partial x}}} \right]\, - M\left( {\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }}} \right)\delta \left( {x - x_{0} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{2}\frac{\partial }{\partial x}\left[ {A_{11} \left( x \right)\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} \frac{{dw_{0} (x)}}{dx}} \right] + \frac{1}{2}\frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {B_{11} \left( x \right)\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} } \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{\partial }{\partial x}\left[ {A_{11} \left( x \right) \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} \frac{{dw_{0} (x)}}{dx}} \right] + \frac{\partial }{\partial x}\left[ {A_{11} \left( x \right)\frac{\partial w(x,t)}{{\partial x}}\left( {\frac{{dw_{0} (x)}}{dx}} \right)^{2} } \right]\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = I_{0} \left( x \right)\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} + \frac{\partial }{\partial x}\left[ {I_{1} \left( x \right)\frac{{\partial^{2} u(x,t)}}{{\partial t^{2} }}} \right] - \frac{\partial }{\partial x}\left[ {I_{2} \left( x \right)\frac{{\partial^{3} w(x,t)}}{{\partial x\partial t^{2} }}} \right] + F\cos \left( {\omega t} \right)\,, \hfill \\ \end{gathered}$$

(5)

with the axial stiffness terms (D_11, B₁₁ and A₁₁) and the area moments of inertia (I_2, I₁ and I₀) about the z axis defined as [36]

$$\left[ \begin{gathered} I_{2} \left( x \right) \hfill \\ I_{1} \left( x \right) \hfill \\ I_{0} \left( x \right) \hfill \\ \end{gathered} \right] = \int\limits_{ - h/2}^{h/2} {b\left[ \begin{gathered} z^{2} \hfill \\ z \hfill \\ 1 \hfill \\ \end{gathered} \right]\left\{ {\rho_{m} - \alpha_{2} \left( z \right)\left[ {V_{CNT} \left( x \right)\rho_{CNT} + V_{m} \left( x \right)\rho_{m} } \right] + V_{CNT} \left( x \right)\left( {\rho_{CNT} - \rho_{m} } \right)} \right\}} dz,$$

(6)

$$\left[ \begin{gathered} D_{11} \left( x \right) \hfill \\ B_{11} \left( x \right) \hfill \\ A_{11} \left( x \right) \hfill \\ \end{gathered} \right] = \int\limits_{ - h/2}^{h/2} {b\left[ \begin{gathered} z^{2} \hfill \\ z \hfill \\ 1 \hfill \\ \end{gathered} \right]\left\{ {\frac{{E_{m} - \alpha_{1} \left( z \right)\left[ {V_{CNT} \left( x \right)e_{1} \,E_{CNT} + V_{m} \left( x \right)E_{m} } \right] + V_{CNT} \left( x \right)\left( {e_{1} \,E_{CNT} - E_{m} } \right)}}{{1 - \nu^{2} \left( x \right)}}} \right\}} dz,$$

(7)

where subscripts _m and _CNT denote the matrix and CNT properties, V is the volume fraction and e₁ is the effective coefficient indicating the efficiency of CNTs in strengthening the Young’s modulus of the composite, and α₁ and α₁ are the porosity terms affecting the Young’s modulus and density terms respectively. For symmetric porosity variation through the thickness, the stiffness and inertia terms B₁₁ and I₁ will be zero.

2.2 Solution method

Since the equations of motion include different parameters with a wide range of scale, new non-dimensional parameters are defined to decrees the scale differences as [36]

$$\begin{gathered} \,\,\,w^{*} = \frac{w}{h},\,\,\,w_{0}^{*} = \frac{{w_{0} }}{h},\,\,\,u^{*} = \frac{u}{h},\,\,\,\,x^{*} = \frac{x}{L},\,\,\,x_{0}^{*} = \frac{{x_{0} }}{L},\,\,\,z^{*} = \frac{z}{h},\,\,\,\,\,\,\Omega = \omega \sqrt {\frac{{L^{4} I_{0,m} }}{{D_{11,m} }}} \hfill \\ t^{*} = \sqrt {\frac{{D_{11,m} }}{{L^{4} I_{0,m} }}} t,\,\,\,\,\gamma = \sqrt{\frac{L}{h}} ,\,\,\,\,I_{0}^{*} = {\frac{{I_{0} }}{{I_{0,m} }}} ,\,\,\,\,I_{1}^{*} = {\frac{{I_{1} }}{{I_{0,m} L}}} ,\,\,\,\,I_{2}^{*} = {\frac{{I_{2} }}{{I_{0,m} L^{2} }}} ,\,\,\,\, \hfill \\ A_{11}^{*} = h^{2} \frac{{A_{11} }}{{D_{11,m} }},\,\,\,\,B_{11}^{*} = h\frac{{B_{11} }}{{D_{11,m} }},\,\,\,\,D_{11}^{*} = \frac{{D_{11} }}{{D_{11,m} }},\,\,\,\,F^{*} = \frac{{FL^{4} }}{{D_{11,m} h}},\,\,\,\,M^{*} = \frac{M}{{I_{0,m} L}},\, \hfill \\ \end{gathered}$$

(8)

and the nonlinear coupled Eqs. (4) and (5) are rewritten using the non-dimensional parameters in Eq. (8) as

$$\begin{gathered} - I_{0} \left( x \right)\left( {\frac{{\partial u^{2} (x,t)}}{{\partial t^{2} }}} \right) + I_{1} \left( x \right)\left( {\frac{{\partial^{3} w(x,t)}}{{\partial x\partial t^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{\partial }{\partial x}\left\{ {A_{11} \left( x \right)\left[ {\gamma^{4} \frac{\partial u(x,t)}{{\partial x}} + \frac{1}{2}\gamma^{2} \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} + \gamma^{2} \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)\left( {\frac{{dw_{0} (x)}}{dx}} \right)} \right]} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{\partial }{\partial x}\left\{ {B_{11} \left( x \right)\gamma^{2} \left[ {\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right]} \right\} - M\left( {\frac{{\partial^{2} u(x,t)}}{{\partial t^{2} }}} \right)\delta \left( {x - x_{0} } \right) = 0, \hfill \\ \end{gathered}$$

(9)

$$\begin{gathered} - I_{0} \left( x \right) \left( {\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }}} \right) + \frac{\partial }{\partial x}\left[ {I_{2} \left( x \right) \left( {\frac{{\partial^{3} w(x,t)}}{{\partial x\partial t^{2} }}} \right)} \right] - \frac{\partial }{\partial x}\left[ {I_{1} \left( x \right) \left( {\frac{{\partial^{2} u(x,t)}}{{\partial t^{2} }}} \right)} \right]\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{\partial^{2} }}{{\partial x^{2} }}\left\{ {D_{11} \left( x \right) \left[ {\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right]} \right\} - \frac{\partial }{\partial x}\left\{ {B_{11} \left( x \right) \left[ {\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right]\left( {\frac{\partial w(x,t)}{{\partial x}} + \frac{{dw_{0} (x)}}{dx}} \right)} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{\partial^{2} }}{{\partial x^{2} }}\left\{ {B_{11} \left( x \right) \left[ {\frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} + \gamma^{2} \frac{\partial u(x,t)}{{\partial x}} + \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)\left( {\frac{{dw_{0} (x)}}{dx}} \right)} \right]} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{\partial }{\partial x}\left\{ {A_{11} \left( x \right) \left[ {\gamma^{2} \frac{\partial u(x,t)}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} } \right]\left( {\frac{\partial w(x,t)}{{\partial x}} + \frac{{dw_{0} (x)}}{dx}} \right)} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{\partial }{\partial x}\left\{ {A_{11} \left( x \right) \left( {\frac{{dw_{0} (x)}}{dx}\frac{\partial w(x,t)}{{\partial x}}} \right)\left( {\frac{\partial w(x,t)}{{\partial x}} + \frac{{dw_{0} (x)}}{dx}} \right)} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - M\left( {\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }}} \right)\delta \left( {x - x_{0} } \right) = F\cos \left( {\Omega t} \right). \hfill \\ \end{gathered}$$

(10)

The superscript * is removed from Eqs. (9) and (10) for the sake of brevity. The axial and transverse motion of the hollow beam are written by assuming the first 2N modes of vibration and neglecting the shear effects using Galerkin’s scheme as

$$u\left( {x,t} \right) = \sum\limits_{j = 1}^{N} {r_{j} \left( t \right)\phi_{j} } \left( x \right),$$

(11)

$$w\left( {x,t} \right) = \sum\limits_{i = 1}^{N} {p_{i} \left( t \right)\psi_{i} } \left( x \right),$$

(12)

the governing coupled Eqs. (9) and (10) are rewritten as

$$\begin{gathered} I_{0} \left( x \right)\sum\limits_{i = 1}^{N} {\phi_{i} } \ddot{r}_{i} \left( t \right) + M\sum\limits_{i = 1}^{N} {\phi_{i} } \delta \left( {x - x_{0} } \right)\ddot{r}_{i} \left( t \right) - I_{1} \left( x \right)\sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{i} }}{dx}} \right)} \ddot{p}_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d }{d x}\left[ {A_{11} \left( x \right)\gamma^{4} \sum\limits_{i = 1}^{N} {\left( {\frac{{d\phi_{i} }}{dx}} \right)} } \right]r_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d }{d x}\left\{ {A_{11} \left( x \right)\gamma^{2} \sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{0} }}{dx}} \right)\left( {\frac{{d\psi_{i} }}{dx}} \right)} - B_{11} \left( x \right)\gamma^{2} \sum\limits_{i = 1}^{N} {\left( {\frac{{d^{2} \psi_{i} }}{{dx^{2} }}} \right)} } \right\}p_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d }{d x}\left\{ {\frac{1}{2}A_{11} \left( x \right)\gamma^{2} \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} } } \right\}p_{i} \left( t \right)p_{j} \left( t \right) = 0, \hfill \\ \end{gathered}$$

(13)

$$\begin{gathered} I_{0} \left( x \right)\sum\limits_{i = 1}^{N} {\psi_{i} } \ddot{p}_{i} \left( t \right) + M\sum\limits_{i = 1}^{N} {\psi_{i} } \delta \left( {x - x_{0} } \right)\ddot{p}_{i} \left( t \right) - \frac{d }{dx}\left[ {I_{2} \left( x \right) \sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{i} }}{dx}} \right)} } \right]\ddot{p}_{i} \left( t \right) + \frac{d }{dx}\left[ {I_{1} \left( x \right) \sum\limits_{i = 1}^{N} {\phi_{i} } } \right]\,\ddot{r}_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{{d^{2} }}{{dx^{2} }}\left\{ {D_{11} \left( x \right)\sum\limits_{i = 1}^{N} {\left( {\frac{{d^{2} \psi_{i} }}{{dx^{2} }}} \right)} } \right\}p_{i} \left( t \right) + \frac{d }{dx}\left\{ {B_{11} \left( x \right) \sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{0} }}{dx}} \right)\left( {\frac{{d^{2} \psi_{i} }}{{dx^{2} }}} \right)} } \right\}p_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{d^{2} }}{{dx^{2} }}\left\{ {B_{11} \left( x \right) \sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{0} }}{dx}} \right)\left( {\frac{{d\psi_{i} }}{dx}} \right)} } \right\}p_{i} \left( t \right) - \frac{d }{dx}\left\{ {A_{11} \left( x \right)\sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{0} }}{dx}} \right)^{2} \left( {\frac{{d\psi_{i} }}{dx}} \right)} } \right\}p_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d }{dx}\left\{ {A_{11} \left( x \right) \gamma^{2} \sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{0} }}{dx}} \right)\left( {\frac{{d\phi_{i} }}{dx}} \right)} } \right\}r_{i} \left( t \right) - \frac{{d^{2} }}{{dx^{2} }}\left\{ {B_{11} \left( x \right)\gamma^{2} \sum\limits_{i = 1}^{N} {\left( {\frac{{d\phi_{i} }}{dx}} \right)} } \right\}r_{i} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{d }{dx}\left\{ {B_{11} \left( x \right)\sum\limits_{j = 1}^{N} {\sum\limits_{i = 1}^{N} {\left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d^{2} \psi_{j} }}{{dx^{2} }}} \right)} } } \right\}p_{i} \left( t \right)p_{j} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{d^{2} }}{{dx^{2} }}\left\{ {\frac{1}{2}B_{11} \left( x \right) \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} } } \right\}p_{i} \left( t \right)p_{j} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d}{dx}\left\{ {\frac{3}{2}A_{11} \left( x \right) \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\left( {\frac{{d\psi_{0} }}{dx}} \right)\left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} } } \right\}p_{i} \left( t \right)p_{j} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d}{dx}\left\{ {A_{11} \left( x \right)\gamma^{2} \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\left( {\frac{{d\phi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} } } \right\}r_{i} \left( t \right)p_{j} \left( t \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{d }{dx}\left\{ {\frac{1}{2}A_{11} \left( x \right)\sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\sum\limits_{j = 1}^{N} \, \left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)\left( {\frac{{d\psi_{k} }}{dx}} \right)} } } \right\}p_{i} \left( t \right)p_{j} \left( t \right)p_{k} \left( t \right)\, = F\cos \left( {\Omega t} \right), \hfill \\ \end{gathered}$$

(14)

which can be sorted as

$$M_{11} \ddot{r} + M_{12} \ddot{p} + C_{1} \dot{r} + KL_{11} r + KL_{12} p + KN_{11} p^{2} = 0,$$

(15)

$$M_{22} \ddot{p} + M_{21} \ddot{r} + C_{2} \dot{p} + KL_{21} r + KL_{22} p + KN_{21} p^{2} + KN_{22} rp + KN_{23} p^{3} = F,$$

(16)

with

$$\,r = \left[ {r_{1} ,r_{2} ,r_{3} ,...,r_{N} } \right],$$

(17)

$$\,p = \left[ {p_{1} ,p_{2} ,p_{3} ,...,p_{N} } \right],$$

(18)

$$\,KN_{11} \left( {l,i,j} \right) = - \int\limits_{0}^{1} \, \varphi_{l} \left( x \right)\frac{d }{d x}\left\{ {\frac{1}{2}A_{11} \left( x \right)\gamma^{2} \left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} \right\}dx,$$

(19)

$$\begin{gathered} \,KN_{21} \left( {l,i,j} \right) = \int\limits_{0}^{1} \, \psi_{l} \frac{d }{d x}\left\{ {B_{11} \left( x \right)\left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d^{2} \psi_{j} }}{{dx^{2} }}} \right) } \right\}dx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \int\limits_{0}^{1} \, \psi_{l} \frac{{d^{2} }}{{d x^{2} }}\left\{ {\frac{1}{2}B_{11} \left( x \right) \left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} \right\}dx \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \int\limits_{0}^{1} \, \psi_{l} \frac{d }{d x}\left\{ {\frac{3}{2}A_{11} \left( x \right) \left( {\frac{{d\psi_{0} }}{dx}} \right)\left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} \right\}dx, \hfill \\ \end{gathered}$$

(20)

$$\,KN_{22} \left( {l,i,j} \right) = - \int\limits_{0}^{1} \, \psi_{l} \frac{d }{d x}\left\{ {A_{11} \left( x \right)\gamma^{2} \left( {\frac{{d\phi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)} \right\}dx,$$

(21)

$$\,KN_{23} \left( {l,i,j,k} \right) = - \int\limits_{0}^{1} \, \psi_{l} \frac{d }{d x}\left\{ {\frac{1}{2}A_{11} \left( x \right){ { \left( {\frac{{d\psi_{i} }}{dx}} \right)\left( {\frac{{d\psi_{j} }}{dx}} \right)\left( {\frac{{d\psi_{k} }}{dx}} \right)} } } \right\}dx,$$

(22)

and the linear coefficients M₁₁, M₁₂, KL₁₁, KL₁₂, KL₂₁ and KL₂₂ are given in Ref. [31]. Using the given assumptions and employing a dynamic equilibrium technique for appropriate beam base functions, the dynamic equilibrium coefficients are written in an exponential series as

$$p_{n} = \sum\limits_{m = - N}^{N} {A_{mn} e^{in\Omega t} } ,$$

(23)

$$r_{n} = \sum\limits_{m = - N}^{N} {B_{mn} e^{in\Omega t} } ,$$

(24)

where A_mn and B_mn are the dynamic equilibrium coordinates and the dynamic complex equilibrium equation are obtained by substituting Eqs. (23) and (24) into Eqs. (15) and (16) as [37]

$$\left\{ { - n^{2} \Omega^{2} \left[ M \right] + in\Omega \left[ C \right] + \left[ K \right]} \right\}\left\{ \begin{gathered} r_{n} \hfill \\ p_{n} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} 0 \hfill \\ F_{n\,}^{{{\text{external}}}} \hfill \\ \end{gathered} \right\} + \left\{ \begin{gathered} NL1_{n\,}^{{{\text{system}}}} \hfill \\ NL2_{n\,}^{{{\text{system}}}} \hfill \\ \end{gathered} \right\},$$

(25)

where $F_{n}^{{{\text{external}}}}$ is the external actuating force on each mode of transverse motion, and $NL1_{n}^{{{\text{system}}}}$ and $NL2_{n}^{{{\text{system}}}}$ are the nonlinear terms of the axial and transverse motions, respectively. By considering all the 2 N modes of vibration in axial and transverse equations, Eq. (25) is rewritten as

$$\left[ T \right]\left\{ R \right\} = \left\{ {F_{\,}^{{{\text{external}}}} } \right\} + \left\{ {NL_{\,}^{{{\text{system}}}} } \right\},$$

(26)

where [T] is a complex matrix defined and $\left\{ R \right\}$ is the amplitudes of the motion defined as

$$\left[ T \right] = \left\{ { - n^{2} \Omega^{2} \left[ M \right] + in\Omega \left[ C \right] + \left[ K \right]} \right\},$$

(27)

$$\left\{ R \right\} = \left\{ \begin{gathered} r \hfill \\ p \hfill \\ \end{gathered} \right\}.$$

(28)

For the next step, using Eq. (26), an equivalent root-finding equation is written as

$$G\left( {R,\Omega } \right) = \left[ T \right]\left\{ R \right\} - \left\{ {F_{\,}^{{{\text{external}}}} } \right\} - \left\{ {NL_{\,}^{{{\text{system}}}} } \right\} = 0,$$

(29)

and the differential of Eq. (29) is written as

$$\frac{dR}{{d\Omega }} = - \left( {\frac{{\partial G\left( {R,\Omega } \right)}}{\partial R}} \right)^{ - 1} \left( {\frac{{\partial G\left( {R,\Omega } \right)}}{\partial \Omega }} \right).$$

(30)

By putting frequency parameter as the input, the amplitudes of the equations of motion are obtained. It should be mentioned that this sequential method fails when the singularity is obtained at ∂G(R,Ω)/∂R (at the turning point) [38]. Accordingly, a continuation term (α_arc) should be added to the system and parameters R and Ω are defined as a function of this parameter as [39]

$$R = R\left( {\alpha_{{{\text{arc}}}} } \right),\,\,\,\,\Omega = \Omega \left( {\alpha_{{{\text{arc}}}} } \right),$$

(31)

where Eq. (30) is rewritten by the definition given in Eq. (31) as [38]

$$\left( {\frac{{\partial G\left( {R,\Omega } \right)}}{\partial R}} \right)\frac{dR}{{d\alpha_{{{\text{arc}}}} }} + \left( {\frac{{\partial G\left( {R,\Omega } \right)}}{\partial \Omega }} \right)\frac{d\Omega }{{d\alpha_{{{\text{arc}}}} }} = \left[ {\frac{{\partial G\left( {R,\Omega } \right)}}{\partial R}\,\,\,\,\frac{{\partial G\left( {R,\Omega } \right)}}{\partial \Omega }\,} \right]\left\{ \begin{gathered} \frac{dR}{{d\alpha_{{{\text{arc}}}} }} \hfill \\ \frac{d\Omega }{{d\alpha_{{{\text{arc}}}} }} \hfill \\ \end{gathered} \right\} = 0.$$

(32)

The tangent vector $\left\{ \begin{gathered} \frac{dR}{{d\alpha_{{{\text{arc}}}} }} \hfill \\ \frac{d\Omega }{{d\alpha_{{{\text{arc}}}} }} \hfill \\ \end{gathered} \right\}$ has unit length with normalising α_arc as [40]

$$\left( {\frac{d\Omega }{{d\alpha_{{{\text{arc}}}} }}} \right)^{2} + \left( {\frac{{dR_{1} }}{{d\alpha_{{{\text{arc}}}} }}} \right)^{2} + \ldots + \left( {\frac{{dR_{N} }}{{d\alpha_{{{\text{arc}}}} }}} \right)^{2} + \ldots + \left( {\frac{{dR_{2N - 1} }}{{d\alpha_{{{\text{arc}}}} }}} \right)^{2} + \left( {\frac{{dR_{2N} }}{{d\alpha_{{{\text{arc}}}} }}} \right)^{2} = 1.$$

(33)

Accordingly, an additional equation for updating α_arc along with R and omega is written using Eq. (33) as

$$\begin{gathered} - \left( {\alpha_{{{\text{arc}}}} - \alpha_{{{\text{arc}}}}^{{{\text{old}}}} } \right)^{2} + \left( {R_{1} - R_{1}^{{{\text{old}}}} } \right)^{2} + \ldots + \left( {R_{N} - R_{N}^{{{\text{old}}}} } \right)^{2} + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, \ldots + \left( {R_{2N - 1} - R_{2N - 1}^{{{\text{old}}}} } \right)^{2} + \left( {R_{2N} - R_{2N}^{{{\text{old}}}} } \right)^{2} = \Theta \left( {R,\Omega ,\alpha_{{{\text{arc}}}} } \right) = 0. \hfill \\ \end{gathered}$$

(34)

The iteration process starts from an initial guess which in this study, the initial guess is made by solving the linear part of Eq. (29). Equations (32) and (34) are solved simultaneously using the initial guess and the process is repeated to reach a converged result. Then the frequency is evolved by [41]

$$\Omega_{{{\text{new}}}} = \Omega_{{{\text{old}}}} + \Delta \Omega ,$$

(35)

and also, the dynamic equilibrium coefficients by

$$A_{mn} = A_{mn} + \Delta A_{mn} ,$$

(36)

$$B_{mn} = B_{mn} + \Delta B_{mn} ,$$

(37)

and the process is repeated.

3 CNT fibre effect on nonlinear coupled response

For AFG CNT strengthened imperfect beams, the equations of motion and solution procedure to obtain the nonlinear dynamic response are presented in the previous section. In this section, by defining the problem with the geometrical and physical properties as in Ref. [36] b = 0.2 m, h = 0.1 m, L = 2 m, E_m = 2.5 GPa, E_CNT = 5646.6 GPa, ρ_m = 1190 kg/m³, ρ_CNT = 1400 kg/m³, k = 1, V_CNT,total = 5% and V_CNT,left = 2.5%, e₁ = 0.14, ν = 0.3 and non-dimensional external force as F = 5 with a modal damping 0.075, the influence of various parameters on the nonlinear forced vibration behaviour of the system with pinned- pinned boundary conditions is discussed.

One of the main analysis of this paper is to examine the effect of adding CNT fibres to imperfect beam models and show the impact on the nonlinear response. In the previous study [36], the improvements in the linear response of the system has been investigated and here, the nonlinear frequency response will be presented to clarify the nonlinear response of the system to the presence of an external harmonic load.

To this end, firstly, the influence of AFG varying the CNT volume fraction is analysed for a beam with symmetric porous closed cell as [42, 43]

$${\text{Symmetric}} \to \left\{ \begin{gathered} \alpha_{1} \left( x \right) = \alpha_{10} \cos \left( {\frac{\pi x}{a}} \right) \hfill \\ \alpha_{2} \left( x \right) = \alpha_{20} \cos \left( {\frac{\pi x}{a}} \right) \hfill \\ \end{gathered} \right.,$$

(38)

$${\text{Closed-cell cellular}} \to \alpha_{20} = 1.121\left( {\frac{{\alpha_{1} \left( {x_{i} } \right)}}{{\alpha_{10} }}} \right)^{ - 1} \left[ { - \sqrt[{2.3}]{{1 - \alpha_{1} \left( {x_{i} } \right)}} + 1} \right].$$

(39)

with α₁₀ = 0.2, geometry imperfection A₀ = 0.5 and mass imperfection of M = 5 at x₀ = 0.3. For this imperfect beam model, CNT distribution is assumed as V_cnt,Total = 5% linear variation through the length with V_cnt,Left = [1%, 2%, 3%]. Results for transverse dynamic equilibrium coordinates can be seen in Fig. 2 with respect to non-dimensional frequency parameter (Ω^0.5) showing that increasing the CNT distribution variation has a substantial effect in varying the amplitude response of the system and increasing the V_CNT,Left for this beam model sweeps the excitation frequency to the right side. Besides, it can be seen that increasing the V_CNT,Left from 1 to 3% leads to lower coupling between the transverse modes by increasing the maximum amplitude of the first generalised coordinate and decreasing it for the other two coordinates.

Fig. 2

Influence of the CNT fibre distribution through the length on the transverse amplitude-frequency response of imperfect AFG CNT strengthened porous beam a V_CNT,L = 1%, b V_CNT,L = 2%, and c V_CNT,L = 3%

Frequency amplitude responses for axial dynamic equilibrium coordinates are shown in Fig. 3 which in contrast to the transverse response, increasing the CNT volume fraction in the left side of the beam from 1 to 3% decreases the peak of the first axial coordinate and increases the peak of the second coordinate. Besides, increasing the CNT volume fraction for this beam model sweeps the excitation frequency to the right side.

Fig. 3

Influence of the CNT fibre distribution through the length on the axial amplitude-frequency response of imperfect AFG CNT strengthened porous beam a V_CNT,L = 1%, b V_CNT,L = 2%, and c V_CNT,L = 3%

Moreover, the influence of the V_cnt,Total inside the matrix is analysed by considering uniform CNT distribution in the beam and varying the CNT volume fraction as V_cnt,Total = [1%, 2%, 3%]. Figure 4 shows the influence of the CNT fibres on the transverse vibration response of the imperfect beam model showing that the frequency response of the system sweeps to the right side for all the coordinates by increasing the fibre volume fraction. The maximum amplitude of the first transverse coordinate does not change by this variation but the second and third transverse coordinates lose amplitude.

Fig. 4

Influence of the total volume of CNT fibre on the transverse amplitude-frequency response of imperfect AFG CNT strengthened porous beam a V_CNT,Total = 1%, b V_CNT,Total = 2%, and c V_CNT,Total = 3%

For the axial motion, the influence of the CNT fibres volume fraction is shown in Fig. 5 indicating that increasing V_cnt,Total from 1 to 3 percent leads to lower amplitude response for the first and third coordinates while not changing it for the second coordinate. The frequency response of the system sweeps to the right side for all the coordinates by increasing V_cnt,Total.

Fig. 5

Influence of the total volume of CNT fibre on the axial amplitude-frequency response of imperfect AFG CNT strengthened porous beam a V_CNT,Total = 1%, b V_CNT,Total = 2%, and c V_CNT,Total = 3%

4 Geometrical imperfection effect on nonlinear coupled response

In this section, by defining the problem with the geometrical and physical properties as previous section, the influence of the geometrical imperfection on the nonlinear forced vibration response of the system with simply-supported boundary conditions is discussed. For the case of having a beam with uniform porosity of α₁₀ = 0.4 with open-cell model as [43, 44]

$${\text{Uniform}} \to \left\{ {\begin{array}{*{20}c} {\alpha_{1} = \alpha_{10} } \\ {\alpha_{2} = \alpha_{20} } \\ \end{array} } \right.\,,$$

(40)

$${\text{Open-cell solids}} \to \, \alpha_{20} = - \sqrt {1 - \alpha_{10} } + 1\,\,,$$

(41)

without the mass imperfection, the frequency response of the beam is presented in Fig. 6 for the first three transverse dynamic coordinates of a geometrically perfect beam model with respect to non-dimensional excitation frequency parameter, and in Figs. 7 and 8 for having geometrical imperfection as A₀ = 0.5 and A₀ = 1, respectively. It can be seen that by adding the geometrical imperfection to the system, the stiffness hardening behaviours of geometrically perfect beam model changes to stiffness softening for the given properties.

Fig. 6

Transverse amplitude-frequency response of geometrically perfect AFG CNT strengthened porous beam (uniform open-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 7

Transverse amplitude-frequency response of geometrically imperfect (A₀ = 0.5) AFG CNT strengthened porous beam (uniform open-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 8

Transverse amplitude-frequency response of geometrically imperfect (A₀ = 1.0) AFG CNT strengthened porous beam (uniform open-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Moreover, the max amplitude of the first generalised coordinate increases first by adding geometrical imperfection as A₀ = 0.5 but decreases after increasing the imperfection to A₀ = 1. However, the second generalised transverse coordinate’s maximum amplitude increases by increasing the geometrical imperfection indicating a higher coupling between modes by having this type of imperfection.

For the axial motion, by considering the geometrical imperfection as A₀ = 0.5 and A₀ = 1, the coupling between the equations of motion leads to nonlinear frequency response in axial direction which is shown in Figs. 9 and 10 for A₀ = 0.5 and A₀ = 1, respectively. For the case of axial dynamic equilibrium coordinates, increasing the geometrical imperfection from 0.5 to 1 leads to higher maximum amplitudes for all the first three axial coordinates.

Fig. 9

Axial amplitude-frequency response of geometrically imperfect (A₀ = 0.5) AFG CNT strengthened porous beam (uniform open-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 10

Axial amplitude-frequency response of geometrically imperfect (A₀ = 1.0) AFG CNT strengthened porous beam (uniform open-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Moreover, for the case of having linear porosity of α₁₀ = 0.4 for closed-cell model as [36]

$${\text{Linear}} \to \left\{ \begin{gathered} \alpha_{1} \left( x \right) = \alpha_{10} \left( {1 + x} \right) \hfill \\ \alpha_{2} \left( x \right) = \alpha_{20} \left( {1 + x} \right) \hfill \\ \end{gathered} \right.,$$

(42)

in contrast to the uniform porous model, the coupling between the axial and transverse geometrically perfect frequency responses exist due to un-symmetric porosity through the thickness. Figures 11, 12, 13 show the first three transverse dynamic coordinates of linear porous beam model having A₀ = 0, 0.5 and 1, respectively. It can be seen that for this type of porosity, increasing the geometrical imperfection to A₀ = 0.5 and A₀ = 1.0 leads to significant change in the frequency response from hardening to softening behaviour with more complicated responses compared to the uniform porosity model; however, the maximum amplitude response follows the same variation as uniform porous model.

Fig. 11

Transverse amplitude-frequency response of geometrically perfect AFG CNT strengthened porous beam (linear closed-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 12

Transverse amplitude-frequency response of geometrically imperfect (A₀ = 0.5) AFG CNT strengthened porous beam (linear closed-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 13

Transverse amplitude-frequency response of geometrically imperfect (A₀ = 1.0) AFG CNT strengthened porous beam (linear closed-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

For the axial coordinates in the linear porous model, frequency-amplitude responses are shown in Figs. 14, 15, 16 for A₀ = 0, 0.5 and 1, respectively. It can be seen that the first dynamic equilibrium axial coordinate has higher maximum amplitude in uniform model compared to the linear model for A₀ = 0.5 while this is opposite for A₀ = 1. Besides, for both linear and uniform porous models, considering the geometrical imperfection sweeps the frequency response peak to higher excitation frequencies.

Fig. 14

Axial amplitude-frequency response of geometrically perfect AFG CNT strengthened porous beam (linear closed-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 15

Axial amplitude-frequency response of geometrically imperfect (A₀ = 0.5) AFG CNT strengthened porous beam (linear closed-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

Fig. 16

Axial amplitude-frequency response of geometrically imperfect (A₀ = 1.0) AFG CNT strengthened porous beam (linear closed-cell porosity with α₁ = 0.4) a first coordinate, b second coordinate, and c third coordinate

5 Porosity imperfection effect on nonlinear coupled response

For the given properties at Sect. 3, the influence of imperfection porosity type on the nonlinear frequency response of the system is analysed in this section. To this end, for linear porous closed-cell model, the porosity parameter is varied as α₁₀ = [0.0, 0.1, 0.2] by having geometrical imperfection of A₀ = 0.5 and the transverse frequency response coordinates are shown in Fig. 17. Similarly, for non-symmetric closed-cell porous model as [36]

$${\text{Non-symmetric}} \to \left\{ \begin{gathered} \alpha_{1} \left( x \right) = \alpha_{10} \cos \left( {\frac{\pi x}{a} - \frac{\pi }{4}} \right) \hfill \\ \alpha_{2} \left( x \right) = \alpha_{20} \cos \left( {\frac{\pi x}{a} - \frac{\pi }{4}} \right) \hfill \\ \end{gathered} \right.,$$

(43)

Fig. 17

Influence of porosity on the transverse amplitude-frequency response of geometrically imperfect AFG CNT strengthened porous beam—linear porous closed-cell model a α₁ = 0.00, b α₁ = 0.10, and c α₁ = 0.20

the same analysis it done and the results are shown in Fig. 18 for the transverse frequency responses; it can be seen that for transverse motion, the maximum amplitude-frequency response coordinates do not change significantly in magnitude for the non-symmetric model. For the linear porous model, increasing the porosity term from 0 to 0.2 slightly increases the peak of the amplitude response for the first transverse coordinate. Besides, the frequency response of the beam model sweeps to left by increasing the porosity parameter.

Fig. 18

Influence of porosity on the transverse amplitude-frequency response of geometrically imperfect AFG CNT strengthened porous beam—un-symmetric porous closed-cell model a α₁ = 0.00, b α₁ = 0.10, and c α₁ = 0.20

For the axial motion, increasing the porosity term from 0 to 0.2 leads to higher coupling between the first two axial coordinates in both the linear (Fig. 19) and un-symmetric (Fig. 20) porous models by decreasing the max value for the amplitude of the first axial coordinate and increasing the amplitude of the second one. The third coordinate loses amplitude in both porous models by increasing the porosity of the system. Similar to the transverse coordinates, the frequency response of the beam model sweeps to left by increasing the porosity parameter and the porosity effect in non-symmetric closed-cell porous model is considerably lower than the linear porous closed-cell model.

Fig. 19

Influence of porosity on the axial amplitude-frequency response of geometrically imperfect AFG CNT strengthened porous beam—linear porous closed-cell model a α₁ = 0.00, b α₁ = 0.10, and c α₁ = 0.20

Fig. 20

Influence of porosity on the axial amplitude-frequency response of geometrically imperfect AFG CNT strengthened porous beam—un-symmetric porous closed-cell model a α₁ = 0.00, b α₁ = 0.10, and c α₁ = 0.20

6 Mass imperfection effect on nonlinear coupled response

Another important imperfection in manufacturing and operating CNT strengthened beams is mass imperfection. In this section, the influence of having mass imperfection and its position on the nonlinear dynamic response of the system is shown.

6.1 Mass imperfection position effect

For the case of having a beam with symmetric porous α₁₀ = 0.2 closed-cell model, geometrical imperfection A₀ = 0.3 and mass imperfection of M = 10 is considered; the rest of the properties are as defined at Sect. 3. For this CNT strengthened beam model, the influence of the position of the mass imperfection is analysed by having x₀ = [0.0, 0.3, 0.5] and shown in Fig. 21 for transverse dynamic equilibrium coordinates; it can be seen that the position of the mass imperfection has a significant effect in varying the nonlinear frequency response in which for x₀ = 0.5, the amplitudes of all the first three coordinates increase significantly.

Fig. 21

Influence of the mass imperfection position on the transverse amplitude-frequency response of imperfect AFG CNT strengthened porous beam a x₀ = 0.00, b x₀ = 0.30, and c x₀ = 0.50

For the axial motion, the dynamic equilibrium coordinates are shown in Fig. 22 by having x₀ = [0.0, 0.3, 0.5]; it can be seen that moving the position of the mass imperfection from 0 to 0.5 increases the amplitudes of the first and third axial coordinates but decreases the amplitude of the second coordinate. It should also be mentioned that increasing the position of the mass imperfection from 0 to 0.5 sweeps the frequency response of the beam model to the left side.

Fig. 22

Influence of the mass imperfection position on the axial amplitude-frequency response of imperfect AFG CNT strengthened porous beam a x₀ = 0.00, b x₀ = 0.30, and c x₀ = 0.50

6.2 Mass imperfection weight effect

The influence of the mass imperfection weight is analysed by having CNT strengthened beam model with non-symmetric closed-cell porosity with α₁₀ = 0.3, geometry imperfection A₀ = 0.5 and the mass imperfection position 0.5. Results are shown in Fig. 23 for transverse dynamic equilibrium coordinates; it can be seen that increasing the mass imperfection weight sweeps the curves to the left side and increases the peak and nonlinearity in the first and third coordinates of the transverse response.

Fig. 23

Influence of the mass imperfection on the transverse amplitude-frequency response of imperfect AFG CNT strengthened porous beam a M = 5, b M = 10, and c M = 20

Similarly, for the axial motion, the results for axial coordinates are shown in Fig. 24 indicating that all the three axial coordinates show higher peak of amplitude by increasing the weight of the mass imperfection.

Fig. 24

Influence of the mass imperfection on the axial amplitude-frequency response of imperfect AFG CNT strengthened porous beam a M = 5, b M = 10, and c M = 20

7 Conclusions

A comprehensive analysis on the nonlinear dynamics of imperfect beams strengthened with CNT fibres was presented in this study for the first time by grading the CNTs through the length of the beam. The beam was assumed with geometrical and mass imperfection together with porosity imperfection. The geometrical imperfection was presented by assuming a slight curve in the beam and the porosity was assumed to vary through the thickness of the beam. The porosity was modelled by assuming open cell, closed cell and simple form of the formulation, and the variation through the thickness was presented using a uniform, un-symmetric, symmetric and linear variations. The coupled axial and transverse equations of motion were presented. They show nonlinear coupling due to porosity, imperfections and large deformations. The equations of motion were solved using a combination of the Galerkin scheme and a dynamic equilibrium technique. By examining the nonlinear dynamic behaviour of the system, the following outcomes were obtained:

• For the studied case, geometric imperfection has a significant effect in varying the nonlinear behaviour from hardening to softening.

• For the symmetric beam, the axial/transverse coupling is insignificant while for an un-symmetric beam, the axial/transverse coupling is relevant and both the axial and transverse coordinates show rich nonlinear dynamics.

• The type of the porosity and its variation has a direct effect in the nonlinear response of the system for both the axial and transverse coordinates.

• The system shows high sensitivity to the mass imperfection and its position. Increasing the mass weight and moving it to the middle of the beam shifts the resonance towards smaller frequency.

• It is shown that the CNTs have a significant effect on the nonlinear response of imperfect beams and decrease the max value for the amplitude of the first coordinate of both axial and transverse motions.

• The distribution of the CNTs have also been examined. An increase of the nonuniformity of CNT grading shifts the resonance towards larger frequency.

Imperfection in the system lead to complicated nonlinear frequency response. This shows the importance of considering these imperfections to accurately model the beam structure. This investigation can be extended to different types of fibre-reinforced structures.

Appendix A

For a hollow beam model, by having a geometrical imperfection and neglecting the shear deformation, the nonzero stress-deformation and strain-deformation terms are written as [36]

$$\varepsilon_{xx} = \frac{\partial u(x,t)}{{\partial x}} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} + \frac{\partial w(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx}\,\,,$$

(A1)

$$\sigma_{xx} = \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} \left( {x,z} \right)}}\left[ {\frac{\partial u(x,t)}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \frac{\partial w(x,t)}{{\partial x}}\frac{{dw_{0} (x)}}{dx}} \right]\,,$$

(A2)

where E is the Young’s modulus, v is the Poisson ratio, w and u are the transverse and axial displacements in z and x directions and w₀ is the geometrical imperfection. It is assumed that the Young’s modulus and the Poisson ratio vary as a function of the position (x, z) within the beam, as a consequence of the porosity and the functionally graded distribution of the CNT along the length. Since the CNT volume fraction varies along the length and the porosity varies along the thickness of the beam, the Young’s modulus and density are defined as [35]

$$\begin{gathered} \left\{ \begin{gathered} E\left( {x,z} \right) \hfill \\ \rho \left( {x,z} \right) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} E_{m} \hfill \\ \rho_{m} \hfill \\ \end{gathered} \right\} - \left[ {\left\{ \begin{gathered} E_{m} \hfill \\ \rho_{m} \hfill \\ \end{gathered} \right\}V_{m} \left( x \right) + \left\{ \begin{gathered} e_{1} \,E_{CNT} \hfill \\ \rho_{CNT} \hfill \\ \end{gathered} \right\}V_{CNT} \left( x \right)} \right]\left\{ \begin{gathered} \alpha_{1} \left( z \right) \hfill \\ \alpha_{2} \left( z \right) \hfill \\ \end{gathered} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {\left\{ \begin{gathered} e_{1} \,E_{CNT} \hfill \\ \rho_{CNT} \hfill \\ \end{gathered} \right\} - \left\{ \begin{gathered} E_{m} \hfill \\ \rho_{m} \hfill \\ \end{gathered} \right\}} \right)V_{CNT} \left( x \right)\,, \hfill \\ \end{gathered}$$

(A3)

where subscripts _m and _CNT denote the matrix and CNT properties, V is the volume fraction and e₁ is the effective coefficient indicating the efficiency of CNTs in strengthening the Young’s modulus of the composite. Parameters α₁ and α₂ are the porosity terms affecting the Young’s modulus and density terms respectively with porosity coefficients α₁₀ and α₂₀ which for closed-cell cellular models, open-cell solids and simplified models are related together by [42, 43]

$$\alpha_{20} = \left\{ \begin{gathered} \frac{{1.121\left( {1 - \sqrt[{2.3}]{{1 - \alpha_{1} \left( z \right)}}} \right)}}{{\left( {\frac{{\alpha_{1} \left( z \right)}}{{\alpha_{10} }}} \right)}} \to \left( {\text{Closed-cell cellular}} \right) \hfill \\ 1 - \sqrt {1 - \alpha_{10} } \, \to \left( {\text{Open-cell solids}} \right) \hfill \\ \hfill \\ \alpha_{10} \to \left( {\text{Simplified models}} \right) \hfill \\ \end{gathered} \right.,$$

(A4)

where α₁ and α₂ can vary in the thickness direction following a specific function which will be discussed further. Besides, the CNT volume fraction varies through the length as [36]

$$\left\{ \begin{gathered} V_{m} (x) = 1 - V_{CNT} (x), \hfill \\ V_{CNT} (x) = V_{CNT - L} \left( {1 - \frac{x}{L}} \right)^{k} + V_{CNT - R} \left[ {1 - \left( {1 - \frac{x}{L}} \right)^{k} } \right]\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le x \le L\,, \hfill \\ \end{gathered} \right.$$

(A5)

where the subscripts _R and _L denote the right and left ends of the beam and k is the variation power term. The potential and kinetic energy terms are written as [36]

$$U = \frac{1}{2}\mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} \left( x \right)}} \left[ {\frac{\partial u(x,t)}{{\partial x}} - z\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w(x,t)}{{\partial x}}} \right)^{2} + \left( {\frac{\partial w(x,t)}{{\partial x}}} \right)\left( {\frac{{dw_{0} (x)}}{dx}} \right)} \right]^{2} dAdx,$$

(A6)

$$\begin{gathered} K = \frac{1}{2}M\mathop \int\limits_{0}^{L} \left[ {\left( {\frac{\partial w(x,t)}{{\partial t}}} \right)^{2} + \left( {\frac{\partial u(x,t)}{{\partial t}}} \right)^{2} } \right]\delta_{d} \left( {x - x_{0} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\frac{1}{2}\mathop \int\limits_{0}^{L} \mathop \int\limits_{A}^{ } \rho \left( {x,z} \right)\left[ {\left( {\frac{\partial u(x,t)}{{\partial t}} - z\frac{{\partial^{2} w(x,t)}}{\partial x\partial t}} \right)^{2} + \left( {\frac{\partial w(x,t)}{{\partial t}}} \right)^{2} } \right]dAdx. \hfill \\ \end{gathered}$$

(A7)

In Eq. (A7), δ_d is the Dirac delta function, M represents the lumped mass imperfection, and x₀ is the axial position of M.