Abstract
This paper presents the free vibration and buckling analyses of functionally graded carbon nanotube-reinforced (FG-CNTR) laminated non-rectangular plates, i.e., quadrilateral and skew plates, using a four-nodded straight-sided transformation method. At first, the related equations of motion and buckling of quadrilateral plate have been given, and then, these equations are transformed from the irregular physical domain into a square computational domain using the geometric transformation formulation via discrete singular convolution (DSC). The discretization of these equations is obtained via two-different regularized kernel, i.e., regularized Shannon’s delta (RSD) and Lagrange-delta sequence (LDS) kernels in conjunctions with the discrete singular convolution numerical integration. Convergence and accuracy of the present DSC transformation are verified via existing literature results for different cases. Detailed numerical solutions are performed, and obtained parametric results are presented to show the effects of carbon nanotube (CNT) volume fraction, CNT distribution pattern, geometry of skew and quadrilateral plate, lamination layup, skew and corner angle, thickness-to-length ratio on the vibration, and buckling analyses of FG-CNTR-laminated composite non-rectangular plates with different boundary conditions. Some detailed results related to critical buckling and frequency of FG-CNTR non-rectangular plates have been reported which can serve as benchmark solutions for future investigations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In modern engineering applications, structural components with different shapes are subjected to diverse mechanical conditions. Therefore, different behaviors such as stress, static, or dynamic buckling and free vibrations of structural elements have been largely studied till now [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Among these structural components, plates with different shapes, i.e., circular, annular, sector, trapezoidal, rectangular, triangular, and skew types for different purposes, find many uses in different engineering designs such as aerospace and aeronautics, automobile, mechanical, and ship industries. Therefore, examining the buckling and vibrational behaviors of plates with different geometries gains importance. Hence, many studies have been presented to examine the mechanical behaviors of various kinds of plates using different analytical and numerical approaches. Kitipornchai et al. [21] considered the elastic buckling of thick skew plate Rayleigh–Ritz method as a solution procedure. Liew et al. [22] used the shear deformation theory of Mindlin’s for modeling of the free vibration behavior of laminated plates with different geometry. Wang et al. [23] proposed a kind of Rayleigh–Ritz method for buckling analysis of thick plates as well as presented some detailed results supplied for Mindlin plates. Xiang et al. [24] examined the elastic buckling of skew Mindlin plates under shear loads using Rayleigh–Ritz method. Liew and Han [25] introduced a mapping technique to apply the differential quadrature method for bending analysis of plates in conjunction with the Reissner–Mindlin thick plate theory. Some detailed results on buckling and free vibration of skew fiber-reinforced composite laminates based on thin and thick plate theories have been investigated by Wang [26,27,28] and detailed results are reported. Anlas and Goker [29] studied the vibration of skew laminated composite plates with simply supported and clamped edges using orthogonal polynomials and the Ritz method. Ferreira [30] analyzed the stability and bending of laminated composite plates using the multiquadric radial basis function in conjunctions with the meshless method. Meshless based radial basis functions and finite point formulation are discussed for static, stability, and vibration analysis of composite plates with different geometries by Ferreira et al. [31, 32]. Karami and Malekzadeh [33] applied the differential quadrature transformation to the vibration problem of plates. Civalek [34] proposed the differential quadrature and harmonic differential quadrature methods for buckling analysis of plates with different shapes. Huang and Li [35] gave some detailed results about bending and buckling of anti-symmetric laminated plates via the first-order shear deformation theory and moving least square differential quadrature method. Liew et al. [36] employed a mesh-free radial basis function method for the buckling analysis of non-uniformly loaded thick plates. Leung et al. [37] proposed a trapezoidal p-element for vibration analysis of plates with quadrilateral shapes. Free vibration response of skew fiber-reinforced composite and laminates using a shear deformable finite-element model is present by Garg et al. [38]. Civalek and Acar [39] analyzed the bending of Mindlin plates resting on two-parameter elastic foundations using the discrete singular convolution method. Free vibration analysis of plates with different shapes is presented by Civalek [40] using the harmonic and polynomial differential quadrature methods. Nguyen et al. [41] presented an iso-geometric finite-element formulation based on Bézier extraction of the non-uniform rational B-splines in combination with a generalized unconstrained higher order shear deformation theory for laminated composite plates. Kalita et al. [42] developed a structural optimization framework for frequencies of skew laminated plates with different boundary conditions and the number of layers by combining the high accuracy of finite-element method with iterative improvement capability of metaheuristic algorithms. Mishra and Barik [43] gave the non-uniform rational B-spline augmented finite-element method for stability analysis of arbitrary thin plates. Alihemmati and Tadi Beni [44] developed the three-dimensional mesh-free Galerkin method for structural analysis of general polygonal geometries and the capability of the method is shown with the free vibration analysis of a general pentagon plate.
In engineering applications, the desired characteristics of structural members are being safety, functional, aesthetic, and affordability. The use of non-uniform, non-homogeneous, and reinforced elements is beneficial to ensure the said conditions, as well as the strength and structural efficiency, is increased, while the total cost and weight are reduced. Therefore, structural elements composed of composite materials have a wide range of utilizations, in the recent engineering applications. Fiber-reinforced composites are one of the composite materials that consist of fibers in a matrix and have major advantages over the conventional structural materials. They have a comprehensive range of applications as aircraft, wind turbines, racing bicycles, radar bonnets, rackets, cooling towers, and the automotive industry. To produce high performance structural and multifunctional composites for various potential applications, CNTs can be used as reinforcing constituents instead of conventional fibers because of their superior properties such as high elastic modulus, tensile strength, and low density. The discovery of CNTs in 1991 Iijima [45] gave rise to accelerate the developments in nanotechnology. CNTs have received a great deal of attention due to the extraordinary mechanical, chemical, thermal, physical, and electrical properties [46,47,48,49,50,51,52,53,54].
However, the applications of CNTs to the composites can be delayed because of the weak interfacial bonding between CNTs and matrix. This problem can be abolished using a new type of composites called functionally graded materials (FGMs), which are characterized with smooth and continuous variations in both compositional profiles. FGMs are inhomogeneous composite materials that occurring of two or more materials with different properties (as ceramic and metal) that the properties are changed gradually and continuously throughout one or more directions, i.e., height (traditional FGM), length (axially FGM), and both of them (bi-directional FGM) unlike in laminated composites. The concept of FGMs was first presented during a spacecraft project as a thermal barrier material for propulsion and airframe structural systems of the spacecraft in 1984 by Japanese scientists [55]. Since then, structures made of FGMs in a variety of geometries like the rectangular, circular, ring, and annular sectors have been used extensively in space transportation, nuclear reactors, defense industries, biomedicine, and chemical plants. For this reason, it is crucial to determine the mechanical behaviors of structures made of FGMs. Consequently, a number of studies have been performed on this topic by different researchers [56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91].
With the development of modern industries and different engineering applications, FGMs and CNTs are started to use together for creating a novel type of composites named functionally graded carbon nanotube-reinforced composites (FG-CNTRC) which has superiorities of both materials. Then, several studies have been performed to examine the mechanical responses of FG-CNTRCs. Some fundamental formulation and benchmark results have been given by Shen [92, 93] and Shen and Zhang [94]. Aragh et al. [95] developed Eshelby–Mori–Tanaka approach for vibration analysis of continuously graded CNTR cylindrical panels. Malekzadeh et al. [96] presented the buckling analysis of FG arbitrary straight-sided quadrilateral plates rested on the two-parameter elastic foundation under in-plane loads. Static and free vibration modeling of CNTRC plates with the first-order shear deformation plate theory is studied using FEM by Zhu et al. [97]. Alibeigloo and Liew [98] examined the bending behavior of the FG-CNTRC plate using the theory of elasticity by the three-dimensional theory of elasticity and state-space method under thermal loading. Lei et al. [99,100,101,102] studied on the dynamic analysis of FG-CNTRC plates via kp-Ritz method, in detail. Malekzadeh and Heydarpour [103] applied the Navier-layerwise differential quadrature method for three-dimensional static and free vibration analysis of FG-CNTRC laminated plates. Some detailed parametric results are presented also for CNTR plates and panels by Zhang et al. [104, 105]. Malekzadeh and Shojaee [106] performed the buckling analysis of quadrilateral laminated plates with CNTRC. Tounsi et al. [107] analyzed the thermal buckling of double-walled CNTR beams. Malekzadeh and Zarei [108] gave some benchmark results on free vibration of FG composites and CNTRC plates. Lei et al. [109] applied the element-free meshless method for buckling analysis of functionally graded CNTRC skew plates on elastic foundations. Previous studies on FGM composites and CNTRC plates and shells are reviewed by Liew et al. [110]. Zhang et al. [111,112,113,114,115,116] performed the buckling, post-buckling vibration analyses of CNTRC plates with diverse shapes. Free vibration analysis of thick FG-CNTRC plates with arbitrary geometry based on the HSDT and FSDT is presented by Ansari et al. [117, 118] using the differential quadrature method. Garcia-Madias et al. [119] gave an efficient finite-element method in conjunctions with the Hu–Washizu principle for static and dynamic analysis of skew plates for CNTRC material. Kiani [120,121,122] examined the free vibration of functionally graded CNTR several types of composite plates under different loadings. Lei et al. [123] discussed the effects of foundation parameters on vibrational behavior CNTRC thick quadrilateral Plplates. Free vibration and buckling responses of a pressurized FG-CNTR conical shell under axial compression are analyzed using harmonic differential quadrature method by Mehri et al. [124]. Mirzaei and Kiani [125] used the Ritz method with Chebyshev basis polynomials for vibration analysis of FGCNTRC plates with cutout. Setoodeh and Shojaee [126] employed a transformer weighting differential quadrature method to the nonlinear free vibration problem of CNTRC quadrilateral plates. Tornabene et al. [127] examined the effect of agglomeration on the natural frequencies of FG-CNTR laminated composite shells. Kiani [128] examined the shear buckling response of CNTRC rectangular plates in the thermal environment. Wu and Li [129] proposed a general three-dimensional model for frequencies of FGM CNTRC plates with various boundary conditions. Thermo-mechanical buckling analysis of embedded FG-CNTRC truncated conical shells is performed by Duc et al. [130]. Fantuzzi et al. [131] discussed bending analysis for laminated nanocomposite plates via shear deformable plate theory. Thermo-mechanical stability response of sandwich nanocomposite plates with FG-CNTR layers surrounded by an elastic matrix subjected to the magnetic field is investigated based on the parabolic shear deformation plate theory by Shokravi [132]. In another study, the mechanical response of CNTRC skew laminated plates under a transverse dynamic load is perused by Zhang and Xiao [133]. Mehar and his coauthors [134,135,136,137] examined the large amplitude–frequency, bending, and free vibration responses of CNTRC structures in the thermal environment are examined by the finite-element method. The effective material properties of the structure are estimated according to the Mori–Tanaka approach. Kiani and Mirzaei [138] investigated the shear buckling behavior of FG-CNTRC plates with the aid of the Ritz method. Nguyen-Quang et al. [139] proposed an extension of the iso-geometric approach for the dynamic response of laminated carbon CNTRC plates integrated with piezoelectric layers. Zghal et al. [140] analyzed the free vibration of FG-CNTRC shell structures. Ebrahimi et al. [141] investigated the free vibration response of sandwich plates with porous electro-magneto-elastic functionally graded materials as face sheets and FG-CNTRC as the core. Mallek et al. [142] presented a geometrically nonlinear finite shell element to predict the nonlinear dynamic behavior of piezolaminated FG-CNTRC shell, to enrich the existing research results on FG-CNTRC structures. Tornabene et al. [143] proposed a multiscale approach for the analysis of three-phase CNT/polymer/fiber laminates. Free vibration analysis of CNTR magneto-electro-elastic plates is examined by Vinyas [144] via the finite-element method.
In this paper, the free vibration and buckling analyses of FG-CNTR laminated non-rectangular plates, i.e., quadrilateral and skew plates, are performed using a four-nodded straight-sided transformation method. The geometric transformation of the DSC method is used to coordinate transformation from the physical domain to the computational domain. Besides, two-different singular kernels are used to the discretization of a singular convolution. After convergence and comparative studies, some detailed parametric results have been obtained for frequencies and buckling loads of non-rectangular plates for various lamination schemes, CNT distributions, geometric parameters of plates, CNT volume fraction numbers, skew angles, loading, and different plate edge conditions. To the best knowledge of authors, this is the first attempt in which the DSC coordinate transformation has been applied for free vibration and buckling analysis of functionally graded composites and CNTR laminated composite plates with the non-rectangular domain.
2 Material properties of FG-CNTR laminated composite plates
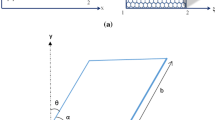
Figure 1 shows arbitrary straight-sided laminated non-rectangular plates made of perfectly bonded FG-CNTR. It is assumed that the material properties vary along the thickness direction. To estimate the material properties of FG structures, several rules of the mixture are developed like power-law, exponential, sigmoid, and Mori–Tanaka homogenization scheme as [145,146,147]:
Power law:
Sigmoid:
Exponential:
Mori–Tanaka scheme:
In view of Eqs. (4a) and (4b), Young’s modulus and Poisson’s ratio can be given as:
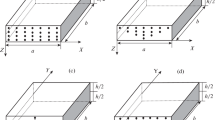
where \(P_{{\text{m}}}\) and \(P_{{\text{c}}}\) are the volume fraction of constituents at the upper (\(z = - h/2\)) and the lower (\(z = h/2)\) surfaces of the structure, respectively. \(K_{\left( z \right)}\) and \(\mu_{\left( z \right)}\) are, respectively, the effective bulk and shear modulus. Also, \(k\) represents the material property gradient index and the subscripts c and m stand the ceramic and metal phase, respectively. The distributions of CNTs through the thickness direction of FG-CNTR laminated non-rectangular plates are defined with uniform distribution (UD) and three types of FG distributions (FG-O, FG-V, and FG-X), as shown in Fig. 2. The volume fractions of said distributions are as follows [92, 93]:
\(V_{CNT}^{*}\) is the volume fraction of CNT which can be described as:
Here, mCNT, ρCNT and ρm denote the mass fraction of CNTs, and the densities of CNTs and matrix, respectively; and Vm is the volume fraction of the matrix. Additionally, the properties of FG-CNTRC can be described as:
where E11, E22, G12 and v12 are the effective Young’s modulus, shear modulus, and Poisson’s ratio of FG-CNTR layer, respectively; \(E_{11}^{CNT} ,E_{22}^{CNT} ,G_{12}^{CNT}\), and \(\nu_{12}^{CNT}\) are Young’s modulus, shear modulus, and Poisson’s ratio of CNTs, respectively; \(\eta_{1} ,\eta_{2} \;{\text{and}}\;\eta_{3}\) are the efficiency parameters of CNTs; Em and vmare Young’s modulus and Poisson’s ratio of matrix, respectively.
3 The method of discrete singular convolution
Effective and fast numerical solution of mathematical physics and engineering problems is of significant interest and important for numerical discretization of physical problems modeling. The method of DSC has become a preferred method by many researchers in recent 10 years due to its simplicity and fast convergence characteristics for different applications. Furthermore, the mathematical basis of the method of discrete singular convolution is older and based on the theory of distributions and the theory of wavelets [148, 149]. In different DSC applications, many DSC kernels such as regularized Shannon’s delta (RSD), regularized Dirichlet, regularized Lagrange, and regularized de la Vall´ee Poussin kernels were used in different applications in area of mathematical physics, computational fluid dynamics, and vibration problems in solid mechanics. The method of discrete singular convolution first used at the end of the 90 s by Wei and his coauthors [150,151,152,153], in which they have proposed some singular kernels, namely, Hilbert, Abel, and delta types, in some mathematical physics and computational mechanics problems. Then, the method of DSC has been utilized in different problems in the area of mathematical physics and computational solid and fluid mechanics [154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170]. It was completely shown and proven by many scientists in different areas via different examples that the method of discrete singular convolution (DSC) has good accuracy, easy for applications, efficiency, and rapid convergence. For a general definition of the method, let be consider a singular convolution as below [150]:
where \(T(t - x)\) is a singular kernel and η(t) as an element of the space of the test function. In application, singular kernels of delta type are generally used [152]:
Kernel \(T(x) = \delta (x)\) is important for the interpolation of surfaces and curves. With a sufficiently smooth approximation, it is more effective to consider a DSC [153]:
where F(t) is an approximation to F(t) and {xk}is a proper set of discrete points on which the Eq. (12) is well defined. During the regularization, two different kernels have been used in this study. These are Regularized Shannon’s Delta (RSD) kernel and Lagrange-delta sequence (LDS) kernel. Shannon’s kernel is regularized via below function:
Equation (13) can also be used to supply discrete approximations to the singular convolution kernels of the delta type:
where \(\mathop \delta \nolimits_{\Delta } (x - \mathop x\nolimits_{k} ) = \Delta \mathop \delta \nolimits_{\alpha } (x - \mathop x\nolimits_{k} )\) and superscript (n) denotes the nth-order derivative, and 2M + 1 is the computational bandwidth which is centered around x and is usually smaller than the whole computational domain. The essence of the DSC is that the partial derivative of a function f(x) and its derivatives with respect to the x coordinate at a grid point xi is approximated by a linear sum of discrete values f (xk) in a narrow bandwidth [x − xM, x + xM]. This can be expressed as [151]:
Second-order derivative at x = xi of the DSC kernels for directly is given as:
The discretized forms of Eq. (7) can then be expressed as:
When the regularized Shannon’s kernel (RSK) is used, the detailed expressions for \(\mathop \delta \nolimits_{\Delta ,\sigma } (x)\), \(\mathop \delta \nolimits_{\Delta ,\sigma }^{(1)} (x)\), \(\mathop \delta \nolimits_{\Delta ,\sigma }^{(2)} (x)\),\(\mathop \delta \nolimits_{\Delta ,\sigma }^{(3)} (x)\) and \(\mathop \delta \nolimits_{\Delta ,\sigma }^{(4)} (x)\) can be easily obtained for xxk. For example, the first- and second-order derivatives are given as [164]:
Lagrange-delta sequence (LDS) kernel is defined for i = 0,1,…, N−1 and j = −M,…,M and given via below function [151, 153, 164, 167, 168]:
Here, \(\mathop W\nolimits_{i,j}^{(n)}\) are the weighting coefficients and these coefficients for the first derivative can be given as:
The weighting coefficients for higher order derivatives are also defined as:
for i = 0,1,…, N−1 and j = −M,…,M, j ≠ 0, and n = 2,3,…,2 M:
Using uniform N grid points for the computational domain x0 < …. < xN−1, with a total of 2 M fictitious grid points, x−M < …. < x−1 and xN < …. < xN−1+M, that is:
When Lagrange kernel is used, related derivatives can also be given as:
4 Four-nodded transformation
The field of arbitrary straight-sided FG-CNTR laminated non-rectangular plate in the Cartesian x–y-coordinate can be mapped into that for the natural— plane, as shown in Fig. 3. Using the transformation equations, the physical domain can be mapped into the computational domain as:
where xi and yi are the coordinates of node i in the physical domain, N is the number of grid points, and \(\mathop \Phi \nolimits_{i} (\xi ,\eta )\); i = 1,2,3,…,N are the interpolation or shape functions. Interpolation function can be defined as:
After the well-known chain rule, related differential derivatives of this function can be written as:
where ξi and ηi are the coordinates of node i in the ξ−η plane, and \(J_{ij}\) are the elements of the Jacobian matrix. These are expressed as follows:
Using this transformation, related derivatives with respect to the –x and y-coordinate can be written, respectively, as:
or
The discrete form of the second-order derivatives with respect to the –x and y-coordinate can be written respectively, as:
5 Buckling of FG-CNTR laminated non-rectangular plates
5.1 Thin isotropic plate
The related governing equation for buckling of thin FG-CNTR plate is given as:
\(D\) is the rigidity of FG-CNTR plate, h is the thickness, \(N_{x}\) and \(N_{y}\) are the applied compressive loads in the x and y directions, respectively, \(N_{xy}\) is the shear forces, w is the deflection, and x and y are the mid-plane Cartesian coordinate. We can define the below differential operators for brevity:
and
Thus, the fourth-order derivatives can be given in terms of the second-order derivatives, that is:
Consequently, related derivatives in the computational domain can be listed for related derivations:
Using the differential operators for fourth-order statements in Eq. (39), the normalized governing equation takes the following form:
Employing the transformation rule, the governing Eq. (52) then becomes:
The discretized governing equations are given by:
Now introducing:
where \(\nabla^{2}\) is the Laplace operator. Thus, fourth-order equation takes the following simple form:
Substituting Eqs. (54) into Eq. (56), and using the fourth-order operator, we find:
For convenience and simplicity, the following new variables have been used in the above equations:
in which the \(G_{\xi } ,G_{\eta }\) and \(G_{\xi \eta }\) take the following values:
We have the following equation for buckling:
For the computations, simply supported and clamped edges are considered.
Simply supported edge (S)
Clamped edge (C)
Here, n and s denote the normal and tangential directions of the plate, respectively. It is known that proper boundary conditions must be satisfied to obtain a unique solution for a differential equation. For this purpose, consider a uniform grid having the following form:
Consider a column vector W given as:
with \((N_{x} + 1)(N_{y} + 1)\) entries \(W_{i,j} = W(X_{i} ,Y_{j} ); \, (i = 0,1,...,N_{x} ; \, j = 0,1,...,N_{y} )\). Let us define the \((N_{x} + 1)(N_{y} + 1)\) differentiation matrices \({\text{D}}_{r}^{n} (r = X,Y;n = 1,2,...)\), with their elements are given by:
where \(\delta_{\sigma ,\Delta }^{(n)} (r_{i} - r_{j} ), \, (r = x,y)\) is a DSC kernel of delta type. For RSD kernel, the differentiation in Eq. (51) can be given by:
In this stage, we consider the following relation between the inner nodes and outer nodes on the left boundary:
or
After rearrangement, one obtains:
where parameter \(a_{i} ,(i = 1,2,...,M)\) can be determined by the boundary conditions. Thus, the first- and second-order derivatives of \(W\) on the left boundary are approximated by:
Similarly, the first- and second-order derivatives of \(f\) on the right boundary (at \(X_{N - 1}\)) are approximated by:
or
Consequently, we obtain the following relation:
Hence, the first- and second-order derivatives of \(f\) on the right boundary are given by:
For simply supported boundary conditions, the related equations are given by:
As stated by Wei and coauthors [150,151,152,153], Eq. (78) is satisfied by choosing \(a_{i} = - 1\) for i = 1,2,…,M,. This is called the anti-symmetric extension. For clamped edge, similar statements can be given as:
Also, these equations given by (80) are satisfied by choosing \(a_{i} = 1\) for i = 1,2,…,M,. This is called the symmetric extension. Thus, DSC form of the related boundary conditions can be given as below:
i) For simply supported edge (S):
ii) For clamped edge (C):
Thus, Eq. (61) is rewritten as:
Here, \({\text{I}}_{\xi } \, \) and \({\text{ I}}_{\eta }\) are the \((N_{r} + 1)^{2} ; \, (r = \xi ,\eta )\) unit matrix and \(\otimes\) denotes the tensor product:
5.2 Thick laminated plate
Based on the first-order shear deformation theory, the governing equations for buckling of FG-CNTR thick plates are given as:
Here, \(N_{x} ,N_{xy} {\text{ and }}N_{y}\) are the in-plane applied forces. Also, mass inertias are given as:
Here, ρ and h denote the density and total thickness of the plate, respectively. The bending moments and shear forces are given as:
As similar to thin plate, related Eqs. (87–89) have also been transformed via DSC method.
6 Free vibration of FG-CNTR laminated non-rectangular plates
6.1 Thick laminated plate
Using the shear deformation theory, governing equations of motion for free vibration of thick plate have been written as:
Related differential terms in Eqs. (96a–96c) can be defined as:
in which Aij and Dij are the stretching and bending stiffnesses, and k is the shear correction factor. Boundary conditions are as follows:
-
Simply supported (S)
$$ w = 0 $$(112)$$ \begin{gathered} M_{n} = n_{x}^{2} \left[ {D_{11} \frac{{\partial \theta_{x} }}{\partial x} + D_{12} \frac{{\partial \theta_{y} }}{\partial y} + D_{16} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad + 2n_{x} n_{y} \left[ {D_{16} \frac{{\partial \theta_{x} }}{\partial x} + D_{26} \frac{{\partial \theta_{y} }}{\partial y} + D_{66} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad + n_{y}^{2} \left[ {D_{12} \frac{{\partial \theta_{x} }}{\partial x} + D_{22} \frac{{\partial \theta_{y} }}{\partial y} + D_{26} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] = 0 \hfill \\ \end{gathered} $$(113)$$ \begin{gathered} M_{ns} = (n_{x}^{2} - n_{y}^{2} )\left[ {D_{16} \frac{{\partial \theta_{x} }}{\partial x} + D_{26} \frac{{\partial \theta_{y} }}{\partial y} + D_{66} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad + n_{x} n_{y} \left[ {D_{12} \frac{{\partial \theta_{x} }}{\partial x} + D_{22} \frac{{\partial \theta_{y} }}{\partial y} + D_{26} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad - n_{x} n_{y} \left[ {D_{11} \frac{{\partial \theta_{x} }}{\partial x} + D_{12} \frac{{\partial \theta_{y} }}{\partial y} + D_{16} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] = 0 \hfill \\ \end{gathered} $$(114) -
Clamped (C)
$$ w = 0 $$(115)$$ \theta_{n} = n_{x} \theta_{x} + n_{y} \theta_{y} = 0 $$(116)$$ \theta_{s} = n_{x} \theta_{y} - n_{y} \theta_{x} = 0. $$(117) -
Free edge (F)
$$ Q_{n} = 0 $$(118)$$ \begin{gathered} M_{n} = n_{x}^{2} \left[ {D_{11} \frac{{\partial \theta_{x} }}{\partial x} + D_{12} \frac{{\partial \theta_{y} }}{\partial y} + D_{16} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad + 2n_{x} n_{y} \left[ {D_{16} \frac{{\partial \theta_{x} }}{\partial x} + D_{26} \frac{{\partial \theta_{y} }}{\partial y} + D_{66} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad + n_{y}^{2} \left[ {D_{12} \frac{{\partial \theta_{x} }}{\partial x} + D_{22} \frac{{\partial \theta_{y} }}{\partial y} + D_{26} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] = 0 \hfill \\ \end{gathered} $$(119)$$ \begin{gathered} M_{ns} = (n_{x}^{2} - n_{y}^{2} )\left[ {D_{16} \frac{{\partial \theta_{x} }}{\partial x} + D_{26} \frac{{\partial \theta_{y} }}{\partial y} + D_{66} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad + n_{x} n_{y} \left[ {D_{12} \frac{{\partial \theta_{x} }}{\partial x} + D_{22} \frac{{\partial \theta_{y} }}{\partial y} + D_{26} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] \hfill \\ \quad - n_{x} n_{y} \left[ {D_{11} \frac{{\partial \theta_{x} }}{\partial x} + D_{12} \frac{{\partial \theta_{y} }}{\partial y} + D_{16} \left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right)} \right] = 0. \hfill \\ \end{gathered} $$(120)
Following harmonic function is used before derivation:
Substituting Eqs. (119) into Eq. (96), we obtain the following discrete form:
In the above equations, discrete singular convolution-based new differential operators are also listed below:
In the above coefficient, the discretization derivatives via DSC can be given as:
6.2 Thin isotropic plate
For free vibration analysis of the isotropic case, the governing equation can be given by:
The transverse displacement w for free vibration is taken as:
Substituting Eq. (143) into Eq. (142), one obtains the normalized equation:
where \(X = x/a\), \(Y = y/b\), \(\lambda = a/b\), \(\Omega^{2} = \rho ha^{4} \omega^{2} /D\). Now introducing:
where ∇2 is the Laplace operator. Thus, Eq. (144) takes the following simple form:
Consider the following differential operators before discretizing the governing differential equations:
Thus, the fourth-order derivatives can be given in terms of the second-order derivatives, that is:
After the transformation process, the following form can be given for the first-, second-, and the fourth-order derivatives, respectively:
and
Using the differential operators in Eq. (152), the normalized governing equation, i.e., Eq. (146), takes the following form:
or
Employing the transformation rule, the governing Eq. (154) becomes:
Finally, DSC analog of the governing equations as:
For convenience and simplicity, the following new variable is introduced:
Such that the governing equations of plate for free vibration can be expressed by:
To obtain the discretized form of Eq. (158) in its natural coordinate, we apply Eq. (152) to below equation:
On substituting Eq. (158) into Eq. (159), the governing equation can now be given by:
Therefore, the governing equation for free vibration is as follows:
If the obtained results are related to unsymmetrical cases, FSDT is used for vibration and buckling. These equations are briefly given below.
6.3 Buckling analysis
Based on the first-order shear deformation theory, the governing equations for buckling of laminated plates are given as:
where u, v and w are displacements in the x-, y-, and z-directions, respectively. \(u_{0}\), \(v_{0}\), and \(w_{0}\) denote displacements of mid-plane of the plate. z defines transverse coordinate. Also, the strain components of the plate are given as:
where \(\varepsilon_{xx}\) and \(\varepsilon_{yy}\) are axial strains. \(\gamma_{xy}\), \(\gamma_{xz}\) and \(\gamma_{yz}\) are angular strains.
The second variation of total potential energy is written as:
where \(\sigma_{xx}\) and \(\sigma_{yy}\) are axial stresses. \(\tau_{xy}\), \(\tau_{xz}\) and \(\tau_{yz}\) are shear stresses. Also, \(\varepsilon_{xx}\) and \(\varepsilon_{yy}\) denote axial strains, \(\gamma_{xy}\), \(\gamma_{xz}\) and \(\gamma_{yz}\) explain the shear strains. Resulting equations can be given as:
Here,
The in-plane and out-of-plane boundary conditions for arbitrary edges of plates:
where \(n_{x}\) and \(n_{y}\) are unit normal vector of the x- and y-axes, respectively.
The resultant forces and moments of FSDT plate can be written as follows:
where,
6.4 Vibration analysis
Using the same equations, vibration equations of laminated composite plates according to the FSDT are written as follows:
where u, v, and w are displacements in the x-, y-, and z- directions, respectively. \(u_{0}\), \(v_{0}\), and \(w_{0}\) denote displacements of mid-plane of the plate. z defines transverse coordinate. Also, the strain components of the plate are given as:
where \(\varepsilon_{xx}\) and \(\varepsilon_{yy}\) are axial strains. \(\gamma_{xy}\) \(\gamma_{xz}\) and \(\gamma_{yz}\) are angular strains. Additionally, \(\kappa\) is curvature. On the other hand:
The following equations are obtained by implementing Hamilton’s Principle to the total potential energy of plate:
where \(k_{W}\) and \(k_{P}\) is presented the stiffness of Winkler and Pasternak elastic foundations, respectively. \(N_{xx}\), \(N_{yy}\) and \(N_{xy}\) are in-plane forces. \(M_{xx}\), \(M_{yy}\) and \(M_{xy}\) explain the moments. \(Q_{x}\) and \(Q_{y}\) denote the transverse forces. Also, \(I_{0}\), \(I_{1}\) and \(I_{2}\) present the mass inertia moments. These expressions are defined as follows:
where \(K_{s}\) is shear correction factor. Resulting equations are as follows:
where,
7 Numerical results and discussion
This section aims to demonstrate the accuracy and convergence of the present DSC transformation through free vibration and buckling analysis of thin and thick FG-CNTRC laminated plates with skew and quadrilateral shapes given in Fig. 4. First, convergence and comparative studies are carried out to check the accuracy of the present DSC solutions for two kernels, in this section. Many available exact and numerical results in the literature are used for comparisons.
At first, a convergence study has been made for isotropic case. In Tables 1 and 2, the convergence and accuracy of the first three non-dimensional natural frequencies of CCCC and SSSS supported the isotropic quadrilateral plates and buckling of isotropic skew plates which are presented. In these tables, the results of two other numerical methods based on the differential quadrature (DQ) and finite-element methods (FEM) are also listed [123, 171]. The results converge as the number of grid points increases in each direction. It is also shown that the skew angles and h/a ratio are significant effect on the convergence of the results. An excellent convergence trend for vibration and buckling with the increase in the number of grid points can be seen. The results have a closer agreement with the results of [96, 123, 171].
The numerical results for laminated (45/−45/45/−45/45) CNTR quadrilateral plates with clamped and simply supported edges with different grid numbers in each direction and different side-to-thickness ratio are tabulated in Tables 3 and 4 via DSC methods based on Shannon’s kernel and Lagrange-delta kernel. In Table 3, a comparison between the critical buckling loads presented DSC results and critical buckling values for SSSS quadrilateral plates given by Malekzadeh and Shojae [106] have also shown. It is concluded from the table that the present numerical results for two different kernels are in close agreement with the literature. It is also shown that the convergence of the DSC–Shannon’s kernel is much better than the DSC–Lagrange-delta kernel. Another comparison study is related to the vibration problem of laminated (45/−45/45/−45/45) CNTR quadrilateral plates with clamped edges with different grid numbers in each direction and different modes are listed in Table 4. Results reported by Malekzadeh and Zarei [108] are also shown in Table 4 for comparison. It can be again observed from Table 4 that there is a very good agreement between the results confirming the accuracy of the DSC method. It is clearly shown from these tables that the present DSC method converges very fast as the number of grid points increases. It can also be clear that using Nx = 11 grid points in x-direction can convergence all modes for plates. Furthermore, reasonable exact results have been obtained using the 13 grids in y-direction (Ny = 13). From the results shown in Tables 1, 2, 3, 4, we find that when 13 × 13 grid density is used, the present results have a good agreement with the earlier study for vibration and buckling. The slight difference between our DSC results from the results given by reference approaches may result from different plate theories and different calculation schemes.
To investigate the effects of some parameters on the frequency values of angle-ply laminated (45/−45/..) skew plates, new analyses are made and presented in this section. For this purpose, the following material properties are used: E1 /E2 = 40; E2 = E3; G12 = 0.6 E2; G13 = G23 = 0.5 E2; υ12 = υ13 = υ23 = 0.25. The effects of skew angles, thickness, boundary conditions, and modes are listed in Tables 5, 6, 7 for laminated skew plates. It is concluded from these tables that increase in skew angle results in lower frequency values for all-type boundary conditions. It is found that the frequency parameter increases as the thickness of the plate increases. It is also interesting to note that the frequency values increased slowly with the increasing value of number of layers.
In Tables 8 and 9, the critical buckling load ratios for composite angle-ply laminated (45/−45/..) skew plates with different parameters under uni-axial and bi-axial loadings are presented for the values of h/a = 0.1; b/a = 1; E1 /E2 = 10; E2 = E3; G12 = 0.5 E2; G13 = G23 = 0.5 E2; υ12 = υ13 = υ23 = 0.33. It is shown that the critical load decreases with increasing the skew angles. It can be also seen that the critical buckling loads corresponding to clamped boundary conditions are higher than those based on the simply supported types of boundary conditions. Furthermore, skew plates under uni-axial loads show the highest buckling loads compared to bi-axial loading for all types of boundary and ply number.
Variation of the values of the first three frequencies with two-different boundary conditions and two different DSC kernels for angle ply laminated (45/−45/45/−45/45) skew plates with different grid numbers is given in Table 10 for UD-CNT composites. It is clearly shown that the frequency values increase with the increasing of mode numbers.
To study the effects of CNT distributions, VCNT numbers, skew angles, thickness-to-length ratio, and boundary conditions, on the vibration frequency of CNTR skew and quadrilateral plates, the frequency values of CNTR plates with clamped and simply supported edges are obtained and presented in Tables 11, 12, 13, 14, 15 for four types FG-CNT distribution. It can be concluded that the increase of volume fraction value of FG-CNT increases the frequency parameter for all case FG-CNT distribution under study. Among the four possible cases of distribution patterns of FG-CNT across the plate thickness, FG-X CNTR plates always have the highest frequency parameters and FG-O CNTR plates have the lowest frequency parameters of the skew plate. It is also found that the frequency parameter increases as the thickness of the plate increases. Also, the frequency values decrease significantly as the skew angle of skew plate increases. Furthermore, the VCNT distribution pattern plays a significant role in the frequency values of the plates. For frequency values of higher modes, the regularized Shannon’s delta kernel gives better results than the Lagrange-delta sequence kernel.
Finally, some detailed results have been calculated via the DSC method for critical buckling loads of FG-CNTR laminated quadrilateral plates in Tables 16, 17, 18. These tables show the critical buckling loads of CCCC and SSSS laminated (45/−45/45/−45/45) CNTR quadrilateral plates under uni-axial and bi-axial loading. The results have been obtained for three different for two different VCNT distribution patterns and four different FG-CNT types. Among the different FG patterns of CNTs across the thickness, FG-X CNTR plates feature the highest values of buckling loads, while FG-O plates feature the lowest buckling loads. As also expected, quadrilateral plates under uni-axial loads show the highest buckling loads compared to bi-axial loading. As can be seen from the results, under the same material, geometric and CNT distributions, buckling loads of CCCC edges are always higher than SSSS edges. It is worth mentioning that an increased enrichment of CNTs within the matrix from 0.11 to 0.17 yields to an increase of the buckling loads, for all loading conditions and CNT distributions.
8 Conclusions
This article is concerned with developing a discrete singular convolution formulation to perform the buckling and vibration analyses of FG-CNTR laminated non-rectangular plates within the framework of first-order shear deformation and classical plate theories. For this aim, the irregular physical domain for plates is transformed into a regular computational domain via geometric transformation procedure using the DSC method. The material properties of FG-CNTR laminated non-rectangular plates are assumed to vary along the thickness based on the various FG-CNT distribution patterns adopted. A general transformation process in conjunction with the second-order transformation is applied to transform the physical real domain into the computational domain. The computational efficiency of the present DSC method is shown by considering different examples related to buckling and vibration. It is believed that the numerical results presented in this study via the DSC method may be useful for right design and analysis of FG-CNTR laminated non-rectangular plates and also may provide a useful technique from vibration and buckling behavior. Numerical results reveal that the volume fractions of CNTs, distribution types of CNTs, boundary conditions, skew angles, thickness-to-length ratio, number of layers, and geometrical parameters have an obvious effect on the vibration and buckling behavior of the FG-CNTR laminated non-rectangular plates.
References
Timoshenko SP, Gere JM (1963) Theory of elastic stability. Springer, Berlin, Heidelberg
Leissa AW (1969) Vibration of plates. US Gov Print Off, Nasa-SP160, Washington
Civalek Ö (2004) Geometrically non-linear static and dynamic analysis of plates and shells resting on elastic foundation by the method of polynomial differential quadrature. Firat University, Elazig (in Turkish)
Qatu MS (2004) Vibration of laminated shells and plates. Elsevier Ltd, Amsterdam
Reddy JN (2004) Mechanics of laminated composite plates and shells : theory and analysis. CRC Press, Boca Raton
Wang CM, Wang CY, Reddy JN (2004) Exact solutions for buckling of structural members. CRC Press, Boca Raton
Reddy JN (2006) Theory and analysis of elastic plates and shells. CRC, Boca Raton
Civalek Ö (2008) Free vibration analysis of symmetrically laminated composite plates with first-order shear deformation theory (FSDT) by discrete singular convolution method. Finite Elem Anal Des 44:725–731. https://doi.org/10.1016/j.finel.2008.04.001
Ferreira AJM (2008) MATLAB codes for finite element analysis: solids and structures (Solid mechanics and its applications). Springer, Berlin
Chakraverty S (2009) Vibration of plates. CRC Press, Boca Raton
Shen H-S (2009) Functionally graded materials: nonlinear analysis of plates and shells. CRC Press, Boca Raton
Shen HS (2017) Postbuckling behavior of plates and shells. World Scientific, Singapore
Chajes A (1974) Principles of structural stability theory. Prentice-Hall, Upper Saddle River
Brush DO, Almroth BO (1975) Buckling of bars, plates, and shells. McGraw-Hill, New York
Simitses GJ (1976) An introduction to the elastic stability of structures. Prentice-Hall, Englewood Cliffs
Whitney JM, Ashton JE (1987) Structural analysis of laminated anisotropic plates. Technomic Pub Co., USA
Iyengar NGR (1988) Structural stability of columns and plates. Ellis Horwood series in civil engineering, John-Wiley, New York
Bažant ZP, Cedolin L (1991) Stability of structures: elastic, inelastic, fracture, and damage theories. Oxford University Press, Oxford
Civalek Ö (1998) Finite element analysis of plates and shells. Fırat University, Elazığ (in Turkish)
Jones RM (1999) Mechanics of composite materials. Taylor & Francis, Oxfordshire
Kitipornchai S, Xiang Y, Wang CM, Liew KM (1993) Buckling of thick skew plates. Int J Numer Methods Eng 36:1299–1310. https://doi.org/10.1002/nme.1620360804
Liew KM, Xiang Y, Kitipornchai S, Wang CM (1993) Vibration of thick skew plates based on mindlin shear deformation plate theory. J Sound Vib 168:39–69. https://doi.org/10.1006/jsvi.1993.1361
Wang CM, Liew KM, Xiang Y, Kitipornchai S (1993) Buckling of rectangular mindlin plates with internal line supports. Int J Solids Struct 30:1–17. https://doi.org/10.1016/0020-7683(93)90129-U
Xiang Y, Wang CM, Kitipornchal S (1995) Buckling of skew mindlin plates subjected to in-plane shear loadings. Int J Mech Sci 37:1089–1101. https://doi.org/10.1016/0020-7403(95)00014-O
Liew KM, Han J-B (1997) A four-node differential quadrature method for straight-sided quadrilateral reissner/mindlin plates. Commun Numer Methods Eng 13:73–81. https://doi.org/10.1002/(SICI)1099-0887(199702)13:2<73:AID-CNM32>3.0.CO;2-W
Wang S (1997) Buckling analysis of skew fibre-reinforced composite laminates based on first-order shear deformation plate theory. Compos Struct 37:5–19. https://doi.org/10.1016/S0263-8223(97)00050-0
Wang S (1997) Free vibration analysis of skew fibre-reinforced composite laminates based on first-order shear deformation plate theory. Comput Struct 63:525–538. https://doi.org/10.1016/S0045-7949(96)00357-4
Wang S (1997) Vibration of thin skew fibre reinforced composite laminates. J Sound Vib 201:335–352. https://doi.org/10.1006/jsvi.1996.0745
Anlas G, Göker G (2001) Vibration analysis of skew fibre-reinforced composite laminated plates. J Sound Vib 242:265–276. https://doi.org/10.1006/jsvi.2000.3366
Ferreira AJM (2003) A formulation of the multiquadric radial basis function method for the analysis of laminated composite plates. Compos Struct 59:385–392. https://doi.org/10.1016/S0263-8223(02)00239-8
Ferreira AJM, Roque CMC, Martins PALS (2003) Analysis of composite plates using higher-order shear deformation theory and a finite point formulation based on the multiquadric radial basis function method. Compos Part B Eng 34:627–636. https://doi.org/10.1016/S1359-8368(03)00083-0
Ferreira AJM, Roque CMC, Neves AMA et al (2011) Buckling and vibration analysis of isotropic and laminated plates by radial basis functions. Compos Part B Eng 42:592–606. https://doi.org/10.1016/j.compositesb.2010.08.001
Karami G, Malekzadeh P (2003) Application of a new differential quadrature methodology for free vibration analysis of plates. Int J Numer Methods Eng 56:847–868. https://doi.org/10.1002/nme.590
Civalek Ö (2004) Application of differential quadrature (DQ) and harmonic differential quadrature (HDQ) for buckling analysis of thin isotropic plates and elastic columns. Eng Struct 26:171–186. https://doi.org/10.1016/j.engstruct.2003.09.005
Huang YQ, Li QS (2004) Bending and buckling analysis of antisymmetric laminates using the moving least square differential quadrature method. Comput Methods Appl Mech Eng 193:3471–3492. https://doi.org/10.1016/j.cma.2003.12.039
Liew KM, Chen XL, Reddy JN (2004) Mesh-free radial basis function method for buckling analysis of non-uniformly loaded arbitrarily shaped shear deformable plates. Comput Methods Appl Mech Eng 193:205–224. https://doi.org/10.1016/j.cma.2003.10.002
Leung AYT, Xiao C, Zhu B, Yuan S (2005) Free vibration of laminated composite plates subjected to in-plane stresses using trapezoidal p-element. Compos Struct 68:167–175. https://doi.org/10.1016/j.compstruct.2004.03.011
Garg AK, Khare RK, Kant T (2006) Free vibration of skew fiber-reinforced composite and sandwich laminates using a shear deformable finite element model. J Sandw Struct Mater 8:33–53. https://doi.org/10.1177/1099636206056457
Civalek Ö, Acar MH (2007) Discrete singular convolution method for the analysis of Mindlin plates on elastic foundations. Int J Press Vessel Pip 84:527–535. https://doi.org/10.1016/j.ijpvp.2007.07.001
Civalek Ö (2009) Fundamental frequency of isotropic and orthotropic rectangular plates with linearly varying thickness by discrete singular convolution method. Appl Math Model 33:3825–3835. https://doi.org/10.1016/j.apm.2008.12.019
Nguyen LB, Thai CH, Nguyen-Xuan H (2016) A generalized unconstrained theory and isogeometric finite element analysis based on Bézier extraction for laminated composite plates. Eng Comput 32:457–475. https://doi.org/10.1007/s00366-015-0426-x
Kalita K, Dey P, Haldar S, Gao XZ (2019) Optimizing frequencies of skew composite laminates with metaheuristic algorithms. Eng Comput. https://doi.org/10.1007/s00366-019-00728-x
Mishra BP, Barik M (2019) NURBS-augmented finite element method for stability analysis of arbitrary thin plates. Eng Comput 35:351–362. https://doi.org/10.1007/s00366-018-0603-9
Alihemmati J, Beni YT (2020) Developing three-dimensional mesh-free Galerkin method for structural analysis of general polygonal geometries. Eng Comput 36:1059–1068. https://doi.org/10.1007/s00366-019-00749-6
Iijima S (1991) Helical microtubules of graphitic carbon. Nature. https://doi.org/10.1038/354056a0
Ajayan PM, Stephan O, Colliex C, Trauth D (1994) Aligned carbon nanotube arrays formed by cutting a polymer resin-nanotube composite. Science (-80) 265:1212–1214. https://doi.org/10.1126/science.265.5176.1212
Odom TW, Huang JL, Kim P, Lieber CM (1998) Atomic structure and electronic properties of single-walled carbon nanotubes. Nature 391:62–64. https://doi.org/10.1038/34145
Kataura H, Kumazawa Y, Maniwa Y et al (1999) Optical properties of single-wall carbon nanotubes. Synth Met 103:2555–2558. https://doi.org/10.1016/S0379-6779(98)00278-1
Rochefort A, Avouris P, Lesage F, Salahub DR (1999) Electrical and mechanical properties of distorted carbon nanotubes. Phys Rev B Condens Matter Mater Phys 60:13824–13830. https://doi.org/10.1103/PhysRevB.60.13824
Salvetat JP, Bonard JM, Thomson NB et al (1999) Mechanical properties of carbon nanotubes. Appl Phys A Mater Sci Process 69:255–260. https://doi.org/10.1007/s003390050999
Thostenson ET, Ren Z, Chou TW (2001) Advances in the science and technology of carbon nanotubes and their composites: a review. Compos Sci Technol 61:1899–1912. https://doi.org/10.1016/S0266-3538(01)00094-X
Yakobson BI, Avouris P (2001) Mechanical properties of carbon nanotubes. Carbon nanotubes. Springer, Berlin, pp 287–327
Li YH, Wei J, Zhang X et al (2002) Mechanical and electrical properties of carbon nanotube ribbons. Chem Phys Lett 365:95–100. https://doi.org/10.1016/S0009-2614(02)01434-3
Sawaya S, Akita S, Nakayama Y (2007) Correlation between the mechanical and electrical properties of carbon nanotubes. Nanotechnology 18:35702. https://doi.org/10.1088/0957-4484/18/3/035702
Koizumi M (1993) The concept of FGM. Ceram Trans Funct Graded Mater 34:3–10
Ganapathi M, Prakash T, Sundararajan N (2006) Influence of functionally graded material on buckling of skew plates under mechanical loads. J Eng Mech 132:902–905. https://doi.org/10.1061/(ASCE)0733-9399(2006)132:8(902)
Zhao X, Lee YY, Liew KM (2009) Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. J Sound Vib 319:918–939. https://doi.org/10.1016/j.jsv.2008.06.025
Sun J, Xu X, Lim CW (2014) Buckling of functionally graded cylindrical shells under combined thermal and compressive loads. J Therm Stress 37:340–362. https://doi.org/10.1080/01495739.2013.869143
Van TH, Duc ND (2014) Nonlinear response of shear deformable FGM curved panels resting on elastic foundations and subjected to mechanical and thermal loading conditions. Appl Math Model 38:2848–2866. https://doi.org/10.1016/j.apm.2013.11.015
Chaht FL, Kaci A, Houari MSA et al (2015) Bending and buckling analyses of functionally graded material (FGM) size-dependent nanoscale beams including the thickness stretching effect. Steel Compos Struct 18:425–442. https://doi.org/10.12989/scs.2015.18.2.425
Tadi Beni Y, Mehralian F, Razavi H (2015) Free vibration analysis of size-dependent shear deformable functionally graded cylindrical shell on the basis of modified couple stress theory. Compos Struct 120:65–78. https://doi.org/10.1016/j.compstruct.2014.09.065
Barati MR, Sadr MH, Zenkour AM (2016) Buckling analysis of higher order graded smart piezoelectric plates with porosities resting on elastic foundation. Int J Mech Sci 117:309–320. https://doi.org/10.1016/j.ijmecsci.2016.09.012
Demir Ç, Mercan K, Civalek O (2016) Determination of critical buckling loads of isotropic, FGM and laminated truncated conical panel. Compos Part B Eng 94:1–10. https://doi.org/10.1016/j.compositesb.2016.03.031
Tadi Beni Y (2016) Size-dependent analysis of piezoelectric nanobeams including electro-mechanical coupling. Mech Res Commun 75:67–80. https://doi.org/10.1016/j.mechrescom.2016.05.011
Tadi Beni Y (2016) Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. J Intell Mater Syst Struct 27:2199–2215. https://doi.org/10.1177/1045389X15624798
Abdelaziz HH, Meziane MAA, Bousahla AA et al (2017) An efficient hyperbolic shear deformation theory for bending, buckling and free vibration of FGM sand wich plates with various boundary conditions. Steel Compos Struct 25:693–704. https://doi.org/10.12989/scs.2017.25.6.693
Akgöz B, Civalek Ö (2017) Effects of thermal and shear deformation on vibration response of functionally graded thick composite microbeams. Compos Part B Eng 129:77–87. https://doi.org/10.1016/J.COMPOSITESB.2017.07.024
Malekzadeh P, Alibeygi Beni A (2010) Free vibration of functionally graded arbitrary straight-sided quadrilateral plates in thermal environment. Compos Struct 92:2758–2767. https://doi.org/10.1016/j.compstruct.2010.04.011
Huynh TA, Luu AT, Lee J (2017) Bending, buckling and free vibration analyses of functionally graded curved beams with variable curvatures using isogeometric approach. Meccanica 52:2527–2546. https://doi.org/10.1007/s11012-016-0603-z
Zouatnia N, Hadji L, Kassoul A (2017) An analytical solution for bending and vibration responses of functionally graded beams with porosities. Wind Struct An Int J 25:329–342. https://doi.org/10.12989/was.2017.25.4.329
Avcar M, Mohammed WKM (2018) Free vibration of functionally graded beams resting on Winkler-Pasternak foundation. Arab J Geosci 11:232. https://doi.org/10.1007/s12517-018-3579-2
Chakraverty S, Pradhan KK (2018) Flexural vibration of functionally graded thin skew plates resting on elastic foundations. Int J Dyn Control 6:97–121. https://doi.org/10.1007/s40435-017-0308-8
Chen M, Jin G, Ma X et al (2018) Vibration analysis for sector cylindrical shells with bi-directional functionally graded materials and elastically restrained edges. Compos Part B Eng 153:346–363. https://doi.org/10.1016/j.compositesb.2018.08.129
Duc ND, Khoa ND, Thiem HT (2018) Nonlinear thermo-mechanical response of eccentrically stiffened Sigmoid FGM circular cylindrical shells subjected to compressive and uniform radial loads using the Reddy’s third-order shear deformation shell theory. Mech Adv Mater Struct 25:1156–1167. https://doi.org/10.1080/15376494.2017.1341581
Gao K, Gao W, Chen D, Yang J (2018) Nonlinear free vibration of functionally graded graphene platelets reinforced porous nanocomposite plates resting on elastic foundation. Compos Struct 204:831–846. https://doi.org/10.1016/j.compstruct.2018.08.013
Hussain M, Naeem MN, Isvandzibaei MR (2018) Effect of Winkler and Pasternak elastic foundation on the vibration of rotating functionally graded material cylindrical shell. Proc Inst Mech Eng Part C J Mech Eng Sci 232:4564–4577. https://doi.org/10.1177/0954406217753459
Rajasekaran S, Khaniki HB (2018) Bending, buckling and vibration analysis of functionally graded non-uniform nanobeams via finite element method. J Brazil Soc Mech Sci Eng 40: https://doi.org/10.1007/s40430-018-1460-6
Sari MS, Al-Rbai M, Qawasmeh BR (2018) Free vibration characteristics of functionally graded Mindlin nanoplates resting on variable elastic foundations using the nonlocal elasticity theory. Adv Mech Eng 10:168781401881345. https://doi.org/10.1177/1687814018813458
Zenkour AM, Sobhy M (2010) Thermal buckling of various types of FGM sandwich plates. Compos Struct 93:93–102. https://doi.org/10.1016/j.compstruct.2010.06.012
Shafiei N, She GL (2018) On vibration of functionally graded nano-tubes in the thermal environment. Int J Eng Sci 133:84–98. https://doi.org/10.1016/j.ijengsci.2018.08.004
Yang T, Tang Y, Li Q, Yang XD (2018) Nonlinear bending, buckling and vibration of bi-directional functionally graded nanobeams. Compos Struct 204:313–319. https://doi.org/10.1016/j.compstruct.2018.07.045
Alizadeh M, Fattahi AM (2019) Non-classical plate model for FGMs. Eng Comput 35:215–228. https://doi.org/10.1007/s00366-018-0594-6
Avcar M (2019) Free vibration of imperfect sigmoid and power law functionally graded beams. Steel Compos Struct 30:603–615. https://doi.org/10.12989/scs.2019.30.6.603
Javani M, Kiani Y, Eslami MR (2019) Rapid heating vibrations of FGM annular sector plates. Eng Comput. https://doi.org/10.1007/s00366-019-00825-x
Khiloun M, Bousahla AA, Kaci A et al (2019) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT. Eng Comput. https://doi.org/10.1007/s00366-019-00732-1
Kwon H, Bradbury CR, Leparoux M (2011) Fabrication of functionally graded carbon nanotube-reinforced aluminum matrix composite. Adv Eng Mater 13:325–329. https://doi.org/10.1002/adem.201000251
Setoodeh A, Ghorbanzadeh M, Malekzadeh P (2012) A two-dimensional free vibration analysis of functionally graded sandwich beams under thermal environment. Proc Inst Mech Eng Part C J Mech Eng Sci 226:2860–2873. https://doi.org/10.1177/0954406212440669
Thai HT, Kim SE (2013) Closed-form solution for buckling analysis of thick functionally graded plates on elastic foundation. Int J Mech Sci 75:34–44. https://doi.org/10.1016/j.ijmecsci.2013.06.007
Taj MNAG, Chakrabarti A (2013) Buckling analysis of functionally graded skew plates: an efficient finite element approach. Int J Appl Mech. https://doi.org/10.1142/S1758825113500415
Duc ND, Quan TQ (2014) Nonlinear response of imperfect eccentrically stiffened FGM cylindrical panels on elastic foundation subjected to mechanical loads. Eur J Mech A/Solids 46:60–71. https://doi.org/10.1016/j.euromechsol.2014.02.005
Phung-Van P, Nguyen-Thoi T, Luong-Van H, Lieu-Xuan Q (2014) Geometrically nonlinear analysis of functionally graded plates using a cell-based smoothed three-node plate element (CS-MIN3) based on the C0-HSDT. Comput Methods Appl Mech Eng 270:15–36. https://doi.org/10.1016/j.cma.2013.11.019
Shen HS (2009) Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments. Compos Struct 91:9–19. https://doi.org/10.1016/j.compstruct.2009.04.026
Shen HS (2012) Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite cylindrical shells. Compos Part B Eng 43:1030–1038. https://doi.org/10.1016/j.compositesb.2011.10.004
Shen HS, Zhang CL (2010) Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite plates. Mater Des 31:3403–3411. https://doi.org/10.1016/j.matdes.2010.01.048
Aragh BS, Barati AHN, Hedayati H (2012) Eshelby-Mori-Tanaka approach for vibrational behavior of continuously graded carbon nanotube-reinforced cylindrical panels. Compos Part B Eng 43:1943–1954. https://doi.org/10.1016/j.compositesb.2012.01.004
Malekzadeh P, Golbahar Haghighi MR, Alibeygi Beni A (2012) Buckling analysis of functionally graded arbitrary straight-sided quadrilateral plates on elastic foundations. Meccanica 47:321–333. https://doi.org/10.1007/s11012-011-9436-y
Zhu P, Lei ZX, Liew KM (2012) Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos Struct 94:1450–1460. https://doi.org/10.1016/j.compstruct.2011.11.010
Alibeigloo A, Liew KM (2013) Thermoelastic analysis of functionally graded carbon nanotube-reinforced composite plate using theory of elasticity. Compos Struct 106:873–881. https://doi.org/10.1016/j.compstruct.2013.07.002
Lei ZX, Liew KM, Yu JL (2013) Large deflection analysis of functionally graded carbon nanotube-reinforced composite plates by the element-free kp-Ritz method. Comput Methods Appl Mech Eng 256:189–199. https://doi.org/10.1016/j.cma.2012.12.007
Lei ZX, Liew KM, Yu JL (2013) Free vibration analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method in thermal environment. Compos Struct 106:128–138. https://doi.org/10.1016/j.compstruct.2013.06.003
Lei ZX, Zhang LW, Liew KM, Yu JL (2014) Dynamic stability analysis of carbon nanotube-reinforced functionally graded cylindrical panels using the element-free kp-Ritz method. Compos Struct 113:328–338. https://doi.org/10.1016/j.compstruct.2014.03.035
Lei ZX, Zhang LW, Liew KM (2015) Vibration analysis of CNT-reinforced functionally graded rotating cylindrical panels using the element-free kp-Ritz method. Compos Part B Eng 77:291–303. https://doi.org/10.1016/j.compositesb.2015.03.045
Malekzadeh P, Heydarpour Y (2015) Mixed Navier-layerwise differential quadrature three-dimensional static and free vibration analysis of functionally graded carbon nanotube reinforced composite laminated plates. Meccanica 50:143–167. https://doi.org/10.1007/s11012-014-0061-4
Zhang LW, Lei ZX, Liew KM, Yu JL (2014) Static and dynamic of carbon nanotube reinforced functionally graded cylindrical panels. Compos Struct 111:205–212. https://doi.org/10.1016/j.compstruct.2013.12.035
Zhang LW, Lei ZX, Liew KM (2015) Free vibration analysis of functionally graded carbon nanotube-reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method. Compos Struct 120:189–199. https://doi.org/10.1016/j.compstruct.2014.10.009
Malekzadeh P, Shojaee M (2013) Buckling analysis of quadrilateral laminated plates with carbon nanotubes reinforced composite layers. Thin-Walled Struct 71:108–118. https://doi.org/10.1016/j.tws.2013.05.008
Tounsi A, Benguediab S, Adda Bedia EA et al (2013) Nonlocal effects on thermal buckling properties of double-walled carbon nanotubes. Adv Nano Res 1:1–11. https://doi.org/10.12989/anr.2013.1.1.001
Malekzadeh P, Zarei AR (2014) Free vibration of quadrilateral laminated plates with carbon nanotube reinforced composite layers. Thin-Walled Struct 82:221–232. https://doi.org/10.1016/j.tws.2014.04.016
Lei ZX, Zhang LW, Liew KM (2015) Buckling of FG-CNT reinforced composite thick skew plates resting on Pasternak foundations based on an element-free approach. Appl Math Comput 266:773–791. https://doi.org/10.1016/j.amc.2015.06.002
Liew KM, Lei ZX, Zhang LW (2015) Mechanical analysis of functionally graded carbon nanotube reinforced composites: a review. Compos Struct 120:90–97. https://doi.org/10.1016/j.compstruct.2014.09.041
Zhang LW, Lei ZX, Liew KM (2015) Vibration characteristic of moderately thick functionally graded carbon nanotube reinforced composite skew plates. Compos Struct 122:172–183. https://doi.org/10.1016/j.compstruct.2014.11.070
Zhang LW, Lei ZX, Liew KM (2015) Buckling analysis of FG-CNT reinforced composite thick skew plates using an element-free approach. Compos Part B Eng 75:36–46. https://doi.org/10.1016/j.compositesb.2015.01.033
Zhang LW, Liew KM, Reddy JN (2016) Postbuckling of carbon nanotube reinforced functionally graded plates with edges elastically restrained against translation and rotation under axial compression. Comput Methods Appl Mech Eng 298:1–28. https://doi.org/10.1016/j.cma.2015.09.016
Zhang LW, Xiao LN, Zou GL, Liew KM (2016) Elastodynamic analysis of quadrilateral CNT-reinforced functionally graded composite plates using FSDT element-free method. Compos Struct 148:144–154. https://doi.org/10.1016/j.compstruct.2016.04.006
Zhang LW (2017) On the study of the effect of in-plane forces on the frequency parameters of CNT-reinforced composite skew plates. Compos Struct 160:824–837. https://doi.org/10.1016/j.compstruct.2016.10.116
Zhang L, Lei Z, Liew K (2017) Free vibration analysis of FG-CNT reinforced composite straight-sided quadrilateral plates resting on elastic foundations using the IMLS-Ritz method. J Vib Control 23:1026–1043. https://doi.org/10.1177/1077546315587804
Ansari R, Shahabodini A, Faghih Shojaei M (2016) Vibrational analysis of carbon nanotube-reinforced composite quadrilateral plates subjected to thermal environments using a weak formulation of elasticity. Compos Struct 139:167–187. https://doi.org/10.1016/j.compstruct.2015.11.079
Ansari R, Torabi J, Hassani R (2019) A comprehensive study on the free vibration of arbitrary shaped thick functionally graded CNT-reinforced composite plates. Eng Struct 181:653–669. https://doi.org/10.1016/j.engstruct.2018.12.049
García-Macías E, Castro-Triguero R, Saavedra Flores EI et al (2016) Static and free vibration analysis of functionally graded carbon nanotube reinforced skew plates. Compos Struct 140:473–490. https://doi.org/10.1016/j.compstruct.2015.12.044
Kiani Y (2016) Free vibration of functionally graded carbon nanotube reinforced composite plates integrated with piezoelectric layers. Comput Math with Appl 72:2433–2449. https://doi.org/10.1016/j.camwa.2016.09.007
Kiani Y (2016) Free vibration of FG-CNT reinforced composite skew plates. Aerosp Sci Technol 58:178–188. https://doi.org/10.1016/j.ast.2016.08.018
Kiani Y (2017) Free vibration of carbon nanotube reinforced composite plate on point Supports using Lagrangian multipliers. Meccanica 52:1353–1367. https://doi.org/10.1007/s11012-016-0466-3
Lei ZX, Zhang LW, Liew KM (2016) Vibration of FG-CNT reinforced composite thick quadrilateral plates resting on Pasternak foundations. Eng Anal Bound Elem 64:1–11. https://doi.org/10.1016/j.enganabound.2015.11.014
Mehri M, Asadi H, Wang Q (2016) Buckling and vibration analysis of a pressurized CNT reinforced functionally graded truncated conical shell under an axial compression using HDQ method. Comput Methods Appl Mech Eng 303:75–100. https://doi.org/10.1016/j.cma.2016.01.017
Mirzaei M, Kiani Y (2016) Free vibration of functionally graded carbon-nanotube-reinforced composite plates with cutout. Beilstein J Nanotechnol 7:511–523. https://doi.org/10.3762/bjnano.7.45
Setoodeh AR, Shojaee M (2016) Application of TW-DQ method to nonlinear free vibration analysis of FG carbon nanotube-reinforced composite quadrilateral plates. Thin-Walled Struct 108:1–11. https://doi.org/10.1016/j.tws.2016.07.019
Tornabene F, Fantuzzi N, Bacciocchi M, Viola E (2016) Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos Part B Eng 89:187–218. https://doi.org/10.1016/j.compositesb.2015.11.016
Kiani Y (2016) Shear buckling of FG-CNT reinforced composite plates using Chebyshev-Ritz method. Compos Part B Eng 105:176–187. https://doi.org/10.1016/j.compositesb.2016.09.001
Wu C-P, Li H-Y (2016) Three-dimensional free vibration analysis of functionally graded carbon nanotube-reinforced composite plates with various boundary conditions. J Vib Control 22:89–107. https://doi.org/10.1177/1077546314528367
Duc ND, Cong PH, Tuan ND et al (2017) Thermal and mechanical stability of functionally graded carbon nanotubes (FG CNT)-reinforced composite truncated conical shells surrounded by the elastic foundations. Thin-Walled Struct 115:300–310. https://doi.org/10.1016/j.tws.2017.02.016
Fantuzzi N, Tornabene F, Bacciocchi M, Dimitri R (2017) Free vibration analysis of arbitrarily shaped functionally graded carbon nanotube-reinforced plates. Compos Part B Eng 115:384–408. https://doi.org/10.1016/j.compositesb.2016.09.021
Shokravi M (2017) Buckling of sandwich plates with FG-CNT-reinforced layers resting on orthotropic elastic medium using Reddy plate theory. Steel Compos Struct 23:623–631. https://doi.org/10.12989/scs.2017.23.6.623
Zhang LW, Xiao LN (2017) Mechanical behavior of laminated CNT-reinforced composite skew plates subjected to dynamic loading. Compos Part B Eng 122:219–230. https://doi.org/10.1016/j.compositesb.2017.03.041
Mehar K, Panda SK, Mahapatra TR (2017) Thermoelastic nonlinear frequency analysis of CNT reinforced functionally graded sandwich structure. Eur J Mech A/Solids 65:384–396. https://doi.org/10.1016/j.euromechsol.2017.05.005
Mehar K, Panda SK, Patle BK (2018) Stress, deflection, and frequency analysis of CNT reinforced graded sandwich plate under uniform and linear thermal environment: a finite element approach. Polym Compos 39:3792–3809. https://doi.org/10.1002/pc.24409
Mehar K, Panda SK, Mahapatra TR (2018) Thermoelastic deection responses of CNT reinforced sandwich shell structure using finite-element method. Sci Iran 25:2722–2737. https://doi.org/10.24200/sci.2017.4525
Mehar K, Kumar Panda S (2018) Thermal free vibration behavior of FG-CNT reinforced sandwich curved panel using finite element method. Polym Compos 39:2751–2764. https://doi.org/10.1002/pc.24266
Kiani Y, Mirzaei M (2018) Rectangular and skew shear buckling of FG-CNT reinforced composite skew plates using Ritz method. Aerosp Sci Technol 77:388–398. https://doi.org/10.1016/j.ast.2018.03.022
Nguyen-Quang K, Vo-Duy T, Dang-Trung H, Nguyen-Thoi T (2018) An isogeometric approach for dynamic response of laminated FG-CNT reinforced composite plates integrated with piezoelectric layers. Comput Methods Appl Mech Eng 332:25–46. https://doi.org/10.1016/j.cma.2017.12.010
Zghal S, Frikha A, Dammak F (2018) Free vibration analysis of carbon nanotube-reinforced functionally graded composite shell structures. Appl Math Model 53:132–155. https://doi.org/10.1016/j.apm.2017.08.021
Ebrahimi F, Farazmandnia N, Kokaba MR, Mahesh V (2019) Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng Comput. https://doi.org/10.1007/s00366-019-00864-4
Mallek H, Jrad H, Wali M, Dammak F (2019) Nonlinear dynamic analysis of piezoelectric-bonded FG-CNTR composite structures using an improved FSDT theory. Eng Comput. https://doi.org/10.1007/s00366-019-00891-1
Tornabene F, Bacciocchi M, Fantuzzi N, Reddy JN (2019) Multiscale approach for three-phase CNT/polymer/fiber laminated nanocomposite structures. Polym Compos 40:E102–E126. https://doi.org/10.1002/pc.24520
Vinyas M (2019) A higher-order free vibration analysis of carbon nanotube-reinforced magneto-electro-elastic plates using finite element methods. Compos Part B Eng 158:286–301. https://doi.org/10.1016/j.compositesb.2018.09.086
Mori T, Tanaka K (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall 21:571–574. https://doi.org/10.1016/0001-6160(73)90064-3
Chi S-H, Chung Y-L (2006) Mechanical behavior of functionally graded material plates under transverse load—Part I: analysis. Int J Solids Struct 43:3657–3674. https://doi.org/10.1016/j.ijsolstr.2005.04.011
Chi S-H, Chung Y-L (2006) Mechanical behavior of functionally graded material plates under transverse load—Part II: numerical results. Int J Solids Struct 43:3675–3691. https://doi.org/10.1016/j.ijsolstr.2005.04.010
Hoffman DK, Wei GW, Zhang DS, Kouri DJ (1998) Shannon-Gabor wavelet distributed approximating functional. Chem Phys Lett 287:119–124. https://doi.org/10.1016/S0009-2614(98)00130-4
Wei GW, Kouri DJ, Huffman DK (1998) Wavelets and distributed approximating functional. Comput Phys Commun 112:1–6. https://doi.org/10.1016/s0010-4655(98)00051-4
Wei GW (2001) A new algorithm for solving some mechanical problems. Comput Methods Appl Mech Eng 190:2017–2030. https://doi.org/10.1016/S0045-7825(00)00219-X
Wei GW, Zhao YB, Xiang Y (2001) The determination of natural frequencies of rectangular plates with mixed boundary conditions by discrete singular convolution. Int J Mech Sci 43:1731–1746. https://doi.org/10.1016/S0020-7403(01)00021-2
Wei GW (2001) Vibration analysis by discrete singular convolution. J Sound Vib 244:535–553. https://doi.org/10.1006/jsvi.2000.3507
Wei GW, Zhao YB, Xiang Y (2002) Discrete singular convolution and its application to the analysis of plates with internal supports. Part 1: theory and algorithm. Int J Numer Methods Eng 55:913–946. https://doi.org/10.1002/nme.526
Wan DC, Zhou YC, Wei GW (2002) Numerical solution of incompressible flows by discrete singular convolution. Int J Numer Methods Fluids 38:789–810. https://doi.org/10.1002/fld.253
Yang SY, Zhou YC, Wei GW (2002) Comparison of the discrete singular convolution algorithm and the Fourier pseudospectral method for solving partial differential equations. Comput Phys Commun 143:113–135. https://doi.org/10.1016/S0010-4655(01)00427-1
Civalek Ö (2007) Linear vibration analysis of isotropic conical shells by discrete singular convolution (DSC). Struct Eng Mech 25:127–130. https://doi.org/10.12989/sem.2007.25.1.127
Akgöz B, Civalek Ö (2011) Nonlinear vibration analysis of laminated plates restingon nonlinear two-parameters elastic foundations. Steel Compos Struct 11:403–421. https://doi.org/10.12989/scs.2011.11.5.403
Civalek Ö (2013) Nonlinear dynamic response of laminated plates resting on nonlinear elastic foundations by the discrete singular convolution-differential quadrature coupled approaches. Compos Part B Eng 50:171–179. https://doi.org/10.1016/j.compositesb.2013.01.027
Civalek Ö, Akgöz B (2013) Vibration analysis of micro-scaled sector shaped graphene surrounded by an elastic matrix. This paper is dedicated to Professor Guo-Wei Wei. Comput Mater Sci 77:295–303. https://doi.org/10.1016/j.commatsci.2013.04.055
Mercan K, Civalek Ö (2016) DSC method for buckling analysis of boron nitride nanotube (BNNT) surrounded by an elastic matrix. Compos Struct 143:300–309. https://doi.org/10.1016/j.compstruct.2016.02.040
Civalek Ö (2017) Free vibration of carbon nanotubes reinforced (CNTR) and functionally graded shells and plates based on FSDT via discrete singular convolution method. Compos Part B Eng 111:45–59. https://doi.org/10.1016/j.compositesb.2016.11.030
Mercan K, Civalek Ö (2017) Buckling analysis of Silicon carbide nanotubes (SiCNTs) with surface effect and nonlocal elasticity using the method of HDQ. Compos Part B Eng 114:34–45. https://doi.org/10.1016/j.compositesb.2017.01.067
Shao Z, Shen Z, He Q, Wei G (2003) A generalized higher order finite-difference time-domain method and its application in guided-wave problems. IEEE Trans Microw Theory Tech 51:856–861. https://doi.org/10.1109/TMTT.2003.808627
Shao Z, Wei GW, Zhao S (2003) DSC time-domain solution of Maxwell’s equations. J Comput Phys 189:427–453. https://doi.org/10.1016/S0021-9991(03)00226-2
Wang Y, Zhao YB, Wei GW (2003) A note on the numerical solution of high-order differential equations. J Comput Appl Math 159:387–398. https://doi.org/10.1016/S0377-0427(03)00541-7
Zhou YC, Patnaik BSV, Wan DC, Wei GW (2003) DSC solution for flow in a staggered double lid driven cavity. Int J Numer Methods Eng 57:211–234. https://doi.org/10.1002/nme.674
Ng CHW, Zhao YB, Wei GW (2004) Comparison of discrete singular convolution and generalized differential quadrature for the vibration analysis of rectangular plates. Comput Methods Appl Mech Eng 193:2483–2506. https://doi.org/10.1016/j.cma.2004.01.013
Yu S, Zhao S, Wei GW (2005) Local spectral time splitting method for first- and second-order partial differential equations. J Comput Phys 206:727–780. https://doi.org/10.1016/j.jcp.2005.01.010
Civalek Ö (2006) Vibration analysis of conical panels using the method of discrete singular convolution. Commun Numer Methods Eng 24:169–181. https://doi.org/10.1002/cnm.961
Zhang L, Xiang Y, Wei GW (2006) Local adaptive differential quadrature for free vibration analysis of cylindrical shells with various boundary conditions. Int J Mech Sci 48:1126–1138. https://doi.org/10.1016/j.ijmecsci.2006.05.005
Karunasena W, Liew KM, Al-Bermani FGA (1996) Natural frequencies of thick arbitrary quadrilateral plates using the pb-2 Rritz method. J Sound Vib 196:371–385. https://doi.org/10.1006/jsvi.1996.0489
Acknowledgements
This work was supported by the Research Center for Interneural Computing of China Medical University of Taiwan. Ömer Civalek would like to thank the committee member of Research Center for Interneural Computing of China Medical University of Taiwan for their help via solution of differential equations.
Author information
Authors and Affiliations
Contributions
ÖC: conceptualization, modeling and software, methodology, validation, ınvestigation, formal analysis, writing -original draft, and supervision. MA: software, writing, editing, resources, visualization, formal analysis, and computational analysis.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Civalek, Ö., Avcar, M. Free vibration and buckling analyses of CNT reinforced laminated non-rectangular plates by discrete singular convolution method. Engineering with Computers 38 (Suppl 1), 489–521 (2022). https://doi.org/10.1007/s00366-020-01168-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-020-01168-8