1 Introduction

The exceptional mechanical, electrical and thermal characteristics of graphene have led to attracting tremendous attention from the research community. Graphene-based nanocomposite materials can be one of the most promising applications of graphene nanosheets. Using graphene platelet (GPL) as composite nanofiller makes the enhancement of multifunctional property possible. Recently, some studies have been carried out to analyze the mechanical behavior of multilayer functional graded graphene platelet-reinforced composite (FG-GPLRC) structures. Yang et al. [1] reported the buckling and postbuckling response of laminated FG-GPLRC Timoshenko beams using the differential quadrature method. Song et al. [2] predicted the free and forced vibrations of multilayer FG-GPLRC first-order shear deformable plates using the Navier solution. Feng et al. [3] investigated the nonlinear bending characteristic of laminated FG-GPLRC Timoshenko beams via the Ritz method. Wu et al. [4] examined the dynamic stability of laminated FG-GPLRC nanocomposite beams based on Bolotin’s method.

Due to the rapid advancement in materials science and technology, the miniaturized FG materials can provide a new opportunity for design of efficient micro- and nano-electromechanical systems and devices [5,6,7]. As a result, size dependency in mechanical behaviors of these small-scale structures is worth studying. In the last decade, several unconventional continuum theories of elasticity have been employed to study the size-dependent characteristics of microstructures [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].

Generally, in the previous investigations, it has been observed that the size effect in type of stress nonlocality has a softening-stiffness influence, while the strain gradient size dependency leads to a hardening-stiffness effect. Accordingly, Lim et al. [36] proposed a more comprehensive size-dependent continuum theory namely nonlocal strain gradient elasticity which includes both softening and stiffening influences to describe the size dependency in a more accurate way. Afterwards, a few studies have been performed on the basis of nonlocal strain gradient elasticity theory. Li and Hu [37] reported the size-dependent critical buckling loads of nonlinear Euler–Bernoulli nanobeams based upon nonlocal strain gradient theory of elasticity. They also presented the size-dependent frequency of wave motion on fluid-conveying carbon nanotubes via nonlocal strain gradient theory [38]. Yang et al. [39] established a nonlocal strain gradient beam model to evaluate the critical voltages corresponding to pull-in instability FG carbon nanotube-reinforced actuators at nanoscale. Simsek [40] used the nonlocal strain gradient theory to capture the size effects on the nonlinear natural frequencies of FGM Euler–Bernoulli nanobeams. Sahmani and Aghdam [41,42,43,44] employed the theory of nonlocal strain gradient elasticity to analyze the nonlinear instability of micro/nanoshells under various types of loading condition. Li et al. [45] anticipated the size-dependent nonlinear free vibration response of porous nanobeams based on the nonlocal strain gradient Euler–Bernoulli beam model. Radwan and Sobhy [46] studied the nonlocal strain gradient dynamic deformation response of graphene sheets on a viscoelastic foundation under a time harmonic thermal load. Wang et al. [47] predicted the transverse-free vibrations of axially moving nanobeams on the basis of nonlocal strain gradient Euler–Bernoulli beam model. Sahmani and Aghdam [48,49,50,51] put the nonlocal strain gradient elasticity theory to use for size-dependent analysis of nonlinear mechanical behavior of GPLRC micro/nanostructures. Zeighampour et al. [52] examined the wave propagation in viscoelastic cylindrical nanoshells surrounded by an elastic medium via a developed nonlocal strain gradient shell model.

The main objective of this work is to analyze the size-dependent nonlinear primary resonance of harmonic excited FG-GPLRC laminated microbeams based upon the nonlocal strain gradient hyperbolic shear deformable beam model. With the aid of the Hamilton’s principle, the non-classical nonlinear differential equations of motion are constructed. On the basis of the Halpin–Tsai micromechanical scheme, the effective material properties of laminated FG-GPLRC microbeams are achieved. Thereafter, a numerical solution methodology using generalized differ-ential quadrature method together with the Galerkin tech-nique was reported and the nonlocal strain gradient frequency response andamplitude response associated with the primary resonance of FG-GPLRC laminated microbeams was obtained.

2 Nonlocal strain gradient refined beam model

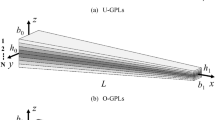
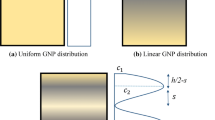
Figure 1 illustrates a six-layer FG-GPLRC microbeam with length L, width b, thickness h and the attached coordinate system. The thicknesses of all six layers are the same equal to \(h_{l} = h/6\). Based upon the related dispersion pattern, the weight fraction of GPLs varies layer by layer of the laminated microbeam. In accordance with Fig. 1, three different patterns of GPL dispersion namely X-GPLRC, O-GPLRC and A-GPLRC are taken into consideration together with the uniform one (U-GPLRC). As a consequence, for each type of GPL dispersion pattern, the GPL volume fraction associated with k-th layer can be given as [6],

$$\begin{aligned} U - {\text{GPLRC}}:\;\;V_{\text{GPL}}^{\left( k \right)} & = V_{\text{GPL}}^{*} , \\ X - {\text{GPLRC}}:\;\;V_{\text{GPL}}^{\left( k \right)} & = 2V_{\text{GPL}}^{*} \left( {\left| {2k - n_{\text{L}} - 1} \right|/n_{\text{L}} } \right), \\ O - {\text{GPLRC}}:\;\;V_{\text{GPL}}^{\left( k \right)} & = 2V_{\text{GPL}}^{*} \left( {1 - \left( {\left| {2k - n_{\text{L}} - 1} \right|/n_{\text{L}} } \right)} \right), \\ A - {\text{GPLRC}}:\;\;V_{\text{GPL}}^{\left( k \right)} & = V_{\text{GPL}}^{*} \left( {\left( {2k - 1} \right)/n_{\text{L}} } \right), \\ \end{aligned}$$
(1)

in which \(n_{\text{L}}\) represents the total number of layers and \(V_{\text{GPL}}^{*}\) stands for the total GPL volume fraction of the laminated micro/nanobeam as shown below:

$$V_{\text{GPL}}^{*} = \frac{{W_{\text{GPL}} }}{{W_{\text{GPL}} + \left( {\frac{{\rho_{\text{GPL}} }}{{\rho_{\text{m}} }}} \right)\left( {1 - W_{\text{GPL}} } \right)}},$$
(2)

where \(\rho_{\text{GPL}}\) and \(\rho_{\text{m}}\) in order denote the mass densities associated with GPLs and the polymer matrix of the laminated microbeam made from the FG-GPLRC nanocomposite. Also, \(W_{\text{GPL}}\) is the GPL weight fraction.

Fig. 1
figure 1

A FG-GPLRC laminated micro/nanobeam with various GPL distributions

Full size image

With the aid of the Halpin–Tsai scheme [53], the Young’s modulus relevant to k-th layer of the FG-GPLRC containing randomly oriented reinforcements can be extracted as,

$$E^{\left( k \right)} = \left( {\frac{3}{8}\frac{{1 + \lambda_{\text{L}} \eta_{\text{L}} V_{\text{GPL}}^{\left( k \right)} }}{{1 - \eta_{\text{L}} V_{\text{GPL}}^{\left( k \right)} }} + \frac{5}{8}\frac{{1 + \lambda_{\text{T}} \eta_{\text{T}} V_{\text{GPL}}^{\left( k \right)} }}{{1 - \eta_{\text{T}} V_{\text{GPL}}^{\left( k \right)} }}} \right)E_{\text{m}} ,$$
(3)

in which \(E_{\text{m}}\) denotes the Young’s modulus of the polymer matrix, and,

$$\eta_{\text{L}} = \frac{{\frac{{E_{\text{GPL}} }}{{E_{\text{m}} }} - 1}}{{\frac{{E_{\text{GPL}} }}{{E_{\text{m}} }} + \lambda_{\text{L}} }},\quad \eta_{\text{T}} = \frac{{\frac{{E_{\text{GPL}} }}{{E_{\text{m}} }} - 1}}{{\frac{{E_{\text{GPL}} }}{{E_{\text{m}} }} + \lambda_{\text{T}} }},\quad \lambda_{\text{L}} = \frac{{2L_{\text{GPL}} }}{{h_{\text{GPL}} }},\quad \lambda_{\text{T}} = \frac{{2b_{\text{GPL}} }}{{h_{\text{GPL}} }},$$
(4)

where \(E_{\text{GPL}} , L_{\text{GPL}} , b_{\text{GPL}} , h_{\text{GPL}}\) are, respectively, the Young’s modulus, length, width and thickness of GPL nanofillers.

Additionally, on the basis of the rule of mixture [54], the Poisson’s ratio and mass density of the k-th layer of the FG-GPLRC laminated microbeam can be obtained as,

$$\begin{aligned} \nu^{\left( k \right)} & = \nu_{\text{m}} \left( {1 - V_{\text{GPL}}^{\left( k \right)} } \right) + \nu_{\text{GPL}} V_{\text{GPL}}^{\left( k \right)} , \\ \rho^{\left( k \right)} & = \rho_{\text{m}} \left( {1 - V_{\text{GPL}}^{\left( k \right)} } \right) + \rho_{\text{GPL}} V_{\text{GPL}}^{\left( k \right)} , \\ \end{aligned}$$
(5)

where \(\nu_{\text{m}}\) and \(\rho_{\text{m}}\) stand for the Poisson’s ratio and mass density of the polymer matrix, respectively. Also, \(\nu_{\text{GPL}}\) and \(\rho_{\text{GPL}}\) denote, respectively, the Poisson’s ratio and mass density of GPL reinforcements.

Based upon the hyperbolic shear deformation beam theory, the displacement field along different coordinate directions can be written as,

$$u_{x} \left( {x,z,t} \right) = u\left( {x,t} \right) - zw_{,x} \left( {x,t} \right) + \left[ {z\cosh \left( {1/2} \right) - h\sinh \left( {z/h} \right)} \right]\psi \left( {x,t} \right),$$
(6a)
$$u_{z} \left( {x,z,t} \right) = w\left( {x,t} \right),$$
(6b)

where u and w in order are the displacement components of the FG-GPLRC laminated microbeam along x- and z-axis. Additionally, \(\psi\) represents the rotation with respect to the cross-section of the microbeam at neutral plane, normal about y-axis.

Consequently, the non-zero strain components are derived as,

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{,x} + \left( {\frac{1}{2}} \right)w_{,x}^{2} - zw_{,xx} + \left[ {z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right]\psi_{,x} } \\ {\left[ {\cosh \left( {\frac{1}{2}} \right) - \cosh \left( {\frac{z}{h}} \right)} \right]\psi } \\ \end{array} } \right\}.$$
(7)

As it has been reported previously, the nonlocal elasticity theory and strain gradient elasticity theory do not consider size effect comprehensively. The nonlocal theory cannot take the higher-order stresses into account. On the other hand, the strain gradient theory has the capability to consider only local higher-order strain gradients. Motivated by this fact, Lim et al. [36] proposed a combination of these theories namely nonlocal strain gradient elasticity theory which assess small-scale effects more reasonably. Accordingly, the total nonlocal strain gradient stress tensor \(\varLambda\) for a beam-type structure can be defined as seen below [36],

$$\varLambda_{xx} = \sigma_{xx} - \sigma_{xx,x}^{*} ,$$
(8a)
$$\varLambda_{xz} = \sigma_{xz} - \sigma_{xz,x}^{*} ,$$
(8b)

where \(\sigma\) and \(\sigma^{*}\) are the stress and higher-order stress tensors.

In accordance with the method of Eringen, the constitutive equation relevant to the total nonlocal strain gradient stress tensor of a FG-GPLRC laminated microbeam can be derived as,

$$\left\{ {\begin{array}{*{20}c} {\varLambda_{xx} - \mu^{2} \varLambda_{xx,xx} } \\ {\varLambda_{xz} - \mu^{2} \varLambda_{xz,xx} } \\ \end{array} } \right\}_{\left( k \right)} = \left[ {\begin{array}{*{20}c} {Q_{11}^{\left( k \right)} } & 0 \\ 0 & {Q_{44}^{\left( k \right)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} - l^{2} \varepsilon_{xx,xx} } \\ {\varepsilon_{xz} - l^{2} \varepsilon_{xz,xx} } \\ \end{array} } \right\}_{\left( k \right)} ,$$
(9)

in which,

$$Q_{11}^{\left( k \right)} = \frac{{E^{\left( k \right)} }}{{1 - \left( {\nu^{\left( k \right)} } \right)^{2} }},\quad Q_{44}^{\left( k \right)} = \frac{{E^{\left( k \right)} }}{{2\left( {1 + \nu^{\left( k \right)} } \right)}},$$
(10)

and \(\mu\) and \(l\) in order are the nonlocal parameter and strain gradient parameter. Thereafter, the nonlocal strain gradient constitutive relations for a hyperbolic shear deformable FG-GPLRC laminated microbeam can be expressed as,

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} - \mu^{2} \varLambda_{xx,xx} } \\ {\varLambda_{xz} - \mu^{2} \varLambda_{xz,xx} } \\ \end{array} } \right\}_{\left( k \right)} \\ & \quad = \left[ {\begin{array}{*{20}c} {Q_{11}^{\left( k \right)} } & 0 \\ 0 & {Q_{44}^{\left( k \right)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{,x} + \left( {\frac{1}{2}} \right)\left( {w_{,x} } \right)^{2} - zw_{,xx} + \left[ {z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right]\psi_{,x} } \\ {\left[ {\cosh \left( {\frac{1}{2}} \right) - \cosh \left( {\frac{z}{h}} \right)} \right]\psi } \\ \end{array} } \right\}_{\left( k \right)} \\ & \quad \quad - l^{2} \left\{ {\begin{array}{*{20}c} {u_{,xxx} + w_{,x} w_{,xxx} + w_{,xx}^{2} - zw_{,xxxx} + \left[ {z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right]\psi_{,xxx} } \\ {\left[ {\cosh \left( {\frac{1}{2}} \right) - \cosh \left( {\frac{z}{h}} \right)} \right]\psi_{,xx} } \\ \end{array} } \right\}_{\left( k \right)} . \\ \end{aligned}$$
(11)

Therefore, within the framework of the nonlocal strain gradient hyperbolic shear deformable beam model, the total strain energy of a FG-GPLRC laminated microbeam can be written as,

$$\begin{aligned} \varPi_{\text{s}} & = \frac{1}{2}\mathop \smallint \limits_{0}^{L} \mathop \smallint \limits_{S} \left\{ {\sigma_{ij} \varepsilon_{ij} + \sigma_{ij}^{*} \nabla \varepsilon_{ij} } \right\}{\text{d}}S{\text{d}}x \\ & = \frac{1}{2}\mathop \smallint \limits_{0}^{L} \left\{ {N_{xx} \left[ {u_{,x} + \left( {\frac{1}{2}} \right)w_{,x}^{2} } \right] - M_{xx} w_{,xx} + R_{xx} \psi_{,x} + Q_{x} \psi } \right\}{\text{d}}x, \\ \end{aligned}$$
(12)

where S represents the cross-sectional area of the FG-GPLRC laminated microbeam. Also, the stress resultants can be achieved in the following forms,

$$\begin{aligned} N_{xx} - \mu^{2} N_{xx,xx} & = A_{11}^{*} \left[ {u_{,x} + \left( {\frac{1}{2}} \right)w_{,x}^{2} - l^{2} \left( {u_{,xxx} + w_{,x} w_{,xxx} + w_{,xx}^{2} } \right)} \right] \\ & \quad + B_{11}^{*} \left( { - w_{,xx} + l^{2} w_{,xxxx} } \right) + C_{11}^{*} \left( {\psi_{,x} - l^{2} \psi_{,xxx} } \right) \\ M_{xx} - \mu^{2} M_{xx,xx} & = B_{11}^{*} \left[ {u_{,x} + \left( {\frac{1}{2}} \right)w_{,x}^{2} - l^{2} \left( {u_{,xxx} + w_{,x} w_{,xxx} + w_{,xx}^{2} } \right)} \right] \\ & \quad + D_{11}^{*} \left( { - w_{,xx} + l^{2} w_{,xxxx} } \right) + F_{11}^{*} \left( {\psi_{,x} - l^{2} \psi_{,xxx} } \right) \\ R_{xx} - \mu^{2} R_{xx,xx} & = C_{11}^{*} \left[ {u_{,x} + \left( {\frac{1}{2}} \right)w_{,x}^{2} - l^{2} \left( {u_{,xxx} + w_{,x} w_{,xxx} + w_{,xx}^{2} } \right)} \right] \\ & \quad + F_{11}^{*} \left( { - w_{,xx} + l^{2} w_{,xxxx} } \right) + G_{11}^{*} \left( {\psi_{,x} - l^{2} \psi_{,xxx} } \right) \\ Q_{x} - \mu^{2} Q_{x,xx} & = A_{44}^{*} \left( {\psi - l^{2} \psi_{,xx} } \right), \\ \end{aligned}$$
(13)

in which,

$$\begin{aligned} \left\{ {N_{xx} ,M_{xx} ,R_{xx} } \right\} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {\mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \varLambda_{xx}^{\left( k \right)} \left\{ {1,z,z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right\}{\text{d}}z} \right) \\ Q_{x} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \varLambda_{xz}^{\left( k \right)} \left\{ {\cosh \left( {\frac{1}{2}} \right) - \cosh \left( {\frac{z}{h}} \right)} \right\}{\text{d}}z, \\ \end{aligned}$$
(14)

and,

$$\begin{aligned} \left\{ {A_{11}^{*} ,B_{11}^{*} ,C_{11}^{*} } \right\} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {Q_{11}^{\left( k \right)} \mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \left\{ {1,z,z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right\}{\text{d}}z} \right) \\ \left\{ {D_{11}^{*} ,F_{11}^{*} ,G_{11}^{*} } \right\} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {Q_{11}^{\left( k \right)} \mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \left\{ {z^{2} ,z^{2} \cosh \left( {\frac{1}{2}} \right) - zh\sinh \left( {\frac{z}{h}} \right),\left[ {z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right]^{2} } \right\}{\text{d}}z} \right) \\ A_{44}^{*} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {Q_{44}^{\left( k \right)} \mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \left\{ {\cosh \left( {\frac{1}{2}} \right) - \cosh \left( {\frac{z}{h}} \right)} \right\}{\text{d}}z} \right). \\ \end{aligned}$$
(15)

Furthermore, the kinetic energy of a FG-GPLRC laminated microbeam modeled via the nonlocal strain gradient hyperbolic shear deformable beam model can be expressed as,

$$\begin{aligned} \varPi_{\text{T}} & = \frac{1}{2}\mathop \smallint \limits_{0}^{L} \mathop \smallint \limits_{S} \rho \left\{ {\left( {u_{x,t} } \right)^{2} + \left( {u_{z,t} } \right)^{2} } \right\}{\text{d}}S{\text{d}}x \\ & = \frac{1}{2}\mathop \smallint \limits_{0}^{L} \left\{ {I_{0} \left( {u_{,t} } \right)^{2} - 2I_{1} u_{,t} w_{,xt} + 2I_{2} u_{,t} \psi_{,t} + I_{3} \left( {w_{,xt} } \right)^{2} - 2I_{4} w_{,xt} \psi_{,t} + I_{5} \left( {\psi_{,t} } \right)^{2} + I_{0} \left( {w_{,t} } \right)^{2} } \right\}{\text{d}}x, \\ \end{aligned}$$
(16)

where,

$$\begin{aligned} \left\{ {I_{0} , I_{1} ,I_{2} } \right\} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {\rho^{\left( k \right)} \mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \left\{ {1,z,z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right\}{\text{d}}z} \right) \\ \left\{ {I_{3} , I_{4} ,I_{5} } \right\} & = b\mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {\rho^{\left( k \right)} \mathop \smallint \limits_{{z_{k - 1} }}^{{z_{k} }} \left\{ {z^{2} ,z^{2} \cosh \left( {\frac{1}{2}} \right) - zh\sinh \left( {\frac{z}{h}} \right),\left[ {z\cosh \left( {\frac{1}{2}} \right) - h\sinh \left( {\frac{z}{h}} \right)} \right]^{2} } \right\}{\text{d}}z} \right). \\ \end{aligned}$$
(17)

Additionally, the work done by the transverse force \({\fancyscript{q}}\) can be defined as follows:

$$\varPi_{\text{P}} = \mathop \smallint \limits_{0}^{L} {\fancyscript{q}}\left( {x,t} \right)w{\text{d}}x.$$
(18)

Thereby, using the Hamilton’s principle, the governing differential equations in terms of the stress resultants can be derived as,

$$N_{xx,x} = I_{0} u_{,tt} - I_{1} w_{,xxt} + I_{2} \psi_{,tt} ,$$
(19a)
$$M_{xx,xx} + \left( {N_{xx} w_{,x} } \right)_{,x} + {\fancyscript{q}} = I_{0} w_{,tt} + I_{1} u_{,xtt} - I_{3} w_{,xxtt} + I_{4} \psi_{,xtt} ,$$
(19b)
$$R_{xx,x}- Q_{x}= I_{2} u_{,tt}-I_{4} w_{,xtt}+ I_{5} \psi_{,xtt}$$
(19c)

Thereafter, by inserting Eqs. (13) in (19a, 19b), the nonlinear size-dependent equations of motion can be rewritten as,

$$\begin{aligned} & A_{11}^{*} \left[ {u_{,xx} + w_{,x} w_{,xx} - l^{2} \left( {u_{,xxxx} + 3w_{,xx} w_{,xxx} + w_{,x} w_{,xxxx} } \right)} \right] \\ & \quad \quad + B_{11}^{*} \left( { - w_{,xxx} + l^{2} w_{,xxxxx} } \right) + C_{11}^{*} \left( {\psi_{,xx} - l^{2} \psi_{,xxxx} } \right) \\ & \quad = I_{0} \left( {u_{,tt} - \mu^{2} u_{,xxtt} } \right) - I_{1} \left( {w_{,xxt} - \mu^{2} w_{,xxxxt} } \right) + I_{2} \left( {\psi_{,tt} - \mu^{2} \psi_{,xxtt} } \right), \\ \end{aligned}$$
(20a)
$$\begin{aligned} & B_{11}^{*} \left[ {u_{,xxx} + w_{,xx}^{2} + w_{,x} w_{,xxx} - l^{2} \left( {u_{,xxxxx} + 3w_{,xxx}^{2} + 4w_{,xx} w_{,xxxx} + w_{,x} w_{,xxxxx} } \right)} \right] \\ & \quad \quad + D_{11}^{*} \left( { - w_{,xxxx} + l^{2} w_{,xxxxxx} } \right) + F_{11}^{*} \left( {\psi_{,xxx} - l^{2} \psi_{,xxxxx} } \right) + A_{11}^{*} \varGamma_{1} - l^{2} A_{11}^{*} \varGamma_{2} \\ & \quad \quad - \mu^{2} A_{11}^{*} \varGamma_{3} + \mu^{2} l^{2} A_{11}^{*} \varGamma_{4} - B_{11}^{*} \varGamma_{5} + l^{2} B_{11}^{*} \varGamma_{6} + \mu^{2} B_{11}^{*} \varGamma_{7} - \mu^{2} l^{2} B_{11}^{*} \varGamma_{8} + C_{11}^{*} \varGamma_{9} \\ & \quad \quad - l^{2} C_{11}^{*} \varGamma_{10} - \mu^{2} C_{11}^{*} \varGamma_{11} + \mu^{2} l^{2} C_{11}^{*} \varGamma_{12} \\ & \quad = I_{0} \left( {w_{,tt} - \mu^{2} w_{,xxtt} } \right) + I_{1} \left( {u_{,xtt} - \mu^{2} u_{,xxxtt} } \right) - I_{3} \left( {w_{,xxtt} - \mu^{2} w_{,xxxxtt} } \right) \\ & \quad \quad + I_{4} \left( {\psi_{,xtt} - \mu^{2} \psi_{,xxxtt} } \right) - {\fancyscript{q}} + \mu^{2} {\fancyscript{q}}_{,xx} , \\ \end{aligned}$$
(20b)
$$\begin{aligned} & C_{11}^{*} \left[ {u_{,xx} + w_{,x} w_{,xx} - l^{2} \left( {u_{,xxxx} + 3w_{,xx} w_{,xxx} + w_{,x} w_{,xxxx} } \right)} \right] + F_{11}^{*} \left( { - w_{,xxx} + l^{2} w_{,xxxxx} } \right) \\ & \quad \quad + G_{11}^{*} \left( {\psi_{,xx} - l^{2} \psi_{,xxxx} } \right) - A_{44}^{*} \left( {\psi - l^{2} \psi_{,xx} } \right) \\ & \quad = I_{2} \left( {u_{,tt} - \mu^{2} u_{,xxtt} } \right) - I_{4} \left( {w_{,xtt} - \mu^{2} w_{,xxxtt} } \right) + I_{5} \left( {\psi_{,tt} - \mu^{2} \psi_{,xxtt} } \right), \\ \end{aligned}$$
(20c)

in which,

$$\begin{aligned} \varGamma_{1} & = u_{,xx} w_{,x} + u_{,x} w_{,xx} + \left( {3/2} \right)w_{,xx} w_{,x}^{2} \\ \varGamma_{2} & = u_{,xxxx} w_{,x} + u_{,xxx} w_{,xx} + 4w_{,x} w_{,xx} w_{,xxx} + \left( {w_{,xx} + w_{,xxxx} } \right)w_{,x}^{2} \\ \varGamma_{3} & = u_{,xxxx} w_{,x} + 3u_{,xxx} w_{,xx} + 3u_{,xx} w_{,xxx} + u_{,x} w_{,xxxx} + 3w_{,xx}^{3} + 9w_{,x} w_{,xx} w_{,xxx} + \left( {3/2} \right)w_{,x}^{2} w_{,xxxx} \\ \varGamma_{4} & = u_{,xxxxxx} w_{,x} + 3u_{,xxxxx} w_{,xx} + 3u_{,xxxx} w_{,xxx} + u_{,xxx} w_{,xxxx} + 10w_{,xxxx} w_{,xx}^{2} + 12w_{,xx} w_{,xxx}^{2} \\ & \quad + 14w_{,x} w_{,xxx} w_{,xxxx} + 8w_{,x} w_{,xx} w_{,xxxxx} + 6w_{,x} w_{,xx} w_{,xxx} \\ & \quad + \left( {w_{,xxxx} + w_{,xxxxx} } \right)w_{,x}^{2} + 2w_{,xx}^{3} \\ \varGamma_{5} & = w_{,x} w_{,xxx} + w_{,xx}^{2} \\ \varGamma_{6} & = w_{,xx} w_{,xxxx} + w_{,x} w_{,xxxxx} \\ \varGamma_{7} & = 3w_{,xxx}^{2} + 4w_{,xx} w_{,xxxx} + w_{,x} w_{,xxxxx} \\ \varGamma_{8} & = w_{,xxxx}^{2} + 3w_{,xxx} w_{,xxxxx} + 3w_{,xx} w_{,xxxxxx} + w_{,x} w_{,xxxxxxx} \\ \varGamma_{9} & = w_{,xx} \psi_{,x} + w_{,x} \psi_{,xx} \\ \varGamma_{10} & = w_{,xx} \psi_{,xxx} + w_{,x} \psi_{,xxxx} \\ \varGamma_{11} & = w_{,xxxx} \psi_{,x} + 3w_{,xxx} \psi_{,xx} + 3w_{,xx} \psi_{,xxx} + w_{,x} \psi_{,xxxx} \\ \varGamma_{12} & = w_{,xxxx} \psi_{,xxx} + 3w_{,xxx} \psi_{,xxxx} + 3w_{,xx} \psi_{,xxxxx} + w_{,x} \psi_{,xxxxxx} . \\ \end{aligned}$$
(21)

To perform the numerical solving process in a more general form, the following dimensionless parameters are taken into consideration,

$$\begin{aligned} & X = \frac{x}{L},\quad U = \frac{u}{h},\quad W = \frac{w}{h},\quad \varPsi = \psi , \\ & \eta_{1} = \frac{l}{L},\quad \eta_{2} = \frac{\mu }{L},\quad \beta = \frac{h}{L} \\ & T = \frac{t}{L}\sqrt {\frac{{A_{11}^{*} }}{{I_{0} }}} ,\quad \left\{ {a_{11}^{*} ,a_{44}^{*} ,b_{11}^{*} ,c_{11}^{*} ,d_{11}^{*} ,f_{11}^{*} ,g_{11}^{*} } \right\} \\ & \;\;\; = \left\{ {\frac{{A_{11}^{*} }}{{A_{11}^{*} }},\frac{{A_{44}^{*} }}{{A_{11}^{*} }},\frac{{B_{11}^{*} }}{{A_{11}^{*} h}},\frac{{C_{11}^{*} }}{{A_{11}^{*} h}},\frac{{D_{11}^{*} }}{{A_{11}^{*} h^{2} }},\frac{{F_{11}^{*} }}{{A_{11}^{*} h^{2} }},\frac{{G_{11}^{*} }}{{A_{11}^{*} h^{2} }}} \right\} \\ & \left\{ {I_{0}^{*} ,I_{1}^{*} , I_{2}^{*} , I_{3}^{*} , I_{4}^{*} ,I_{5}^{*} } \right\} = \left\{ {\frac{{I_{0} }}{{I_{0} }},\frac{{I_{1} }}{{I_{0} h}},\frac{{I_{2} }}{{I_{0} h}},\frac{{I_{3} }}{{I_{0} h^{2} }},\frac{{I_{4} }}{{I_{0} h^{2} }},\frac{{I_{5} }}{{I_{0} h^{2} }}} \right\},\quad {\mathcal{Q}} = \frac{{{\fancyscript{q}}L^{2} }}{{A_{11}^{*} h}}. \\ \end{aligned}$$
(22)

As a result, the dimensionless form of the size-dependent nonlinear governing differential equations of motion can be expressed as,

$$\begin{aligned} & a_{11}^{*} \left[ {U_{,XX} + \beta W_{,X} W_{,XX} - \eta_{1}^{2} \left( {U_{,XXXX} + 3\beta W_{,XX} W_{,XXX} + \beta W_{,X} W_{,XXXX} } \right)} \right] - b_{11}^{*} \left( {W_{,XXX} - \eta_{1}^{2} W_{,XXXXX} } \right) \\ & \quad \quad + c_{11}^{*} \left( {\varPsi_{,XX} - \eta_{1}^{2} \varPsi_{,XXXX} } \right) \\ & \quad = I_{0}^{*} \left( {U_{,TT} - \eta_{2}^{2} U_{,XXTT} } \right) - I_{1}^{*} \left( {W_{,XXT} - \eta_{2}^{2} W_{,XXXXT} } \right) + I_{2}^{*} \left( {\varPsi_{,TT} - \eta_{2}^{2} \varPsi_{,XXTT} } \right), \\ \end{aligned}$$
(23a)
$$\begin{aligned} & b_{11}^{*} \left[ {U_{,XXX} + \beta W_{,XX}^{2} + \beta W_{,X} W_{,XXX} - \eta_{1}^{2} \left( {U_{,XXXXX} + 3\beta W_{,XXX}^{2} + 4\beta W_{,XX} W_{,XXXX} + \beta W_{,X} W_{,XXXXX} } \right)} \right] \\ & \quad \quad - d_{11}^{*} \left( {W_{,XXXX} - \eta_{1}^{2} W_{,XXXXXX} } \right) + f_{11}^{*} \left( {\varPsi_{,XXX} - \eta_{1}^{2} \varPsi_{,XXXXX} } \right) + a_{11}^{*} \tilde{\varGamma }_{1} - \eta_{1}^{2} a_{11}^{*} \tilde{\varGamma }_{2} \\ & \quad \quad - \eta_{2}^{2} a_{11}^{*} \tilde{\varGamma }_{3} + \eta_{2}^{2} \eta_{1}^{2} a_{11}^{*} \tilde{\varGamma }_{4} - b_{11}^{*} \tilde{\varGamma }_{5} + \eta_{1}^{2} b_{11}^{*} \tilde{\varGamma }_{6} + \eta_{2}^{2} b_{11}^{*} \tilde{\varGamma }_{7} - \eta_{2}^{2} \eta_{1}^{2} b_{11}^{*} \tilde{\varGamma }_{8} + c_{11}^{*} \tilde{\varGamma }_{9} \\ & \quad \quad - \eta_{1}^{2} c_{11}^{*} \tilde{\varGamma }_{10} - \eta_{2}^{2} c_{11}^{*} \tilde{\varGamma }_{11} + \eta_{2}^{2} \eta_{1}^{2} c_{11}^{*} \tilde{\varGamma }_{12} \\ & \quad = I_{0}^{*} \left( {W_{,TT} - \eta_{2}^{2} W_{,XXTT} } \right) + I_{1}^{*} \left( {U_{,XTT} - \eta_{2}^{2} U_{,XXXTT} } \right) - I_{3}^{*} \left( {W_{,XXTT} - \eta_{2}^{2} W_{,XXXXTT} } \right) \\ & \quad \quad + I_{4}^{*} \left( {\varPsi_{,XTT} - \eta_{2}^{2} \varPsi_{,XXXTT} } \right) - {\mathcal{Q}} + \eta_{2}^{2} {\mathcal{Q}}_{,XX} , \\ \end{aligned}$$
(23b)
$$\begin{aligned} & c_{11}^{*} \left[ {U_{,XX} + \beta W_{,X} W_{,XX} - \eta_{1}^{2} \left( {U_{,XXXX} + 3\beta W_{,XX} W_{,XXX} + \beta W_{,X} W_{,XXXX} } \right)} \right] - f_{11}^{*} \left( {W_{,XXX} - \eta_{1}^{2} W_{,XXXXX} } \right) \\ & \quad \quad + g_{11}^{*} \left( {\varPsi_{,XX} - \eta_{1}^{2} \varPsi_{,XXXX} } \right) - a_{44}^{*} \left( {\varPsi - \eta_{1}^{2} \varPsi_{,XX} } \right) \\ & \quad = I_{2}^{*} \left( {U_{,TT} - \eta_{2}^{2} U_{,XXTT} } \right) - I_{4}^{*} \left( {W_{,XTT} - \eta_{2}^{2} W_{,XXXTT} } \right) + I_{5}^{*} \left( {\varPsi_{,TT} - \eta_{2}^{2} \varPsi_{,XXTT} } \right), \\ \end{aligned}$$
(23c)

where,

$$\begin{aligned} \tilde{\varGamma }_{1} & = \beta U_{,XX} W_{,X} + \beta U_{,X} W_{,XX} + \left( {3/2} \right)\beta^{2} W_{,XX} W_{,X}^{2} \\ \tilde{\varGamma }_{2} & = \beta U_{,XXXX} W_{,X} + \beta U_{,XXX} W_{,XX} + 4\beta^{2} W_{,X} W_{,XX} W_{,XXX} + \beta^{2} \left( {W_{,XX} + W_{,XXXX} } \right)W_{,X}^{2} \\ \tilde{\varGamma }_{3} & = \beta \left[ {U_{,XXXX} W_{,X} + 3U_{,XXX} W_{,XX} + 3U_{,XX} W_{,XXX} + U_{,X} W_{,XXXX} } \right] \\ & \quad + \beta^{2} \left[ {3W_{,XX}^{3} + 9W_{,X} W_{,XX} W_{,XXX} + \left( {3/2} \right)W_{,X}^{2} W_{,XXXX} } \right] \\ \tilde{\varGamma }_{4} & = \beta \left[ {U_{,XXXXXX} W_{,X} + 3U_{,XXXXX} W_{,XX} + 3U_{,XXXX} W_{,XXX} + U_{,XXX} W_{,XXXX} } \right] \\ & \quad + \beta^{2} \left[ {10W_{,XXXX} W_{,XX}^{2} + 12W_{,XX} W_{,XXX}^{2} + 14W_{,X} W_{,XXX} W_{,XXXX} } \right. \\ & \quad \left. { + 8W_{,X} W_{,XX} W_{,XXXXX} + 6W_{,X} W_{,XX} W_{,XXX} + \left( {W_{,XXXX} + W_{,XXXXX} } \right)W_{,X}^{2} + 2W_{,XX}^{3} } \right] \\ \tilde{\varGamma }_{5} & = \beta W_{,X} W_{,XXX} + \beta W_{,XX}^{2} \\ \tilde{\varGamma }_{6} & = \beta W_{,XX} W_{,XXXX} + \beta W_{,X} W_{,XXXXX} \\ \tilde{\varGamma }_{7} & = 3\beta W_{,XXX}^{2} + 4\beta W_{,XX} W_{,XXXX} + \beta W_{,X} W_{,XXXXX} \\ \tilde{\varGamma }_{8} & = \beta W_{,XXXX}^{2} + 3\beta W_{,XXX} W_{,XXXXX} + 3\beta W_{,XX} W_{,XXXXXX} + \beta W_{,X} W_{,XXXXXXX} \\ \tilde{\varGamma }_{9} & = W_{,XX} \varPsi_{,X} + W_{,X} \varPsi_{,XX} \\ \tilde{\varGamma }_{10} & = W_{,XX} \varPsi_{,XXX} + W_{,X} \varPsi_{,XXXX} \\ \tilde{\varGamma }_{11} & = W_{,XXXX} \varPsi_{,X} + 3W_{,XXX} \varPsi_{,XX} + 3W_{,XX} \varPsi_{,XXX} + W_{,X} \varPsi_{,XXXX} \\ \tilde{\varGamma }_{12} & = W_{,XXXX} \varPsi_{,XXX} + 3W_{,XXX} \varPsi_{,XXXX} + 3W_{,XX} \varPsi_{,XXXXX} + W_{,X} \varPsi_{,XXXXXX} . \\ \end{aligned}$$
(24)

3 Numerical solution methodology

Herein, to capture the nonlinear nonlocal strain gradient frequency of a FG-GPLRC microbeam, a solving process on the basis of the GDQ numerical method is utilized [55]. Based upon the Chebyshev–Gauss–Lobatto scheme, a set of mesh points within X domain can be obtained as,

$$X_{i} = \left( {1/2} \right)\left[ {1 - \cos \left( {\pi \left( {i - 1} \right)/\left( {N - 1} \right)} \right)} \right],\quad i = 1,2, \ldots ,N.$$
(25)

Consequently, the discretized nonlinear governing equations of motion can be written in terms of mass matrix, damping matrix and stiffness matrix as below,

$${\mathbf{\mathcal{M}}}{\mathbf{\ddot{p}}} + {\mathbf{\mathcal{C}}}{\dot{\mathbf{p}}} + {\mathbf{\mathcal{K}}}_{\varvec{L}} {\mathbf{p}} + {\mathbf{\mathcal{K}}}_{\varvec{N}} = {\mathbf{\mathcal{Q}}}\cos \left( {\varOmega T} \right).$$
(26)

The derivative operators corresponding to each order can be introduced as,

$${\mathcal{D}}_{ij}^{r} = \left\{ {\begin{array}{*{20}l} {I_{X} } \hfill & {\quad r = 0} \hfill \\ {\frac{{\mathop \prod \nolimits_{j = 1,j \ne i}^{N} \left( {X_{k} - X_{j} } \right)}}{{\left( {X_{i} - X_{j} } \right)\mathop \prod \nolimits_{i = 1,i \ne j}^{N} \left( {X_{j} - X_{i} } \right)}}} \hfill & {\quad r = 1,\;i,j = 1,2, \ldots ,N} \hfill \\ {r\left( {{\mathcal{D}}_{ij}^{1} {\mathcal{D}}_{ii}^{r - 1} - \frac{{{\mathcal{D}}_{ij}^{r - 1} }}{{\left( {X_{i} - X_{j} } \right)}}} \right)} \hfill & {\quad r = 2,3, \ldots ,N - 1,\;i,j = 1,2, \ldots ,N} \hfill \\ { - \mathop \sum \limits_{i = 1, i = j}^{N} {\mathcal{D}}_{ij}^{r} } \hfill & {\quad r = 1,2,, \ldots ,N - 1,\;i,j = 1,2, \ldots ,N} \hfill \\ \end{array} } \right.$$
(27)

where \(I_{X}\) represents the identity matrix.

Also, the time derivative operator corresponding to each order can be introduced explicitly in the following matrix forms,

$${\mathcal{D}}_{\text{T}}^{\left( 1 \right)} = {\mathbb{A}}_{ij} \quad {\text{where}}\;\left\{ {\begin{array}{*{20}l} {{\mathbb{A}}_{1,1} = 0} \hfill \\ {{\mathbb{A}}_{i,1} = \left( { - 1} \right)^{i - 1} \cot \left[ {\frac{{\pi \left( {i - 1} \right)}}{{N_{t} }}} \right]} \hfill \\ {{\mathbb{A}}_{i,j} = \left( { - 1} \right)^{{N_{t} - j + 1}} \cot \left[ {\frac{{\pi \left( {N_{t} - j + 1} \right)}}{{N_{t} }}} \right]} \hfill \\ {{\mathbb{A}}_{i + 1,j + 1} = {\mathbb{A}}_{ij} } \hfill \\ \end{array} } \right.\quad i,j = 2,3, \ldots ,N_{t} ,$$
(28)
$${\mathcal{D}}_{\text{T}}^{\left( 2 \right)} = {\mathbb{B}}_{ij} \quad {\text{where}}\;\left\{ {\begin{array}{*{20}l} {{\mathbb{B}}_{1,1} = - \frac{{N_{t}^{2} }}{12} - \frac{1}{6}} \hfill \\ {{\mathbb{B}}_{i,1} = \frac{{\left( { - 1} \right)^{i - 1} }}{{2\sin^{2} \left[ {\frac{{\pi \left( {i - 1} \right)}}{{N_{t} }}} \right]}}} \hfill \\ {{\mathbb{B}}_{i,j} = \frac{{\left( { - 1} \right)^{{N_{t} - j + 1}} }}{{2\sin^{2} \left[ {\frac{{\pi \left( {N_{t} - j + 1} \right)}}{{N_{t} }}} \right]}}} \hfill \\ {{\mathbb{B}}_{i + 1,j + 1} = {\mathbb{B}}_{ij} } \hfill \\ \end{array} } \right.\quad i,j = 2,3, \ldots ,N_{t} ,$$
(29)

4 Numerical results and discussion

On the basis of the developed nonlocal strain gradient beam model, the size-dependent frequency response and amplitude response associated with the primary resonance of harmonic excited FG-GPLRC laminated microbeams are predicted. In the preceding numerical results, the damping parameter is assumed as \({\mathbf{\mathcal{C}}} = 0.02\). Also, the geometric parameters of the FG-GPLRC laminated microbeams are selected as \(h = 24\;{\text{nm}}\) for \(n_{L} = 6\) and \(b = h,\;\;L = 20h\), \(h_{\text{GPL}} = 0.3\;{\text{nm}}\), \(L_{\text{GPL}} = 5\;{\text{nm}}\), and \(b_{\text{GPL}} = 2.5\;{\text{nm}}\). In addition, \(\omega_{\text{L}}\) stands for the linear natural frequency of the FG-GPLRC laminated microbeam. The material properties of the polymer matrix and GPL reinforcements are tabulated in Table 1.

Table 1 Material properties of the polymer matrix and GPL reinforcements [56, 57]
Full size table

Herein, the validity of the given solution is checked. To this end, by ignoring the strain gradient terms, the nonlocal natural frequencies of a simply supported carbon nanotube with different slenderness ratios are calculated and compared with those presented by Sahmani and Ansari [58] using the GDQ method and molecular dynamics simulation. As shown in Table 2, a very good agreement is found which confirms the validity of the given solution for the problem.

Table 2 Comparison of natural frequencies of simply supported carbon nanotubes obtained by the nonlocal beam model and molecular dynamics simulations (THz)
Full size table

Figures 2 and 3 illustrate the nonlocal strain gradient frequency response of the harmonic excited FG-GPLRC laminated microbeams corresponding to different values of the nonlocal parameter and strain gradient parameter, respectively. It can be seen that the nonlocality size effect leads to an increase in the peak of the jump phenomenon in the vibration amplitude and it occurs at a higher excitation frequency. However, by changing the end supports from simply supported to clamped one, the significance of this pattern reduces. On the other hand, by taking the strain gradient size dependency into account, the peak of the jump phenomenon decreases and it is shifted to a lower excitation frequency. It is shown again that through changing the boundary conditions from simply supported–simply supported (SS–SS) to clamped–clamped (C–C), these observations related to the strain gradient size effect become negligible.

Fig. 2
figure 2

Size-dependent frequency esponse of the soft excited FG-GPLRC laminated micro/nanobeams corresponding to different nonlocal parameters and boundary conditions (\({\mathbf{\mathcal{Q}}} = 0.01, U - {\text{GPLRC}}, V_{\text{GPL}} = 0.1, l = 0\;{\text{nm}}\))

Full size image
Fig. 3
figure 3

Size-dependent frequency response of the soft excited FG-GPLRC laminated micro/nanobeams corresponding to different strain gradient parameters and boundary conditions (\({\mathbf{\mathcal{Q}}} = 0.01, U - {\text{GPLRC}}, V_{GPL} = 0.1, \mu = 0\;{\text{nm}}\))

Full size image

Figures 4 and 5 display the nonlocal strain gradient amplitude response curves of the harmonic excited FG-GPLRC laminated microbeams corresponding to different values of the nonlocal parameter and strain gradient parameter, respectively. It is observed that by increasing the excitation amplitude, the vibration amplitude increases up to the first bifurcation point. After that, increment in the vibration amplitude continues via reduction in the value of excitation amplitude up to the second bifurcation point. It is found that the nonlocality causes a decrease in the excitation amplitudes associated with both the bifurcation points, but its effect on the first one is more significant. However, the strain gradient size dependency has an opposite influence and leads to an increase. Furthermore, it is indicated that by changing the end supports from simply supported to clamped one, the influence of the nonlocality on the excitation amplitudes associated with the first and second bifurcation points increases and decreases, respectively. But for the strain gradient size dependency, its influence on the excitation amplitudes associated with both the bifurcation points reduces by changing the boundary conditions from SS–SS to C–C.

Fig. 4
figure 4

Size-dependent amplitude response of the soft excited FG-GPLRC laminated micro/nanobeams corresponding to different nonlocal parameters and boundary conditions (\(\varOmega = 1.3\omega ,U - {\text{GPLRC}}, V_{\text{GPL}} = 0.1, l = 0\;{\text{nm}}\))

Full size image
Fig. 5
figure 5

Size-dependent amplitude response of the soft excited FG-GPLRC laminated micro/nanobeams corresponding to different strain gradient parameters and boundary conditions (\(\varOmega = 1.3\omega ,U - {\text{GPLRC}}, V_{\text{GPL}} = 0.1, \mu = 0\;{\text{nm}}\))

Full size image

5 Concluding remarks

The prime aim of this investigation was to anticipate the nonlocal strain gradient nonlinear primary resonance of the harmonic excited FG-GPLRC laminated microbeams with different GPL dispersion patterns and various boundary conditions. To this purpose, the nonlocal strain gradient theory of elasticity was applied to the refined hyperbolic shear deformation beam theory to construct a more comprehensive size-dependent beam model. Via a numerical solving process, the nonlocal strain gradient frequency response and amplitude response are captured.

It was indicated that the nonlocality size effect leads to an increase in the peak of the jump phenomenon in the vibration amplitude and it occurs at a higher excitation frequency. However, by changing the end supports from simply supported to clamped one, the significance of this pattern reduces. On the other hand, by taking the strain gradient size dependency into account, the peak of the jump phenomenon decreases and it is shifted to a lower excitation frequency. It was observed that for all types of boundary conditions and GPL dispersion pattern, the significance of strain gradient size dependency on the linear frequency of the harmonic excited FG-GPLRC laminated microbeam is more than that of the nonlocal size effect. Moreover, it was seen that the nonlocality causes a decrease in the excitation amplitudes associated with both the bifurcation points, but its effect on the first one is more significant. However, the strain gradient size dependency has an opposite influence and leads to an increase.