On the dynamics of axially functionally graded CNT strengthened deformable beams

Abstract

In this study, by functionally grading carbon nanotube (CNT) fibres through the axial direction of deformable beams, a new model for strengthening such structures is formulated. The strengthened deformable beam is additionally supported by a varying elastic foundation which is modelled via the Winkler–Pasternak elastic foundation. CNT distribution in the longitudinal direction is modelled using a power-law function presenting general forms of variation from linear to parabolic models. Equations of motion are determined using Hamilton’s principle and are solved by employing the generalised differential quadrature approach method. A comprehensive parametric investigation is presented in order to indicate the influence of having CNT fibres distributed functionally through the length. It is shown that grading CNT fibres axially have a significant effect in varying the natural frequency parameter. Moreover, the influence of having Winkler–Pasternak elastic bed on the free vibration of such structures is discussed considering different types of foundation stiffness variation through the length. A comprehensive comparison study is presented to verify the current methodology and formulation by using previous literature for foundation modelling and FE modelling for linearly varying CNT’s longitudinal distribution, which for all the cases, a good agreement between the results is observed.

1 Introduction

One main concern of engineers in designing structures is the durability of the structure while undergoing different types of static and dynamic loadings. This importance has created a key research topic on manufacturing, modelling and analysing reinforced structures. Composite structures are a great example of the engineered structures with optimised stiffness in at least one direction [1].

1.1 Application and importance

A well-known class of composite structures is fibre strengthened structures which are made of a base material (matrix) and at least one element for reinforcing the structure (fibre). These types of fibre reinforcements, which could also be observed in nature [2,3,4], have a long history of utilisation in biomechanics and body tissues [5, 6] automotive industry [7] and repairing and strengthening structures [8]. One of the successful models of strengthened structures is carbon nanotube (CNT) strengthened structures where the CNTs, with significant stiffness properties, play the role of fibres in the composite structure.

The importance, difficulties and achievements in producing CNT strengthened structures have widely been discussed in past years (interested readers are referred to Refs. [9, 10] for more details). In general, small-scale structures such as micro/nanobeams, micro/nanoplates and micro/nanotubes show different mechanical response due to molecular interactions forces which have been discussed previously in Refs. [11,12,13,14,15,16,17,18,19]. Although it can easily be understood that the structural behaviour is modified by adding CNT fibres to the base matrix, the effect intensity of adding CNT fibres and the amount to be added for different base materials to reach the demanded mechanical behaviour should be investigated. Thus, some studies mainly focused on the mechanical characteristics of different base materials strengthened with different amounts of CNT fibres [20].

Moreover, since adding the CNT fibres could increase the costs notably, it is important to manage the usage and positioning the fibres, especially for high volume productions. Accordingly, it is more beneficial to optimise the mechanical properties of the base matrix in the direction(s) and region(s) in which the structure needs to behave more firmly. A proper way to do this is to align the CNT fibre through the required direction(s) that the structure is confronting mechanical loadings which could be useful in decreasing the total CNT usage [21, 22].

Furthermore, positioning the CNT fibres in a proper way through the structure following an optimised model could significantly affect the total CNT usage. This means having a higher volume fraction of CNT fibres in the regions that require more stiffness and decreasing it in the regions with lower mechanical loading, as reported by Kwon et al. [23] who successfully fabricated CNT strengthened structures in which the volume fraction, of CNT has been functionally graded through the structure using a powder metallurgy route method.

1.2 Literature review

Since there are unlimited ways to functionally grade the CNT fibres through the structure, it is important to know which function could be appropriate regarding the type of loading and the mechanical condition. For different types of structures, researchers have studied the mechanical behaviour of FG CNT strengthened structures in the past in which beams, as the most important structural element, have attracted extensive attention. For instance, in the framework of nonlinear dynamics, Ke et al. [24] analysed the nonlinear oscillation behaviour of CNT strengthened beams with CNT through-thickness varying volume fraction; the Timoshenko beam theory with geometrical nonlinearities has been used to formulate the structure. CNTs were assumed to be aligned through the axial direction with the possibility to linearly increase the volume fraction through the thickness. It was shown that increasing the CNT volume fraction leads to higher natural frequencies in both uniformly distributed and FG graded fibre models; they [25] also studied the dynamic behaviour of such structures with the same assumptions indicating the influence of increasing the CNT volume fraction on the stability of the strengthened structure.

In the framework of linear dynamic analysis, both free and nonlinear vibration responses of CNT reinforced beams with grading through thickness have been investigated. Lin and Xiang [26] have examined the vibration behaviour of first- and third-order beams strengthened with CNTs. CNT was distributed functionally through the thickness of the beam using type A and X models. It was shown that the natural frequency parameter increases significantly by increasing the CNT volume fraction from 12 to 17%. Ansari et al. [27] investigated the forced vibration response of FG CNT strengthened through the thickness via the Timoshenko beam theory. Different types of CNT distribution had been studied considering von-Karman geometrical nonlinearity. It was shown that type O CNT distribution model has the highest peak amplitude compared to other types of CNT positioning.

For the case of stability analysis, Mayandi and Jeyaraj [28] used a finite element method for analysing the mechanical behaviour of FG CNT strengthened beams. It was shown that critical buckling temperature for type X CNT distribution is higher than type O and V; this importance indicated the effect of CNT distribution on the mechanical behaviour of such structures. Other types of structures strengthened with FG CNTs through the thickness direction have also been analysed; interested readers are referred to as Refs. [29,30,31,32,33]. A detailed literature review on the recent progress of FG CNT strengthened structures can be found in Ref. [10].

1.3 Novelty and problem definition

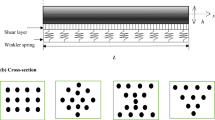
It can be seen that in all of the discussed valuable literature, grading CNT has been applied through the thickness direction and the mechanical behaviour for different types of CNT distribution has been discussed. However, another important model of grading CNT in a structure especially beams is by grading the CNT fibres through the axial direction. Axially functionally grading (AFG) the CNT fibres could help in setting the natural frequencies in the desired range as well as varying the strength of the structure through the length. A schematic view of a beam in which the CNT fibres are graded through the length is presented in Fig. 1 where the beam is located on an elastic foundation of combination of Pasternak and Winkler type. This study aims to present a new general model of this class and analyse the free dynamics response of such structures while considering the presence of a varying Winkler–Pasternak foundation.

Fig. 1

Schematic model of an axially CNT strengthened beam resting on an elastic foundation of Winkler–Pasternak type. The lower graph shows the variation of CNT volume fraction from the left end to the right end of the beam following a specific function

2 Problem formulation

2.1 CNT strengthened composite structures

For structures strengthened with CNTs (such as CNT strengthened beams), the composite properties could be obtained using different rule of mixtures. However, by aligning and grading the CNT distribution through the axial direction (Fig. 1), the properties become dependent on the volume fraction of CNT and the base matrix defined as V_m(x) and V_CNT(x), respectively, where the subs CNT and m represent the properties related to the CNT fibres and the base matrix. Accordingly, the material properties of AFG CNT strengthened one-dimensional structures could be written as [34]

$$ \begin{aligned} E(x) & = V_{{m}} (x)E_{{m}} + e_{1} \,V_{\text{CNT}} (x)E_{{11,{\text{CNT}}}} , \\ \nu (x) & = V_{\text{CNT}} (x)\nu_{\text{CNT}} + V_{{m}} (x)\nu_{{m}} , \\ \rho (x) & = V_{\text{CNT}} (x)\rho_{\text{CNT}} + V_{{m}} (x)\rho_{{m}} , \\ \end{aligned} $$

(1)

where ν, E, ρ, e₁ and G indicate Poisson’s ratio, Young modulus, mass density, effective coefficient and the shear modulus, respectively. As mentioned previously, it is assumed that the volume fraction of CNT fibres varies through the length of the beam following a specific function. Figure 1 presents a view of the variation of CNT volume fraction from the left end of the beam to the right. Similar types of grading models have been previously studied in structures with functionally graded physical properties variation due to material changes in axial [17, 35,36,37,38], thickness [39,40,41,42,43,44,45,46] or both directions [47,48,49,50,51]. To have a general form of AFG CNT strengthened model, the volume fraction of CNT fibres through the length has been presented by utilising a power-law distribution function as [26]

$$ \begin{aligned} V_{\text{CNT}} (x) & = \left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)\left( {1 - \frac{x}{L}} \right)^{k} + V_{\text{CNT-R}} ,\quad 0 \le x \le L; \\ V_{{m}} (x) & = 1 - V_{\text{CNT}} (x), \\ \end{aligned} $$

(2)

where V_CNT-L and V_CNT-R are the volume fractions of CNT fibres at the left and right ends of the beam, respectively; parameter k presents the power term which by having k = 0, CNT strengthened model with constant CNT volume fraction will be obtained and by having k = 1, linear variation model will be achieved. The total volume fraction of CNT in the beam could be presented as

$$ V_{\text{CNT-Total}} = \frac{{\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)}}{k + 1} + V_{\text{CNT-R}} . $$

(3)

It can easily be seen that for k = 0 the total volume fraction of CNT will be equal to the CNT volume fraction at the left end.

2.2 Strengthened beam formulation

For a general structure model, constitutive stress–strain law is written as [52]

$$ \{ \sigma \} [Q]\{ \varepsilon \} \to \left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{zz} \hfill \\ \sigma_{xy} \hfill \\ \sigma_{xz} \hfill \\ \sigma_{yz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {Q_{11} } &\quad {Q_{21} } &\quad {Q_{31} } &\quad {Q_{41} } &\quad {Q_{51} } &\quad {Q_{61} } \\ {Q_{12} } &\quad {Q_{22} } &\quad {Q_{32} } &\quad {Q_{42} } &\quad {Q_{52} } &\quad {Q_{62} } \\ {Q_{13} } &\quad {Q_{23} } &\quad {Q_{33} } &\quad {Q_{43} } &\quad {Q_{53} } &\quad {Q_{63} } \\ {Q_{14} } &\quad {Q_{24} } &\quad {Q_{34} } &\quad {Q_{44} } &\quad {Q_{54} } &\quad {Q_{64} } \\ {Q_{15} } &\quad {Q_{25} } &\quad {Q_{35} } &\quad {Q_{45} } &\quad {Q_{55} } &\quad {Q_{65} } \\ {Q_{16} } &\quad {Q_{26} } &\quad {Q_{36} } &\quad {Q_{46} } &\quad {Q_{56} } &\quad {Q_{66} } \\ \end{array} } \right]^{\text{T}} \left\{ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \varepsilon_{zz} \hfill \\ \varepsilon_{xy} \hfill \\ \varepsilon_{xz} \hfill \\ \varepsilon_{yz} \hfill \\ \end{aligned} \right\}, $$

(4)

where Q indicates the stiffness matrix, σ is the stress term, and ε is the strain term. For orthotropic structures, this equation is simplified as [53]:

$$ \{ \sigma \} = [Q]\{ \varepsilon \} \to \left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{zz} \hfill \\ \sigma_{xy} \hfill \\ \sigma_{xz} \hfill \\ \sigma_{yz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {Q_{11} } &\quad {Q_{21} } &\quad {Q_{31} } &\quad 0 &\quad 0 &\quad 0 \\ {Q_{21} } &\quad {Q_{22} } &\quad {Q_{32} } &\quad 0 &\quad 0 &\quad 0 \\ {Q_{31} } &\quad {Q_{32} } &\quad {Q_{33} } &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad {Q_{44} } &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {Q_{55} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {Q_{66} } \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \varepsilon_{zz} \hfill \\ \varepsilon_{xy} \hfill \\ \varepsilon_{xz} \hfill \\ \varepsilon_{yz} \hfill \\ \end{aligned} \right\}, $$

(5)

and accordingly, for the Euler–Bernoulli beam theory, the constitutive stress–strain law is written as [54]

$$ \begin{aligned} \sigma_{xx} & = Q_{11} (x)\varepsilon_{xx} = \frac{{E_{11} (x)}}{{1 - \nu^{2} (x)}}\varepsilon_{xx} , \\ \varepsilon_{xx} & = \frac{\partial \eta (x,t)}{\partial x} - z\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}. \\ \end{aligned} $$

(6)

where $\eta$ and $\xi$ are the axial and transverse displacement terms, respectively. Moreover, the beam is assumed to be resting on a Winkler–Pasternak foundation which could vary through the axial direction. In a general form, the elastic foundation is defined using power-law varying function with the following stiffness coefficients [55]

$$ \begin{aligned} K_{\text{W}} (x) = K_{\text{W0}} \left[ {1 - \alpha \left( {\frac{x}{L}} \right)^{n} } \right], \hfill \\ K_{\text{P}} (x) = K_{\text{P0}} \left[ {1 - \beta \left( {\frac{x}{L}} \right)^{m} } \right], \hfill \\ \end{aligned} $$

(7)

where K_W and K_P are the Winkler and Pasternak foundation stiffness terms which are assumed to be a function of length parameter x. The Winkler elastic foundation term is presented with an initial value of K_W0, a coefficient and power term α and n, respectively; similarly, Pasternak foundation term is also presented using an initial value, coefficient and power term K_P0, $\beta$ and m, respectively. For the given assumptions, material property variations and beam theory, the potential and kinetic energy terms and the external work due to the foundation are formulated as

$$ \begin{aligned} U & = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{A}^{ } \sigma_{xx}^{{}} \varepsilon_{xx} {\text{d}}A{\text{d}}x = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{A}^{ } \frac{{E_{11} (x)}}{{1 - \nu^{2} (x)}} \left[ {\frac{\partial \eta (x,t)}{\partial x} - z\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right]^{2} {\text{d}}A{\text{d}}x, \\ K & = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{A}^{ } \rho (x)\left[ {\left( {\frac{\partial \xi (x,t)}{\partial t}} \right)^{2} + \left( {\frac{\partial \eta (x,t)}{\partial t} - z\frac{{\partial^{2} \xi (x,t)}}{\partial x\partial t}} \right)^{2} } \right]{\text{d}}A{\text{d}}x, \\ W_{\text{F}} & = \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {K_{\text{W}} (x)\xi^{2} (x,t) + K_{\text{P}} (x)\left( {\frac{\partial \xi (x,t)}{\partial x}} \right)^{2} } \right]{\text{d}}x. \\ \end{aligned} $$

(8)

By using Hamilton’s principle, one can reach to the equations of motion as:

$$ \begin{aligned} \delta u & \to - I_{0} (x)\left( {\frac{{\partial \eta^{2} (x,t)}}{{\partial t^{2} }}} \right) + I_{1} (x)\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x\partial t^{2} }}} \right) \\ & \quad + \frac{\partial }{\partial x}\left[ {A_{11} (x)\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)} \right] - \frac{\partial }{\partial x}\left[ {B_{11} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)} \right] = 0, \\ \delta w & \to - I_{0} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial t^{2} }}} \right) + \frac{\partial }{\partial x}\left[ {I_{2} (x)\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x\partial t^{2} }}} \right)} \right] - \frac{\partial }{\partial x}\left[ {I_{1} (x)\left( {\frac{{\partial^{2} \eta (x,t)}}{{\partial t^{2} }}} \right)} \right]\, \\ & \quad + \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {B_{11} (x)\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)} \right] - \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {D_{11} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)} \right] \\ & \quad - K_{\text{W}} (x)\xi (x,t) + \frac{\partial }{\partial x}\left[ {K_{\text{P}} (x)\left( {\frac{\partial \xi (x,t)}{\partial x}} \right)} \right] = 0, \\ \end{aligned} $$

(9)

in conjunction with the following boundary equations

$$ \begin{aligned} & \left. {A_{11} (x)\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)\delta \eta (x,t)} \right|_{x = 0}^{x = L} - \left. {B_{11} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)\delta \eta (x,t)} \right|_{x = 0}^{x = L} = 0, \\ & \left. {\frac{\partial }{\partial x}\left[ {B_{11} (x)\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)} \right]\delta \xi (x,t)} \right|_{x = 0}^{x = L} - \left. {\frac{\partial }{\partial x}\left[ {D_{11} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)} \right]\delta \xi (x,t)} \right|_{x = 0}^{x = L} = 0, \\ & \left. {B_{11} (x)\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)\delta \left( {\frac{\partial \xi (x,t)}{\partial x}} \right)} \right|_{x = 0}^{x = L} - \left. {\left[ {D_{11} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)} \right]\delta \left( {\frac{\partial \xi (x,t)}{\partial x}} \right)} \right|_{x = 0}^{x = L} = 0. \\ \end{aligned} $$

(10)

By having symmetric material distribution through the thickness, I₀, I₁ and I₂ as the inertia terms become

$$ \left\{ \begin{aligned} I_{0} (x) \hfill \\ I_{2} (x) \hfill \\ \end{aligned} \right\} = \left[ {\rho_{{m}} + \left( {\rho_{\text{CNT}} - \rho_{{m}} } \right)V_{\text{CNT}} (x)} \right]\left\{ \begin{aligned} A \hfill \\ I \hfill \\ \end{aligned} \right\},\quad I_{1} = 0, $$

(11)

and A₁₁, B₁₁ and D₁₁ are the stiffness terms written as

$$ \left\{ \begin{aligned} A_{11} (x) \hfill \\ D_{11} (x) \hfill \\ \end{aligned} \right\} = \frac{{E_{{m}} + \left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)V_{\text{CNT}} (x)}}{{1 - \nu^{2} (x)}}\left\{ \begin{aligned} A \hfill \\ I \hfill \\ \end{aligned} \right\},\quad B_{11} = 0, $$

(12)

leading to simplified equations of motion and boundary equations as

$$ \begin{aligned} \delta u & \to - I_{0} (x)\left( {\frac{{\partial \eta^{2} (x,t)}}{{\partial t^{2} }}} \right) + \frac{\partial }{\partial x}\left[ {A_{11} (x)\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)} \right] = 0, \\ \delta w & \to - I_{0} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial t^{2} }}} \right) + \frac{\partial }{\partial x}\left[ {I_{2} (x)\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x\partial t^{2} }}} \right)} \right] - \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {D_{11} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)} \right] \\ & \quad - K_{\text{W}} (x)\xi (x,t) + \frac{\partial }{\partial x}\left[ {K_{\text{P}} (x)\left( {\frac{\partial \xi (x,t)}{\partial x}} \right)} \right] = 0, \\ \end{aligned} $$

(13)

$$ \begin{aligned} & {\text{BC1:}}\;\;\left. {\eta (x,t)} \right|_{0}^{L} = 0\quad {\text{or}}\quad \left. {\frac{\partial \eta (x,t)}{\partial x}} \right|_{0}^{L} = 0, \\ & {\text{BC2:}}\;\;\left. {\left[ {\frac{{\partial D_{11} (x)}}{\partial x}\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right) + D_{11} (x)\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x^{3} }}} \right)} \right]} \right|_{0}^{L} = 0\quad {\text{or}}\quad \left. {\xi (x,t)} \right|_{0}^{L} = 0, \\ & {\text{BC3:}}\;\;\left. {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right|_{0}^{L} = 0\quad {\text{or}}\quad \left. {\frac{\partial \xi (x,t)}{\partial x}} \right|_{0}^{L} = 0. \\ \end{aligned} $$

(14)

Substituting Eqs. (11) and (12) into Eqs. (13) and (14) and by neglecting the Poisson’s ratio variation due to very small variations of this parameter, equations of motion are rewritten as

$$ \begin{aligned} & - \left[ {\rho_{{m}} + \left( {\rho_{\text{CNT}} - \rho_{{m}} } \right)V_{\text{CNT}} (x)} \right]\left( {\frac{{\partial \eta^{2} (x,t)}}{{\partial t^{2} }}} \right) \\ & \quad + \frac{{\left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}}}{{1 - \nu^{2} }}\left( {\frac{\partial \eta (x,t)}{\partial x}} \right) \\ & \quad + \frac{{E_{{m}} + \left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)V_{\text{CNT}} (x)}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} \eta (x,t)}}{{\partial x^{2} }}} \right) = 0, \\ \end{aligned} $$

(15)

$$ \begin{aligned} & - \left[ {\rho_{{m}} + \left( {\rho_{\text{CNT}} - \rho_{{m}} } \right)V_{\text{CNT}} (x)} \right]A\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial t^{2} }}} \right) \\ & \quad + \left[ {\left( {\rho_{\text{CNT}} - \rho_{{m}} } \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}} \right]I\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x\partial t^{2} }}} \right) \\ & \quad + \left[ {\rho_{{m}} + \left( {\rho_{\text{CNT}} - \rho_{{m}} } \right)V_{\text{CNT}} (x)} \right]I\left( {\frac{{\partial^{4} \xi (x,t)}}{{\partial x^{2} \partial t^{2} }}} \right)\, \\ & \quad - \frac{{\left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)\frac{{\partial^{2} V_{\text{CNT}} (x)}}{{\partial x^{2} }}}}{{1 - \nu^{2} }}I\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right) \\ & \quad - 2\frac{{\left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}}}{{1 - \nu^{2} }}I\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x^{3} }}} \right) \\ & \quad - \frac{{E_{{m}} + \left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)V_{\text{CNT}} (x)}}{{1 - \nu^{2} }}I\frac{{\partial^{4} \xi (x,t)}}{{\partial x^{4} }} \\ & \quad + K_{\text{P}} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right) + \frac{{\partial K_{\text{P}} (x)}}{\partial x}\left( {\frac{\partial \xi (x,t)}{\partial x}} \right) - K_{\text{W}} (x)\xi (x,t) = 0, \\ \end{aligned} $$

(16)

together with boundary conditions as:

$$ \begin{aligned} & {\text{BC1:}}\;\;\left. {\frac{\partial \eta (x,t)}{\partial x}} \right|_{0}^{L} = 0\quad {\text{or}}\quad \left. {\eta (x,t)} \right|_{0}^{L} = 0, \\ & {\text{BC2:}}\;\;\left. {\left[ {\begin{array}{*{20}l} {\frac{{\left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right)}}{{1 - \nu^{2} }}} \hfill \\ {\quad + \frac{{E_{{m}} + \left( {e_{1} \,E_{{ 1 1 , {\text{CNT}}}} - E_{{m}} } \right)V_{\text{CNT}} (x)}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x^{3} }}} \right)} \hfill \\ \end{array} } \right]} \right|_{0}^{L} = 0\quad {\text{or}}\quad \left. {\xi (x,t)} \right|_{0}^{L} = 0, \\ & {\text{BC3:}}\;\;\left. {\frac{\partial \xi (x,t)}{\partial x}} \right|_{0}^{L} = 0\quad {\text{or}}\quad \left. {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right|_{0}^{L} = 0. \\ \end{aligned} $$

(17)

By defining non-dimensional parameters of:

$$ x^{*} = \frac{x}{L},\quad w^{*} = \frac{\xi }{h},\quad u^{*} = \frac{\eta }{h},\quad t^{*} = t\sqrt {\frac{{E_{{m}} I}}{{\rho_{{m}} AL^{4} }}} ,\quad \gamma = \sqrt {\frac{I}{{AL^{2} }}} ,\quad k_{\text{w}}^{*} = \frac{{k_{\text{w}} L^{4} }}{{E_{{m}} I}},\quad k_{\text{p}}^{*} = \frac{{k_{\text{p}} L^{2} }}{{E_{{m}} I}}, $$

(18)

equations of motion will be rewritten in non-dimensional forms as

$$ \begin{aligned} & - \left[ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)V_{\text{CNT}} (x)} \right]\left( {\frac{{\partial \eta^{2} (x,t)}}{{\partial t^{2} }}} \right) + \frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}}}{{1 - \nu^{2} }}\frac{1}{{\gamma^{2} }}\left( {\frac{\partial \eta (x,t)}{\partial x}} \right)\, \\ & \quad + \frac{{1 + \left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)V_{\text{CNT}} (x)}}{{1 - \nu^{2} }}\frac{1}{{\gamma^{2} }}\left( {\frac{{\partial^{2} \eta (x,t)}}{{\partial x^{2} }}} \right) = 0, \\ \end{aligned} $$

(19)

$$ \begin{aligned} & - \left[ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)V_{\text{CNT}} (x)} \right]\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial t^{2} }}} \right) + \left[ {\left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}} \right]\,\gamma^{2} \left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x\partial t^{2} }}} \right) \\ & \quad + \left[ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)V_{\text{CNT}} (x)} \right]\,\,\gamma^{2} \left( {\frac{{\partial^{4} \xi (x,t)}}{{\partial x^{2} \partial t^{2} }}} \right) \\ & \quad - \frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\frac{{\partial^{2} V_{\text{CNT}} (x)}}{{\partial x^{2} }}}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right) - 2\frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\frac{{\partial V_{\text{CNT}} (x)}}{\partial x}}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x^{3} }}} \right) \\ & \quad - \frac{{1 + \left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)V_{\text{CNT}} (x)}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{4} \xi (x,t)}}{{\partial x^{4} }}} \right) \\ & \quad + K_{\text{P}} (x)\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right) + \frac{{\partial K_{\text{P}} (x)}}{\partial x}\left( {\frac{\partial \xi (x,t)}{\partial x}} \right) - K_{\text{W}} (x)\xi (x,t) = 0, \\ \end{aligned} $$

(20)

which for the sake of brevity the superscript * is removed from the equations. Considering power-law CNT grading function through the length as demonstrated in Eq. (2) and a general form for Winkler–Pasternak foundation varying model in Eq. (7), the equations of motion can still be rewritten as

$$ \begin{aligned} & - \left[ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)V_{\text{CNT}} (x)} \right]\left( {\frac{{\partial \eta^{2} (x,t)}}{{\partial t^{2} }}} \right) \\ & \quad - \frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(k)(1 - x)^{(k - 1)} } \right]}}{{1 - \nu^{2} }}\frac{1}{{\gamma^{2} }}\left( {\frac{\partial \eta (x,t)}{\partial x}} \right) \\ & \quad + \frac{{1 + \left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x)^{k} + V_{\text{CNT-R}} } \right]}}{{1 - \nu^{2} }}\frac{1}{{\gamma^{2} }}\left( {\frac{{\partial^{2} \eta (x,t)}}{{\partial x^{2} }}} \right) = 0, \\ \end{aligned} $$

(21)

$$ \begin{aligned} & - \left[ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x)^{k} + V_{\text{CNT-R}} } \right]} \right]\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial t^{2} }}} \right) \\ & \quad + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(k)(1 - x)^{(k - 1)} } \right]\,\,\gamma^{2} \left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x\partial t^{2} }}} \right) \\ & \quad + \left[ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x)^{k} + V_{\text{CNT-R}} } \right]} \right]\,\,\gamma^{2} \left( {\frac{{\partial^{4} \xi (x,t)}}{{\partial x^{2} \partial t^{2} }}} \right) \\ & \quad - \frac{{1 + \left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x)^{k} + V_{\text{CNT-R}} } \right]}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{4} \xi (x,t)}}{{\partial x^{4} }}} \right) \\ & \quad + 2\frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(k)(1 - x)^{(k - 1)} } \right]}}{{1 - \nu^{2} }}\left( {\frac{{\partial^{3} \xi (x,t)}}{{\partial x^{3} }}} \right) \\ & \quad + \left\{ {K_{\text{P0}} \left( {1 - \beta x^{m} } \right) - \frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(K - 1)(k)(1 - x)^{(k - 2)} } \right]}}{{1 - \nu^{2} }}} \right\}\left( {\frac{{\partial^{2} \xi (x,t)}}{{\partial x^{2} }}} \right) \\ & \quad - m\beta x^{m - 1} \left( {\frac{\partial \xi (x,t)}{\partial x}} \right) - K_{\text{W0}} \left( {1 - \alpha x^{n} } \right)\xi (x,t) = 0. \\ \end{aligned} $$

(22)

It can be seen that the governing equations have x depended coefficients due to the CNT fibre grading through the length and also the foundation variation.

3 Solution procedure

Since the equations of motion contain complicated coefficients varying through the length, generalised differential quadrature (GDQ) method is employed. Accordingly, the transverse displacement term and the corresponding derivations are defined as [56]

$$ W^{(r)} = \sum\limits_{k = 0}^{1} {h_{1k}^{(r)} w_{1}^{(k)} } + \sum\limits_{k = 0}^{1} {h_{Nk}^{(r)} w_{N}^{(k)} } + \sum\limits_{k = 2}^{N - 1} {h_{k0}^{(r)} w_{k}^{{}} } = \sum\limits_{k = 1}^{N + 2} {M_{ik}^{(r)} W_{k}^{{}} } $$

(23)

where h_ij determines the Hermite shape functions defined in [56] which could be represented in one summation using M_ik. Terms w₁, w_N and w_k indicate the deformations at the left end, right end and the nodes in between, respectively. The total number of sampling points is indicated by N in which for higher accuracy, Chebyshev–Gauss–Lobatto model [57] is employed for unevenly sampling which is defined as

$$ x_{n} = \frac{1}{2}\left[ {1 - \cos \left( {\frac{n - 1}{N - 1}\pi } \right)} \right]. $$

(24)

For having harmonic response and by defining $w(x,t) = w(x)e^{{i\omega_{{m}} t}}$, the equations of motion can be rewritten as

$$ \begin{aligned} & \sum\limits_{j = 1}^{N + 2} {\left\{ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x_{j} )^{k} + V_{\text{CNT-R}} } \right]} \right\}M_{ij}^{{}} } \lambda_{{m}}^{2} \\ & \quad - \sum\limits_{j = 1}^{N + 2} {\gamma^{2} \left\{ {\left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(k)(1 - x_{j} )^{(k - 1)} } \right]} \right\}M_{ij}^{(1)} } \lambda_{{m}}^{2} \\ & \quad - \sum\limits_{j = 1}^{N + 2} {\gamma^{2} \left\{ {1 + \left( {\frac{{\rho_{\text{CNT}} }}{{\rho_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x_{j} )^{k} + V_{\text{CNT-R}} } \right]} \right\}M_{ij}^{(2)} } \lambda_{{m}}^{2} \\ & \quad - \sum\limits_{j = 1}^{N + 2} {\frac{{1 + \left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(1 - x_{j} )^{k} + V_{\text{CNT-R}} } \right]}}{{1 - \nu^{2} }}M_{ij}^{(4)} } \\ & \quad + 2\sum\limits_{j = 1}^{N + 2} {\frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(k)(1 - x_{j} )^{(k - 1)} } \right]}}{{1 - \nu^{2} }}M_{ij}^{(3)} } \\ & \quad + \sum\limits_{j = 1}^{N + 2} {\left\{ {\begin{array}{*{20}l} {K_{\text{P0}} \left( {1 - \beta x_{j}^{m} } \right)} \hfill \\ {\quad - \frac{{\left( {e_{1} \,\frac{{E_{{ 1 1 , {\text{CNT}}}} }}{{E_{{m}} }} - 1} \right)\left[ {\left( {V_{\text{CNT-L}} - V_{\text{CNT-R}} } \right)(K - 1)(k)(1 - x_{j} )^{(k - 2)} } \right]}}{{1 - \nu^{2} }}} \hfill \\ \end{array} } \right\}M_{ij}^{(2)} } \\ & \quad - \sum\limits_{j = 1}^{N + 2} {m\beta K_{\text{P0}} x_{j}^{m - 1} M_{ij}^{(1)} } - \sum\limits_{j = 1}^{N + 2} {K_{\text{W0}} \left( {1 - \alpha x_{j}^{n} } \right)M_{ij}^{{}} } = 0, \\ \end{aligned} $$

(25)

where $\lambda_{{m}}$ indicates the non-dimensional natural frequency term defined with respect to the base matrix properties as $\lambda_{{m}} = \omega_{{m}} \sqrt {\rho_{{m}} AL^{4} /E_{{m}} I}$. Depending on the boundary type, the governing equations could be solved in matrix for the natural frequency characteristics.

4 Results and discussion

This section provides a comprehensive verification for the current formulation and methodology presents the convergence of the solution procedure and discusses the dynamic behaviour of the CNT strengthened structure as different mechanical properties vary.

4.1 Verification and comparison

For the first step, the current methodology for solving such problems and the accuracy of the model is discussed. One way to verify the current results is to implement the model (in the absence of the Winkler–Pasternak elastic foundation) in a finite element (FE) software (i.e. ANSYS^® (version 19.2, ANSYS Inc., Canonsburg, PA, US) [58]); to this end, by having geometrical properties as L = 1 m and h = 10 mm, CNT volume fraction variation as V_CNT,total = 5%, V_CNT-L = 2.5%, k = 1, and the properties as in [59]: E_m = 2.5 GPa, E_11,CNT = 5646.6 GPa, v_m = 0.3, ρ_m = 1190 kg/m³, ρ_CNT = 1400 kg/m³ and e₁ = 0.14 (CNT is assumed to be as the armchair (10, 10) in the room temperature). First four frequency terms and mode shapes for linearly CNT volume fraction variation are observed for both GDQM and ANSYS models which the results are presented in Table 1 and Fig. 2 for a clamped–clamped beam and in Table 2 and Fig. 3 for a simply supported beam, respectively. The GDQM results are in a good agreement with those obtained via the FE analysis.

Table 1 Comparison between GDQM and FEM: non-dimensional natural frequency results for a fully clamped linearly AFG CNT strengthened beam model

Fig. 2

First four mode shapes of linearly AFG CNT strengthened clamped–clamped beam model with no foundations: a 1st mode; b 2nd mode; c 3rd mode; d 4th mode

Table 2 Comparison between GDQM and FEM: non-dimensional natural frequency results for a simply supported linearly AFG CNT strengthened beam model

Fig. 3

First four mode-shapes of linearly AFG CNT strengthened simply-supported beam model with no foundations: a 1st mode; b 2nd mode; c 3rd mode; d 4th mode

Since there are no studies in the literature on grading the CNT fibres trough the length of the beam for verification purposes, studies on non-strengthened beams resting on an elastic medium are considered. Accordingly, two different comparative studies for analysing the Winkler varying foundation model and Pasternak foundation are presented in the following.

Firstly, the beam is assumed to be homogeneous laying on a Winkler elastic foundation which varies through the axial direction. For the case of having constant Winkler foundation, the fundamental natural frequency terms for hinged beam model are obtained and compared in Table 3 to those presented by Zhou [60]. Similarly, for linear K_W = K_W0 (1 − αx) and parabolic K_W = K_W0 (1 − αx²) foundation variations through the thickness, the fundamental frequency parameter is obtained for different K_W0 and α terms and verified in Tables 4 and 5. It can be seen that the results are in very good agreement with those presented by Zhou [60].

Table 3 Non-dimensional fundamental natural frequency term of homogeneous beams resting on a constant Winkler foundation

Table 4 Non-dimensional fundamental natural frequency term of homogeneous beams resting on a linearly varying Winkler foundation

Table 5 Non-dimensional fundamental natural frequency term of homogeneous beams resting on a parabolic varying Winkler foundation

Secondly, in order to verify the modelling while considering the presence of Pasternak foundation, a comparison study is performed. Tables 6 and 7 indicate the first natural frequency term of simply supported and clamped beams resting on a Winkler–Pasternak foundation, respectively. Results are shown for different Winkler and Pasternak terms and compared with those presented by Chen et al. [61], which show great agreement between this methodology and previous studies.

Table 6 Non-dimensional fundamental natural frequency term of simply supported beams resting on a Winkler–Pasternak foundation

Table 7 Non-dimensional fundamental natural frequency term of clamped beams resting on a Winkler–Pasternak foundation

After verifying the current solution procedure, the influence of different terms on the free dynamics of AFG CNT strengthened beams is studied in Sects. 4.2, 4.3 and 4.4 for the influence of the varying Winkler elastic parameters, Pasternak term and CNT distribution model, respectively.

4.2 Influence of varying Winkler elastic parameters

The influence of changing the CNT volume fraction together with different Winkler terms is presented. To this end, the volume fraction of CNT at the left end is increased from 0 to 1% with R = V_CNT-L/V_CNT-L = 1.5, and the Pasternak term is assumed to vary with K_P0 = 10 and β = 1.

Figure 4 demonstrates parameters for the first natural frequency of the fixed-end beam for different CNT volume fraction power terms (k = 1, 2 and 3); for both K_W0 = 200 and 750, the natural frequency term for constant Winkler model is larger compared to foundation varying models. By linearly varying the Winkler elastic foundation term, the natural frequency drops in magnitude, however, by increasing the power term (from n = 1–2) the natural frequency term increases but remains lower than that of the constant foundation model. Moreover, it can be noted that increasing the power term k from 1 to 3, the natural frequency increases for all the CNT volume fractions which means that the stiffness of the system has increased.

Fig. 4

Non-dimensional fundamental natural frequency term of clamped AFG CNT strengthened beams with respect to CNT volume fraction for different Winkler foundation models: a k = 1; b k = 2; c k = 3

Moreover, for simply supported AFG CNT strengthened beam model, the fundamental frequency terms are presented in Fig. 5 for k = 1, 2 and 3. Similar to the clamped–clamped beam model, the natural frequency term decreases by changing the constant Winkler model to linear model and increases, respectively, by changing the linear Winkler model to parabolic model; the natural frequency parameter increases for all types of Winkler model while increasing the CNT volume fraction.

Fig. 5

Non-dimensional fundamental natural frequency term of simply-supported AFG CNT strengthened beams with respect to CNT volume fraction for different Winkler foundation models: a k = 1; b k = 2; c k = 3

4.3 Influence of varying Pasternak parameters

Another important term in the analysis of such structures is the Pasternak parameters in the varying elastic foundation model. To demonstrate the influence of these parameters on vibration response of AFG CNT strengthened structures with different CNT volume fractions, Figs. 6 and 7 are presented. Figures 6 and 7, which are, respectively, for the clamped and simply supported beam models, indicate the fundamental frequency term for different Pasternak models for CNT grading power terms k = 1, 2 and 3. It can be noted that increasing the Pasternak term K_P0 leads to higher natural frequency parameters while changing it from a constant stiffness to linearly varying with β = 1 and m = 2 decreases frequencies; in the physical view, the stiffness of the whole system drops. Comparing Figs. 6 and 7 with Figs. 5 and 4, it can be seen that the frequency term of AFG CNT strengthened beam is more sensitive to Winkler parameter variation compared to the Pasternak term variation in the foundation model.

Fig. 6

Non-dimensional fundamental natural frequency term of clamped AFG CNT strengthened beams with respect to CNT volume fraction for different Pasternak foundation models: a k = 1; b k = 2; c k = 3

Fig. 7

Non-dimensional fundamental natural frequency term of simply-supported AFG CNT strengthened beams with respect to CNT volume fraction for different Pasternak foundation models: a k = 1; b k = 2; c k = 3

4.4 Influence of CNT distribution model

The main term in analysing these structures is the effect of CNT distribution by engineering both CNT volume fraction and the grading through the length. To this end, by assuming K_P = 10 and K_W = 200, the fundamental frequency terms are calculated for V_CNT-L = 15% while varying both the power term and the volume fraction of the CNT at the right end. From Fig. 8, it can be noted that increasing the power term and the right-to-left volume fraction ratio, leads to higher fundamental frequency terms for both fully clamped and simply supported AFG CNT strengthened beam models; varying the power term k has its most impact in the lower amounts of k for both boundary condition models.

Fig. 8

Non-dimensional fundamental natural frequency term of AFG CNT strengthened beams with respect to CNT volume fraction: a clamped; b simply supported

Additionally, to have a comprehensive view of the CNT reinforcing effect, all three reinforcement terms (V_CNT-L, V_CNT-R and k) are varied and the free vibration frequency response is obtained. Figures 9 and 10 indicate the frequency terms by varying CNT distribution terms as k = [1, 2, 5], 0 ≤ V_CNT-L ≤ 5% and 1 ≤ R ≤ 3. It can be seen how the power term will significantly change the fundamental frequency parameter for both simply supported and clamped AFG CNT strengthened beam models. The physical explanation for such a significance increase in non-dimensional frequency term is that the stiffness of CNT fibres is considerably higher than the matrix base and hence, adding a small percentage of CNT leads to significant changes in vibration behaviour of the system.

Fig. 9

Non-dimensional fundamental natural frequency term of hinged AFG CNT strengthened beams with respect to CNT volume fraction 1: k = 5; 2: k = 2; 3: k = 1

Fig. 10

Non-dimensional fundamental natural frequency term of clamped AFG CNT strengthened beams with respect to CNT volume fraction 1: k = 5; 2: k = 2; 3: k = 1

5 Conclusions

In this study, a general formulation for free dynamic analysis of AFG CNT strengthened deformable beams was obtained. CNTs are assumed to be aligned and graded through the length following a general form of power-law function. The beam was assumed to be embedded in an elastic environment considering both Winkler and Pasternak effects. The elastic foundation was analysed in different forms as a constant model, linear and parabolic varying through the length direction of the beam. By modelling the problem via Hamilton’s approach and solving using GDQ method, natural frequency parameters were obtained. It was shown that for hinged and clamped beam models, adding CNT fibres to the base matrix could increase the natural frequency and stiffness of the beam significantly; however, the simply supported beam model is slightly more sensitive to the variation of CNT volume fraction through the length. Adding AFG CNT fibres to the base matrix beam has its most impact on varying the fundamental natural frequency terms of the beam model in the low amounts of CNTs and its effect will slightly decrease by reaching to higher amounts of CNT. For a few cases of the model with no foundations, the first four natural frequencies have been obtained using the FEM in ANSYS Workbench [58] which shows a good agreement with the current results.

Furthermore, the influence of having a general varying elastic foundation in conjunction with CNT fibres graded through the length was discussed. It was shown that increasing the constant Winkler and Pasternak terms leads to higher natural frequency terms while increasing the power-term of the Pasternak foundation part decreases the frequency. For the presented varying foundation model, increasing the Winkler power-term from uniformly distributed model to linear model (from n = 0 to n = 1), the first natural frequency term decreases significantly while increasing it from linear to parabolic model (from n = 0 to n = 1) increases the fundamental frequency of the beam. Moreover, for both fully clamped and simply supported beam models, it was seen that for lower volume fractions of CNT fibres, the sensitivity of fundamental frequency to variation of the foundation term is noticeably higher.