Postbuckling analysis of hydrostatic pressurized FGM microsized shells including strain gradient and stress-driven nonlocal effects

Abstract

Herein, with the aid of the newly proposed theory of nonlocal strain gradient elasticity, the size-dependent nonlinear buckling and postbuckling behavior of microsized shells made of functionally graded material (FGM) and subjected to hydrostatic pressure is examined. As a consequence, the both nonlocality and strain gradient micro-size dependency are incorporated to an exponential shear deformation shell theory to construct a more comprehensive size-dependent shell model with a refined distribution of shear deformation. The Mori–Tanaka homogenization scheme is utilized to estimate the effective material properties of FGM nanoshells. After deduction of the non-classical governing differential equations via boundary layer theory of shell buckling, a perturbation-based solving process is employed to extract explicit expressions for nonlocal strain gradient stability paths of hydrostatic pressurized FGM microsized shells. It is observed that the nonlocality size effect causes to decrease the critical hydrostatic pressure and associated end-shortening of microsized shells, while the strain gradient size dependency leads to increase them. In addition, it is found that the influence of the internal strain gradient length scale parameter on the nonlinear instability characteristics of hydrostatic pressurized FGM microsized shells is a bit more than that of the nonlocal one.

1 Introduction

The importance of size dependency phenomenon observed at micron and submicron scales becomes considerable through continuing reduction in the characteristic size of new systems and devices. This point has been experimentally indicated in several experimental studies. Recently, Anwar et al. [1] demonstrated the role of curcumin nanoparticles combined with Tween 80 as permeation enhancer. Blivi et al. [2] anticipated in a quantify way the influence of nano-size effect on the elastic and thermal characteristics of nano-reinforced polymers. Afrand [3] predicted the influence of hybrid nano-additives and functionalized carbon nanotubes on the thermal conductivity of ethylene glycol.

On the other hand, the functionally graded composite materials have been extensively utilized in different structures, the mechanical responses of which have been investigated by various studies in recent years [4,5,6,7,8,9,10].

In addition, this fact cannot be ignored that investigation of size-dependent mechanical responses of microstructures could provide essential information for desirable design procedures for microscaled devices and systems. As a result, some non-classical continuum theories have been developed which are so faster than experimental methods in analysis of size dependency in mechanical behavior of structures at microscale.

One of the indispensable size effects is a nonhomogeneous manner of stress and strain states of microstructures and nanostructures. Lots of studies have been carried out in which these non-classical continuum theories have been put to use for analysis of mechanical behavior of different small-scaled structures [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. More recently, Radić and Jeremić [30] studied the thermal buckling behavior of double-layered graphene sheets using nonlocal continuum elasticity within the frame work of a new first-order shear deformation theory. Wang et al. [31] obtained the boundary conditions related to a microplate modeled by strain gradient elasticity theory. Li [32] studied the thermo-electro-mechanical coupling transverse vibrations of axially moving piezoelectric nanobeams based on the nonlocal elasticity theory for using in self-powered components of nanorobot. Sahmani and Aghdam [33,34,35] predicted the size-dependent nonlinear instability response of hybrid functionally graded exponential shear deformable nanoshells based on the nonlocal continuum elasticity. Ruocco et al. [36] introduced Hencky bar net model in conjunction with the finite difference method for buckling and vibration analysis of nonlocal nanobeams made of axially functionally graded material (FGM). Sahmani and Aghdam [37] analyzed the nonlinear buckling behavior of piezoelectric cylindrical nanoshells on the basis of the nonlocal theory of elasticity. Dastjerdi and Tadi Beni [38] investigated the nonlinear bending behavior of microsectors with variable thickness based upon the nonlocal higher order shear deformation plate theory. Aria and Friswell [39] developed a nonlocal finite element model for buckling and vibration characteristics of FGM nanobeams. Li et al. [40] explored the nonlocal frequency response of nanomechanical mass sensor within the framework of the multi-directional vibrations of a buckled nanoribbon.

Generally, in the previous investigations, it has been observed that the size effect in type of stress nonlocality has a softening influence, while the strain gradient size dependency leads to a stiffening effect. Accordingly, Lim et al. [41] proposed a new size-dependent elasticity theory namely as nonlocal strain gradient theory which includes the both softening and stiffening influences to describe the size dependency in a more accurate way. Subsequently, a few studies have been performed on the basis of nonlocal strain gradient elasticity theory. Sahmani and Aghdam [42,43,44] analyzed the nonlinear mechanical behaviors of lipid supramolecular protein microtubules on the basis of the nonlocal strain gradient elasticity theory. Radic [45] studied the buckling behavior of porous double-layered FGM nanoplates embedded in the Pasternak elastic foundation based upon the nonlocal strain gradient theory. Sahmani and Safaei [46, 47] explored the nonlinear free and forced vibrations of bi-dimensional FGM microbeams under harmonic excitation on the basis of the nonlocal strain gradient elasticity. Jalali and Thai [48] established a nonlocal strain gradient quasi-3D sinusoidal shear deformation plate theory for dynamic instability of viscoelastic FGM nanoplate under biaxially oscillating loading and longitudinal magnetic field. Sahmani et al. [49, 50] and Fattahi et al. [51] employed the nonlocal strain gradient elasticity theory to anticipate the nonlinear mechanical characteristics of different microstructures. Mohammadian et al. [52] investigated the size-dependent lateral vibrations of hetero-junction carbon nanotubes on the basis of the nonlocal strain gradient theory of elasticity. Shen et al. [53] analyzed the size-dependent dynamical behavior of a microtubule under axial, thermal and variable transverse loads simultaneously on the basis of the nonlocal strain gradient theory of elasticity.

The prime objective of the current study is to anticipate the small-scale effects on the nonlinear instability characteristics of hydrostatic pressurized FGM microsized shells via nonlocal strain gradient shell model. For this purpose, the nonlocal strain gradient elasticity theory is implemented into a refined exponential shear deformation shell theory to take simultaneously the both nonlocality and strain gradient micro-size dependency into account. Afterwards, using a two-stepped perturbation technique in conjunction with boundary layer theory of shell buckling, explicit expressions for nonlocal strain gradient load–deflection and load-shortening stability paths of FGM microsized shells are achieved.

2 Nonlocal strain gradient FGM shell model

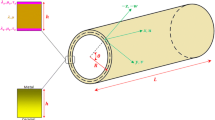
A schematic representation of an FGM microsized shell with length $L$, radius of mid-plane $R$, thickness $h$ and the attached coordinate system is displayed in Fig. 1. As it can be seen, the outer ($z = - h/2$) and inner ($z = h/2)$ free surfaces of the nanoshell are metal rich and ceramic rich, respectively. According to the Mori–Tanaka homogenization scheme, the material properties including the bulk modulus and shear modulus vary through shell thickness as below:

Fig. 1

Schematic representation of an FGM microshell with attached coordinate system

$$\frac{{\lambda_{e} - \lambda_{m} }}{{\lambda_{c} - \lambda_{m} }} = \frac{{V_{c} }}{{1 + V_{m} \left( {\lambda_{c} - \lambda_{m} } \right)/\left( {\lambda_{m} + 4\mu_{m} /3} \right)}}$$

(1a)

$$\frac{{\mu_{e} - \mu_{m} }}{{\mu_{c} - \mu_{m} }} = \frac{{V_{c} }}{{1 + V_{m} \left( {\mu_{c} - \mu_{m} } \right)/\left( {\mu_{m} + \mu_{m} \left( {9\lambda_{m} + 8\mu_{m} } \right)/6\left( {\lambda_{m} + 2\mu_{m} } \right)} \right)}},$$

(1b)

where $\lambda ,\mu , V$ in order represent the bulk modulus, shear modulus and volume fraction. In addition, the subscripts $e, m, c$ denote, respectively, the effective, metal, and ceramic. In addition, one will have

$$V_{c} + V_{m} = 1.$$

(2)

The volume fraction corresponding to the ceramic phase can be expressed as

$$V_{c} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{k} ,$$

(3)

in which $k$. stands for the material property gradient index. As a consequence, the Young’s modulus and Poisson’s ratio of an FGM microshell can be written, respectively, as

$$E\left( z \right) = \frac{{9\lambda_{e} \mu_{e} }}{{3\lambda_{e} + \mu_{e} }}$$

(4)

$$\nu \left( z \right) = \frac{{3\lambda_{e} - 2\mu_{e} }}{{6\lambda_{e} + 2\mu_{e} }}.$$

(5)

On the basis of a refined shell theory incorporating an exponential distribution of the shear deformation, the components of displacement field along different coordinate directions can be given as

$$u_{x} \left( {x,y,z} \right) = u\left( {x,y} \right) - z\frac{{\partial w\left( {x,y} \right)}}{\partial x} + z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \psi_{x} \left( {x,y} \right)$$

(6a)

$$u_{y} \left( {x,y,z} \right) = v\left( {x,y} \right) - z\frac{{\partial w\left( {x,y} \right)}}{\partial y} + z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \psi_{y} \left( {x,y} \right)$$

(6b)

$$u_{z} \left( {x,y,z} \right) = w\left( {x,y} \right) ,$$

(6c)

where $u$, $v$ and $w$ in order denote the mid-plane displacements along $x, y$ and $z$ axis. Moreover, $\psi_{x}$ and $\psi_{y}$ are the rotations of the mid-plane normal about the $y$- and solutions of the problem in a more general$x$-axis, respectively.

According to the von Kármán-Donnell-type kinematics nonlinearity, the strain components of nanoshell in terms of displacement field can be presented as

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} & = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} } \\ {\kappa_{yy}^{\left( 1 \right)} } \\ {\kappa_{xy}^{\left( 1 \right)} } \\ \end{array} } \right\} + ze^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} } \\ {\kappa_{yy}^{\left( 2 \right)} } \\ {\kappa_{xy}^{\left( 2 \right)} } \\ \end{array} } \right\} \\ & = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \\ {\frac{\partial v}{\partial y} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} } \\ {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \\ \end{array} } \right\} - z\left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial y^{2} }}} \\ {2\frac{{\partial^{2} w}}{\partial x\partial y}} \\ \end{array} } \right\} + z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \left\{ {\begin{array}{*{20}c} {\frac{{\partial \psi_{x} }}{\partial x}} \\ {\frac{{\partial \psi_{y} }}{\partial y}} \\ {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \\ \end{array} } \right\} \\ \end{aligned}$$

(7)

$$\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right){\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} \left\{ {\begin{array}{*{20}c} {\psi_{x} } \\ {\psi_{y} } \\ \end{array} } \right\},$$

in which $\varepsilon_{ij}^{0}$, $\kappa_{ij}^{\left( 1 \right)}$, $\kappa_{ij}^{\left( 2 \right)}$ ($i,j = x,y$) represent, respectively, the mid-plane strain components, the first-order curvature components, and the higher order curvature components.

As it was mentioned before, it has been observed that small-scale effects may cause a softening or stiffening influence. Motivated by this fact, Lim et al. [41] proposed a new unconventional continuum theory namely as nonlocal strain gradient elasticity theory which contains the both nonlocal and strain gradient size effects simultaneously. As a result, the total nonlocal strain gradient stress tensor $\varLambda$ can be expressed as below [41]:

$$\varLambda_{ij} = \sigma_{ij} - \nabla \sigma_{ij}^{*} ;\quad i,j = x,y,$$

(8)

where $\sigma$ and $\sigma^{*}$ in order denote the stress and higher order stress tensors which can be expressed as

$$\sigma_{ij} = \mathop \int \limits_{\varOmega } \left\{ {\varrho_{1} \left( {\left| {{\mathcal{X}}^{{\prime }} - {\mathcal{X}}} \right|} \right)C_{ijkl} \varepsilon_{kl} \left( {{\mathcal{X}}^{{\prime }} } \right)} \right\}{\text{d}}\varOmega$$

(9a)

$$\sigma_{ij}^{*} = l^{2} \mathop \int \limits_{\varOmega } \left\{ {\varrho_{2} \left( {\left| {{\mathcal{X}}^{{\prime }} - {\mathcal{X}}} \right|} \right)C_{ijkl} \nabla \varepsilon_{kl} \left( {{\mathcal{X}}^{{\prime }} } \right)} \right\}{\text{d}}\varOmega ,$$

(9b)

in which $C$ is the stiffness matrix, $\varrho_{1}$ and $\varrho_{2}$ are, respectively, the nonlocal kernel functions, ${\mathcal{X}}$ and ${\mathcal{X}}^{{\prime }}$ in order represent a point and any point else in the body, and $l$ stands for the internal length scale parameter. In addition, $\nabla$ is the gradient symbol. Following the method of Eringen, the constitutive relationship corresponding to the total nonlocal strain gradient stress tensor of a two dimensional material can be obtained as

$$\left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\varLambda_{ij} = C_{ijkl} \varepsilon_{kl} - l^{2} C_{ijkl} \nabla^{2} \varepsilon_{kl} ,$$

(10)

where $e_{0} \theta$ represents the nonlocal parameter in such a way that $\theta$ is an internal characteristic constant and $e_{0}$ is a constant related to the selected material. In addition, $\nabla^{2}$ denotes the Laplacian operator. As a result, the nonlocal strain gradient constitutive relations for an FGM microshell can be rewritten as

$$\left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left( {1 - l^{2} \nabla^{2} } \right)\left[ {\begin{array}{*{20}c} {Q_{11} \left( z \right)} & {Q_{12} \left( z \right)} & 0 & 0 & 0 \\ {Q_{12} \left( z \right)} & {Q_{22} \left( z \right)} & 0 & 0 & 0 \\ 0 & 0 & {Q_{44} \left( z \right)} & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} \left( z \right)} & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} \left( z \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ \end{array} } \right\},$$

(11)

in which

$$Q_{11} \left( z \right) = Q_{22} \left( z \right) = \frac{E\left( z \right)}{{1 - \nu \left( z \right)^{2} }},\quad Q_{12} \left( z \right) = \frac{\nu \left( z \right)E\left( z \right)}{{1 - \nu \left( z \right)^{2} }},\quad Q_{44} \left( z \right) = Q_{55} \left( z \right) = Q_{66} \left( z \right) = \frac{E\left( z \right)}{{2\left( {1 + \nu \left( z \right)} \right)}}.$$

The work $\varPi_{P}$ done by the external hydrostatic pressure ${\fancyscript{q}}$ can be expressed as

$$\varPi_{P} = \mathop \int \limits_{S} {\fancyscript{q}}wdS.$$

(12)

In addition, in accordance with the nonlocal strain gradient exponential shear deformation shell model, the total strain energy of an FGM microshell can be given as

$$\begin{aligned} \varPi_{s} & = \frac{1}{2}\mathop \int \limits_{S}^{ } \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2} }} \left\{ {\sigma_{ij} \varepsilon_{ij} + \sigma_{ij}^{*} \nabla \varepsilon_{ij} } \right\}{\text{d}}z{\text{d}}S \\ & = \frac{1}{2}\int\limits_{s} {\left\{ {N_{xx} \varepsilon_{xx}^{0} + N_{yy} \varepsilon_{yy}^{0} + N_{xy} \gamma_{xy}^{0} + M_{xx} \kappa_{xx}^{\left( 1 \right)} + M_{yy} \kappa_{yy}^{\left( 1 \right)} + M_{xy} \kappa_{xy}^{\left( 1 \right)} + H_{xx} \kappa_{xx}^{\left( 2 \right)} + H_{yy} \kappa_{yy}^{\left( 2 \right)} + H_{xy} \kappa_{xy}^{\left( 2 \right)} + Q_{x} \gamma_{xz} + Q_{y} \gamma_{yz} } \right\}{\text{d}}S} , \\ \end{aligned}$$

(13)

where the stress resultants are in the following forms:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {N_{xx} - e_{0}^{2} \theta^{2} \nabla^{2} N_{xx} } \\ {N_{yy} - e_{0}^{2} \theta^{2} \nabla^{2} N_{yy} } \\ {N_{xy} - e_{0}^{2} \theta^{2} \nabla^{2} N_{xy} } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {A_{11}^{*} } & {A_{12}^{*} } & 0 \\ {A_{12}^{*} } & {A_{22}^{*} } & 0 \\ 0 & 0 & {A_{66}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} - l^{2} \nabla^{2} \varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} - l^{2} \nabla^{2} \varepsilon_{yy}^{0} } \\ {\gamma_{xy}^{0} - l^{2} \nabla^{2} \gamma_{xy}^{0} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {B_{11}^{*} } & {B_{12}^{*} } & 0 \\ {B_{12}^{*} } & {B_{22}^{*} } & 0 \\ 0 & 0 & {B_{33}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{xx}^{\left( 1 \right)} } \\ {\kappa_{yy}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{yy}^{\left( 1 \right)} } \\ {\kappa_{xy}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{xy}^{\left( 1 \right)} } \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {B_{11}^{**} } & {B_{12}^{**} } & 0 \\ {B_{12}^{**} } & {B_{22}^{**} } & 0 \\ 0 & 0 & {B_{33}^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{xx}^{\left( 2 \right)} } \\ {\kappa_{yy}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{yy}^{\left( 2 \right)} } \\ {\kappa_{xy}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{xy}^{\left( 2 \right)} } \\ \end{array} } \right\} \\ \end{aligned}$$

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {M_{xx} - e_{0}^{2} \theta^{2} \nabla^{2} M_{xx} } \\ {M_{yy} - e_{0}^{2} \theta^{2} \nabla^{2} M_{xx} } \\ {M_{xy} - e_{0}^{2} \theta^{2} \nabla^{2} M_{xx} } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {B_{11}^{*} } & {B_{12}^{*} } & 0 \\ {B_{12}^{*} } & {B_{22}^{*} } & 0 \\ 0 & 0 & {B_{33}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} - l^{2} \nabla^{2} \varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} - l^{2} \nabla^{2} \varepsilon_{yy}^{0} } \\ {\gamma_{xy}^{0} - l^{2} \nabla^{2} \gamma_{xy}^{0} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {D_{11}^{*} } & {D_{12}^{*} } & 0 \\ {D_{12}^{*} } & {D_{22}^{*} } & 0 \\ 0 & 0 & {D_{33}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{xx}^{\left( 1 \right)} } \\ {\kappa_{yy}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{yy}^{\left( 1 \right)} } \\ {\kappa_{xy}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{xy}^{\left( 1 \right)} } \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {D_{11}^{**} } & {D_{12}^{**} } & 0 \\ {D_{12}^{**} } & {D_{22}^{**} } & 0 \\ 0 & 0 & {D_{33}^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{xx}^{\left( 2 \right)} } \\ {\kappa_{yy}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{yy}^{\left( 2 \right)} } \\ {\kappa_{xy}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{xy}^{\left( 2 \right)} } \\ \end{array} } \right\} \\ \end{aligned}$$

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {H_{xx} - e_{0}^{2} \theta^{2} \nabla^{2} H_{xx} } \\ {H_{yy} - e_{0}^{2} \theta^{2} \nabla^{2} H_{xx} } \\ {H_{xy} - e_{0}^{2} \theta^{2} \nabla^{2} H_{xx} } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {B_{11}^{**} } & {B_{12}^{**} } & 0 \\ {B_{12}^{**} } & {B_{22}^{**} } & 0 \\ 0 & 0 & {B_{33}^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} - l^{2} \nabla^{2} \varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} - l^{2} \nabla^{2} \varepsilon_{yy}^{0} } \\ {\gamma_{xy}^{0} - l^{2} \nabla^{2} \gamma_{xy}^{0} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {D_{11}^{**} } & {D_{12}^{**} } & 0 \\ {D_{12}^{**} } & {D_{22}^{**} } & 0 \\ 0 & 0 & {D_{33}^{**} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{xx}^{\left( 1 \right)} } \\ {\kappa_{yy}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{yy}^{\left( 1 \right)} } \\ {\kappa_{xy}^{\left( 1 \right)} - l^{2} \nabla^{2} \kappa_{xy}^{\left( 1 \right)} } \\ \end{array} } \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {G_{11}^{*} } & {G_{12}^{*} } & 0 \\ {G_{12}^{*} } & {G_{22}^{*} } & 0 \\ 0 & 0 & {G_{33}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{xx}^{\left( 2 \right)} } \\ {\kappa_{yy}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{yy}^{\left( 2 \right)} } \\ {\kappa_{xy}^{\left( 2 \right)} - l^{2} \nabla^{2} \kappa_{xy}^{\left( 2 \right)} } \\ \end{array} } \right\} \\ \end{aligned}$$

(14)

$$\left\{ {\begin{array}{*{20}c} {Q_{x} - e_{0}^{2} \theta^{2} \nabla^{2} Q_{x} } \\ {Q_{y} - e_{0}^{2} \theta^{2} \nabla^{2} Q_{y} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{44}^{*} } & 0 \\ 0 & {A_{55}^{*} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\psi_{x} - l^{2} \nabla^{2} \psi_{x} } \\ {\psi_{y} - l^{2} \nabla^{2} \psi_{y} } \\ \end{array} } \right\},$$

in which

$$\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} } \\ {\varLambda_{yy} } \\ {\varLambda_{xy} } \\ \end{array} } \right\}{\text{d}}z,\quad \left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} } \\ {\varLambda_{yy} } \\ {\varLambda_{xy} } \\ \end{array} } \right\}z{\text{d}}z$$

$$\left\{ {\begin{array}{*{20}c} {H_{xx} } \\ {H_{yy} } \\ {H_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xx} } \\ {\varLambda_{yy} } \\ {\varLambda_{xy} } \\ \end{array} } \right\}z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} {\text{d}}z,\quad \left\{ {\begin{array}{*{20}c} {Q_{x} } \\ {Q_{y} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\varLambda_{xz} } \\ {\varLambda_{yz} } \\ \end{array} } \right\}\left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right){\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} {\text{d}}z$$

(15)

and

$$\left\{ {\begin{array}{*{20}c} {A_{11}^{*} ,B_{11}^{*} ,D_{11}^{*} } \\ {B_{11}^{**} ,D_{11}^{**} ,G_{11}^{*} } \\ \end{array} } \right\} = \mathop \int \limits_{ - h/2}^{h/2} \left[ {Q_{11} \left( z \right)} \right]\left\{ {\begin{array}{*{20}c} {1,z,z^{2} } \\ {z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{4z^{2} }}{{h^{2} }}}} } \\ \end{array} } \right\}{\text{d}}z$$

$$\left\{ {\begin{array}{*{20}c} {A_{22}^{*} ,B_{22}^{*} ,D_{22}^{*} } \\ {B_{22}^{**} ,D_{22}^{**} ,G_{22}^{*} } \\ \end{array} } \right\} = \mathop \int \limits_{ - h/2}^{h/2} \left[ {Q_{22} \left( z \right)} \right]\left\{ {\begin{array}{*{20}c} {1,z,z^{2} } \\ {z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{4z^{2} }}{{h^{2} }}}} } \\ \end{array} } \right\}{\text{d}}z$$

$$\left\{ {\begin{array}{*{20}c} {A_{12}^{*} ,B_{12}^{*} ,D_{12}^{*} } \\ {B_{12}^{**} ,D_{12}^{**} ,G_{12}^{*} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {A_{21}^{*} ,B_{21}^{*} ,D_{21}^{*} } \\ {B_{21}^{**} ,D_{21}^{**} ,G_{21}^{*} } \\ \end{array} } \right\} = \mathop \int \limits_{ - h/2}^{h/2} \left[ {Q_{12} \left( z \right)} \right]\left\{ {\begin{array}{*{20}c} {1,z,z^{2} } \\ {z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{4z^{2} }}{{h^{2} }}}} } \\ \end{array} } \right\}{\text{d}}z$$

(16)

$$\left\{ {\begin{array}{*{20}c} {A_{66}^{*} ,B_{66}^{*} ,D_{66}^{*} } \\ {B_{66}^{**} ,D_{66}^{**} ,G_{66}^{*} } \\ \end{array} } \right\} = \mathop \int \limits_{ - h/2}^{h/2} \left[ {Q_{66} \left( z \right)} \right]\left\{ {\begin{array}{*{20}c} {1,z,z^{2} } \\ {z{\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} ,z^{2} {\text{e}}^{{ - \frac{{4z^{2} }}{{h^{2} }}}} } \\ \end{array} } \right\}{\text{d}}z$$

$$\left\{ {\begin{array}{*{20}c} {A_{44}^{*} } \\ {A_{55}^{*} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{ - h/2}^{h/2} \left[ {Q_{44} \left( z \right)} \right]\left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right){\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} {\text{d}}z} \\ {\mathop \int \limits_{ - h/2}^{h/2} \left[ {Q_{55} \left( z \right)} \right]\left( {1 - \frac{{4z^{2} }}{{h^{2} }}} \right){\text{e}}^{{ - \frac{{2z^{2} }}{{h^{2} }}}} {\text{d}}z} \\ \end{array} } \right\}.$$

By applying the virtual work’s principle to the total strain energy of the hydrostatic pressurized FGM exponential shear deformable microshell, the non-classical governing differential equations are derived as

$$\frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = 0$$

(17a)

$$\frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{yy} }}{\partial y} = 0$$

(17b)

$$\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} + \frac{{N_{yy} }}{R} + N_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }} + {\fancyscript{q}} = 0$$

(17c)

$$\frac{{\partial H_{xx} }}{\partial x} + \frac{{\partial H_{xy} }}{\partial y} - Q_{x} = 0$$

(17d)

$$\frac{{\partial H_{xy} }}{\partial x} + \frac{{\partial H_{yy} }}{\partial y} - Q_{y} = 0.$$

(17e)

With the aim of satisfaction of the first two differential equations at hand, the Airy stress function $f\left( {x,y} \right)$ is introduced as below:

$$N_{xx} = \frac{{\partial^{2} f\left( {x,y} \right)}}{{\partial y^{2} }},\quad N_{yy} = \frac{{\partial^{2} f\left( {x,y} \right)}}{{\partial x^{2} }},\quad N_{xy} = - \frac{{\partial^{2} f\left( {x,y} \right)}}{\partial x\partial y}.$$

(18)

In addition, for a perfect shell-type structure, the compatibility equation relevant to the mid-plane strain components can be read as

$$\frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial y^{2} }} + \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial x^{2} }} - \frac{{\partial^{2} \gamma_{xy}^{0} }}{\partial x\partial y} = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}.$$

(19)

Thereby, through inserting Eq. (18) in the inverse of Eq. (14) and then using Eqs. (17) and (19), the nonlocal strain gradient governing equations can be presented as functions of the displacement field as follows:

$$\begin{aligned} \varphi_{1} \frac{{\partial^{4} f}}{{\partial x^{4} }} & + \left( {\varphi_{7} - 2\varphi_{2} } \right)\frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + \varphi_{1} \frac{{\partial^{4} f}}{{\partial y^{4} }} + \varphi_{4} \frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\left( {\varphi_{3} - \varphi_{8} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \varphi_{4} \frac{{\partial^{4} w}}{{\partial y^{4} }} - \varphi_{6} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} \\ & - \left( {\varphi_{5} - \varphi_{9} } \right)\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial y^{2} }} - \varphi_{6} \frac{{\partial^{3} \psi_{y} }}{{\partial y^{3} }} - \left( {\varphi_{5} - \varphi_{9} } \right)\frac{{\partial^{3} \psi_{y} }}{{\partial x^{2} \partial y}} + \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }} = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} \\ \end{aligned}$$

(20a)

$$\begin{aligned} \left( {1 - l^{2} \nabla^{2} } \right) & \left( {\varphi_{10} \frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\left( {\varphi_{11} + 2\varphi_{12} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \varphi_{10} \frac{{\partial^{4} w}}{{\partial y^{4} }} + \varphi_{13} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} + \left( {\varphi_{14} + 2\varphi_{15} } \right)\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial y^{2} }}} \right. \\ & \quad \left. { + \varphi_{13} \frac{{\partial^{3} \psi_{y} }}{{\partial y^{3} }} + \left( {\varphi_{14} + 2\varphi_{15} } \right)\frac{{\partial^{3} \psi_{y} }}{{\partial x^{2} \partial y}}} \right) - \frac{1}{R}\frac{{\partial^{2} f}}{{\partial x^{2} }} = \left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} f}}{{\partial y^{2} }} - 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} f}}{\partial x\partial y} + \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} f}}{{\partial x^{2} }} + {\fancyscript{q}}} \right) \\ \end{aligned}$$

(20b)

$$\begin{aligned} \varphi_{16} \frac{{\partial^{3} f}}{{\partial x^{3} }} & + \varphi_{17} \frac{{\partial^{3} f}}{{\partial x\partial y^{2} }} + \varphi_{18} \frac{{\partial^{3} w}}{{\partial x^{3} }} + \left( {\varphi_{19} + 2\varphi_{20} } \right)\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }} + \varphi_{21} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + \varphi_{22} \frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} \\ & + \left( {\varphi_{23} + \varphi_{22} } \right)\frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} - A_{44}^{*} \psi_{x} = 0 \\ \end{aligned}$$

(20c)

$$\begin{aligned} \varphi_{16} \frac{{\partial^{3} f}}{{\partial y^{3} }} & + \varphi_{17} \frac{{\partial^{3} f}}{{\partial x^{2} \partial y}} + \varphi_{18} \frac{{\partial^{3} w}}{{\partial y^{3} }} + \left( {\varphi_{19} + 2\varphi_{20} } \right)\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \varphi_{21} \frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }} + \varphi_{22} \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} \\ & + \left( {\varphi_{23} + \varphi_{22} } \right)\frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} - A_{44}^{*} \psi_{y} = 0, \\ \end{aligned}$$

(20d)

where the parameters $\varphi_{i} \left( {i = 1, \ldots ,23} \right)$ are introduced in Appendix A.

In addition, the edge supports at the left and right ends of the FGM microshells are assumed to be clamped. As a result, one will have $w = 0,\quad \frac{\partial w}{\partial x} = 0\;{\text{at}}\;x = 0, L.$

On the other hand, the equilibrium of in the x-axis direction can be expressed as

$$\mathop \int \limits_{0}^{2\pi R} N_{xx} {\text{d}}y + \pi R^{2} {\fancyscript{q}} = 0.$$

(21)

The periodicity condition relevant to a closed shell-type structure reads

$$\mathop \int \limits_{0}^{2\pi R} \frac{\partial v}{\partial y}{\text{d}}y = 0$$

(22)

which can be rewritten as

$$\mathop \int \limits_{0}^{2\pi R} \left( {\varphi_{1} \frac{{\partial^{2} f}}{{\partial x^{2} }} - \varphi_{2} \frac{{\partial^{2} f}}{{\partial y^{2} }} + \varphi_{4} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \varphi_{3} \frac{{\partial^{2} w}}{{\partial y^{2} }} - \varphi_{6} \frac{{\partial \psi_{x} }}{\partial x} - \varphi_{5} \frac{{\partial \psi_{y} }}{\partial y} + \frac{w}{R} - \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} } \right){\text{d}}y = 0.$$

(23)

Furthermore, the unit end-shortening related to the movable boundary conditions at the left and right ends of an FGM exponential shear deformable microshell can be given as

$$\begin{aligned} \frac{{\Delta_{x} }}{L} & = - \frac{1}{2\pi RL}\mathop \int \limits_{0}^{2\pi R} \mathop \int \limits_{0}^{L} \frac{\partial u}{\partial x}{\text{d}}x{\text{d}}y \\ & = - \frac{1}{2\pi RL}\mathop \int \limits_{0}^{2\pi R} \mathop \int \limits_{0}^{L} \left( {\varphi_{1} \frac{{\partial^{2} f}}{{\partial y^{2} }} - \varphi_{2} \frac{{\partial^{2} f}}{{\partial x^{2} }} + \varphi_{3} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \varphi_{4} \frac{{\partial^{2} w}}{{\partial y^{2} }} - \varphi_{5} \frac{{\partial \psi_{x} }}{\partial x} - \varphi_{6} \frac{{\partial \psi_{y} }}{\partial y} - \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right){\text{d}}x{\text{d}}y, \\ \end{aligned}$$

(24)

3 Solving process

3.1 Boundary layer theory of nonlocal strain gradient shell buckling

First, the following dimensionless parameters are put to use to obtain the asymptotic solutions of the problem in a more general framework:

$$X = \frac{\pi x}{L},\quad Y = \frac{y}{R},\quad \beta = \frac{L}{\pi R},\quad \eta = \frac{L}{\pi h},\quad \epsilon = \frac{{\pi^{2} Rh}}{{L^{2} }}$$

$$\left\{ {a_{11}^{*} ,a_{12}^{*} ,a_{33}^{*} ,a_{44}^{*} } \right\} = \left\{ {\frac{{A_{11}^{*} }}{{A_{00} }},\frac{{A_{12}^{*} }}{{A_{00} }},\frac{{A_{44}^{*} }}{{A_{00} }},\frac{{A_{55}^{*} }}{{A_{00} }},\frac{{A_{66}^{*} }}{{A_{00} }}} \right\}\left\{ {g_{11}^{*} ,g_{12}^{*} ,g_{33}^{*} } \right\} = \left[ {\frac{{G_{11}^{*} }}{{A_{00} h^{2} }},\frac{{G_{12}^{*} }}{{A_{00} h^{2} }},\frac{{G_{66}^{*} }}{{A_{00} h^{2} }}} \right]$$

$$\left\{ {\begin{array}{*{20}c} {b_{11}^{*} ,b_{12}^{*} ,b_{66}^{*} ,b_{11}^{**} ,b_{12}^{**} ,b_{66}^{**} } \\ {d_{11}^{*} ,d_{12}^{*} ,d_{66}^{*} ,d_{11}^{**} ,d_{12}^{**} ,d_{66}^{**} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{B_{11}^{*} }}{{A_{00} h}},\frac{{B_{12}^{*} }}{{A_{00} h}},\frac{{B_{66}^{*} }}{{A_{00} h}},\frac{{B_{11}^{**} }}{{A_{00} h}},\frac{{B_{12}^{**} }}{{A_{00} h}},\frac{{B_{66}^{**} }}{{A_{00} h}}} \\ {\frac{{D_{11}^{*} }}{{A_{00} h^{2} }},\frac{{D_{12}^{*} }}{{A_{00} h^{2} }},\frac{{D_{66}^{*} }}{{A_{00} h^{2} }},\frac{{D_{11}^{**} }}{{A_{00} h^{2} }},\frac{{D_{12}^{**} }}{{A_{00} h^{2} }},\frac{{D_{66}^{**} }}{{A_{00} h^{2} }}} \\ \end{array} } \right\}$$

(25)

$$W = \frac{\epsilon w}{h},\quad F = \frac{{\epsilon^{2} f}}{{A_{00} h^{2} }},\quad \left\{ {\varPsi_{X} , \varPsi_{Y} } \right\} = \frac{{\epsilon^{2} L}}{\pi h}\left\{ {\psi_{x} , \psi_{y} } \right\}$$

$${\mathcal{P}}_{q} = \frac{{3^{3/4} qLR^{3/2} }}{{4\pi A_{00} h^{3/2} }},\quad \delta_{q} = \frac{{3^{3/4} q_{x} \sqrt R }}{{4\pi h^{3/2} }},\quad {\mathcal{G}}_{1} = \frac{{e_{0} \theta }}{L},\quad {\mathcal{G}}_{2} = \frac{l}{L},$$

in which $A_{00} = \left( {\lambda_{m} + 2\mu_{m} } \right)h$. As a consequence, the nonlinear nonlocal strain gradient governing differential equations can be deduced in boundary layer-type forms as below:

$$\begin{aligned} \vartheta_{1} \frac{{\partial^{4} F}}{{\partial X^{4} }} & + \left( {\vartheta_{7} - 2\vartheta_{2} } \right)\beta^{2} \frac{{\partial^{4} F}}{{\partial X^{2} \partial Y^{2} }} + \vartheta_{1} \beta^{4} \frac{{\partial^{4} F}}{{\partial Y^{4} }} + \epsilon \left( {\vartheta_{4} \frac{{\partial^{4} W}}{{\partial X^{4} }} + 2\left( {\vartheta_{3} - \vartheta_{8} } \right)\beta^{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial Y^{2} }} + \vartheta_{4} \beta^{4} \frac{{\partial^{4} W}}{{\partial Y^{4} }}} \right) \\ & - \vartheta_{6} \frac{{\partial^{3} \varPsi_{X} }}{{\partial X^{3} }} - \left( {\vartheta_{5} - \vartheta_{9} } \right)\beta^{2} \frac{{\partial^{3} \varPsi_{X} }}{{\partial X\partial Y^{2} }} - \vartheta_{6} \beta^{3} \frac{{\partial^{3} \varPsi_{Y} }}{{\partial Y^{3} }} - \left( {\vartheta_{5} - \vartheta_{9} } \right)\beta \frac{{\partial^{3} \varPsi_{Y} }}{{\partial X^{2} \partial Y}} + \frac{{\partial^{2} W}}{{\partial X^{2} }} = \beta^{2} \left( {\frac{{\partial^{2} W}}{\partial X\partial Y}} \right)^{2} - \beta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }} \\ \end{aligned}$$

(26a)

$$\begin{aligned} \left( {1 - \pi^{2} {\mathcal{G}}_{2}^{2} \nabla^{2} } \right) & \left( {\epsilon^{2} \left( {\vartheta_{10} \frac{{\partial^{4} W}}{{\partial X^{4} }} + 2\left( {\vartheta_{11} + 2\vartheta_{12} } \right)\beta^{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial Y^{2} }} + \vartheta_{10} \beta^{4} \frac{{\partial^{4} W}}{{\partial Y^{4} }}} \right)} \right. \\ & \quad + \epsilon \left( {\vartheta_{13} \frac{{\partial^{3} \varPsi_{X} }}{{\partial X^{3} }} + \left( {\vartheta_{14} + 2\vartheta_{15} } \right)\beta \frac{{\partial^{3} \varPsi_{X} }}{{\partial X^{2} \partial Y}}} \right)\left. { + \epsilon \left( {\vartheta_{13} \beta^{3} \frac{{\partial^{3} \varPsi_{Y} }}{{\partial Y^{3} }} + \left( {\vartheta_{14} + 2\vartheta_{15} } \right)\beta^{2} \frac{{\partial^{3} \varPsi_{Y} }}{{\partial X\partial Y^{2} }}} \right)} \right) \\ & \quad - \frac{{\partial^{2} F}}{{\partial X^{2} }} = \left( {1 - \pi^{2} {\mathcal{G}}_{1}^{2} \nabla^{2} } \right)\left( {\beta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} F}}{{\partial Y^{2} }} + 2\beta^{2} \frac{{\partial^{2} W}}{\partial X\partial Y}\frac{{\partial^{2} F}}{\partial X\partial Y} + \beta^{2} \frac{{\partial^{2} W}}{{\partial Y^{2} }}\frac{{\partial^{2} F}}{{\partial X^{2} }} + \epsilon^{3/2} \frac{4}{3}3^{1/4} {\mathcal{P}}_{q} } \right) \\ \end{aligned}$$

(26b)

$$\begin{aligned} \vartheta_{16} \frac{{\partial^{3} F}}{{\partial X^{3} }} & + \vartheta_{17} \beta^{2} \frac{{\partial^{3} F}}{{\partial X\partial Y^{2} }} + \epsilon \left( {\vartheta_{18} \frac{{\partial^{3} W}}{{\partial X^{3} }} + \left( {\vartheta_{19} + 2\vartheta_{20} } \right)\beta^{2} \frac{{\partial^{3} W}}{{\partial X\partial Y^{2} }}} \right) + \vartheta_{21} \frac{{\partial^{2} \varPsi_{X} }}{{\partial X^{2} }} + \vartheta_{22} \beta^{2} \frac{{\partial^{2} \varPsi_{X} }}{{\partial Y^{2} }} \\ & + \left( {\vartheta_{23} + \vartheta_{22} } \right)\beta \frac{{\partial^{2} \varPsi_{Y} }}{\partial X\partial Y} - a_{44}^{*} \eta^{2} \varPsi_{X} = 0 \\ \end{aligned}$$

(26c)

$$\begin{aligned} \vartheta_{16} \beta^{3} \frac{{\partial^{3} F}}{{\partial Y^{3} }} & + \vartheta_{17} \beta \frac{{\partial^{3} F}}{{\partial X^{2} \partial Y}} + \epsilon \left( {\vartheta_{18} \beta^{3} \frac{{\partial^{3} W}}{{\partial Y^{3} }} + \left( {\vartheta_{19} + 2\vartheta_{20} } \right)\beta \frac{{\partial^{3} W}}{{\partial X^{2} \partial Y}}} \right) + \vartheta_{21} \beta^{2} \frac{{\partial^{2} \varPsi_{Y} }}{{\partial Y^{2} }} + \vartheta_{22} \frac{{\partial^{2} \varPsi_{Y} }}{{\partial X^{2} }} \\ & + \left( {\vartheta_{23} + \vartheta_{22} } \right)\beta \frac{{\partial^{2} \varPsi_{X} }}{\partial X\partial Y} - a_{44}^{*} \eta^{2} \varPsi_{Y} = 0. \\ \end{aligned}$$

(26d)

The clamped boundary conditions at the left and right ends of microshells take the dimensionless form as: $W = 0, \frac{\partial W}{\partial X} = 0\;{\text{at}}\;X = 0, \pi .$

Moreover, the dimensionless load-equilibrium relationship along x-axis takes the following form:

$$\frac{1}{2\pi }\mathop \int \limits_{0}^{2\pi } \beta^{2} \frac{{\partial^{2} F}}{{\partial Y^{2} }}{\text{d}}Y + \frac{2}{3}3^{1/4} \epsilon^{3/2} {\mathcal{P}}_\fancyscript{q} = 0 .$$

(27)

In similar way, the periodicity condition and the unit end-shortening of an FGM exponential shear deformable microshell in dimensionless forms can be rewritten, respectively, as follows:

$$\mathop \int \limits_{0}^{2\pi } \left\{ {\vartheta_{1} \frac{{\partial^{2} F}}{{\partial X^{2} }} - \vartheta_{2} \beta^{2} \frac{{\partial^{2} F}}{{\partial Y^{2} }} + \epsilon \left( {\vartheta_{4} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \vartheta_{3} \beta^{2} \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right) - \vartheta_{6} \frac{{\partial \varPsi_{x} }}{\partial X} - \vartheta_{5} \beta \frac{{\partial \varPsi_{Y} }}{\partial Y} + W - \frac{{\beta^{2} }}{2}\left( {\frac{\partial W}{\partial Y}} \right)^{2} } \right\}{\text{d}}Y = 0$$

(28)

$$\delta_{q} = - \frac{{3^{3/4} }}{{8\pi^{2} \varepsilon^{3/2} }}\mathop \int \limits_{0}^{2\pi } \mathop \int \limits_{0}^{\pi } \left\{ { - \vartheta_{2} \frac{{\partial^{2} F}}{{\partial X^{2} }} + \vartheta_{1} \beta^{2} \frac{{\partial^{2} F}}{{\partial Y^{2} }} + \epsilon \left( {\vartheta_{3} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \vartheta_{4} \beta^{2} \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right) - \vartheta_{5} \frac{{\partial \varPsi_{x} }}{\partial X} - \vartheta_{6} \beta \frac{{\partial \varPsi_{y} }}{\partial Y} - \frac{1}{2}\left( {\frac{\partial W}{\partial X}} \right)^{2} } \right\}{\text{d}}X{\text{d}}Y.$$

(29)

3.2 Perturbation-based solution methodology

As it was explained, the small perturbation parameter $\epsilon$ has been utilized to construct the boundary layer-type nonlocal strain gradient governing equation (26). Now, a two-stepped perturbation technique [54,55,56,57,58] is employed, based on which the independent variables are summarized via the summations of the regular and boundary layer solutions as follows:

$$W = \bar{W}\left( {X,Y,\epsilon } \right) + \tilde{W}\left( {X,Y,\epsilon ,\xi } \right) + \hat{W}\left( {X,Y,\epsilon ,\varsigma } \right)$$

(30a)

$$F = \bar{F}\left( {X,Y,\epsilon } \right) + \tilde{F}\left( {X,Y,\epsilon ,\xi } \right) + \hat{F}\left( {X,Y,\epsilon ,\varsigma } \right)$$

(30b)

$$\varPsi_{X} = \bar{\varPsi }_{X} \left( {X,Y,\epsilon } \right) + \tilde{\varPsi }_{X} \left( {X,Y,\epsilon ,\xi } \right) + \hat{\varPsi }_{X} \left( {X,Y,\epsilon ,\varsigma } \right)$$

(30c)

$$\varPsi_{Y} = \bar{\varPsi }_{Y} \left( {X,Y,\epsilon } \right) + \tilde{\varPsi }_{Y} \left( {X,Y,\epsilon ,\xi } \right) + \hat{\varPsi }_{Y} \left( {X,Y,\epsilon ,\varsigma } \right),$$

(30d)

where the accent character “–” stands for the regular solution, and the accent characters ∼ and ^ represents the boundary layer solutions in order associated with the left ($X = 0$) and right ($X = \pi$) ends of an FGM microshell.

Thereby, each part of the solutions can be altered to the perturbation expansions as below:

$$\bar{W}\left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2} \bar{W}_{i/2} \left( {X,Y} \right) ,\quad \bar{F}\left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2} \bar{F}_{i/2} \left( {X,Y} \right)$$

$$\bar{\varPsi }_{x} \left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i/2} \bar{\varPsi }_{{x_{i/2} }} \left( {X,Y} \right),\quad \bar{\varPsi }_{y} \left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i/2} \bar{\varPsi }_{{y_{i/2} }} \left( {X,Y} \right)$$

$$\tilde{W}\left( {X,Y,\epsilon ,\xi } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 1} \tilde{W}_{i/2 + 1} \left( {X,Y,\xi } \right),\quad \tilde{F}\left( {X,Y,\epsilon ,\xi } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \tilde{F}_{i/2 + 2} \left( {X,Y,\xi } \right)$$

(31)

$$\tilde{\varPsi }_{x} \left( {X,Y,\epsilon ,\xi } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i + 3/2} \tilde{\varPsi }_{{x_{i + 3/2} }} \left( {X,Y,\xi } \right)\varvec{,}\quad \tilde{\varPsi }_{y} \left( {X,Y,\epsilon ,\xi } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \tilde{\varPsi }_{{y_{i/2 + 2} }} \left( {X,Y,\xi } \right)$$

$$\hat{W}\left( {X,Y,\epsilon ,\varsigma } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 1} \hat{W}_{i/2 + 1} \left( {X,Y,\varsigma } \right),\quad \hat{F}\left( {X,Y,\epsilon ,\varsigma } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \hat{F}_{i/2 + 2} \left( {X,Y,\varsigma } \right)$$

$$\hat{\varPsi }_{x} \left( {X,Y,\epsilon ,\varsigma } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i + 3/2} \hat{\varPsi }_{{x_{i + 3/2} }} \left( {X,Y,\varsigma } \right),\quad \hat{\varPsi }_{y} \left( {X,Y,\epsilon ,\varsigma } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \hat{\varPsi }_{{y_{i/2 + 2} }} \left( {X,Y,\varsigma } \right),$$

in which $\xi$ and $\varsigma$ denote the boundary layer variables as follows:

$$\xi = \frac{X}{{\epsilon^{1/2} }},\quad \varsigma = \frac{\pi - X}{{\epsilon^{1/2} }}.$$

(32)

Moreover, it is supposed that

$$\epsilon^{3/2} \frac{4}{3}3^{1/4} q = \mathop \sum \limits_{i = 0} \epsilon^{i} {\mathcal{Q}}_{i} .$$

(33)

Afterwards, to extract the sets of perturbation equations corresponding to the both regular and boundary layer solutions, Eqs. (30) and (31) are inserted in the nonlocal strain gradient governing equation (26) and then the expressions with similar order of $\epsilon$ are collected. A tolerance limit $< 0.001$ is considered to determine the maximum order of $\epsilon$ associated with the convergence of the solution methodology.

An initial buckling mode shape for the FGM exponential shear deformable microshell is assumed to continue the procedure as

$$\bar{W}_{2} \left( {X,Y} \right) = {\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{11}^{\left( 2 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right) .$$

(34)

Now, some mathematical calculations are carried out to obtain the asymptotic solutions corresponding to each independent variable of the problem which are presented in Appendix A. Subsequently, substitution of them in Eqs. (27) and (29) and then rearranging with respect to the second perturbation parameter (${\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon^{2}$) yields, explicit expressions for the nonlocal strain gradient load–deflection and load-shortening stability paths, respectively, as follows:

$${\mathcal{P}}_{q} = \mathop \sum \limits_{i = 0,2,4, \ldots } {\mathcal{P}}_{q}^{\left( i \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon^{2} } \right)^{i} = {\mathcal{P}}_{q}^{\left( 0 \right)} + {\mathcal{P}}_{q}^{\left( 2 \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon^{2} } \right)^{2} + \ldots$$

(35)

$$\delta_{q} = \mathop \sum \limits_{i = 0,2,4, \ldots } \delta_{q}^{\left( i \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon^{2} } \right)^{i} = \delta_{q}^{\left( 0 \right)} + \delta_{q}^{\left( 2 \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon^{2} } \right)^{2} + \ldots$$

(36)

The parameters given in the above equations are introduced in Appendix B. Thereafter, it is supposed that the dimensionless coordinates of the point relevant to the maximum deflection of the FGM microshell are $\left( {X,Y} \right) = \left( {\pi /2m,\pi /2n} \right)$. As a result, one will have

$${\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon^{2} = \epsilon \frac{{w_{m} }}{h} + {\mathcal{S}}_{2} + {\mathcal{S}}_{1} \left( {\epsilon \frac{{w_{m} }}{h} + {\mathcal{S}}_{2} } \right)^{2} ,$$

(37)

where $w_{m}$ represents the maximum deflection of FGM microshell and the symbols ${\mathcal{S}}_{1}$ and ${\mathcal{S}}_{2}$ are presented in Appendix B.

4 Numerical results and discussion

Based upon the developed nonlocal strain gradient FGM shell model, the nonlinear instability characteristics of exponential shear deformable FGM microshells under hydrostatic pressure are anticipated in this section. The material properties of ceramic phase (silicon) and metal phase (aluminum) of FGM microshells are tabulated in Table 1. Moreover, in all of the preceding results, the geometric parameters of nanoshells are selected in such a way that $R/h = 50$ and $L/R = 2$.

Table 1 Material properties of the ceramic and metal phases of an FGM microshell [59]

First, the validity of the present solving process is checked. To this end, the terms related to the nonlocal strain gradient elasticity are eliminated, the critical hydrostatic pressures of isotropic cylindrical shells at usual scale (macroscale) with simply supported end conditions are evaluated and compared with those reported by Kasagi and Sridharan [60] using finite element method, as tabulated in Table 2. A very good agreement is found between two types of the solution methodology which confirms the accuracy of the present solving process.

Table 2 Comparison of the nonlinear critical buckling pressures (psi) for isotropic cylindrical shells $\left( {E = 10^{7} \;{\text{psi}},\quad \nu = 0.33} \right)$

In Table 3, the dimensionless nonlocal strain gradient critical buckling pressures of an FGM microshell under hydrostatic pressure are given corresponding to different values of the small-scale parameters. The percentages presented in the parentheses are the differences between the size-dependent critical buckling pressures with the classical one. It is found that the nonlocality leads to decrease the buckling pressure, while the strain gradient size dependency causes to increases it. In addition, for higher values of the small-scale parameters, the significance of the strain gradient size effect becomes more than that of the nonlocal one.

Table 3 Dimensionless nonlocal strain gradient critical buckling pressures of an FGM microshell corresponding to different values of the small-scale parameters $\left( {h = 1\;{\text{nm}},\quad k = 1} \right)$

Figure 2 shows the nonlocal strain gradient load–deflection stability paths of hydrostatic pressurized FGM microshells corresponding to various values of nonlocal parameter and internal strain gradient length scale parameter. It can be observed that the nonlocality size effect causes to decrease the critical hydrostatic pressure, while the strain gradient size dependency leads to increase it. In addition, by moving to the deeper part of the postbuckling regime, the both types of small-scale effect reduce and the different stability curves tends to each other. In addition, it is seen that the significance of the strain gradient size effect on the nonlinear instability characteristics of hydrostatic pressurized FGM microshells is a bit higher than that of the nonlocality one.

Fig. 2

Dimensionless load–deflection stability paths of nonlocal strain gradient FGM microshells under hydrostatic pressure ($h = 1\;{\text{nm}},\quad k = 1$); a $l = 0\;{\text{nm}},$ b $e_{0} \theta = 0\;{\text{nm}}$

In Fig. 3, the nonlocal strain gradient load-shortening stability curves of hydrostatic pressurized FGM microshells within the both prebuckling and postbuckling domains are depicted. It is revealed that the nonlocality size effect as well as the strain gradient one has no influence on the slope of prebuckling part of the load-shortening response of FGM microshells. It can be seen that the aforementioned one leads to reduce the shortening of nanoshell at the critical buckling point, but the last one causes to increase it.

Fig. 3

Dimensionless load-shortening stability paths of nonlocal strain gradient FGM microshells under hydrostatic pressure ($h = 1\;{\text{nm}},\quad k = 1$); a $l = 0\;{\text{nm}}$, b $e_{0} \theta = 0\;{\text{nm}}$

Plotted in Figs. 4 and 5 are the buckling mode shapes of a nonlocal strain gradient FGM microshell under hydrostatic pressure at the postbuckling domain and in the vicinity of the critical buckling point corresponding to various nonlocal parameters and internal strain gradient length scale parameters, respectively. It can be found that by taking the nonlocal size dependency into consideration, the maximum deflection associated with the postbuckling domain decreases. However, the internal strain gradient length scale parameter causes to increase it. In addition, as it has been considered in the solving process, it is demonstrated that for all values of nonlocal and internal strain gradient length scale parameters, the maximum deflection of nanoshell occurs at a point with dimensionless coordinate of $X = \pi /2m$, where the value of $m$ has been obtained equal to $m = 1$.

Fig. 4

Dimensionless buckling mode shapes of nonlocal strain gradient FGM microshells under hydrostatic pressure ($h = 1\;{\text{nm}},\quad k = 1,\quad l = 0\;{\text{nm}}$)

Fig. 5

Dimensionless buckling mode shapes of nonlocal strain gradient FGM microshells under hydrostatic pressure ($h = 1\;{\text{nm}},\quad k = 1,\quad e_{0} \theta = 0\;{\text{nm}}$)

With the purpose of answering this question that how the shell thickness affects the significance of size-dependent behavior of hydrostatic pressurized FGM microshells, the following critical pressure ratio is introduced as

$${\text{Critical pressure ratio}} = \frac{\text{Buckling pressure obtained via local shell model}}{\text{Buckling pressure obtained via nonlocal strain gradient shell model}}.$$

Figure 6 presents the variation of critical pressure ratio with small-scale parameter (nonlocal parameter or internal strain gradient length scale parameter) for FGM microshells with different shells thicknesses. It is obvious that by increasing the value of small-scale parameter, the critical pressure ratio deviates from the unit value, but this deviation becomes less considerable corresponding to higher shell thickness. This observation indicates that the both nonlocality and strain dependencies play more important role in the nonlinear instability of thinner microshells. The more considerable influence of internal strain gradient length scale parameter in comparison with that of nonlocal parameter on the critical buckling pressure of the microshell is also illustrated as the first one for $l = 4\;{\text{nm}}$ is 13.12% increment and the second one for $e_{0} \theta = 4\;{\text{nm}}$ is $11.16\%$ reduction.

Fig. 6

Variation of the critical pressure ratio with small-scale parameter ($k = 1$)

Figures 7 and 8 in order illustrate the nonlocal strain gradient load–deflection and load-shortening stability paths of FGM microshells corresponding to various small-scale parameters and different values of material property gradient index. It is revealed for all values of material property gradient index, the both nonlocality and strain gradient size dependencies have a considerable influence on the nonlinear instability characteristics of hydrostatic pressurized FGM nanoshells. These influences are a bit more significant for FGM nanoshells with lower value of $k$.

Fig. 7

Dimensionless load–deflection stability paths of nonlocal strain gradient FGM microshells under hydrostatic pressure ($h = 1\;{\text{nm}}$); a $l = 0\;{\text{nm}},$ b $e_{0} \theta = 0\;{\text{nm}}$

Fig. 8

Dimensionless load-shortening stability paths of nonlocal strain gradient FGM microshells under hydrostatic pressure ($h = 1\;{\text{nm}}$); a $l = 0\;{\text{nm}},$ b $e_{0} \theta = 0\;{\text{nm}}$

5 Concluding remarks

Within the framework of a refined exponential shear deformation shell theory, the nonlocal strain gradient elasticity theory was utilized to report the size-dependent nonlinear instability of hydrostatic pressurized FGM microshells in a more comprehensive way. On the basis of Mori–Tanaka homogenization scheme, the effective material properties of FGM microshells were estimated. After that, the boundary layer theory of shell buckling in conjunction with a two-stepped perturbation methodology was employed to capture analytical explicit expressions for nonlocal strain gradient stability paths of FGM microshells. The following conclusions were obtained:

• The nonlocality size effect causes a reduction in the critical hydrostatic pressure and critical shortening of FGM microshells, but the strain gradient size dependency leads to increase them.

• By moving to the deeper part of the postbuckling regime, the both types of small-scale effect decrease. It was observed that the nonlocality size effect as well as the strain gradient one has no influence on the slope of prebuckling part of the load-shortening response of FGM microshells.

• It was seen that by taking the nonlocal size dependency into consideration, the maximum deflection associated with the postbuckling domain decreases. However, the internal strain gradient length scale parameter causes to increase it.

• It was revealed that the influence of internal strain gradient length scale parameter on the critical buckling pressure of nanoshell is a bit more than that of the nonlocal parameter.

• It was found that the both nonlocality and strain gradient size dependencies in the nonlinear instability characteristics are a bit more considerable for FGM microshells with lower value of material property gradient index.

Appendices

Appendix A

$$\varphi_{1} = \frac{{A_{11}^{*} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{2} = \frac{{A_{12}^{*} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{3} = \frac{{A_{11}^{*} B_{11}^{*} - A_{12}^{*} B_{12}^{*} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }}$$

$$\varphi_{4} = \frac{{A_{11}^{*} B_{12}^{*} - A_{12}^{*} B_{11}^{*} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{5} = \frac{{A_{11}^{*} B_{11}^{**} - A_{12}^{*} B_{12}^{**} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }},\quad \varphi_{6} = \frac{{A_{11}^{*} B_{12}^{**} - A_{12}^{*} B_{11}^{**} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }}$$

$$\varphi_{7} = \frac{1}{{A_{66}^{*} }},\quad \varphi_{8} = \frac{{B_{66}^{*} }}{{A_{66}^{*} }},\quad \varphi_{9} = \frac{{B_{66}^{**} }}{{A_{66}^{*} }}$$

$$\varphi_{10} = D_{11}^{*} - B_{11}^{*} \varphi_{3} - B_{12}^{*} \varphi_{4} ,\quad \varphi_{11} = D_{12}^{*} - B_{11}^{*} \varphi_{3} - B_{12}^{*} \varphi_{4}$$

$$\varphi_{12} = D_{66}^{*} - B_{66}^{*} \varphi_{8} ,\quad \varphi_{13} = B_{11}^{*} \varphi_{5} + B_{12}^{*} \varphi_{6} - D_{11}^{**}$$

(38)

$$\varphi_{14} = B_{12}^{*} \varphi_{5} + B_{11}^{*} \varphi_{6} - D_{12}^{**} ,\quad \varphi_{15} = B_{66}^{**} \varphi_{9} - D_{66}^{**}$$

$$\varphi_{16} = B_{12}^{**} \varphi_{1} - B_{11}^{**} \varphi_{2} , \varphi_{17} = B_{11}^{**} \varphi_{1} - B_{12}^{**} \varphi_{2} - B_{66}^{**} \varphi_{7}$$

$$\varphi_{18} = B_{11}^{**} \varphi_{3} + B_{12}^{**} \varphi_{4} - D_{11}^{**} ,\quad \varphi_{19} = B_{12}^{**} \varphi_{3} + B_{11}^{**} \varphi_{4} - D_{12}^{**}$$

$$\varphi_{20} = B_{66}^{**} \varphi_{8} - D_{66}^{** } ,\quad \varphi_{21} = G_{11}^{*} - B_{11}^{**} \varphi_{5} - B_{12}^{**} \varphi_{6}$$

$$\varphi_{22} = G_{66}^{*} - B_{66}^{**} \varphi_{9} ,\quad \varphi_{23} = G_{12}^{*} - B_{11}^{**} \varphi_{6} - B_{12}^{**} \varphi_{5} .$$

This point should be noted that the parameters of $\vartheta_{i} \left( {i = 1, \ldots ,23} \right)$ are the dimensionless form of $\varphi_{i}$.

The solutions in asymptotic forms corresponding to each of independent variables are extracted as below:

$$\begin{aligned} W = {\mathcal{A}}_{00}^{\left( 0 \right)} & + \epsilon^{3/2} \left[ {{\mathcal{A}}_{00}^{{\left( {3/2} \right)}} - {\mathcal{A}}_{00}^{{\left( {3/2} \right)}} \left( {\sin \left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right) + { \cos }\left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} X}}{\sqrt \epsilon }}} - {\mathcal{A}}_{00}^{{\left( {3/2} \right)}} \left( {\sin \left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + { \cos }\left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \\ & + \epsilon^{2} \left[ {{\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{11}^{\left( 2 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right) - {\mathcal{A}}_{00}^{\left( 2 \right)} \left( {\sin \left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right) + { \cos }\left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} X}}{\sqrt \epsilon }}} - {\mathcal{A}}_{00}^{\left( 2 \right)} \left( {\sin \left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + { \cos }\left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \\ & + \epsilon^{3} \left[ {{\mathcal{A}}_{00}^{\left( 3 \right)} + {\mathcal{A}}_{11}^{\left( 3 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right)} \right] \\ & + \epsilon^{4} \left[ {{\mathcal{A}}_{00}^{\left( 4 \right)} + {\mathcal{A}}_{11}^{\left( 4 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{20}^{\left( 4 \right)} \cos \left( {2mX} \right) + {\mathcal{A}}_{02}^{\left( 4 \right)} { \cos }\left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}$$

(39)

$$\begin{aligned} F = & - {\mathcal{B}}_{00}^{\left( 0 \right)} \left( {\beta^{2} X^{2} + \frac{{Y^{2} }}{2}} \right) + \epsilon \left[ { - {\mathcal{B}}_{00}^{\left( 1 \right)} \left( {\beta^{2} X^{2} + \frac{{Y^{2} }}{2}} \right)} \right] \\ & + \epsilon^{2} \left[ { - {\mathcal{B}}_{00}^{\left( 2 \right)} \left( {\beta^{2} X^{2} + \frac{{Y^{2} }}{2}} \right) + {\mathcal{B}}_{11}^{\left( 2 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right)} \right] \\ & + \epsilon^{5/2} \left[ {{\mathcal{A}}_{00}^{{\left( {3/2} \right)}} \left( {b_{10}^{\left( 2 \right)} \sin \left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right) + b_{01}^{\left( 2 \right)} { \cos }\left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} X}}{\sqrt \epsilon }}} + {\mathcal{A}}_{00}^{{\left( {3/2} \right)}} \left( {b_{10}^{\left( 2 \right)} \sin \left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + b_{01}^{\left( 2 \right)} { \cos }\left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \\ & + \epsilon^{3} \left[ { - {\mathcal{B}}_{00}^{\left( 3 \right)} \left( {\beta^{2} X^{2} + \frac{{Y^{2} }}{2}} \right) + {\mathcal{A}}_{00}^{\left( 2 \right)} \left( {b_{10}^{\left( 3 \right)} \sin \left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right) + b_{01}^{\left( 3 \right)} { \cos }\left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} X}}{\sqrt \epsilon }}} + {\mathcal{A}}_{00}^{\left( 2 \right)} \left( {b_{10}^{\left( 3 \right)} \sin \left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + b_{01}^{\left( 3 \right)} { \cos }\left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \\ & + \epsilon^{4} \left[ { - {\mathcal{B}}_{00}^{\left( 4 \right)} \left( {\beta^{2} X^{2} + \frac{{Y^{2} }}{2}} \right) + {\mathcal{B}}_{20}^{\left( 4 \right)} \cos \left( {2mX} \right) + {\mathcal{B}}_{02}^{\left( 4 \right)} \cos \left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}$$

(40)

$$\begin{aligned} \varPsi_{X} & = \epsilon^{2} \begin{array}{*{20}c} {\left[ {{\mathcal{C}}_{11}^{\left( 2 \right)} \cos \left( {mX} \right){ \sin }\left( {nY} \right) + \left( {c_{10}^{\left( 2 \right)} \sin \left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right) + c_{01}^{\left( 2 \right)} \cos \left( {\frac{{\varGamma_{1} X}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} X}}{\sqrt \epsilon }}} } \right.} \\ {\left. { + \left( {c_{10}^{\left( 2 \right)} \sin \left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + c_{01}^{\left( 2 \right)} \cos \left( {\frac{{\varGamma_{1} \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma_{2} \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right]} \\ \end{array} \\ & \quad + \epsilon^{3} \left[ {{\mathcal{C}}_{11}^{\left( 3 \right)} \cos \left( {mX} \right){ \sin }\left( {nY} \right)} \right] + \epsilon^{4} \left[ {{\mathcal{C}}_{11}^{\left( 4 \right)} \cos \left( {mX} \right){ \sin }\left( {nY} \right) + {\mathcal{C}}_{20}^{\left( 4 \right)} { \sin }\left( {2mX} \right)} \right] + O\left( {\epsilon^{5} } \right) \\ \end{aligned}$$

(41)

$$\begin{aligned} \varPsi_{Y} & = \epsilon^{2} \left[ {{\mathcal{D}}_{11}^{\left( 2 \right)} \sin \left( {mX} \right){ \cos }\left( {nY} \right)} \right] + \epsilon^{3} \left[ {{\mathcal{D}}_{11}^{\left( 3 \right)} \sin \left( {mX} \right){ \cos }\left( {nY} \right)} \right] \\ & \quad + \epsilon^{4} \left[ {{\mathcal{D}}_{11}^{\left( 4 \right)} \sin \left( {mX} \right){ \cos }\left( {nY} \right) + {\mathcal{D}}_{02}^{\left( 4 \right)} \sin \left( {2nY} \right)} \right] + O\left( {\epsilon^{5} } \right) , \\ \end{aligned}$$

(42)

in which

$$\varGamma_{1} = \sqrt {\frac{{\sqrt {\frac{1}{{\vartheta_{4}^{2} }}} + \frac{{\vartheta_{4} }}{{\vartheta_{1} \vartheta_{2} + \vartheta_{4}^{2} }}}}{2}} ,\quad \varGamma_{2} = \sqrt {\frac{{\sqrt {\frac{1}{{\vartheta_{4}^{2} }}} - \frac{{\vartheta_{4} }}{{\vartheta_{1} \vartheta_{2} + \vartheta_{4}^{2} }}}}{2}} .$$

(43)

Appendix B

$${\mathcal{P}}_{q}^{\left( 0 \right)} = {\mathcal{U}}_{0} {\mathcal{U}}_{1} {\mathcal{U}}_{8} + {\mathcal{U}}_{2} {\mathcal{U}}_{8} \epsilon^{2}$$

(44)

$$\begin{aligned} {\mathcal{P}}_{q}^{\left( 2 \right)} & = 8{\mathcal{U}}_{1} {\mathcal{U}}_{3} {\mathcal{U}}_{7} {\mathcal{U}}_{8} + \frac{{8{\mathcal{U}}_{1} {\mathcal{U}}_{3} {\mathcal{U}}_{8} \left( {{\mathcal{U}}_{0} {\mathcal{U}}_{1} {\mathcal{U}}_{6} {\mathcal{U}}_{8} H_{20} + {\mathcal{U}}_{0} {\mathcal{U}}_{3} {\mathcal{U}}_{5} H_{20} } \right)}}{{{\mathcal{U}}_{0} {\mathcal{U}}_{1} {\mathcal{U}}_{8} H_{20} - {\mathcal{U}}_{5} }} + \frac{{8{\mathcal{U}}_{1} {\mathcal{U}}_{3} \left( {{\mathcal{U}}_{0} {\mathcal{U}}_{6} + {\mathcal{U}}_{0}^{2} {\mathcal{U}}_{3} H_{20} } \right)}}{{{\mathcal{U}}_{0} {\mathcal{U}}_{1} {\mathcal{U}}_{8} H_{20} - {\mathcal{U}}_{5} }} \\ & \quad + \frac{{8{\mathcal{U}}_{0} {\mathcal{U}}_{1} {\mathcal{U}}_{3} \left( {{\mathcal{U}}_{6} + {\mathcal{U}}_{0} {\mathcal{U}}_{3} } \right)}}{{{\mathcal{U}}_{0} {\mathcal{U}}_{1} {\mathcal{U}}_{8} - {\mathcal{U}}_{5} }} + 16{\mathcal{U}}_{0} {\mathcal{U}}_{3} {\mathcal{U}}_{4} {\mathcal{U}}_{8} \\ \end{aligned}$$

(45)

$$\delta_{q}^{\left( 0 \right)} = \left[ {\frac{{\vartheta_{1} }}{2} - \vartheta_{2} + \left( {\frac{{\left( {2\vartheta_{1} \vartheta_{2} - \vartheta_{2}^{2} } \right)\varGamma_{2} }}{{\pi \vartheta_{1} \left( {\varGamma_{1}^{2} + \varGamma_{2}^{2} } \right)}}} \right)\epsilon^{1/2} } \right]{\mathcal{P}}_{q} + \left[ {\left( {\frac{{3^{1/4} \left( {\varGamma_{1}^{2} + \varGamma_{2}^{2} } \right)\left( {2\vartheta_{1} - \vartheta_{2} } \right)^{2} }}{{6\pi \varGamma_{2} }}} \right)\epsilon } \right]{\mathcal{P}}_{q}^{2}$$

(46)

$$\delta_{q}^{\left( 2 \right)} = \left[ {\frac{{3^{3/4} m^{2} }}{32}} \right]\epsilon^{ - 3/2} ,$$

(47)

where

$$H_{11} = 1 + \pi^{2} {\mathcal{G}}_{1}^{2} \left( {m^{2} + \beta^{2} n^{2} } \right),\quad H_{20} = 1 + 4\pi^{2} {\mathcal{G}}_{1}^{2} m^{2}$$

(48)

$$G_{11} = 1 + \pi^{2} {\mathcal{G}}_{2}^{2} \left( {m^{2} + \beta^{2} n^{2} } \right),$$

where ${\mathcal{U}}_{i} \left( {i = 0, \ldots ,8} \right)$ are constant parameters extracted via the perturbation sets of equations:

$${\mathcal{S}}_{1} = - \left[ {\left( {2\vartheta_{1} - \vartheta_{2} } \right)\left( {{\mathcal{P}}_{q}^{\left( 2 \right)} } \right)} \right]$$

(49)

$${\mathcal{S}}_{2} = - \left( {2\vartheta_{1} - \vartheta_{2} } \right)\left( {{\mathcal{P}}_{q}^{\left( 0 \right)} } \right).$$

(50)