1 Introduction

After the discovery of carbon nanotubes (CNTs) by Iijima (1991), the families of carbon nanostructures such as graphene sheets, carbon nanotubes, and fullerenes provide a new foundation to apply in the different emerging fields of nanoscience and nanotechnology (Chen et al. 2003; Kim et al. 2004; Pumera et al. 2006; Yu et al. 2010) due to their extraordinary physical, mechanical and electrical properties. According to the direction of the rolling of the graphene sheet, carbon nanotubes can be classified into armchair and zigzag which are indicated in Fig. 1. Because of the small scale of such structures, investigation of the behavior of them using experimental methods makes some difficulties that causes the importance of theoretical analyses has been increasing.

Fig. 1
figure 1

Definition of chiral vector for a graphene sheet

Full size image

Liew et al. (2006) proposed a continuum model to analyze the vibrations of multi-layered graphene sheet (MLGS) embedded in an elastic matrix on the basis of the classical plate theory (CLPT). Ansari and Hemmatnezhad (2010) applied the homotopy perturbation method for nonlinear vibration of multi-walled carbon nanotubes embedded in an elastic medium based on the classical continuum mechanics. The nanoscale vibration analysis of MLGS embedded in an elastic medium was studied by Behfar and Naghdabadi (2005). They considered each layer of MLGSs as orthotropic plates whose elastic modulus are different in two perpendicular directions. Based on the CLPT, Kitipornchai et al. (2005) investigated the vibration response of MLGSs with simply-supported boundary conditions using a continuum model. They proposed an explicit formula for the van der Waals interaction between any two sheets of a MLGS.

As the classical continuum models do not have the capability to consider the size-effects in the analyses of nanostructures, using them to predict the behavior of structures at the nanoscale becomes controversial. Hence, the extension of the continuum mechanics to accommodate the size dependence of nanostructures is a topic of major concern. Modified continuum models are one of the most applied theoretical approaches for the investigation of nanomechanics due to their computational efficiency and their capability to produce accurate results which are comparable to those of atomistic models. The application of nonlocal continuum mechanics allowing for the small scale effects in the analyses of nanomaterials has been recommended by many research workers.

The use of nonlocal elasticity to study size-effects in micro and nanoscale structures was pioneered by Peddieson et al. (2003). They studied the bending of micro and nanoscale beams with the concept of nonlocal elasticity and concluded that size-effects could be significant for nano-sized structures and that the magnitude of the size-effects greatly depends on the value of the nonlocal parameter. After that, Nonlocal continuum model has gained much popularity among the researchers because of its efficiency as well as simplicity to analyze the behavior of various nanostructures.

Wang et al. (2006) developed nonlocal elastic beam and shell models to investigate the small-scale effects on the buckling analysis of CNTs under compression. They demonstrated that the buckling solutions for CNTs via local continuum mechanics are overestimated. Various available beam theories were reformulated by Reddy (2007) using the nonlocal differential constitutive relations of Eringen to bring out the effect of the size-effects buckling loads and natural frequencies of the beams at nanoscale. Shen (2010) presented an investigation on the buckling and postbuckling of microtubules subjected to a uniform external radial pressure in thermal environments based on nonlocal shear deformable cylindrical shell. Amara et al. (2010) studied the column buckling of multi-walled carbon nanotubes with large aspect ratios under axial compression coupling with temperature change on the basis of nonlocal theory of thermal elasticity mechanics. Ansari and Sahmani (2012) incorporated Eringen’s nonlocality into different beam theories to include small-scale effects on the axial buckling of single-walled CNTs with different boundary conditions and compared with the results of molecular dynamics simulations. There are so many other studies about buckling and vibration responses of nanostructures in which the nonlocal elasticity continuum models have been utilized (Hu et al. 2008; Kiani 2010; Ansari et al. 2010; Ansari and Sahmani 2013; Radic et al. 2014; Sahmani and Bahrami 2015; El-Borgi et al. 2015; Sari and Al-Kouz 2016; Sahmani and Aghdam 2017a, b, c; Zhang et al. 2017; Sahmani and Fattahi 2017a, b) which show the enormous interest of this extension of continuum mechanics in various fields of nanoscience and nanomechanics.

In this work, axial buckling response of single-layered graphene sheets (SLGSs) is studied based on nonlocal continuum mechanics. To this end, Eringen’s nonlocal elasticity equations are incorporated into the different types of plate theory to develop nonlocal elastic plate models. Generalized differential quadrature (GDQ) method is implemented into the governing differential equations of nonlocal models to discretize them along the simply supported and clamped boundary conditions. Then molecular dynamics (MD) simulations are performed for a series of armchair and zigzag SLGSs with various values of side-length and boundary conditions, the results of which are fitted with those of nonlocal plate models to derive appropriate values of nonlocal parameter.

2 Overview of plate theories

2.1 Introduction

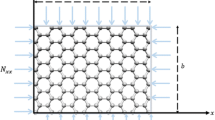
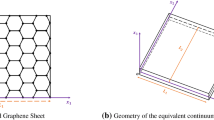
To represent the behavior of plates, there are different plate theories. Consider a uniform square nanoplate with the side length L and thickness h. A coordinate system \((x,y,z)\) is introduced at the one corner of the midplane of the nanoplate, whereas the x axis is taken along the length of the nanoplate, the y axis in the width direction and the z axis is taken along the depth (thickness) direction. The displacement components \((u_{1} , u_{2} , u_{3} )\) along the axes \((x,y,z)\) can be written in a general form as:

$$\begin{aligned} u_{1} & = - z\frac{\partial w}{\partial x} + \psi (z)\left( {\frac{\partial w}{\partial x} + \varphi_{x} } \right) \\ u_{2} & = - z\frac{\partial w}{\partial y} + \psi (z)\left( {\frac{\partial w}{\partial y} + \varphi_{y} } \right) \\ u_{3} & = w(x,t), \end{aligned}$$
(1)

where w is the transverse displacement and \(\varphi_{x} , \varphi_{y}\) are the angular displacements in the x and y directions, respectively. \(\psi (z)\) is the shape function as follows:

For classical plate theory (CLPT): \(\psi \left( z \right) = 0\).

For first-order shear deformation theory (FSDT): \(\psi \left( z \right) = z\).

2.2 Classical plate theory

The simplest and the most well-known plate theory is the classical plate theory which is on the basis of that the straight lines which are vertical to the mid-plane will remain straight and vertical to the mid-plane after deformation. In otherwise, the effects of shear deformation and rotational inertia are not considered in this type of plate theory. On the basis of Eq. (1), the strain–displacement relations appropriate to CLPT can be obtained as:

$$\varepsilon_{xx} = \frac{{\partial u_{1} }}{\partial x} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(2-a)
$$\varepsilon_{yy} = \frac{{\partial u_{2} }}{\partial y} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(2-b)
$$\gamma_{xy} = \frac{{\partial u_{1} }}{\partial y} + \frac{{\partial u_{2} }}{\partial x} = - 2z\frac{{\partial^{2} w}}{\partial x\partial y},$$
(2-c)
$$\gamma_{xz} = \gamma_{yz} = 0.$$
(2-d)

Using the principle of virtual displacement, the following equilibrium equation can be expressed for CLPT as:

$$\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{yy} }}{{\partial y^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} - P\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$
(3)

where P is the critical axial buckling load and \(M = \left\{ {M_{xx} ,M_{yy} ,M_{xy} } \right\}^{T} = \mathop \int \nolimits_{ - h/2}^{h/2} z\left\{ {\sigma_{xx} ,\sigma_{yy} ,\sigma_{xy} } \right\}^{T} dz\).

The governing equation of (3) can be obtained in terms of displacements as:

$$- \frac{{Eh^{3} }}{{12(1 - \nu^{2} )}}\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\nu \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) - \frac{{Eh^{3} }}{6(1 + \nu )}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} - P\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0.$$
(4)

2.3 First-order shear deformation theory

The next type of plate theory is the first-order shear deformation plate theory in which the effects of shear deformation and rotational inertia are taken into account, so the straight lines will no longer remain vertical to the mid-plane of the plate after deformation. However, it is assumed that the transverse shear stress has a linear distribution along the thickness of the plate. Using Eq. (1), the following strain–displacement relations can be obtained as:

$$\varepsilon_{xx} = \frac{{\partial u_{1} }}{\partial x} = z\frac{{\partial \varphi_{x} }}{\partial x},$$
(5-a)
$$\varepsilon_{yy} = \frac{{\partial u_{2} }}{\partial x} = z\frac{{\partial \varphi_{y} }}{\partial y},$$
(5-b)
$$\gamma_{xy} = \frac{{\partial u_{1} }}{\partial y} + \frac{{\partial u_{2} }}{\partial x} = z\left( {\frac{{\partial \varphi_{x} }}{\partial y} + \frac{{\partial \varphi_{y} }}{\partial x}} \right),$$
(5-c)
$$\gamma_{xz} = \frac{{\partial u_{1} }}{\partial z} + \frac{{\partial u_{3} }}{\partial x} = \frac{\partial w}{\partial x} + \varphi_{x} ,$$
(5-d)
$$\gamma_{yz} = \frac{{\partial u_{2} }}{\partial z} + \frac{{\partial u_{3} }}{\partial y} = \frac{\partial w}{\partial y} + \varphi_{y} .$$
(5-e)

Using the principle of virtual displacement, the equilibrium equations can be expressed for FSDT as:

$$\frac{{\partial Q_{xx} }}{\partial x} + \frac{{\partial Q_{yy} }}{\partial y} - P\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$
(6-a)
$$\frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{xx} = 0 ,$$
(6-b)
$$\frac{{\partial M_{yy} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x} - Q_{yy} = 0 ,$$
(6-c)

where \(Q = \left\{ {Q_{xx} ,Q_{yy} } \right\}^{T} = \int \nolimits_{ - h/2}^{h/2} \left\{ {\sigma_{xz} ,\sigma_{yz} } \right\}^{T} dz.\)

The governing equations of (6) can be obtained in terms of displacements as:

$$\kappa Gh\left( {\frac{{\partial \varphi_{x} }}{\partial x} + \frac{{\partial \varphi_{y} }}{\partial y} + \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) - P\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,$$
(7-a)
$$\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} \varphi_{y} }}{\partial x\partial y}} \right) + \frac{{Eh^{3} }}{24(1 + \nu )}\left( {\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial y} + \frac{{\partial^{2} \varphi_{y} }}{{\partial y^{2} }}} \right) - \kappa Gh\left( {\varphi_{x} + \frac{\partial w}{\partial x}} \right) = 0,$$
(7-b)
$$\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\frac{{\partial^{2} \varphi_{y} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} \varphi_{x} }}{\partial x\partial y}} \right) + \frac{{Eh^{3} }}{24(1 + \nu )}\left( {\frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi_{y} }}{\partial x\partial y}} \right) - \kappa Gh\left( {\varphi_{y} + \frac{\partial w}{\partial y}} \right) = 0.$$
(7-c)

3 Nonlocal plate theories for axial buckling of SLGSs

3.1 Review of Eringen’s nonlocal elasticity

The theory of nonlocal elasticity was first considered by Eringen in the 1970’s (Eringen 1972). This concept is inherent in solid state physics where the nonlocal attractions of atoms are prevalent Eringen. In contrast to the classical elasticity, in the nonlocal model the stress at a reference point x in an elastic body depends not only on the strains at x, but also on strains at all other points of the body (Eringen 1972). According to the nonlocal elasticity theory, this fact was attributed to the atomic theory of lattice dynamics and experimental measurements of phonon dispersion (Eringen 1983).

For homogenous and isotropic elastic continuum, the linear nonlocal elasticity theory can be expressed as the following set of equations (Eringen 1983):

$$\sigma_{kl,k} + \rho \left( {f_{l} - \ddot{u}_{l} } \right) = 0 ,$$
(8-a)
$$\sigma_{kl} (x) = \int \nolimits_{V} \alpha \left( {\left| {x - x^{\prime}} \right|,\tau } \right)\sigma_{kl}^{c} (x^{\prime})dV ,$$
(8-b)
$$\sigma_{kl}^{c} (x^{\prime}) = L_{1} e_{rr} (x^{\prime})\delta_{kl} + 2L_{2} e_{kl} (x^{\prime}) ,$$
(8-c)
$$e_{kl} (x^{\prime}) = \frac{1}{2}\left( {\frac{{du_{k} (x^{\prime})}}{{dx^{\prime}_{l} }} + \frac{{du_{l} (x^{\prime})}}{{dx^{\prime}_{k} }}} \right) ,$$
(8-d)

where Eq. (8-a) is the equilibrium relation in which \(\sigma_{kl,l} , \rho , f_{l}\) and \(u_{l}\) are the nonlocal stress tensor, mass density, body force density and displacement vector at a reference point x in the body, respectively. Equation (8-b) is the relation between local (\(\sigma_{kl}^{c}\)) and nonlocal (\(\sigma_{kl,l}\)) stress tensors using the nonlocal modulus (\(\alpha \left( {\left| {x - x^{'} } \right|,\tau } \right)\)). Finally, Eqs. (8-c) and (8-d) are the classical constitutive stress–strain and strain–displacement relationships, respectively. \(L_{1}\) and \(L_{2}\) are the Lame constants.

Eringen (1972) made certain assumptions to simplify Eq. (8-b) to a partial differential equation form as:

$$\left( {1 - \tau^{2} \ell^{2} \nabla^{2} } \right)t_{kl} (x) = \sigma_{kl} (x),\quad \tau = e_{0} \frac{a}{\ell },$$
(9)

where \(t_{kl} = \sigma_{kl,l}\), \(a/\ell\) is the characteristic length ratio and \(e_{0}\) is the nonlocal constant which are appropriate to the material.

3.2 Application of nonlocal elasticity in plate theories

3.2.1 Classical plate theory

Using Eq. (9), the only constitutive relation for nonlocal model of CLPT with elastic medium is obtained as:

$$- \frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\nu \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) - \frac{{Eh^{3} }}{{6\left( {1 + \nu } \right)}}\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} - P\frac{{\partial^{2} w}}{{\partial x^{2} }} + \mu P\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) = 0.$$
(10)

3.2.2 First order shear deformation theory (FSDT)

Using Eq. (9), the constitutive relations for nonlocal model of FSDT with elastic medium can be expressed as:

$$\kappa Gh\left( {\frac{{\partial \varphi_{x} }}{\partial x} + \frac{{\partial \varphi_{y} }}{\partial y} + \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) - P\frac{{\partial^{2} w}}{{\partial x^{2} }} + \mu P\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}} \right) = 0 ,$$
(11-a)
$$\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} \varphi_{y} }}{\partial x\partial y}} \right) + \frac{{Eh^{3} }}{24(1 + \nu )}\left( {\frac{{\partial^{2} \varphi_{x} }}{\partial x\partial y} + \frac{{\partial^{2} \varphi_{y} }}{{\partial y^{2} }}} \right) - \kappa Gh\left( {\varphi_{x} + \frac{\partial w}{\partial x}} \right) = 0,$$
(11-b)
$$\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\frac{{\partial^{2} \varphi_{y} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} \varphi_{x} }}{\partial x\partial y}} \right) + \frac{{Eh^{3} }}{24(1 + \nu )}\left( {\frac{{\partial^{2} \varphi_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi_{y} }}{\partial x\partial y}} \right) - \kappa Gh\left( {\varphi_{y} + \frac{\partial w}{\partial y}} \right) = 0.$$
(11-c)

4 Generalized differential quadrature (GDQ) method

4.1 Introduction

The differential quadrature method is a numerical technique used to solve the initial and boundary value problems (Chen 1996; Noye and Tan 1989; Quan and Chang 1989). This method compared with the other numerical method such as the finite difference methods and finite element methods, and showing excellent numerical results, it needs only applying a few grid points in order to get high-precise solutions, a good convergence and it requires only less computational workload (Bert and Malik 1996; Shu et al. 2000). This method was proposed by Bellman in the early 70 s (Bellman and Casti 1971; Bellman et al. 1972). Then, the technique has been successful employed in a variety of problems in engineering and physical sciences hence attracted many researchers attention in recent years. Al-Saif and Zhu (2002), using the differential quadrature method to solve the coupled incompressible Navier–Stokes equation and heat equation and showing that accurate numerical results can be obtained by the DQM using only a few grid point and requires less storage and computational effort compared to the conventional low-order finite difference method. In another work, Al-saif and Zhu (2003), using the mixed differential quadrature method (MDQM) for solving the coupled two-dimensional incompressible Navier–Stokes equation and heat equation. The results show that the new method is more accurate and has better convergence than the traditional DQM. The purpose of this paper is to introduce and application the differential quadrature method to solving unsteady state two-dimensional convection–diffusion equation. The results demonstrated that high accurate numerical solution by using only a few grid points and requires less storage and computational effort compared to the some numerical methods wealthy from some researchers in the precedent studies.

The GDQ method is one of the most efficient numerical techniques to solve various boundary value problems. Many researchers have recently suggested the application of the generalized differential quadrature (GDQ) method to the analysis of nanostructures. This method has shown superb accuracy, efficiency, convenience and great potential in solving complicated partial differential equations. The basic idea of the differential quadrature method lies in the approximation of partial derivative of a function with respect to a coordinate at a discrete point as a weighted linear sum of the function values at all discrete points along that coordinate direction. Let \(\frac{{\partial^{r} f}}{{\partial x^{r} }}\) be the rth derivative of a function \(f(x)\) which can be expressed as a linear sum of the function values:

$$\left. {\frac{{\partial^{r} f(x)}}{{\partial x^{r} }}} \right|_{{x = x_{P} }} = \mathop \sum \limits_{Q = 1}^{n} A_{PQ}^{(r)} f(x_{P} ),$$
(12)

where n is the number of total discrete grid points used in the approximation process and \(A_{PQ}^{(r)}\) are weighting coefficients. The weighting coefficients of the first derivative are determined by:

$$A_{PQ}^{(1)} = \frac{{M(x_{P} )}}{{\left( {x_{P} - x_{Q} } \right)M(x_{Q} )}} \quad \quad \left( { P, Q = 1,2, \ldots ,n; P \ne Q} \right) ,$$
(13)

where

$$M(x_{P} ) = \mathop \prod \limits_{Q = 1;Q \ne P}^{n} (x_{P} - x_{Q} ).$$
(14)

The weighting coefficients of higher-order derivatives can be obtained through the following recurrence relation:

$$A_{PQ}^{(r)} = \left\{ {\begin{array}{*{20}l} {r\left[ {A_{PQ}^{(r - 1)} A_{PQ}^{(1)} - \frac{{A_{PQ}^{(r - 1)} }}{{x_{p} - x_{q} }}} \right],\quad P \ne Q} \\ \quad { - \mathop \sum \limits_{Q = 1}^{n} A_{PQ}^{(r)} , P = Q \quad (P, Q = 1,2, \ldots ,n; 2 \le r \le n - 1) } \\ \end{array} } \right..$$
(15)

4.2 Implementation of GDQ method along of governing equations

By applying the GDQ method, the discrete counterparts of governing differential equations corresponding to each type of nonlocal plate model can be expressed as:

For CLPT:

$$\begin{aligned} & - \frac{{Eh^{3} }}{{12\left( {1 - \nu ^{2} } \right)}}\left( {\mathop \sum \limits_{{k = 1}}^{{N_{x} }} A_{{pk}}^{{(4)}} W_{{kq}} + 2\nu \mathop \sum \limits_{{k = 1}}^{{N_{x} }} \mathop \sum \limits_{{m = 1}}^{{N_{y} }} A_{{pk}}^{{(2)}} B_{{qm}}^{{(2)}} W_{{km}} + \mathop \sum \limits_{{m = 1}}^{{N_{y} }} B_{{qm}}^{{(4)}} W_{{pm}} } \right) \\ & \quad - \frac{{Eh^{3} }}{{6\left( {1 + \nu } \right)}}\mathop \sum \limits_{{k = 1}}^{{N_{x} }} \mathop \sum \limits_{{m = 1}}^{{N_{y} }} A_{{pk}}^{{(2)}} B_{{qm}}^{{(2)}} W_{{km}} - P\mathop \sum \limits_{{k = 1}}^{{N_{x} }} A_{{pk}}^{{(2)}} W_{{kq}} \\ & \quad + \mu P\mathop \sum \limits_{{k = 1}}^{{N_{x} }} \mathop \sum \limits_{{m = 1}}^{{N_{y} }} A_{{pk}}^{{(2)}} B_{{qm}}^{{(2)}} W_{{km}} = 0. \\ \end{aligned}$$
(16)

For FSDT:

$$\begin{aligned} &\kappa Gh\left( {\mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(1)} \phi_{{x_{kq} }} + \mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(1)} \phi_{{y_{pm} }} + \mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(2)} W_{kq} + \mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(2)} W_{pm} } \right) \hfill \\ &\quad - P\mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(2)} W_{kq} + \mu P\mathop \sum \limits_{k = 1}^{{N_{x} }} \mathop \sum \limits_{m = 1}^{{N_{y} }} A_{pk}^{(2)} B_{qm}^{(2)} W_{km} = 0, \hfill \\ \end{aligned}$$
(17-a)
$$\begin{aligned} &\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(2)} \phi_{{x_{kq} }} + \nu \mathop \sum \limits_{k = 1}^{{N_{x} }} \mathop \sum \limits_{m = 1}^{{N_{y} }} A_{pk}^{(1)} B_{qm}^{(1)} \phi_{{y_{pm} }} } \right) + \frac{{Eh^{3} }}{24(1 + \nu )} \hfill \\ &\quad \left( {\mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(2)} \phi_{{y_{pm} }} } { + \mathop \sum \limits_{k = 1}^{{N_{x} }} \mathop \sum \limits_{m = 1}^{{N_{y} }} A_{pk}^{(1)} B_{qm}^{(1)} \phi_{{x_{pm} }} } \right) - \kappa Gh\left( {\phi_{{x_{pq} }} + \mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(1)} W_{kq} } \right) = 0, \hfill \\ \end{aligned}$$
(17-b)
$$\begin{aligned} &\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}\left( {\mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(2)} \phi_{{y_{pm} }} + \nu \mathop \sum \limits_{k = 1}^{{N_{x} }} \mathop \sum \limits_{m = 1}^{{N_{y} }} A_{pk}^{(1)} B_{qm}^{(1)} \phi_{{x_{pm} }} } \right) + \frac{{Eh^{3} }}{24(1 + \nu )} \hfill \\ &\quad \left( {\mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(2)} \phi_{{x_{kq} }} } { + \mathop \sum \limits_{k = 1}^{{N_{x} }} \mathop \sum \limits_{m = 1}^{{N_{y} }} A_{pk}^{(1)} B_{qm}^{(1)} \phi_{{y_{pm} }} } \right) - \kappa Gh\left( {\phi_{{y_{pq} }} + \mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(1)} W_{pm} } \right) = 0. \hfill \\ \end{aligned}$$
(17-c)

4.3 Implementation of GDQ method along of boundary conditions

Using the GDQ approximation, the discretized counterparts of different boundary conditions relevant to each type of plate theory can be expressed as:

For CLPT:

All edges simply supported (SSSS):

$$W_{pq} = 0, \quad \mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(2)} W_{kq} = 0\quad \quad {\text{at edges}}\,x = 0,L,$$
$$W_{pq} = 0, \quad \mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(2)} W_{pm} = 0 \quad \quad {\text{at edges}}\,y = 0,L.$$

All edges clamped (CCCC):

$$W_{pq} = 0, \quad \mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(1)} W_{kq} = 0\quad \quad {\text{at edges}}\;x = 0,L,$$
$$W_{pq} = 0,\quad \mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(1)} W_{pm} = 0 \quad \quad {\text{at edges}}\;y = 0,L.$$

For FSDT:

All edges simply supported (SSSS):

$$W_{pq} = 0,\quad \mathop \sum \limits_{k = 1}^{{N_{x} }} A_{pk}^{(1)} \phi_{{x_{kq} }} = 0 \quad \quad {\text{at edges}}\;x = 0,L,$$
$$W_{pq} = 0,\quad \mathop \sum \limits_{m = 1}^{{N_{y} }} B_{qm}^{(1)} \phi_{{y_{pm} }} = 0 \quad \quad {\text{at edges}}\;y = 0,L.$$

All edges clamped (CCCC):

$$W_{pq} = 0,\quad \phi_{{x_{pq} }} = 0\quad \quad {\text{at edges}}\;x = 0,L,$$
$$W_{pq} = 0,\quad \phi_{{y_{pq} }} = 0 \quad \quad {\text{at edges}}\;y = 0,L.$$

5 Molecular dynamics simulation

Molecular dynamics simulation is an atomistic method used in the analysis of different nanostructures. Through the fast development of various fields of nanotechnology, MD simulation is considered as a powerful and accurate implement to study systems at the nanoscale. A comparison between different methods of Young’s modulus determination for SWCNTs using MD simulation was made by Agrawal et al. (2006). Hao et al. (2008) investigated the buckling of defective single-walled and double-walled carbon nanotubes under compressive loads by MD simulations. Tachikawa et al. (2009) applied MD simulation to study the dynamics interaction of magnesium on the graphene surface. The fracture behavior of a graphene sheet containing a center crack was studied by Tsai et al. (2010) based on the MD simulation and continuum mechanics. They showed that the strain energy release rate can be an appropriate parameter for describing the fracture of covalently bonded graphene sheet. To present the nonlinear vibrational response of simply supported SLGSs, Shen et al. (2010) fitted the natural frequencies of graphene sheets obtained from MD simulations and nonlocal plate model to estimate the value of small scale parameter.

The essential concept of MD simulation is to evaluate the motions of atoms in the system at different time periods. An appropriate potential field is adopted to simulate the set of the atoms of the system. Currently, the potentials which are available to implement in the MD simulations, can be classified as semi-empirical, empirical and quantum mechanical ones. Some of them are pair potentials such as the non-bonded Lennard-Jones potential (Lennard-Jones 1924) used to incorporate the van der Waals forces in the simulations. The other ones are many body potentials like the Tersoff (1989) potential originally employed to simulate systems consisting of carbon and semi-conductor atoms. One of the most important factors in the MD modeling is the correct choice of potential that is used in a MD simulation. This choice depends on various conditions such as the nature of the simulation, the type of material being simulated and the trade-off between accuracy and computational efficiency.

The molecular dynamics simulator “NanoHive” (Nanorex Inc. 2005) is utilized to perform the simulations presented in the current study. NanoHive is a free open source MD simulator which has certain features that can be used to model different loading conditions of nanostructures (Nanorex Inc. 2005). Quasi-static molecular dynamics simulations are performed on DWCNTs with different chirality, aspect ratios, and boundary conditions. All simulations are established using the Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential (Stuart et al. 2000). The AIREBO potential is an extension of the commonly used REBO potential developed for solid carbon and hydrocarbon molecules (Stuart et al. 2000).

The MD simulations presented here are all performed at constant temperature equal to the room temperature (300 Kelvin). The van Gunstern-Berendsen thermostat (Berendsen et al. 1984) is implemented in such a way that the scaling factor is used after each step of the MD simulation; the velocities of the atoms of system are scaled as the average kinetic energy remains approximately constant. A time step of \(0.5 fs\) is selected with about 35,000 numbers of steps to simulate the axial buckling response of SLGSs.

Compressive axial strain is applied to each SLGS by mathematically changing the coordinate of the carbon atoms (Nanorex Inc. 2005). Then using the NanoHive simulator, various time steps of relaxation are arranged to enable the graphene sheets to reach to the equilibrium configuration. This procedure is repeated for different values of the compressive strain while for a certain value of the strain, the SLGS collapses corresponding to its buckling mode-shape. One layer of atoms at all sides of the SLGSs is fixed in space to simulate simply-supported boundary conditions. However, there are four atomic layers of carbon fixed to simulate clamped boundary conditions. According to this modeling conception, the simply supported and clamped boundary conditions considered in this study are shown in Fig. 2, schematically.

Fig. 2
figure 2

Schematic of single-layered graphene sheet. a One atomic layer at ends of all sides are held fixed to simulate simply-supported boundary conditions. b Four atomic layers at ends of all sides are held fixed to simulate clamped boundary conditions

Full size image

A series of axial buckling simulation are established for a range of zigzag and armchair graphene sheets with simply supported and clamped boundary conditions and different values of side-length. The critical axial buckling loads obtained directly from MD simulations are given in Tables 1 and 2 for armchair and zigzag SLGSs, respectively. It can be observed from the results of MD simulation that armchair SLGSs relatively have higher critical buckling loads compared to zigzag SLGSs especially for lower values of side-length.

Table 1 Critical axial buckling loads of armchair SLGSs obtained from MD simulation (nN)
Full size table
Table 2 Critical axial buckling loads of zigzag SLGSs obtained from MD simulation (nN)
Full size table

6 Numerical results and discussion

6.1 Results of nonlocal elastic plate models

The critical axial buckling loads of SLGSs based on nonlocal elastic plate models are calculated using GDQ method for simply supported and clamped boundary conditions. It is assumed that thickness of graphene sheet \(h = 0.34\), Young’s modulus \(E = 1 TPa\), and Poisson’s ratio \(\nu = 0.16\) (Kitipornchai et al. 2005).

The numerical results presented in Tables 3 and 4 are the critical axial buckling loads of nanosheets corresponding to SSSS and CCCC boundary conditions, respectively. It can be seen from the tables that the critical axial buckling loads obtained from the nonlocal models have different values relevant to the various values of the nonlocal parameter \(\mu\). However, for higher side-lengths, this difference between the critical buckling loads diminishes. It implies that the size-effects reduce with the increase of SLGS’s size. Therefore, an important issue in the application of the nonlocal elasticity models used for nanostructures is the determination of the appropriate value of the nonlocal parameter. Use of the nonlocal models is only beneficial if the correct values of nonlocal parameter are available which are proposed in the next section.

Table 3 Critical axial buckling loads of simply-supported SLGSs obtained from nonlocal plate models (nN)
Full size table
Table 4 Critical axial buckling loads of clamped SLGSs obtained from nonlocal plate models (nN)
Full size table

A critical part of the numerical methods is to show the convergence of their results. Table 5 represents the convergence criteria of GDQ method used to evaluate the critical axial buckling loads of SLGSs with different values of nonlocal parameter and types of boundary conditions. This pattern of convergence of the numerical technique reflects its efficiency and reliability.

Table 5 Convergence study of critical axial buckling loads (nN) of SLGSs with different boundary conditions \((L = 20\,{\text{nm}})\)
Full size table

6.2 Appropriate values of nonlocal parameter

An important issue in the application of the nonlocal elasticity models to SLGSs is the derivation of the appropriate value of nonlocal elasticity parameter \(\mu\) used in the nonlocal plate models. The nonlocal models presented in the Sect. 3 are only efficient if the correct value of the nonlocal parameter is known.

Previous research on finding the correct values of the nonlocal constant for CNTs is very limited. Still, there is no consensus on the value of \(\mu\) that should be used for CNTs. Some recent publications have proposed \(\mu\) values by comparing nonlocal models with molecular dynamics simulation results: Zhang et al. (2005) used a nonlocal Timoshenko beam model to compare axial buckling results with molecular mechanics (MM) simulations of Sears and Brata (2004) and proposed the value of 0.82 for the nonlocal parameter. Hu et al. (2008) compared nonlocal shell models for dispersion of propagating waves in CNTs with results from molecular dynamics simulations and reported \(\mu\) values of 0.6 for transverse waves and 0.2–0.23 for torsional waves. Khademolhosseini et al. (2010) have been used MD simulation and nonlocal continuum shell models to extract effective shell thickness and consistent value of nonlocal parameter for torsional buckling of simply-supported SWCNTs. They presented nonlocal parameters of 0.85 and 0.86 for armchair and zigzag SWCNTs, respectively. Recently, Ansari et al. (2010) performed MD simulations for free vibrations of armchair and zigzag SLGSs with simply-supported and clamped side-length and the results are matched with those of nonlocal plate model to propose the appropriate values of nonlocal parameter corresponding to each type of chirality, nonlocal plate model and boundary conditions.

Due to large scattering of the different values of nonlocal parameter proposed in the previous publications, further investigation about this crucial variable of nonlocal models used for SLGSs seems necessary which makes it possible to understand better the size-effects on responses of SLGSs.

In this work, a nonlinear least-square fitting procedure is utilized to propose the appropriate values of nonlocal parameter by minimizing the Euclidean norm of the difference between the critical buckling loads obtained directly from the MD simulations and those of nonlocal elastic plate models in which \(\mu\) is set as optimization variable. The values of \(\mu\) obtained from the matching procedure are presented in Table 6 for both armchair and zigzag SLGSs corresponding to different types of nonlocal plate model and boundary conditions. To compare the effects of type of chirality, nonlocal plate model, and boundary conditions with each other, Table 7 indicates the influence of each of them separately and it is concluded that boundary conditions have the most significant influence on the recommended values of nonlocal parameter for the axial buckling of SLGSs.

Table 6 Appropriate values of nonlocal parameter corresponding to different types of chirality, nonlocal plate model and boundary conditions
Full size table
Table 7 Comparison between the influences of chirality, nonlocal plate model and boundary conditions on the recommended values of nonlocal parameter
Full size table

Figures 3 and 4 depict the comparison between the critical axial buckling loads obtained directly from MD simulations and those of nonlocal elastic plate models with their proposed appropriate values of nonlocal parameter corresponding to CLPT and FSDT, respectively. It can be seen from the figures that there is an excellent agreement between the two series of the numerical results for both types of boundary conditions which implies the capability of the present nonlocal plate models to predict axial buckling behavior of SLGSs.

Fig. 3
figure 3

Comparison between the results of MD simulations and nonlocal CLPT with its recommended values of nonlocal parameter a armchair SLGSs, b zigzag SLGSs

Full size image
Fig. 4
figure 4

Comparison between the results of MD simulations and nonlocal FSDT with its recommended values of nonlocal parameter a armchair SLGSs, b zigzag SLGSs

Full size image

7 Conclusions

In the present study, axial buckling characteristics of SLGSs with different boundary conditions were investigated. To consider small-scale effects into the buckling analysis, Eringen’s nonlocal elasticity equations were incorporated into various plate theories to develop nonlocal elastic plate models. The discretized forms of the governing differential equations relevant to each type of nonlocal plate model were obtained using generalized differential quadrature (GDQ) method along simply supported and clamped boundary conditions.

Afterward, a series of MD simulations were performed for armchair and zigzag square SLGSs with different side-lengths and boundary conditions, the results of which were matched with those of nonlocal plate models through a nonlinear least-square fitting procedure to find the correct values of nonlocal parameter corresponding to each type of chirality, nonlocal plate model, and boundary conditions. It was observed that the present nonlocal elastic plate models with their recommended values of nonlocal parameter have an excellent capability to predict the axial buckling response of SLGSs.

Moreover, it was found that among the type of boundary conditions, chirality, and nonlocal plate theory, boundary conditions have the most significant influence on the appropriate values of nonlocal parameter for the axial buckling of SLGSs.