1 Introduction

Due to superior mechanical, chemical, thermal and electronic properties, in recent years, nanostructures have been widely interested by many scientists in the micro-electro-mechanical system (MEMs) and nano-electro-mechanical system (NEMs). However, nano experiments and molecular dynamics (MD) simulation is not only difficult but also very expensive, and hence the development of mathematical models in evaluating the mechanical behavior of structures at the nanoscale becomes an urgent problem. In the literature, there are three general types of mathematical models to perform the analysis of nanostructures including atomistic [1], hybrid atomistic continuum mechanics [2] and continuum mechanics. For continuum mechanics, the nonlocal elasticity theory [3, 4], which considers small-scale effects with good accuracy and satisfactory agreements with molecular dynamics has been used. In this theory, the stress at one point is assumed as a function of the strain field at its neighboring. Besides, the inter-atomic forces and the atomic size scales, called the nonlocal parameters, are incorporated into constitutive equations in a nonlocal theory. This nonlocal model showed a good agreement with MD simulations and experiments for free vibration of the nanoplate problems [5–8], and was extensively applied to investigate the various performances of nanoplates [9–21].

Recently, the application of FG materials has been widely spread in nanoscale devices such as thin films [22, 23], and NEMS [24] due to their excellent performance. It is well known that FG materials are the advanced engineering composite materials with continuous variation of material properties from one surface to the other through the thickness and thus eliminate the concentration stress found in laminated composites. Many works have been proposed for the bending, free vibration and buckling analyses of the FG nanoplates considering the small-scale effects. For example, Natarajan et al. [25] investigated the free flexural vibration of FG nanoplates with power-law distribution model and computed the effective properties by the Mori–Tanaka homogenization scheme. Jung and Han [26] studied bending and vibration responses of the Sigmoid FGM nanoplates using the Navier’s solution. Nami et al. [27] analyzed the thermal buckling of the FG rectangular nanoplates with assuming the material properties of FG nanoplates according to the power-law distribution. In this study, the authors used the third-order shear deformation plate theory including nonlocal elasticity to build the governing equations of the nanoplates. Hashemi et al. [28] studied the free vibration of FG circular/annular plates with moderately thick based on the Mindlin plate theory and considered a small-scale effect on natural frequencies. Salehipour et al. [29] established the exact analytical solution of the free vibration of FG micro/nanoplates by the three-dimensional theory of elasticity accounting small-scale effect. Salehipour et al. [30] developed the modified nonlocal elasticity for the examination of the natural frequency of the FG micro/nanoplates. Ansari et al. [31] analyzed the bending and vibration of FG nanoplates with three-dimensional plate theory in conjunction with Eringen’s nonlocal theory. In addition, the use of surface effects or the nonlocal plate theories to investigate for nanostructure behaviors has been conducted in many works. For instance, Karimi et al. [32] combined surface effects and nonlocal refined plate theories to analyze the buckling and vibration of the silver nanoplates. Karimi and Shahidi [33, 34] used the theories of the nonlocal, refined plate, and surface effects to investigate the free vibration response of square and skew magneto-electro-elastic nanoplates resting on elastic foundations. Also, using the Galerkin and Navier’s method to investigate the magnitudes of surface energy stress in synchronous and asynchronous bending/buckling analysis of slanting double-layer was introduced in Ref.[35, 36]. Farajpour et al. [37] developed the Brinson model, nonlocal elasticity and Pasternak foundation model to study the effect of biaxial preload on the vibrational behavior of small-scale composite sheets reinforced by shape memory alloy nanofibers. Karami et al. [38] used the generalized differential quadrature method and nonlocal elasticity theory to examine positive and negative surface effects on the buckling and vibration of nanoplates subjected to biaxial and shear in-plane loadings. In addition, the use of the finite difference method based on surface effects combining with nonlocal elasticity theories was proposed to analyze nanostructures in Refs.[39,40,41,42]. Farajpour et al. [43] proposed an integral form of nonlocal elasticity with two distinct phases to investigate wave propagations in carbon nanotubes conveying nanofluid under the magneto-hygro-mechanical loading. Karimi and Rafieian [44] based on the nonlocal strain gradient and modified couple stress models to investigate the free vibration of BiTiO3–CoFe2O4 nanoplates.

Recently, the nanostructures such as graphene sheets have also been founded to be embedded in various mediums (such as polymer composites) with the aim of enhancing the strength of parent material. To date, some studies have been performed to model the mechanical behaviors of nanostructures embedded in elastic mediums. For example, Wang and Li [45] studied the bending behavior of the nanoplates embedded in an elastic matrix. Narendar and Gopalakrishnan [46] investigated the wave dispersion of a single-layered graphene sheet embedded in an elastic polymer matrix at Terahertz frequency level. Pouresmaeeli et al. [47] examined the vibration of viscoelastic orthotropic nanoplates embedded in a viscoelastic medium. Zenkour and Sobhy [48] investigated thermal buckling of nanoplates resting on the Winkler-Pasternak elastic medium, based on the sinusoidal shear deformation plate theory. Panyatong et al. [49] investigated the bending behavior of nanoplates embedded in an elastic medium including nonlocal elasticity and surface stress. In the above-mentioned works, most of them used analytical solutions to investigate the behavior of FG nanoplates resting on the elastic foundation. However, the analytical solutions are limited or even impossible when the geometry, boundary conditions and types of the load become more complicated. As an alternative, numerical methods have been proposed to overcome the limits of of these problems.

In the other front of developing the numerical methods for plate structures, Shimpi [50] proposed a displacement field with the separation of the bending and shear components to improve the first-order shear deformation theory (FSDT). The most interesting points of this theory are the use of fewer unknowns in the governing equations than the original FSDT and have no requirement of any shear correction factor. Some researchers developed the four-unknown shear deformation theories for the analysis of various problems. Specifically, Mechab et al. [51].conducted the static analysis of the functionally graded plates using the refined plate theory with four unknowns. In this study, the Navier method was used to build the governing equation for the FG plates under the sinusoidal distributed load. Benachour et al. [52] extended the four-unknown refined plate theory and the Navier method to derive the governing equation for free vibration analysis of the FG plates. Thai et al. [53] presented the finite element method using the four-unknown shear deformation theories to study the bending and free vibration analysis for FG plates. Based on the four-unknown shear deformation theories and the nonlocal theory, Sobhy [54] studied the static, free vibration and buckling response of the FG nanoplates resting on the elastic foundation. To the best of authors’ knowledge, most of above-mentioned works only focus on using the finite element method combining the four-unknown shear deformation theories to study for macrostructures, and there have been very few articles using numerical methods for the analysis of FG nanoplates. It hence motivates us to develop a finite element method using the four-unknown shear deformation theory for analysis of the FGP nanoplates.

To fill in the above-mentioned research gaps, this article is performed to develop a finite element method using the four-unknown shear deformation theory and nonlocal theory to accurately describe the stress and the displacement field of the FG nanoplates resting on the elastic foundation. Due to using the techniques of a numerical method, the proposed method will be very suitable to analyze for the complex nanostructures with arbitrary boundary and load conditions. The accuracy and reliability of the proposed method will be demonstrated by comparing the present numerical results with those of published works. Furthermore, the influence of geometrical parameters, material parameters, elastic foundation parameters to the static bending and the free vibrations of the FG nanoplates are also examined. The paper is organized as follows: A brief review of materials and works dealing with this problem is introduced in Sect. 1. Theoretical formulations are presented in Sect. 2. Verification examples, numerical results, and discussions are performed in Sect. 3. Section 4 concludes some highlight results and new contributions of this work.

2 Theoretical formulation

2.1 FG nanoplates resting on elastic foundations

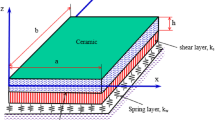
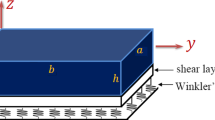
We consider a square FG nanoplate with the length a, the width b and the thickness h, which is made from mixture of ceramics and metals as shown in Fig. 1. The material properties are assumed to change continuously from a top surface (\(z=+h/2\)) to the bottom (\(z=-h/2\)) surface according to a power-law distribution. The FG nanoplates rest on elastic foundations via the Pasternak-type consisting of two overlapping layers. The first layer is expressed as a spring system with the stiffness coefficient \({k}_{w}\), and the second layer is the sliding layer represented as parallel lines with a sliding stiffness coefficient \({k}_{s}.\)

Fig. 1
figure 1

Model of FG nanoplates resting on two-layer elastic foundations

Full size image

The effective property of FG material is given by a power law of volume fraction as:

$$\left\{ {\begin{array}{*{20}l} {P\left( z \right) = P_{m} + \left( {P_{c} - P_{m} } \right)V_{c} } \\ {V_{c} = \left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} } \\ \end{array} } \right.,$$
(1)

where P is the effective material property such as Young's modulus E, mass density ρ, and Poisson's ratio ν; subscripts m and c denote the metallic and ceramic constituents, respectively; and Vc is the volume-fractions of the ceramic, n is the volume-fraction exponent. The volume-fractions of ceramic and metal varying through the thickness via the volume-fraction exponents \(n\) are illustrated in Fig. 2.

Fig. 2
figure 2

Variation of the volume fraction versus the dimensionless thickness

Full size image

2.2 Nonlocal elastic theory

In the classical elasticity theories, the stress tensor at any point only depends on the strain tensor at that point. However, in the nonlocal continuum theory, the stress tensor at a point depends on the strain tensor at all the points of the continuum. According to the nonlocal theory proposed by Eringen [3], the nonlocal constitutive relation of a Hooke solid is given by:

$$\begin{gathered} \sigma_{ij} - \mu \nabla^{2} \sigma_{ij} = \sigma_{ij}^{l} \hfill \\ \sigma_{ij}^{l} = C_{ijkl} \varepsilon_{ij} ;\mu = \left( {e_{0} l} \right)^{2} , \hfill \\ \end{gathered}$$
(2)

where \({\sigma }_{ij}\) is the nonlocal stress tensor; \({\sigma }_{ij}^{l}\) is the local stress tensor; \({C}_{ijkl}\) is the elastic constant-coefficient; \({\varepsilon }_{ij}\) is the local strain tensor; \(\mu\) represents the small-scale effect in nanostructures; \(l\) is an internal characteristic length and \({e}_{0}\) is a constant. \(\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}\) is the two-dimensional Laplacian operator.

2.3 Four-unknown hyperbolic sine shear deformation theory

In present work, the displacement field at any point of the FG nanoplate (\({U}_{1}, {U}_{2}, {U}_{3}\)) is written as [53]:

$$\left\{ {\begin{array}{*{20}l} {U_{1} \left( {x,y,z,t} \right) = u_{0} \left( {x,y,t} \right) - z\frac{{\partial w^{{\text{b}}} }}{\partial x} - f\left( z \right)\frac{{\partial w^{{\text{s}}} }}{\partial x}} \\ {U_{2} \left( {x,y,z,t} \right) = v_{0} \left( {x,y,t} \right) - z\frac{{\partial w^{{\text{b}}} }}{\partial y} - f\left( z \right)\frac{{\partial w^{{\text{s}}} }}{\partial y}} \\ {U_{3} \left( {x,y,z,t} \right) = w^{{\text{b}}} + w^{{\text{s}}} } \\ \end{array} } \right.$$
(3)
$$f\left( z \right) = z - \psi \left( z \right);\,\psi \left( z \right) = h \times \sinh \left( \frac{z}{h} \right) - z \times \cosh \left( \frac{1}{2} \right),$$
(4)

where \({U}_{1}, {U}_{2}, {U}_{3}\) are the displacements in the x, y, and z directions, respectively; \({u}_{0}\) and \({v}_{0}\) are respectively the in-plane displacements of the middle surface; \({w}^{b}\) and \({w}^{s}\) are the bending and shear components of the transverse displacement, respectively. In the general case, the various four unknowns of the displacements \({u}_{0}, {v}_{0}, {w}^{b}\) and \({w}^{s}\) are the function depending on the variables x and y.

The linear strain components of the FG nanoplate are written based on the displacements field in Eq. (3) as follows:

$$\varepsilon_{xx} = \frac{{\partial U_{1} }}{\partial x} = \frac{{\partial u_{0} }}{\partial x} - z\frac{{\partial^{2} w^{{\text{b}}} }}{{\partial x^{2} }} - f\left( z \right)\frac{{\partial^{2} w^{{\text{s}}} }}{{\partial x^{2} }} = u_{0,x} - zw_{,xx}^{{\text{b}}} - f\left( z \right)w_{,xx}^{{\text{s}}}$$
(5)
$$\varepsilon_{yy} = \frac{{\partial U_{2} }}{\partial y} = \frac{{\partial v_{0} }}{\partial y} - z\frac{{\partial^{2} w^{{\text{b}}} }}{{\partial y^{2} }} - f\left( z \right)\frac{{\partial^{2} w^{{\text{s}}} }}{{\partial y^{2} }} = v_{0,y} - zw_{,yy}^{{\text{b}}} - f\left( z \right)w_{,yy}^{{\text{s}}}$$
(6)
$$\begin{aligned} \varepsilon_{xy} & = \frac{{\partial U_{1} }}{\partial y} + \frac{{\partial U_{2} }}{\partial x} = \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} - 2z\frac{{\partial^{2} w^{{\text{b}}} }}{\partial x\partial y} - 2f\left( z \right)\frac{{\partial^{2} w^{{\text{s}}} }}{\partial x\partial y} \\ & = u_{0,y} + v_{0,x} - 2zw_{,xy}^{{\text{b}}} - 2f\left( z \right)w_{,xy}^{{\text{s}}} \\ \end{aligned}$$
(7)
$$\gamma_{xz} = \frac{{\partial U_{1} }}{\partial z} + \frac{{\partial U_{3} }}{\partial x} = g\left( z \right)\frac{{\partial w^{{\text{s}}} }}{\partial x} = g\left( z \right)w_{,x}^{{\text{s}}}$$
(8)
$$\gamma_{yz} = \frac{{\partial U_{2} }}{\partial z} + \frac{{\partial U_{3} }}{\partial y} = g\left( z \right)\frac{{\partial w^{{\text{s}}} }}{\partial y} = g\left( z \right)w_{,y}^{{\text{s}}} ,$$
(9)

where

$$g\left( z \right) = \frac{\partial \psi \left( z \right)}{{\partial z}} = \cosh \left( \frac{z}{h} \right) - \cosh \left( \frac{1}{2} \right).$$
(10)

In Eqs. (8) and (9), the components of the transverse shear strains\({\gamma }_{xz}\),\({\gamma }_{yz}\) are equal to zero on top (\(z=+h/2 )\) and bottom surfaces \(\left(z=-h/2 \right)\) of the FG nanoplate. These formulations can be briefed as vectors as follows:

$${{\varvec{\upvarepsilon}}} = \left\{ {\begin{array}{*{20}l} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ \end{array} } \right\} = {\varvec{\varepsilon}}^{0} + z{\varvec{\varepsilon}}^{1} + f\left( z \right){\varvec{\varepsilon}}^{2} ;{{\varvec{\upgamma}}} = \left\{ {\begin{array}{*{20}l} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = g\left( z \right){\varvec{\gamma}}^{0} ,$$
(11)

where

$${\varvec{\varepsilon}}^{0} = \left\{ {\begin{array}{*{20}l} {u_{0,x} } \\ {v_{0,y} } \\ {u_{0,y} + v_{0,x} } \\ \end{array} } \right\};\;{\varvec{\varepsilon}}^{1} = - \left\{ {\begin{array}{*{20}l} {w_{,xx}^{b} } \\ {w_{,yy}^{b} } \\ {2w_{,xy}^{b} } \\ \end{array} } \right\};\;{\varvec{\varepsilon}}^{2} = - \left\{ {\begin{array}{*{20}l} {w_{,xx}^{s} } \\ {w_{,yy}^{s} } \\ {2w_{,xy}^{s} } \\ \end{array} } \right\};\;\gamma^{0} = \left\{ {\begin{array}{*{20}l} {w_{,x}^{s} } \\ {w_{,y}^{s} } \\ \end{array} } \right\}.$$
(12)

According to the nonlocal elasticity model in Eq. (2), the constitutive relations (between nonlocal stresses and strains) for elastic nanoplates can be given as follows:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{xx} - \mu \nabla^{2} \sigma_{xx} } \\ {\sigma_{yy} - \mu \nabla^{2} \sigma_{yy} } \\ {\sigma_{xy} - \mu \nabla^{2} \sigma_{xy} } \\ {\sigma_{xz} - \mu \nabla^{2} \sigma_{xz} } \\ {\sigma_{yz} - \mu \nabla^{2} \sigma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {C_{11} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & 0 & 0 & 0 \\ 0 & 0 & {C_{66} } & 0 & 0 \\ 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & {C_{44} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{xy} } \\ \end{array} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {{\mathbf{D}}_{b} } & 0 \\ 0 & {{\mathbf{D}}_{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\varvec{\upvarepsilon}}} \\ {{\varvec{\upgamma}}} \\ \end{array} } \right\}$$
(13)

in which \({C}_{ij}\) can be expressed as:

$$\begin{gathered} C_{11} = C_{22} = \frac{E\left( z \right)}{{1 - v\left( z \right)^{2} }};\,C_{12} = \frac{v\left( z \right)E\left( z \right)}{{1 - v\left( z \right)^{2} }};\,C_{66} = C_{55} = C_{44} = \frac{E\left( z \right)}{{2\left( {1 + v\left( z \right)} \right)}} \hfill \\ {\mathbf{D}}_{b} = \left[ {\begin{array}{*{20}l} {C_{11} } & {C_{12} } & 0 \\ {C_{21} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right];\,{\mathbf{D}}_{s} = \left[ {\begin{array}{*{20}l} {C_{55} } & 0 \\ 0 & {C_{44} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(14)

Next, the equations of motion of four unknowns using the hyperbolic sine shear deformation theory are derived from Hamilton’s principle for the FG nanoplate resting on the elastic foundation as:

$$\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left( {\delta U + \delta V - \delta W - \delta T} \right){\text{d}}t = 0,$$
(15)

where \(\delta U,\) \(\delta V, \delta W\) and \(\delta T\) are the variation of the strain energy of the FG nanoplates, the energy stored in the deformed elastic medium, the work done by applied force and the kinetic energy, respectively. The variation of the strain energy can be given as

$$\delta U = \mathop \int \limits_{S}^{{}} \mathop \int \limits_{ - h/2}^{ + h/2} \left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{yy} \delta \varepsilon_{yy} + \sigma_{xy} \delta \varepsilon_{xy} + \sigma_{xz} \delta \gamma_{xz} + \sigma_{yz} \delta \gamma_{xz} } \right){\text{d}}z{\text{d}}S$$
(16)
$$= \int\limits_{{\text{S}}} {\left( {\begin{array}{*{20}l} {N_{xx} \frac{{\partial \delta u_{0} }}{\partial x} - M_{xx} \frac{{\partial^{2} \delta w^{{\text{b}}} }}{{\partial x^{2} }} - L_{xx} \frac{{\partial^{2} \delta w^{{\text{s}}} }}{{\partial x^{2} }} + N_{yy} \frac{{\partial \delta v_{0} }}{\partial y} - M_{yy} \frac{{\partial^{2} \delta w^{{\text{s}}} }}{{\partial y^{2} }}} \hfill \\ { - L_{yy} \frac{{\partial^{2} \delta w^{{\text{s}}} }}{{\partial y^{2} }} + N_{xy} \left( {\frac{{\partial \delta u_{0} }}{\partial y} + \frac{{\partial \delta v_{0} }}{\partial x}} \right) - 2M_{xy} \frac{{\partial^{2} \delta w^{{\text{b}}} }}{\partial x\partial y} - } \hfill \\ {2L_{xy} \frac{{\partial^{2} \delta w^{{\text{s}}} }}{\partial x\partial y} + Q_{xz} \frac{{\partial \delta w^{{\text{s}}} }}{\partial x} + Q_{yz} \frac{{\partial \delta w^{{\text{s}}} }}{\partial y}} \hfill \\ \end{array} } \right)} {\text{d}}S.$$
(17)

The variation of the energy stored in the deformed elastic foundation is expressed by

$$\delta V = \mathop \int \limits_{{\text{S}}}^{{}} R\delta \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right){\text{d}}S,$$
(18)

where \(R={k}_{w}\left({w}^{b}+{w}^{s}\right)-{k}_{s}{\nabla }^{2}\left({w}^{b}+{w}^{s}\right)\) is the reaction force of an elastic foundation.

The variation of work done by applied force can be expressed by

$$\delta W = \mathop \int \limits_{{\text{S}}}^{{}} - q\left( {x,y} \right) \delta \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right){\text{d}}S$$
(19)

The variation of kinetic energy is given by

$$\delta T = \mathop \int \limits_{{\text{S}}}^{{}} \mathop \int \limits_{ - h/2}^{ + h/2} \rho \left( z \right)\left( {\dot{U}_{1} \delta \dot{U}_{1} + \dot{U}_{2} \delta \dot{U}_{2} + \dot{U}_{3} \delta \dot{U}_{3} } \right){\text{d}}z{\text{dS}}$$
(20)
$$= \int\limits_{{\text{S}}} {\left( {\begin{array}{*{20}l} {I_{0} \left( {\dot{u}_{0} \delta \dot{u}_{0} + \dot{v}_{0} \delta \dot{v}_{0} + \left( {\dot{w}^{{\text{b}}} + \dot{w}^{{\text{s}}} } \right)\delta \left( {\dot{w}^{{\text{b}}} + \dot{w}^{{\text{s}}} } \right)} \right) - } \hfill \\ {I_{1} \left( {\dot{u}_{0} \delta \dot{w}_{,x}^{{\text{b}}} + \dot{w}_{,x}^{{\text{b}}} \delta \dot{u}_{0} + \dot{v}_{0} \delta \dot{w}_{,y}^{{\text{b}}} + \dot{w}_{,x}^{{\text{b}}} \delta \dot{v}_{0} } \right) + I_{2} \left( {\dot{w}_{,x}^{{\text{b}}} \delta \dot{w}_{,x}^{{\text{b}}} + \dot{w}_{,y}^{{\text{b}}} \delta \dot{w}_{,y}^{{\text{b}}} } \right) - } \hfill \\ {J_{1} \left( {\dot{u}_{0} \delta \dot{w}_{,x}^{{\text{s}}} + \dot{w}_{,x}^{{\text{s}}} \delta \dot{u}_{0} + \dot{v}_{0} \delta \dot{w}_{,y}^{{\text{s}}} + \dot{w}_{,y}^{{\text{s}}} \delta \dot{v}_{0} } \right) + K_{2} \left( {\dot{w}_{,x}^{{\text{s}}} \delta \dot{w}_{,x}^{{\text{s}}} + \dot{w}_{,y}^{{\text{s}}} \delta \dot{w}_{,y}^{{\text{s}}} } \right) + } \hfill \\ {J_{2} \left( {\dot{w}_{,x}^{{\text{b}}} \delta \dot{w}_{,x}^{{\text{s}}} + \dot{w}_{,x}^{{\text{s}}} \delta \dot{w}_{,x}^{{\text{b}}} + \dot{w}_{,y}^{{\text{b}}} \delta \dot{w}_{,y}^{{\text{s}}} + \dot{w}_{,y}^{{\text{s}}} \delta \dot{w}_{,y}^{{\text{b}}} } \right)} \hfill \\ \end{array} } \right){\text{d}}S} ,$$
(21)

where \(S\) is the area of the element.

By substituting Eqs. (16), (18), (19) and (20) into Eq. (15) and integrating by parts, the equations of motion of FG nanoplates can be obtained as:

$$\delta u_{0} :N_{xx,x} + N_{xy,y} = I_{0} \ddot{u}_{0} - I_{1} \ddot{w}_{,x}^{{\text{b}}} - J_{1} \ddot{w}_{,x}^{{\text{s}}}$$
(22)
$$\delta v_{0} :N_{yy,y} + N_{xy,x} = I_{0} \ddot{v}_{0} - I_{1} \ddot{w}_{,y}^{{\text{b}}} - J_{1} \ddot{w}_{,y}^{{\text{s}}}$$
(23)
$$\begin{gathered} \delta w^{{\text{b}}} :M_{xx,xx} + 2M_{xy,xy} + M_{yy,yy} + q\left( {x,y} \right) - k_{w} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) + k_{{\text{s}}} \nabla^{2} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) \hfill \\ = I_{0} \left( {\ddot{w}^{{\text{b}}} + \ddot{w}^{{\text{s}}} } \right) + I_{1} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - I_{2} \nabla^{2} \ddot{w}^{{\text{b}}} - J_{2} \nabla^{2} \ddot{w}^{{\text{s}}} \hfill \\ \end{gathered}$$
(24)
$$\begin{aligned} & \delta w^{{\text{s}}} :L_{xx,xx} + 2L_{xy,xy} + L_{yy,yy} + Q_{xz,x} + Q_{yz,y} + q\left( {x,y} \right) - k_{w} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) \\ & \quad + k_{{\text{s}}} \nabla^{2} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) \\ & = I_{0} \left( {\ddot{w}^{{\text{b}}} + \ddot{w}^{{\text{s}}} } \right) + J_{1} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - J_{2} \nabla^{2} \ddot{w}^{{\text{b}}} - K_{2} \nabla^{2} \ddot{w}^{{\text{s}}} , \\ \end{aligned}$$
(25)

where the dot (.) superscript convention indicates differentiation with respect to the time variable t; \(q\left(x,y\right)\) is the transverse load, and \(({I}_{i, }{J}_{j}, {K}_{k})\) are the mass moment of inertia defined by

$$(I_{0} ,I_{1} ,I_{2} ,J_{1} ,J_{2} ,K_{2} ) = \mathop \int \limits_{{\frac{ - h}{2}}}^{\frac{h}{2}} \left( {1,z,z^{2} ,f\left( z \right),zf\left( z \right),f\left( z \right)^{2} } \right)\rho \left( z \right){\text{d}}z.$$
(26)

The local stress resultants are given as

$$\left\{ {N_{ij}^{l} ;M_{ij}^{l} ;L_{ij}^{l} } \right\} = \mathop \int \limits_{{\frac{ - h}{2}}}^{\frac{h}{2}} \sigma_{ij}^{l} \left\{ {1;z;f\left( z \right)} \right\}{\text{d}}z;ij = xx,yy,xy$$
(27)
$$\left\{ {Q_{xz}^{l} ;Q_{yz}^{l} } \right\} = \mathop \int \limits_{{\frac{ - h}{2}}}^{\frac{h}{2}} \left\{ {\sigma_{xz}^{l} ;\sigma_{yz}^{l} } \right\}g\left( z \right){\text{d}}z.$$
(28)

Substituting Eq. (11) into Eq. (13) and subsequent results into Eqs. (27) and (28), the stress resultants in terms of displacement fields \(({u}_{0}, {v}_{0}, {w}^{b}\) and \({w}^{s})\) for a nonlocal model can be introduced as follows:

$$\left\{ {N_{xx} N_{yy}N_{xy}}\right\}^{T} - \mu \nabla^{2} \left\{ {N_{xx}N_{yy}N_{xy} } \right\}^{T} = {\varvec{A}\varepsilon }^{0} + {\varvec{B}\varepsilon }^{1} + {\varvec{B}}^{b} {\varvec{\varepsilon}}^{2} ;$$
(29)
$$\left\{ {M_{xx} M_{yy} M_{xy} } \right\}^{T} - \mu \nabla^{2} \left\{ {M_{xx} M_{yy} M_{xy} } \right\}^{T} = {\varvec{B}\varepsilon }^{0} + {\varvec{B}\varepsilon }^{1} + {\varvec{F}}^{b} {\varvec{\varepsilon}}^{2} ;$$
(30)
$$\left\{ {L_{xx} L_{yy} L_{xy} } \right\}^{T} - \mu \nabla^{2} \left\{ {L_{xx} L_{yy} L_{xy} } \right\}^{T} = {\varvec{B}}^{b} {\varvec{\varepsilon}}^{0} + {\varvec{F}}^{b} {\varvec{\varepsilon}}^{1} + {\varvec{H}\varepsilon }^{2} ;$$
(31)
$$\left\{ {Q_{xz} Q_{yz} } \right\}^{T} - \mu \nabla^{2} \, \left\{ {Q_{xz} Q_{yz} } \right\}^{T} = {\varvec{A}}^{b} {\varvec{\gamma}}^{0} ;$$
(32)

where:

$$\left( {{\varvec{A}},{\varvec{B}},{\varvec{B}}^{b} ,{\varvec{F}},{\varvec{F}}^{b} ,{\varvec{H}}} \right) = \mathop \int \limits_{{\frac{ - h}{2}}}^{\frac{h}{2}} {\varvec{D}}_{b} (1,z,f\left( z \right),z^{2} ,zf\left( z \right),f\left( z \right)^{2} ){\text{d}}z;{\varvec{A}}^{b} = \mathop \int \limits_{{\frac{ - h}{2}}}^{\frac{h}{2}} {\varvec{D}}_{s} g^{2} \left( z \right){\text{d}}z,$$
(33)

Next, substituting Eqs. (29)–(33) into Eqs. (22)–(25), the equations of motion can be rewritten in terms of displacements as follows:

$$N_{xx,x} + N_{xy,y} = \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} \ddot{u}_{0} - I_{1} \ddot{w}_{,x}^{{\text{b}}} - J_{1} \ddot{w}_{,x}^{{\text{s}}} } \right)$$
(34)
$$N_{xy,x} + N_{yy,y} = \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} \ddot{v}_{0} - I_{1} \ddot{w}_{,y}^{{\text{b}}} - J_{1} \ddot{w}_{,y}^{{\text{s}}} } \right)$$
(35)
$$\left( {1 - \mu \nabla^{2} } \right)\left( {\begin{array}{*{20}l} {\left ({M_{xx,xx} + 2M_{xy,xy} + M_{yy,yy} } \right)}= \hfill \\ { - q\left( {x,y} \right) + k_{w} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) - k_{s} \nabla^{2} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) + } \hfill \\ {I_{0} \left( {\ddot{w}_{{}}^{{\text{b}}} + \ddot{w}_{{}}^{{\text{s}}} } \right) + I_{1} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - I_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{b}}} - J_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{s}}} } \hfill \\ \end{array} } \right)$$
(36)
$$\left( {1 - \mu \nabla^{2} } \right)\left( {\begin{array}{*{20}l} {L_{xx,xx} + 2L_{xy,xy} + L_{yy,yy} + Q_{xz,x} + Q_{yz,y} = } \hfill \\ { - q\left( {x,y} \right) + k_{w} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) - k_{s} \nabla^{2} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right)} \hfill \\ { + I_{0} \left( {\ddot{w}_{{}}^{{\text{b}}} + \ddot{w}_{{}}^{{\text{s}}} } \right) + J_{1} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - J_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{b}}} - K_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{s}}} } \hfill \\ \end{array} } \right)$$
(37)

Finally, the variation form or weak forms can be obtained for Eqs. (34)–(37) by multiplying them with (\({\delta u}_{0}, {\delta v}_{0}, {\delta w}^{b} and {\delta w}^{s})\) respectively, and integrating over the element domain \(S\) and adding together the same sides of each equation, we obtain the following results

$$\mathop \int \limits_{{\text{S}}} \left( {N_{xx} \delta u_{0,x} + N_{xy} \delta u_{0,y} - \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} \ddot{u}_{0} - I_{1} \ddot{w}_{,x}^{{\text{b}}} - J_{1} \ddot{w}_{,x}^{{\text{s}}} } \right)\delta u_{0} } \right){\text{d}}S = 0$$
(38)
$$\mathop \int \limits_{{\text{S}}} \left( {N_{xy} \delta v_{0,x} + N_{yy} \delta v_{0,y} - \left( {1 - \mu \nabla^{2} } \right)\left( {I_{0} \ddot{v}_{0} - I_{1} \ddot{w}_{,y}^{{\text{b}}} - J_{1} \ddot{w}_{,y}^{{\text{s}}} } \right)\delta v_{0} } \right){\text{d}}S = 0$$
(39)
$$\int\limits_{{\text{S}}} {\left( {\begin{array}{*{20}l} {M_{xx} \delta w_{,xx}^{{\text{b}}} + 2M_{xy} \delta w_{,xy}^{{\text{b}}} + M_{yy} \delta w_{,yy}^{{\text{b}}} - } \hfill \\ {\left( {1 - \mu \nabla^{2} } \right)\left( {\begin{array}{*{20}l} { - q\left( {x,y} \right) + k_{w} \left( {w^{{\text{b}}} + w^{{\text{s}}} } \right) - k_{s} \nabla^{2} \left( {w^{E} + w^{{\text{E}}} } \right) + } \hfill \\ {I_{0} \left( {\ddot{w}_{{}}^{{\text{b}}} + \ddot{w}_{{}}^{{\text{s}}} } \right) + I_{1} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - I_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{b}}} - J_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{s}}} } \hfill \\ \end{array} } \right)\delta w^{{\text{b}}} } \hfill \\ \end{array} } \right)} {\text{d}}S = 0$$
(40)
$$\int\limits_{{\text{S}}} {\left( {\begin{array}{*{20}l} {L_{xx} \delta w_{,xx}^{{\text{s}}} + 2L_{xy} \delta w_{,xy}^{{\text{s}}} + L_{yy} \delta w_{,yy}^{{\text{s}}} + Q_{xz} \delta w_{,x}^{{\text{s}}} + Q_{yz} \delta w_{,y}^{{\text{s}}} - } \hfill \\ {\left( {1 - \mu \nabla^{2} } \right)\left( {\begin{array}{*{20}l} { - q\left( {x,y} \right) + k_{w} \left( {w^{b} + w^{{\text{s}}} } \right) - k_{s} \nabla^{2} \left( {w^{{\text{b}}} + w^{s} } \right)} \\ { + I_{0} \left( {\ddot{w}_{{}}^{{\text{b}}} + \ddot{w}_{{}}^{{\text{s}}} } \right) + J_{1} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - J_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{b}}} - K_{2} \nabla^{2} \ddot{w}_{{}}^{{\text{s}}} } \\ \end{array} } \right)\delta w^{{\text{s}}} } \hfill \\ \end{array} } \right)} {\text{d}}S = 0$$
(41)

2.4 Finite element formulation

In this work, the four-node plate element with 8 degrees of freedom for each node as shown in Fig. 3 is used, the nodal displacement vector can be defined as follows

$${\varvec{q}}_{{\text{e}}} = \left[ {\begin{array}{*{20}l} {{\varvec{q}}_{1}^{{\text{T}}} } & {{\varvec{q}}_{2}^{{\text{T}}} } & {{\varvec{q}}_{3}^{{\text{T}}} } \\ \end{array} {\varvec{q}}_{4}^{{\text{T}}} } \right]^{{\text{T}}}$$
(42)
Fig. 3
figure 3

Four-node element plate

Full size image

The displacements at the node \(i, (i=1/4)\) are expressed as:

$${\varvec{q}}_{i} = \left\{ {\begin{array}{*{20}l} {u_{0i} } & {v_{0i} } & {w_{i}^{{\text{b}}} } & {w_{i}^{{\text{s}}} } & {w_{i,x}^{{\text{b}}} } & {w_{i,x}^{{\text{s}}} } & {w_{i,y}^{{\text{b}}} } & {w_{i,y}^{{\text{s}}} } \\ \end{array} } \right\}$$
(43)

The displacement field of the plate element is interpolated through the displacement node as:

$$\left\{ {\begin{array}{*{20}l} {u_{0} = {\varvec{N}}_{u} {\varvec{q}}_{e} ;v_{0} = {\varvec{N}}_{v} {\varvec{q}}_{e} ;w^{{\text{b}}} = {\varvec{N}}_{wb} {\varvec{q}}_{e} ;w^{{\text{s}}} = {\varvec{N}}_{ws} {\varvec{q}}_{e} ;} \\ {w_{i,x}^{{\text{b}}} = {\varvec{N}}_{wb,x} {\varvec{q}}_{e} ;w_{i,y}^{{\text{b}}} = {\varvec{N}}_{wb,y} {\varvec{q}}_{e} ;w_{i,x}^{{\text{s}}} = {\varvec{N}}_{ws,x} {\varvec{q}}_{e} ;w_{i,y}^{{\text{s}}} = {\varvec{N}}_{ws,y} {\varvec{q}}_{e} } \\ \end{array} } \right.,$$
(44)

where \({{\varvec{N}}}_{u},{{\varvec{N}}}_{v},{{\varvec{N}}}_{wb},{{\varvec{N}}}_{ws}\) are the shape functions with size (1 × 32)

$$\left\{ {\begin{array}{*{20}l} {N_{u} = \left[ {\begin{array}{*{20}c} {N_{1}^{{\left( 1 \right)}} } & {N_{2}^{{\left( 1 \right)}} } & {N_{3}^{{\left( 1 \right)}} } & {N_{4}^{{\left( 1 \right)}} } \\ \end{array} } \right];\;N_{v} = \left[ {\begin{array}{*{20}l} {N_{1}^{{\left( 2 \right)}} } & {N_{2}^{{\left( 2 \right)}} } & {N_{3}^{{\left( 2 \right)}} } & {N_{4}^{{\left( 2 \right)}} } \\ \end{array} } \right];} \\ {N_{{wb}} = \left[ {\begin{array}{*{20}l} {N_{1}^{{\left( 3 \right)}} } & {N_{2}^{{\left( 3 \right)}} } & {N_{3}^{{\left( 3 \right)}} } & {N_{4}^{{\left( 3 \right)}} } \\ \end{array} } \right];\;N_{{ws}} = \left[ {\begin{array}{*{20}l} {N_{1}^{{\left( 4 \right)}} } & {N_{2}^{{\left( 4 \right)}} } & {N_{3}^{{\left( 4 \right)}} } & {N_{4}^{{\left( 4 \right)}} } \\ \end{array} } \right];} \\ \end{array} } \right.$$
(45)

The shape functions \({{\varvec{N}}}_{i}^{(j)}\left(j=1\div4\right)\) in Eq. (45) have the size (1 × 8)

$$\left\{ {\begin{array}{*{20}l} {N_{i}^{{\left( 1 \right)}} = \left\{ {\begin{array}{*{20}l} {\lambdabar _{i} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right\}};\, \\ {N_{i}^{{\left( 2 \right)}} = \left\{ {\begin{array}{*{20}l} 0 & {\lambdabar _{i} } & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right\}};\, \\ {N_{i}^{{\left( 3 \right)}} = \left\{ {\begin{array}{*{20}l} 0 & 0 & {\hbar _{{3i - 2}} } & 0 & {\hbar _{{3i - 1}} } & 0 & {\hbar _{{3i}} } & 0 \\ \end{array} } \right\}};\, \\ {N_{i}^{{\left( 4 \right)}} = \left\{ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hbar _{{3i - 2}} } & 0 & {\hbar _{{3i - 1}} } & 0 & {\hbar _{{3i}} } \\ \end{array} } \right\}.} \\ \end{array} } \right.,$$
(46)

where \(\lambdabar_{i}(i=1\div4)\) is the Lagrange interpolation functions and \({\hbar }_{k }(k=1\div12)\) is the Hermit interpolation functions. The functions are given by Appendix A.

Next, substituting Eq. (44) into Eqs. (38) and (41), the finite element model for the static and vibration analysis of the FG nanoplates resting on the elastic foundation, respectively, can be expressed as:

$${\varvec{M}}_{e} {\ddot{\varvec{q}}}_{e} + {\varvec{K}}_{e} {\varvec{q}}_{e} = 0,$$
(47)
$${\varvec{K}}_{e} {\varvec{q}}_{e} = {\varvec{P}}_{e}$$
(48)

in which \({{\varvec{K}}}_{e}\) represent the stiffness matrices; \({{\varvec{M}}}_{e}\) is the mass matrices and \({{\varvec{P}}}_{e}\) is the load vector of each nanoplate element and the matrices are computed as:

$${\varvec{K}}_{e} = {\varvec{K}}_{e}^{{\text{b}}} + {\varvec{K}}_{e}^{{\text{s}}} + {\varvec{K}}_{e}^{{{\text{fou}}}}$$
(49)

with

$${\varvec{K}}_{e}^{{\text{b}}} = \mathop \int \limits_{{\text{S}}} \left[ {\begin{array}{*{20}l} {{\varvec{B}}_{1}^{{\text{T}}} } & {{\varvec{B}}_{2}^{{\text{T}}} } & {{\varvec{B}}_{3}^{{\text{T}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\varvec{A}} & {\varvec{B}} & {{\varvec{B}}^{{\text{b}}} } \\ {\varvec{B}} & {\varvec{F}} & {{\varvec{F}}^{{\text{b}}} } \\ {{\varvec{B}}^{{\text{b}}} } & {{\varvec{F}}^{{\text{b}}} } & {\varvec{H}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\varvec{B}}_{1} } \\ {{\varvec{B}}_{2} } \\ {{\varvec{B}}_{3} } \\ \end{array} } \right]{\text{d}}S$$
(50)
$${\varvec{K}}_{e}^{{\text{s}}} = \mathop \int \limits_{{\text{S}}}^{{}} \left( {{\varvec{B}}_{1}^{{\text{b}}} } \right)^{{\text{T}}} {\varvec{A}}^{{\text{b}}} {\varvec{B}}_{1}^{{\text{b}}} {\text{d}}S$$
(51)
$${\varvec{K}}_{e}^{{{\text{fou}}}} = \int\limits_{{\text{S}}} {\left( {\begin{array}{*{20}l} {k_{w} \left[ {{\varvec{B}}_{w}^{{\text{T}}} {\varvec{B}}_{w} + \mu \left( {{\varvec{B}}_{wx}^{{\text{T}}} {\varvec{B}}_{wx} + {\varvec{B}}_{wy}^{{\text{T}}} {\varvec{B}}_{wy} } \right)} \right] + k_{{\text{s}}} \left( {{\varvec{B}}_{wx}^{{\text{T}}} {\varvec{B}}_{wx} + {\varvec{B}}_{wy}^{{\text{T}}} {\varvec{B}}_{wy} } \right)} \\ { + \mu k_{s} \left( {{\varvec{B}}_{wx2}^{{\text{T}}} {\varvec{B}}_{wx2} + {\varvec{B}}_{wy2}^{{\text{T}}} {\varvec{B}}_{wy2} + {\varvec{B}}_{wx2}^{{\text{T}}} {\varvec{B}}_{wy2} + {\varvec{B}}_{wy2}^{{\text{T}}} {\varvec{B}}_{wx2} } \right)} \\ \end{array} } \right)} {\text{d}}S$$
(52)
$$\user2{\rm M}_{e} = \mathop \int \limits_{{\text{S}}} \left[ {{\varvec{N}}^{{\text{T}}} {\varvec{D}}_{m} {\varvec{N}} + \mu \left( {{\varvec{N}}_{x}^{{\text{T}}} {\varvec{D}}_{m} {\varvec{N}}_{x} + {\varvec{N}}_{y}^{{\text{T}}} {\varvec{D}}_{m} {\varvec{N}}_{y} } \right)} \right]{\text{d}}S$$
(53)
$$\begin{aligned} {\varvec{P}}_{e} & & = \mathop \int \limits_{{\text{S}}} \left( {1 - \mu \nabla^{2} } \right)q\left( {x,y} \right){\varvec{B}}_{w}^{T} {\text{d}}S \\ & \quad = \mathop \int \limits_{{\text{S}}} q{\varvec{B}}_{w}^{T} {\text{d}}S - \mu \mathop \int \limits_{{\text{S}}} q\left( {x,y} \right)\left( {{\varvec{B}}_{w,xx}^{T} + {\varvec{B}}_{w,yy}^{T} } \right){\text{d}}S - \mu \mathop \int \limits_{{\text{S}}} {\varvec{B}}_{w}^{T} \left( {q_{,xx} \left( {x,y} \right) + q_{,yy} \left( {x,y} \right)} \right){\text{d}}S \\ \end{aligned}$$
(54)

in which the unknown variables are the strain matrices and defined in Appendix B.

3 Numerical results and discussions

In this section, several numerical examples are performed to investigate the influences of some geometric parameters, material properties, the elastic foundations, the nonlocal parameters and the various boundary conditions on the responses of the bending and the free vibration of FG nanoplates resting on the elastic foundation. In most examples of this paper, the FG nanoplates are made from the material properties: \(Al/{Al}_{2}{O}_{3}\) with the ceramics are \({Al}_{2}{O}_{3}\); \(Al\) represents the metals. The length of the nanoplates is a = 10 nm. For finite element analysis, this work uses Gauss integral 2 × 2 to calculate the stiffness matrices, the mass matrices and the load vector of the nanoplate elements. The boundary condition symbols are used in this study: C (clamped), S (simple supported), and F (free) as shown in Fig. 4.

Fig. 4
figure 4

Boundary conditions of the nanoplates

Full size image

For convenience in comparing its numerical results with the exact solutions in the literature, the following dimensionless forms are given:

$$\begin{aligned} {\text{w}}^{**} & = {\text{w}}_{{\max}} \times \frac{{100E_{c} h^{3} }}{{q_{0} a^{4} }};\,{\text{w}}_{1} = {\text{w}}_{{\max}} \times \frac{{100E_{c} h^{3} }}{{12\left( {1 - v^{2} } \right)q_{0} a^{4} }};\,\sigma_{xx}^{**} \left( z \right) = \frac{10h}{{q_{0} a}}\sigma_{xx} \left( {\frac{a}{2},\frac{b}{2},z} \right);\, \\ \sigma_{xy}^{**} \left( z \right) & = \frac{10h}{{q_{0} a}}\sigma_{xy} \left( {0,0,z} \right);\, \sigma_{xz}^{**} \left( z \right) = \frac{10h}{{q_{0} a}}\sigma_{xz} \left( {0,\frac{b}{2},z} \right); \,\\ \Omega^{*} & = \omega_{11} \frac{{a^{2} }}{h}\sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-\nulldelimiterspace} {E_{c} }}} ;\,\Omega = \omega_{11} h\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}} ;\,\Omega_{1} = \omega_{11} h\sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-\nulldelimiterspace} {E_{c} }}} \\ K_{w} & = \frac{{(k_{w} a^{4} )}}{{D_{c} }};\,K_{s} = \frac{{(k_{s} a^{2} )}}{{D_{c} }};\,K_{w} 1 = \frac{{(k_{w} a^{4} )}}{{D_{m} }};K_{s} 1 = \frac{{(k_{s} a^{2} )}}{{D_{m} }};D_{c} = \frac{{(E_{c} h^{3} )}}{{12(1 - \nu_{c}^{2} )}};D_{m} = \frac{{(E_{m} h^{3} )}}{{12(1 - \nu_{m}^{2} )}} \\ \end{aligned}$$

The sinusoidal distributed load has the form of \(q(x,y)={q}_{0}sin(\frac{\pi x}{a})sin(\frac{\pi y}{b})\), \(where {q}_{0}\) is the maximum load at the central point of the plate.

3.1 Convergence and accuracy study

Before evaluating the accuracy and the convergence of the present finite formulation for analysis of FG nanoplates, this part conducts some analysis of the FG plates and compares their results with those available in the literature. Firstly, we investigate the bending and free vibration responses of the simply supported FG plate (the length \(a=10\) and \(h=1\)) subjected to the sinusoidal load. Table 1 provides the results of dimensionless deflection \({\text{w}}_{1}\) by the proposed method for the uniform meshes \(2\times 2, 4\times 4. 8\times 8. 10\times 10. 16\times 16\) and \(20\times 20\) and compared with the results by Thai et al. [55, 56]. From Table 1, it is observed that the numerical results of the bending and free vibration responses of the present method agree well with those given in Ref [55]. with mesh size \(10\times 10\), and those in Ref [56]. with mesh size \(8\times 8\), respectively. Hence in this paper, the model of the nanoplates will use the mesh size \(10\times 10\) and \(8\times 8\) for the bending and the free vibration analysis, respectively.

Table 1 The convergence of dimensionless deflection \({w}_{1}\) and fundamental frequency \({\Omega }_{1}\) of SSSS square plate under sinusoidal loads (a/h = 10)
Full size table

Next, Table 2 presents the numerical results of the dimensionless central deflections \({w}^{**},\) the dimensionless in-plane normal stress \({\sigma }_{xx}^{**}(h/2)\), the dimensionless in-plane shear stress \({\sigma }_{xy}^{**}(-h/3)\) and the dimensionless transverse shear stress \({\sigma }_{xz}^{**}(0)\) of the simply supported \({Al}_{2}{O}_{3}/Al\) square plate (with the length and thickness ratio a/h = 10) subjected to sinusoidal load with the volume-fraction exponent varying from 0 to 5 (n = 0, 1, 2, 5) and the various foundation stiffness \({K}_{w}\) and \({K}_{s}\). It is found that the present results match well with the exact solution produced by Ameur et al. [57].

Table 2 The dimensionless deflection of the simply supported FG plate resting on the elastic foundation under the sinusoidal distributed load
Full size table

Next, Table 3 shows the numerical results of the dimensionless center deflection of the isotropic nanoplates subjected to the uniform load \({q}_{0}=1\). The nanoplate has the length and thickness ratio \(a/h=10\), width-to-length ratio \(b/a=1,2\); and the material properties \(E=30\times {10}^{6}, v=0.3\). The results of the proposed method are compared with the Navier’s exact solution of Aghababaei and Reddy [58]. It is seen that the present results are in a good agreement with those given in Ref.[58].

Table 3 The dimensionless deflection and stress of the simply supported isotropic nanoplates versus to the variation of length-to-width ratio and nonlocal coefficient under the sinusoidal distributed load
Full size table

Next, Table 4 displays the numerical results of the dimensionless frequency \(\Omega\) of the square FG nanoplates made from \({Si}_{3}{N}_{4}/{SU}_{3}{S}_{3}{O}_{4}\) as given in Table 5. The FG nanoplates have the length-to-thickness ratio (\(a/h=5, 10, 20, 50\)), the nonlocal coefficient \(\mu =0/4\) and the volume-fraction exponent varies from 0 and \(\infty\) (\(n=0, 1, 5, \infty )\). It can be seen that the present results agree well with the Navier’s exact solutions performed by Sobhy [59]. Table 6 shows the results of the dimensionless frequency \(\Omega\) of the square FG nanoplates with aluminum at the bottom surface and zirconia at the top surface \((Al/{Al}_{2}{O}_{3})\) resting on the elastic foundation. The various foundation stiffness coefficient \({K}_{w1}\), \({K}_{s1}\), the volume-fraction exponent \(n\) \((n=0.5 and 2\)), the nonlocal coefficient \(\mu =1\) and length-to-thickness ratio \(a/h=5\) are examined in this table. It can be found that the increase of the elastic foundation stiffness leads to the increase of the dimensionless fundamental frequency \(\Omega\) and the increase of the volume-fraction exponents \(n\) leads to the reduce of the dimensionless fundamental frequency \(\Omega\). This implies that the increase of the volume-fraction exponents \(n\) makes the FG nanoplates become weaker. It is seen again that the present finite element formulation shows a very good agreement with those produced by Panyatong et al. [60].

Table 4 The dimensionless fundamental frequency \(\Omega\) of the simply supported FG nanoplates versus to the variation of the volume-fraction exponent \(n\), the nonlocal coefficient \(\mu\) and the length- to-thickness ratio \(a/h\)
Full size table
Table 5 Material properties of the FG nanoplates
Full size table
Table 6 The dimensionless fundamental frequency \(\Omega\) of the simply supported FG nanoplates versus to the variation of the volume-fraction exponent \(n\) and the elastic foundation coefficient \((\mu =1, a/h =5, SSSS)\)
Full size table

Through the above-compared results, it can be found that the proposed finite element formulation is accurate and reliable. In addition, it is suitable for analysis of the thick and thin nanoplates which do not requirement any shear correction factor.

3.2 Static bending problem

This sub-section investigates the effects of the nonlocal coefficient \(\mu\), the elastic foundation stiffnesses \({K}_{w}\), \({K}_{s}\), the volume-fraction exponent \(n\) and the geometric parameters such as length-to-thickness ratio (\(a/h)\), width-to-length ratio \(b/a)\), the various boundary conditions on the maximum deflection \({w}^{**}\), the in-plane normal stress \({\sigma }_{xx}^{**}(z)\), the in-plane shear stress \({\sigma }_{xy}^{**}(z)\) and the transverse shear stress \({\sigma }_{xz}^{**}(z)\) of the FG nanoplates resting on elastic foundation. The material properties of FG nanoplates are given in Table 5.

Table 3 presents the results of the dimensionless central deflection \({w}^{**}\) and comparison with those given by Aghababaei and Reddy [58]. In addition, Table 3 also shows the values of the in-plane normal stress \({\sigma }_{xx}^{**} (h/2)\), the in-plane shear stress \({\sigma }_{xy }^{**}(-h/3)\) and the transverse shear stress \({\sigma }_{xz}^{**}(0)\). It is seen that the obtained results agree well with published results in Ref.[58]. It is also found that the increase of the nonlocal coefficient \(\mu\) leads to the increase of the transverse displacements, the in-plane normal stress, the in-plane shear stress and the transverse shear stress. This is because the increase of the nonlocal coefficient \(\mu\) leads to the larger detachment of the distance between molecules and thus makes the structural stiffness decrease.

Table 7 and Table 8 show the dimensionless central deflection \({w}^{**}\) and the in-plane normal stress \({\sigma }_{xx}^{**} (h/2)\) of the simply supported nanoplates resting on the elastic foundation subjected to the uniform distribution load and the sinusoidal distribution load, respectively. The variation of the elastic foundation coefficient, the volume-fraction exponent \((n=0.5, 1, 5, 10)\) and the nonlocal coefficient \(\mu\) (from \(0\) to \(4)\) are examined in these tables. The results show that the values of the dimensionless central deflection \({w}^{**}\) and the in-plane normal stress \({\sigma }_{xx}^{**} (h/2)\) of the FG nanoplates without resting on elastic foundation increase rapidly as the nonlocal coefficient \(\mu\) and the volume-fraction exponent n increase. However, it is noted for the case of the FG nanoplates resting on the elastic foundation that the dimensionless central deflection \({w}^{**}\) and the in-plane normal stress \({\sigma }_{xx}^{**} (h/2)\) increase slowly versus to the increase of the elastic foundation coefficient. It is observed that the elastic foundation makes the nanoplates become much harder and hence makes both the displacement and stress of nanoplates decrease.

Table 7 The dimensionless deflection and maximum in-plane normal stress of the FG nanoplates resting on the elastic foundation versus to the variation of the volume-fraction exponent and nonlocal coefficient under the uniform distributed load
Full size table
Table 8 The dimensionless deflection and maximum in-plane normal stress of the FG nanoplates resting on the elastic foundation versus to the variation of the volume-fraction exponent and nonlocal coefficient under the sinusoidal distributed load
Full size table

Let us next consider the FG nanoplates with the length-to-thickness ratio a/h = 10 resting on the elastic foundation with the foundation stiffness \({K}_{w}={K}_{s}=10\) under the sinusoidally distributed load. Table 9 shows the influence of the boundary conditions on the dimensionless central deflection \({w}^{**}\) of the FG nanoplates. The obtained results of FG nanoplates with the different boundary conditions can help fill in the gap that the analytical method is missing in published works. The values of displacement decrease gradually corresponding to the following order of boundary conditions: CFFF, CCFF, SSSS, CFCF, CSSS, CCCS, CCCC.

Table 9 The variation of the dimensionless deflection of the FG nanoplates resting on the elastic foundation under the sinusoidal distributed load versus to the variation of the boundary condition, the nonlocal coefficient \(\mu\) and the volume-fraction exponent \(n\)
Full size table

Table 10 presents the values of the dimensionless central deflection \({w}^{**}\) of the FG nanoplates resting on the elastic foundation with the foundation stiffness \({K}_{w}=30; {K}_{s}=10\) subjected to sinusoidally distributed load. We consider the FG nanoplates with the volume-fraction exponent n = 1, the change of nonlocal coefficient, the length-to-thickness ratio and the various boundary conditions. it can be observed that the increase of the nonlocal coefficient and the volume-fraction exponent n leads to the increase of the dimensionless central deflection. In addition, it can be seen that the present finite element method eliminates the shear locking phenomenon and obtains good results when the thickness of the FG nanoplates becomes very thin.

Table 10 The variation of the dimensionless deflection of the FG nanoplates resting on the elastic foundation versus to the variation of the boundary condition, the nonlocal coefficient \(\mu\) and the length-to-thickness ratio \(a/h\)
Full size table

Figure 5 illustrates the dimensionless central deflection \({w}^{**}\), the in-plane normal stress \({\sigma }_{xx}^{**} (z)\), the in-plane shear stress \({\sigma }_{xy }^{**}(z)\) and the transverse shear stress \({\sigma }_{xz}^{**}(z)\) of the simply supported FG nanoplates resting on the elastic foundation. In Fig. 5a, it can be seen that the dimensionless central deflections of the FG nanoplates increase rapidly corresponding to the increase of the volume-fraction exponent \(n\) from 0 to 2. However, they increase more slowly corresponding to the increase of the volume-fraction exponent \(n\) from 2 to 10. Figure 5b, Fig. 5c and Fig. 5d depict the in-plane normal stress \({\sigma }_{xx}^{**} (z)\), the in-plane shear stress \({\sigma }_{xy}^{**} (z)\) and the transverse shear stress \({\sigma }_{xz}^{**} (z)\) at points on the vertical line passing through the centroid of FG nanoplates with \(a/h=10\). It is noted that the values of the in-plane normal stress \({\sigma }_{xx}^{**} (z)\), the in-plane shear stress \({\sigma }_{xy }^{**}(z)\) are not equal zero at the point \(z/h=0\) in Fig. 5b and Fig. 5c. In addition, when \(n=1.5\) the in-plane normal stress \({\sigma }_{xx}^{**} (z)\) and the in-plane shear stress \({\sigma }_{xy }^{**}(z)\) have the value of zero at \(z/h\approx 0.1481\). The transverse shear stress \({\sigma }_{xz}^{**} (z)\) obtains the maximum value at \(z/h\approx 0.220\).

Fig. 5
figure 5

The effect of nonlocal coefficient \(\mu\) and \(n\) versus to (a) \(to the dimensionless deflection,\) b to the in-plane normal stress \({\sigma }_{xx}^{**}\)(\(z\)); c to the in-plane shear stress \({\sigma }_{xy }^{**}\)(\(z)\); d to the transverse shear stress \({\sigma }_{xz}^{**}\)(\(z)\) of FG nanoplates resting on elastic foundations \({(K}_{w}=10, {K}_{s}=10,a/h=10, n=1.5, SSSS)\)

Full size image

Figure 6 shows the dimensionless deflection \({w}^{**}\) of the full clamped FG nanoplates resting on the elastic foundation under sinusoidally distributed load. The influences of length-to-thickness ratio \(a/h\) and the volume-fraction exponent \(n\) on the deflection of nanoplates are examined. It is observed that the dimensionless deflections \({w}^{**}\) decreases rapidly when the length-to-thickness ratio \(a/h\) increases from 5 to 10. However, they decrease slowly in the case of variation from 10 to 20. Figure 6b, Fig. 6c and Fig. 6d depict the in-plane normal stress \({\sigma }_{xx}^{**} (z)\), the in-plane shear stress \({\sigma }_{xy}^{**} (z)\) and the transverse shear stress \({\sigma }_{xz}^{**} (z)\) at points on the vertical line passing through the centroid of FG nanoplates with the length-to-thickness ratio \(a/h=10\).

Fig. 6
figure 6

The effects of length-to-thickness ratio \(a/h\) and the volume-fraction exponent \(n\) versus to: a the dimensionless deflection; b the in-plane normal stress \({\sigma }_{xx}^{**}\) (\(z)\); c the in-plane shear stress \({\sigma }_{xy }^{**}\)(\(z)\); d the transverse shear stress \({\sigma }_{xz}^{**}\)(\(z)\) of FG nanoplates resting on elastic foundations \(({K}_{w}=10, {K}_{s}=10, a/h =10, \mu =1, CCCC)\)

Full size image

Figure 7a shows the dimensionless deflection \({w}^{**}\) of the simply supported FG nanoplates resting on the elastic foundation under sinusoidal distributed load versus to the variations of the foundation stiffness and the length-to-thickness ratio \(a/h\). Figure 7b, Fig. 7c and Fig. 7d illustrate the in-plane normal stress \({\sigma }_{xx}^{**} \left(z\right),\) the in- plane shear stress \({\sigma }_{xy}^{**} (z)\) and the transverse shear stress \({\sigma }_{xz}^{**} (z)\) at points on the vertical line passing through the centroid of FG nanoplates versus to the variation of the foundation stiffness. It is clear seen that when the volume-fraction exponent \(n\) is constant, the transverse shear stress \({\sigma }_{xz}^{**} (z)\) has the same shape and different value.

Fig. 7
figure 7

The effect of length-to-thickness ratio \(a/h\) and the foundation stiffness \({K}_{w}, {K}_{s}\) versus to: a the dimensionless deflection; b the in-plane normal stress \({\sigma }_{xx}^{**}\)(\(z)\); c the in-plane shear stress \({\sigma }_{xy}^{**}\)(\(z)\); d the transverse shear stress \({\sigma }_{xz}^{**}\)(\(z)\) of FG nanoplates resting on elastic foundations \((n=1.5, \mu =1)\)

Full size image

Figure 8 show the dimensionless deflection \({w}^{**}\) and the in-plane normal stress \({\sigma }_{xx}^{**} (h/2)\) of the FG nanoplates \((n=1.5,\mu =1, a/h=10)\) resting on the elastic foundation under sinusoidally distributed load versus to the variations of the foundation stiffness, the volume-fraction exponent \(n\) and the boundary conditions. From Fig. 8c and Fig. 8d, it can be found that the displacements of FG plates decrease linearly with the increase of the parameter \({K}_{w}\) but decrease nonlinear with the increase of the parameter \({K}_{s}\).

Fig. 8
figure 8

The effect of the volume-fraction exponent \(n\) and the boundary conditions on: a the dimensionless deflection; b the in-plane normal stress \((h/2) ({K}_{w}=10, {K}_{s}=10)\)

Full size image

3.3 Free vibration problem

This sub-section considers the influences of the elastic foundations, the nonlocal coefficient, the volume-fraction exponent, the geometric parameters and the boundary conditions versus to the free vibration of the FG nanoplates.

Table 11 presents the effects of the various boundary conditions \(and\) the variation of the volume-fraction exponent and the nonlocal coefficient versus to the dimensionless fundamental frequency \({\Omega }^{*}\) of the FG nanoplates \((a/h=10)\) resting on elastic foundation. It is seen that the dimensionless fundamental frequency \({\Omega }^{*}\) decreases gradually via the following order of boundary conditions: CCCC, CCCS, CSCS, CSSS, CFCF, SSSS, CSFS, SFSS. It is also found that the increase of the nonlocal coefficient makes the FG nanoplates become softer, and hence makes the dimensionless fundamental frequency decrease. These results again help fill in the gap of those that the analytical method is missing.

Table 11 The effect of the boundary condition, the nonlocal coefficient \(\mu\) and the volume-fraction exponent \(n\) \(({ a/h=10,K}_{w1}=50, { K}_{s1}=50)\) on the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation. \(.\)
Full size table

Figure 9a illustrates the variation of the dimensionless fundamental frequency of the FG nanoplates with the volume-fraction exponents \(n=2\) resting on the elastic foundation versus to the variation of the length-to-thickness \(a/h\). It can be seen that the dimensionless fundamental frequency of the FG nanoplates decreases rapidly when the length-to-thickness ratio \(a/h\) varies from 5 to 15. However, they decrease slowly when the length-to-thickness ratio \(a/h\) varies from 20 to 50. Figure 9b demonstrates the effect of the volume-fraction exponents \(n\) and the nonlocal coefficient on the variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation. It is seen that the dimensionless fundamental frequency decreases rapidly when the volume-fraction exponent varies from 0 to 2, but decreases slowly when the volume-fraction exponent varies from 2 to 10.

Fig. 9
figure 9

The variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation \({(K}_{w1}=50, { K}_{s1}=10,CCCC)\) with the various nonlocal coefficient versus to the variation of a the length-to-thickness \(a/h\) (\(n=2)\); b the volume-fraction exponents \(n\) (\(a/h=20)\)

Full size image

Figure 10 demonstrates the variation of the fundamental frequency \({\Omega }^{*}\) of the FG nanoplates resting on the elastic foundation\((n=1, \mu =1, CCCC\)) with different foundation parameters versus to the variations of width-to-length \(b/a\) and of the volume-fraction exponents \(n\) (\(a/h=20)\) and of the length-to-thickness\(a/h, (b/a=1)\). Figure 11 shows the variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation \(({\mu =1,K}_{w1}=10, {K}_{s1}=10)\) in the various boundary conditions versus to the variations of the length-to-thickness \(a/h\) (\(n=1\)) and of the volume-fraction exponent \(n\) (\(h=10\)). Figure 12 presents the variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation \((n=1.5, a/h=10, CCCC )\) with different nonlocal coefficients versus to the variations of the elastic foundation coefficient\({K}_{w1}\), \(({K}_{s1}=\) 10) and of \({K}_{s1},\) \(\left({K}_{w1}=50\right).\) The results from these figures show that the increase of the width-to-length ratio makes the nanoplates become softer and thus makes the fundamental frequency \({\Omega }^{*}\) decrease. Furthermore, the increase of the elastic foundation stiffness leads to the increase of the fundamental frequency. Form Fig. 12, it can be seen that the fundamental frequency \({\Omega }^{*}\) depends linearly on the elastic foundation coefficient \({K}_{w1}\) but depends nonlinearly on the elastic foundation coefficient\({K}_{s1}\).

Fig. 10
figure 10

The variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation \((n=1, \mu =1, CCCC\)) with different foundation parameters versus to the variation of: a the width-to-length ratio \(b/a, (a/h=20);\) b the length-to-thickness \(a/h, (b/a=1)\)

Full size image
Fig. 11
figure 11

The variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation \(({\mu =1,K}_{w1}=10, {K}_{s1}=10)\) in the various boundary conditions versus to the variations of: a the length-to-thickness \(a/h\) (\(n=1\)); b the volume-fraction exponent \(n\) (\(h=10\))

Full size image
Fig. 12
figure 12

The variation of the dimensionless fundamental frequency of the FG nanoplates resting on the elastic foundation \((n=1.5, a/h=10, CCCC)\) with different nonlocal coefficients versus to the variations of: a the elastic foundation coefficient \({K}_{w1}\), \(({K}_{s1}=\) 10); and b\({K}_{s1},\) \(\left({K}_{w1}=50\right)\)

Full size image

Figure 13 shows the variations of the first six fundamental frequencies \(10{\omega }_{i}h\sqrt{\frac{{\rho }_{m}}{{E}_{m}}}(i=1/6)\) of the FG nanoplates versus to the variations of the nonlocal parameter \(\mu\), volume-fraction exponent \(n\) and elastic foundation coefficient \({K}_{w1}\). It can be seen that the increase of the nonlocal parameter and the volume-fraction exponent \(n\) leads to the decrease of all fundamental frequencies in which the mode (3,2) and mode (3,3) have the largest decrease. For example, the value of the fundamental frequency of the FG nanoplates of the mode (3,3) decreases more than 2.5 times, from 6.02 (with nonlocal parameter \(\mu =0\)) to 2.365 (with nonlocal parameter \(\mu =4\)). The volume-fraction exponent \(n\) has a significant influence on the fundamental frequency of the FG nanoplates when \(n\) changes from 0 to 2 and the value of the modes decreases negligibly with \(n\ge 2\). Figure 14 shows the nine mode shapes of the FG nanoplates resting on the elastic foundation. It can be found that the nanoplates resting on the elastic foundation still have the same shapes as the nanoplates without the elastic foundation.

Fig. 13
figure 13

The variations of the first six fundamental frequencies of the FG nanoplates (\(a/h=10,SSSS\)) versus to the variations of: a the nonlocal parameter \(\mu ;\) b the volume-fraction exponent \(n;\) c the elastic foundation coefficient \({K}_{w1};\) d the elastic foundation coefficient \({K}_{s1}\)

Full size image
Fig. 14
figure 14

The first nine mode shapes of FG nanoplates resting on the elastic foundation

Full size image

4 Conclusions

A finite element formulation using four-unknown shear deformation theory is developed for bending and free vibration analysis of the FG nanoplates resting on the elastic medium foundation. In this formulation, a four-node quadrilateral element with eight degrees of freedom per node and the four-unknown variables are approximated by Lagrangian and Hermitian interpolation functions to form the finite element formulation of the stiffness matrices, the mass matrices and the load vectors of the FG nanoplates with the second derivatives. Therefore, it is clear that this element is the most suitable for investigating the bending and free vibration responses of the FG nanoplates resting on the elastic medium foundation. The accuracy and the reliability of the present method have been validated by comparing its numerical results to those available in the literature. In addition, the analyses of the effects of various parameters on the bending and the free vibration of the FG nanoplates resting on the elastic foundation have been examined. It is thus very promising to extend the present method for the analysis of the FG porous nanoplates with laws of variable thickness resting on elastic foundation, the FG porous plate resting on elastic foundation subjected to other loads, and the FG porous nanoshells resting on the elastic foundation. It is noted that the proposed method also exists a limit regarding using high-order shape functions to approximate displacement fields of the FG nanoplates. This limit in somehow leads to a rather high computation cost and hence should be a topic for improvement in coming studies.