1 Introduction

Quantum coherence (QC) is a broad concept that encompasses all kinds of superpositions within both single and multipartite quantum systems [1, 2]. When the off-diagonal elements of a density matrix are nonzero, it indicates the presence of QC. Baumgratz et al. [2] introduced a quantum resource theory of QC, where the \(l_1\)-norm of coherence effectively quantifies the degree of QC. In the context of multipartite systems, QC can arise from various forms of separable and nonseparable correlations, such as entanglement and quantum discord (QD) [3,4,5,6,7]. Even within these separable and nonseparable correlations, there are additional types of correlations based on their operational interpretation, including Bell nonlocality (BNL) and quantum steering (QS). Together, these different notions form a hierarchy of correlations that are essential for understanding the nature of different types of quantum resources in quantum information and processing.

Figure 1 illustrates the hierarchy of quantum correlations, where each layer represents a subset of the one encompassing it, with QC being the largest and most inclusive, and BNL being the most specific and restrictive. This hierarchical structure visually represents how each type of quantum correlations may build upon the previous ones, showcasing their interrelations and dependencies [8,9,10].

Entanglement refers to the remarkable nonseparable quantum correlations between particles, where the state of one particle instantaneously influences the state of another, regardless of distance [11,12,13]. QD extends beyond entanglement, encompassing some quantum correlations residing in both separable and nonseparable states shared between subsystems of a quantum system [5,6,7]. However, in general, it has been shown that quantum correlations may be detected even in the absence of both entanglement and QD [14]. For pure nonseparable states, QD and entanglement are equivalent [6, 7], but this is not the case for mixed states.

QS [15,16,17,18] represents a unique form of quantum correlations. In a scenario where two distant observers share an entangled quantum state, QS describes the ability of one observer to remotely influence the state of the other observer’s system. While entanglement entails quantum correlations between quantum particles regardless of distance, QS introduces an asymmetry in the observer’s roles. In a QS scenario, one observer can manipulate the state of the other observer’s system, but the reverse may not always hold. This fundamental asymmetry sets QS apart and raises intriguing questions about the relationship between QS, entanglement, and BNL.

BNL is a concept that arises from the violation of certain inequalities known as Bell inequalities [19, 20]. These inequalities describe limits on quantum correlations that can occur between distant systems within a classical framework. When these inequalities are violated, it implies that the quantum correlations between the systems cannot be explained by local hidden variables (underlying properties or information that determine the outcome of measurements)and suggests a form of BNL in quantum mechanics. From Bell inequalities, we now understand that entanglement and BNL are synonymous in a pure state, meaning that entanglement implies BNL and vice versa. However, the situation is not clear and simple for mixed states, even in two-qubit systems [21,22,23,24].

The measures of BNL, entanglement, QD, and QS are intricately connected, making it difficult to clearly differentiate them, even in systems with two or three qubits. The complexity is underscored by the requirement of 15 independent parameters to fully characterize a density matrix, even for two-qubit mixed state systems, highlighting the intricate nature of quantum correlations. While entanglement is a cornerstone of quantum information theory, it does not fully encapsulate the correlations present in mixed states. The lack of a straightforward mathematical relationship among these measures, combined with the challenges of distinguishing separable states from entangled ones, indicates that enhancing one type of correlation does not necessarily lead to improvements in others. This complexity necessitates the assessment of multiple metrics, as different quantum resources may become more significant under varying conditions. This study qualitatively explores the trends and hierarchy of these correlations within a two-qubit Heisenberg model, providing insights into their interrelations and the circumstances under which each type of correlation may dominate.

A one-dimensional Heisenberg spin chain is a theoretical model generally used in condensed matter physics to describe a linear array of interacting quantum spins [25,26,27,28,29,30,31,32]. Each spin interacts with its nearest neighbors, exhibiting phenomena such as quantum phase transitions and quantum correlations. In quantum technologies, Heisenberg spin chains offer potential for quantum simulation [33, 34], computing [35, 36], metrology and sensing [37,38,39], quantum criticality and multipartite entanglement [40], and communication [41, 42]. Entanglement properties of spin chains can be harnessed for quantum communication protocols, where one can use spin chains as quantum channels to transfer quantum states between distant parties securely and with higher fidelity compared to classical communication channels [43].

In this work, we take the most general two-qubit Heisenberg XYZ model under a sinusoidally controlled magnetic field applied to an individual spin site with asymmetric spin–orbit coupling interaction called Dzyaloshinsky-Moriya (DM) interaction and symmetric exchange coupling known as Kaplan–Shekhtman–Entin-Wohlman–Aharony (KSEA) interaction, and study the behavior of all the aforementioned quantifiers with changes in the model parameters.

To elucidate the occurrence of weak ferromagnetism observed in certain rhombohedral antiferromagnets, Dzyaloshinsky [44,45,46] developed a phenomenological approach grounded in the Landau theory of second-order phase transitions. This approach highlighted that the appearance of a nonzero net magnetization in the system is attributed to the antisymmetric mixed term in the expansion of the thermodynamic potential. Additionally, Dzyaloshinsky noticed that in antiferromagnetic crystals with tetragonal lattices, weak ferromagnetism can be induced by the symmetric mixed term in the corresponding thermodynamic potential. In 1960, Moriya [47] improved the understanding by formulating a microscopic theory of anisotropic superexchange interaction, extending the Anderson theory of superexchange to include spin–orbit coupling. Through perturbation theory, Moriya identified the primary anisotropy contribution to the interaction between neighboring spins as the DM interaction. Moriya also revealed a second-order correction term involving a symmetric traceless tensor. While historically considered negligible, Kaplan and subsequently Shekhtman et al. [47,48,49] argued for the significance of the symmetric term. This term, called KSEA interaction as mentioned before, can restore the O(3) invariance of the isotropic Heisenberg system, a property disrupted by the DM term. This reevaluation of the interaction emphasizes its importance in understanding weak ferromagnetism in antiferromagnetic systems.

Fig. 1
figure 1

Conventional hierarchy breakdown of quantum coherence and correlations, i.e., BNL \(\subseteq\) QS \(\subseteq\) quantum entanglement \(\subseteq\) QD \(\subseteq\) QC

Full size image

Finally, we also consider a teleportation protocol by employing the two-qubit Heisenberg spin chain as a channel to study how the channel parameters can impact the fidelity of the teleported state. Heisenberg XYZ model has already been experimentally studied, such as in Rydberg or dipolar atoms, through a combination of dipole interactions with engineered optical pumping [50]. Floquet-engineered XXZ spin coupling in bulk systems and optical tweezer arrays have been demonstrated in [51, 52]. Similarly, this model has been recently realized in multiple experiments, notably in dipolar-octupolar (DO) Kramers compounds Ce\(_2\)(Sn, Zr)\(_2\)O\(_7\) and Nd\(_2\)Zr\(_2\)O\(_7\) [53,54,55]. Moreover, the XYZ model has been realized in Weyl-Heisenberg ferromagnets [56].

1.1 Motivation and contribution of this study

This study aims to enhance our understanding of various quantum resources in quantum information processing, particularly in quantum teleportation. While entanglement is vital for teleportation, the complexities of mixed states affected by thermal and quantum noise necessitate the consideration of additional quantum correlations, such as BNL, QS, QD, and \(l_1\)-norm of QC. Utilizing the Heisenberg XYZ spin model, we explore how the Gibbs thermal state acts as a mixed state channel for teleportation, incorporating various control parameters like magnetic fields and interactions such as DM and KSEA. This approach allows us to investigate how these factors influence the different coherence and correlation measures constituting the hierarchy of quantum resources and the fidelity of teleportation. Our contribution lies in systematically quantifying these quantum resources and analyzing their collective impact on teleportation fidelity. We also examine the robustness of these resources under varying temperature conditions, providing insights into optimizing quantum communication protocols.

1.2 Organization

The scheme of this paper is as follows: in Sect. 2, we define and explain the different notions of QC and quantum correlation measures. In Sect. 3, we briefly introduce the spin-1/2 Heisenberg XYZ model, diagonalize the system, and come up with the thermal state of the model. In Sect. 4, we present a simple teleportation scheme based on the considered model to be implemented. Section 5 presents the results and discussion, and finally, Sect. 6 concludes this paper.

2 Quantum resources

2.1 \(l_1\)-norm quantum coherence

QC is a fundamental concept that arises from the superposition principle in quantum mechanics. A rigorous framework to quantify coherence as a resource, known as the resource theory of QC, has been previously developed [1, 2]. This theory identifies the set of incoherent states \(\mathcal {I}\) which are diagonal in a reference basis \(\{|i\rangle \}\):

$$\begin{aligned} \delta \in \mathcal {I} \iff \delta = \sum _i \delta _i |i\rangle \langle i|. \end{aligned}$$
(1)

The free operations are the incoherent operations that map incoherent states to incoherent states. Revealing and quantifying QC is essential to enable quantum correlations and information processing.

Accordingly, Baumgratz et al. [2] proposed the \(l_1\)-norm of quantum coherence as a quantifier of coherence, given by

$$\begin{aligned} Q(\rho ) = \sum _{i\ne j} |\langle i|\rho |j\rangle | = \sum _{i,j} |\rho _{ij}| - \sum _i |\rho _{ii}|, \end{aligned}$$
(2)

where \(\rho\) is the density operator of the considered system.

2.2 Quantum discord

QD measures nonclassical correlations between subsystems in a quantum system, capturing quantumness not explained by classical means. QD quantifies differences between quantum and classical mutual information.

QD indicates the difference between total and classical correlation for a two-qubit system [5,6,7, 57]. That is, QD for a bipartite quantum X state, \(\rho _{X}\) is expressed as

$$\begin{aligned} D(\rho _{X}) = \min \{q_1,~q_2\}, \end{aligned}$$
(3)

where

$$\begin{aligned} q_j = H(\rho _{11}+\rho _{33}) + \sum ^4_{i=1} \lambda _i \log _2 \lambda _i + w_j, \end{aligned}$$
(4)

here, \(\lambda _i\)’s represent the eigenvalues of density matrix \(\rho _{X}\), and

$$\begin{aligned} w_1= & {} H(\xi ), \end{aligned}$$
(5)
$$\begin{aligned} w_2= & {} -\sum _i \rho _{ii} \log _2 \rho _{ii} - H(\rho _{11}+\rho _{33}), \end{aligned}$$
(6)

with

$$\begin{aligned} H(\xi )=-\xi \log _2 \xi - (1-\xi )\log _2(1-\xi ), \end{aligned}$$
(7)

and

$$\begin{aligned} \xi =\frac{1}{2}\left\{ 1+\sqrt{[1-2(\rho _{33}+\rho _{44})]^2+4(|\rho _{14}|+|\rho _{23}|)^2}\right\} . \end{aligned}$$
(8)

2.3 Concurrence

Concurrence is an entanglement monotone used to quantify the degree of entanglement in arbitrary two-qubit states [4, 58]. For a given density matrix \(\rho\), concurrence \(C(\rho )\) of two qubits is defined as follows

$$\begin{aligned} C(\rho ) = \max \{0, \lambda _1 - \lambda _2 - \lambda _3 - \lambda _4\}. \end{aligned}$$
(9)

where \(\lambda _i\)’s are the square roots of the eigenvalues of the matrix (non-Hermitian) \(\rho (\sigma _y \otimes \sigma _y) \rho ^* (\sigma _y \otimes \sigma _y)\) in decreasing order. As before, \(\sigma _y\) represents the y-component of Pauli matrices, and \(\rho ^*\) denotes the complex conjugate of \(\rho\). Note that the measure (9) takes values between 0 and 1, indicating the absence of entanglement when \(C(\rho ) = 0\) and maximal entanglement when \(C(\rho ) = 1\).

2.4 Quantum steering

Erwin Schrödinger proposed steering as an extension of the Einstein-Podolsky-Rosen paradox [15]. Though initially overlooked as nonlocal correlations, it later sparked significant advancements. Steerable states exhibit quantum advantages in device-independent quantum cryptography [59], secure teleportation [60], randomness generation [61], and subchannel discrimination [62]. The three-setting linear steering inequality [63, 64] is based on the assumption that either Alice or Bob are allowed three measurement observables on their respective subsystems. It is a crucial tool for detecting and quantifying steering in a state, particularly in a two-qubit system which reads

$$\begin{aligned} \frac{1}{\sqrt{3}} \sum _{i=1}^3 \textrm{Tr}(A_i \otimes B_i\rho ) \le 1, \end{aligned}$$
(10)

where \(A_i = a_i \cdot \sigma\) and \(B_i = b_i \cdot \sigma\) are Hermitian operators acting on qubits A and B, respectively. Here, \(a_i, b_i \in \mathbb {R}^3\) are two unit vectors with \(\{b_1, b_2, b_3\}\) being orthogonal to each other, and Pauli matrices \(\sigma = (\sigma _1=\sigma _x, \sigma _2=\sigma _y, \sigma _3=\sigma _z)\). Any violation of the inequality (10) implies that \(\rho\) is steerable, and the maximal violation gives a measure of steering [64]. Explicitly,

$$\begin{aligned} S(\rho ) = \max _{\{A_i,B_i\}} \left\{ \frac{1}{\sqrt{3}} \sum _{i=1}^3 \textrm{Tr}(A_i \otimes B_i\rho ) \right\} \end{aligned}$$
(11)

represents the maximum violation of the three-setting linear steering inequality.

2.5 Bell nonlocality

In order to quantify BNL and enable a more thorough comparison of quantum correlations, one can use the Bell inequality violation. The normalized form of BNL measure can be written as [65,66,67,68,69]

$$\begin{aligned} \mathcal {B}(\rho )= \max \left\{ 0, \frac{\mathcal {B}_{CHSH }-2}{\mathcal {B}_{\text {max}}-2}\right\} , \end{aligned}$$
(12)

where \(0\le \mathcal {B}(\rho )\le 1\) since \(\mathcal {B}_{CHSH }\le \mathcal {B}_{\text {max}}=2\sqrt{2}\) for a two-qubit system \(\rho\). Notice, \(\mathcal {B}_{CHSH }\) is the maximum violation of Bell Clauser–Horne–Shimony–Holt (CHSH) inequality, which for an X-shaped density matrix is given by [68,69,70]:

$$\begin{aligned}&\mathcal {B}_{CHSH } = 2\max \Big \{ 2\sqrt{2|\rho _{14}|^2 + 2|\rho _{23}|^2}, \sqrt{4(|\rho _{14}| + |\rho _{23}|)^2 + \gamma ^2} \Big \}, \end{aligned}$$
(13)

with \(\gamma =\rho _{11} - \rho _{22} - \rho _{33} + \rho _{44}\).

3 Heisenberg XYZ model

The Hamiltonian describing a general Heisenberg XYZ model under the influence of an inhomogeneous magnetic field, including DM and KSEA interactions, is given by

$$\begin{aligned} \hat{\mathcal {H}}_N=\hat{\mathcal {H}}_H+\hat{\mathcal {H}}_B+\hat{\mathcal {H}}_{DM }+\hat{\mathcal {H}}_{KSEA }, \end{aligned}$$
(14)

The initial term \(\hat{\mathcal {H}}_H\) accounts for Heisenberg spin exchange interactions, with \(\hat{\mathcal {H}}_B\) as the Zeeman Hamiltonian representing the influence of the inhomogeneous external magnetic field on the system. Additionally, \(\hat{\mathcal {H}}_{DM }\) and \(\hat{\mathcal {H}}_{KSEA }\) represent the DM interaction and KSEA interaction, respectively. This total Hamiltonian (14) can be explicitly written as [71, 72]

$$\begin{aligned} \hat{\mathcal {H}}_N &=\sum _{i=1}^{N-1}\big \{ J_x \hat{\sigma }_i^x\otimes \hat{\sigma }_{i+1}^x + J_y \hat{\sigma }_{i}^y\otimes \hat{\sigma }_{i+1}^y + J_z \hat{\sigma }_{i}^z\otimes \hat{\sigma }_{i+1}^z \\&\quad+\overrightarrow{\textbf{B}}_{i}\cdot (\overrightarrow{{{\sigma }}}_{i}\otimes \mathbb {I}_2)+\overrightarrow{\textbf{B}}_{i+1}\cdot (\mathbb {I}_2\otimes \overrightarrow{{\sigma }}_{i+1})\\&\quad+ \overrightarrow{\mathbf {\mathcal {D}}}\cdot (\overrightarrow{\mathbf {{\sigma }}}_{i}\times \overrightarrow{ {{\sigma }}}_{i+1})+ \overrightarrow{{{\sigma }}}_{i}\cdot \Gamma \cdot \overrightarrow{{{\sigma }}}_{i+1}\big \}, \end{aligned}$$
(15)

here,

$$\begin{aligned} \Gamma = \begin{pmatrix} 0 &{} \Gamma _{z} &{} \Gamma _{y} \\ \Gamma _{z} &{} 0 &{} \Gamma _{x} \\ \Gamma _{y} &{} \Gamma _{x} &{} 0 \\ \end{pmatrix}. \end{aligned}$$
(16)

The interaction between neighboring spin sites is determined by the real spin–spin coupling coefficients along the x, y, and z directions, denoted as \(J_k\) for \(k = x, y, z\). Antiferromagnetic coupling is indicated by positive values of \(J_k\), while negative values represent ferromagnetic coupling. The standard Pauli spin operators, denoted as \(\hat{\sigma }_i^k\), define the spin vector on the ith site as \(\overrightarrow{\mathbf {{\sigma }}}_{i} = (\hat{\sigma }_i^x, \hat{\sigma }_i^y, \hat{\sigma }_i^z)\). Moreover, \(\overrightarrow{\textbf{B}}_{i}=(B_{i}^x,B_{i}^y,B_{i}^z)\) represents the magnetic flux density contributing to Zeeman splitting at the ith spin site. The DM interaction vector is defined by \(\overrightarrow{\mathbf {\mathcal {D}}}=(\mathcal {D}_x,\mathcal {D}_y,\mathcal {D}_z)\) and serves as the anti-symmetric exchange coupling responsible for spin–orbit coupling in specific materials. Note that the KSEA interaction (\(\Gamma\)) introduces an anisotropic symmetric interaction [71,72,73,74].

To simplify our analysis, we focus on a bipartite Heisenberg XYZ model restricted to interactions between two specific spin sites. This model is limited to a two-spin system and does not consider interactions between arbitrary pairs within a longer chain or under periodic boundary conditions. For this two-spin model, we further simplify by assuming that \(\overrightarrow{\textbf{B}}_{1} = (0,0,B\cos {\theta })\), \(\overrightarrow{\textbf{B}}_{2} = (0,0,B\sin {\theta })\), \(\overrightarrow{\mathbf {\mathcal {D}}} = (0,0,\mathcal {D}_z)\), and specifying that \(\Gamma _x = \Gamma _y = 0\) while \(\Gamma _z \ne 0\). Consequently, the Hamiltonian in Eq. (15) with these assumptions can be explicitly written as

$$\begin{aligned} \begin{aligned} \hat{\mathcal {H}} =&J_x~ \hat{\sigma }_1^x\otimes \hat{\sigma }_{2}^x + J_y~ \hat{\sigma }_{1}^y\otimes \hat{\sigma }_{2}^y + J_z~ \hat{\sigma }_{1}^z\otimes \hat{\sigma }_{2}^z \\&+ B~[\cos {\theta }(\hat{\sigma }_{1}^z\otimes \mathbb {I}_2) + \sin {\theta }(\mathbb {I}_2\otimes \hat{\sigma }_{2}^{z})] \\&+ \mathcal {D}_z~ (\hat{\sigma }_1^x\otimes \hat{\sigma }_{2}^y - \hat{\sigma }_{1}^y\otimes \hat{\sigma }_{2}^x)\\&+ \Gamma _z~ (\hat{\sigma }_1^x\otimes \hat{\sigma }_{2}^y + \hat{\sigma }_{1}^y\otimes \hat{\sigma }_{2}^x). \end{aligned} \end{aligned}$$
(17)

As we know, this Hamiltonian (17) has a standard X-structured matrix form. Using the standard computational basis \(\{\left| 00\right\rangle , \left| 01\right\rangle , \left| 10\right\rangle , \left| 11\right\rangle \}\), it can be expressed in a simplified form

$$\begin{aligned} \hat{\mathcal {H}} = \begin{pmatrix} J_z+B(\cos {\theta }+\sin {\theta }) &{} 0 &{} 0 &{} -2 i \Gamma _z +J_x-J_y \\ 0 &{} -J_z+B(\cos {\theta }-\sin {\theta }) &{} 2 i \mathcal {D}_z+J_x+J_y &{} 0 \\ 0 &{} -2 i \mathcal {D}_z+J_x+J_y &{} -J_z-B(\cos {\theta }-\sin {\theta }) &{} 0 \\ 2 i \Gamma _z +J_x-J_y &{} 0 &{} 0 &{} J_z-B(\cos {\theta }+\sin {\theta }) \end{pmatrix}. \end{aligned}$$
(18)

The diagonalization of \(\hat{\mathcal {H}}\) (18) results in four eigenvalues, given by

$$\begin{aligned} \begin{aligned} E_{1,2}&= \pm {\mathcal {K}_1} + J_z, \quad E_{3,4}= \pm {\mathcal {K}_2} - J_z, \end{aligned} \end{aligned}$$
(19)

with expressions

$$\begin{aligned} \mathcal {K}_1=\sqrt{k_1^2+B^2\left( \cos {\theta }+\sin {\theta }\right) ^2} \end{aligned}$$

and

$$\begin{aligned} \mathcal {K}_2=\sqrt{k_2^2+B^2\left( \cos {\theta }-\sin {\theta }\right) ^2}, \end{aligned}$$

where

$$\begin{aligned} k_1=\sqrt{\left( J_x-J_y\right) ^2+4 \Gamma _z^2}, \end{aligned}$$
$$\begin{aligned} k_2=\sqrt{\left( J_x+J_y\right) ^2+4 \mathcal {D}_z^2}. \end{aligned}$$

The state of a system in the thermal equilibrium with the absolute temperature T is described by the Gibbs density operator

$$\begin{aligned} \rho _T = \frac{1}{\mathcal {Z}} e^{-\hat{\mathcal {H}}/\kappa T}, \end{aligned}$$
(20)

where \(\mathcal {Z}=\textrm{Tr}[\exp (-\hat{\mathcal {H}}/\kappa T]\) is partition function with the Boltzmann constant \(\kappa\) (considered as \(\kappa =1\) for simplification purpose).

Using now Hamiltonian (18) and density operator (20), we obtain the following density matrix at thermal equilibrium

$$\begin{aligned} \rho _T=\left( \begin{array}{cccc} a^- &{} 0 &{} 0 &{} c \\ 0 &{} b^- &{} d &{} 0 \\ 0 &{} d^* &{} b^+ &{} 0 \\ c^* &{} 0 &{} 0 &{} a^+ \end{array}\right) , \end{aligned}$$
(21)

where the nonzero elements read

$$\begin{aligned} \begin{aligned}&a^{\pm } =\frac{e^{- J_z/T}}{\mathcal {Z}}\left\{ \cosh \left( \mathcal {K}_1/T\right) \pm \left[ B(\cos {\theta }+\sin {\theta }) / \mathcal {K}_1\right] \Theta _1\right\} , \\&b^{\pm } =\frac{e^{J_z/T}}{\mathcal {Z}}\left\{ \cosh \left( \mathcal {K}_2/T\right) \pm \left[ B(\cos {\theta }-\sin {\theta }) / \mathcal {K}_2\right] \Theta _2\right\} , \\&c =-\frac{e^{- J_z/T}}{\mathcal {Z}}\left[ \left( -2 i \Gamma _z+J_x-J_y\right) / \mathcal {K}_1\right] \Theta _1, \\&d =-\frac{e^{J_z/T}}{\mathcal {Z}}\left[ \left( 2 i \mathcal {D}_z+J_x+J_y\right) / \mathcal {K}_2\right] \Theta _2, \end{aligned} \end{aligned}$$
(22)

where \(\Theta _{(1)2}=\sinh \left( \mathcal {K}_{(1)2}/T\right)\), and

$$\begin{aligned} Z=2\left[ e^{- J_z/T} \cosh \left( \mathcal {K}_1/T\right) +e^{ J_z/T} \cosh \left( \mathcal {K}_2/T\right) \right] , \end{aligned}$$
(23)

The state presented in Eq. (21) has an X structure. Thus, the explicit expressions of the aforementioned quantifiers based on thermal state elements (22) can be derived straightforwardly.

For example, the \(l_1\)-norm of quantum coherence (2) can be obtained as

$$\begin{aligned} Q(\rho _T)=|c|+|c^*|+|d|+|d^*|. \end{aligned}$$
(24)

Moreover, the analytical expression of QD for our thermal state (21) would be given by Eq. (3) with considering \(\rho _{11}=a^-\), \(\rho _{22}=b^-\), \(\rho _{33}=b^+\), \(\rho _{44}=a^+\), \(\rho _{14}=c\), and \(\rho _{23}=d\).

Regarding the analytical form of QS (11), one needs to simply obtain \(\textrm{Tr}(A_i \otimes B_i\rho _T)\). Explicitly, we have

$$\begin{aligned} \begin{aligned} S(\rho _{T}) =&\big \{8 (c c^*+d d^*) - 4 a^- (b^- + b^+) \\&- 4 a^+ (b^- - b^+) + 1\big \}^{1/2}. \end{aligned} \end{aligned}$$
(25)

Besides, the concurrence (9) can be derived as

$$\begin{aligned} C(\rho _{T})=2\max \left\{ 0, t_1, t_2\right\} , \end{aligned}$$
(26)

where \(t_1=|d|-\sqrt{a^- a^+}\) and \(t_2=|c|-\sqrt{b^- b^+}\).

Finally, the normalized form of BNL function (12) is found to be

$$\begin{aligned} \mathcal {B}(\rho _T)= \max \left\{ 0, (2 \max \{m_1, m_2\}-2)/(2\sqrt{2}-2)\right\} , \end{aligned}$$
(27)

where \(m_1=\sqrt{4(|c| + |d|)^2 + (a^- - b^- - b^+ + a^+)^2}\) and \(m_2=\sqrt{8(|c|^2 + |d|^2)}\).

Fig. 2
figure 2

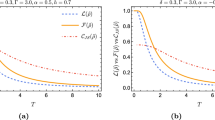
The variations of \(l_1\)-norm quantum coherence (a), QD (b), concurrence (c), QS (d), BNL (e), and average fidelity (f) as a function of temperature T at \(J_x=0.8\), \(J_y=0.5\), \(J_z=0.3\), \(\mathcal {D}_z=0\), \(\Gamma _z=0\) when the magnetic field is applied to single spin (\(\theta =0\)), and when a same magnetic field is applied to both spins (\(\theta =\pi /4\)). Black horizontal lines show \(S(\rho _T)=1\) in d and \(\mathcal {F}(\rho _T)=2/3\) in f

Full size image

4 Quantum teleportation

In this section, we examine the teleportation protocol, considering \(\rho _T\) as the quantum channel state, assuming the input state is an arbitrary unknown pure state consisting of two qubits such as

$$\begin{aligned} |\psi _{\text {in}}\rangle = \cos (\alpha /2)|10\rangle + e^{i\phi } \sin (\alpha /2)|01\rangle , \end{aligned}$$
(28)

where \(\alpha\) and \(\phi\) represent the amplitude and phase of the target state to be teleported, respectively. The quantum channel is known as a completely positive and trace-preserving operator. Through this process, an input state is mapped to an output state.

When a quantum state is teleported via the mixed channel \(\rho _{\text {ch}}\), the resulting output replica state \(\rho _{\text {out}}\) is achieved by performing joint measurements and local unitary transformations on the input state \(\rho _{\text {in}}=|\psi _{\text {in}}\rangle \langle \psi _{\text {in}}|\)

$$\begin{aligned} \rho _{\text{ out } }=\sum _{i, j \in \{0, x, y, z\}} p_i p_j\left( \sigma ^i \otimes \sigma ^j\right) \rho _{\text{ in } }\left( \sigma ^i \otimes \sigma ^j\right) , \end{aligned}$$
(29)

where \(\sigma ^0=\mathbb {I}_2\), and \(p_i={\text {Tr}}\left( q^i \rho _{\text{ ch }}\right)\) satisfies the condition \(\sum _i p_i=1\). Moreover, we have \(q^0=|\Psi ^{-}\rangle \langle \Psi ^{-}|\), \(q^1=| \Phi ^{-}\rangle \langle \Phi ^{-}|\), \(q^2=| \Psi ^{+}\rangle \langle \Psi ^{+}|\), and \(q^3=|\Phi ^{+}\rangle \langle \Phi ^{+}|\) in which \(|\Psi ^{ \pm }\rangle\) and \(|\Phi ^{ \pm }\rangle\) are four Bell states. Here, let us suppose that the quantum channel is a thermal state (21), i.e. \(\rho _{\textrm{ch}}=\rho _T\).

The quality of the teleported state is determined by the criterion of fidelity \(F(\rho _{\text {in}}, \rho _{\text {out}})\), defined as

$$\begin{aligned} F(\rho _{\text {in}}, \rho _{\text {out}}) = \left( \textrm{Tr}\sqrt{\sqrt{\rho _{\text {in}}}\rho _{\text {out}}\sqrt{\rho _{\text {in}}}}\right) ^2. \end{aligned}$$
(30)

Based on the above definition, the average fidelity of teleportation \(\mathcal {F}\) is given by

$$\begin{aligned} \mathcal {F}= \frac{1}{4\pi }\int _{0}^{2\pi } \text {d}\phi \int _{0}^{\pi } \text {d}\alpha F(\rho _{\text {in}}, \rho _{\text {out}})\sin \alpha . \end{aligned}$$
(31)

The maximum classical average fidelity threshold is observed at \(\mathcal {F} = 2/3\). Beyond this point, we transition into the quantum average fidelity regime. The proximity of the quantum average fidelity to unity signifies reduced information leakage, indicating optimal conditions for quantum teleportation.

In our case (density matrix (21)), the analytical form of average fidelity is derived by

$$\begin{aligned} \mathcal {F}(\rho _{T})=\frac{2}{3}(b^- +b^+)^2 +\frac{1}{3}(a^- +a^+)^2+\frac{1}{3}(d +d^*)^2. \end{aligned}$$
(32)

5 Results and discussion

In this investigation, our objective is to analyze various quantum coherence and correlation measures within the Heisenberg XYZ model, using it as a quantum resource channel for teleporting a target quantum state \(|\psi _{\text {in}}\rangle = \cos (\alpha /2)|10\rangle + e^{i\phi } \sin (\alpha /2)|01\rangle\). The goal is to enhance average quantum teleportation fidelity beyond 2/3 by adjusting parameters such as magnetic field, bath temperature, and DM and KSEA interactions, thereby enhancing the channel’s quantum resources. We consider an antiferromagnetic spin chain characterized by anisotropic spin–spin coupling constants (a random case): \(J_x = 0.8\), \(J_y = 0.5\), and \(J_z = 0.3\).

5.1 Impact of magnetic field

First, our focus is on the impact of applying a magnetic field to either one spin (\(\theta = 0\) or \(\theta = \pi /2\)) or to both spins (\(\theta = \pi /4\)) with \(B=1\) on quantum resources and teleportation fidelity in the absence of DM and KSEA interactions. Figure 2 illustrates the variations of quantum resources and teleportation fidelity with temperature under zero DM and KSEA interactions, comparing two distinct fixed magnetic field values.

Fig. 3
figure 3

The behaviors of \(l_1\)-norm quantum coherence (a), QD (b), concurrence (c), QS (d), BNL (e), and average fidelity (f) versus temperature T at \(J_x=0.8\), \(J_y=0.5\), \(J_z=0.3\), \(\theta =\pi /4\), and \(\Gamma _z=0\) for different fixed values of \(\mathcal {D}_z\)

Full size image

In Fig. 2a, b, the \(l_1\) norm of quantum coherence and QD are shown as functions of temperature. At low temperatures, peak values are higher when the same magnetic field is applied to both spins (dashed blue curve) compared to when it is applied to just one spin (solid green curve). Both measures decrease with increasing temperature. This result does not surprise us because the temperature can diminish the QC and correlation due to thermal fluctuations in the system.

Figure 2c–e depict the behaviors of concurrence, QS, and BNL versus T, respectively. The entanglement captured by concurrence disappears after \(T\approx 1.9\). Note that at low temperatures, peak values of concurrence are greater when the same magnetic field is applied to both spins (dashed blue curve). Our findings show that for \(0.7 \le T \le 0.9\), the channel state is steerable without BNL, as \(S(\rho _T) > 1\) in Fig. 2d. Between \(T \approx 0.7\) and \(T \approx 1.9\), the channel state remains entangled (see Fig. 2c) but without BNL (see Fig. 2e). More precisely, BNL decreases to zero before concurrence and discord as the channel becomes thermally mixed. Notice, \(Q(\rho _T)\) and \(D(\rho _T)\) show more robustness compared to \(C(\rho _T)\), \(\mathcal {S}(\rho _T)\), and \(\mathcal {B}(\rho _T)\). Thus, the mixed entangled states can exist without violating Bell inequalities or exhibiting BNL. These highlight the hierarchical relationship between the mentioned quantum resources.

Our results in Fig. 2 indicate that applying the same magnetic field to both qubits significantly enhances average teleportation fidelity (see Fig. 2f), QC, and correlations at low temperatures. These enhancements diminish at higher temperatures due to thermal effects [75, 76]. However, fidelity remains above the classical limit \(\mathcal {F}(\rho _T)=2/3\) at low temperatures for both \(\theta = 0\) and \(\theta = \pi /4\), with maximum fidelity achieved for \(\theta = \pi /4\).

From Fig. 2, we conclude that applying the same magnetic field to both qubits enhances teleportation fidelity and quantum correlations more significantly across different temperatures compared to applying it to just one qubit. The hierarchy of quantum resources, i.e., BNL \(\subseteq\) QS \(\subseteq\) quantum entanglement \(\subseteq\) QD \(\subseteq\) QC depicted in Figs. 1 and 2, demonstrates that the BNL function is the weakest measure, while the \(l_1\)-norm of coherence is the strongest indicator of nonclassical characteristics.

Given that using the same magnetic field control for both spins enhances QC and correlations as well as average teleportation fidelity at low temperatures, we will adopt \(\theta =\pi /4\) as the standard setting and explore other model parameters to improve these measures against the increasing of temperature.

Fig. 4
figure 4

The behaviors of \(l_1\)-norm quantum coherence (a), QD (b), concurrence (c), QS (d), BNL (e), and average fidelity (f) versus temperature T at \(J_x=0.8\), \(J_y=0.5\), \(J_z=0.3\), \(\theta =\pi /4\), and \(\mathcal {D}_z=0\) for different fixed values of \(\Gamma _z\)

Full size image

5.2 Impact of DM interaction

Next, we examine the impact of different fixed values of DM interaction, without introducing KSEA interaction, on the quantum resources and the average fidelity of teleportation. This analysis is presented in Fig. 3 where the considered functions are evaluated against temperature T for various fixed values of DM interaction: \(\mathcal {D}_z = 0.5\) (dashed black), \(\mathcal {D}_z = 1.0\) (solid red), \(\mathcal {D}_z = 1.5\) (dashed green), and \(\mathcal {D}_z = 2.0\) (solid blue).

We observe that although DM interaction does not increase the peak values of these functions, it aids in maintaining high peak values of quantum resources even at significantly higher temperatures (compare with Fig 2 when \(\mathcal {D}_z = 0\)). Thus, we can consider its effect as a positive influence on all QC and correlations of the quantum channel. For instance, when \(\mathcal {D}_z = 0.5\), BNL diminishes to zero around \(T \approx 0.9\), whereas for \(\mathcal {D}_z = 2.0\), it decreases to zero at \(T \approx 2.5\), marking more than a five-fold improvement in the sustainability of BNL. A similar trend is observed for QD and concurrence, with even higher T values. Notably, among all quantum resources, BNL is the most delicate, followed by QS.

Despite achieving maximal entanglement at near-zero temperatures, the average teleportation fidelity remains greater than the classical limit of 2/3, indicating successful but not maximal teleportation. At low temperatures, the value of teleportation fidelity slightly decreases with larger DM interactions. However, this underscores that the maximal entanglement in a mixed-state situation does not always guarantee ideally successful teleportation, even at the lowest T values. Thus, increasing the DM interaction decreases the peak value of the average fidelity of teleportation while making it stable at higher temperatures. Nevertheless, this shows that maintaining the nonclassical characteristics at higher temperatures with increased DM interaction does not guarantee enhanced values of average teleportation fidelity.

In summary, increasing DM interaction generally enhances all the quantum correlations and coherence in our work but does not significantly increase the peak value of average teleportation fidelity, although it helps maintain these values at higher T. Again, the hierarchy of quantum resources, as depicted in Fig. 1, is held.

5.3 Impact of KSEA interaction

Finally, we explore the impact of various fixed values of KSEA interaction, without introducing DM interaction, on quantum resources and the average fidelity of teleportation. This analysis is illustrated in Fig. 4 when we have plotted all functions against T for different fixed values of KSEA interaction: \(\Gamma _z = 0.5\) (dashed black), \(\Gamma _z = 1.0\) (solid red), \(\Gamma _z = 1.5\) (dashed green), and \(\Gamma _z = 2.0\) (solid blue) with zero value of \(\mathcal {D}_z\). One can observe that, unlike DM interaction, KSEA interaction increases the peak values of these measures [compare with Fig 3 when \(\Gamma _z = 0\)]. Besides, it helps to maintain high peak values of QC and quantum correlations even at significantly higher temperatures. In general, its effect is positive on all quantum resources of the quantum channel. For instance, when \(\Gamma _z = 0.5\), BNL diminishes to zero around \(T \approx 0.2\), whereas for \(\Gamma _z = 2.0\), it decreases to zero at \(T \approx 1.8\), marking a more than nine-fold improvement in the sustainability of BNL. A similar trend is observed for QD and concurrence. Again, among all quantum resources, BNL remains the most delicate, followed by QS.

Despite achieving maximal entanglement at very low temperatures, the average teleportation fidelity only remains greater than the classical limit (2/3) when KSEA interaction is very small (look at Fig. 4f). Namely, at \(\Gamma _z = 0.5\), the average fidelity of teleportation is greater than 2/3 at near-zero temperatures, whereas increasing KSEA interaction does not help in achieving fidelity greater than 2/3 even at low temperatures. This shows that increasing the KSEA interaction does not enhance teleportation fidelity and can not guarantee successful teleportation. This observation aligns with findings in other studies, such as [77], which indicates that teleportation fidelity is not solely determined by entanglement measures such as concurrence and purity. Specifically, even states with higher concurrence and purity may exhibit lower teleportation fidelity due to the influence of other nonlocal properties that are not captured by these traditional metrics. Therefore, our results further emphasize that increasing KSEA interaction, despite enhancing entanglement, does not guarantee successful teleportation, as the fidelity is also influenced by additional state parameters beyond concurrence and purity.

Although a large value of KSEA interaction does not enhance the average fidelity of teleportation, it is beneficial for enhancing QC and correlations (quantum resources). Therefore, increasing KSEA interaction enhances all the correlations and coherence but does not increase the peak value of average teleportation fidelity. While it helps maintain these values at higher T. Overall, the impact of KSEA interaction on teleportation fidelity is negative.

Achieving a quantum advantage for teleportation is unsuccessful across all temperatures with different fixed KSEA interaction values. Although QC and correlations generally persist at nonzero levels for even higher temperatures, indicating the presence of BNL, entanglement, discord, and steering, successful quantum teleportation (greater than \(\mathcal {F}(\rho _T)=2/3\)) is not achieved in this scenario. Additionally, we find that the channel state exhibits BNL and steerability, as well as entanglement, yet teleportation remains unachievable.

6 Conclusion and outlook

In this study, we conducted a comprehensive comparative analysis of various coherence and correlation measures, including Bell nonlocality, quantum steering, quantum entanglement, quantum discord, and \(l_1\) norm of quantum coherence, within the context of a two-qubit Heisenberg XYZ model under the Dzyaloshinsky-Moriya (DM) and Kaplan-Shekhtman-Entin-Wohlman-Aharony (KSEA) interactions with variable Zeeman splitting. We treated the Gibbs thermal state of this model as a quantum channel for teleportation, evaluating the average teleportation fidelity. These coherence and correlation measures, along with average teleportation fidelity, were systematically examined as functions of temperature while varying key channel parameters such as the Zeeman splitting, KSEA interaction, and DM interaction.

Our findings indicate that the presence of entanglement in the context of the Heisenberg spin channel does not inherently guarantee successful teleportation, particularly in mixed-state scenarios. This conclusion not only aligns with but also extends the insights from previous works, including the study by Nandi et al. [77] on two-qubit X-states. There are other proposals that somehow patronize our study by Adhikari et al. [78]. We have shown that applying a magnetic field to both spins instead of one spin significantly enhances quantum coherence and teleportation fidelity. However, these enhancements deteriorate with increasing temperature due to thermal fluctuations, underscoring the critical role of temperature in degrading quantum properties.

Moreover, our results indicate that while increasing the DM interaction maintains higher peak values of quantum resources at elevated temperatures, it does not significantly boost the average teleportation fidelity, which remains above the classical threshold of \(2/3\). This finding underscores that maximal entanglement in mixed states does not guarantee successful teleportation, corroborating Nandi et al.’s [77] conclusions that entanglement alone cannot ensure teleportation success. Similarly, while both DM and KSEA interactions generally increase the strength of all coherence and correlations, they fail to provide significant support for the teleportation process. Also, our analysis reveals that increasing KSEA interaction fails to improve teleportation fidelity, echoing Nandi et al.’s [77] assertion that higher concurrence and purity do not always translate into improved teleportation fidelity. Besides, Nandi et al. [77] emphasized the detrimental effects of noise and decoherence on teleportation fidelity in two-qubit X-states, highlighting that even with maximal entanglement, the fidelity is compromised by the mixed nature of the states involved. Our study aligns with this perspective, demonstrating that despite the presence of maximal entanglement, the mixed-state nature impairs teleportation fidelity.

We also scrutinized various quantum resources within the traditional hierarchy of quantum resources and found that this hierarchy remains valid in our model. Specifically, Bell nonlocality emerges as the most fragile correlation, while the \(l_1\)-norm of coherence stands out as the most robust indicator, capable of capturing all forms of quantum coherence. This refined understanding of quantum resources provides a more comprehensive framework for analyzing teleportation fidelity in mixed-state scenarios.