1 Introduction

In 1935, Schrödinger tried to interpret the Einstein-Podolsky-Rosen (EPR) paradox by establishing correlations between two quantum systems that were too strong to be explained classically; this phenomenon is commonly referred to as EPR-steering [1, 2]. The concept of steering involves one remote user using a pair of entangled states to influence or steer their partner’s state through local measurements. As per the hierarchy of quantum correlations, steerable states are a strict superset of the states that can demonstrate Bell nonlocality and a strict subset of the entangled states [3,4,5]. Quantum steering has recently received significant attention in the field of quantum information research and has been the subject of both experimental and theoretical investigations [6, 7]. For example, the experimental quantum steering has been studied through the implementation of generalized entropic criteria and dimension-bounded steering inequalities, where two or three measurement setups are used on each side [8]. Steering game based on the all-versus-nothing criterion has been experimentally demonstrated [9]. The asymmetric property of EPR steering is relevant for experimental and potential applications in quantum information as a one-sided device-independent quantum key distribution [10], quantum teleportation [11], and optimal prepare-and-measure scenarios [12]. Moreover, for different quantum systems, the possibility of quantum steering is experimentally interpreted, including photon polarizations in a linear-optical setup [13], Bohmian trajectories [14], a family of the natural two-qubit state [15], and non-Gaussian state [16].

In the theoretical framework, researchers have developed asymmetric criteria of steering correlation for a pair of arbitrary continuous variables [3]. Additionally, Walborn et al. [17] have utilized the entropic uncertainty relations to express the steering inequality for arbitrary discrete observables. The violation of the Clauser-Horne-Shimony-Holt inequality has also been employed to discuss the degree of steerability [18, 19]. Furthermore, some investigations have been conducted on the violation of steering inequality and its degree for various quantum systems, including a three-mode optomechanical system [20], Heisenberg chain models [21, 22], two-level or three-level detectors [23, 24], and qubit-qubit as well as qubit-qutrit states [25,26,27].

On the other hand, the essential conceptions of squeezed spin systems were introduced by Kitagawa and Ueda in 1993 [28]. The entropy squeezing for a bipartite system has been obtained for three discrete observables in N-dimensional Hilbert space and employing the discrete Shannon entropy [29]. The violation of two conditional entropy squeezing factors represents a magnificent indicator of entanglement [30]. Meanwhile, the entropy squeezing of multi-qubit inside a cavity system has been considered a hot research topic, such as two-qubit interacting with two-mode cavity field [31], qutrit state in a cavity filed [32], and the effect of classical field and nonlinear term on the qubit-field interaction [33].

Our motivation is to introduce how entropy squeezing can be employed as an indicator of the degree of steerability. As the distinction between steering and entanglement lies in non-locality, quantified through conditional entropy, we employ the entropy squeezing—a commonly used entanglement indicator—transformed into conditional entropy squeezing to signify steering. Overall, as the discrete conditional Shannon entropy is used as a measure of steerability, so do the two conditional entropy squeezing factors express the steering?

This paper is organized as follows: In Sect. 2, we present the steerability based on conditional entropy squeezing. In Sect. 3, the main results of our paper are discussed in detail. Finally, the conclusion is given in Sect. 4.

2 Steerability based on conditional entropy squeezing

In order to gain a better understanding of the relationship between entropy squeezing and normalized Entropic Uncertainty Relation (EUR)-steering for bipartite subsystems A and B, we can take advantage of the definition provided by Walborn et al. [17]. The mathematical framework of EUR-steering inequality concerning an even N-dimensional Hilbert space along with the local hidden state for a pair of arbitrary discrete observables is expressed as [17]

$$\begin{aligned} \sum _{i=1}^{N+1}H \left( R^B_i|R^A_i \right) \ge \frac{N}{2} \ln \left( \frac{N}{2} \right) + \left( 1+\frac{N}{2} \right) \ln \left( 1+\frac{N}{2} \right) , \end{aligned}$$
(1)

where \( \{R^A_i\}\) and \(\{R^B_i\} \) are the eigenvectors of the discrete observables \( {\hat{R}}^A \) and \( {\hat{R}}^B \), respectively, and N is the total number of different eigenvectors. \(H(R^B|R^A) \ge \sum _{\lambda } P(\lambda ) H_Q(R^B|\lambda ) \) denotes the corresponding local hidden state constraint for discrete observables, which is defined by the conditional information entropy \(H_Q(R^B|\lambda ) \) of the probability distribution \( P_Q(R^B|\lambda ) \) with the hidden variable \(\lambda \). In two-dimensional Hilbert space \( N =2 \), by employing the Pauli spin operators \(\{\sigma _x,\sigma _y,\sigma _z\}\) as measurements, the EUR-steering from A to B is realized only if the following condition is violated [17, 34]

$$\begin{aligned} H \left( \sigma _x^B|\sigma _x^A \right) +H \left( \sigma _y^B|\sigma _y^A \right) +H \left( \sigma _z^B|\sigma _z^A \right) \ge 2\ln 2, \end{aligned}$$
(2)

where

$$\begin{aligned} \begin{aligned} H \left( \sigma _i^B|\sigma _i^A \right)&= H \left( {\hat{\rho }}_{AB} \right) _i - H \left( {\hat{\rho }}_A \right) _i\\ {}&= - \sum _{n,m=1}^{2} P_i^{n,m} \ln P_i^{n,m}+ \sum _{l=1}^{2} P_i^{l} \ln P_i^{l}. \end{aligned} \end{aligned}$$
(3)

here \( P_i^{n,m}=\langle \phi ^i_n, \phi ^i_m|\hat{\rho }_{AB}|\phi ^i_n, \phi ^i_m \rangle \) and \( P_i^{n}= \langle \phi ^i_n |\hat{\rho }_{A}|\phi ^i_n \rangle \) are the probability distribution of an arbitrary two-qubit state \(\hat{\rho }_{AB}\) and reduced single qubit state \(\hat{\rho }_{A}\), respectively, where \( |\phi ^i_{n} \rangle \) and \( |\phi ^i_{m} \rangle \) represent the two possible eigenvectors of \( \sigma _i \), and \(\hat{\rho }_{A}=Tr_B[\hat{\rho }_{AB}] \).

In this paper, we assume that the density state \( {\hat{\rho }}_{AB} \) with real components in the standard basis \( \{|00\rangle , |01\rangle , |10\rangle , |11\rangle \} \) can be written as

$$\begin{aligned} {\hat{\rho }}_{AB}=\begin{pmatrix} \rho _{11}&{} \quad 0 &{} \quad 0&{} \quad \rho _{14}\\ 0&{} \quad \rho _{22}&{} \quad \rho _{23}&{} \quad 0\\ 0&{} \quad \rho _{23}&{} \quad \rho _{33} &{} \quad 0\\ \rho _{14}&{} \quad 0&{} \quad 0&{} \quad \rho _{44} \end{pmatrix}. \end{aligned}$$
(4)

Note that \({\hat{\rho }}_{AB}\) satisfies the common conditions \({\hat{\rho }}_{AB}\ge 0\) and \(Tr[{\hat{\rho }}_{AB}]=1\).

By applying state (4) in Eq. (2) and violating EUR-steering inequality, one can obtain

$$\begin{aligned} \begin{aligned} {\mathcal {I}}_{AB}=&\sum _{i=1}^{3} \sum _{j=1}^{4}\frac{1 + x_{ij}}{2} \ln (1+x_{ij})\\ {}&- \sum _{k=1}^{2}(1 + a_{k}) \ln (1+a_{k})\le 2 \ln 2, \end{aligned} \end{aligned}$$
(5)

where the summations in the first term in Eq. (5) are related to the three Pauli spin operators and probability distribution of the two-qubit system \(\hat{\rho }_{AB}\), respectively, and \( x_{ij} \) are obtained by

$$\begin{aligned} \begin{aligned}&x_{11}=x_{12}=-x_{13}=-x_{14}=2 (\rho _{14}+\rho _{23}),\\ {}&x_{21}=x_{22}=-x_{23}=-x_{24}=2(\rho _{23}-\rho _{14}),\\ {}&x_{31}=3\rho _{11}-(\rho _{22}+\rho _{33}+\rho _{44}), \\&x_{32}=3\rho _{22}-(\rho _{11}+\rho _{33}+\rho _{44}),\\ {}&x_{33}=3\rho _{33}-(\rho _{11}+\rho _{22}+\rho _{44}),\\&x_{34}=3\rho _{44}-(\rho _{11}+\rho _{22}+\rho _{33}). \end{aligned} \end{aligned}$$
(6)

Likewise, the summation in the second term in Eq. (5) is related to the probability distribution of the reduced state \(\hat{\rho }_{A}\), and \( a_{k} \) would be given by

$$\begin{aligned} \begin{aligned} a_{k}=(-1)^k (\rho _{11}+\rho _{22}-\rho _{33}-\rho _{44}). \end{aligned} \end{aligned}$$
(7)

However, the one-way normalized EUR-steering is quantified based on observable A measurements as follows [35]

$$\begin{aligned} S^{A\longrightarrow B}=\max \bigg \{0,\frac{{\mathcal {I}}_{AB}-2\ln 2}{{\mathcal {I}}_{max}-2\ln 2}\bigg \}, \end{aligned}$$
(8)

where \({\mathcal {I}}_{max}= 6 \ln 2 \) when the system is prepared in Bell states.

On the other hand, if we define the function \( \Xi \left( \sigma _i^B|\sigma _i^A \right) = e^{H \left( \sigma _i^B|\sigma _i^A \right) } \), then the inequality (2) can be reformulated as

$$\begin{aligned} \Xi \left( \sigma _x^B|\sigma _x^A \right) \Xi \left( \sigma _y^B|\sigma _y^A \right) \ge \frac{4}{\Xi \left( \sigma _z^B|\sigma _z^A \right) }, \end{aligned}$$
(9)

where

$$\begin{aligned} \Xi \left( \sigma _i^B|\sigma _i^A \right) = \sum _{n,m=1}^{2} \bigg (P_i^{n,m}\bigg )^{P_i^{n,m}} \times \sum _{l=1}^{2} \bigg (P_i^{l}\bigg )^{P_i^{l}}. \end{aligned}$$
(10)

According to Ref. [29], the fluctuations in component \( \Xi (\sigma _i^B|\sigma _i^A)\) are said to be “squeezed in entropy” if the squeezing factor \( E(\sigma _i^B|\sigma _i^A) \) satisfies the condition

$$\begin{aligned} E\big (\sigma ^B_i|\sigma ^A_i \big )=\frac{2}{\sqrt{\Xi \big (\sigma _z^B|\sigma _z^A \big )}}-\Xi \big (\sigma _i^B|\sigma _i^A \big ), \end{aligned}$$
(11)

with \( i=x,y \). From the previous condition, we can depict the upper bounds or the lower bounds of the normalized EUR-steering degree. If the state is maximally entangled, then the upper and lower bounds in condition (11) are identical. Hence, bidirectional steerability and the average of conditional entropy squeezing factor have similar behavior. In partially entangled states, the normalized EUR steerability is restricted between the upper and lower bounds. Therefore, the average of the two components of conditional entropy squeezing \( E(\sigma _i^B|\sigma _i^A) \) represents an indicator for quantum steerability. In any case, we can define the quantum steerability based on the average of entropy squeezing as

$$\begin{aligned} {\mathcal {Z}}^{A\longrightarrow B}{\mathop {=}\limits ^{ \text{ def } }}\max \left\{ 0,\frac{E\big (\sigma _x^B|\sigma _x^A \big )+E \big (\sigma _y^B|\sigma _y^A \big )}{2}\right\} , \end{aligned}$$
(12)

where \( E(\sigma _x^B|\sigma _x^A)\) and \(E(\sigma _y^B|\sigma _y^A) \) are defined in Eq. (11). Hereinafter, we provide a comparative study between the average of conditional entropy squeezing and one-way quantum steering for some different quantum systems.

3 Some results and discussion

Here, we study the relationship between one-way steering and the average conditional entropy squeezing for a class of two-qubit state, which reads

$$\begin{aligned} {\hat{\rho }}_{AB}=\nu |\phi \rangle \langle \phi |+ (1-\nu ) |\psi \rangle \langle \psi |, \end{aligned}$$
(13)

where \( |\phi \rangle =\frac{|01\rangle +|10\rangle }{\sqrt{2}} \), \( |\psi \rangle =\frac{|00\rangle +|11\rangle }{\sqrt{2}} \), and \( \nu \) is the setting state parameter. The state (13) is maximally entangled for \(\nu =1\) and \(\nu =0\), partially entangled for \( \nu \in (0,0.5) \cup (0.5,1)\), and disentangled for \(\nu =0.5\).

Fig. 1
figure 1

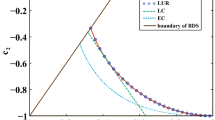
Comparative study between a \( E(\sigma _x^B|\sigma _x^A) \) (dotted curve), \( E(\sigma _y^B|\sigma _y^A) \) (dashed curve), and one-way normalized EUR-steering \( S^{A\longrightarrow B} \) (solid curve) for the state (13), and b the average of conditional entropy squeezing \( {\mathcal {Z}}^{A\longrightarrow B} \) (dashed curve) and one-way normalized EUR-steering \( S^{A\longrightarrow B} \) (solid curve)

Full size image

In Fig. 1, we have performed a comparative analysis of the normalized EUR-steering and entropy squeezing for a composite system consisting of a two-qubit state represented by Eq. (13). Through our analysis, we have observed interesting relationships between these two measures. Figure 1a clearly demonstrates that the extent of normalized EUR-steering is bounded by the two conditional entropy squeezing factors. Specifically, when the normalized EUR-steering is maximized, we observe that the two conditional entropy squeezing factors become identical. Conversely, when the normalized EUR-steering is minimized, the two conditional entropy squeezing factors are separated. This finding indicates that the values of \( E(\sigma _x^B|\sigma _x^A) \) and \( E(\sigma _y^B|\sigma _y^A) \) can be considered as upper and lower bounds of normalized EUR-steering, respectively. Furthermore, we have investigated the average of the two conditional entropy squeezing factors and its relation with the normalized EUR-steering. Figure 1b illustrates that at maximally entangled states with \( \nu =0 \) and \( \nu =1 \), the average of entropy squeezing (\( {\mathcal {Z}}^{A\longrightarrow B} \)) aligns closely with the normalized EUR-steering \( S^{A\longrightarrow B} \). However, at a lower degree of steering, corresponding to a partially entangled state, we observe deviations between the behaviors of normalized EUR-steering and the average of entropy squeezing. Nevertheless, even in these cases, \( {\mathcal {Z}}^{A\longrightarrow B} \) remains a reliable indicator for expressing the presence of steerability in the system.

3.1 Some quantum processes

In this subsection, we will compare in detail the effect of some quantum processes on the functions \( {\mathcal {Z}}^{A\longrightarrow B} \) and \( S^{A\longrightarrow B} \), namely acceleration process, decoherence via a stochastic dephasing channel, and swapping process.

3.1.1 Acceleration process

Let two qubits be simultaneously or separately accelerated in Rindler space. This space delineates two distinct sectors, denoted as Regions I and II. In this context, the accelerated particle is situated within the first region (Region I), while the anti-accelerated particle occupies the second region (Region II). The computational basis \( \{0,1\} \) in this space for regions I and II can be defined as [36]

$$\begin{aligned} \begin{aligned}&|0_k\rangle = \cos r_k |0_k\rangle _I |0_k\rangle _{II}+ \sin r_k |1_k\rangle _I |1_k\rangle _{II},\\ {}&|1_k\rangle = |1_k\rangle _I |0_k\rangle _{II}, \end{aligned} \end{aligned}$$
(14)

where \( r_k\in [0,\pi /4] \) is the acceleration parameter of the qubit \( k=A,B \). By substituting in the state (13) and tracing over the degrees of the region II, one can get the accelerated state as

$$\begin{aligned} \begin{aligned} {\hat{\rho }}_{AB}^\textrm{acc}&= {\mathcal {A}}_{11} |00\rangle \langle 00| + {\mathcal {A}}_{22}|01\rangle \langle 01|+ {\mathcal {A}}_{33}|10\rangle \langle 10|\\ {}&\quad + {\mathcal {A}}_{44} |11\rangle \langle 11| +( {\mathcal {A}}_{14} |00\rangle \langle 11|+{\mathcal {A}}_{23} |10\rangle \langle 01|+h.c.), \end{aligned} \end{aligned}$$
(15)

where

$$\begin{aligned} \begin{aligned}&{\mathcal {A}}_{11}= \frac{\nu }{2} \cos ^2 r_a \cos ^2 r_b,\ {\mathcal {A}}_{22}= \cos ^2 r_a \left( \frac{\nu }{2} \sin ^2r_b +\frac{1-\nu }{2} \right) ,\\&{\mathcal {A}}_{33}=\cos ^2 r_b \left( \frac{\nu }{2} \sin ^2r_a + \frac{1-\nu }{2} \right) , \\ {}&{\mathcal {A}}_{44}= \sin ^2 r_a \left( \frac{\nu }{2} \sin ^2r_b + \frac{1-\nu }{2} \right) + \frac{1-\nu }{2} \sin ^2r_b +\frac{\nu }{2}, \\&{\mathcal {A}}_{14}=\frac{\nu }{2}\cos r_a \cos r_b, \ {\mathcal {A}}_{23}=\frac{1-\nu }{2}\cos r_a \cos r_b. \end{aligned} \end{aligned}$$
(16)
Fig. 2
figure 2

Average of conditional entropy squeezing \( {\mathcal {Z}}^{A\longrightarrow B} \) (dashed curve) and one-way normalized EUR-steering \( S^{A\longrightarrow B} \) (solid curve) for accelerated state (15) with \(\nu =1\). a \( r_a=r \), \( r_b=0 \) and b \( r_a= r_b=r \)

Full size image

In Fig. 2, we present an investigation into the impact of the accelerated process on a two-qubit state. Specifically, we aim to explore the relationship between the normalized EUR-steering and average entropy-squeezing measures under this process. We assumed that the two-qubit state is maximally entangled with \(\nu =1\) as a fixed parameter. In Fig. 2a, we observe that when only one qubit is accelerated with \( r_a=r \) and \( r_b=0 \), the normalized EUR-steering is maximized at lower values of the acceleration parameter. As the acceleration parameter increases, we see a decrease in the degree of steering. Interestingly, we note that the normalized EUR-steering and the entropy squeezing are identical across different values of the acceleration parameter r. This indicates a consistent relationship between these measures regardless of the acceleration applied to the system. On the other hand, when both qubits are accelerated simultaneously with \( r_a= r_b=r \), Fig. 2b reveals an intriguing trend. As the acceleration parameter increases, the rate of decrease in steering becomes more pronounced. This finding suggests that accelerating two qubits simultaneously increases the suppression of steering. However, it is important to note that despite this trend, the two measures, namely normalized EUR-steering and entropy squeezing, exhibit little variations with respect to the acceleration parameter.

3.1.2 Noisy channel process

To examine the two functions (8) and (12) under noisy channel models, we can express the temporal density operator in terms of Kraus operators as

$$\begin{aligned} {\hat{\rho }}_{AB}(t)= \sum _{i,j} K_i^A(t) K_j^B(t) {\hat{\rho }}_{AB}(0) (K_i^A (t) K_j^B (t))^\dagger , \end{aligned}$$
(17)

here \( {\hat{\rho }}_{AB}(0) \) is defined in Eq. (13), while \( K_i^k(t)\) and \( K_j^k(t)\) with \(k=A, B \) are the time-dependent Kraus operators for different noise channels. For example, we use the Kraus operators of amplitude-damping noise [37], which are defined by [38]

$$\begin{aligned} K_1 (t)=|0\rangle \langle 0|+\sqrt{1-p(t)} |1\rangle \langle 1|, \quad K_2 (t)=\sqrt{p(t)} |0\rangle \langle 1|, \end{aligned}$$
(18)

where

$$\begin{aligned} p(t)= e^{-g t}\left[ \cos (\lambda t/2)+ \frac{g}{\lambda } \sin (\lambda t/2) \right] ^2 \end{aligned}$$

pertains to a non-Markovian amplitude-damping channel with \(\lambda =\sqrt{ g(2\gamma - g)}\), where g is a decay rate which depends on the reservoir correlation time and \( \gamma \) is the coupling strength related to qubit relaxation time [38].

Likewise, the Kraus operators for purely dephasing noise channels can be defined as [39]

$$\begin{aligned} K_1 (t)=|0\rangle \langle 0|+q(t) |1\rangle \langle 1|, \quad K_2(t)=\sqrt{1-q^2(t)} |1\rangle \langle 1|, \end{aligned}$$
(19)

where

$$\begin{aligned} q(t)=\exp \left\{ -\dfrac{\gamma }{2} \left( t+g^{-1} [\exp (-g t)-1]\right) \right\} . \end{aligned}$$
Fig. 3
figure 3

Average of conditional entropy squeezing \( {\mathcal {Z}}^{A\longrightarrow B} \) (dashed curve) and one-way normalized EUR-steering \( S^{A\longrightarrow B} \) (solid curve) for amplitude-damping noise, where a \(\nu =1\), \( g=0.01 \), b \(\nu =1\), \(g=0.1 \) and c \(\nu =0.1\), \(g=0.1 \). It is evident that the two measures are perfectly aligned in scenarios of maximum entanglement \(\nu =1\), whereas a slight deviation emerges in cases of partial entanglement, e.g., \(\nu =0.1\)

Full size image

Figure 3 presents a comprehensive examination of the impact of amplitude-damping noise on the degree of steerability, with the normalized EUR-steering and entropy squeezing serving as the quantifying measurements. In Fig. 3a, we observe that, by selecting a small value for the damping rate (\( g=0.01 \)), the normalized EUR-steering oscillates between its maximum and lower bounds. This oscillatory behavior is consistent with the properties of steerability under the influence of amplitude-damping noise. Indeed, the oscillatory patterns in \({\mathcal {Z}}^{A\longrightarrow B} \) and \(S^{A\longrightarrow B} \) are telltale signs of non-Markovianity associated with p(t). It is noteworthy that the two measures, normalized EUR-steering and entropy squeezing, coincide perfectly with the scaled time parameter. This convergence of the two measurements further reinforces their equivalence in capturing the system’s dynamics. Moving to Fig. 3b, we examine the effect of increasing decay rates within the range of g (specifically with \( g=0.1 \) and maximally entangled state with \( \nu =1 \)). As the scaled time escalates \( \gamma t \), we gradually observe the normalized EUR-steering oscillating with an increase in the upper bounds. On the other hand, in the case of a partially entangled state with a parameter value of \( \nu =0.1 \), it can be observed from Fig. 3c that a clear separation between the two measures over time. Furthermore, as the scaled time increases, the upper bounds of the steering degree exhibit a decrease in value. Remarkably, the maximum bounds of steering continue to expand as time progresses, indicating a growing influence of the amplitude-damping noise on the steerability of the system. Just like in the previous case, the normalized EUR-steering and average entropy-squeezing measurements in this scenario remain parallel, underscoring their identical nature. This consistent agreement can be attributed to the initial state being maximally entangled.

Fig. 4
figure 4

Average of conditional entropy squeezing \( {\mathcal {Z}}^{A\longrightarrow B} \) (dashed curve) and one-way normalized EUR-steering \( S^{A\longrightarrow B} \) (solid curve) under purely dephasing channel, where a \(\nu =1\), \( g=0.01 \), b \(\nu =1\), \(g=0.1 \) and c \(\nu =0.1\), \(g=0.1 \)

Full size image

Figure 4 provides a detailed analysis of the effect of dephasing noise on the degree of steering, utilizing the normalized EUR-steering and entropy squeezing as the measurement criteria. Moreover, the comparison between these two measures under the influence of the dephasing noise channel is examined. In the first, we consider an initial state that is maximally entangled with \( \nu =1 \). Initially, we note that while the entropy squeezing and normalized EUR-steering measures display similarities in their general behavior, they are not entirely identical as the scaled time progresses. At the onset, both measures exhibit their maximum bounds. However, as time increases, we observe a notable distinction between the maximum bounds of entropy squeezing and normalized EUR-steering. Interestingly, the maximum bounds of entropy squeezing surpass those of normalized EUR-steering. This disparity suggests that the influence of dephasing noise imposes a more pronounced impact on the entropy squeezing measure compared to normalized EUR-steering. In the context of partial entanglement \( \nu =0.1 \) with \( g=0.1 \), our observations indicate a rapid decay of steering and a decrease in the upper bounds of steering during the initial stages of the interaction. This suggests that partial entanglement has a significant impact on the dynamics of steering. Furthermore, it is important to note that the time evolution of the steered system is influenced by the degree of entanglement. As the entanglement decreases, the decay of steering becomes more pronounced, implying a decreasing ability to remotely control and influence the entangled particles.

Notably, despite the difference in the maximum bounds between the two measures, they still portray parallel trends. As the scaled time continues to grow, we witness a decrease in the degrees of steering for both measures. This observation implies that the detrimental effects of dephasing noise manifest as a reduction in the correlation between the entangled subsystems. Besides, it is evident that increasing the damping rate of the dephasing channel exacerbates this decreasing effect on the steering degrees.

3.1.3 Swapping process

Let us consider two different sources, \( S_{12} \) and \( S_{34} \), which generate pairs of two-qubit states \( \rho _{12} \) and \( \rho _{34} \), respectively. Qubits 1 and 4 are far apart, while qubits 3 and 2 remain close. The swapping process is aimed to measure the amount of quantum normalized EUR-steering between qubits 1 and 4 by performing a joint Bell measurement on qubits 2 and 3. The post-measurement state \( \rho _{14} \) is calculated by [40]

$$\begin{aligned} \rho _{14}=Tr_{23} \bigg [\frac{M_i. \rho _{1234}. M_i^\dagger }{Tr[M_i. \rho _{1234}. M_i^\dagger ]}\bigg ], \end{aligned}$$
(20)

where \( \rho _{1234}=\hat{\rho }_{AB} \otimes \hat{\rho }_{AB}\), such that the two sources generate the state \(\hat{\rho }_{AB}\) defined in Eq. (13). Moreover, \( M_i = I_2 \otimes |\Phi _i\rangle \langle \Phi _i|\otimes I_2\) in which \(I_2\) is a \(2\times 2\) identity matrix and \(|\Phi _i\rangle \)’s stand for the usual four Bell states.

Fig. 5
figure 5

Average of conditional entropy squeezing \( {\mathcal {Z}}^{A\longrightarrow B} \) (dashed curve) and one-way normalized EUR-steering \( S^{A\longrightarrow B} \) (solid curve) under swapping process with \( |\Phi _i\rangle =|\psi \rangle \)

Full size image

Finally, Fig. 5 focuses on analyzing the effects of the swapping process on the behavior of normalized EUR-steering and conditional entropy squeezing concerning the state parameter \( \nu \). The post-measurement state \( \rho _{14} \) at \( |\Phi _i\rangle =|\psi \rangle \) is studied to understand how the swapping process influences the behavior of the quantum system. The findings indicate that the steerability degree significantly decreases when the two-qubit state is initially in a partially entangled state. Furthermore, when compared to Fig. 1, it is noticeable that the unsteerable region expands during the swapping process. However, when the two-qubit state is maximally entangled, the two measures are equal. Hence, conditional entropy squeezing serves as an excellent indicator of the level of normalized EUR-steering present under this process.

4 Conclusion and outlook

We have proposed a new method for quantifying one-way quantum normalized EUR-steering in an arbitrary two-qubit system using the average of conditional entropy squeezing. We derived the explicit analytical expressions of normalized EUR-steering and conditional entropy squeezing. A comparative analysis of the two measures was conducted on a free maximally mixed two-qubit state, either restricted two-qubit state by using acceleration, noisy channels, or swapping processes.

For the free maximally mixed two-qubit state, our results highlight the interconnectedness between normalized EUR-steering and entropy squeezing. We demonstrated that the conditional entropy squeezing factors serve as bounds for normalized EUR-steering, which represented the upper and lower limits. Additionally, we established the average of entropy squeezing as a valuable indicator of steerability, particularly at a maximally entangled state.

The effects of the accelerated process on a two-qubit state were demonstrated. We observed that the behavior of normalized EUR-steering and entropy squeezing depends on whether one or both qubits are accelerated. In the former case, the degree of normalized EUR-steering decreases with increasing acceleration, while in the latter case, the rate of decrease in steering is amplified. Nonetheless, despite these variations, the measures of normalized EUR-steering and entropy squeezing remain stable and invariant with respect to the acceleration parameter.

Under the amplitude-damping noise, our results showed that under a specific small damping rate, the normalized EUR-steering experiences oscillatory behavior. By allowing the decay rate to increase, the normalized EUR-steering experiences oscillatory behavior with expanding boundaries. Notably, the normalized EUR-steering and entropy-squeezing measurements remained indistinguishable throughout these processes, further validating their correlation. On the other hand, the effect of dephasing noise on the degree of steering was evaluated. While the two measures differ in terms of their maximum bounds, they exhibit similar overall trends. Specifically, as the scaled time increases, both measures demonstrate a decrease in the degree of steering. This decreasing effect is amplified by enhancing the damping rate of the dephasing channel.

Finally, the swapping process significantly diminishes the steerability degree when the initial state of the two-qubit is partially entangled. For maximally entangled states, the two measures coincide.

In conclusion, it is evident that entropy squeezing serves as a measure of steering primarily in the context of a maximally entangled state. However, when considering partially entangled states or situations where entanglement is constrained by external factors, entropy squeezing remains a highly reliable indicator of steering. By assessing the degree of entropy squeezing in such scenarios, valuable insights can be gained regarding the presence and extent of quantum steering. Note that entropy squeezing is a tool for indicating and understanding quantum steering, even in cases where maximal entanglement may not be achieved.