1 Introduction

Numerous processes to generate the two-qubit information resources, namely, quantum correlations [1,2,3] and quantum coherence [4] have been exploited and used in several real physical systems. These significant concepts have tremendous advantages in different aspects of modern physics from information science to condensed matter theory [5, 6]. The quantum entanglement [2, 7,8,9,10,11], a direct result of the superposition principle, is considered at the forefront of resources which stimulates the advance of quantum technology. The occurrence of this purely quantum phenomenon manifests in an instantaneous disturbance of any part of a pair of spatially separated particles immediately after the other part undergoes a local measurement [7, 8]. This is done as if a certain channel is configured to secure a nonlocal correlation between the entangled system components. Such nonlocality makes the involved system enjoys by its distinguishing feature of being able to be described only as a whole rather than in its parts. Therefore, the nonlocality concept is a quintessential property of quantum entanglement. It is regarded as a fundamental resource for many quantum technology applications, such as quantum teleportation [12, 13], quantum dense coding [14], quantum cryptography [15], quantum metrology [16] and so on. Besides its excellent technological applications, nonlocality provides a new understanding of many conceptual issues in quantum physics. In terms of the Bell nonlocality concept [1, 8], the nonlocal character of a quantum state lies in the violation of the Bell inequalities. Strictly speaking, the realization of violation of the Bell inequalities for a quantum system led to the conclusion that there is an entanglement phenomenon [17]. In this respect, Buscemi has been establish a closer relationship between entanglement and nonlocality and shown that all entangled states are necessarily nonlocal [18].

Whenever the multipartite system is correlated, any local measurement made on one of its constituents is necessarily accompanied by a degree of uncertainty. This uncertainty is regarded as a primary tool to characterize the nonlocal correlation between the multipartite system parts. The uncertainty principle was recognized as one of the most striking features of quantum mechanics that genuinely differentiates the classical world from the quantum one [19,20,21,22]. Specifically, the famous Heisenberg uncertainty principle states that the momentum \({\hat{p}}\) and position \({\hat{x}}\) of a physical system cannot be simultaneously and precisely assigned [19, 20]. Aside from momentum and position, Robertson [21] and Schrödinger [23] showed that such limitation can be generalized to any arbitrary two incompatible observables. To make a connection between the uncertainty relation and quantum information theory, the entropic uncertainty relation was introduced [24, 25]. It is shown that this new version of uncertainty has attracted special attention in the literature (see for instance Refs. [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] and references therein). From an applicative point of view, the entropic uncertainty relation provides valuable physical resources for many quantum information tasks achievement; such as entanglement witnessing [43], quantum metrology [44], cryptographic security [45], quantum randomness [46], probing quantum correlations [47, 48] and quantum key distribution [49].

Quantum correlations in finite-dimensional systems are broadly recognized as crucial resources to improve the performance of quantum protocols in comparison to their classical analogue [50]. But the proper use of such quantum correlations is often obstructed by the decoherence phenomenon. Among the decoherence process, we distinguish intrinsic decoherence which was initially addressed by Milburn [51] and after intensively studied in many seminal works [52,53,54,55,56]. The Milburn intrinsic decoherence was mainly introduced to modify the usual Schrödinger equation that governs the quantum system time evolution. In fact, Milburn approach is based on the assumption wherein over sufficiently short time steps, the system under consideration does not evolve continuously under the effect of a unitary evolution, but rather according to a stochastic sequence of identical unitary phase transformations. It is worth mentioning that the influence of intrinsic decoherence in quantum systems was intensively addressed in many works (see, for instance, [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]).

In the present work, we shall explore the intrinsic decoherence approach for engendering pairwise information resources, such as the two-qubit Bell nonlocality, entropic uncertainty, and entanglement. In this context, we deal with a two neighboring spin-1/2 particles coupled via the Heisenberg XYZ interaction subjected to a transverse magnetic field and under the interplay z-components of DM (z–DM) along with KSEA (z–KSEA) interactions  controlled by the intrinsic decoherence effect. The characterization and quantification of quantum correlations as well as entropic uncertainty in this investigating model were recently studied [73, 74]. Usually, the choice of Heisenberg spin systems is motivated by the fact that such quantum systems are the potential candidate for implementing quantum communication and many other quantum information tasks.

This paper is outlined as follows. The Sect. 2 is devoted to reviewing some preliminaries about the quantum correlations that can be employed in this work. In Sect. 3, we introduce the model describing the quantum system consisting of a two-spin Heisenberg XYZ model under an external transverse homogeneous magnetic field by considering also the effects of the spin–orbit coupling both antisymmetric as well as symmetric contributions directed along the z-axis and studying its intrinsic evolution in the ambit of the Milburn master equation. The dynamical behaviors of the investigated quantum correlations in terms of the different parameters characterizing the considered system are examined and discussed through Sect. 4. Finally, our main results are summarized in Sect. 5.

2 Two-qubit information resource quantifiers

  • Bell nonlocality (BL) Here, let us use the maximal amounts of the two-qubit Bell function \(B_{\max }(t)\) as an indicator of two-qubit nonlocality [75, 76]. This two-qubit nonlocality satisfies \(B_{\max }(t)>2\), namely Bell-CHSH inequality is violated [77]. The analytical representation of the two-qubit Bell function \(B_{\max }(t)\) is given by [78]

    $$\begin{aligned} {B}_{\max }(t) =2 \sqrt{\xi _{1}+\xi _{2}}, \end{aligned}$$
    (1)

    in which \(\xi _{1}\) and \(\xi _{2}\) are the two largest eigenvalues of the matrix \({T}^{\dagger }{T}\) with \({T}=[t_{ij}]\) which is the correlation matrix [76] of a two-qubit state \({\hat{M}}_{AB}\), and its elements are given by

    $$\begin{aligned} t_{ij}=tr\{{\hat{M}}_{AB}(\sigma ^i \otimes \sigma ^{j})\}, \end{aligned}$$
    (2)

    where \(\sigma ^{i,j}\) (\(i,j=x,y,z\)) are the Pauli spin matrices. In our investigation, the BL is quantified by

    $$\begin{aligned} BL ({\hat{M}}_{AB}) ={B}_{\max }(t)-1. \end{aligned}$$
    (3)

    This means that two-qubit state has BL when this function satisfies \(BL ({\hat{M}}_{AB})>1\).

  • Concurrence (CE) The CE is one of the most common entanglement measures for a bipartite quantum system \({\hat{M}}_{AB}\). The CE is defined as [79, 80]

    $$\begin{aligned} CE ({\hat{M}}_{AB})=\max \{0,\sqrt{\mu _{1}}-\sqrt{\mu _{2}}-\sqrt{\mu _{3}}-\sqrt{\mu _{4}}\,\}, \end{aligned}$$
    (4)

    where \(\mu _{i}\)’s are the positive eigenvalues of the matrix \(R={\hat{M}}_{AB}(\sigma ^{y}\otimes \sigma ^{y}) {\hat{M}}^{*}_{AB} (\sigma ^{y}\otimes \sigma ^{y})\) in decreasing order with \({\hat{M}}^{*}_{AB}\) which is the complex conjugate of density matrix \({\hat{M}}_{AB}\). In general, \(0\le CE ({\hat{M}}_{AB})\le 1\).

  • Entropic uncertainty (EU) The concept of uncertainty was first proposed by Heisenberg [19] in 1927, and then it was formulated by Kennard [20] and Robertson [21] in terms of a standard deviation. After that, some researchers introduced new relations based on the Shannon and von Neumann entropies [81, 82]. Amongst them, let us use the relation provided by Berta et al. [83] for a two-particle system with a quantum memory (B), which may be correlated with the measured particle (A). This scenario can be run between two legitimate characters called Alice and Bob. The uncertainty of Bob about measurement outcome of Alice is bounded by [83]

    $$\begin{aligned} S(P\left| B \right. ) + S(Q\left| B \right. ) \ge S(A\left| B \right. ) + \log _2 \frac{1}{c}, \end{aligned}$$
    (5)

    where \(S(A\left| B \right) = S({\hat{M}}_{AB}) - S({\hat{M}}_B)\) is the conditional von Neumann entropy of density operator \({\hat{M}}_{AB}\) with \(S({\hat{M}}) = - tr({\hat{M}} \log _2 {\hat{M}})\) (for a general density matrix \({\hat{M}}\)). And \(c=\max _{i,j}\lbrace |\langle p_i | q_j \rangle |^{2} \rbrace\) where \(|p_i\rangle\) and \(|q_j\rangle\) are eigenstates of the incompatible observables P and Q. In the left-hand side, \(S(X\left| B\right. ) = S({\hat{M}}_{XB} ) - S({\hat{M}}_B )\) with \(X \in \left\{ {P, Q}\right\}\) being the conditional von Neumann entropy of post measurement states \(\begin{aligned} {\hat{M}}_{PB} =\sum \nolimits _i {(| {p_i }\rangle _{A}\langle {p_i } | \otimes \mathbf{{I}}_{B})}{\hat{M}}_{AB} (| {p_i }\rangle _{A} \langle {p_i } | \otimes \mathbf{{I}}_{B}),\nonumber \end{aligned}\) \(\begin{aligned} {\hat{M}}_{QB} =\sum \nolimits _j {(| {q_j }\rangle _{A}\langle {q_j } | \otimes \mathbf{{I}}_{B})} {\hat{M}}_{AB} (| {q_j }\rangle _{A} \langle {q_j }| \otimes \mathbf{{I}}_{B}).\nonumber \end{aligned}\) Herein, \({\hat{M}}_B = tr_A ({\hat{M}}_{AB} )\) and \(\mathbf{{I}}_{B}\) is the identity operator. According to Eq. (5), by resorting the incompatibility P and Q with the Pauli spin-1/2 operators \(\sigma ^x\) and \(\sigma ^z\), respectively, the EU, left-hand side of Eq. (5), can be expressed as

    $$\begin{aligned} EU ({\hat{M}}_{AB}) \equiv S({\hat{M}}_{\sigma ^x B}) + S({\hat{M}}_{\sigma ^z B})-2S({\hat{M}}_B). \end{aligned}$$
    (6)

3 Physical model and its dynamics

This section considers a Heisenberg XYZ model consisting of two qubits, say A and B, under the external transverse uniform magnetic field with DM and KSEA (DM–KSEA) interactions governed along the z-axis as [73, 74]

$$\begin{aligned} {\hat{H}}= & {} \sum _{i=x,y,z}J_{i}\sigma ^{i}_{A}\sigma ^{i}_{B}\nonumber \\&+ \sum _{j=1,2}\left\{ D^{z}_{j}(\sigma ^{x}_{A}\sigma ^{y}_{B}+(-1)^{j} \sigma ^{y}_{A}\sigma ^{x}_{B})\right\} +{ \sum _{k=A,B} B^{z}_{k}\sigma ^{z}_{k},} \end{aligned}$$
(7)

where \(\sigma ^{x,y,z}_{A,B}\)’s denote the standard Pauli matrices which are spanned by the lower \(|0\rangle _{k}\) and upper \(|1\rangle _{k} (k=A,B)\) states. \(B^{z}_{k}\) is the transverse homogeneous magnetic field in the z-direction at k-site. \(D^{z}_{1}\) is the strength of z–DM interaction resulting to orbit–spin coupling antisymmetric contribution, \(D^{z}_{2}\) represents the symmetric orbit–spin coupling contribution of the z–KSEA interaction, and \(J_{i}\) is the symmetrical spin–spin exchange coupling constants. Note that the special case \(D_1^z = D_2^z\) corresponds to a uniform spin-orbit interaction.

In the two-qubit standard computational basis states \(\{|\varpi _{1}\rangle =|11\rangle ,|\varpi _{2}\rangle =|10\rangle , |\varpi _{3}\rangle =|01\rangle , |\varpi _{4}\rangle =|00\rangle \}\), the Hamiltonian which represents that case is given by Eq. (7), and its the eigenstates \(|E_{l}\rangle (l=1,2,3,4)\) and the eigenvalues \(E_{l}\) are

$$\begin{aligned} |E_{1}\rangle= & {} \Lambda ^{+}_{\alpha }(W^{+}_{\alpha }|\varpi _{1}\rangle +|\varpi _{4}\rangle ),\quad E_{1}=J_{z}+\alpha ,\nonumber \\ |E_{2}\rangle= & {} \Lambda ^{+}_{\beta }(W^{+}_{\beta }|\varpi _{2}\rangle +|\varpi _{3}\rangle ), \quad E_{2}=-J_{z}+\beta ,\nonumber \\ |E_{3}\rangle= & {} \Lambda ^{-}_{\beta }(W^{-}_{\beta }|\varpi _{2}\rangle +|\varpi _{3}\rangle ),\quad E_{3}=-J_{z}-\beta ,\nonumber \\ |E_{4}\rangle= & {} \Lambda ^{-}_{\alpha }(W^{-}_{\alpha }|\varpi _{1}\rangle +|\varpi _{4}\rangle ),\quad E_{4}=J_{z}-\alpha , \end{aligned}$$
(8)

with

$$\begin{aligned} \Lambda ^{\pm }_{\alpha }= & {} \sqrt{\frac{1}{2} \pm \frac{1}{2\alpha } (B^{z}_{A}+B^{z}_{B})}, \quad \Lambda ^{\pm }_{\beta }=\sqrt{\frac{1}{2} \pm \frac{1}{2\beta } (B^{z}_{A}-B^{z}_{B})}, \nonumber \\ W^{\pm }_{\alpha }= & {} \pm \frac{J_{x}-J_{y}+2i D^{z}_{2}}{\alpha \pm (B^{z}_{A}+B^{z}_{B})},\quad W^{\pm }_{\beta }=\pm \frac{J_{x}+J_{y}-2i D^{z}_{1}}{\beta \pm (B^{z}_{A}-B^{z}_{B})},\nonumber \\ \alpha= & {} \sqrt{(B^{z}_{A}+B^{z}_{B})^{2}+(J_{x}-J_{y})^{2}+4(D^{z}_{2})^{2}}, \nonumber \\ \beta= & {} \sqrt{(B^{z}_{A}-B^{z}_{B})^{2}+(J_{x}+J_{y})^{2}+4(D^{z}_{1})^{2}}. \end{aligned}$$
(9)

Here, Milburn model [51] is used to explore the dynamics of the two-qubit information resources. The Milburn equation is given by

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}t} {\hat{M}}_{AB} =-i[{\hat{H}},{\hat{M}}_{AB}]-\frac{\gamma }{2}[{\hat{H}},[{\hat{H}},{\hat{M}}_{AB}]], \end{aligned}$$
(10)

where \({\hat{M}}_{AB}\) is a general density matrix of the two-qubit and \(\gamma\) is the decoherence parameter.

Using the eigenvalues \(E_{l}\) and the eigenstates \(|E_{l}\rangle\), the general solution for Eq. (10) is described by the following density matrix \({\hat{M}}_{AB}(t)\) [57]

$$\begin{aligned} { {\hat{M}}_{AB}(t)= \!\!\!\!\sum ^{4}_{m, n=1} \!\!\!\!\Lambda _{mn}(t) \,I_{mn}(t) \,\langle E_{m}|{\hat{M}}(0)|E_{n}\rangle \, |E_{m}\rangle \langle E_{n}|,} \end{aligned}$$
(11)

with the Schrödinger unitary interaction \(\Lambda _{mn}(t)\) and the intrinsic decoherence \(I_{mn}(t)\) terms which are described by

$$\begin{aligned} \Lambda _{mn}(t)= e^{-i(E_{m}-E_{n})t}, \qquad I_{mn}(t)=e^{ -\frac{\gamma }{2} (E_{m}-E_{n})^{2}t}. \end{aligned}$$
(12)

To obtain a particular analytical solution for Eq. (11), we consider that the two qubits are initially started with two different initial states; the uncorrelated state \({\hat{M}}(0)= |\varpi _{1}\rangle \langle \varpi _{4}|\) and the maximally correlated Bell state

$$\begin{aligned} {\hat{M}}(0)= \frac{1}{2} \left[ (|\varpi _{1}\rangle +|\varpi _{4}\rangle ) (\langle \varpi _{1}|+\langle \varpi _{4}|)\right] . \end{aligned}$$
(13)

In the following, let us use the case of the uncorrelated state to explore the generation of the the two-qubit information resources via BL, CE, and EU. While the case of the maximally correlated Bell state will be used to investigate the robustness of the two-qubit information resources against the Schrödinger unitary interaction and the intrinsic decoherence.

4 Dynamics of two-qubit information resources

4.1 For initial separable state

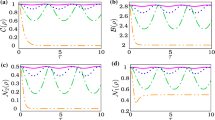
The dynamics of the BL, CE, and EU are depicted in Fig. 1 for specific values of \(J_{x}=-1\), \(J_{y}=-0.5\), \(J_z=2\), and \(D^{z}_{1}=D^{z}_{2}=1\) for different values of transverse uniform magnetic field \(B=B^{z}_{A}=B^{z}_{B}\) and in the absence of the intrinsic decoherence \(\gamma =0\) when initial state is separable \({\hat{M}}(0)= |\varpi _{1}\rangle \langle \varpi _{4}|\). As shown in this figure, all criteria oscillate during the time and their frequencies increase with growing magnitude of B when \(B>1/2\). As mentioned before, the initial state is uncorrelated and hence, BL and CE started from one and zero, respectively, and then they evolve between their minimal and maximal values within the time. Conversely, EU begins from its maximal value and it fluctuates in the opposite way of BL and CE.

Fig. 1
figure 1

The dynamics of the BL, CE, and EU are shown for \(J_{x}=-1\), \(J_{y}=-0.5\), \(J_z=2\), and \(D^{z}_{1}=D^{z}_{2}=1\) when the two-qubit system is initially in the uncorrected state \({\hat{M}}(0)= |\varpi _{1}\rangle \langle \varpi _{4}|\) in the absence of the intrinsic decoherence with different transverse uniform magnetic fields. \(B=0\) in a, \(B=0.5\) in b, \(B=2\) in c, and \(B=5\) in d

Full size image

In Fig. 2, all parameters are the same as in Fig. 1 but the system is affected by the intrinsic decoherence, that is \(\gamma =0.02\). It is obvious that BL, CE, and EU fluctuate but their amplitudes become less and finally, they reach steady values. According to this figure, they get the fixed values more quickly with increasing transverse homogeneous magnetic field B. One may conclude that the external magnetic field and intrinsic decoherence have a destructive effect on the quantum correlations when they affect the system simultaneously. Hence, Bob’s information about the results of Alice’s measurements in a decoherence environment decreases with increasing B during the time.

Fig. 2
figure 2

The dynamics of the BL, CE, and EU are shown as in Fig. 1 but under the intrinsic decoherence effect, \(\gamma =0.02\)

Full size image

Figure 3 is devoted to study of the behavior of BL, CE, and EU in the absence and presence of decoherence for different values of the z–DM and z–KSEA interactions \(D=D_{1}^{z}=D_{2}^{z}\) and the other parameters are the same in Fig. 1b. As displayed in this figure, all functions oscillate throughout the time and when DM and KSEA interactions are applied, their frequencies and sudden change points increase in the absence of decoherence [compare plots Fig. 3a and b]. In the presence of decoherence as well as DM–KSEA interactions, all quantities become fixed after some fluctuations (see Fig. 3d). However, there is no considerable difference between absence and presence of decoherence by comparing plots Fig. 3a and c, in the case that the DM–KSEA interactions are turned off.

Fig. 3
figure 3

The dynamics of BL, CE, and EU are shown as in Fig. 1b but for different strengths of z–DM and z–KSEA interactions. \(D=0\) in a and \(D=2\) in b. Graphs c and d as in a and b but under the intrinsic decoherence effect, \(\gamma =0.02\)

Full size image

4.2 For initial maximally correlated state

The time evolution of the robustness quantum information resources is shown in Fig. 4 for specific values of exchange couplings and D, and different values of transverse uniform magnetic field B with and without intrinsic decoherence when the two-qubit state is maximally entangled \({\hat{M}}(0)= [ (|\varpi _{1}\rangle +|\varpi _{4}\rangle ) (\langle \varpi _{1}|+\langle \varpi _{4}|)]/2\) at the beginning time. It is obvious that BL and CE begin from their maximal values (BL(t=0)=\(2\sqrt{2}-1\approx 1.8284\) and CE(t=0)=1) as expected from the assumed initial state, and conversely, EU starts from zero. Therefore, Bob can correctly guess Alice’s results at the initial moment the system interacts with the environment. By comparing plots Fig. 4a, b with c, d respectively, one can find that they oscillate over time but in the case of the existence of decoherence, their vibrations and sudden change points become less and they can be vanish faster for larger amount of B.

Fig. 4
figure 4

The dynamics of the robustness quantum information resources are shown for \(J_{x}=-1\), \(J_{y}=-0.5\), \(J_z=2\), and \(D^{z}_{1}=D^{z}_{2}=1\) when the two-qubit system is initially in the maximally correlated state \({\hat{M}}(0)= \frac{1}{2}[ (|\varpi _{1}\rangle +|\varpi _{4}\rangle ) (\langle \varpi _{1}|+\langle \varpi _{4}|)]\) in the absence of the intrinsic decoherence with different transverse uniform magnetic fields. \(B=0\) in (a) and \(B=1\) in (b). Graphs c and d as in a and b but under the intrinsic decoherence effect, \(\gamma =0.02\)

Full size image

Finally, in Fig. 5 the dynamics of BL, CE, and EU have been drawn for those parameters in Fig. 1b and different values of DM–KSEA interactions \(D=D_{1}^{z}=D_{2}^{z}\). This figure is similar to Fig. 3 except that the beginning state is a maximally entangled state and hence, there is no any uncertainty to measure incompatible observables at \(t=0\). Thus, we can see the destructive effects of D and intrinsic decoherence when they are used simultaneously. It is worth nothing that in all cases, the behavior of EU is in opposite way of BL and CE during the time. In the other words, EU lessens with growing BL and CE.

Fig. 5
figure 5

The dynamics of the robustness quantum information resources are shown as in Fig. 1b but for different strength of DM and KSEA interactions. \(D=0\) in a and \(D=2\) in b. Graphs c and d as in a and b but under the intrinsic decoherence effect, \(\gamma =0.02\)

Full size image

5 Concluding remarks and outlook

In this work, we have studied the dynamics of Bell nonlocality, entanglement, and entropic uncertainty for a two-qubit Heisenberg XYZ model with DM–KSEA interactions under intrinsic decoherence and different initial states. Specifically, we examined the time evolution of the BL, CE, and EU under the effect of DM–KSEA interactions, transverse uniform magnetic field, and intrinsic decoherence. The results showed that the symmetric and antisymmetric orbit–spin couplings greatly affect the oscillations behaviors and sudden change points of quantum correlations. It was also found that external magnetic field and intrinsic decoherence have a significant effect on the dynamical behavior of quantum quantifiers. More precisely, we observed that by tuning DM–KSEA interactions as well as magnetic field strength to appropriate values, one can reach maximal Bell nonlocality and entanglement, resulting in smaller measurement uncertainty even under intrinsic decoherence effects. Thereby, Bob would be able to guess Alice’s results with high precision, which is extremely required in realistic quantum information processing. Thus, we think our investigations may be beneficial to assist us to understand the behaviors of the quantum correlations and entropic measurement uncertainty in open quantum systems and their controlling.