1 Introduction

To explain the phenomenon of weak ferromagnetism observed in some rhombohedral antiferromagnets, Dzyaloshinsky [1, 2] developed a phenomenological approach based on the Landau theory of second-order phase transitions and showed that the antisymmetric mixed (in magnetization components) term in the expansion of the thermodynamic potential is responsible for the appearance of nonzero net magnetization of the system. Shortly after [3], he also noticed that in antiferromagnetic crystals with the tetragonal lattices, weak ferromagnetism can be caused by the symmetric mixed term in the expansion of the corresponding thermodynamic potential.

Later on, in 1960, Moriya [4, 5] developed a microscopic theory of anisotropic superexchange interaction by extending the Anderson theory of superexchange to include spin–orbit coupling. Using perturbation theory, he found that the leading anisotropy contribution to the interaction between two neighboring spins \({{\varvec{\sigma }}}_1\) and \({{\varvec{\sigma }}}_2\) is given by

$$\begin{aligned} {\mathcal {H}}_{\mathrm{DM}}={{\mathbf {D}}}\cdot ({{\varvec{\sigma }}}_1\times {{\varvec{\sigma }}}_2), \end{aligned}$$
(1)

where \({{\mathbf {D}}}=(D_x,D_y,D_z)\) is a constant vector that characterizes a substance. This interaction reproduces Dzyaloshinsky’s antisymmetric term and is now referred to as the Dzyaloshinsky–Moriya (DM) interaction. In addition, Moriya found the second-order correction term [4, 5]

$$\begin{aligned} {\mathcal {H}}_{\mathrm{KSEA}}={{\varvec{\sigma }}}_1 \cdot {\tilde{\Gamma }}\cdot {{\varvec{\sigma }}}_2, \end{aligned}$$
(2)

where \({\tilde{\Gamma }}\) is a symmetric traceless tensor. For a long time, this interaction was assumed to be negligible compared with the antisymmetric contribution (1). However, more later Kaplan [6] and then Shekhtman et al. [7, 8] argued the importance of the symmetric term because it can restore the O(3) invariance of the isotropic Heisenberg system which is broken by the DM term. For this reason, the interaction (2) began to be called the Kaplan–Shekhtman–Entin-Wohlman–Aharony (KSEA) interaction [9, 10] (see also reference 14 in [11]).

We will discuss two-site systems with the Hamiltonian

$$\begin{aligned} {\mathcal {H}}={\mathcal {H}}_{\mathrm{Z}} + {\mathcal {H}}_{\mathrm{H}} + {\mathcal {H}}_{\mathrm{DM}} + {\mathcal {H}}_{\mathrm{KSEA}}, \end{aligned}$$
(3)

where \({\mathcal {H}}_{\mathrm{Z}}\) is the Zeeman energy and \({\mathcal {H}}_{\mathrm{H}}\) the anisotropic exchange Heisenberg interactions. Behavior of quantum correlations in different particular cases of the model (3) was considered in numerous papers. The behavior of thermal entanglement in two-qubit completely isotropic (XXX) Heisenberg chain in the absence of an external field, but in the presence of DM interaction with a nonzero of only one, \(D_z\), component of the Dzyaloshinsky vector \({{\mathbf {D}}}\) was considered in [12]. The author of this paper found that the DM interaction can excite entanglement. Thermal entanglement in the partially anisotropic (XXZ) Heisenberg model with \(D_z\) or \(D_x\) component of Dzyaloshinsky vector was studied in [13]. Quantum entanglement in anisotropic Heisenberg XXZ chain with only \(D_z\) component was also discussed in [14]. The authors established that while the anisotropy suppresses the entanglement, the DM interaction can restore it. The effect of DM interaction on the quantum entanglement in the Heisenberg XYZ chain was observed in [15] in the absence of magnetic field. Thermal quantum discord in the anisotropic Heisenberg XXZ model with DM interaction and without any external field was investigated in [16]. Concurrence and quantum discord in two-qubit anisotropic Heisenberg XXZ model with DM interaction along the z-direction was considered in [17] where it was found that the tunable parameter \(D_z\) may play a constructive role to the quantum correlations in thermal equilibrium. Quantum discord of two-qubit anisotropy XXZ Heisenberg chain with DM interaction under uniform magnetic field was investigated in [18]. In the recent papers [19, 20], the thermal quantum entanglement and discord in two-qubit XYZ chain with DM interaction were discussed. As a whole, one can conclude that the most results have been obtained for the spin pairs with DM interactions when the exchange Heisenberg couplings are isotropic or, rarer, anisotropic. The external magnetic field was taken into account much less frequently. Finally, there are no publications where the quantum correlations (entanglement, discord, etc.) in Heisenberg dimers were discussed in the presence of KSEA interactions. Our research fills these gaps to a certain extent.

The structure of this paper is as follows. In the next section, we write down the Hamiltonian in an expanded form and establish its relationship with the density matrix. Sections 3 and 4 deal with the X and CS quantum states what gives the key that opens the way, first, to the group-theoretical analysis in Sect. 5 and then, in Sect. 6, to the results for the \(D_y\) and \({\Gamma }_y\) pair components of Dzyaloshinsky vector and \(\hat{\Gamma }\) tensor. Section 7 is devoted to the classification of fifteen Hamiltonians and density matrices. Finally, in the last Sect. 8, we briefly summarize the results obtained and note the remaining unsolved problems.

2 Hamiltonian and density matrix

The DM interaction (1) can be written in an expanded form as

$$\begin{aligned} {{\mathbf {D}}}\cdot ({{\varvec{\sigma }}}_1\times {{\varvec{\sigma }}}_2) =D_x(\sigma _1^y\sigma _2^z-\sigma _1^z\sigma _2^y) +D_y(\sigma _1^z\sigma _2^x-\sigma _1^x\sigma _2^z) +D_z(\sigma _1^x\sigma _2^y-\sigma _1^y\sigma _2^x), \end{aligned}$$
(4)

where \({{\varvec{\sigma }}}_i\) denotes the vector of Pauli matrices at site \(i=1,2\); \({{\varvec{\sigma }}}_i=(\sigma _i^x,\sigma _i^y,\sigma _i^z)\). Similarly for the KSEA term (2):

$$\begin{aligned} {{\varvec{\sigma }}}_1 \cdot {\tilde{\Gamma }}\cdot {{\varvec{\sigma }}}_2&=(\sigma _1^x,\sigma _1^y,\sigma _1^z) \left( \begin{array}{lll} 0&{}{\Gamma }_z&{}{\Gamma }_y\\ {\Gamma }_z&{}0&{}{\Gamma }_x\\ {\Gamma }_y&{}{\Gamma }_x&{}0 \end{array} \right) \left( \begin{array}{c} \sigma _2^x\\ \sigma _2^y\\ \sigma _2^z \end{array} \right) \nonumber \\&={\Gamma }_x(\sigma _1^y\sigma _2^z+\sigma _1^z\sigma _2^y) +{\Gamma }_y(\sigma _1^z\sigma _2^x+\sigma _1^x\sigma _2^z) +{\Gamma }_z(\sigma _1^x\sigma _2^y+\sigma _1^y\sigma _2^x), \end{aligned}$$
(5)

where \({\Gamma }_x\), \({\Gamma }_y\), and \({\Gamma }_z\) are the elements of the tensor \({\tilde{\Gamma }}\). As a result, the Hamiltonian (3) is rewritten as

$$\begin{aligned} {\mathcal {H}}&=B_1^x\sigma _1^x + B_1^y\sigma _1^y + B_1^z\sigma _1^z + B_2^x\sigma _2^x + B_2^y\sigma _2^y + B_2^z\sigma _2^z\nonumber \\&\quad + J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z\nonumber \\&\quad + D_x(\sigma _1^y\sigma _2^z-\sigma _1^z\sigma _2^y)+D_y(\sigma _1^z\sigma _2^x-\sigma _1^x\sigma _2^z)+D_z(\sigma _1^x\sigma _2^y-\sigma _1^y\sigma _2^x)\nonumber \\&\quad + {\Gamma }_x(\sigma _1^y\sigma _2^z+\sigma _1^z\sigma _2^y)+{\Gamma }_y(\sigma _1^z\sigma _2^x+\sigma _1^x\sigma _2^z)+{\Gamma }_z(\sigma _1^x\sigma _2^y+\sigma _1^y\sigma _2^x), \end{aligned}$$
(6)

where \(B_i^\alpha \)\((i=1,2\); \(\alpha =x,y,z)\) are the components of the external magnetic fields \({\mathbf {B}}_1\) and \({\mathbf {B}}_2\) (with the incorporated gyromagnetic ratios or g-factors) and \(J_\alpha \)\((\alpha =x,y,z)\) are the Heisenberg exchange couplings.

We will be able to study the systems only in some special cases of the Hamiltonian (6). For them, we will be interested in systems in a state of thermal equilibrium. The corresponding Gibbs density matrix is given as

$$\begin{aligned} \rho =\frac{1}{Z}\exp (-{\mathcal {H}}/T), \end{aligned}$$
(7)

where T is the temperature in energy units and Z the partition function. Thus, the Hamiltonian and density matrix of any system are connected via the functional relation.

Quantum correlations contained in composite quantum states are the focus of quantum information science. Many measures have been proposed to quantify these correlations, such as quantum entanglement, quantum discord, and one-way quantum work deficit [21,22,23,24,25,26,27,28]. It should be emphasized that the quantum correlation measures must satisfy a number of criteria [29] (see also the review [24]). In particular, as a necessary condition, the measures must be invariant under any local unitary transformations.

3 XYZ chain with \(D_z\) and \({\Gamma }_z\) couplings

We begin the analysis with quantum states having the X form. In accord with definition, X matrix can have nonzero entries only on the main diagonal and anti-diagonal. The portrait of such a sparse matrix resembles the letter “X,” which allowed to give it such a name [30]. Algebraic characterization of X states in quantum information has been done by Rau [31]. It is important to note that both the sums and the products of X matrices are again the X matrices; that is, the set of X matrices is algebraically closed. In particular, a function (decomposable in a Taylor series) of X matrix is the X matrix.

In the most general form, the Hermitian X matrix corresponding to the Hamiltonian (6) can be written as

$$\begin{aligned} {\mathcal {H}}_{zz}= \left( \begin{array}{cccc} J_z+B_1^z+B_2^z&{}\cdot &{}\cdot &{}J_x-J_y-2i{\Gamma }_z\\ \cdot &{}-J_z+B_1^z-B_2^z &{}J_x+J_y+2iD_z&{}\cdot \\ \cdot &{}J_x+J_y-2iD_z\ &{}-J_z-B_1^z+B_2^z&{}\cdot \\ J_x-J_y+2i{\Gamma }_z&{}\cdot &{}\cdot &{}J_z-B_1^z-B_2^z \end{array} \right) , \end{aligned}$$
(8)

where the points are put instead of zero entries. In Eq. (8), \(B_1^z\) and \(B_2^z\) are the z-components of external fields applied at the 1st and 2nd qubits, respectively, \((J_x,J_y,J_z)\) the vector of interaction constants of the Heisenberg part of interaction, \(D_z\) the z-component of Dzyaloshinsky vector, and \({\Gamma }_z\) the z-component in the KSEA interaction. Thus, this model contains seven real independent parameters: \(B_1^z\), \(B_2^z\), \(J_x\), \(J_y\), \(J_z\), \(D_z\), and \({\Gamma }_z\).

On the other hand, “any four-by-four matrix—and, therefore, the Hamiltonian matrix in particular—can be written as a linear combination of the sixteen double-spin matrices” [32, Sect. 12-2]. For the traceless X matrix (8), the linear combination of “double-spin matrices” is given as

$$\begin{aligned} {\mathcal {H}}_{zz}=B_1^z\sigma _1^z + B_2^z\sigma _2^z + J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z + J_{xy}\sigma _1^x\sigma _2^y + J_{yx}\sigma _1^y\sigma _2^x, \end{aligned}$$
(9)

where

$$\begin{aligned} J_{xy}=D_z + {\Gamma }_z,\quad J_{yx}=-D_z + {\Gamma }_z. \end{aligned}$$
(10)

Due to the functional relation (7), the Gibbs density matrix also has the X form with seven real parameters:

$$\begin{aligned} \rho _{zz}&= \left( \begin{array}{cccc} a&{}\cdot &{}\cdot &{}u\\ \cdot &{}b &{}v&{}\cdot \\ \cdot &{}v^*\cdot &{}c&{}\cdot \\ u^*&{}\cdot &{}\cdot &{}d \end{array} \right) =\frac{1}{4}(\sigma _0\otimes \sigma _0 + s_1^z\sigma _z\otimes \sigma _0 + s_2^z\sigma _0\otimes \sigma _z \nonumber \\&\quad + c_1\sigma _x\otimes \sigma _x + c_2\sigma _y\otimes \sigma _y + c_3\sigma _z\otimes \sigma _z + c_{12}\sigma _x\otimes \sigma _y + c_{21}\sigma _y\otimes \sigma _x), \end{aligned}$$
(11)

where the asterisk denotes complex conjugation, \(s_1^z\), \(s_2^z\), \(c_1\), \(c_2\), \(c_3\), \(c_{12}\), and \(c_{21}\) are the unary and binary correlation functions, and

$$\begin{aligned} \sigma _0= \left( \begin{array}{ll} 1&{}0\\ 0&{}1 \end{array} \right) ,\quad \sigma _x= \left( \begin{array}{ll} 0&{}1\\ 1&{}0 \end{array} \right) ,\quad \sigma _y= \left( \begin{array}{cc} 0&{}-i\\ i&{}0 \end{array} \right) ,\quad \sigma _z= \left( \begin{array}{cc} 1&{}0\\ 0&{}-1 \end{array} \right) \end{aligned}$$
(12)

are the unit and Pauli spin operators in the standard representation. Due to the nonnegativity definition and normalization condition of any density operator, \(a,b,c,d\ge 0\), \(a+b+c+d=1\), \(ad\ge |u|^2\), and \(bc\ge |v|^2\).

One can now calculate different quantum correlations in the X quantum states. The methods of calculating quantum correlations for the two-qubit X quantum states have been developed in a number works. The concurrence, a measure of quantum entanglement, is given by [30]

$$\begin{aligned} C=2\max \left\{ 0,|u|-\sqrt{bc},|v|-\sqrt{ad}\right\} . \end{aligned}$$
(13)

There are considerable studies on the quantum discord and one-way quantum work deficit. For instance, the quantum discord of two-qubit X quantum states was considered in Refs. [33,34,35] (and references therein). One may present the quantum discord as a formula

$$\begin{aligned} Q=\min \{Q_0, Q_{{\tilde{\theta }}}, Q_{\pi /2}\}, \end{aligned}$$
(14)

where the subfunctions (branches) \(Q_0\) and \(Q_{\pi /2}\) are the analytical expressions (corresponding to the discord with optimal measurement angles 0 and \(\pi /2\), respectively) and only the third branch \(Q_{{\tilde{\theta }}}\) requires one-dimensional searching of the optimal state-dependent measurement angle \({\tilde{\theta }}\in (0,\pi /2)\) (for details see in Refs. [36,37,38,39]).

Very similar situation takes place for the one-way quantum work deficit [40,41,42]. We may again write the one-way quantum work deficit of two-qubit X state in a semi-analytical form:

$$\begin{aligned} {\Delta }=\min \{\Delta _0, \Delta _{\vartheta }, \Delta _{\pi /2}\}, \end{aligned}$$
(15)

where the branches \(\Delta _0\) and \(\Delta _{\pi /2}\) are known in the analytical form, while the third branch \(\Delta _{\vartheta }\) also requires to perform numerical minimization to obtain state-dependent minimizing polar angle \(\vartheta \in (0,\pi /2)\) (see [42,43,44,45]).

So, the theory to calculate quantum correlations of X quantum states is well developed. This gives a possibility to calculate and investigate different quantum correlations for the two-qubit systems in a nonuniform field in z-direction, with completely anisotropic Heisenberg interactions, and with arbitrary z-components of DM and KSEA interactions.

4 XYZ chain with \(D_x\) and \({\Gamma }_x\) couplings

Let us take the centrosymmetric (CS) quantum state now. The CS matrix \(n\times n\) is defined by the relations for its matrix elements as follows: \(a_{ij}=a_{n+1-i,n+1-j}\) [46]. It is easy to check that the sum and product of CS matrices are the CS matrix, i.e., this family of matrices as well as X matrices is algebraically closed.

Most general Hermitian CS matrix of fourth order looks as

$$\begin{aligned} \rho _{xx}= \left( \begin{array}{llll} a&{}\mu &{}\nu &{}c\\ \mu ^*&{}b&{}d&{}\nu ^*\\ \nu ^*&{}d&{}b&{}\mu ^*\\ c&{}\nu &{}\mu &{}a \end{array} \right) , \end{aligned}$$
(16)

where a, b, c, and d are real quantities, while \(\mu \) and \(\nu \) are complex.

The Hamiltonian with CS symmetry reads

$$\begin{aligned} {\mathcal {H}}_{xx}= \left( \begin{array}{cccc} J_z&{}B_2^x-iJ_{zy}&{}B_1^x-iJ{yz}&{}J_x-J_y\\ B_2^x+iJ_{zy}&{}-J_z&{}J_x+J_y&{}B_1^x+iJ_{yz}\\ B_1^x+iJ_{yz}&{}J_x+J_y&{}-J_z&{}B_2^x+iJ_{zy}\\ J_x-J_y&{}B_1^x-iJ_{yz}&{}B_2^x-iJ_{zy}&{}J_z \end{array} \right) . \end{aligned}$$
(17)

This Hamiltonian in the Bloch form is written as

$$\begin{aligned} {\mathcal {H}}_{xx}=B_1^x\sigma _1^x + B_2^x\sigma _2^x + J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z + J_{yz}\sigma _1^y\sigma _2^z + J_{zy}\sigma _1^z\sigma _2^y. \end{aligned}$$
(18)

The latter can be rewritten in the form

$$\begin{aligned} {\mathcal {H}}_{xx}&=B_1^x\sigma _1^x + B_2^x\sigma _2^x + J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z\nonumber \\&\quad + D_x(\sigma _1^y\sigma _2^z - \sigma _1^z\sigma _2^y) + {\Gamma }_x(\sigma _1^y\sigma _2^z + \sigma _1^z\sigma _2^y), \end{aligned}$$
(19)

where

$$\begin{aligned} D_x=\frac{1}{2}(J_{yz}-J_{zy}),\quad {\Gamma }_x=\frac{1}{2}(J_{yz}+J_{zy}) \end{aligned}$$
(20)

are the x-components of Dzyaloshinsky vector and \({\tilde{\Gamma }}\) tensor, respectively.

So here we have the two-qubit anisotropic Heisenberg spin cluster with \(D_x\) and \({\Gamma }_x\) terms of DM and KSEA interactions and additionally in the nonuniform external fields applied in the transverse x-direction.

In Ref. [47] and then in Refs. [36, 37], it has been shown that by means of double Hadamard transformation \(H\otimes H\), where

$$\begin{aligned} H=\frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1&{}1\\ 1&{}-1 \end{array} \right) =H^t \end{aligned}$$
(21)

is the Hadamard transform, any CS matrix \(4\times 4\) is reduced to the X form (and vice versa). Indeed, taking into account relations

$$\begin{aligned} H\sigma _x H=\sigma _z,\quad H\sigma _y H=-\sigma _y,\quad H\sigma _z H=\sigma _x \end{aligned}$$
(22)

simple calculations yield

$$\begin{aligned} (H\otimes H){\mathcal {H}}_{xx}(H\otimes H)&=B_1^x\sigma _1^z + B_2^x\sigma _2^z + J_z\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_x\sigma _1^z\sigma _2^z\nonumber \\&\quad + D_x(\sigma _1^x\sigma _2^y - \sigma _1^y\sigma _2^x) - {\Gamma }_x(\sigma _1^x\sigma _2^y + \sigma _1^y\sigma _2^x). \end{aligned}$$
(23)

Thus, the CS Hamiltonian is returned to the X case up to a reassignment of seven parameters.

As a result, the discovered remarkable transformation \(H\otimes H\) allows to find correlation functions using the corresponding solutions for the X states. Knowing the solution for X state, we now able to calculate such quantum correlations as quantum entanglement, discord, and one-way work deficit for the CS case of XYZ model in the transverse external fields and not only with DM but also with KSEA interaction.

5 Group-theoretical view on the quantum states

To find the key to solve the XYZ model with the components \(D_y\) and \({\Gamma }_y\) of the DM and KSEA interactions, we analyze the symmetry of the CS matrix using group-theoretical methods. In addition, in the future this case will serve us as a heuristic example.

In the most general case, the four-by-four CS matrix is written as

$$\begin{aligned} A_{CS}= \left( \begin{array}{cccc} A_1&{}A_2&{}A_3&{}A_4\\ A_5&{}A_6&{}A_7&{}A_8\\ A_8&{}A_7&{}A_6&{}A_5\\ A_4&{}A_3&{}A_2&{}A_1 \end{array} \right) , \end{aligned}$$
(24)

where the entries are arbitrary real or complex values. The CS matrix is symmetric about its center. On the other hand, we may say that CS matrix is such a matrix that commutes with the operator [48]

$$\begin{aligned} U_{xx}= \left( \begin{array}{cccc} \cdot &{}\cdot &{}\cdot &{}1\\ \cdot &{}\cdot &{}1&{}\cdot \\ \cdot &{}1&{}\cdot &{}\cdot \\ 1&{}\cdot &{}\cdot &{}\cdot \end{array} \right) . \end{aligned}$$
(25)

It is clear that \(U_{xx}^2\) equals the unity matrix. One may also claim that the commutativity condition with this operator generates the CS matrix, i.e., the most general matrix that commutes with \(U_{xx}\) is the CS matrix.

Let us find out what consequences the symmetry of matrix (24) lead to. For this purpose, we perform a group-theoretical analysis. The transformation \(U_{xx}\) together with the identity transformation E makes up the group \(\{E,U_{xx}\}\). This group is of second order and has two irreducible representations \({\Gamma }^{(1)}\) and \({\Gamma }^{(2)}\). The \(4\times 4\) unit matrix and the matrix (25) together give the original representation \(\Gamma \) of this group in the space of the matrix (24). The characters of \(\Gamma \) (traces of representation matrices) equal \(\chi (E)=4\) and \(\chi (U_{xx})=0\). Knowing them, we can find the multiplicities \(a_1\) and \(a_2\) with which the irreducible representations \({\Gamma }^{(1)}\) and \({\Gamma }^{(2)}\), respectively, are contained in \(\Gamma \).

Table 1 Character table of the group \(\{E,U_{xx}\}\)
Full size table

For this purpose, it is sufficient to make use of the character table for the group (Table 1) and the formula [49]

$$\begin{aligned} a_\mu =\frac{1}{g}\sum _G\chi ^{(\mu )}(G)^*\chi (G), \end{aligned}$$
(26)

where g is the order of the group, \(\chi ^{(\mu )}(G)\) the character of the element G in the \(\mu \)-th irreducible representation, and \(\chi (G)\) the character of the same element in the original representation. Simple calculations yield

$$\begin{aligned} a_1=2,\quad a_2=2. \end{aligned}$$
(27)

This imply that in the basis where the representation \(\Gamma \) of the Abelian group \(\{E,U_{xx}\}\) is completely reducible, the matrix (24) will take a block-diagonal form with two subblocks \(2\times 2\).

Quasidiagonalizing transformation is constructed from the eigenvectors of the operator \(U_{xx}\) and can be written as

$$\begin{aligned} R=\frac{1}{\sqrt{2}} \left( \begin{array}{cccc} 1&{}\cdot &{}\cdot &{}1\\ \cdot &{}1&{}1&{}\cdot \\ \cdot &{}1&{}-1&{}\cdot \\ 1&{}\cdot &{}\cdot &{}-1 \end{array} \right) =R^t. \end{aligned}$$
(28)

This transformation is orthogonal and symmetric (coincides with its transposition). After this transformation, the CS matrix (24) takes the quasidiagonal form

$$\begin{aligned} RA_{CS}R= \left( \begin{array}{cccc} A_1+A_4&{}A_2+A_3&{}\cdot &{}\cdot \\ A_5+A_8&{}A_6+A_7&{}\cdot &{}\cdot \\ \cdot &{}\cdot &{}A_6-A_7&{}A_5-A_8\\ \cdot &{}\cdot &{}A_2-A_3&{}A_1-A_4 \end{array} \right) . \end{aligned}$$
(29)

Note that another useful way to practically quasidiagonalize different matrices is to use for them so-called motion integrals [50].

The resulting quasidiagonal form allows it easy to extract all eigenvalues of any CS matrix and, in particular, of the Hamiltonian and density matrix. In turn, in some cases, this opens a possibility to direct calculation of quantum correlations, for example the quantum entanglement of two-qubit quantum CS states [51].

Importantly, the matrix \(U_{xx}\) can be written as a direct product of Pauli matrices,

$$\begin{aligned} U_{xx}=\sigma _x\otimes \sigma _x. \end{aligned}$$
(30)

It is this property that allowed to reduce the problem to the known case by applying the local unitary transformation (double Hadamard transformation) and calculate any quantum correlations of CS states using the results for the X quantum states.

It is arisen a question either to consider another combinations \(U_{\alpha \beta }=\sigma _\alpha \otimes \sigma _\beta \) (\(\alpha ,\beta =0, x, y, z\)) with all possible Pauli matrices including the unit matrix \(\sigma _0\). Take, for instance,

$$\begin{aligned} U_{zz}=\sigma _z\otimes \sigma _z= \left( \begin{array}{llll} 1&{}\cdot &{}\cdot &{}\cdot \\ \cdot &{}-1&{}\cdot &{}\cdot \\ \cdot &{}\cdot &{}-1&{}\cdot \\ \cdot &{}\cdot &{}\cdot &{}1 \end{array} \right) . \end{aligned}$$
(31)

Simple calculations show that the most general matrix that commutes with \(U_{zz}\) has the X form:

$$\begin{aligned} A_X= \left( \begin{array}{cccc} A_1&{}\cdot &{}\cdot &{}A_2\\ \cdot &{}A_3&{}A_4&{}\cdot \\ \cdot &{}A_5&{}A_6&{}\cdot \\ A_7&{}\cdot &{}\cdot &{}A_8 \end{array} \right) . \end{aligned}$$
(32)

So we can now give a new definition for the X matrix; namely, it is such a matrix that commutes with the matrix \(U_{zz}=\sigma _z\otimes \sigma _z\) or, in other words, is invariant under the transformations of the group \(\{E,U_{zz}\}\).

In the following sections, we will continue to develop such a group-theoretical approach.

6 XYZ chain with \(D_y\) and \({\Gamma }_y\) couplings

We return to the consideration of spin systems. Let us now take the direct product of two \(\sigma _y\) matrices,

$$\begin{aligned} U_{yy}=\sigma _y\otimes \sigma _y= \left( \begin{array}{cccc} \cdot &{}\cdot &{}\cdot &{}-1\\ \cdot &{}\cdot &{}1&{}\cdot \\ \cdot &{}1&{}\cdot &{}\cdot \\ -1&{}\cdot &{}\cdot &{}\cdot \end{array} \right) , \end{aligned}$$
(33)

and find the most general matrix that commutes with it. Carrying out the necessary calculations, we get the matrix

$$\begin{aligned} A_{yy}= \left( \begin{array}{llll} A_1&{}A_2&{}A_3&{}A_4\\ A_5&{}A_6&{}A_7&{}A_8\\ -A_8&{}A_7&{}A_6&{}-A_5\\ A_4&{}-A_3&{}-A_2&{}A_1 \end{array} \right) . \end{aligned}$$
(34)

Note that a family of matrices with such a structure is algebraically closed.

Again performing a group-theoretical analysis, as in previous section, we find that the matrix (34) can be reduced to a block-diagonal form also with two subblocks of second orders. The quasidiagonalizing transformation is built from eigenvectors of \(U_{yy}\), Eq. (33), and can be written as

$$\begin{aligned} S=\frac{1}{\sqrt{2}} \left( \begin{array}{rrrr} -1&{}\cdot &{}\cdot &{}1\\ \cdot &{}1&{}1&{}\cdot \\ \cdot &{}1&{}-1&{}\cdot \\ 1&{}\cdot &{}\cdot &{}1 \end{array} \right) =S^t. \end{aligned}$$
(35)

Calculations yield

$$\begin{aligned} SA_{yy}S= \left( \begin{array}{cccc} A_1-A_4&{}-A_2-A_3&{}\cdot &{}\cdot \\ -A_5+A_8&{}A_6+A_7&{}\cdot &{}\cdot \\ \cdot &{}\cdot &{}A_6-A_7&{}A_5+A_8\\ \cdot &{}\cdot &{}A_2-A_3&{}A_1+A_4 \end{array} \right) . \end{aligned}$$
(36)

This results opens a way to extract all eigenvalues of any \(A_{yy}\) matrix.

Taking into account hermiticity condition, one can write the density matrix with the discussed symmetry:

$$\begin{aligned} \rho _{yy}= \left( \begin{array}{llll} a&{}\mu &{}\nu &{}c\\ \mu ^*&{}b&{}d&{}-\nu ^*\\ \nu ^*&{}d&{}b&{}-\mu ^*\\ c&{}-\nu &{}-\mu &{}a \end{array} \right) . \end{aligned}$$
(37)

Similar structure has the Hamiltonian

$$\begin{aligned} {\mathcal {H}}_{yy}= \left( \begin{array}{cccc} J_z&{}-iB_2^y+J_{zx} &{}-iB_1^y+J{xz}&{}J_x-J_y\\ iB_2^y+J_{zx}&{}-J_z&{}J_x+J_y&{}-iB_1^y-J_{xz}\\ iB_1^y+J_{xz}&{}J_x+J_y&{}-J_z&{}-iB_2^y-J_{zx}\\ J_x-J_y&{}iB_1^y-J_{xz} &{}iB_2^y-J_{zx}&{}J_z \end{array} \right) . \end{aligned}$$
(38)

In the Bloch form, this Hamiltonian is given by

$$\begin{aligned} {\mathcal {H}}_{yy}=B_1^y\sigma _1^y + B_2^y\sigma _2^y + J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z + J_{zx}\sigma _1^z\sigma _2^x + J_{xz}\sigma _1^x\sigma _2^z. \end{aligned}$$
(39)

In terms of the DM and KSEA couplings, this equation is rewritten as

$$\begin{aligned} {\mathcal {H}}_{yy}&=B_1^y\sigma _1^y + B_2^y\sigma _2^y + J_x\sigma _1^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z \nonumber \\&\quad + D_y(\sigma _1^z\sigma _2^x - \sigma _1^x\sigma _2^z) + {\Gamma }_y(\sigma _1^z\sigma _2^x + \sigma _1^x\sigma _2^z), \end{aligned}$$
(40)

where

$$\begin{aligned} D_y=\frac{1}{2}(J_{zx}-J_{xz}),\quad {\Gamma }_y=\frac{1}{2}(J_{zx}+J_{xz}) \end{aligned}$$
(41)

are the y-components of Dzyaloshinsky vector and \({\tilde{\Gamma }}\) tensor, respectively. So, we come to the completely anisotropic Heisenberg modes in the “transverse” external field and with independent \(D_y\) and \({\Gamma }_y\) terms of DM and KSEA interactions.

As already noted above, it is important to find local unitary transformations. The Hadamard transform diagonalizes the spin matrix \(\sigma _x\). It easy to check that the Pauli matrix \(\sigma _y\) is diagonalized by the unitary transformation

$$\begin{aligned} Y=\frac{1}{\sqrt{2}} \left( \begin{array}{ll} 1&{}1\\ i&{}-i \end{array} \right) . \end{aligned}$$
(42)

(This operator can be called a Y-transform because it diagonalizes the matrix \(\sigma _y\).) In the proper representation of the matrix \(\sigma _y\),Footnote 1

$$\begin{aligned} Y^\dagger \sigma _x Y=\sigma _y,\quad Y^\dagger \sigma _y Y=\sigma _z,\quad Y^\dagger \sigma _z Y=\sigma _x. \end{aligned}$$
(43)

Double transformation of Y reduces the Hamiltonian \({\mathcal {H}}_{yy}\) to the X form. Indeed,

$$\begin{aligned} (Y\otimes Y)^\dagger {\mathcal {H}}_{yy}(Y\otimes Y)&=B_1^y\sigma _1^z + B_2^y\sigma _2^z + J_z\sigma _1^x\sigma _2^x + J_x\sigma _1^y\sigma _2^y + J_y\sigma _1^z\sigma _2^z \nonumber \\&\quad + D_y(\sigma _1^x\sigma _2^y - \sigma _1^y\sigma _2^x) + {\Gamma }_y(\sigma _1^x\sigma _2^y + \sigma _1^y\sigma _2^x). \end{aligned}$$
(44)

The same is valid for the density matrix \(\rho _{yy}\): It is also reduced to the X form by the local unitary transformation consisting of direct product of two Y transforms.

So, we have found a way which allows to calculate the quantum correlations in the XYZ system with arbitrary components \(D_y\) and \({\Gamma }_y\) using the known formulas for the X states. At the same time, the way found shows the equivalence of quantum correlation properties in the system under discussion and in the X (and CS) system.

7 Classification of quantum states

The examples considered in the previous sections provide us with a starting point to explore the invariance under local operations to extend the known results and get new quantum states. Consider now the mixed products of spin matricesFootnote 2

$$\begin{aligned} U_{\alpha \beta }=\sigma _\alpha \otimes \sigma _\beta \quad (\alpha ,\beta =0,x,y,z), \end{aligned}$$
(45)

where \(\sigma _0\), \(\sigma _x\), \(\sigma _y\), and \(\sigma _z\) are given by Eq. (12). The matrices commuting with each given operator \(U_{\alpha \beta }\) form algebraically closed families. One should be noted that such U-operators, up to common coefficients, coincide with the generators of SU(4) group [52,53,54,55].

Repeating calculations similar to Sect. 5, we find, as above, that the characters of the initial representation of any group \(\{E,U_{\alpha \beta }\}\) are still equal to four and zero, and therefore, the multiplicities are again \(a_1=a_2=2\). As a result, any matrix that commutes with the matrix \(U_{\alpha \beta }\) can be reduced to the block-diagonal form with two subblocks of second order. Quasidiagonalizing transformations are constructed from the eigenvectors of the given matrix \(U_{\alpha \beta }\).

Finding for each operator \(U_{\alpha \beta }\) the matrix originated from the condition of commutativity and then taking its Hermitian form, we arrive at a collection of quantum states (and Hamiltonians) which is shown in Table 2.

Table 2 Fifteen quantum states/Hamiltonians generated by U-operators and, in braces, spin matrix septets required for their Bloch decompositions
Full size table

Each quantum state (and hence Hamiltonian) is supplied by a set of Pauli matrices over which the quantum state or Hamiltonian is decomposed in the form of a linear combination.

We can look at Table 2 as a four-by-four matrix. Using this table, it is easy to find the Hamiltonians and density matrices of different spin models. Let us consider the first row. The corresponding Hamiltonians are written as

$$\begin{aligned} {\mathcal {H}}_{0x}&={\mathbf {B}}_1{{\varvec{\sigma }}}_1 + B_2^x\sigma _2^x + J_x\sigma _1^x\sigma _2^x +J_{zx}\sigma _1^z\sigma _2^x + J_{yx}\sigma _1^y\sigma _2^x,\end{aligned}$$
(46)
$$\begin{aligned} {\mathcal {H}}_{0y}&={\mathbf {B}}_1{{\varvec{\sigma }}}_1 + B_2^y\sigma _2^y + J_y\sigma _1^y\sigma _2^y +J_{zy}\sigma _1^z\sigma _2^y + J_{xy}\sigma _1^x\sigma _2^y,\end{aligned}$$
(47)
$$\begin{aligned} {\mathcal {H}}_{0z}&={\mathbf {B}}_1{{\varvec{\sigma }}}_1 + B_2^z\sigma _2^z + J_z\sigma _1^z\sigma _2^z +J_{yz}\sigma _1^y\sigma _2^z + J_{xz}\sigma _1^x\sigma _2^z. \end{aligned}$$
(48)

System (46) by means of local unitary transform \(\sigma _0\otimes H\) and system (47) by the local unitary transformation \(\sigma _0\otimes Y\) are reduced to a structure of the model (48):

$$\begin{aligned} (\sigma _0\otimes H){\mathcal {H}}_{0x}(\sigma _0\otimes H)\rightarrow {\mathcal {H}}_{0z},\quad (\sigma _0\otimes Y)\dagger {\mathcal {H}}_{0y}(\sigma _0\otimes Y)\rightarrow {\mathcal {H}}_{0z}. \end{aligned}$$
(49)

Thus, all quantum correlations in these three spin systems are the same.

The mixed members can be rewritten through the DM and KSEA interactions. For example,

$$\begin{aligned} {\mathcal {H}}_{0z}&={\mathbf {B}}_1{{\varvec{\sigma }}}_1 + B_2^z\sigma _2^z + J_z\sigma _1^z\sigma _2^z + D_x(\sigma _1^y\sigma _2^z-\sigma _1^z\sigma _2^y) + {\Gamma }_x(\sigma _1^y\sigma _2^z+\sigma _1^z\sigma _2^y) \nonumber \\&\quad +D_y(\sigma _1^z\sigma _2^x - \sigma _1^x\sigma _2^z) + {\Gamma }_y(\sigma _1^z\sigma _2^x + \sigma _1^x\sigma _2^z) \end{aligned}$$
(50)

with additional conditions \({\Gamma }_x=D_x\) and \({\Gamma }_y=-D_y\) in accord with Eqs. (20) and (41). The corresponding density matrix has a characteristic, “checkerboard” structure

$$\begin{aligned} \rho _{0z}= \left( \begin{array}{llll} a&{}\cdot &{}\nu &{}\cdot \\ \cdot &{}b&{}\cdot &{}\delta \\ \nu ^*&{}\cdot &{}c&{}\cdot \\ \cdot &{}\delta ^*&{}\cdot &{}d \end{array} \right) . \end{aligned}$$
(51)

A partial transposition of \(\rho _{0z}\), namely \(\rho _{0z}^{t_2}\), does not change the density matrix: \(\rho _{0z}^{t_2}=\rho _{0z}\). Consequently, all eigenvalues stay nonnegative, and therefore, in accordance with the positive partial transpose (PPT) criterion [56, 57], the state (51) is separable, i.e., its quantum entanglement (and with it the entanglement of systems with the Hamiltonians \({\mathcal {H}}_{0x}\) and \({\mathcal {H}}_{0y}\)) is identically equal to zero.

Consider now the systems from the first column of Table 2. They are

$$\begin{aligned} {\mathcal {H}}_{x0}&=B_1^x\sigma _1^x + {\mathbf {B}}_2{{\varvec{\sigma }}}_2 + J_x\sigma _1^x\sigma _2^x +J_{xy}\sigma _1^x\sigma _2^y + J_{xz}\sigma _1^x\sigma _2^z,\end{aligned}$$
(52)
$$\begin{aligned} {\mathcal {H}}_{y0}&=B_1^y\sigma _1^y + {\mathbf {B}}_2{{\varvec{\sigma }}}_2 + J_y\sigma _1^y\sigma _2^y +J_{yz}\sigma _1^y\sigma _2^z + J_{yx}\sigma _1^y\sigma _2^x,\end{aligned}$$
(53)
$$\begin{aligned} {\mathcal {H}}_{z0}&=B_1^z\sigma _1^z + {\mathbf {B}}_2{{\varvec{\sigma }}}_2 + J_z\sigma _1^z\sigma _2^z +J_{zx}\sigma _1^z\sigma _2^x + J_{zy}\sigma _1^z\sigma _2^y. \end{aligned}$$
(54)

The cross (helical) interactions in these Hamiltonians can also be given in the form of DM–KSEA interactions. These models again pass one into another by the local unitary transformations consisting of the corresponding direct products of operators H, Y, and \(\sigma _0\). The density matrix corresponding to the Hamiltonian \({\mathcal {H}}_{z0}\) has a block-diagonal (and therefore direct sum) form (see Table 2)

$$\begin{aligned} \rho _{z0}= \left( \begin{array}{llll} a&{}\mu &{}\cdot &{}\cdot \\ \mu ^*&{}b&{}\cdot &{}\cdot \\ \cdot &{}\cdot &{}c&{}\nu \\ \cdot &{}\cdot &{}\nu ^*&{}d \end{array} \right) = \left( \begin{array}{ll} a&{}\mu \\ \mu ^*&{}b \end{array} \right) \oplus \left( \begin{array}{ll} c&{}\nu \\ \nu ^*&{}d \end{array} \right) . \end{aligned}$$
(55)

The quantum entanglement of this state as well as the states corresponding to the Hamiltonians \({\mathcal {H}}_{x0}\) and \({\mathcal {H}}_{y0}\) equals zero, again in accordance with the PPT criterion.

The Hamiltonians (46)–(48) are pairwise connected with the Hamiltonians (52)–(54) using the spin exchange operator P introduced by Dirac (see [32, Sect. 12-2]),

$$\begin{aligned} P=\frac{1}{2}(1+{\varvec{\sigma }}_1{\varvec{\sigma }}_2)= \left( \begin{array}{cccc} 1&{}\cdot &{}\cdot &{}\cdot \\ \cdot &{}\cdot &{}1&{}\cdot \\ \cdot &{}1&{}\cdot &{}\cdot \\ \cdot &{}\cdot &{}\cdot &{}1 \end{array} \right) =P^t. \end{aligned}$$
(56)

This operator exchanges the first and second qubits (\(1\rightleftharpoons 2\)) and swaps them (similar to the mirror reflection in the plane that separates the qubits):

$$\begin{aligned} P\sigma _\alpha \otimes \sigma _\beta P=\sigma _\beta \otimes \sigma _\alpha ,\quad P\sigma _1^\alpha \sigma _2^\beta P=\sigma _1^\beta \sigma _2^\alpha . \end{aligned}$$
(57)

The matrix (56) is an orthogonal transformation that permutes the second and third rows and columns of any matrix of the fourth order. One should emphasize that this transformation is not local, and therefore, generally speaking, it changes the value of quantum correlation because the quantum discord and one-way work deficit depend on which qubit the measurement was performed. As noted in [24, 58], the discord is not a symmetric quantity, and there are “left” and “right” discords of the same system. However, if simultaneously with the permutation P, the measured qubit is changed in the discussed systems, then the value of discord (and deficit) will remain unchanged. As an example, \(P\rho _{0z}P\rightarrow \rho _{z0}\) and the “right” discord passes to the “left” one and vice versa.

Now we turn to the consideration of the “inner” part of Table 2, i.e., the systems and their quantum states with the Cartesian indexes \(\alpha ,\beta =x,y,z\) only. “Diagonal” stares (\(\rho _{xx}\), \(\rho _{yy}\), and \(\rho _{zz}\)) have already been discussed in detail in previous sections. All of them are related by local unitary transformations, and therefore, the quantum correlations are the same and can be calculated using formulas available for the X state.

The “off-diagonal” Hamiltonians from the upper triangle part of the table are written as follows

$$\begin{aligned} {\mathcal {H}}_{xy}&=B_1^x\sigma _1^x + B_2^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z +J_{xy}\sigma _1^x\sigma _2^y + J_{yx}\sigma _1^y\sigma _2^x +J_{yz}\sigma _1^y\sigma _2^z +J_{zx}\sigma _1^z\sigma _2^x,\end{aligned}$$
(58)
$$\begin{aligned} {\mathcal {H}}_{xz}&=B_1^x\sigma _1^x + B_2^z\sigma _2^z + J_y\sigma _1^y\sigma _2^y +J_{zx}\sigma _1^z\sigma _2^x + J_{xz}\sigma _1^x\sigma _2^z +J_{zy}\sigma _1^z\sigma _2^y +J_{yx}\sigma _1^y\sigma _2^x,\end{aligned}$$
(59)
$$\begin{aligned} {\mathcal {H}}_{yz}&=B_1^y\sigma _1^y + B_2^z\sigma _2^z + J_x\sigma _1^x\sigma _2^x +J_{zy}\sigma _1^z\sigma _2^y + J_{yz}\sigma _1^y\sigma _2^z +J_{zx}\sigma _1^z\sigma _2^x +J_{xy}\sigma _1^x\sigma _2^y. \end{aligned}$$
(60)

These Hamiltonians can be expressed via DM–KSEA interactions. For instance,

$$\begin{aligned} {\mathcal {H}}_{xy} =B_1^x\sigma _1^x + B_2^y\sigma _2^y + J_z\sigma _1^z\sigma _2^z +{\varvec{D}}\cdot ({{\varvec{\sigma }}}_1\times {{\varvec{\sigma }}}_2) +{{\varvec{\sigma }}}_1 \cdot {\tilde{\Gamma }} \cdot {{\varvec{\sigma }}}_2 \end{aligned}$$
(61)

with conditions \({\Gamma }_x=D_x\) and \({\Gamma }_y=D_y\), whereas \({\Gamma }_z\) and \(D_z\) are arbitrary independent quantities. The Hamiltonians of a lower part of the “off-diagonal” systems are

$$\begin{aligned} {\mathcal {H}}_{yx}&=B_1^y\sigma _1^y + B_2^x\sigma _2^x + J_z\sigma _1^z\sigma _2^z +J_{xy}\sigma _1^x\sigma _2^y + J_{yx}\sigma _1^y\sigma _2^x +J_{zy}\sigma _1^z\sigma _2^y +J_{xz}\sigma _1^x\sigma _2^z,\end{aligned}$$
(62)
$$\begin{aligned} {\mathcal {H}}_{zx}&=B_1^z\sigma _1^z + B_2^x\sigma _2^x + J_y\sigma _1^y\sigma _2^y +J_{zx}\sigma _1^z\sigma _2^x + J_{xz}\sigma _1^x\sigma _2^z +J_{yz}\sigma _1^y\sigma _2^z +J_{xy}\sigma _1^x\sigma _2^y,\end{aligned}$$
(63)
$$\begin{aligned} {\mathcal {H}}_{zy}&=B_1^z\sigma _1^z + B_2^y\sigma _2^y + J_x\sigma _1^x\sigma _2^x +J_{zy}\sigma _1^z\sigma _2^y + J_{yz}\sigma _1^y\sigma _2^z +J_{yx}\sigma _1^y\sigma _2^x +J_{xz}\sigma _1^x\sigma _2^z. \end{aligned}$$
(64)

Remarkably, all these six “off-diagonal” Hamiltonians (58)–(60) and (62)–(64) are reduced to the Hamiltonian of the X model by local unitary transformations composed of the operators H, Y, and \(\sigma _0\). Indeed,

$$\begin{aligned} (H\otimes Y)^\dagger {\mathcal {H}}_{xy}(H\otimes Y)\rightarrow {\mathcal {H}}_{zz},\quad (H\otimes \sigma _0){\mathcal {H}}_{xz}(H\otimes \sigma _0)\rightarrow {\mathcal {H}}_{zz}, \end{aligned}$$
(65)

similarly for other cases.

So, out of fifteen quantum states, nine (\(\rho _{\alpha \beta }\) with \(\alpha ,\beta =x,y,z\)) are transformed among themselves by local unitary transformations. Their quantum correlations are complete identical to each other and are calculated by the formulas for the X state.

The quantum states of the six remaining models are separable and therefore without quantum entanglement. These models consist of two equal subclasses \(\rho _{0\alpha }\) and \(\rho _{\alpha 0}\) (\(\alpha =x,y,z\)) in each of which the quantum discord and other quantum correlations are equivalent to each other since the states are connected via local unitary transformations. Moreover, the states from different subclasses are paired trough the spin exchange transformation P thanks to which the “right” quantum discord of one member of a pair equals the “left” discord of other member of the same pair. Unfortunately, among both subclasses there is no one quantum state for which the quantum discord is known. However, most recently Zhou et al. [59] have evaluated the “right” and “left” quantum discords for the quantum sate

$$\begin{aligned} \rho =\frac{1}{4}(1+{\varvec{s}}_1{\varvec{\sigma }}_1+c_3\sigma _1^z\sigma _2^z) \end{aligned}$$

(see Theorem 2.3 in their paper [59]). It would be interesting to extend this result to the general “checkerboard” (\(\rho _{0z}\)) or two-block-\((2\times 2)\)-diagonal \((\rho _{z0})\) quantum states.

8 Results and perspectives

We have analyzed fifteen types of two-spin systems in an external field, with the exchange bounds, and with indirect interactions occurring through the orbital magnetic moments. The structures of Hamiltonians and density matrices are presented in an obvious form (Table 2).

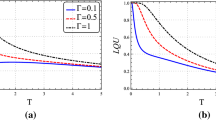
The originality and new feature of our results in comparison with other works [12,13,14,15,16,17,18,19,20] is that we take into account not only the DM interactions, but also the KSEA ones. The latter interactions make their own changes in the behavior of quantum correlations. For example, in recent work [19] a local minimum was found due to DM couplings (black line in Fig. 6c of Ref. [19]). This behavior is reproduced by the dotted line in Fig. 1. We also performed calculations for nonzero values of the constant \({\Gamma }_z\) shown by curves 1 and 2 in Fig. 1. It is seen that the KSEA interactions suppress the local minimum of the quantum discord.

Fig. 1
figure 1

Quantum discord Q vs temperature T for the model (8) by \(B_1^z=B_2^z=0\), \(J_x=-1\), \(J_y=-1.5\), \(J_z=-2\), \(D_z=1.8\), and \({\Gamma }_z=0\) (dotted line), 0.3 (solid line 1), 0.5 (solid line 2)

Full size image

We have classified fifteen types of quantum states, each of which contains seven parameters. A detailed study of the behavior of quantum correlations in them will require a separate extensive work in the future.

We have also shown that, from viewpoint of quantum correlation properties, all systems are divided into two groups: the systems with the X quantum states (up to local unitary transformations) for which the developed theory for the calculation of quantum correlations is available and systems with checkerboard-like or block-diagonal non-X quantum states in which the quantum entanglement is absent, whereas the question about the quantum discord and other quantum correlations remains open.