1 Introduction

Studying solid-state physical systems under multiple interactions has recently attracted particular focus. The unprecedented possibility of taking advantage of these systems has opened the door to constructing new quantum-based technologies (Dowling and Milburn 2003). Quantum superposition and entanglement (Einstein et al. 1935) are two surprising aspects of the quantum theory and are found to be imperative resources for achieving speedup in information processing (Nielsen and Chuang 2002) and for realizing several non-local tasks and classically unattainable applications (Ekert et al. 1992; Kim et al. 2001; Mansour and Dahbi 2020; Cruz et al. 2022) within the realm of classical physics. Further, it has been demonstrated that even when entanglement is lost, quantum information processing tasks may still be performed in the case of particular mixed states due to the presence of nonclassical correlations beyond entanglement (Adesso et al. 2016; Melo-Luna et al. 2017). On the other side, decoherence (Schlosshauer 2019) effects present a grave challenge to the beneficial applications of quantum mechanics because it prevents the retention and controllable handling of qubits.

Previously many studies focused on measuring and characterizing quantum resources in the framework of intrinsic and standard decoherence models in different quantum systems (Dahbi et al. 2023; Yin et al. 2022; Essakhi et al. 2022; Mohamed and Eleuch 2020; Mohamed et al. 2022; Chaouki et al. 2022; Hashem et al. 2022; Mansour and Dahbi 2020; Haddadi et al. 2022; Maleki 2017; Wu et al. 2017; Li et al. 2021; El Anouz et al. 2022; Mohamed et al. 2022; Mansour et al. 2021; Naveena et al. 2022; Muthuganesan and Chandrasekar 2021). Although many methods were introduced to measure quantum systems, assessing the quantumness of multipartite systems is still a challenging task Adesso et al. (2016); Schlosshauer (2005); Coopmans et al. (2022). For specific quantum systems, quantum discord (QD) Ollivier and Zurek (2001) was the first quantifier introduced to capture nonclassical correlations. QD measures the difference between total correlations and classical correlations in a quantum system. However, it is a strenuous measure to calculate, and analytical expressions of QD were only obtained for two-qubit states (Luo 2008; Henderson and Vedral Aug 2001) and quantum X-states ( see for instance the works (Wang et al. 2010; Chen et al. 2011; Haddadi et al. 2019; Baba et al. 2020) and references therein). A rigorous mathematical characterization on the computational difficulties of quantum discord is provided in Huang (2014), demonstrating that computing quantum discord is an NP-complete problem. Quantum correlations have been studied in many quantum systems, such as Heisenberg spin chain models (for instance, spin-1 Heisenberg chains (Malvezzi et al. 2016), anisotropic spin-1/2 XY chain in transverse magnetic field (Mofidnakhaei et al. 2018) ) and quantum dot systems such as two coupled double quantum dots systems (Filgueiras et al. 2020; Dahbi et al. 2022; Elghaayda et al. 2022; Ferreira et al. 2022), gravitational cat states (Dahbi et al. 2022), and many other realizable physical systems (Obada et al. 2013; Mohamed and Eleuch 2022; Elghaayda et al. 2022; Mohamed et al. 2022)). Recently, considerable attention has been dedicated to studying the influence of the Dzyaloshinsky-Moriya (DM) interaction and the Kaplan-Shekhtman-Entin-Wohlman-Aharony (KSEA) interaction on the quantum features of specific quantum systems (Oumennana et al. 2022; Khedif et al. 2021; Xie and Liu 2022; Oumennana et al. 2022). The Dzyaloshinsky–Moriya (DM) interaction is a spin-orbit coupling mechanism that induces an antisymmetric exchange that adds to the total magnetic exchange interaction between two nearby spins (more details can be found in Moriya (1960)). The DM Hamiltonian of two spins is found to be \({\hat{H}} _{\textrm{DM}} = \varvec{D}. ( \varvec{S}_1 \times \varvec{S}_2)\), where \(\varvec{D}\) is a constant vector. In addition, Moriya found the second-order correction term, \(H_\textrm{KSEA}=\varvec{S}_1.\Gamma .\varvec{S}_2\), where \(\Gamma\) is a symmetric traceless tensor. However, he assumed that this term is negligible compared to the antisymmetric contribution until (Kaplan 1983), and then Shekhtman et al. (1992) proved otherwise. It was shown that the symmetric KSEA is important for recovering the broken \(\textrm{SU}(2)\) symmetry caused by the DM interaction (Citro and Orignac 2002).

Quantum coherence is another quantum feature that one should deal with. This latter emanates from the superposition principle of quantum states and is a valuable resource to be preserved due to its pivotal role in quantum information processing (Pan et al. 2017) and quantum thermodynamics (Narasimhachar and Gour 2015). It was indeed proven that long-lasting quantum coherence is vital for overcoming classical limitations of measurement accuracy in quantum metrology (Pires et al. 2018). Moreover, growing interest is accorded to the role played by quantum coherence in some biological mechanisms (Lambert et al. 2013), such as photosynthesis (Scholes 2011) and bird navigation (Ritz 2011). Similarly to quantum correlations and entanglement, several quantifiers were introduced to capture quantum coherence in quantum systems appropriately, e.g. relative entropy of coherence and \(l_1\)-norm of coherence (Baumgratz et al. 2014) as well as intrinsic randomness (Yuan et al. 2015).

In this article, we investigate the evolution of correlated coherence and quantum correlations quantified by quantum discord in a two-qubit XXZ Heisenberg spin chain under intrinsic decoherence effects with an applied magnetic field, KSEA and DM interactions using the Milburn’s decoherence model (Milburn 1991). We mainly focus on how the Hamiltonian parameters and the initial state affect the dynamical behavior of correlated coherence and quantum discord. We look at two different extended Werner-like states to show how the choice of the initial state is essential to suppress the effects of specific interactions.

The rest of this work is as follows. In Sect. 2, we give a short overview of the quantum resources indicators used in this study. The Hamiltonian of the considered physical model is introduced in Sect. 3, and the evolved density matrix corresponding to the system is derived for the parameterized initial state considered. In Sect. 4 we present the results obtained for the dynamics of correlated coherence and quantum discord under the influence of intrinsic decoherence with the combined impact of KSEA and DM interactions. Finally, we conclude the main findings from the proposed model in Sect. 5.

2 Quantum information indicators

This part defines the correlated coherence, used as a quantum coherence quantifier, and the quantum discord operated to quantify nonclassical correlations.

2.1 Correlated coherence

Quantum coherence is a basis-dependent property of a quantum state that arises from the superposition of system states reflected by the non-diagonal components of the density matrix on a given basis. Here, we consider a conveniently computable coherence measure, specifically the \(l_1\)–norm of coherence (Baumgratz et al. 2014). The \(l_1\)-norm of coherence is a trustworthy key indicator that meets the requirements of a good coherence measure and can be obtained for a given density matrix \(\varrho\). Baumgratz et al. (Baumgratz et al. 2014) has demonstrated that a quantum system’s coherence is given as

$$\begin{aligned} {\mathcal {C}}_{l_{1}}(\varrho )= \min _{\eta \in {\mathfrak {I}}} |\varrho - \eta |, \end{aligned}$$
(1)

where \({\mathfrak {I}}\) is a set containing all incoherent states, that is \({\mathcal {C}}_{l_{1}}(\eta ) =0\) for all \(\eta \in {\mathfrak {I}}\). The \(l_{1}\)-norm coherence can be obtained by means of the non-diagonal entries of \(\varrho\) as

$$\begin{aligned} {\mathcal {C}}_{l_{1}}(\varrho ) = \sum _{i\ne j} \sqrt{\varrho _{ij} \varrho _{ij}^*} , \end{aligned}$$
(2)

where \(^{*}\) refers to the complex conjugate. It should be noted that the total \(l_1\)-norm coherence of a state \(\varrho\), living in Hilbert space of dimension d, should not exceed \(d-1\). Correlated coherence is yet another metric of coherence that can provide information about the quantumness of a particular state. For any given bipartite state \(\varrho\), correlated coherence is defined as the total coherence subtracting local coherences. The definition of the \(l_1\)-norm based correlated coherence (Baumgratz et al. 2014) reads as

$$\begin{aligned} {\mathcal {C}}_{cc} (\varrho ) := {\mathcal {C}}_{l_1} (\varrho )-{\mathcal {C}}_{l_1} (\varrho _A)-{\mathcal {C}}_{l_1} (\varrho _B), \end{aligned}$$
(3)

where \(\varrho _A = tr_B \varrho\) and \(\varrho _B = tr_A \varrho\) are the reduced density matrices of local subsystems.

2.2 Quantum discord

QD (Ollivier and Zurek 2001) quantifies quantum correlations inhibited in a composite system. In a two-qubit system, QD is defined by removing the existing classical correlations from the quantum mutual information of the system as

$$\begin{aligned} {{\mathcal {D}}}(\varrho )= {{\mathcal {I}}}(\varrho )-{\mathcal C}(\varrho ), \end{aligned}$$
(4)

with

$$\begin{aligned} {{\mathcal {I}}}(\varrho )={{\mathcal {S}}}(\varrho _B)+ {{\mathcal {S}}}(\varrho _A)-{{\mathcal {S}}}(\varrho ) \end{aligned}$$
(5)

and

$$\begin{aligned} {{\mathcal {C}}}(\varrho )={{\mathcal {S}}}(\varrho _A)- min_{\{\pi _{i}^{B}\}}\sum _{i}p_{i}{{\mathcal {S}}}(\varrho _{A|i}). \end{aligned}$$
(6)

\({{\mathcal {S}}}(\varrho )=-tr(\varrho \log _2 \varrho )\) is the von Neumann entropy. \(\varrho _A\) and \(\varrho _B\) are the reduced density operators corresponding, respectively, to the subsystems A and B. \({\left\{ \pi _{B}^{i}\right\} }={|i_{B} \rangle \langle i_{B} |}\) is the complete ensemble of orthonormal projectors acting only on the second subsystem B.

\(\varrho _{A|i} = tr_{B}(\pi _{B}^{i}\varrho \pi _{B}^{i}) / p_{i}\) is the resulting state of the first subsystem A after obtaining the result i on B, and \(p_{i}= tr_{AB} ( \pi _B^i \varrho \pi _B^i)\) is the probability of having i as a result. Following the relations (5) and (6), the quantum discord (4) can be rewritten as Henderson and Vedral (2001); Fanchini et al. (2010)

$$\begin{aligned} \displaystyle {{\mathcal {D}}}(\varrho ) = min_{ \left\{ \pi _B^i \right\} }[{\mathcal S}(\varrho /{\left\{ \pi _{B}^{i}\right\} } ]+{{\mathcal {S}}}(\varrho _B) -{{\mathcal {S}}}(\varrho ). \end{aligned}$$
(7)

In general, for arbitrary quantum states, finding analytical formulas for QD is complicated due to the minimization process required for conditional entropy. It was only possible to obtain approximate analytical expressions (Huang 2013) for a limited number of states, such as the X-states. For X-states

$$\begin{aligned} \varrho = {\begin{bmatrix} {{\varrho _{11}}}&{}0&{}0&{}{{\varrho ^* _{14}}}\\ 0&{}{{\varrho _{22}}}&{}{{\varrho ^* _{23}}}&{}0\\ 0&{}{\varrho _{23}}&{}{{\varrho _{33}}}&{}0\\ {\varrho _{14}}&{}0&{}0&{}{{\varrho _{44}}} \end{bmatrix}} \end{aligned}$$
(8)

the quantum discord is redefined by the succeeding expression (Wang et al. 2010; Ali et al. 2010)

$$\begin{aligned} {{\mathcal {D}}}(\varrho ) = \min \{{{\mathcal {Q}}}{{\mathcal {D}}}_1, {{\mathcal {Q}}}{{\mathcal {D}}}_2\}, \end{aligned}$$
(9)

with

$$\begin{aligned} {{\mathcal {Q}}}{{\mathcal {D}}}_{i}= f(\varrho _{11 }+\varrho _{33 }) +\sum _{k=1}^{4} \lambda _k \log _2(\lambda _k)+{{\mathcal {D}}}_{i}. \end{aligned}$$

\({{\mathcal {D}}}_1= f(\Lambda )\), \({\mathcal D}_2=-\sum _{n=1}^{4}\varrho _{nn} \log _2(\varrho _{nn}) - f(\varrho _{11 }+\varrho _{33})\), \(\Lambda =\frac{1}{2} \Big (1 + \Big ((1-2(\varrho _{33 }+\varrho _{44 }))^2+4 (|\varrho _{14}|+|\varrho _{23}|)^2\Big )^{1/2} \Big )\) and \(f(x)=-x \log _2(x)-(1-x) \log _2(1-x)\) is the binary Shannon entropy. \(\lambda _k\)’s denote the eigenvalues of the density matrix \(\varrho\).

As a point worth highlighting here, it was demonstrated in Ref. (Tan et al. 2016) that correlated coherence can unify numerous ideas of quantumness, such as quantum discord, within the same paradigm and that the concept of correlated coherence recognizes similarities between quantum correlations and quantum entanglement. So, the quantum features of correlations derive from the quantum features of coherence.

3 Two-qubit XXZ model

We consider the model as a two-qubit system operating spin polarization of two nearest spin-1/2 XXZ particles. The particles are exposed to the interplay of an external homogeneous magnetic field and the combination of DM and KSEA interactions along the z-axis. The associated Hamiltonian is solvable and is represented as Oumennana et al. (2022)

$$\begin{aligned} {\hat{H}}= & {} J_z \sigma _{1}^{z}\sigma _{2}^{z}+ J(\sigma _{1}^{x}\sigma _{2}^{x}+ \sigma _{1}^{y}\sigma _{2}^{y})+ D_z\left( \sigma _{1}^{x}\sigma _{2}^{y}-\sigma _{1}^{y}\sigma _{2}^{x}\right) \nonumber \\+ & {} \Gamma _z \left( \sigma _{1}^{x}\sigma _{2}^{y}+\sigma _{1}^{y}\sigma _{2}^{x}\right) + B (\sigma _1^z + \sigma _2^z), \end{aligned}$$
(10)

where \(\sigma _{\mu }^{i=x,y,z}\) \((\mu =1,2)\) are the typical Pauli matrices corresponding to the spin \(\mu\), while \(J_z\) and J are real coupling coefficients denoting, respectively, the anisotropy coupling constant defining the symmetric spin-spin exchange interaction in the z-direction, and the interaction coupling constant. The B is a parameter, restricted to \(B \ge 0\), that indicates the strength of the magnetic field. Besides, the \(\Gamma _z\) and \(D_z\) parameters reflect the z-KSEA and z-DM interactions, which result in symmetric and anti-symmetric spin-orbit coupling contributions, respectively. We assume that the two-spin XXZ model behaves as in the antiferromagnetic case, \(J > 0\) and \(J_z > 0\). It is worth stating that all parameters are considered to be dimensionless. The Hamiltonian (10) can be written on the two-qubit basis, \(\lbrace \vert \Downarrow \Downarrow \rangle , \vert \Downarrow \Uparrow \rangle , \vert \Uparrow \Downarrow \rangle , \vert \Uparrow \Uparrow \rangle \rbrace\), as

$$\begin{aligned} \displaystyle {\hat{H}} = \left( \begin{array}{cccc} J_z+2B&{}0&{}0&{}-2i\mathrm{\Gamma }_z\\ 0&{}-J_z &{} 2 J+2iD_z&{}0\\ 0&{}-2iD_z + 2J &{}-J_z&{}0\\ 2i\mathrm{\Gamma }_z&{}0&{}0&{}-2B+J_z \end{array} \right) . \end{aligned}$$
(11)

The eigenvalues and the associated eigenvectors of the aforementioned Hamiltonian \({\hat{H}}\) are

$$\begin{aligned} {\mathcal {V}}_1&= J_z+ \chi , \quad {\mathcal {V}}_2 = -J_z+ \omega ,\\&{\mathcal {V}}_3= -J_z- \omega , \quad {\mathcal {V}}_4 = J_z- \chi , \end{aligned}$$
$$\begin{aligned} \vert u_1\rangle&= \sqrt{\frac{\chi +2B}{2\chi }}\left( |\Downarrow \Downarrow \rangle +\frac{ 2i\mathrm{\Gamma }_z}{{\chi +2B}}\vert \Uparrow \Uparrow \rangle \right) , \\ \vert u_2\rangle&= \frac{1}{\sqrt{2}}\left( |\Downarrow \Uparrow \rangle +\frac{2 J-2iD_z}{\omega } \vert \Uparrow \Downarrow \rangle \right) , \\ \vert u_3\rangle&= \frac{1}{\sqrt{2}} \left( |\Downarrow \Uparrow \rangle -\frac{2 J-2iD_z}{\omega }\vert \Uparrow \Downarrow \rangle \right) , \\ \vert u_4\rangle&= \sqrt{\frac{\chi -2B}{2\chi }}\left( |\Downarrow \Downarrow \rangle -\frac{2i\mathrm{\Gamma }_z}{\chi -2B}\vert \Uparrow \Uparrow \rangle \right) , \end{aligned}$$

with \(\chi = 2(B^2+\Gamma _{z}^{2})^{1/2}\) and \(\omega =2(J^2+D_{z}^{2})^{1/2}\). To introduce intrinsic decoherence, we use Milburn’s decoherence model (Milburn 1991), which assumes that quantum systems evolve continually in an arbitrary sequence of identical unitary transformations instead of unitary evolution. The following equation describes such evolution (Milburn 1991)

$$\begin{aligned} \frac{d\varrho _t}{dt} = \frac{1}{\gamma }\Bigl (\exp (-i\gamma {\hat{H}})\varrho _t \exp (i\gamma {\hat{H}})-\varrho _t\Bigr ), \end{aligned}$$
(12)

here, \(\varrho _t\) is the density matrix associated to the Hamiltonian \({\hat{H}}\), and \(\gamma\) is the intrinsic decoherence parameter. Thus in the limit of \(\gamma ^{-1} \rightarrow \infty\), there is no intrinsic decoherence, and Eq. (12) is reduced to the typical von Neumann equation characterizing an isolated quantum system. Milburn altered the Schrödinger equation in order for quantum coherence to be spontaneously destroyed throughout the evolution of the quantum system. The ensuing equation is obtained

$$\begin{aligned} \frac{d\varrho _t}{dt}=-\frac{\gamma }{2}[{\hat{H}},[{\hat{H}},\varrho _t]]-i [{\hat{H}},\varrho _t]. \end{aligned}$$
(13)

where \(\frac{\gamma }{2}[{\hat{H}},[{\hat{H}},\varrho _t]]\) designates the non-unitary evolution under the intrinsic decoherence in our considered two-qubit system. A proper solution for the equation (13) is obtained using the Kraus operators \({{\hat{M}}}_{l}\) (Milburn 1991)

$$\begin{aligned} \varrho _t= \sum ^{\infty }_{l=0} {{\hat{M}}}_l(t) \varrho ^{t=0}{{\hat{M}}}^{\dagger } _l{}(t) \end{aligned}$$
(14)

with \(\varrho ^{t=0}\) being the density matrix at \(t=0\) of the considered system and \({{\hat{M}}}_{l}\) are given by

$$\begin{aligned} \displaystyle {{\hat{M}}}_l(t) = \Big (\frac{\gamma ^{l} t^{l}}{l!}\Big )^{1/2} { {\hat{H}}}^l \exp \left( -i{ {\hat{H}}}t\right) \exp \left( -\frac{\gamma t}{2}{{\hat{H}}}^{2}\right) , \end{aligned}$$

with \(\sum ^{\infty }_{l=0} {{\hat{M}}}_l(t) {{\hat{M}}}^{\dagger }_l{}(t) ={\mathbb {I}}\). Finally, the evolved state of the two-spin XXZ quantum system described by \({\hat{H}}\) under intrinsic decoherence effects can be obtained by Milburn (1991)

$$\begin{aligned} \displaystyle \varrho _t= & {} \sum _{j,k} \exp \left( -\frac{\gamma t}{2}({{\mathcal {V}}}_j-{{\mathcal {V}}}_{k})^{2}- i({{\mathcal {V}}}_{j}-{{\mathcal {V}}}_{k})t\right) \nonumber \\\times & {} \langle u_{j}\vert \varrho ^{t=0}\vert u_{k}\rangle \vert u_{j}\rangle \langle u_{k}\vert , \end{aligned}$$
(15)

where \({{\mathcal {V}}}_{j,k}\) and \(\vert u_{j,k}\rangle\) are, respectively, the eigenvalues of the Hamiltonian \({\hat{H}}\) (11) and their corresponding eigenstates. The time-dependent density matrix in Eq. (15) represents the state of the two-qubit XXZ Heisenberg spin model at some time t. It is written as a function of an initial state \(\varrho ^{t=0}\), which will be considered in the following to be a Werner-like state. Equation (15) allows us to describe how the system resources change as the state of the system is evolving under the intrinsic decoherence effects characterized by \(\gamma\). Following, we use correlated coherence and quantum discord to study how intrinsic decoherence affects coherence and nonclassical correlations in the two-spin XXZ Heisenberg model under the different supposed interactions. For a complete characterization of the influence of intrinsic decoherence on the system, we take into account two possible scenarios of the initial state

$$\begin{aligned} \vert \Psi _1\rangle= & {} \cos \left( \theta /2\right) \vert \Downarrow \Downarrow \rangle +\sin \left( \theta /2\right) \vert \Uparrow \Uparrow \rangle , \end{aligned}$$
(16)
$$\begin{aligned} \vert \Psi _2\rangle= & {} \cos \left( \theta /2\right) \vert \Downarrow \Uparrow \rangle +\sin \left( \theta /2\right) \vert \Uparrow \Downarrow \rangle . \end{aligned}$$
(17)

where \(\vert 0\rangle \equiv \vert \Downarrow \rangle\) and \(\vert 1\rangle \equiv \vert \Uparrow \rangle\), denoting spin-down and spin-up, respectively. We shall study intrinsic decoherence according to two samples of Bell-like initial states. To do that, we combine the states in Eqs. (16)–(17) using a parametrization and then solve the dynamical equation. The results for each sample initial state can be obtained by dealing with the parametrization parameters. Thus, the initial state looks as follows

$$\begin{aligned} \varrho ^{t=0} = \alpha _1 \varrho ^{t=0} _1 + \alpha _2 \varrho ^{t=0} _2, \end{aligned}$$
(18)

where \(\varrho ^{t=0} _i = p \vert \Psi _i\rangle \langle \Psi _i\vert + (1-p)/4 ~ I_4\), \(0 \le p \le 1\) denoting the level of purity in the initial state, \(0 \le \theta <\pi\) and \(\alpha _1\) and \(\alpha _2\) are the parametrization parameters taking either zero or one in each of the two scenarios. We note that when Bell-like states reduce to Bell states, those of EWL states reduce to Werner states (Werner 1989). The parameterized initial state is follows

$$\begin{aligned} \displaystyle \varrho ^{t=0} = \left(\begin{array}{cccc} \frac{1}{4} \left(\alpha _1 (2 p \cos (\theta )+p+1)-\alpha _2 (p-1)\right) & 0 & 0 & \frac{1}{2} \alpha _1 p \sin (\theta ) \\ 0 & \frac{1}{4} \left(\alpha _2 (2 p \cos (\theta )+p+1)-\alpha _1 (p-1)\right) & \frac{1}{2} \alpha _2 p \sin (\theta ) & 0 \\ 0 & \frac{1}{2} \alpha _2 p \sin (\theta ) & \frac{1}{4} \left(\alpha _2 (-2 p \cos (\theta )+p+1)-\alpha _1 (p-1)\right) & 0 \\ \frac{1}{2} \alpha _1 p \sin (\theta ) & 0 & 0 & \frac{1}{4} \left(\alpha _1 (-2 p \cos (\theta )+p+1)-\alpha _2 (p-1)\right) \\\end{array}\right). \end{aligned}$$

To simplify calculations, all terms that correspond to the product \(\alpha _1 \alpha _2\) in \(\varrho ^{t}\) cancel in both situations and thus can be omitted. By solving the Milburn’s equation, one finds that the time-dependent density matrix encoding both cases takes the form

$$\begin{aligned} \varrho ^t = \begin{pmatrix} \varrho _{11} &{} 0 &{} 0 &{} \varrho _{14} \\ 0 &{} \varrho _{22} &{} \varrho _{23} &{} 0 \\ 0 &{} \varrho _{23}^{*} &{} \varrho _{33} &{} 0 \\ \varrho _{14}^* &{} 0 &{} 0 &{} \varrho _{44} \end{pmatrix}. \end{aligned}$$
(19)

The time-evolution preserves the X-structure of the initial extended Werner-like (EWL) state for any choice between the two initial states. The following table gives the properties of the density matrix for each case.

\(\vert \Psi _i\rangle\)

\((\alpha _1, \alpha _2)\)

\(\varrho _{ij} \ne 0\)

\(\vert \Psi _1\rangle\)

(1, 0)

(\(\varrho _{11}, \varrho _{14}, \varrho _{22}, \varrho _{44})\), with \(\varrho _{33} = \varrho _{22}, \varrho _{41} = \varrho _{14}^*\)

\(\vert \Psi _2\rangle\)

(0, 1)

(\(\varrho _{11}, \varrho _{22}, \varrho _{23}, \varrho _{33})\), with \(\varrho _{11} = \varrho _{44}, \varrho _{32} = \varrho _{23}^*\)

For the combined initial state in (18), we get the following density matrix entries

$$\begin{aligned} \displaystyle \varrho _{11}&= \frac{\alpha _1}{\chi ^2} \left( B^2 (2 p \cos (\theta )+p+1)+p \Gamma _z e^{-2 \gamma t \chi ^2} \left( 2 \cos (\theta ) \Gamma _z \cos (2 t \chi )-\chi \sin (\theta ) \sin (2 t \chi )\right) +(p+1) \Gamma _z^2\right) -\frac{1}{4} \alpha _2 (p-1), \\ \varrho _{14}&= \frac{\alpha _1 p e^{-2 \gamma t \chi ^2}}{2 \chi ^2} \left( \chi \sin (\theta ) (\chi \cos (2 t \chi )-2 i B \sin (2 t \chi ))+2 \cos (\theta ) \Gamma _z \left( -2 i B e^{2 \gamma t \chi ^2}+2 i B \cos (2 t \chi )+\chi \sin (2 t \chi )\right) \right) , \\ \varrho _{22}&= \frac{\alpha _2}{4 \omega } \Big (\left( 2 p e^{-2 \gamma t \omega ^2} \Big (\left( 2 D_z \sin (\theta ) \sin (2 t \omega )+\omega \cos (\theta ) \cos (2 t \omega )\right) +(p+1) \omega \right) -\alpha _1 (p-1) \omega \Big )\Big ), \\ \varrho _{23}&= \frac{\alpha _2 p e^{-2 \gamma t \omega ^2}}{\omega ^2} \left( J-i D_z\right) \left( -2 i D_z \sin (\theta ) \cos (2 t \omega )+2 J \sin (\theta ) e^{2 \gamma t \omega ^2}+i \omega \cos (\theta ) \sin (2 t \omega )\right) , \\ \varrho _{33}&= \frac{\alpha _2}{4 \omega } \Big ( \left( (p+1) \omega -2 p e^{-2 \gamma t \omega ^2} \left( 2 D_z \sin (\theta ) \sin (2 t \omega )+\omega \cos (\theta ) \cos (2 t \omega )\right) \right) -\alpha _1 (p-1) \omega \Big ), \\ \varrho _{44}&= \frac{\alpha _1}{\chi ^2} \left( B^2 (-2 p \cos (\theta )+p+1)+p \Gamma _z e^{-2 \gamma t \chi ^2} \left( \chi \sin (\theta ) \sin (2 t \chi )-2 \cos (\theta ) \Gamma _z \cos (2 t \chi )\right) +(p+1) \Gamma _z^2\right) -\frac{1}{4} \alpha _2 (p-1). \end{aligned}$$

The populations of the system combining both scenarios are given implicitly as

$$\begin{aligned} \displaystyle \lambda _1= & {} \frac{1}{2} \left( -\sqrt{4 \left| \varrho _{23}\right| {}^2+\left( \varrho _{22}-\varrho _{33}\right) {}^2}+\varrho _{22}+\varrho _{33}\right) ,\\ \lambda _2= & {} \frac{1}{2} \left( \sqrt{4 \left| \varrho _{23}\right| {}^2+\left( \varrho _{22}-\varrho _{33}\right) {}^2}+\varrho _{22}+\varrho _{33}\right) , \\ \displaystyle \lambda _3= & {} \frac{1}{2} \left( -\sqrt{4 \left| \varrho _{14}\right| {}^2+\left( \varrho _{11}-\varrho _{44}\right) {}^2}+\varrho _{11}+\varrho _{44}\right) ,\\ \lambda _4= & {} \frac{1}{2} \left( \sqrt{4 \left| \varrho _{14}\right| {}^2+\left( \varrho _{11}-\varrho _{44}\right) {}^2}+\varrho _{11}+\varrho _{44}\right) . \end{aligned}$$

We use the following notation to locate the matrix density and populations for each case:

$$\begin{aligned} \varrho ^t = {\left\{ \begin{array}{ll} \varrho ^t _1, &{} \text {if}\ \alpha _1 = 1, \alpha _2 = 0 \\ \varrho ^t _2, &{} \text {if}\ \alpha _1 = 0, \alpha _2 = 1 \end{array}\right. }. \end{aligned}$$
(20)

By combining the two cases in (20), correlated coherence writes as

$$\begin{aligned} \displaystyle {\mathcal {C}}_{cc} (\varrho ^t)= & {} \frac{\alpha _1 p e^{-2 \gamma t \chi ^2}}{\chi ^2} \Bigg [\Big (2 B \chi \sin (\theta ) \sin (2 t \chi )+4 B \cos (\theta )\nonumber \\\times & {} \Gamma _z \left( e^{2 \gamma t \chi ^2}-\cos (2 t \chi )\right) \Big ){}^2\nonumber \\+ & {} \left( \chi ^2 \sin (\theta ) \cos (2 t \chi )+2 \chi \cos (\theta ) \Gamma _z \sin (2 t \chi )\right) {}^2\Bigg ]^{1/2}\nonumber \\+ & {} \frac{\alpha _2 p e^{-2 \gamma t \omega ^2}}{\omega } \Bigg [\Big (\omega \cos (\theta ) \sin (2 t \omega )-2 D_z \sin (\theta ) \nonumber \\\times & {} \cos (2 t \omega )\Big ){}^2+4 J^2 \sin ^2(\theta ) e^{4 \gamma t \omega ^2}\Bigg ]^{1/2}. \end{aligned}$$
(21)

One can check that \(\varrho _{14}\) and \(\varrho _{23}\) are the sole non-zero off-diagonal elements, storing all information about the system’s coherence for each studied case. As well, one can easily verify that local coherence, (\({\mathcal {C}}^L (\varrho ) = {\mathcal {C}}_{l_1} (\varrho _A) + {\mathcal {C}}_{l_1} (\varrho _B) = 0\)), is always zero and thus correlated coherence is the system’s total coherence. Similarly, quantum discord is obtained implicitly as

$$\begin{aligned} {{\mathcal {Q}}}{{\mathcal {D}}}_{1}= & {} \log _2 \left( \frac{(1-\Lambda )^{\Lambda }}{\Lambda ^{\Lambda }-\Lambda ^{\Lambda +1}} \prod _{i=1}^4 \lambda _i^{\lambda _i} \left( \frac{\beta }{1-\beta }\right) {}^{-\beta }\right) \nonumber \\- & {} \log _2 \left( -\beta +1\right) , \end{aligned}$$
(22)
$$\begin{aligned} {{\mathcal {Q}}}{{\mathcal {D}}}_{2}= & {} \log _2 \left( \prod _{i=1}^4 \lambda _i^{\lambda _i} \times \prod _{j=1}^4 \varrho _{jj}^{-\varrho _{jj}} \right) , \end{aligned}$$
(23)

where \(\Lambda = \frac{1}{2} \left( \sqrt{4 \left( \varrho _{14}+\varrho _{23}\right) {}^2+\left( 1-2 \left( \varrho _{33}+\varrho _{44}\right) \right) {}^2}+1\right)\), \(\beta = \varrho _{11}+\varrho _{33}\) and \(\lambda _i\)’s are the populations of the system. Quantum discord is then computed by plugging Eq. (22) and Eq. (23) in Eq. (9).

4 Results and analysis

This section presents the obtained findings regarding correlated coherence and quantum discord. To sweeten our learning of the dynamical aspect of quantum correlations and coherence in the two-qubit XXZ Heisenberg model, we considered two kinds of EWL states. We then depict the behavior of coherence and quantum correlations as a function of time and all the parameters in the Hamiltonian as well as the level of purity of the initial state, the Bloch angle, and the decoherence rate.

Fig. 1
figure 1

Time-evolution of coherence (correlated coherence) a and quantum correlations (quantum discord) b. Case 1 (\(\varrho ^t \equiv \varrho ^t _1\)) and case 2 (\(\varrho ^t \equiv \varrho ^t _2\)), versus decoherence rates \(\gamma\)

Full size image

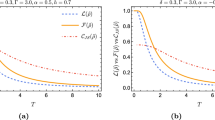
In Fig. 1, we plot the correlated coherence and quantum discord as functions of time t for both initial EWL states \(\varrho _{1}^{t=0}\) and \(\varrho _{2}^{t=0}\) for some decoherence rates \(\gamma\). We notice that both measures show oscillatory behavior due to intrinsic decoherence. At the initial time \(t=0\), the two quantifiers start from the same equal nonzero value for both initial states \(\varrho _{1}^{t=0}\) and \(\varrho _{2}^{t=0}\), that is \({\mathcal {C}}_{cc}(\varrho _{1}^{t=0}) = {\mathcal {C}}_{cc}(\varrho _{2}^{t=0}) \approx 0.495\) and \({\mathcal {D}}(\varrho _{1}^{t=0}) = {\mathcal {D}}(\varrho _{2}^{t=0}) \approx 0.262\). Without intrinsic decoherence \(\gamma =0\), both measures display non-damping oscillations and fluctuate between their minimum and maximum values for an infinite time scale. For \(\gamma > 0\), as time increases, correlated coherence and quantum discord experience damped oscillations and get closer to a stable value after an adequate period suggesting that the system has evolved to a steady state. When \(t \rightarrow +\infty\), the attained steady state becomes independent on \(\gamma\) but on the initial Werner-like state and the Hamiltonian parameters, namely p and \(\theta\). Also, it is marked that a more considerable \(\gamma\) drives the quick decline of correlated coherence and discord; it causes the number and size of their oscillations to drop at some point, causing the system’s state to transition into a steady state quickly. The coherence and correlation deterioration are due to the damping terms \(e^{-2 \gamma t \chi ^2}\) (in the case of \(\varrho _{1}^t\)) and \(e^{-2 \gamma t \omega ^2}\) (in the case of \(\varrho _{2}^t\)); these functions reduce the coherence and quantum correlations amplitude after each incrementing t or \(\gamma\). Similarly, we can mark identical routines for all the different cases.

In the asymptotic limit, \(t \rightarrow \infty\), quantum coherence and quantum correlations reach their stable value. The higher the steady-state correlation, the more the system will be appropriate for achieving quantum-based tasks. In the same conditions of \(\Gamma _z = J = 0.5, B = D_z = 0.1, p = 0.7, \theta = \pi /4\) and \(\gamma > 0\), we numerically find the value of correlated coherence as \({\mathcal {C}}_{cc}(\varrho _{1}^{t \rightarrow \infty }) \approx 0.095\) and \({\mathcal {C}}_{cc}(\varrho _{2}^{t \rightarrow \infty }) \approx 0.485\). Similarly, for quantum discord, we find \({\mathcal {D}}(\varrho _{1}^{t \rightarrow \infty }) \approx 0.007\) and \({\mathcal {D}}(\varrho _{2}^{t \rightarrow \infty }) \approx 0.212\).

Remarkably, we encountered that \({\mathcal {C}}_{cc}(\varrho _{1}^{t \rightarrow \infty })<{\mathcal {C}}_{cc}(\varrho _{2}^{t \rightarrow \infty })\) and \({\mathcal {D}}(\varrho _{1}^{t \rightarrow \infty }) < {\mathcal {D}}(\varrho _{2}^{t \rightarrow \infty })\), this means that the system sustains more superposition and correlations when it is prepared in the initial state \(\varrho _{2}^{t = 0}\). On the other hand, when the system is initially prepared in the Werner-like state \(\varrho _{1}^{t = 0}\), its steady state is still a weakly correlated mixed state that sustains low superposition.

Fig. 2
figure 2

Time-evolution of coherence (correlated coherence) a and quantum correlations (quantum discord) b. Case 1 (\(\varrho ^t \equiv \varrho ^t _1\)): versus B. Case 2 (\(\varrho ^t \equiv \varrho ^t _2\)): versus \(D_z\)

Full size image

Figure 2 shows the dynamics of correlated coherence and quantum discord versus time t for various values of the DM interaction strength \(D_{z}\) and the homogeneous magnetic field B. It is worth noting, as it was shown analytically above, that the DM interaction does not affect the system when the considered initial state is \(\varrho _{1}^{t=0}\) as \(D_{z}\) does not appear in the expressions of the entries of the evolved density matrix \(\varrho _{1}^{t}\). Likewise, the effect of the magnetic field B can not be studied for \(\varrho _{2}^{t}\) since the structure of the initial EWL state \(\varrho _{2}^{t=0}\) totally suppresses its contribution.

In Fig. 2a, we notice that for growing intensities of the magnetic field B, the oscillatory behavior of correlated coherence within \(\varrho _{1}^{t}\) swiftly declines as the amplitudes are shrinking, and \({\mathcal {C}}_{cc} (\varrho _{1}^{t})\) rapidly stabilizes on a nonzero frozen state. Furthermore, the oscillations are slightly phase-shifted, and when \(B\ne 0\), the peaks presenting the maximal values reached over time are broader for more diminutive intensities of B. We again observe that the lower bound of the oscillations is unsteady, as it can increase or decrease over time. When the external magnetic field is non-existing (\(B=0\)), correlations are damped over time due to intrinsic decoherence, and we regard the collapse and regeneration phenomena. On the other hand, quantum discord (Fig. 2b) exhibits erratic oscillations; they are indeed damped over time but present successive small and irregular spikes. Physically, since the Milburn model is characterized by the associated magnetic field B, the irregular oscillatory behavior of correlated coherence and discord in the case \(\varrho ^t \equiv \varrho _1 ^t\), could be due to an ongoing information flow between the magnetic field and the two-qubit XXZ spin system. For the second density matrix \(\varrho ^{t}\equiv \varrho _{2}^{t}\), we see that the same behavior is manifested by both quantum measures with the mere difference that oscillations are regular and that correlated coherence records higher values than quantum discord. At \(t=0\), the quantum correlations and correlated coherence amounts are nonzero. Their initial recorded quantities do not depend on the DM interaction’s strength \(D_{z}\) since they are fixed when the initial state is given. In the absence of the DM interaction \(D_{z}=0\), both measures record the highest values. In contrast, for increasing \(D_{z}\) values, the oscillations’ frequency increases despite being quickly damped. The oscillations get damped and saturate to a stable value for a finite time. This might be explained through the many-body localization-delocalization viewpoint (Doggen et al. 2018). Meanwhile, for \(\varrho ^{t}\equiv \varrho _{1}^{t}\) and \(\gamma >0\), the steady states of correlated coherence and discord are closely related to both B and \(\Gamma _z\), it turns out that there is a competition between B and \(\Gamma _z\). In more specific terms, the steady states increase/decrease by increasing/decreasing either B or \(\Gamma _z\) until \(B = \Gamma _z\), the point at which the steady-state reaches its maximum value. This result indicates that B and \(\Gamma _z\) cancel each other so that the steady states of correlated coherence and discord remain dependent only on p and \(\theta\). We note that for all \(\gamma > 0\), the maximum steady state recorded for \(\theta = \pi /4\) and \(p = 0.7\) remains constant for all nonzero intensities \(B = \Gamma _{z}\), numerically, \({\mathcal {C}}_{cc} (\varrho _1 ^{t \rightarrow \infty }) \approx 0.2474\) and \({\mathcal {D}} (\varrho _1 ^{t \rightarrow \infty }) \approx 0.0543\).

For the second configuration \(\varrho ^{t}\equiv \varrho _{2}^{t}\), we see that as the DM interaction strength grows, the value of the steady state decreases. In contrast, the steady state of correlated coherence and quantum discord improves as the spin-spin interaction coupling becomes strong. For \(\gamma >0\) and \(J=D_z \ne 0\), the steady state can be modified by changing p and \(\theta\). These results highlight the initial state’s impact on the system’s whole evolution and suggest that its quantum resources could be tweaked and enhanced by modifying certain parameters.

Fig. 3
figure 3

Time-evolution of coherence 3a and quantum correlations 3b. Case 1 (\(\varrho ^t \equiv \varrho ^t _1\)): versus \(\Gamma _z\). Case 2 (\(\varrho ^t \equiv \varrho ^t _2\)): versus J

Full size image

In Fig. 3, we depict the influence of the strength of the KSEA interaction (\(\Gamma _{z}\)) and the spin-spin coupling J on correlated coherence and quantum discord for both considered initial states. We specify again that the effect of the first parameter is examined only in the first case where \(\varrho ^{t}\equiv \varrho _{1}^{t}\), while the influence of the anisotropy parameter J can solely be examined when \(\varrho ^{t}\equiv \varrho _{2}^{t}\).

The first salient observation regarding the evolution of correlated coherence and quantum discord in the first considered case \(\varrho ^{t}\equiv \varrho _{1}^{t}\), is that both appear to be stable for \(\Gamma _{z}=0\) for short periods. However, they eventually decrease for sufficiently long periods. In the absence of the KSEA interaction, the expression of correlated coherence reduces to \({\mathcal {C}}_{cc} (\varrho _{1}^{t})=pe^{-2\gamma t\times 4B^{2}}\sin {\theta }\), and we can numerically perceive its time evolution. Correlated coherence exhibits the same oscillatory pattern in the presence of the KSEA interaction (\(\Gamma _{z}\ne 0\)). However, as \(\Gamma _{z}\) decreases, the lower bound of oscillations is higher, and the minimum values shift to the right. As KSEA interaction strengthens, the frequency of oscillations decreases and coherence becomes less erratic. Quantum discord displays identical behavior as correlated coherence with lower quantities. In distinction, we spot in the dynamical behavior of QD the resurgence of the collapse and revival phenomena and the previously mentioned pattern of minor successive increases and decreases when oscillations reach their minimum values.

In the second case \(\varrho ^{t}\equiv \varrho _{2}^{t}\), we observe that for increasing interaction coupling constant J, the frequency of oscillations of both quantifiers increases, but the amplitudes shrink. For \(J=0\), the lower bounds of both measures nearly drop to zero at the same instants t, at \(t\approx 2\) and \(t\approx 10\), and we see that correlated coherence displays sharp peaks at these instants. Once again, it is apparent that the initial amounts of quantum correlations and correlated coherence are not related to the parameters that do not figure in the initial state.

Fig. 4
figure 4

Time-evolution of coherence (a) and quantum correlations (b). Case 1 (\(\varrho ^t \equiv \varrho ^t _1\)) and case 2 (\(\varrho ^t \equiv \varrho ^t _2\)), versus the Bloch angle \(\theta\)

Full size image

In Fig. 4, we visualize the effect of the angle \(\theta\) on correlated coherence and quantum discord dynamics. Unlike the previous figures where the initial values, at \(t=0\), of \({\mathcal {C}}_{cc} (\varrho ^{t})\) and \({{\mathcal {D}}}(\varrho ^{t})\) are not dependent on the strengths of the parameters \(\gamma\) (Fig. 1), \(D_{z}\) and B (Fig. 2), J and \(\Gamma _{z}\) (Fig. 3), we notice in Fig. 4 that the initial amounts of quantum correlations and correlated coherence are related to the value of the angle \(\theta\).

Clearly, as the value of \(\theta\) rises, not only the initial recorded values are higher, but also those recorded during the time evolution. The angle \(\theta\) does not affect the frequency of oscillations, but it affects the quantities of correlated coherence and nonclassical correlations within the system. Moreover, oscillations are in phase when \(\varrho ^{t}\equiv \varrho _{2}^{t}\), unlike the first case \(\varrho ^{t}\equiv \varrho _{1}^{t}\) where oscillations are slightly phase-shifted to the right for decreasing \(\theta\) values.

For \(\theta =\frac{\pi }{2}\), which is the angle value for which the Bell-like states (16–17) reduce to the maximally entangled Bell states and the EWL becomes a Werner state, \({\mathcal {C}}_{cc} (\varrho ^{t})\) and \({{\mathcal {D}}}(\varrho ^{t})\), present the higher quantities. Still, they are roughly invariant as they present timid fluctuations when \(\varrho ^{t}\equiv \varrho _{2}^{t}\). Another worth noting remark is the collapse and revival phenomena exhibited in the dynamical behavior of quantum discord when \(\varrho ^{t}\equiv \varrho _{1}^{t}\), in addition to the pattern of the small spikes in the lower bound of QD.

Fig. 5
figure 5

Time-evolution of coherence 5a and quantum correlations 5b. Case 1 (\(\varrho ^t \equiv \varrho ^t _1\)) and case 2 (\(\varrho ^t \equiv \varrho ^t _2\)), versus the level of purity p

Full size image

In Fig. 5, we show the impact of the level of purity p in the initial state on correlated coherence and quantum discord for both considered states \(\varrho _{1}^{t}\) and \(\varrho _{2}^{t}\). When \(p=0\), the system presents zero coherence and zero discord since the initial state (18) reduces to \(\varrho ^{t=0}=\varrho _{1}^{t=0}=\varrho _{2}^{t=0}=\frac{1}{4}I_{4}\) which is an incoherent separable state. As it is shown in Fig. 5a, b, the evolved density matrix corresponding to \(p=0\) does not contain discord-type correlations (\({{\mathcal {D}}}(\varrho _{1}^{t})={{\mathcal {D}}}(\varrho _{2}^{t})=0\)) nor correlated coherence (\({\mathcal {C}}_{cc} (\varrho _{1}^{t})={\mathcal {C}}_{cc} (\varrho _{2}^{t})=0\)). Raising the purity level, p, improves quantum correlations and coherence within the system, whereas it does not affect the frequency of their oscillations. Both quantifiers, given both cases \(\varrho ^{t=0}=\varrho _{1}^{t=0}\) and \(\varrho ^{t=0}=\varrho _{2}^{t=0}\), display damped oscillations. Nevertheless, we recognize in the first case the collapse and revival phenomenon, which is not manifested when \(\varrho ^{t=0}=\varrho _{2}^{t=0}\). As mentioned earlier, the initial amounts of quantum discord and correlated coherence in the system are those of the initial state given, so it is only natural that they are exclusively dependent on the purity level p and the angle \(\theta\). In all figures, it can be seen that the values of quantum coherence and correlations for both cases are the same before the system starts to evolve (at \(t=0\)). This is because both Bell-like states have the same superposition and the same amount of entanglement. Furthermore, correlated coherence is always more significant than the nonclassical correlations measured by QD for both initial states.

5 Conclusion

By utilizing correlated coherence and quantum discord, the dynamics of correlated coherence and quantum discord versus intrinsic decoherence rate are investigated in the two-spin XXZ model under the interplay of two different types of interactions. We found that correlated coherence and quantum discord dynamics depend on all system parameters except the anisotropy coupling \(J_z\), which has no effects. The two measures go up and down in a pattern that gets smaller and quieter as time passes. In particular, we find that the initial state affects the system’s dynamics significantly because it allows it to avoid specific interactions. We also found that the maximum value of the steady state gets smaller by increasing \(B, \Gamma _z\), and \(D_z\), but increasing J makes the steady state bigger. We show that it is possible to have more robust quantum resources by engineering an appropriate initial state for the system. Moreover, we found that the exchange of information between the system and the magnetic field causes quantum discord to have irregular oscillations for the case \(\rho ^t \equiv \rho _1 ^t\). We note that the only part contributing to the correlated coherence dynamic is total coherence because local coherence is always zero, meaning that the reduced density matrices of the subsystems are incoherent states. The results of this work give a more in-depth understanding of the influence of specific interactions and initial state and their consequences on the coherence and discord dynamics of the considered quantum system.