1 Introduction

Quantum entanglement is the fundamental characteristic of quantum mechanics, and it is also an important resource for quantum communication and quantum computation [1]. Recently, much attention has been paid to the thermal entanglement in the spin model [2, 3] since it plays a key role in quantum information processing tasks. The experimental observation of thermal entanglement in a spin chain formed in the compound \(\hbox {Na}_{2}\hbox {Cu}_{5}\hbox {Si}_{4}\hbox {O}_{14}\) has been reported [4]. In particular, the properties of Heisenberg model with the Dzyaloshinskii–Moriya (DM) interaction (arising from spin–orbit coupling) have been studied extensively which can cause another type of anisotropy [5–8]. The \(\hbox {Cs}_{2}\hbox {CuCl}_{4}\), Cu benzoate, and kagomé antiferromagnet can be described by the DM interaction. Many physical systems, such as optical lattices, superconductors, and nuclear spins also have been simulated by the model. It is now well established that at low temperatures these systems exhibit new types of magnetic order and novel quantum phases [9]. Moreover, quantum teleportation has been comprehensively studied in both theoretical and experimental works. Quantum teleportation can be adopted to test the existence of entanglement and how much entanglement there is in a quantum state. Quantum teleportation not only is relevant to quantum communication, but also is a universal computational primitive for quantum computation. It is worthwhile to study the entanglement teleportation in the condensed matter physics.

Recently, Li et al. [8] examined the Heisenberg model with different DM interactions. They found that a more efficient control parameter can be obtained by adjusting the direction of the DM interaction, no matter in the antiferromagnetic case or in the ferromagnetic case. Inspired by this, if we use the Heisenberg model with different DM interactions to perform quantum teleportation protocol, we will also have another means to manipulate the output entanglement and the fidelity of entanglement teleportation. As far as we are aware, the entanglement in the system must be maintained a long time in order to fulfill the quantum task. The unavoidable interaction of a system with its surroundings always makes entanglement decay with time [10]. It is difficult to keep the coherence of a quantum state as the quantum system correlates with its external environment. So, all the discussion must be including the environmental effect on the system [10, 11]. In recent years, there have been many proposals to solve the decoherence problem which is responsible for the quantum-to-classical transition. The general investigation method for this problem is tracing out all other degrees except the quantum states of interest. However, Milburn [12] has given a simple model of intrinsic decoherence based on the assumption that for sufficiently short time steps the system does not evolve continuously under unitary evolution but rather in a stochastic sequence of identical unitary transformations [13–15]. The effects of intrinsic decoherence on the dynamics of entanglement have been studied in a number of works. For example, Hu [15] has shown that the ideal spin channels will be destroyed by the intrinsic decoherence environment. Yu [16] has discussed the intrinsic decoherence effects on the entanglement of a two-qubit XYZ model. Also, the results of reference [17] has demonstrated that an inhomogeneous magnetic field can reduce the effects of intrinsic decoherence. Fan has found that the phase decoherence rate makes the original harmonic vibration with respect to time decay to a stable value [18]. All those works enrich our understanding of the decoherence mechanism. However, how the different DM interactions affect the dynamics of entanglement teleportation and the fidelity of entanglement teleportation has not been reported. We will not only study how much entanglement is teleported through the channel, but also consider the quality of the entanglement teleportation protocol by the fidelity.

In this paper, we will investigate the influence of the intrinsic decoherence on the entanglement and entanglement teleportation of a two-qubit and three-qubit Heisenberg XYZ model with different DM interactions. The outline of this work is as follows. In Sect. 2, we introduce the Hamiltonian of the two-qubit model with different DM interactions and present the exact solution of the model. In Sect. 3, we discuss the effect of different DM interactions on the evolution of entanglement. In Sect. 4, entanglement teleportation processes via the above system and the effect of initial state on the fidelity are investigated. In Sect. 5, we extend our result to three-qubit DM system and study the effect of decoherence on the average fidelity. Finally, in Sect. 6, we summarize our results and draw our conclusions.

2 Model and solution

The Hamiltonian \(H_{z} \) for a two-qubit anisotropic Heisenberg XYZ model with \(z\)-component DM interaction is

$$\begin{aligned} H_z =J(1+\gamma )\sigma _1^x \sigma _2^x +J(1-\gamma )\sigma _1^y \sigma _2^y +J_z \sigma _1^z \sigma _2^z +D_{z} (\sigma _1^x \sigma _2^y -\sigma _1^y \sigma _2^x), \end{aligned}$$
(1)

where \(J\) is the isotropic coupling coefficient and \(J_z \) is the anisotropic coupling coefficient. They both can be obtained by combining bare exchange interactions with an applied field [19]. \(J>0\) and \(J_z>0\) correspond to the antiferromagnetic. \(J<0\) and \(J_z<0\) correspond to the ferromagnetic. \(\gamma \) is the anisotropic parameter. \(D_{z}\) is the \(z\)-component DM interaction parameter, and \(\sigma ^{i} (i=x, y, z)\) are Pauli matrices. The eigenvalues and eigenvectors of the Hamiltonian \(H_{z} \) are given by

$$\begin{aligned} E_{z1}= & {} J_z +2J\gamma , \nonumber \\ E_{z2}= & {} J_z -2J\gamma , \nonumber \\ E_{z3}= & {} -J_z +2\sqrt{J^{2}+D_z^2}, \nonumber \\ E_{z4}= & {} -J_z -2\sqrt{J^{2}+D_z^2},\nonumber \\ |\psi _{z1,z2}\rangle= & {} \frac{|00>\pm |11>}{\sqrt{2}}, \nonumber \\ |\psi _{z3,z4}\rangle= & {} \frac{|01>\pm \chi |10>}{\sqrt{2}}, \end{aligned}$$
(2)

where \(\chi =\frac{J-iD_z}{\sqrt{J^{2}+D_z^2}}\).

The Hamiltonian \(H_{x} \) for a two-qubit anisotropic Heisenberg XYZ model with \(x\)-component DM interaction is

$$\begin{aligned} H_x =J(1+\gamma )\sigma _1^x \sigma _2^x +J(1-\gamma )\sigma _1^y \sigma _2^y +J_z \sigma _1^z \sigma _2^z +D_{x} (\sigma _1^y \sigma _2^z -\sigma _1^z \sigma _2^y). \end{aligned}$$
(3)

Except for \(D_{x}\), the meanings of the other parameters are the same as those in Eq. (1). The eigenvalues and eigenvectors of the Hamiltonian \(H_{x}\) are given by

$$\begin{aligned} E_{x1}= & {} 2J-J_z , \nonumber \\ E_{x2}= & {} 2J\gamma +J_z , \nonumber \\ E_{x3}= & {} -J(1+\gamma )+\sqrt{[J(1-\gamma )+J_z]^{2}+4D_x^{2}}, \nonumber \\ E_{x4}= & {} -J(1+\gamma )-\sqrt{[J(1-\gamma )+J_z]^{2}+4D_x^{2}}, \nonumber \\ \left| {\psi _{x1}} \right\rangle= & {} \frac{|01>+|10>}{\sqrt{2}}, \nonumber \\ \left| {\psi _{x2}} \right\rangle= & {} \frac{|00>+|11>}{\sqrt{2}}, \nonumber \\ \left| {\psi _{x3}} \right\rangle= & {} \frac{\sin \varphi _1 |00>-i\cos \varphi _1 |01>+i\cos \varphi _1 |10>-\sin \varphi _1 |11>}{\sqrt{2}}, \nonumber \\ \left| {\psi _{x4}} \right\rangle= & {} \frac{\sin \varphi _2 |00>+i\cos \varphi _2 |01>-i\cos \varphi _2 |10>-\sin \varphi _2 |11>}{\sqrt{2}}, \end{aligned}$$
(4)

here \(\varphi _{1,2} =\hbox {arc}\tan \left( {\frac{2D_x}{\sqrt{[J( 1-\gamma )+J_z]^{2}+4D_x^{2}}\mp J(1-\gamma )\pm J_z}}\right) \).

The master equation describing the intrinsic decoherence under the Markovian approximations is given by [12, 14]

$$\begin{aligned} \frac{d\rho (t)}{dt}=-i\left[ {H,\rho (t)}\right] -\frac{1}{2}\Gamma \left[ {H,\left[ {H,\rho (t)}\right] }\right] , \end{aligned}$$
(5)

where \(\Gamma \) is the intrinsic decoherence rate. The formal solution of the above master equation can be expressed as

$$\begin{aligned} \rho (t)=\sum \limits _{k=0}^\infty {\frac{(t)^{k}}{k!}} M^{k}\rho (0)M^{\dag k}, \end{aligned}$$
(6)

where \(\rho (0)\) is the density operator of the initial state and \(M^{k}\) is defined by

$$\begin{aligned} M^{k}=H^{k}e^{-iHt}e^{-\frac{t}{2}\Gamma H^{2}}. \end{aligned}$$
(7)

According to the Eq. (6), it is easy to show that, under intrinsic decoherence, the dynamics of the density operator \(\rho (t)\) for the above-mentioned system which is initially in the state \(\rho (0)\) is given by

$$\begin{aligned} \rho (t)=\sum \limits _{mn} {\exp \left[ {-\frac{\Gamma t}{2}(E_m -E_n)^{2}-i\left( {E_m -E_n}\right) t} \right] } \times \left\langle {\psi _m \left| {\rho (0)} \right. } \right. \left| {\psi _n} \right\rangle \left| {\psi _m} \right\rangle \left\langle {\psi _n} \right| ,\nonumber \\ \end{aligned}$$
(8)

where \(E_m, E_n \) and \(\left| {\psi _m} \right\rangle , \left| {\psi _n} \right\rangle \) are the eigenvalues and the corresponding eigenvectors of \(H_{z/x}\) given in Eqs. (2) and (4). Here, we will choose \(\left| {\varphi (0)} \right\rangle =\cos \alpha \left| {01} \right\rangle +\sin \alpha \left| {10} \right\rangle \) as the initial state for two-qubit Heisenberg XYZ model.

3 Entanglement evolutions

To quantify the amount of entanglement associated with \(\rho (t)\), we consider the concurrence, which is defined as [20, 21]

$$\begin{aligned} C=\max \left[ {0,\hbox { 2max}\left( {\lambda _i}\right) -\sum \limits _i^4 {\lambda _i}} \right] , \end{aligned}$$
(9)

where \(\lambda _i \) are the square roots of the eigenvalues of the matrix \(R=\rho (t)S\rho ^{{*}}(t)S, \rho (t)\) is the density matrix, \(S=\sigma _1^y \otimes \sigma _2^y \), and the asterisk stands for the complex conjugate.

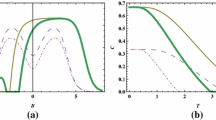
In Fig. 1, we depict the concurrence as a function of the coupling coefficients \(J\) and the time under different initial conditions. As is shown in Fig. 1a, there is no difference between ferromagnetic case and antiferromagnetic case because the concurrence is a symmetric function about \(J=0\). This can be explained from Eq. (2), for the eigenvalues are the same if we change the sign of \(J\). The concurrence is a decreasing function with respect to \(|J|\) when the initial state is a separable state, and it is an increasing function for the entangled state. In Fig. 1b, we see that the concurrence is an asymmetric function with the \(J=0\) for the \(D_x \) system because the eigenvalues will change if we alter the sign of \(J\). So the evolution of entanglement is different for the antiferromagnetic case and the ferromagnetic case. When the initial state angle become \(\alpha =\pi /4\), the entanglement is 1 and it is independent of any parameters.

Fig. 1
figure 1

Concurrence versus the real coupling coefficients \(J\) and the time under different initial states with the Hamiltonian being Eq. (1) (a), Eq. (3) (b). \(\gamma =0.2, J_z =1, D_{z/x}=2, \Gamma =0.02\).

Full size image

In Fig. 2, the entanglement is plotted versus the coupling coefficients \(J_z\) and the time. From Fig. 2a, we see that the entanglement is also a symmetric function about \(J_z=0\) because the expression of the density matrix for this system is independent of \(J_z\). After enough time of decoherence, the entanglement becomes a constant value, while the system becomes a stable state when time \(\rightarrow \infty \). In Fig. 2b, the entanglement is an asymmetric function with respect to \(J_z=0\) except for \(\alpha =\pi /4\) (the entanglement assumes its maximum 1 under this condition). We can note that with the increase in time the entanglement behaves as an oscillatory function, especially for ferromagnetic case.

Fig. 2
figure 2

Concurrence versus the real coupling coefficients \(J_z\) and the time under different initial states with the Hamiltonian being Eq. (1) (a), Eq. (3) (b). \(J=1, \gamma =0.5, D_{z/x}=2, \Gamma =0.02\)

Full size image

In Fig. 3, we give the plot of the entanglement as a function of the DM interaction \(D_{z/x} \) and the time. Except the initial state \(\left| {10} \right\rangle \), the other figures in Fig. 3a show that the entanglement is a monotonic decreasing function with respect to \(D_z \). For a fixed \(D_z \), the entanglement will quickly become a stable value with the increase in time because the stable decoherence time is short for this condition. In Fig. 3b, except \(\alpha =\pi /4\) case, the entanglement will oscillate with the increase in \(D_x \) and eventually become a stable value. This result can be explained by seeking the limiting value of the concurrence equation.

Fig. 3
figure 3

Concurrence versus the DM interaction \(D_{z/x} \) and the time under different initial states with the Hamiltonian being Eq. (1) (a), Eq. (3) (b). \(J=1, \gamma =0.6, J_z=1.5, \Gamma =0.02\)

Full size image

Fig. 4 gives the results about how the initial state affects the entanglement. In Fig. 4a, with the increasing of the time, the entanglement will quickly become a stable value. The maximal stable value of concurrence occurs at \(\alpha =\pi /4\) and \(\alpha ={3\pi }/4\). The dependence of entanglement on initial state angle \(\alpha \) periodically changes, and the period is \(\pi /2\). In Fig. 4b, we find that the region of the entanglement will change if we alter the sign for \(J\) or \(J_z\), but the results will not be affected if their signs change together. The period is \(\pi /2\) for the same signs of \(J\) and \(J_z\), but the period is \(\pi \) for different signs of \(J\) and \(J_z\).

Fig. 4
figure 4

Concurrence versus the initial state angle \(\alpha \) and the time with the Hamiltonian being Eq. (1) (a), Eq.  (3) (b). a \(J=1, \gamma =0.2, J_z=2, D_z=0.5, \Gamma =0.02\). b \(\gamma =0.2, D_x=0.5, \Gamma =0.02\)

Full size image

4 The effect of initial state on the entanglement teleportation and the fidelity

The above model can be used as a quantum channel to transmit unknown state. After we input a state from one end, the state will be destroyed, and then, we can apply a local measurement in the form of linear operators, after that we will get the output state from another end. Now we use two copies of the above state \(\rho (t)\otimes \rho (t^{\prime })\) as resource and input state \(\left| {\psi _{\mathrm{in}}} \right\rangle =\cos (\theta /2)|10\rangle +e^{i\phi }\sin (\theta /2)|01\rangle (0\le \theta \le \pi ,0\le \phi \le 2\pi )\). The output replica state can be obtained by \(\rho _{out} (t)=\sum _{i,j} {p_{ij} (\sigma _i \otimes \sigma _j)} \rho _{in} (\sigma _i \otimes \sigma _j)\) [22], where \(\sigma _i ({i=0,x,y,z})\) denote the unit matrix \(I\) and three components of the Pauli matrix, respectively, \(\rho _{in} =\left| \psi \right\rangle _{in} \left\langle \psi \right| \) and \(p_{ij} =tr\left[ {E^{_i}\rho (t)} \right] tr\left[ {E^{_j}\rho (t)} \right] , \sum {p_{ij} =1} \). \(\rho (t)\) is the quantum state of the channel, \(E^{0}=\left| {\psi _{\mathrm{Bell}}^2} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^2} \right| , E^{1}=\left| {\psi _{\mathrm{Bell}}^3} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^3} \right| , E^{2}=\left| {\psi _{\mathrm{Bell}}^0} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^0} \right| , E^{3}=\left| {\psi _{\mathrm{Bell}}^1} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^1} \right| \) and \(\left| {\psi _{\mathrm{Bell}}^{0,3}} \right\rangle ={\left( {\left| {00} \right\rangle \pm \left| {11} \right\rangle } \right) }/{\sqrt{2}}, \left| {\psi _{\mathrm{Bell}}^{1,2}} \right\rangle ={\left( {\left| {01} \right\rangle \pm \left| {10} \right\rangle } \right) }/{\sqrt{2}}\).

In Fig. 5, the output entanglement \(C_{out} \) as a function of the initial state angle \(\alpha \) and the time is plotted for the \(D_{z/x} \) system. From the figures, we find that the maximal output entanglement is decreasing when the input state angle \(\theta \) varied from \(\pi /2\) to \(\pi /6\). The periodic dependence of output entanglement on the angle \(\alpha \) also exists in the figures. \(\pi /2\) and \(\pi \) are the periodicity for the \(D_z \) system and the \(D_x\) system, respectively. Moreover, in Fig. 5b, the behavior of the output entanglement is totally different when the initial state angle \(\alpha \in (0,\pi /2)\) and \(\alpha \in (\pi /2,\pi )\).These results demonstrate that how to choose initial state is very important.

Fig. 5
figure 5

Entanglement of output state versus the initial state angle \(\alpha \) and the time \(t\) with the Hamiltonian being Eq. (1) (a), Eq. (3) (b). \(J=1, \gamma =0.2, D_{z/x} =0.5, \phi =0, \Gamma =0.02\), (a), (b)

Full size image

The fidelity between \(\rho _{in} \) and \(\rho _{\mathrm{out}} \) characterizes the quality of the teleported state \(\rho _{\mathrm{out}} \). When the input is a pure state, we can apply the concept of fidelity as a useful indicator of teleportation performance of a quantum channel. If the quantum channel is maximal entangled, the best entanglement teleportation will be obtained. The fidelity of \(\rho _{in} \) and \(\rho _{\mathrm{out}} \) is defined to be [23, 24]

$$\begin{aligned} F(\rho _{in}, \rho _{out})=\{tr[\sqrt{(\rho _{{in}})^{1/2}\rho _{out} (\rho _{in})^{1/2}}]\}^{2}. \end{aligned}$$
(10)

By averaging over all possible input state, the average fidelity \(F_\mathrm{A}\) of teleportation can be formulated as

$$\begin{aligned} F_\mathrm{A} =\frac{\int _0^{2\pi } {d\phi \int _0^\pi {F\sin \theta d\theta }}}{4\pi }. \end{aligned}$$
(11)

In Fig. 6, the average fidelity \(F_\mathrm{A}\) is plotted as a function of the time under different initial state \(\alpha \). For the purpose of transmitting \(\rho _{in} \) with better fidelity than any classical communication protocol, we require Eq. (11) to be strictly greater than 2/3 [25]. Figure 6a gives the evolution of fidelity for the \(D_{z/x} \) system when the initial state is \(\left| {10} \right\rangle \). In this figure, the \(D_x \) system behaves inferior to the classical communication and the \(D_z \) system performs better. If we change the initial state from \(\left| {10} \right\rangle \) to \({\left( {\sqrt{3}\left| {10} \right\rangle +\left| {01} \right\rangle }\right) }/2\), the result in Fig. 6b shows that the two kinds of system all behave better than the former condition. The entanglement will become a stable constant value with the increase in time, and this is meaningful for quantum information processing. In Fig. 6c, d, we choose the initial state as \(\sqrt{2}{\left( {\left| {10} \right\rangle +\left| {01} \right\rangle }\right) }/2\) and \(\left| {\varphi (0)} \right\rangle =0.9238\left| {01} \right\rangle +0.3826\left| {10} \right\rangle \), respectively, the \(D_x \) system has a better average fidelity than the \(D_z \) system. From Fig. 6, we find that the initial state is one of the significant factors to determine what kinds of system are suitable as quantum channel.

Fig. 6
figure 6

Dynamics of the average fidelity for \(D_z =2\) (blue solid line) and \(D_x=2\) (red dotted line). \(J=1, \gamma =0.4, J_z =0.5, \Gamma =0.02\) (Color figure online)

Full size image

The asymptotic behavior of the fidelity versus the model parameters \(\alpha \) is shown in the Fig. 7. The asymptotic fidelity \(F_\mathrm{A} \) demonstrates periodicity too. This means that we can implement teleportation process in proper angle and get optimal fidelity. We note that the period is \(\pi /2, \pi \) for the \(D_z\) and the \(D_x\) systems, respectively.

Fig. 7
figure 7

Asymptotical behavior of the fidelity versus the initial state angle \(\alpha . J=1, \gamma =0.8, J_z=2, \Gamma =0.02\). a \(D_z=2\), b \(D_x=2\)

Full size image

5 The decoherence of the fidelity for the three-qubit model

The three-qubit Hamiltonian of XYZ model with different DM interactions is expressed as follows,

$$\begin{aligned} H_z= & {} J\left( {1+\gamma }\right) \left( {\sigma _1^x \sigma _2^x +\sigma _2^x \sigma _3^x}\right) +J\left( {1-\gamma }\right) \left( {\sigma _1^y \sigma _2^y +\sigma _2^y \sigma _3^y}\right) +J_z \left( {\sigma _1^z \sigma _2^z +\sigma _2^z \sigma _3^z}\right) \nonumber \\&\quad +\,D_{z} \left( {\sigma _1^x \sigma _2^y -\sigma _1^y \sigma _2^x +\sigma _2^x \sigma _3^y -\sigma _2^y \sigma _3^x}\right) , \end{aligned}$$
(12)
$$\begin{aligned} H_x= & {} J(1+\gamma )\left( {\sigma _1^x \sigma _2^x +\sigma _2^x \sigma _3^x}\right) +J(1-\gamma )\left( {\sigma _1^y \sigma _2^y +\sigma _2^y \sigma _3^y}\right) +J_z \left( {\sigma _1^z \sigma _2^z +\sigma _2^z \sigma _3^z}\right) \nonumber \\&\quad +\,D_{x} \left( {\sigma _1^y \sigma _2^z -\sigma _1^z \sigma _2^y +\sigma _2^y \sigma _3^z -\sigma _2^z \sigma _3^y}\right) , \end{aligned}$$
(13)

Taking into account the decoherence factors, we use the above three-qubit state \(\chi _{\textit{ABC}}\) as a quantum resource. The joint state of the two receivers conditioned on the sender measurement result \(j\) is described by [26]

$$\begin{aligned} \rho _{\textit{BC}}^j =\frac{1}{p_j}tr_{\textit{SA}} \left[ {\left( {\Pi _{\textit{SA}}^j \otimes I_{\textit{BC}}}\right) \left( {\tau _{in} \otimes \chi _{\textit{ABC}}}\right) } \right] , \end{aligned}$$
(14)

here \(\Pi _{\textit{SA}}^1 =\left| {\psi _{\mathrm{Bell}}^0} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^0} \right| , \Pi _{\textit{SA}}^2 =\left| {\psi _{\mathrm{Bell}}^3} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^3} \right| , \Pi _{\textit{SA}}^3 =\left| {\psi _{\mathrm{Bell}}^1} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^1} \right| \), and \(\Pi _{\textit{SA}}^4 =\left| {\psi _{\mathrm{Bell}}^2} \right\rangle \left\langle {\psi _{\mathrm{Bell}}^2} \right| \). \(I_{\textit{BC}}\) is the identity operator on the subsystem BC, and \(j\) is the outcome of the measurement. \(\tau _{in} =\left| \psi \right\rangle _s \left\langle \psi \right| \) is the density matrix for input state \(\left| \psi \right\rangle _s =\cos \frac{\theta }{2}\left| 0 \right\rangle _s +e^{i\phi }\sin \frac{\theta }{2}\left| 1 \right\rangle _s \). \(p_j =tr_{\textit{SABC}} \left[ {\left( {\Pi _{\textit{SA}}^j \otimes I_{\textit{BC}}}\right) \left( {\kappa _s \otimes \chi _{\textit{ABC}}}\right) }\right] \). In order to successfully carry out the teleportation protocol, two receivers perform\( j\)-dependent unitary operations \(U_B^j =U_C^j =U^{j}\) on the systems B and C, respectively. So

$$\begin{aligned} \tau _B^j =\tau _C^j =\tau ^{j}=U^{j}\rho ^{j}U^{j\dagger }, \end{aligned}$$
(15)

where \(U^{j}\) could be one of the Pauli matrices or the identity matrix. \(\rho ^{j}=\rho _B^j =tr_C \rho _{\textit{BC}}^j =\rho _C^j =tr_B \rho _{\textit{BC}}^j \). The average fidelity between \(\tau _{in} \) and \(\tau _{\mathrm{out}} \) characterizes the quality of the teleportation protocol

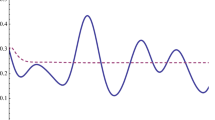
$$\begin{aligned} F_\mathrm{A} =\frac{\int _0^{2\pi } {d\phi \int _0^\pi {\sin \theta d\theta \sum \limits _{i=1}^4 {p_j tr\left( {\tau _{out}^j \tau _{in}} \right) }}}}{4\pi }. \end{aligned}$$
(16)

In Fig. 8, the average fidelity \(F_\mathrm{A}\) is plotted as a function of the time. The \(D_x \) system behaves better than the classical communication, and the \(D_z \) system will exhibit damped oscillation below the value of 2/3. From this figure and Fig. 6, we notice that the \(D_x \) system is more favorable to resist decoherence in most cases.

Fig. 8
figure 8

Dynamics of the average fidelity for \(D_z=1\) (blue solid line) and \(D_x=1\) (red dotted line). The initial state is \(W\) state \(\left| W \right\rangle =\left( {\left| {001} \right\rangle +\left| {010} \right\rangle +\left| {010} \right\rangle } \right) /\sqrt{3}. J=1, \gamma =0.2, J_z=1.2, \Gamma =0.02\) (Color figure online)

Full size image

6 Summary

In summary, we have investigated the entanglement and the fidelity of entanglement teleportation for Heisenberg XYZ model with different Dzyaloshinskii–Moriya interactions when the Milburn’s intrinsic decoherence taken into consideration. After comparing the two different DM interactions, we can clearly find which one can get stable entanglement and high fidelity. The results demonstrate that after reaching the maximum decoherence time the entanglement will keep in a steady value for some initial state. With the change of initial state angle, the entanglement, the output entanglement, and the asymptotic fidelity all will exhibit periodicity. The \(D_x \) system is more favorable to resist decoherence and get a high fidelity both in two-qubit teleportation protocol and in three-qubit teleportation protocol. These results are valuable in quantum information processing based on the solid-state qubit.