Introduction

As one of the first steps in building a project, it is essential to carefully analyze the soil-bearing capacity of shallow footing, among the most crucial construction criteria [1, 2]. Because bearing capacity depends on various soil parameters, obtaining a precise estimation is vital for several geotechnical engineering operations. The maximum settlement ratio, equal to 0.1 of the foundation width, determines the final operational stress (Full). Many scientists have debated and developed formulae to offer an accurate estimate of the Fult of foundations on layered soils, including Meyerhof and Hanna [3], Florkiewicz [4], and Lotfizadeh and Kamalian [5]. So far, various analytical and numerical techniques have been used to study the bearing capacity. However, classical methodologies and laboratory techniques cannot be used without investing significant money and time. In contrast, due to their outstanding competence in many industrial applications, artificial intelligence approaches may be employed as low-cost but reliable models for evaluating geotechnical factors like bearing capacity.

The primary goal of evaluating bearing capacity (Fult) is to reduce the likelihood of high settlement when the constructions above' real-world pressures have been imposed [6,7,8,9]. The soil characteristics, which correlate to the layers under the foundation and include cohesiveness and internal friction angle, unit weight, dilation angle, elastic modulus, poison's ratio, and imposed loads on the footing, are the most crucial variables in determining the bearing capacity [10]. Generally, the Fult is the maximum applied stress for a foundation settling to footing width ratio (S/B), corresponding to 10% of the footing width [11, 12]. The bearing capacity of a thin footing is affected by a variety of factors, including multilayer soil condition, geological condition, footing width, failure model taken into account during the assessment, soil type, and position of the firm soil (e.g., soil layer pattern) [13,14,15,16]. Numerous neural network-based models have recently been developed to aid Fult estimation in single homogeneous soil conditions [14, 17,18,19]. Several finite element method (FEM) simulations [20,21,22,23,24] were also performed in addition to the experimental laboratory testing as part of a practical strategy to support the findings. The results demonstrated that the Fult rises with increasing relative density rate, footing width, and setback distance and falls with decreasing slope angle. Ismail and Jeng [25] examined the load-settlement characteristic of piles using a high-order neural network model (HON-PILE). The findings showed that the HON estimates outperformed traditional ANN techniques [26]. The new model claims to achieve superior forecasts than current theoretical models. A general regression neural network (GRNN) was created by Sarkar et al. [27] to forecast SPT-N based on soil value in Khulna City, Bangladesh. A thorough geotechnical and geological assessment of the city and its surroundings was conducted to broadly generalize the subsurface state of the investigation region depending on SPT measurements and the type of soil. And over 2326 fieldwork SPT values (N) were gathered from 42 clusters of 143 boreholes scattered across a 37 km2 region to suggest the GRNN model. Consequently, the city was split into four geological formations and three geotechnical areas. The results from the GRNN model forecast accurately and could be applied to future city design compared to the actual site investigation. Adaptive neuro-fuzzy inference systems (ANFISs), artificial neural networks (ANN), and other relevant, efficient simulations were made available by introducing soft computing technologies for various engineering computations emphasizing estimating jobs [28]. For load-settlement relation evaluation, such models have also been effectively employed [13, 29]. In this regard, Padmini et al. [30] applied three models to forecast the eventual bearing capacity of weak soil, including ANN, neuro-fuzzy, and fuzzy (on cohesionless soil). Their findings demonstrated that intelligent simulations outperformed well-known carrying capacity theories. To determine the final bearing capacity of shallow foundations laying on rock masses, Alavi and Sadrossadat [31] used linear genetic programming. Metaheuristic algorithms suggest effective methods for a variety of optimization issues [32]. The efficiency of widely used predictive models such as the ANN, support vector machines (SVMs), and ANFIS is improved using them [33, 34]. In terms of implementing metaheuristic algorithms for bearing capacity assessment, multiple algorithms were utilized to increase the validity of the described models [1, 14, 35]. Moayedi et al. [36] used the biogeography-based optimization (BBO) technique on ANN and ANFIS to estimate the failure probability of shallow footings. The findings show that the employed approach may improve the ANFIS's classification accuracy for ANFIS (from 97.6 to 98.5%) and the ANN (from 98.2 to 98.4%). Similarly, Moayedi et al. [37] contrasted the efficacy of the dragonfly algorithm (DA) and the Harris Hawks optimization (HHO) to optimize the computing variables of the ANN. As mentioned earlier, their analysis showed that both algorithms can handle the job. Regarding the area under the curve (AUC) values, the DA, with an AUC of 0.942 and an error of 0.1171, outperformed the HHO, with an AUC of 0.915 and an error of 0.1350.

The objective of the current study was to utilize the ERWCA-ANN artificial intelligence approach, in combination with MLP, to establish a robust predictive network. This network was intended to accurately estimate the load-settlement relationship specific to a particular engineering problem, incorporating key factors influencing the load-settlement trend, including the soil's bearing capacity.

To achieve this objective, a comprehensive dataset was assembled through numerous finite element simulations. The subsequent sections detailed the database compilation process, as well as the optimization and modeling procedures undertaken during the implementation of the proposed solution, which harnessed machine learning techniques. Ultimately, the study entailed an assessment of the outcomes derived from each approach. Furthermore, a thorough examination of the influential factors was conducted, thus facilitating a comprehensive discussion of their impacts.

Established database

In this study, the effectiveness of the intelligent models is trained and validated using a finite element data set. A shallow footing was deliberately developed on two-layered soil using the Mohr–Coulomb constitutive models. Triangular components with 15 nodes were used to evaluate the system. To create the input parameters, data about the seven critical system components—the angle of friction (FA), unit weight (UW) \(\left( {\frac{kN}{{m^{3} }}} \right)\) elastic modulus (EM) \(\left( {\frac{kN}{{m^{3} }}} \right)\), Poisson's ratio (PR) (v), dilation angle (DA), and setback distance (SD) (m)—is gathered. The objective is then attained using the settlement (m) values of 901 implemented stages. Figure 1 displays soil types and data collection. Also, the values of all input variables are given in Table 1.

Fig. 1
figure 1

A 3D view of soil types and data collection

Full size image
Table 1 Soil types and input values
Full size table

The predicted values that were produced vary from 0 to 10 cm. Conversely, settlement values greater than 5 cm suggest errors, while settlement values less than 5 cm suggest the system's stability. In this view, the numbers 0 and 1 stand for stability and error, respectively. The descriptive statistical analysis for every parameter is also included in Table 2.

Table 2 Descriptive statistics of the compressive strength and key factors
Full size table

For the 80–20 split ratio, 721 samples were chosen randomly as training data. These data are provided to intelligent models to deduce the correlation between the stability values (SV) and conditioning variables. After the SV behavior has been derived, the models are then utilized in the remaining 180 samples to gauge how well they function under stranger circumstances.

Methodology

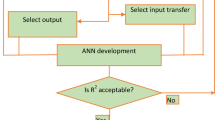
This study employs a sophisticated non-linear intelligent model known as ERWCA-MLP to accurately determine soil bearing capacity. A comprehensive dataset of eight hundred and eighty samples, encompassing diverse soil qualities and layer thicknesses, was meticulously analyzed to achieve this objective while assessing their influencing factors. To construct the aforementioned models, a library consisting of seven inputs and one output (Fy) was established. This procedure is depicted in Fig. 2. The subsequent sections provide comprehensive insights into the methodologies harnessed throughout this investigation.

Fig. 2
figure 2

Schematic view of the data provision process

Full size image

Multilayer perceptron (MLP)

The soil's bearing capacity can be estimated through a unique artificial intelligence system known as ERWCA-MLP, which is grounded in multilayer perceptron (MLP) methodologies. Initially introduced by McCulloch and Pitts [38], artificial neural networks (ANNs) form the foundation of this approach. The initial training approach for ANNs, stems from a multitude of principles grounded in theories and neuro-physiological facts [32]. Researchers have extensively explored the development of both simple and nonlinear mathematical models inspired by human neurons [39,40,41,42,43], resulting in various architectures or topologies [44, 45]. The models constructed using ANN techniques involve training a network and evaluating the anticipated outcomes against a predefined test dataset. In this context, Fig. 3 illustrates the architecture of the ANN employed for soil bearing capacity forecasting.

Fig. 3
figure 3

The MLP structure utilized in this study

Full size image

Evaporation rate-based water cycle algorithm

Sadollah et al. [46] proposed the ER-WCA by modifying the water cycle algorithm. It is a population-based optimizer that has proven adept at coping with various regression [47] and classification [48] problems. As explained, the WCA algorithm is the fundamental theory underlying this paradigm. This algorithm simulates the water cycle found in nature. Water transpiration and evaporation combine to form clouds. The water then returns to the earth in the form of various precipitations.

Regarding convergence speed and precision, the WCA outperforms the majority of other optimizers. The algorithm's functionality in all dimensions contributes to this advantage [49]. Compared to the binary WCA, the ER-WCA has a more optimal equilibrium between exploitation and exploration, resulting in greater precision and faster convergence. This algorithm may be expressed in several phases. First, the population is generated randomly, and initial members (i.e., streams, rivers, and seas) are formed. A cost function is applied to each stream to monitor the minimization of the error. Next, flow intensity (FI) is calculated for the members, and the positions are exchanged accordingly. The rivers flow to the sea, and the evaporation rate (ER) is determined. Based on the obtained ER, the position of the members is updated. Some mathematical explanations are presented in the following. Considering highly fitted members as rivers and the rest as streams, the candidate streams (\(CS\)) array is defined as follows:

$$CS = \left[ {x_{1} , x_{2} , \ldots , x_{K} } \right]$$
(1)

in which \(K\) represents the dimension of the problem. Assuming \(K_{pop}\) as the population size, generating the population is expressed by Eq. (2):

$$Total\,\, population = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {Sea} \\ {River_{1} } \\ {River_{2} } \\ \end{array} } \\ \vdots \\ { Stream_{{K_{sr + 1} }} } \\ {Stream_{{K_{sr + 2} }} } \\ \vdots \\ { Stream_{{K_{pop} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{1}^{1} } & {x_{2}^{1} } & \cdots & {x_{K}^{1} } \\ {x_{1}^{2} } & {x_{2}^{2} } & \cdots & {x_{2}^{K} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{1}^{{K_{pop} }} } & {x_{2}^{{K_{pop} }} } & \cdots & {x_{N}^{{k_{pop} }} } \\ \end{array} } \right]$$
(2)

Equation (3) gives the FI:

$${\text{Cos}} t_{i} = f \left( {x_{1}^{i} , x_{1}^{i} , \ldots , x_{K}^{i} } \right)\quad i = 1, 2, \ldots , K_{pop}$$
(3)

Moreover, Eqs. (4) and (5) reflect the process of designating the streams to the rivers and the sea:

$$C_{n} = Cost_{n} - Cost_{{K_{sr + 1} }} \quad n = 1, 2, \ldots , K_{sr}$$
(4)
$$NS_{n} = round \left\{ {\left| {\frac{{C_{n} }}{{\mathop \sum \nolimits_{n = 1}^{{K_{sr} }} C_{n} }}} \right.| \times K_{streams} } \right\},\quad n = 1, 2, \ldots , K_{sr}$$
(5)

where \(K_{sr}\) shows the number of individuals who opted for the best-fitted ones. Subsequently, \(K_{Stream}\) denotes the number of the remaining individuals.

The ERWCA is a nature-inspired optimization algorithm inspired by the water cycle process in nature. It's important to note that the specific advantages of ERWCA may vary depending on its implementation details, problem context, and empirical performance in comparison to other optimization algorithms. Empirical validation and benchmarking against established optimization methods are essential steps to assess its effectiveness and competitiveness in practical applications. Like many nature-inspired optimization algorithms, ERWCA likely balances exploration (searching for new solutions) and exploitation (exploiting known solutions) effectively. This balance can help it converge to high-quality solutions efficiently. ERWCA is likely based on a simple conceptual framework, mimicking the water cycle process. This simplicity can make it easier to understand, implement, and apply compared to more complex optimization algorithms. As with many nature-inspired algorithms, ERWCA is likely versatile and applicable to various problem domains. It can be used for optimization problems in engineering, economics, finance, and other fields. Indeed, nature-inspired algorithms often exhibit robustness to noise and uncertainty in the optimization landscape. ERWCA may also possess this characteristic, making it suitable for noisy or uncertain optimization problems. ERWCA may be amenable to parallelization, allowing it to leverage parallel computing resources for faster convergence and scalability to large-scale optimization problems. They also typically have low computational complexity, making them suitable for optimization problems with computational constraints. ERWCA may offer a balance between solution quality and computational cost. In addition, ERWCA likely offers opportunities for customization and parameter tuning to adapt to specific problem characteristics and optimization requirements. This flexibility allows users to tailor the algorithm to their needs effectively.

Results and discussion

The primary goal of this research is to forecast the soil's bearing capacity under two soil layers. To estimate the Fy, the traits that had the most significant impact on its computation were determined. The 20 and 80% parameters were randomly selected for the testing and training databases. Levenberg–Marquardt's (LM) back-propagation training technique was utilized for the analysis. Because of its efficiency and ease, this method has been used in numerous investigations successfully [13, 50,51,52,53]. The number of neurons in the hidden layer is one of the most critical aspects in constructing an ANN design. This number typically ranges from one to 10, depending on recommendations derived from previous experiments and the characteristics of the dataset utilized in this study. In this regard, the performance indices of the MLPs are presented in Table 3.

Table 3 MLP network optimization
Full size table

As previously mentioned, the primary objective of the current study was to enable the algorithm to determine the optimal weights and biases matrix for the MLP. To achieve this goal, an MLP with one hidden layer consisting of five neurons (determined through a trial-and-error approach) was initially recommended as the base model. Consequently, the MLP under consideration had a total count of 751 input/output variables. This process was carried out using the MATLAB 2020 programming language. It is important to note that, in this investigation, the activation functions for the hidden and output neurons were selected as "tangent-sigmoid (i.e., Tansig)" and "purelin," respectively. Subsequently, the ERWCA method was integrated to create the ERWCA-MLP neural ensemble quantitatively.

Hybridizing the MLP Using metaheuristic algorithm

Combining the Evaporation Rate-based Water Cycle Algorithm (ERWCA) with a Multilayer Perceptron (MLP) neural network can be a promising approach for optimization problems, particularly in the context of training MLP models. By combining ERWCA with MLP, you leverage the strengths of both optimization techniques to effectively train neural networks while exploring the search space for optimal solutions. This hybrid approach can potentially lead to improved convergence, better generalization, and enhanced performance of MLP models in various tasks. Two techniques are combined based on the below mathematical phases.

Initialization of MLP Parameters: Use ERWCA to initialize the weights and biases of the MLP. ERWCA can explore the search space to find an initial set of parameters that may lead to better performance during training.

Optimization of MLP Parameters: Apply ERWCA to optimize the parameters of the MLP during training. This includes adjusting the weights and biases of the MLP based on the performance of the network on the training data.

Objective Function: Define an objective function that measures the performance of the MLP model. This could be a loss function, such as mean squared error for regression tasks or cross-entropy loss for classification tasks.

Fitness Evaluation: Use the objective function to evaluate the fitness of each candidate solution generated by ERWCA. In the context of optimizing MLP parameters, the fitness would correspond to the performance of the MLP model on a validation set.

Updating Parameters: Apply ERWCA's optimization mechanisms, such as evaporation, precipitation, and infiltration, to update the parameters of the MLP. This involves modifying the weights and biases of the MLP based on the performance feedback obtained from the objective function.

Iterative Optimization: Iterate the optimization process until convergence criteria are met or a maximum number of iterations is reached. During each iteration, ERWCA explores the search space to find better parameter configurations for the MLP.

Validation and Testing: After optimization, evaluate the performance of the trained MLP model on a separate validation set to assess its generalization ability. Additionally, test the final model on a held-out test set to evaluate its performance on unseen data.

Hyperparameter Tuning: Conduct hyperparameter tuning for both ERWCA and the MLP to optimize their respective parameters. This may include adjusting parameters such as population size, evaporation rate, learning rate, and network architecture.

Following the ensemble's formation, a population-based trial-and-error procedure determined the optimal metaheuristic algorithm's complexity [54]. To achieve this, ten different population numbers were used to examine the ERWCA-MLP network. One thousand times were run through the model to reduce error. This method's objective function (OF) was configured to assess the training error within every repetition as the root-mean-square error (RMSE). Equation (1) represents this function. The resulting RMSEs for the studied population numbers are shown in Fig. 4. Additionally, this image shows the convergence curve of the most precise model.

$$RMSE = \sqrt {\frac{1}{N}\mathop \sum \limits_{I = 1}^{N} \left[ {\left( {Y_{{i_{observed} }} - Y_{{i_{predicted} }} } \right)} \right]^{2} }$$
(1)

where N is the number of data, and \(Y_{{i_{observed} }}\) and \(Y_{{i_{predicted} }}\) stand for the observed and predicted stability values.

Fig. 4
figure 4

Variation of the MSE versus iteration to find the best fit ERWCA structures

Full size image

Improving the ERWCA-MLP algorithm's most crucial factor is crucial for obtaining the most significant prediction result from the model. The initial parametric inquiry strategy used, such as choosing the best-fit ANN design, required a set of error and trial advances to optimize the forecasting ability of the hybrid ERWCA-MLP system. As a result, various models were created utilizing various population size values, including 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500. The adjustments in the original settings had a significant impact on the findings. It was shown that increasing the number of nodes causes the estimated and measured network outcomes to converge more closely. Compared to other parameters, it is discovered that the version with 300 swarms is the optimal value.

The initial step taken earlier than employing hybrid intelligence solutions is determining the appropriate MLP network architecture. In the second step, the four structures of the ERWCA-MLP must be optimized. By employing the RMSE reduction process, the performance of the above-cited trial and error procedure was estimated. Given the error procedures presented in Fig. 6, the invasive weed optimizer model with a population size of 500 indicated the optimum efficiency reflected as its lower root means square error value. As a result, such a structure was presented as the optimum ERWCA-MLP in a population size of 500 architecture for further evaluations of the capacity of friction for driven piles installed in cohesive soils. A reliable procedure of prediction, which is applied through ANN hybrid models, is required to be created from several steps, such as (1) data normalization and processing, (2) choosing an appropriate hybrid technique, and eventually (3) determining the appropriate hybrid structure of the developed technique, obtainable through a trial-and-error process. Besides its faster training process, the IWO proposed models provided higher accuracies in predicting shaft friction capacity for the installed, driven piles. Figure 5 shows the ERWCA-MLP models in predicting the driven piles' final bearing capacity and the measured data for training and testing datasets. The obtained results of the model of ERWCA-MLP based on \(R^{2}\) values were 0.98953, 0.99305, 0.99466, 0.99605, 0.9953, 0.99364, 0.99523, 0.99435, 0.99499 and 0.99631 for the testing datasets, respectively, for size of population equal to 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500 and 0.9902, 0.9934, 0.9945, 0.9959, 0.9958, 0.9936, 0.9952, 0.9947, 0.9946 and 0.9964 for training datasets, for size of population equal to 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500. According to the results, the developed hybrid ERWCA-MLP model in a population size of 500 accurately predicts the ultimate bearing capacity of the installed, driven piles.

Fig. 5
figure 5figure 5

The results of accuracy for the different ERWCAMLP proposed models

Full size image

As of yet, \(R^{2}\) parameters have supported the ability of the metaheuristic algorithm to create a more potent MLP. The ERWCA-MLP application's outcomes are compared in this part to assess the model's effectiveness. The chosen model's testing and training results for forecasting the soil's bearing capacity are premised on its \(R^{2}\) are shown in Table 4. As shown in Table 4, points were assigned based on the estimated \(R^{2}\) for every population size. The system that produced the most reliable results in each phase was chosen based on the total scores. Regarding \(R^{2}\) for the training and testing phases, Table 4 shows that the population size of 500 achieved the most outstanding results (\(R^{2}\) = 0.9964 and 0.99631 for testing and training).

Table 4 Network results based on statistical indices for ten proposed ERWCA-MLP swarm size
Full size table

Accuracy assessment criteria

Accuracy assessment criteria are metrics used to evaluate the performance of predictive models, classifiers, or algorithms by comparing their predictions or classifications with actual observed values or ground truth. These criteria provide quantitative measures of how well a model performs on a given dataset. These accuracy assessment criteria provide valuable insights into the performance of predictive models and classifiers, helping practitioners evaluate their effectiveness, identify areas for improvement, and make informed decisions in various domains such as machine learning, statistics, and data science. Choosing the most appropriate criteria depends on the specific characteristics of the dataset and the goals of the analysis. As an example, accuracy measures the proportion of correctly classified instances out of the total number of instances in the dataset. It is calculated as the sum of true positives and true negatives divided by the total number of instances. While accuracy is intuitive and easy to interpret, it may not be suitable for imbalanced datasets where one class dominates the others. Precision measures the proportion of true positive predictions among all positive predictions made by the classifier. It is calculated as the ratio of true positives to the sum of true positives and false positives. Precision is useful when the cost of false positives is high. MAE and MSE are metrics used to assess the accuracy of regression models by measuring the average difference or squared difference between predicted and observed values. Lower values of MAE and MSE indicate better model performance. RMSE is the square root of the mean squared error and provides a measure of the average magnitude of errors in the predicted values. Like MAE and MSE, lower values of RMSE indicate better model performance.

The efficiency error of the systems was measured using the two error parameters of RMSE and mean absolute error (MAE). The MAE's formula is expressed in Eq. (2).

$$MAE = \frac{1}{N}\mathop \sum \limits_{I = 1}^{N} \left| {Y_{{i_{observed} }} - Y_{{i_{predicted} }} } \right|$$
(2)

In this section, the capabilities of the best-fit algorithms are evaluated to assess their suitability for simulations. As is widely recognized, the results from the training phase indicate the model's learning capacity, while findings from the testing phase illustrate its ability to generalize to unseen scenarios. Figures 6 and 7 depict the projected and actual results of ensemble models for each of the ten population sizes—50, 100, 150, 200, 250, 300, 350, 400, 450, and 500. Figure 6 illustrates that the errors of various training ERWCAMLP structures are consistently low, indicating close alignment between target and output trends. Figure 7 displays the error frequencies for different training ERWCAMLP structures, revealing that the current optimization process has effectively reduced errors across all population sizes.

Fig. 6
figure 6figure 6figure 6

Value of errors different training ERWCAMLP structures

Full size image
Fig. 7
figure 7figure 7figure 7

Value of errors for different testing ERWCAMLP structures

Full size image

There are two components to evaluating the models that have been used. The testing and training errors of the developed ERWCA-MLP are characterized quantitatively by the MSE and MAE. Figures 8 and 9 provide the findings, including a visual evaluation of the soil's projected and actual bearing capacity and a histogram of the inaccuracies. Based on these results, combining the ERWCA evolutionary approach with the MLP has successfully enabled it to learn more about and estimate the soil's bearing capacity.

Fig. 8
figure 8figure 8figure 8

The error frequency for different training ERWCAMLP structures

Full size image
Fig. 9
figure 9figure 9figure 9

The error frequency for different testing ERWCAMLP structures

Full size image

For the size of the population of 50, 100, 150, 200, 250, 300, 350, 400, 450, and 500, respectively, the values obtained of RMSE and MAE for the typical ANN during the training stage were (0.21222, 0.21259, 0.20904, 0.21093, 0.20856, 0.20787, 0.21366, 0.21039, 0.21422, 0.21288) and (0.1627, 0.16375, 0.15858, 0.15944, 0.16102, 0.15 The training error ranges were, respectively, [− 0.0031228, 0.21236], [− 0.00086137, 0.21276], [0.00016558, 0.20921], [0.0027594, 0.21108], [− 0.00078537, 0.20872], [0.0027133, 0.20802], [− 0.0097779, 0.2136], [− 0.011612, 0.21023], [− 0.010712, 0.21412], and [− 0.00059669, 0.21305].

All of the neural-metaheuristic groups outperformed the ANN in the testing stage, like the previous step, demonstrating how well the algorithms adjusted this instrument's computational biases and weights. The RMSE decreased from 0.3465 to 0.3076, 0.3122, 0.2985, and 0.2745. The MAE decreased from 0.3055 to 0.2555, 0.2592, 0.2430, and 0.1783. Figure 9 shows the graph of the errors as well as the discrepancies between the expected and actual stability levels (assigned as errors). The extent of the variations in the ERWCA-MLP products are as follows: [− 0.010956, 0.21565], [− 0.0068661, 0.21722], [− 0.0056265, 0.2153], [− 0.0018814, 0.21719], [− 0.0057661, 0.21232], [− 0.0032159, 0.21094], [− 0.016106, 0.21991], [− 0.015968, 0.21231], [− 0.014801, 0.21675].

Taylor diagrams

A graphical tool used in meteorology and climate research to assess how well several datasets compare to a reference dataset is called a Taylor diagram, after Karl E. Taylor. It is often used to evaluate the effectiveness of climate models, numerical simulations, or other model outputs compared to observational data. The graphic shows how each dataset's standard deviation, correlation, and centered root mean square difference (RMSD) concerning the reference dataset are related. With the help of these graphic, researchers may rapidly determine which datasets are more knowledgeable and provide a thorough overview of model performance across all dimensions. Overall, Taylor diagrams are useful tools for evaluating and comparing models, and they may help in model development by pointing out areas that need work. In terms of variability, correlation, and general agreement with observational data, they provide a thorough tool to display and assess model performance. It provides a graphical depiction of the degree of conformity between observations and a pattern or group of patterns and was first proposed by Taylor in 2001 [55]. The correlation, the centered root-mean-square difference, and the standard deviations are used to gauge how similar the two patterns are. These graphs are very useful for comparing the performance of many models or analyzing complicated models with many different features, as in IPCC. The Taylor diagram in Fig. 10 illustrates how the existing database compares how well different models can reproduce the regional distribution of annual average precipitation. Four models were subjected to statistical analysis, and each model was given a label. The placement of each label on the map shows how well the predicted precipitation pattern for that model matches the data.

Fig. 10
figure 10

Taylor diagrams

Full size image

Discussion

It is widely acknowledged that metaheuristic algorithms have the potential to enhance the performance metrics of artificial neural networks (ANNs). This positive impact has been extensively documented across various engineering disciplines [56,57,58], particularly in geotechnical engineering [59,60,61,62]. Building upon this understanding, this study investigates the optimization capabilities of an innovative metaheuristic approach known as ERWCA.

A methodology was devised utilizing ERWCA, followed by the implementation of a multilayer perceptron (MLP) to tackle the significant geotechnical challenge of assessing bearing capacity. The ERWCA-MLP model demonstrated remarkable precision. Based on the findings of this research, a rapid, cost-effective, and accurate method for predicting soil bearing capacity can be developed by integrating neural computing with metaheuristic techniques. This approach contrasts with conventional methods that rely on time-consuming and potentially costly experiments, such as laboratory research and finite element analysis. Furthermore, comparison with traditional approaches revealed the potential benefits of employing metaheuristic methods to enhance efficiency. In practical terms, this study advocates for leveraging real-world events as strong motivators to optimize the computational settings of MLP.

In conclusion, the combination of MLP neural networks with ER-WCA presents a promising approach for solving engineering classification problems. Integrating MLP, a powerful machine learning technique, with ER-WCA, a nature-inspired optimization algorithm, offers several advantages. While MLP enables the learning of intricate patterns and relationships within engineering data, ER-WCA enhances the optimization process by leveraging principles from the water cycle and evaporation rates. The hybrid MLP-ER-WCA method has shown promising results in engineering classification problems. By effectively adjusting the weights and biases of the MLP network through the ER-WCA optimization process, the model achieves improved accuracy and convergence while mitigating issues like local optima and overfitting. ER-WCA's ability to explore the solution space and exploit optimal regions enables the hybrid model to effectively handle complex and nonlinear engineering classification problems. Combining global search capabilities with MLP's learning capabilities enhances the model's robustness and generalization performance. The hybrid MLP-ER-WCA method holds potential for various engineering classification applications, including fault diagnosis, image recognition, and pattern recognition. It offers benefits in enhancing decision-making processes and improving the accuracy and efficiency of classification systems.

Conclusions

This study delves into the optimization capabilities of the novel metaheuristic technique ERWCA. A strategic framework was devised using this technique, coupled with a multilayer perceptron, to address the prominent geotechnical challenge of determining bearing capacity. This methodological fusion was then applied to predict the load-settlement behavior of shallow footings near slopes, necessitating consideration of numerous input variables such as unit weight (UW) (kN/m3), elastic modulus (EM) (kN/m2), friction angle (FA), dilation angle (DA), Poisson's ratio (PR) (v), and setback distance (SD) (m). Given the complexity of this engineering problem, a robust strategy was imperative. The optimal complexity of the metaheuristic algorithm was determined through a population-based trial-and-error process. The objective function of this approach was designed to assess training error, quantified by RMSE and R2. Notably, a population size of 500 yielded exceptional results, achieving the highest R2 values (0.9964 and 0.99631 for testing and training phases, respectively). In conclusion, the fusion of the Multilayer Perceptron with the Evaporation Rate-based Water Cycle Algorithm showcases substantial promise in addressing engineering estimation challenges. However, it is essential to acknowledge that further research and validation are necessary to investigate the applicability and performance of the hybrid methodology in different engineering domains and real-world scenarios. Comparative studies with other optimization algorithms and machine learning approaches can provide insights into the strengths and weaknesses of the ERWCA-MLP method and its competitiveness.