Estimating Bearing Capacity of Strip Footings over Two-Layered Sandy Soils Using the Characteristic Lines Method

Abstract

A study on the bearing capacity of strip footings over sandy-layered soils has been conducted using the stress characteristic lines method. Traditional bearing capacity theories for specifying the ultimate bearing capacity of shallow foundations are based on the idea that the bearing layer is homogenous and infinite. In practice, layered soils are mainly being used. The stress characteristic lines method is a powerful numerical tool that can solve stability problems in geotechnical engineering. In the present paper, an appropriate algorithm is derived for estimating the static bearing capacity of strip footing located on two-layered soils using the stress characteristic lines method. Numerical and experimental examples are presented, to validate the proposed algorithm. Graphs and equations illustrate the effective depth of strip footings located on two-layered soils. If the friction angles of the top and bottom layers are 30° and 35°, respectively, the depth effect of the top layer is estimated to be 0.76 of the foundation’s width.

1 Introduction

Soil is the basis of construction, so the study of bearing capacity of foundations is crucial to soil mechanics and geotechnical engineering. Also, calculations on bearing capacity of foundations located on the non-homogeneous soil are important. The methods for computing bearing capacity on layered soils (Michalowski and Shi [1]) vary from calculating the average strength parameters (Bowels [2]), which is based on limit equilibrium considerations (Mayerhof [3], Reddy and Srinivasan [4]), to applying more rigorous limit analysis approaches (Chen and Davidson [5], Florkiewicz [6], Michalowski and Shi [7]). Experimental methods have been the basis for semi-empirical approaches (Brown and Meyerhof [8], Meyerhof and Hanna [9], Buttons Analysis [10]). These methods show how the ratio of the top layer thickness to the footing width affects the total bearing capacity for layered soils.

The stress characteristic lines method introduced by Sokolovski [11], Booker, Davis [12] and Atkinson [13] is one of the most effective numerical methods used for the estimation on bearing capacity of strip foundations. The important advantage of this method over other numerical methods is that it neither requires the customary and troublesome meshing nor the use of complex and specific soil behavior models. The stress characteristics method uses only the stress field, rather than the strain field, and performs its computations with higher speed and simplicity. Although the stress characteristic lines method belongs to the plastic equilibrium world, it does not obtain the upper or lower limit of the collapse load. If a stress field is found in the non-plastic zone, and does not breach the failure criteria (commonly Mohr–Coulomb), the obtained response can thus be said to have a lower limit to the collapse load.

In the present paper, the bearing capacity factors of smooth strip footing over two-layered sandy soils are calculated using the stress characteristic lines method. Initially, an algorithm is proposed to calculate the static bearing capacity of the smooth strip footing located on the two-layered sandy soil. In the proposed algorithm, introduced by Booker and Davis [12], the basic calculations for homogeneous soils are extended to two-layered sandy soils. Numerical and experimental examples are then analyzed to validate the offered algorithm. In the end, a specific applied example is analyzed, followed by detailed simple tables and graphs to illustrate its practical applications.

2 Fundamentals of Characteristic Lines Method

This section deals with the class of 2D plane strain problems. Three components of stress must follow the 2D form of the equilibrium equations:

$$\frac{{\partial \sigma_{x} }}{{\partial_{x} }} + \frac{{\partial \tau_{xy} }}{{\partial_{y} }} = \gamma \times \cos \varepsilon ,$$

(1a)

$$\frac{{\partial \tau_{xy} }}{{\partial_{x} }} + \frac{{\partial \sigma_{y} }}{{\partial_{y} }} = \gamma \times \sin .$$

(1b)

The unit weight $\gamma$ is fixed, and $\varepsilon$ indicates the angle of volumetric force with axis x. The soil is modeled as a homogenous rigid-perfectly plastic Mohr–Coulomb material:

$$\left( {\sigma_{x} - \sigma_{y} } \right)^{2} + 4 \times \tau_{xy}^{2} = \left( {\sigma_{x} + \sigma_{y} + 2 \times c \times \cot \varphi } \right)^{2} \times sin_{\varphi }^{2} .$$

(2)

Stresses are shown in terms of auxiliary variables: where R is the radius of Mohr’s circle and p is the circle center from the origin of the coordinates (Fig. 1). $\theta$ is the angle between the main big stress with axis x (Fig. 2):

$$\sigma_{\text{x}} = p + R \times \cos 2\theta ,$$

(3a)

$$\sigma_{y} = p - R \times \cos 2\theta ,$$

(3b)

$$\tau_{xy} = R \times \sin 2\theta .$$

(3c)

Fig. 1

Mohr’s circle of stresses in the collapse mode

Fig. 2

Situation of big main stress axis ($\sigma 1$) and characteristic lines $\alpha$ and $\beta$ in the Cartesian coordinate system

Therein:

$$R = p \times \sin \varphi + c \times \cos \varphi .$$

(4)

The equilibrium equations system (Eq. 1a, 1b) may be rewritten in simpler terms based on the new variables of p and $\theta$ as follows:

$$\frac{{\partial_{p} }}{{\partial_{x} }} \times \left( {1 + \sin \varphi \times \cos 2\theta } \right) + \frac{{\partial_{p} }}{{\partial_{y} }} \times \sin \varphi \times \sin 2\theta + \;2 \times R \times \left( { - \frac{{\partial_{\theta } }}{{\partial_{x} }} \times \sin 2\theta + \frac{{\partial_{\theta } }}{{\partial_{y} }} \times \cos 2\theta } \right) = \gamma \times \cos \varepsilon ,$$

(5a)

$$\frac{{\partial_{p} }}{{\partial_{x} }} \times \sin \varphi \times \sin 2\theta + \frac{{\partial_{p} }}{{\partial_{y} }}\left( {1 - \sin \varphi \times \sin 2\theta } \right) + \;2 \times R \times \left( { + \frac{{\partial_{\theta } }}{{\partial_{x} }} \times \cos 2\theta + \frac{{\partial_{\theta } }}{{\partial_{y} }} \times \sin 2\theta } \right) = \gamma \times \sin \varepsilon .$$

(5b)

The characteristic lines equivalent to equation system Eq. 5a and 5b are shown in the following equation:

$$\frac{dy}{dx} = \tan \left( {\theta - \mu } \right),$$

(6a)

$$\frac{dy}{dx} = \tan \left( {\theta + \mu } \right).$$

(6b)

Therein:

$$\mu = \frac{\pi }{4} - \frac{\varphi }{2}.$$

(7)

Equation (6a) and (6b) indicate the characteristic lines of $\alpha$ and $\beta$ (see Fig. 2). Now, the equation system (Eq. 5a, 5b) cited in the Cartesian coordinate system can be replaced with the characteristic lines of $\alpha$ and $\beta$ as axes using the following relations:

$$- \sin 2\mu \times \frac{\partial p}{{\partial s_{\alpha } }} + 2 \times R \times \frac{\partial \theta }{{\partial s_{\alpha } }} + \gamma \times \left[ {\sin \left( { - \varepsilon + 2\mu } \right) \times \frac{\partial x}{{\partial s_{\alpha } }} + \cos \left( { - \varepsilon + 2\mu } \right) \times \frac{\partial y}{{\partial s_{\alpha } }}} \right] = 0,$$

(8a)

$$\sin 2\mu \times \frac{\partial p}{{\partial s_{\beta } }} + 2 \times R \times \frac{\partial \theta }{{\partial s_{\beta } }} + \gamma \times \left[ {\sin \left( { - \varepsilon - 2\mu } \right) \times \frac{\partial x}{{\partial s_{\beta } }} + \cos \left( { - \varepsilon - 2\mu } \right) \times \frac{\partial y}{{\partial s_{\beta } }}} \right] = 0.$$

(8b)

Signs $\frac{\partial }{{\partial s_{\alpha } }}$ and $\frac{\partial }{{\partial s_{\beta } }}$ present the derivative to the arc length along the characteristic lines $\alpha$ and $\beta ,$ respectively.

3 Algorithm for Solving the Problem Based on the Characteristic Lines Method

Figures 3 (homogeneous soil) and 4 (layered soil) show a complete mesh of the characteristic lines for the right half of a smooth strip footing problem.

Fig. 3

Array of characteristic lines under the right half of the smooth foundation located on a single-layer soil

Fig. 4

Array of characteristic lines under the right half of the smooth foundation located on a two-layer soil

Three plastic zones are located under the foundation:

• 1. Cauchy zone (OTQ) whose boundary conditions, including the coordinates and variables p and $\theta$, are known along a non-characteristic curve thereof (boundary OT).

• 2. Goursat zone (OQR) whose boundary conditions, including the coordinates and variables p and $\theta$, are known along its two characteristic curves (OQ and point O that is a characteristic curve $\beta$ with an infinitesimal arc length).

• 3. Mixed zone (ORS) whose boundary conditions are known to be in the direction of the characteristic curve (OR), while its other boundary conditions (e.g., $\theta$) are in the direction of the non-characteristic curve (boundary OS).

Calculation of solution points occurs clockwise (from OT to OS).

BCTL¹ is a computer program that uses the stress characteristics method to solve the classical geotechnical bearing capacity of a solid footing resting on two-layered soil. The two conditions considered in this study include cohesionless soil with friction and self-weight, and the cohesionless, weightless soil with friction and uniform surface surcharge.

The following assumptions were made during this research:

• The soil modeled as a rigid perfectly plastic Mohr–Coulomb material was thought to be homogeneous (for each stratum).

• The unit weight $\gamma$ and friction angle $\varphi$ were fixed during the running program.

• Plane strain analyses can be performed.

• The soil–foundation interface was considered smooth.

• A uniform surcharge pressure q can be used on the soil next to the foundation.

3.1 Solving the Cauchy Zone Problem

3.1.1 Homogeneous Soil

The characteristics method is based on the following factors. If the characteristics of point A (on an $\alpha$ characteristic) and point B (on a $\beta$ characteristic) are known, the third point (P) specification (p, $\theta$, x, y) can be obtained by integrating the governing equations at the same time (Fig. 5). This can be done by rewriting the equation systems Eqs. 6a, 6b and 8a, 8b.

$$y_{P} - y_{A} = \tan \left[ {\frac{{\theta_{P} + \theta_{A} }}{2} - \mu } \right] \times \left( {x_{P} - x_{A} } \right),$$

(9a)

$$y_{P} - y_{B} = \tan \left[ {\frac{{\theta_{P} + \theta_{B} }}{2} + \mu } \right] \times \left( {x_{P} - x_{B} } \right),$$

(9b)

Fig. 5

Array of characteristic lines in the Cauchy zone (homogeneous soil)

and

$$- \sin \left( {2\mu } \right) \times \left[ {p_{\text{P}} - p_{\text{A}} } \right] + \left[ {R_{\text{A}} + R_{\text{P}} } \right] \times \left[ {\theta_{\text{P}} - \theta_{\text{A}} } \right] = - \gamma \times \sin \left( { - \varepsilon + 2\mu } \right) \times \left[ {x_{\text{P}} - x_{\text{A}} } \right] - \gamma \times \cos \left( { - \varepsilon + 2\mu } \right) \times \left[ {y_{\text{P}} - y_{\text{A}} } \right] ,$$

(10a)

$$\sin \left( {2\mu } \right) \times \left[ {p_{\text{P}} - p_{\text{B}} } \right] + \left[ {R_{\text{B}} + R_{\text{P}} } \right] \times \left[ {\theta_{\text{P}} - \theta_{\text{B}} } \right] = - \gamma \times \sin \left( { - \varepsilon - 2\mu } \right) \times \left[ {x_{\text{P}} - x_{\text{B}} } \right] - \gamma \times \cos \left( { - \varepsilon - 2\mu } \right) \times \left[ {y_{\text{P}} - y_{\text{B}} } \right].$$

(10b)

To attain the new point by solving the four nonlinear Eqs. (9a, 9b, 10a, 10b), it is proper and customary to choose a midpoint finite difference scheme, in conjunction with a fixed-point iteration strategy (Martin [14]).

• Solve Eqs. (9a, 9b) for x _p and y _p (with supposed $\theta_{p}$).

• Solve Eqs. (10a, 10b) for p _P and $\theta_{p}$.

• Check convergence.

• Test each of the four components for convergence.

  $$\left| {x_{p}^{\text{new}} - x_{p}^{\text{old}} } \right| \le {\text{Tol}}.$$
  $$\left| {y_{p}^{\text{new}} - y_{p}^{\text{old}} } \right| \le {\text{Tol}}.$$
  $$\left| {p_{p}^{\text{new}} - p_{p}^{\text{old}} } \right| \le {\text{Tol}}.$$
  $$\left| {\theta_{p}^{\text{new}} - \theta_{p}^{\text{old}} } \right| \le {\text{Tol}}.$$

  If any part of these relations fail, $x_{p}^{\text{old}} = x_{p}^{\text{new}}$, $y_{p}^{\text{old}} = y_{p}^{\text{new}}$, $p_{p}^{\text{old}} = p_{p}^{\text{new}}$, $\theta_{p}^{\text{old}} = \theta_{p}^{\text{new}} ,$ then repeat from step one.

• Backup strategy.

3.1.2 Two-Layer Soil

The vertical and shear stresses of two-layer soil are equal at the boundary line (Fig. 6), and the following equation can be obtained:

$$\sigma_{xt} = \sigma_{xb} ,$$

(11a)

$$\tau_{xyt} = \tau_{xyb} ,$$

(11b)

where t represents the top layer and b the bottom layer.

Fig. 6

Status of stresses at a two-layer boundary

Referring to Eqs. 3a, 3b, 3c, 4, 11a and 11b, the following results are obtained:

$$p_{t} + {\text{R}}_{\text{t}} \times \cos 2\theta_{t} = p_{b} + R_{b} \times \cos 2\theta_{b} ,$$

(12a)

$$R_{t} \times \sin 2\theta_{t} = R_{b} \times \sin 2\theta_{b} .$$

(12b)

Therein:

$$R_{t} = p_{t} \times \sin \varphi_{t} + c_{t} \times \cos \varphi_{t} ,$$

(13a)

$$R_{b} = p_{b} \times \sin \varphi_{b} + c_{b} \times \cos \varphi_{b} ,$$

(13b)

where $p_{t}$, $\theta_{t}$ and $\varphi_{t}$ are considered top layers, $\varphi_{b}$ is known as bottom layer, and sandy-layered soils are calculated as $c_{b}$ = c _t  = 0. As illustrated in Eqs. 12a and 12b, $p_{b}$ and $\theta_{b}$ are obtained for points A and B on the boundary line. The problem is solved to obtain the values of new point P (Figs. 7, 8). The friction angle and the unit weight of the bottom layer are used for Eqs. 9a, 9b, 10a and 10b.

Fig. 7

Effect of layer change in the Cauchy zone (the bottom layer is stronger than the top layer)

Fig. 8

Effect of layer change in the Cauchy zone (the top layer is stronger than the bottom layer)

3.2 Solving the Goursat Zone Problem

3.2.1 Homogeneous Soil

Referring to Fig. 3, point O in the Goursat zone is a characteristic boundary of $\beta$ with zero length. Once the arc shares its first point with the Cauchy zone, thereby making the variables p and $\theta$ easily noticeable, it then shares its last point with the mixed zone, where the variable $\theta$ is specified. Once the Cauchy zone problem is solved, the variables (x, y, p and $\theta$) on OQ become known. The solution strategy, as with one used in the Cauchy zone, progresses along the characteristic boundary OQ and consequently solves the Goursat zone.

3.2.2 Two-Layer Soil

Different modes may be developed at the two-layer boundary. For example, two modes may be analyzed as follows:

3.2.2.1 Mode 1: x _B $\le$ x _p (Fig. 9)

When x _A, x _B and x _p are located on the top layer, the solving procedure is similar to that described for the single-layer soil (x denotes the point height from the ground). Similarly, when x _A, x _B and x _p are located on the bottom layer, the solving procedure is similar to that of foregoing and friction angle, and the equations are calculated according to the soil’s unit weight in the bottom layer. Initially, the new points A and B replace the old points on the boundary line. The new point value (p, $\theta$) is then calculated for the bottom layer using Eq. 12a and 12b. And finally, specifications of new point P are obtained using Eqs. 9a, 9b, 10a and 10b.

Fig. 9

Schematic effect of layer change in the Goursat zone

3.2.2.2 Mode 2: x _B $>$ x _P (Fig. 10)

Similar to mode 1, if x _A, x _B and x _p are located on the top layer in mode 2, the solving procedure is similar to that described for the single-layer (homogeneous) soil. When x _A, x _B and x _p are located on the bottom layer, the solving procedure is similar to that of the foregoing and friction angle, in which the equations are calculated according to the soil’s unit weight in the bottom layer. Considering that point B is located on the bottom layer and point A on the top layer, six equations (Eqs. 9a, 9b, 10a, 10b, 12a and 12b) should be solved simultaneously for obtaining specifications of point P (in this mode, the boundary height based on height P is either slightly higher or lower, see Fig. 4).

Fig. 10

Schematic effect of layer change in the Goursat and mixed zone

3.3 Solving Mixed Zone

3.3.1 Homogeneous Soil

Once the Goursat problem is solved, positions p and $\theta$ along the last characteristic line $\alpha$ (line OR) are thus obtained. This characteristic line is the known characteristic boundary of the mixed zone. The Goursat zone procedure is applied to solve the mixed zone problem, which can thus determine contact pressure distribution under the right side of the foundation (OS line). For the vertical ($\sigma_{x}$) element, the integral of the contact pressure results in the vertical collapse force ($p_{x}$). The obtained value is doubled due to the existing symmetry.

3.3.2 Two-Layer Soil Model

In the two-layer soil model, if the height of points A, B and P are located in the top or bottom layer, a homogeneous procedure is implemented. Otherwise, the second mode in the Goursat zone is applied (Fig. 10). That is to say, even if point B is located in the bottom layer and point A in the top layer, six equations—Eqs. 9a, 9b, 10a, 10b, 12a and 12b—should be solved simultaneously to obtain the specifications of new point P (in this mode, the boundary height based on height P is somewhat higher or lower, see Fig. 4).

4 Comparison to Other Methods

4.1 Calculation of N _γ Value for Homogenous Soil

The research of Sokolovski [15], Bolton and Lau [16] and Martin [14] on determining N _γ value through the stress characteristic lines method was compared to that done in this study. In all researches, the properties of both layers were of similar to homogeneous soil. Nonetheless, the comparison showed a slight difference between what was derived from the stress characteristic lines method and the obtained values for homogeneous soil by other researchers (see Table 1).

Table 1 The value of N _γ for homogeneous soils

4.2 Calculation of N _γ Value for Layered Soils

The experimental data obtained by Verma et al. [17] for the plate load test on the bearing capacity of sandy-layered soils is used in this study for further comparison. Table 2 illustrates the properties of the two layers.

Table 2 Properties of two-layer soil

Table 3 compares the results of the two layers when the properties are the same, and Table 4 illustrates the two sandy-layered soils. Test results for the computed N _γ values obtained for this paper showed minor differences from those obtained by Kamalian et al. [18] and Martin [14] and major differences with those by the Verma test.

Table 3 The value of Nγ for homogeneous soils

Table 4 The value of Nγ for layered soils ($\varphi_{t}$ = 39, $\varphi_{b}$ = 32)

Nevertheless, most researchers have noted that the observed values of the ultimate bearing capacity factor (N _γ ) are much greater than those calculated. The common reasons for this are: (1) the stress characteristic method is a lower bound analysis method, which normally results in failure loads lower than the exact failure load; (2) the obtained bearing capacity factor (N _γ ) from the stress characteristic lines method is calculated for the smooth footing, while it is obtained for rough footing in the Verma test. The mentioned results suggest that the change in layer thickness affects not only the ultimate bearing capacity factor (N _γ ), but also the effective depth factor (X). The effective depths for both the Verma test and those performed for this study are illustrated in Table 5.

Table 5 Effective depth factor (X) versus the thickness of the top layer to width of the footing

The drawings in Fig. 11, which are based on Table 5, illustrate the effective depth factors (X) versus top layer thickness (H)/width of square test plate or width of strain footing (B) (40 cm in this case).

Fig. 11

Effective depth factor (X) versus (H/B)

As observed in Table 5, if the top layer thickness is more than 1.133 × B (B is the width of the foundation), the effective depth remains constant (as seen in this study). As a result, N _γ corresponds to their values for homogeneous soil.

The effective depth of sandy-layered soils is given by the following equations:

$${\text{Verma test}} {:}\, X = 0.73 \times \left( {\frac{H}{B}} \right) + 0.64\;\;\,\;0.5 < \frac{H}{B} < 2,$$

(14)

$${\text{This study}} {:} \ X = 0.254 \times \left( {\frac{H}{B}} \right) + 0.845\;\;\;\;\;0 \le \frac{H}{B} \le 1.133.$$

(15)

5 Parametric study

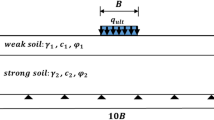
In this section, the BCTL program is used on two layers of soil (weak sand layer overlain strong sand layer). The bearing capacity coefficients (N _γ , N _q ) have been studied and an equation foreseeing the effective depth is developed based on BCTL.

5.1 Computation of N _γ

For smooth strip footing on sandy-layered soils with no surcharge (c _t  = c _b  = 0, q = 0), the bearing capacity is given by:

$$q_{u} = 0.5 \times \gamma \times B \times N_{\gamma } \;,{\text{where}}\;N_{\gamma } = f\left( {\varphi_{t} ,\varphi_{b} ,\frac{H}{B}} \right).$$

(16)

Also for smooth strip footing:

$$\theta_{f} = 0\;{\text{and}}\;\theta_{gr} = \frac{\pi }{2},$$

where $\theta_{f}$ denotes the angle of the strip smooth footing and $\theta_{gr}$ represents the free area of the land next to the foundation. The issue of strong soil layer overlain by weaker soil layer has been studied in the past. The N _γ value cannot be fixed directly using BCTL (i.e., with q = 0). It is proper to fix c _t  = c _b  = 0, γ _t  = 10 KN/m³, γ _b  = 13.5 KN/m³, B = 2 m and H/B = 0.3 and let $q \to 0$; the average bearing pressure q _u then corresponds directly to the bearing capacity factor, N _γ . The analyses below is carried out with q = 10⁻⁵ KN/m².

The BCTL N _γ values are shown in Tables 6, 7 and 8 and Fig. 12. The internal friction angle of the bottom layer ($\varphi_{b}$) increases by one-degree steps.

Table 6 $N_{\gamma }$ values, $\varphi_{t}$ = 25

Table 7 $N_{\gamma }$ values, $\varphi_{t}$ = 30

Table 8 $N_{\gamma }$ values, $\varphi_{t}$ = 35

Fig. 12

$N_{\gamma }$ values for various internal friction angles

Also for fixed c _t  = c _b  = 0, $\varphi_{t}$ = 30, $\varphi_{b}$ = 35, $\gamma_{t}$ = 10 KN/m³, $\gamma_{b}$ = 13.5 KN/m³, q = 10⁻⁵ KN/m² and B = 2 m. Table 9 and Fig. 13 show the values of N _γ and q _u for smooth strip footing for different H/B. When the thickness of the top layer is constant in the case of layered soil, and if the bottom layer is stronger than the top layer, the N _γ values increase as the internal friction angle of the bottom layer increases.

Table 9 The value of N _γ for layered soil ($\varphi_{t}$ = 30, $\varphi_{b}$ = 35)

Fig. 13

$N_{\gamma }$ values versus the ratio of H/B

Table 10 shows the effective depth values (X) for different H/B ratios.

Table 10 Effective depth factor (X) versus the thickness of the top layer to the width of footing (B = 2 m)

The drawing in Fig. 14 is based on Table 10, illustrating the effective depth factors (X) versus top layer thickness (H)/width of the trip footing (B).

Fig. 14

Effective depth factor (X) versus (H/B)

The effective depth of sandy-layered soils ($\varphi_{t}$ = 30 and $\varphi_{b}$ = 35) is given by the following equation:

$$X = - 0.268 \times \left( {\frac{H}{B}} \right) + 0.96\;\;\;\frac{H}{B} \le 0.757.$$

(17)

5.2 Computation of N _q

To isolate the N _q term, a weightless and cohesionless soil was considered as the bearing capacity obtained solely from a uniform surface surcharge (q). The bearing capacity is given by:

$$q_{u} = q \times N_{q} \;,\;{\text{where}}\;N_{q} = f\left( {\varphi_{t} ,\varphi_{b} ,\frac{H}{B}} \right).$$

(18)

It is proper to fix c _t  = c _b  = 0, γ _t  = 10 KN/m³, γ _b  = 13.5 KN/m³, B = 2 m, H/B = 0.3 and q = 10 KN/m². The BCTL N _q values are shown in Tables 11, 12 and 13 and Fig. 15. The internal friction angle of the bottom layer ($\varphi_{b}$) increases by one-degree steps.

Table 11 N_q values, $\varphi_{t}$ = 25

Table 12 N_q values, $\varphi_{t}$ = 30

Table 13 N_q values, $\varphi_{t}$ = 35

Fig. 15

N _q values

6 Conclusions

In this paper, a new algorithm is proposed to better calculate the bearing capacity of smooth strip foundations located on two-layered sandy soils using the stress characteristic lines method. Numerical and experimental examples, including Verma [17], are analyzed to validate the proposed algorithm.

Two cases were considered for this study, in which the top sandy layer was either stronger or weaker than the bottom layer. The following conclusions were made:

• 1. When the top layer is weaker than the bottom one, an effective depth for the top layer is formed. If it is less than its actual depth, the top layer controls the bearing capacity and behaves as a homogenous layer. In the case of $\varphi_{t}$ = 30, $\varphi_{b}$ = 35 and $\left( {\frac{H}{B}} \right)_{cr} = 0.76.$.

• 2. As long as the depth of the top layer does not exceed its effective depth, the bearing capacity factors increase with the friction angle of the bottom layer.

• 3. When the top layer is stronger than the bottom layer, increasing the depth of the top layer increases the bearing capacity factors of the two-layered soil.

• 4. An equation for the initial estimation of the effective depth was developed based on the obtained results.