1 Introduction

The real-world complicated problems due to nonlinear constraints, interdependencies among variables and large solution spaces need to be optimized using capable techniques. Optimization, as a core component in problem solving, refers to find the best value of a set of variables for an objective function subject to a given set of constraints. The performances, benefits and great successes of such processes have widely been notified in the literature [10, 22, 48].

A design problem in rock engineering using uniaxial compressive strength (UCS) and elasticity modulus (E) usually involves many parameters of which some are highly sensitive. These two strength index properties of rocks have significantly been quoted in design approaches of civil, mining and construction engineering-oriented applications (e.g., tunneling, dam design, rock blasting, slope stability, rock mass classification, rock failure criteria, foundation engineering, underground excavation). Concerning approved and recognized difficulties in direct measurements of these parameters in both economical aspects and significant technical challenges in weak or highly weathered rocks [2, 4, 14, 16, 31, 37], producing optimized models that can provide more accurate results is demanded. From a practical perspective, a variety of predictive models for UCS and E have widely been highlighted using simpler indirect test methods through different statistical and multivariate techniques [4, 27, 37, 38, 40, 51, 55]. However, the accuracy of such empirical relations due to the large variability of rock properties cannot be generalized. Furthermore, the drawbacks of statistical techniques in the effectiveness of auxiliary factors (e.g., porosity, mineralogy and mineral composition, density and weathering degree), uncertainty of experimental tests as well as inaccurate prediction in a wide expanded range of data should be considered [1, 39, 41]. In recent years, such limitations in producing predictive models tremendously have been recuperated using different artificial intelligence techniques [2, 14, 20, 46]. Table 1 shows a brief summary of immense successes in producing more efficient predictive models for both UCS and E in rock engineering.

Table 1 Summary of some recently used techniques to predict UCS and E
Full size table

Further, it was approved that incorporated ANN-based models with metaheuristic algorithms can lead to remarkable progress in predictability level [2, 14, 29]. The metaheuristic algorithms as a subcategory of optimization processes have extensively been grown through the last two decades and outlined considerable popularity in a wide range of practical engineering applications, finance, planning, scheduling and designing [6, 18, 26, 28, 50]. These state-of-the-art algorithms have been drawn from various nature-inspired sources and aim to improve fitness function. Imperialistic competitive algorithm [12], firefly [53], gray wolf optimizer [36], ant colony [21], honey beam [42], particle swarm optimization [33], artificial bee colony [32] and simulated annealing [34] are some of these metaheuristics that have actively been incorporated with artificial intelligence models for a variety of engineering tasks. Efficiency, flexibility and model independent are some of the main substantial features of these algorithms [6, 14, 17, 54]. The performance of such algorithms not only takes relatively much less time than traditional optimization techniques but also provides appropriate accomplishments when the learning rule is not efficient or fails to deliver satisfactory results [17]. However, they cannot guarantee that the best solution found after termination criteria is satisfied or indeed its global optimal solution to the problem [2, 14, 26, 54].

Among these optimization methods, the imperialist competitive algorithm (ICA) is one of the recently developed metaheuristics inspired by socio-political behaviors [12]. This global search population-based algorithm is a component of swarm intelligence technique which can provide an evolutionary computation without the requirement to the gradient of the function in its optimization process.

The UCS and E almost are predicted using localized data in terms of single objective models. This implies that developing a multi-objective model that can provide acceptable accuracy is greatly of interest. Furthermore, the approved performance of metaheuristics in different sizes of the search spaces motives for optimizing such multi-objective models in rock engineering problems. Comparing with the previous studies, this paper presents a robust automated hybrid multi-objective model, where the strength index properties were predicted through an optimum generalized feedforward network (GFFN) incorporated with ICA. Replacing the GFFN instead of the usual multilayer perceptron to increase the computability of the model and machine-driven tuned optimal internal parameters which yield the best performance are the main features of this study. The models were managed using 208 datasets corresponding to different physical and mechanical parameters (porosity, n; density, γ; water absorption, w; rock class, point load index, Is; and P-wave velocity, Vp) from almost all over quarry locations of Iran. It was observed that the classification error in GFFN for UCS and E from 19.1% and 23.8% was significantly decreased to 14.3% and 16.7% in ICA-GFFN. The assessed performance showed that the developed hybrid ICA-GFFN as a feasible tool can effectively be applied to provide more precise results than GFFN. Two different sensitivity analyses were applied to identify the most and least effective parameters on predicted UCS and E.

The remainder of this paper is organized as follows. A summary of ICA is presented in Sect. 2. The study is turned toward the modeling procedure, applied datasets and hybridizing layout in Sect. 3. Discussion, validation and analysis of the obtained results then were placed in Sect. 4. The summary of remarkable findings then was outlined in conclusions.

2 The process of ICA

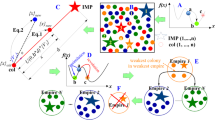
ICA is a recently developed evolutionary and robust optimization algorithm inspired by imperialist competitiveness based on the extending policy for the power and rule of a government beyond its own borders [12]. This algorithm mathematically is configured using a series of parameters including number of country (Ncou), number of imperialist (Nimp), number of decades (Ndec), number of colonies (Ncol), direction of moved colony toward the imperialist (β), deviation parameter (θ), arbitrary parameter describing the search condition (φ) and effective factor on the total power of empire (ζ). As presented in Table 2, the initial guess of these parameters can be set using previous studies [5, 8, 12,13,14, 29].

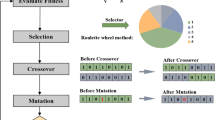
Table 2 The range of used ICA parameters in previous studies
Full size table

More insights about the organized formula can be found in [12,13,14, 29]. Here, only a brief description about the theoretical concept is presented. This algorithm can be divided into eight essential steps including generating the initial empires, moving the colonies of an empire toward the imperialist, revolution, exchanging positions of the imperialist and colony, total power of an empire, imperialistic competition, elimination of empires and convergence. To start the ICA, the country and cost function should be defined. Among the initial generated population (Ncou), those with minimum cost are selected to be imperialists and the rest play the role of colonies (Ncol). Then, the imperialistic empires begin to compete with each other to attract more colonies. Therefore, the colonies are moved toward an imperialist peak or new minimum area (assimilation process) to improve their situations and find better solutions. The movement process of colonies due to partially absorbed colonies can have a direct or deviated path toward the imperialist. The position of trapped colonies is then excited by sudden random changes using the revolution process to escape from possible local optimum in the search space. The performance of revolution can be compared with a mutation in the genetic algorithm in preventing the early convergence to local optima [29]. Hence, if the new position of the colony possesses a lower cost function than the imperialist, the position of imperialist and colony will be exchanged. The more empire power, the more attracted colonies; thus, the weakest empire because of losing colonies is gradually collapsed and eliminated. This implies that all the countries then should be converged to only one robust empire in the domain of the problem as the desired solution.

Accordingly, the competition process among the empires represents the possession probability of each empire (pn) based on its total power and is calculated using normalized total cost of empire as follows:

$$p_{n} = \left| {\frac{{NTC_{n} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{\text{imp}} }} NTC_{i} }}} \right|;\; \mathop \sum \limits_{i = 1}^{{N_{\text{imp}} }} p_{i} = 1$$
(1)

where TCn and NTCn denote the total and normalized cost of the nth empire.

The distribution mechanism of ICA is the probability density function (PDF) which compared to a genetic algorithm requires less computation effort.

3 Overview of applied model

3.1 Summary on GFFN

The multilayer perceptrons (MLPs) as the main core of feedforward networks have widely been updated during the last decades. These structures are trained slowly but easy to use and can approximate any input/output map subjected to different internal characteristics. The GFFN is configured by replacing the perceptrons of the hidden layer in MLPs with the generalized shunting inhibitory neurons (GSN) (Fig. 1). This organization provides a subcategory of MLPs that is an extended form of the shunting inhibitory artificial neural networks (SIANNs) [19, 30]. The output of the jth neuron in the hidden layer (Oj) using a set of adaptive weights (wi,j and wjk) subjected to nonlinear activation functions (f and g) are expressed as follows:

$$O_{j} = \frac{{b_{j} + f(\mathop \sum \nolimits_{i} w_{ij} x_{i} + w_{jk} )}}{{a_{j} + g(\mathop \sum \nolimits_{i} c_{ij} x_{i} + c_{jk} )}}$$
(2)

where xi is the ith input; cji is the “shunting inhibitory” connection weight from input i to neuron j and wij denotes the connection weight from input i to neuron j. wj0 and cj0 are bias constants, and aj is a positive constant that represents the passive decay rate of the neuron where bj is the output bias. f and g are activation functions, respectively.

Fig. 1
figure 1

The mathematical model of GSN in data processing

Full size image

This reveals that the GSNs perform the nonlinear transformation on input datasets to speed up the training procedure and enhance the computability level to save the required memory. It also facilitates more freedom to select optimum topology and provides higher resolution in complex nonlinear decision classifiers [3, 11, 14, 24, 30]. Jumping over one or more layers is another characteristic of the GSN which allows neurons to operate as adaptive nonlinear filters [1, 11, 14, 24, 30]. Such ability in this classifier provides greater flexibility and more efficient performance than MLP in the same number of neurons [1, 11, 14]. The number of neurons in hidden layers and corresponding arrangements, activation function, learning rate and training algorithm are the main internal characteristics components which should be set to produce an optimum structure [1, 14, 15, 24]. The network error (E) of the kth output neuron and corresponding root mean square error (RMSE) is defined using the actual and predicted values (xk and yk) as follows:

$$E = \frac{1}{2}\mathop \sum \limits_{i = 1}^{n} \left( {x_{k} - y_{k} } \right)^{2} \to RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{k} - y_{k} } \right)^{2} }}{n}}$$
(3)

To reduce the error between the desired and actual outputs, the weights are optimized using an updating procedure for the (n + 1)th pattern subjected to

$$\Delta w_{ik} = - \eta \frac{\partial E\left( W \right)}{{\partial w_{ik} }}$$
(4)
$$w_{ik} \left( {n + 1} \right) = w_{ik} \left( n \right) + \nabla w_{ik} \left( n \right)$$
(5)

where η is the learning rate.

3.2 Organized datacenter

In the current study, a number of 208 datasets comprising the rock class, point load index (Is), P-wave velocity (VP), porosity (n), water absorption (w) and density (γ) from 47 quarry locations in Iran were acquired and compiled (Table 3). These datasets are the updated version of [14] with a greater number of instances containing both UCS and E. A sample of gathered datasets and executed simple descriptive statistical analyses are presented in Tables 4 and 5. The rock classes including sedimentary, igneous, digenetic and metamorphic were assigned and coded from 1 to 4, respectively.

Table 3 The specification of acquired datasets
Full size table
Table 4 A brief presentation of compiled datasets
Full size table
Table 5 Descriptive statistics of acquired datasets
Full size table

Different strategies for randomization are used in optimization to alleviate the computational burden associated with robust control techniques. In this paper, the randomized data split into three sets for training, testing and validation was used. Comparing the K-fold cross-validation, elimination of the selection bias, balancing the groups with respect to uncertainties, and the statistical tests are the basic benefits of randomized data. The K-fold cross-validation always requires to be checked for stable performance over all the folds. Furthermore, insufficiently distributed data in the folds or significant differences from others provide instability in model performance. Such discrepancies then should be removed using some other different cross-validation methods. Trusting just to final aggregated score for the R2 will miss a lot of information about models’ performance. The compiled components were then randomized by 55%, 25% and 20% to provide training, testing and validation sets. Further, the datasets due to different units were normalized within the range of [0, 1] using:

$${\text{Norm}}\;{\text{scaled}}\;{\text{value}} = \frac{{x - x_{\hbox{min} } }}{{x_{\hbox{max} } - x_{\hbox{min} } }}$$
(6)

This procedure provides dimensionless input data which are necessary to improve the learning speed and model stability.

3.3 Assessment of optimum hybrid model

Combining a developed optimum GFFN with ICA is the overview of the hybridized layout in this study. An optimum network structure needs to be managed through internal characteristics, where there is no unified accepted method for such critical arrangements [1, 24]. Therefore, to decrease the complexities, it is advised to make the internal characteristics as few as possible [57]. However, there is no guarantee that can capture all possible alternatives for optimal solutions. In the current study, this drawback was covered using an automated iterative trial–error integrated with the constructive technique. Referring to Fig. 2a, the optimum GFFN model was captured by examining different training algorithms and activation functions. This strategy in addition to monitored error improvements was applied to escape from local minima, early convergence and prevent the overfitting problem. Quick propagation (QP), conjugate gradient descent (CGD), momentum (MO), quasi-Newton (QN) and Levenberg–Marquardt (L–M) were implemented as training algorithms. Logistic (Log), hyperbolic tangent (HyT), linear (Lin) and squash (Sq) were also used as activation transfer functions for hidden and output layers. The value of 0.7 for the learning rate was set for all implemented algorithms and the step sizes of hidden layers were changed in the domain of [1.0–0.001]. Furthermore, the sum of squares and cross-entropy were also employed as output error function, respectively. Following the embedded loops (1 and 2) in Fig. 2a, the number of neurons is a user-defined parameter that can frequently be increased to evaluate a wide range of topologies subjected to different training algorithms and activation functions. The root mean square error (RMSE) and iteration number were organized as termination criteria. If the RMSE is not achieved, then the number of iteration (in this study set for 1000) as the second stopping metric is implemented.

Fig. 2
figure 2

Simplified diagram of optimizing process for a GFFN and b hybrid ICA-GFFN in this study

Full size image

This implies on wide ranges of monitored topologies (> 860) even with similar architecture but various internal characteristics (e.g., number of neurons, layer arrangements, training algorithm, activation functions) that was run three times to control whether the stopping criteria are satisfied (Table 6). Accordingly, the RMSE and the network correlation (R2) of each tested structure were calculated. As an example of executed effort, the variation of calculated RMSE based on the number of neurons as well as some of the tested topologies with different layer arrangements subjected to HyT activation transfer function is presented in Fig. 3a, b. The minimum RMSE for optimum GFNN architecture was observed in number of neurons 12 correspond to 6-7-5-2 topology (Fig. 3b). The performance of the optimum model then is assessed using different accuracy criteria and statistical error indices.

Table 6 Implemented training algorithms and characteristics of corresponding optimum GFFN model
Full size table
Fig. 3
figure 3

a Variation of network RMSE using different training algorithms against the number of neurons subjected to HyT activation functions and b a series of examined structures with 12 neurons

Full size image

To improve the predictability level of the developed optimum GFFN model, the procedure of Fig. 2a was incorporated into ICA. This metaheuristic algorithm by adjusting the weights and biases can minimize the error of optimum GFFN. However, for an appropriate optimizing process, the effective ICA parameters (Table 2) should properly be selected. These parameters can be determined using previous studies [5, 8, 12,13,14, 29]. Here, for β, θ and ζ, the values 2, π/4 and 0.02 were considered. The proper Ncou was specified through the analyzed R2 and minimum RMSE of 12 trained hybrid models using the introduced GFFN structure (Table 7). By applying a similar process, the monitored approximate boundary for low variation of RMSE against the Ncou was characterized as the optimum Ndec (Fig. 4). The Nimp similarly was determined through the calculated R2 and RMSE of ICA-GFFN models (Table 8). To provide the output, the hybrid ICA-GFFN model then was trained using the optimized GFFN structure (6-7-5-2) but subjected to ascertained ICA parameters (Table 9). To assess the capacity of the network performance and evaluate the predictability level, the results of randomized training and testing datasets are reflected in Fig. 5a–d. The monitoring of error improvement for models was also carried out to control the overfitting and trapping in local minima (Fig. 5e). This criterion refers to network performance predictability during the last and/or each iteration and, consequently, can detect the situation when the network is not improving, and further training is unavailing.

Table 7 Characterizing the Ncou among the trained models
Full size table
Fig. 4
figure 4

Performance of ICA-GFFN models using different Ncou to find the optimum Ndec

Full size image
Table 8 Determination of Nimp using both training and testing datasets
Full size table
Table 9 Handled parameters for optimization process in this study
Full size table
Fig. 5
figure 5

Predictability of optimum GFFN and hybrid ICA-GFFN models for a and c E and b, d UCS using randomized training and testing datasets as well as e error improvement of applied models

Full size image

4 Validation and discussion

Model evaluation as an important part of a data science project is utilized to quantify the improved facilities regarding previous versions. The confusion matrix as a compact representation of the model performance is the source of many scoring metrics for classification tasks [45]. Moreover, it is a benefit to identify the system confusing for different classes. The confusion matrixes of GFFN, ICA-GFFN and conducted multivariate regression (MVR) models (Eqs. 7–10) for randomized datasets were calculated. A sample of carried out efforts for hybrid ICA-GFFN using validation datasets is presented in Table 10.

Table 10 Confusion matrix of ICA-GFFN model for UCS and E
Full size table
$$UCS = - 124.97 + 3.54\left( {rock clss} \right) + 44.4\gamma - 0.49n + 0.18w + 6.75V_{P} + 7.65I_{{S\left( {50} \right) }} R^{2} = 0.67$$
(7)
$$E = - 47.5 + 0.79\left( {rock\;clss} \right) + 9.93\gamma + 0.02n + 0.91w + 1.99V_{P} + 5.06I_{{S\left( {50} \right)}} \quad R^{2} = 0.60$$
(8)
$$UCS = 2.004\;rock class^{0.305} \gamma^{0.268} n^{ - 0.093} w^{0.062} V_{P}^{1.406} I_{{S\left( {50} \right)}}^{0.524} \quad R^{2} = 0.54$$
(9)
$$E = 0.194\;rock class^{0.574} \gamma^{1.615} n^{ - 0.096} w^{0.925} V_{P}^{0.53} I_{{S\left( {50} \right)}}^{1.003} \quad R^{2} = 0.49$$
(10)

Accordingly, the calculated correct classification rate (CCR) and classification error (CE) and then the improvement progress of all models were compared, and the results are presented in Tables 11 and 12, respectively. Further, the accuracy performance of all models was pursued and cross-examined using known statistical error indices, respectively (Table 12). Mean absolute percentage error (MAPE) is one of the most popular indexes for a description of the accuracy and size of the forecasting error. The performance of the model can be evaluated using variance account for (VAF) as an intrinsically connected index between predicted and actual values. The generic index of agreement (IA) [49] indicates the compatibility of modeled and observations. The formulation of these indices can widely be found in statistical textbooks. Higher values of VAF, IA and R2 as well as smaller values of MAPE and RMSE exhibit better model performance (Table 12).

Table 11 Compared CCR and CE of the models for validation and test datasets
Full size table
Table 12 Improvement of progresses for the applied models
Full size table

The precision-recall curve as a useful tool to measure the success of prediction can reflect the relevant and corresponding number of truly turned results (Precision) as well as show the tradeoff between them for different thresholds (recall). Therefore, both high precision and recall express an ideal performance which returns many results and all are labeled correctly. The high precision shows a low false-positive rate while high recall refers to a low false-negative rate. Thereby, a large area under the curve is connected to both high recall and precision returning accurate as well as the majority of all positive results. High recall but low precision returns many data but most of predictions comparing to training are labeled incorrect and vice versa in high precision but low recall. In Fig. 6, the precision-recall curves for GFFN, ICA-GFFN and generated multivariate regressions (MVR) using the same randomized datasets are presented.

Fig. 6
figure 6

Comparing the area under computed precision-recall curves for MVR, GFNN and ICA-GFFN

Full size image

The robustness and performance capacity of sensitivity analyses in the presence of uncertainty for the purpose of model calibration, determining the importance of inputs and enhancing the predictability of a system has been approved [2, 15, 43]. This also implies that removing the least effective inputs may lead to the development of better results [25]. Here, the effectiveness of input parameters on predicted outputs using two sensitivity analyses methods known as the Cosine amplitude and partial derivative (PaD) [15, 25] according to Eqs. 11 and 12 is identified and reflected in Fig. 7.

$$R_{ij} = \frac{{\mathop \sum \nolimits_{k = 1}^{m} \left( {x_{ik} \times x_{jk} } \right)}}{{\sqrt {\mathop \sum \nolimits_{k = 1}^{m} x_{ik}^{2} \mathop \sum \nolimits_{k = 1}^{m} x_{jk}^{2} } }}, x_{i} \;{\text{and}}\;x_{j} :{\text{elements}}\;{\text{of}}\;{\text{data}}\;{\text{pairs}}$$
(11)
$${\text{contribution}} \;{\text{of}} \;i{\text{th}}\;{\text{variable}} = \frac{{SSD_{i} }}{{\mathop \sum \nolimits_{i} SSD_{i} }};\;SSD_{i} = \mathop \sum \limits_{p} \left( {\frac{{\partial O_{k}^{p} }}{{\partial x_{i}^{p} }}} \right)^{2}$$
(12)

where O pk and x pi are the output and input values for pattern P, and SSDi is the sum of the squares of the partial derivatives.

Fig. 7
figure 7

Influence of input parameters on predicted UCS and E using different sensitivity analyses

Full size image

5 Conclusion

A new efficient multi-objective GFFN model using an iterative trial and error procedure integrated with the constructive technique was proposed and applied on a comprehensive dataset of building stones of Iran to predict the UCS and E. Comparison of numerous structures subjected to different internal characteristics that showed a four-layer GFFN model with 6-7-5-2 topology (12 neurons in two hidden layers) can be selected as the optimum. The predictability of the introduced GFFN model then successfully with at least 8% improvement progress was optimized using ICA. According to established confusion matrixes, the correct classification rate of UCS and E from 52.3% and 45.2% in MVR models increased to 85.7% and 83.3% in hybrid ICA-GFFN. Furthermore, the GFFN and hybrid ICA-GFFN with at least a 24% improvement in progress showed the superior capability to MVR models. The compared areas under precision-recall curves show that incorporating with ICA provides 80.2% accuracy in the prediction process. This implies that proposed ICA-GFFN as a viable tool for optimizing multi-objective problems decreases the classification errors which can be interpreted as more precious results. Accordingly, the models were evaluated using statistical criteria where the ICA-GFFN with 6.14, 0.178, 95.80 and 0.96 for UCS and 7.22, 0.241, 91.55 and 0.95 for E corresponding to MAPE, RMSE, VAF and R2 reflected better performance capacities than GFFN. The calculated IA index (0.90 for UCS and 0.88 for E) was another supplementary indicator that showed that the ICA-GFFN model produces closer predicted values to observations. The implemented sensitivity analyses showed that Is, VP and n are the most effective factors on predicted UCS and E values. The result of sensitivity analyses can also be interpreted as the appropriate trend with previous empirical correlations which mostly have been established by these three factors and thus the obtained MVR correlations in this paper also can be calibrated with these effective factors.