1 Introduction

During the recent decade, investigating the bearing capacity of multilayered soils using novel mathematical solutions has attracted appreciable attention in the field of geotechnical engineering. In this sense, various analytical and experimental methods are developed to compute the bearing capacity of different soils (or reinforced concrete) [1, 2]. These models are based on limit equilibrium theories and small-scale modelling, respectively. Terzaghi et al. [3], for instance, presented a model assuming the unique bearing capacity for soils even for the multi-layered soils. The homogeneous soil layers and natural soils deposited in stratums are scarcely observed in nature. Due to different strength parameters as well as soil stiffness in each layer of soil, some differences should be considered in exploring the ultimate bearing capacity of a single soil layer and a multi-layer one. About the small-scale laboratory modellings, achieving a reliable model for calculating the bearing capacity of the multilayered soils is not viable, because of some shortcomings associated with such methods.

Nowadays, investigating the concept of the bearing capacity of footings comprises a vast literature. Plenty of experimental and analytical works have been carried out to focus on better understanding the layered soils. It can be said that the main aim of these researches lies in achieving the most reliable solutions in such conditions. Among those, the numerical methods such as Frydman and Burd [4] and Silvestri [5] examined the bearing capacity of strip foundations rested on the sand by performing limit equilibrium approaches. In research by Lotfizadeh and Kamalian [6], the bearing capacity of conventional strip footings was estimated through a numerical simulation (i.e., by the characteristic lines method) when it is installed on layered sandy soil. The main findings of their research was a good algorithm developed for predicting the strip foundation’s bearing capacity placed on double-layered soils.

Moreover, analytical approaches consist of slip line [7], limit analysis [8], and limit equilibrium [9]. In the mentioned analysis, a new parameter, namely the modified friction angle (ψ′), was used. Note that, ψ′ is obtained based on apparent friction angle (φ) coupled with dilatancy angle (ψ) of the sand. Then, they considered the friction angle (i.e., in a practical range) to calculated bearing capacity factors of Nq and Nγ. Finally, the obtained results were compared with the results of previous works. It was shown that the results are adequate. Ghazavi and Eghbali [10] successfully used an analytical approach based on the limit equilibrium method for calculating the ultimate bearing capacity of a shallow footing rested on layered (two layers) sandy soil.

A laboratory study conducted by Keskin and Laman [11] investigated the bearing capacity of a shallow strip foundation located near a sandy soil slope. Five critical factors, including the relative density of sand, slope angle, setback distance of the proposed footing from the sloping margin, and footing width, were taken to influence the ultimate bearing capacity of the foundations. Comparing the real and obtained results indicated a good agreement between them in terms of load-settlement and the overall trend of behaviour. Additionally, some finite element methods were executed on a prototype slope to support the reliability of the experimental findings. According to the results, the magnitude of the proposed variable (i.e., the ultimate bearing capacity) is directly proportional to the relative density of sand, footing width, and setback distance, and also is adversely proportional to the slope angle.

Moreover, various intelligent approaches have been widely used to simulate the bearing capacity of soils (and rocks and reinforced concrete) under different conditions [12,13,14,15]. Moayedi and Hayati [16] employed feedforward neural network (FFNN), general regression neural network (GRNN), radial basis neural network (RBNN), support vector machine (SVM), adaptive neuro-fuzzy inference system (ANFIS), and tree regression fitting model (TREE) for evaluating the bearing capacity of shallow strip footing on a homogeneous sandy slope. The computed correlation values of 0.9233 and 0.9095, respectively, in the training and testing phases, revealed the superiority of the FFNN model.

As mentioned, typical predictive models have been successfully used for analyzing the bearing capacity of various footings. This is a while, few studies have focused on achieving a more successful prediction by applying the optimization techniques [17,18,19,20,21] which can be considered as a gap of knowledge in this field. Hence, looking for more reliable prediction of bearing capacity, the main objective of the current research is to enhance the efficiency of two popular artificial intelligence tools, namely artificial neural network and adaptive neuro-fuzzy inference system for analyzing the bearing capacity using biogeography-based optimization algorithm. It should be noted that according to the best knowledge of the authors, the used evolutionary technique has not been hired before for this aim. Another novelty of this work lies in establishing a classification model instead of direct estimation of the settlement of the proposed footing. The results are evaluated in several ways, and the efficiency of the BBO algorithm on optimizing the performance of the mentioned models is discussed.

2 Evolutionally prediction algorithms

2.1 Conventional biogeography-based optimization

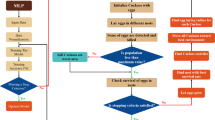
The name biogeography-based optimisation (BBO) [22] implies a natural-inspired search algorithm that follows the biogeography science for optimisation. This model explores the distribution of different species over time and space [22]. Figure 1 shows the general flowchart of the BBO algorithm. Similar to other existing optimization techniques, it is a population-based method. Similar to particles in particle swarm optimization (PSO) and chromosomes in the genetic algorithm (GA), some so-called individuals “habitat” is the possible solutions of the BBO.

Fig. 1
figure 1

The flowchart of the BBO classification algorithm

Full size image

Consequently, a habitat suitability index (HSI) is defined to evaluate the goodness of each. In his sense, high-HSIs represent a promising solution, and a poor one is demonstrated by low-HIS values. Through an immigration process, the attributes of a solution emigrate from a high-HIS to low-HIS ones. In this way, two operators, namely, emigration and immigration, perform to enhance a solution to the defined problem. Optimization of a problem is a repetitive process and entails defining an objective function (OF). An error criterion (e.g., mean square error) is usually specified for this aim. Generally, it is expected that this process decreases the values of the OF in each iteration. Finally, the habitat which reaches the lowest OF is considered as the solution to the problem. In the case of artificial intelligence techniques (e.g., artificial neural network and fuzzy-based tools), the BBO aims to find the optimal values of their computational parameters [16]. Finally, the obtained optimal values are used to reconstruct the proposed model.

2.2 Artificial neural network

Artificial neural networks (ANNs) are known as one of the most capable predictive models which were theoretically introduced by [23]. These models have been extensively used in many studies [24,25,26,27,28,29,30]. Among different types of ANNs, the multi-layer perceptron is one of the most commonly used tools which distinguishes its self by three types of layer [16, 31,32,33,34,35,36]. Each layer contains some computational units called neurons. In the first stage of the training, the data are received by input neurons, and they perform to release the output to the next layer (i.e., hidden layer). After completing the neurons lied in this layer, the final output is produced from the last layer (output layer). The analytical performance of the MLP for a layer with M neurons is described as follows:

$$O_{j} = F \left( { \mathop \sum \limits_{m = 1}^{M} (IW) + b_{j } } \right).$$
(1)

In which, I shows the input vector, W and b denote particular weight and bias term of the proposed neuron. In addition, F symbolises the activation function.

2.3 An adaptive neuro-fuzzy inference system

Incorporating the neural learning capability of ANNs with fuzzy inference system (FIS), Jang [37] introduced an adaptive neuro-fuzzy inference system (ANFIS). The ANN aims to make a more flexible FIS in this model. The ANFIS has been extensively used for many engineering works [38]. The performance of ANFIS comprises five steps which are performed in five layers. In this way,

Every node in layer 1 contains adaptive nodes as:

$$O_{1,i} = \mu A_{i} (x)$$
(2)
$$O_{1,i} = \mu B_{i} (y)$$
(3)

where \(x\,\,\,{\text{and}}\,\,y\) are the input nodes, \(A\,\,{\text{and}}\,\,B\) are the linguistic variables, and \(\mu A_{i} (x)\,\,\,{\text{and}}\,\,\,\mu B_{i} (y)\) represent the membership functions of the proposed node.

In layer 2, the output of each node is calculated as follows:

$$O_{2,i} = W_{i} = \mu A_{i} (x)\mu B_{i} (y),\quad i = 1,2$$
(4)

where \(W_{i}\) is the response of each node.

The normalized outputs of layer 2 are the nodes of the next layer:

$$O_{3,i} = \bar{w}_{l} = \left[ {\frac{{w_{i} }}{{w_{1} + w_{2} }}} \right],\quad i = 1,2$$
(5)

For the layer number 4, a node function is applied as follows:

$$O_{4,i} = \bar{w}_{l} f_{i} = \bar{w}_{l} \left( {p_{i} x + q_{i} y + r_{i} } \right)$$
(6)

in which \(\bar{w}_{l}\) represents the normalised firepower of the previous layer, \(p_{i} ,q_{i} ,\,\,{\text{and}}\,\,\,r_{i}\) are the specific result parameters.

The overall response of the ANFIS is obtained in layer five from the summation of all input signals:

$$O_{5,i} = \sum \bar{w}_{l} f_{i} = \frac{{\sum w_{i} f_{i} }}{{\sum w_{i} }},\quad i = 1,2$$
(7)

3 Data collection and methodology

The required database was collected from a series of finite element-based simulation of shallow footing (e.g., a total of 901 simulations) located on double layered soil with different properties. The foundation is analyzed by assuming 2D axisymmetric conditions. Both the footing and soil are modelled by 15-node triangular elements with the Mohr–Coulomb (MC) as the material model. The finite element simulation was undertaken to provide the measured result database. For the intelligent simulation of this study, the settlement (Uy (m)) was considered as the target variable influenced by seven conditioning factors. The obtained Uy varied from 0 to 0.10. Therefore, the values of less than 0.05 were considered to indicate the failure (shown by 1). Likewise, the values more than 0.05 were considered to indicate stability (confirmed by 0). In the next step, regarding the famous ratio of 80:20%, the dataset was divided into the training (i.e., 721 samples) and testing (i.e., 180 samples) parts for developing and evaluating the proposed models. The small portion of the data set provided for the training from the numerical simulation is tabulated in Table 1.

Table 1 The small portion of the data set provided for the training
Full size table

4 Results and discussion

The main aim of this research is to present a suitable optimization of ANN and ANFIS predictive models for analyzing the bearing capacity of a two-layered soil with different properties. To this end, a total of 901 finite element-based simulations of shallow footing located on double layered soil were done. Seven factors consisting of elastic modulus, applied stress, friction angle, setback distance, dilation angle, unit weight, Poisson’s ratio, were considered as the settlement essential parameters. The dataset was randomly divided into two parts, with 80% for the training and 20% for the testing phases. For changing into a classification problem, regarding the obtained settlements, the target variable was presented in two situations of “Stable” and “Failed”.

4.1 Optimizing the models using conventional BBO

After providing and pre-processing the required data, the biogeography-based optimization technique was combined with ANFIS and MLP to improve their performance. Note that, the programming language of MATLAB was used for coding the proposed BBO–MLP and BBO–FIS ensembles. Remarkably, based on the author’s experience as well as a trial and error process, five hidden neurons and 7 clusters were selected for constructing the MLP and ANFIS, respectively. As explained, in the case of artificial intelligence models, any optimization algorithm enhances their performance through finding the optimal values for computational parameters, i.e., weights and biases in MLP and parameters if membership functions in ANFIS. It is also well established that other than the appropriate population size, these ensembles need enough repetitions to achieve an acceptable result. With this in mind, both BBO–MLP and BBO–FIS were tested with six population sizes, including 5, 15, 30, 50, 75, and 100, within 1000 repetitions. The error criterion of mean square error (MSE) was defined as the objective function in this study. Besides, this criterion, as well as a mean absolute error (MAE), were used to evaluate the performance of the implemented techniques. The following equations denote the MSE and MAE, respectively

$${\text{MSE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{{i_{\text{observed}} }} - Y_{{i_{\text{predicted}} }} } \right)^{2}$$
(8)
$${\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{{i_{\text{observed}} }} - Y_{{i_{\text{predicted}} }} } \right)$$
(9)

in which N shows the number of involved instances, and Yi observed, and Yi predicted stand for the desired and estimated values of settlement, respectively.

The results of the convergence process are presented in Fig. 2a, b, respectively, for BBO–MLP and BBO–FIS. As is seen, all performed networks yield very close results. Accordingly, the BBO–MLP with population size = 50 and BBO–FIS with population size = 15 reached the lowest MSE. In overall, the FIS-based networks reach their best performance sooner in comparison with MLP-based systems. Hence, the convergence curves of the BBO–ANFIS are presented for the first 500 epochs. The classification results of the used models are evaluated and compared in the next part.

Fig. 2
figure 2

The results obtained for a, b MLP, c, d, FIS, e, f BBO–MLP, and g, h BBO–FIS prediction

Full size image

4.2 Evaluation of the BBO, BBO–MLP, and BBO–FIS

In this part, actual targets are compared with the estimated ones to evaluate the performance of the applied models. As explained supra, two possible values of 0 and 1 indicate the stability and failure of the proposed soil in this study. The performance error of the implemented MLP, FIS, BBO–MLP, and BBO–FIS, is measured using two well-known criteria, namely MSE and MAE. In addition, the receiver operating characteristic (ROC) curve is plotted for the results of each model. Remarkably, the area under this curve (AUROC) is an excellent representative of the accuracy of the prediction in diagnostic problems. This diagram shows a trade-off between the false-positive and false-negative rates for every likely cutoff. For plotting the ROC, false-positive rate (FPR) of the prediction results is drawn on the x-axis versus true-positive rate (TPR) on the y-axis. Let TN and FN be the true-negative and false-negative, respectively, the FPR and TPR parameters are defined as follows:

$${\text{TPR}} = \frac{\text{TP}}{{{\text{TP}} + {\text{FN}}}}$$
(10)
$${\text{FPR}} = 1 - \frac{\text{TN}}{{{\text{TN}} + {\text{FP}}}}$$
(11)

The graphical comparison between the actual and predicted response variable is presented in Fig. 2 alongside the corresponding ROC curves. From these charts, it is seen that the optimised versions of MLP and FIS tools have presented more consistent results, which represents an excellent efficiency for the used BBO algorithm.

Based on the calculated MSEs of 0.0563, 0.0581, 0.0499, and 0.0514, respectively, for the MLP, FIS, BBO–MLP, and BBO–FIS prediction, it can be deduced that applying the BBO algorithm is a right way for decreasing the prediction error. Although, referring to the obtained MAEs of 0.1283, 0.1223, 0.1164, and 0.1320, the calculated error of the improved FIS is slightly higher than the typical FIS, the calculated AUROCs support the results of the MSE. Accordingly, the prediction accuracy of the used FIS experienced a significant increase from 97.6 to 98.5%. Besides, more area covered by the ROC curve of the BBO–MLP (Accuracy = 98.4%) shows that this model presented a slightly better approximation compared to unreinforced MLP (Accuracy = 98.2%).

In the last part, a score-based ranking system is also developed to determine the most capable model of the study. In this way, a score is assigned to each model based on the prediction accuracy in terms of each one of MSE, MAE, and AUROC indices. Then, the summation of these scores equates a total ranking score (TRS), which determines the final ranks. The higher value of TRS, the more accuracy of the model. Table 2 summarizes the ranking results. In this sense, the BBO–FIS featured as the most successful model in terms of MSE and MAE, and the second accurate model in terms of AUROC.

Table 2 The ranking system developed based on the obtained accuracy criteria
Full size table

All in all, concerning the obtained TRSs of 6, 5, 11, and 8, respectively, for the MLP, FIS, BBO–MLP, and BBO–FIS, the MLP-based ensemble is introduced as the most reliable approach for analyzing the veering capacity of the considered multi-layered soil in this study. After that, the BBO–FIS outperformed MLP and FIS. In addition, comparing the typical MLP and FIS, the neural learning theory surpassed fuzzy learning.

5 Conclusions

Due to the crucial role of analyzing the bearing capacity of the soils in many civil engineering projects, this issue has attracted increasing attention. In the current study, we presented a novel optimization of ANN and ANFIS predictive models to estimate the settlement of a shallow footing located on a double layered soil with different properties. To this end, after providing a proper dataset form several FEM simulations, the biogeography-based optimization algorithm was synthesized with a multilayer perceptron neural network as well as a fuzzy inference system to improve their performance. After an extensive trial and error process, it was shown that the BBO–MLP with population size = 50 and BBO–FIS with population size = 15 reached the lowest objective function. Additionally, three accuracy indices, namely MSE, MAE, and AUROC, were defined to evaluate the results. In overall, based on the computed value of MSE (0.0563, 0.0581, 0.0499, and 0.0514, respectively, for the MLP, FIS, BBO–MLP, and BBO–FIS), MAE (0.1283, 0.1223, 0.1164, and 0.1320), and AUROC (0.982, 0.976, 0.984, and 0.985), it was revealed that applying the proposed BBO algorithm helps both MLP and FIS to enjoy more prediction accuracy compared to their unreinforced versions. Finally, referring to the developed ranking system, the BBO–MLP emerged as the most promising model, followed by BBO–FIS, MLP, and FIS.