1 Introduction

Ultimate bearing capacity has been defined as the value of maximum pressure that soil can support without occurring failure [1, 2]. Currently, the influences of the ultimate bearing capacity in the case of shallow strip footings have been highly considered by scholars in the field of geotechnical engineering design as a major issue. It is called a major problem, because is considered as the interface among soil and upper structures. There are different analytical procedures that are according to limit equilibrium theory [3]. In the literature, there are various solutions that can be widely used to predict and measure the bearing capacity parameter. In previous attempts, different analytical and experimental methods, including limit analysis [4], experimental methods [5], analytical methods [6], limit equilibrium [7], and numerical methods [8] have been proposed in the case of the footings’ bearing capacity set on the slope crest.

Natural soils that are deposited in layers of homogeneous soil are rarely discovered. The ultimate bearing capacity in the case of the multi-layer soil is not commonly treated such as a single layer of soil, since, for each layer, the soil stiffness and stability factors are distinct. Many scholars have focused on theories related to the bearing capacity for multi-layered soil. In this way, two cases which may be deemed as inhomogeneous sands layer are: (1) stronger soil that placed onto a layer of weaker soil and (2) weaker sand that placed onto a layer of solid soil [9]. The usual computational approaches commonly consider designing the ultimate bearing capacity or qult by Eqs. 1 and 2 that are suggested in Refs. [3, 10]:

$$q_{{{\text{ult-Terzaghi}}\,\left( { 1 9 4 3} \right)}} = c^{\prime}N_{c} + qN_{q} + \frac{1}{2}\gamma BN_{\gamma }$$
(1)
$$q_{{{\text{ult-Hasen}}\,\left({ 1 9 7 0} \right)}} = c^{\prime}N_{c} d_{c} S_{c} + q^{\prime}N_{q} d_{q} S_{q} + \frac{1}{2}\gamma BN_{\gamma } d_{\gamma } S_{\gamma }.$$
(2)

In above relations, \(N_{c}\), \(N_{q}\), and \(N_{\gamma }\) stand for the parameters of the bearing capacity that are based on the overburden pressure (q), the internal friction angle (\(\varphi\)), footing width (B), cohesion (\(c^{\prime}\)), and soil unit weight (\(\gamma\)).

Recently, various data mining models like artificial neural network (ANN) and fuzzy systems have been promisingly used to deal with geotechnical issue including bearing capacity [11,12,13,14,15]. In this regards, Maizir et al. [16] explained approaches of the finite element and also ANN for predicting the pile bearing capacity in the case of sandy soil. They used ANN models to predict the bearing capacity utilizing dynamic load test information, and compared the results of a finite-element approach with an empirical method. They found that finite-element and ANNs’ approaches have almost the same results for the ultimate load. In addition, they showed that axial bearing capacity of piles is entirely changeable. Likewise, Ziaee et al. [17] suggested a novel design equation about predicting the bearing capacity of shallow structures on rock masses by taking into account ANN model. They simulated the bearing capacity with considering internal friction angle about the rock mass, joint spacing ratio for basis width, rate of rock mass, and unindicated compressive rock strength. Moreover, they used general data sets of plate load, rock socket, footing load test in the large-scaled state, and centrifuge rock socket outcomes for expanding the model. The results of their research proved an appropriate efficiency of the derivative model to predict the bearing capacity of shallow bases. The suggested estimating relation is considerably more efficient compared to traditional relations. Lee and Lee [18] used error back propagation neural networks for estimating the ultimate bearing capacity about piles. They verified the applicability of the ANNs with outcomes of model pile load measurements and showed that the maximum difference between experimental and prediction data is around 25%. Moayedi and Hayati [19] showed the outcomes of various non-linear machine learning as well as soft computing-based algorithm [e.g., radial basis neural network (RBNN), support vector machine (SVM), regression fitting model (TREE), etc.]. They evaluated them by taking into account different statistical indices. After performing this task, the most precise algorithm was suggested for estimating the solution. They have also compared the estimated data with the FEM data and showed good validity for FFNN solutions.

Moreover, many scholars have employed evolutionary knowledge for enhancing the results of regular predictive models in many engineering problems [20,21,22,23,24,25,26]. Moayedi et al. [27] used different evolutionary algorithms such as differential evolution (DE) and genetic algorithm along with particle swarm optimization for optimizing machine learning models to estimate the ultimate bearing capacity in the case of shallow footing on multi-layered soil state. They stated that all optimized methods have a promising performance. However, the algorithm of PSO–ANN showed better performance than other methods. Likewise, Moayedi and Armaghani [28] have suggested and evaluated an ANN optimized with imperialism competitive algorithm (ICA) approach to predict the bearing capacity about driven pile into cohesionless soil. By means of various accuracy criteria and high validity, the expanded ICA-ANN algorithm was deduced, and they suggested it as a novel model about deep foundation engineering.

Although famous optimization techniques (e.g., PSO, ICA, GA, etc.) have been widely used to solve the problem of bearing capacity, utilizing and evaluating more-state-of-the-art colleague algorithms are considered as a gap of knowledge in this field. Hence, the pivotal objective of the current effort lies in presenting and evaluating two novel state-of-the-art hybrid techniques, namely Harris hawks optimization (HHO) and dragonfly algorithm (DA) for investigating the bearing capacity in the position of a classification issue. Notably, the literature survey (to the best knowledge of the authors) indicates that our proposed algorithms have not been previously used in the same field of study. Meanwhile, receiving operating characteristic (ROC) diagram is used to evaluate the classification accuracy of the models.

2 Methodology

2.1 Artificial neural network

Mimicking the interactions between the neurons in the biological neural network, the basic theory of artificial neural network (ANN) was first discussed by McCulloch and Pitts [29]. The most outstanding merit of this method is its capability for mapping the non-linear interactions between some dependent and independent parameters ASCE Task Committee [30]. Figure 1 shows a general structure of a widely used type of ANNs, namely multi-layer perceptron (MLP).

Fig. 1
figure 1

The structure of an MLP neural network

Full size image

In general, the MLP uses Levenberg–Marquardt (LM) [31, 32], which is a powerful approximation to Newton’s method [33]. In comparison with conventional gradient descent (GD) technique, the LM has shown higher robustness [34, 35]. More specifically, it aims to minimize the sum of squares function (V(x)) as follows:

$$V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) = \sum\limits_{i = 1}^{N} {e_{i}^{2} (x)}$$
(3)
$$\Delta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} = - \left[ {\nabla^{2} \,V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right]^{ - 1} \,\nabla V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ).$$
(4)

In the above relations, \(\,\nabla^{2} \,V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )\) and \(\nabla V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )\,\) are the Hessian and gradient matrixes, respectively.

Next, assuming \(J(x)\) as the Jacobean matrix, then we have the following:

$$\begin{aligned} & \nabla V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) = J(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )e(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) \\ & \nabla^{2} V(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) = J^{T} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )J(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) + S(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ), \\ & S(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) = \sum\limits_{i = 1}^{N} {e_{i} \nabla^{2} e_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} . \\ \end{aligned}$$
(5)

When \(S(x) \approx 0\), Eq. 4 can be expressed as follows:

$$\Delta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} = \left[ {J^{\text{T}} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )J(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )} \right]^{ - 1} J^{\text{T}} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ).$$
(6)

Finally, let λ determine the behavior of the algorithm, then the LM is expressed as follows:

$$\Delta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} = \left[ {J^{\text{T}} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )J(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ) + \lambda I} \right]^{ - 1} J^{\text{T}} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} )\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ).$$
(7)

2.2 Harris hawks optimization

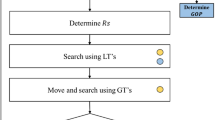
The name Harris hawks optimization (HHO) implies a recently developed optimization technique suggested by Heidari et al. [36]. This algorithm mimics the cooperative behavior of Harris’ hawks to address various optimization problems. By performing a good teamwork, the hawks aim to hunt the prey in some steps including tracing, encircling, approaching, and finally attacking. These hawks do a co-called maneuvering “surprise pounce” for catching an escaping hunt. As shown in Fig. 2, two main phases of the HHO are exploration and exploitation, where a middle phase is defined for transferring between them.

Fig. 2
figure 2

Different phases of Harris hawks optimization (after Heidari et al. [36])

Full size image

The first phase comprises waiting, seeking, and discovering the proposed prey. Let \(X_{\text{rabit}}\) stand for the rabbit position, and then, the position of the hawks is defined as follows:

$$X\left( {{\text{iter}} + 1} \right) = \left\{ {\begin{array}{*{20}l} {X_{\text{rand}} \left( {\text{iter}} \right) - r_{1} \left| {X_{\text{rand}} \left( {\text{iter}} \right) - 2r_{2} X\left( {\text{iter}} \right)} \right.} \hfill & { \quad {\text{if}}\;q \ge 0 \cdot 5} \hfill \\ {\left( {X_{\text{rabit}} \left( {\text{iter}} \right) - X_{\text{m}} \left( {\text{iter}} \right)} \right) - r_{3} \left( {{\text{LB}} + r_{4} \left( {{\text{UB}} - {\text{LB}}} \right)} \right)} \hfill & {\quad {\text{if}}\;q < 0 \cdot 5} \hfill \\ \end{array} } \right.,$$
(8)

where \(X_{\text{rand}}\) is one of the existing hawks which is proposed randomly. Moreover, \(r_{i}\) (i = 1, 2, 3, 4, q) is a random number which ranges in [0, 1]. In addition, \(X_{m}\) denotes the average position. Considering \(X_{i}\) and N as the place of the hawks and their size, respectively, \(X_{m}\) is calculated by the following equation:

$$X_{m} \left( {\text{iter}} \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} X_{i} \left( {\text{iter}} \right).$$
(9)

At the second stage, let T and \(E_{0} \in \left( { - 1. 1} \right)\) be the maximum size about the repetitions and the initial energy, the escaping energy of the hunt (E), which can change the exploration and exploitation, is formulated as follows:

$$E = 2E_{0} \left( {1 - \frac{\text{iter}}{T}} \right).$$
(10)

In this part, based on the magnitude of \(\left| E \right|\), it is decided to start the exploration phase (\(\left| E \right| \ge 1\)) or exploiting the neighborhood of the solutions (\(\left| E \right| < 1\)).

In the last phase, regarding the value of \(\left| E \right|\), the hawks decide to apply a soft (\(\left| E \right| \ge 0.5\)) or hard besiege (\(\left| E \right| < 0.5\)) to catch it from several directions. Remarkably, the escaping probability of the target is calculated by the parameter r, so that if it is larger than 0.5, the hunt successfully escapes and vice versa [37].

2.3 Dragonfly algorithm

Inspired by migration (dynamic swarm) and hunting (static swarm) behavior of Dragonfly herds, Mirjalili [38] proposed Dragonfly algorithm (DA) for the first time. It has shown a high capability for optimizing various engineering problems [39,40,41]. The Dragonflies‏’ life has two stages. The first stage, called nymph, is longer and the second stage is known as puberty. The hunting operation gets started by making some small groups for investigating a small region. And they change their position suddenly for hunting small insects. This is while they construct large groups during the migration [42]. As Fig. 3 illustrates, this algorithm draws on five stages of separation, alignment, cohesion, attracting to prey, and distraction from the enemy.

Fig. 3
figure 3

Different phases of the DA algorithm (after Mirjalili [38])

Full size image

Mathematically, the values belonging to the separation, alignment, cohesion, attraction to food, and confusion of enemy actions are computed by Eqs. 11, 12, 13, 14, and 15, respectively:

$$S_{i} = - \mathop \sum \limits_{j = 0}^{n} X - X_{j}$$
(11)
$$A_{i} = - \frac{{\mathop \sum \nolimits_{j = 0}^{n} V_{j} }}{n}$$
(12)
$$C_{i} = - \frac{{\mathop \sum \nolimits_{j = 0}^{n} X_{j} }}{n} - X$$
(13)
$$F_{i} = X^{f} - X$$
(14)
$$E_{i} = X^{e} - X,$$
(15)

in which X, Xf, and Xe stand for the positions of the proposed dragonfly, the food source, and the enemy, respectively. Moreover, Vj denotes the jth dragonfly velocity, and also n shows and the number of involved members.

Furthermore, assuming a, s, e, f, c, e, and w as the weights pertaining to related element, Eqs. 16 and 17 are used to update the dragonflies’ position for trying different weight solutions [38]:

$$\Delta X_{i \cdot j} = \left( {sS_{j} + aA_{j} + cC_{j} + fF_{j} + eE_{j} } \right) + w \Delta X_{i - 1 \cdot j - 1}$$
(16)
$$X_{i \cdot j} = X_{i - 1 \cdot j - 1} + \Delta X_{i \cdot j} .$$
(17)

The terms e and w in above relations can be calculated by Eqs. 18 and 19. Note that, in exploration (i.e., the dynamic phase), the alignment values of dragonflies are aimed to be larger than cohesion values. Aversely, the cohesion values are projected to be larger in exploitation (i.e., the static phase) to have the capability of attacking.

$$e = 0 \cdot 1 - i *\left( {\frac{ 0 \cdot 1}{{\frac{I}{2}}}} \right)$$
(18)
$$w = 0 \cdot 9 - i*\left( {\frac{ 0 \cdot 9 - 0 \cdot 4}{I}} \right),$$
(19)

where a, s, and c symbolize random numbers in the extent [0 − 2e], i is the going repetition, and f shows a random number in the extent [0 − 2]. Also, the term I denotes the number of repetitions [43, 44].

3 Data collection

T data set which was used to train the intelligent models of this research was the outcome of an extensive finite-element modeling, investigating a shallow footing in 2D axisymmetric conditions. The proposed footing was analyzed on a two-layered soil. This is worth noting that both members of the designed system (i.e., the footing and soil) are analyzed by 15-node triangular elements. Besides, the Mohr–Coulomb is considered for the material model. A total of 901 stages were implemented by considering seven effective factors including unit weight (kN/m3), friction angle, elastic modulus (kN/m2), dilation angle, Poisson’s ratio (v), applied stress (kN/m), and setback distance (m), where the settlement (m) is extracted as the output. The values of the settlement ranged in [0–0.10 m]. To change the problem into the classification mode, the target data were classified into two categories: (1) the settlements below 0.05 represent the failure of the system and were presented by 1, and (2) the settlements above 0.05 represent the stability of the system and were presented by 0. In the following, similar to many previous studies [45, 46], the acquired data set was divided into the training and testing groups containing 80% (i.e., 721 rows) and 20% (i.e., 180 rows) of whole samples, respectively. Figure 4 shows the distribution of the considered key factors.

Fig. 4
figure 4

Distribution of bearing capacity influential factors versus the settlement

Full size image

4 Results and discussion

This paper addresses two novel optimizations of ANN for analyzing the bearing capacity of a two-layered soil with different properties. The proposed optimization techniques are Harris hawks optimization and dragonfly algorithm, which were incorporated with an MLP network to find the most appropriate structure of it. To create the required data set, seven key factors of unit weight, friction angle, elastic modulus, dilation angle, Poisson’s ratio, applied stress, and setback distance were considered to implement 901 finite-element simulations for shallow footing located on double-layered soil. The settlement was then acquired as the output. Out of 9 rows, 80% (i.e., 721 samples) were randomly selected to train the proposed MLP, HHO-MLP, and DA-MLP models and the remaining 20% (i.e., 180 samples) were used to evaluate the accuracy of the predictions. In this regard, mean square error and mean absolute error were defined as follows to measure the error of the performance:

$${\text{MSE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{{i_{\text{observed}} }} - Y_{{i_{\text{predicted}} }} } \right)^{2}$$
(20)
$${\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {Y_{{i_{\text{observed}} }} - Y_{{i_{\text{predicted}} }} } \right),$$
(21)

in which \(Y_{{i_{\text{observed}} }}\) and \(Y_{{i_{\text{predicted}} }}\) represent the observed and predicted settlements, respectively. Also, N stands for the number of samples. Moreover, the area under the receiving operating characteristic curve (AUC) criteria was used to measure the accuracy of classification. The ROC curve is a good indicator of the accuracy of natural hazard modeling [47] which plots the specificity versus the sensitivity [47,48,49].

4.1 Optimizing the MLP using HHO and DA conventional algorithms

The most proper structure of the models was determined by executing an extensive tail and error process. Note that all modes were coded and implemented in the programming language of MATLAB. At first, it was found that the MLP with six neurons in its hidden layer presets more reliable prediction among the MLPs with the number of neurons varying from 1 to 10. Therefore, this structure was used as the basic model for the HHO-MLP and DA-MLP ensembles. Following this, the HHO and DA were applied to the MLP to find the best values for computational parameters (i.e., the connecting weights and biases). Based on the population size, ten different structures of the HHO-MLP and DA-MLP networks were tested within 1000 repetitions to achieve the best complexity of the models. In this sense, the population size varied from 10 to 100 with ten intervals. The MSE was defined as the objective function for measuring the performance error at the end of each iteration. Notably, each structure performed six times to ensure about the repeatability of them.

Figure 5a, b shows the results of the sensitivity analysis of the HHO-MLP and DA-MLP models. As is seen, the HHO keeps reducing the MSE until the last try, while the DA stops this procedure after nearly 500th iteration. According to these charts, the lowest objective function is obtained for the HHO-MLP (MSE = 0.117559367) and DA-MLP (MSE = 0.097887729) with the population sizes of 50 and 60, respectively. This is worth noting that the elite HHO took around 1662 s for optimizing the MLP, while this value was 924 s for the DA.

Fig. 5
figure 5

Executed sensitivity analysis based on the population size

Full size image

4.2 Accuracy assessment of the MLP, HHO-MLP, and DA-MLP predictive models

In this section, the performance of the used predictive models is evaluated in both training and testing stages by means of three well-known accuracy indices of MSE, MAE, and AUC. Figure 6 illustrates the results. In this figure, the observed classification values (i.e., 0 and 1) are graphically compared with the estimated values. In addition, the error (i.e., the difference between the observed and predicted classification values) is depicted alongside the histogram of the errors. Based on the results, the training outputs of the MLP, HHO-MLP, and DA-MLP range in [− 0.2689 to 1.0562], [− 0.3487 to 1.0947], and [− 0.1778 to 1.0862], respectively. As for the testing results, these extents were [− 0.2341 to 1.0724], [− 0.3367 to 1.1137], and [− 0.1629 to 1.0852]. According to Fig. 6, the prediction results of the reinforced MLPs have more consistency with the targets, compared to the typical MLP. It shows the efficiency of the applied HHO and DA evolutionary algorithms. In the following, the results are evaluated more accurately.

Fig. 6
figure 6

The results obtained for a, b MLP, c, d HHO-MLP, and e, f DA-MLP predictions, respectively, for the training and testing samples

Full size image

After drawing the ROC curves related to the training and testing results, the area under those curves is calculated to indicate the classification accuracy. The obtained AUCs, as well as the calculated MSEs and MAEs, are presented in Table 1 to develop a ranking system. In this system, a ranking score is assigned to each model based on the obtained criteria. Finally, the total ranking score (TRS) (i.e., the summation of the training and testing scores) determines the most successful model.

Table 1 The developed ranking system based on obtained accuracy criteria
Full size table

As the table denotes, in the training phase, the MSE error criterion decreased from 0.1283 to 0.1175 (i.e., by 8.42%) and 0.0978 (i.e., by 23.77%), respectively, by applying the HHO and DA algorithms. Likewise, the MAE was reduced from 0.3045 to 0.2927 (i.e., by 3.88%) and 0.2605 (i.e., by 14.45%). Also, these algorithms helped the MLP to increase the classification accuracy from 91.6 to 94.4% and 96.8%. As for the testing phase, the MSE fell from 0.1416 to 0.1350 (i.e., by 4.66%) and 0.1171 (i.e., by 17.30%). The decrease of the testing MAE from 0.3230 to 0.3200 (i.e., by 0.93%) and 0.2904 (i.e., by 10.09%) is another evidence for the effectiveness of the applied algorithms in improving the applicability of the MLP. Besides, the generalization accuracy of the MLP rose from 89.0 to 91.5% and 94.2%.

All in all, according to the results of the developed ranking system, the DA-based ensemble (TRS = 18) outperformed two other models in terms of all three MSE, MAE, and AUC, in both training and testing phases. After that, the HHO-based ensemble (TRS = 12) presented a more reliable approximation than the unreinforced MLP (TRS = 6).

A remarkable point is the time-effectiveness of the applied metaheuristic algorithms. Figure 7 compares the calculation time of the optimized HHO and DA algorithms within 1000 repetitions. As explained previously, the DA has a faster convergence as it reaches the lowest error with nearly 500 tries. This is while the HHO continues decreasing the error until the end. Therefore, it can be deduced that these algorithms minimized the objective function in approximately 1662 (HHO with population size = 50 and the number of iterations = 1000) and 460 s (DA with population size = 60 and the number of iterations = 500). Hence, in addition to the accuracy, the DA is also more effective in terms of the calculation time.

Fig. 7
figure 7

The performance time of the used HHO-MLP and DA-MLP

Full size image

5 Conclusions

Having a reliable approximation of bearing capacity is a fundamental task in geotechnical engineering. Due to the complexity of such problems, many scholars have employed hybrid evolutionary algorithms for dealing with them. The pivotal aim of this research was to investigate the potential of Harris hawks optimization and dragonfly algorithm in optimizing the performance of artificial neural network applied for stability analysis of a two-layered soil. The results of the executed sensitivity analysis showed that the HHO and DA with the population sizes of 50 and 60 performed better than other structures. Also, the calculated accuracy criteria revealed that both HHO and DA were successful and can be promisingly used for optimizing the weights and biases of the MLP. From comparison viewpoint, it was deduced that the outputs of the DA-MLP are in better consistency with the desired classification values. Finally, the authors believe that comparing the efficiency of the DA algorithm with other existing optimization approaches is a good idea for future works.