1 Introduction

Blasting as a powerful and fast but cost-effective tool widely have been applied to accomplish rock handling in civil (e.g. dam, road, tunnel), mining (e.g. underground, open pit, quarries) and construction purposes [1,2,3]. However, the industry experts and independent analysts believe that most of the blast-produced energy is wasted due to ground vibration and partial of this loss may then cause for fly-rock debris, air blast, back break, and seismic waves [1, 4,5,6]. Moreover, other possible induced blasting dangers (e.g. block size, environmental and utilities impacts, local disruptions, and premature detonation/misfires) are underestimated. The peak particle velocity (PPV) as an indicator index of undesirable ground vibration measurements is used to control the structural damage criteria and decrease the possible risk of blasting on environmental complaints [1, 7,8,9,10]. Therefore, providing predictive PPV-based models for assessing the effect of induced ground vibration is great of interest.

Traditionally, the PPV is estimated by empirical–statistical predictors [11,12,13,14,15,16]. However, such predictors due to incorporating of only limited numbers of influential parameters are not consistent and almost represent different scores of accuracies [7, 17, 18]. Despite presented updates using other related parameters [19,20,21], the PPV models in wide expanded range of data cannot simulate the process efficiently and thus provide unreliable predictions [1, 6, 22].

With parallel of progress in numerical simulation tools, soft computing-based techniques also have been applied to develop PPV predictive models. In literatures, capability of artificial neural network (ANNs) [1, 9, 10, 23], ANFIS and fuzzy logic [22, 24,25,26], support vector machine [27,28,29], and hybrid intelligent models [2, 30,31,32] in producing more precise results than other conventional or regression analyses have been highlighted.

Hybridized architectures aim to combine and optimize different knowledge schemes and learning strategies to solve a computational task [33, 34]. In this perspective, the metaheuristic algorithms (MAs) due to flexibility, effective dealing with complex constraints, problem-independent strategies, and user-defined special conditions [35, 36] have contributed to large number of new systems designs to overcome on limitations of individual models. Therefore, integrating the ANNs-MAs can provide innovative intelligent computational frameworks. Such computational intelligence incorporations have shown remarkable progress in predictability level of developed PPV models [26, 30, 32, 37,38,39,40,41]. Almost in all these literatures, the multilayer perceptrons (MLPs) is the core of hybridizing. Dense MLPs lead to high variance and thus slow training that is deemed insufficient to converge to a solution for modern advanced computer vision tasks. Moreover, large numbers of total parameters corresponding to characteristic of fully connected layers should be adjusted that can make redundancy in such high dimensions. However, if proper internal characteristics are set, the MLPs can approximate any input/output map.

Owing to the lack of a unified framework, comparative performance and conceptual analysis of various hybrid models often have been remained difficult. These issues motives for developing novel hybridized models using other subclass of ANNs.

In this paper, an optimum PPV-predictive model using generalized feedforward neural network (GFFN) structure integrated with a novel automated intelligent setting parameter approach is presented. The model then was hybridized with two prominent swarm-intelligence MAs including firefly and imperialist competitive algorithms (FMA and ICA). Applying the GFFN enhances the computing power, while automating process tunes the optimal hyper parameters. This implies that the performance of optimized FMA and ICA in different size of the search spaces are investigated. The adopted models were applied on 78 compiled datasets of a quarry in west of Iran (Table 1). Compared predictability and accuracy level using different metrics demonstrated superior performance in hybrid GFFN-FMA than GFFN-ICA and optimum GFFN. The importance of the used components then also was identified using sensitivity and weight analyses.

Table 1 The relevant parameters in adjustment of FMA
Full size table

2 Hybridizing and optimization

Optimization techniques lead to more efficient and cost-effective procedures to find an optimal solution among various iteratively compared responses. The classical methods lead to a set of nonlinear simultaneous equations that may be difficult to solve, while the computing capacities can be enhanced by utilizing the MAs and intelligent computer-aided activities [36]. This implies that combinatorial incorporations of ANNs-MAs can capture the feasible solution with less computational effort than traditional approaches [33, 34, 36, 42]. As presented in Fig. 1, the MAs are categorized in practical-oriented branches of optimization techniques. However, an algorithm may not exactly fit into each category. It can be a mixed type or hybrid, which uses some combination of deterministic components with randomness, or combines one algorithm with another to design more efficient system.

Fig. 1
figure 1

An overview on subcategories of optimization algorithms

Full size image

Therefore, in the design of hybrid architectures, the incorporation and interaction of applied techniques are more important than merging different methods to create ever-new techniques [34, 42].

2.1 FMA

Referring to Fig. 1, the FMA is a swarm population-based stochastic intelligence method inspired by the flashing behavior of fireflies [43] with approved efficiency in solving the hardest global and local optimization problems [44]. This algorithm (Fig. 2) is formulated using introduced parameters in Table 1 which depend on the problem should appropriately be tuned.

Fig. 2
figure 2

Mathematical concept of FMA and relevant parameters

Full size image

The FMA aims to optimize the I (Table 1) as the objective function. Accordingly, better fireflies have smaller error and thus higher intensity. As presented in Table 1, I and β for each firefly are functions of distance coordinate in which γ plays crucial role on the convergence speed. This parameter in most optimizing problems typically varies within [0.1–10] interval (Table 1).

According to level of I, the optimal solution in population is found through the individual fitness function (FT) for any binary combination of fireflies using:

$${{s}_{i}^{\rm new} }= {s}_{i}^{t} + {{\beta }_{0}} {e}^{-\gamma {{r}_{ij}^{2}}}\left({s}_{j}-{s}_{i} \right)+{\alpha }_{t}\left({\rm rand}-0.5\right)$$
(1)

where αt varies within [0, 1] interval. The rand function corresponds to a random number of solutions I. sj is a solution with lower FT than si and (sj-si) represents the updated step size.

In each iteration, the FT is compared with the previous results to keep only one new solution [34]. Briefly, using FT the position of moved firefly i towards the brighter one (new solution) in the current population is evaluated using:

$${s}_{i}^{\mathrm{new}}=\left\{\begin{array}{ll}{s}_{i} {s}_{i}={s}_{\rm best}\to \text{no new solution} \\ {s}_{i}^{\mathrm{new}} {s}_{j}={s}_{\rm best}\to \text{one new solution} \\ {s}_{ij}^{\rm new \,with} {\mathrm{FT}}_{\rm best} {\rm otherwise} \to \text{at least two better solutions}\end{array}\right.$$
(2)

The third condition means that the FTbest (the lowest) is retained while others are discarded.

2.2 ICA

ICA is an evolutionary and robust optimization algorithm inspired by imperialist competitive through expanding power and political system [45]. Like other evolutionary algorithms, ICA also starts with a random initial ensemble of countries (Ncou) in which those with minimum cost are selected to be imperialists (Nimp) and the rests play the role as colonies (Ncol). The outcome of configured formulation in this algorithm is to eliminate the weakest empires through a competition process according to total power of an empire (Fig. 3). The more empire power, the more attracted colonies, and thus all the countries are converged to only one robust empire in the domain of the problem as the desired solution.

Fig. 3
figure 3

Scheme of ICA competition process

Full size image

Similar to other evolutionary algorithms, the involved parameters in ICA (Table 2) should also properly be adjusted. Appropriate initial guess for these parameters (Table 2) can be set through the previous studies [33, 45,46,47].

Table 2 The range of used ICA parameters in the previous studies
Full size table

The total power of nth empire (TCn) as summation of the power of imperialist and its attracted colonies is expressed by:

$$\mathrm{TCn} = \mathrm{cost} ({\rm imperialist}) \xi \times {\rm mean} \{ {\rm cost ({\rm colonies of} n {\rm n} {\rm empire})}$$
(3)

where ξ theoretically falls within [0, 1] interval. The total power is affected by imperialist power in small value of ξ and can be influenced by the mean power of colonies in large ξ value. Thus, usually the value of ξ is considered close to 0.

Accordingly, the competition process among the empires represents the possession probability of each empire (pn) based on its total power and is calculated using normalized total cost of empire as:

$${p}_{n}=\left|\frac{{\mathrm{NTC}}_{n}}{\sum _{i=1}^{{N}_{\rm imp}}{\mathrm{NTC}}_{i}}\right|; \sum _{i=1}^{{N}_{\rm imp}}{p}_{i}=1$$
(4)

where TCn and NTCn denote the total and normalized cost of nth empire.

3 Layout of GFFN model

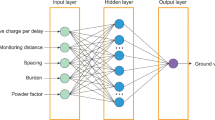
ANNs are simple simulation of human brain structure in learning the nonlinear models through the interconnected processing neurons. In the MLPs (Fig. 4A), as the main core of ANNs the result of mth neuron in output layer (Om) is expressed using:

$$O_{m} = g\underbrace {{(bk\sum _{j} f\overbrace {{(b_{j} \sum x_{i} w_{{ij}} )}}^{{z_{j} }}.w_{{jk}} }}_{{y_{k} }}$$
(5)

where xi denotes the inputs. f and g are the applied activation function on the hidden and output layers. zj shows the output of jth neuron in hidden layer using assigned weights (wij). Accordingly, the weight of hidden to output layer is shown by wjk. bj, and bk are the biases for setting the threshold values.

Fig. 4
figure 4

Implemented the GSN in data processing

Full size image

As presented in Fig. 4B, replacing the perceptron with generalized shunting neuron (GSN) can provide considerable plausibility. The shunting model [48] due to spatial extent of the dendritic tree and receiving two inputs (one excitatory and one inhibitory) dedicates the GFFN (Fig. 4C) in which the connecting system can jump over one or more layers [49]. This ability allows neurons to operate as adaptive nonlinear filters and provide higher flexibility [33, 46, 49,50,51].

In GFFN, the input lines are rectified in a postsynaptic neuron in such way that excitatory input transmits the signals in preferred directions while in the null direction the response of the excitatory synapse is shunted by the simultaneous activation of the inhibitory synapse [49]. Therefore, in the same number of neurons, the GFFN due to using shunting inhibition and applied GSN not only often solve the problem much more efficiently than MLPs [33, 50, 52], but also can speed up the training procedure and enhance the computability level to save the memory. This characteristic then utilizes more freedom to select optimum topology and get higher resolution in complex nonlinear decision classifiers [1, 33, 49, 50]. To produce the output of jth neuron in hidden layer (zj), all input is summed and passed through activation function as:

$${z}_{j}=\frac{{b}_{j}+f(\sum _{i}{w}_{ji}{x}_{j}+{w}_{jo})}{{a}_{j}+g(\sum _{i}{c}_{ji}{x}_{i}+{c}_{jo})}$$
(6)

where xi and xj show the inputs to the ith and jth neurons. wj0 and cj0 are bias constants. aj is a positive constant represents the passive decay rate of the neuron and bj reflects the output bias. wji and cji express the connection weight from the ith inputs to the jth neuron, where cji refers to “shunting inhibitory” connection weight.

The network error (E) of the kth output neuron in tth iteration in terms of the actual (tk) and predicted values (\({o}_{k}^{t}\)) then is defined as:

$${E}_{\rm train}^{t}=\frac{1}{2}\sum _{i=1}^{n}{\left({o}_{k}^{t}-{t}_{k}\right)}^{2}=\frac{1}{2}\sum _{i=1}^{n}{\left(g\left(\sum _{j=1}^{J}{w}_{jk}{z}_{j}^{t}\right)-{t}_{k}\right)}^{2}$$
(7)

To reduce the error between the desired and actual outputs, the weights are optimized using an updating procedure for (t + 1)th pattern subjected to:

$$w_{{ik}}^{{t + 1}} = w_{{ik}}^{t} \underbrace {{ - \eta \frac{{\partial E(W)}}{{\partial w_{{ik}} }}}}_{{\nabla w_{{ik}}^{t} }}$$
(8)

where η is the learning rate.

4 Case study and acquired datasets

In the current study, a number 78 monitored PPV from the Alvand–Qoly quarry at 5 km distance from Bijar town in Kurdistan province of Iran (Fig. 5) was used. This mine with 124 million tones of deposit in an area of 15.93km2 is the resource of limestone for Kurdistan cement industry. The PPV values have been recorded during the blasting of benches with 13.5 m depth and 1 m subdrill, where the distances between located geophones to shot point vary between 241 and 1500 m. The statistical description of employed data is given in Table 3. These data were normalized within [0, 1] interval and then randomized into 55%, 25%, and 20% to generate the training, testing, and validation sets.

Fig. 5
figure 5

Generated digital elevation model of studied area

Full size image
Table 3 Simple descriptive statistical analyses of datasets
Full size table

5 Configuring the hybrid predictive models

The learning algorithm of ANNs in weight space intends to minimize the output error and converge to a locally optimal solution. However, there is no guarantee in finding a global solution. This implies that adjustment of internal characteristics (e.g., number of neurons, activation function, learning rate, and layer organization) to capture an appropriate network size is a difficult task, where there is no unified accepted method [51, 53].

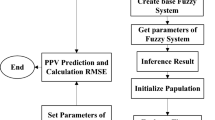
As presented in Fig. 6, in this paper an automated setting parameter procedure using a trial–error method was designed to find the optimum topology of predictive GFFN model. The proposed parameter setting approach aims to capture the optimal of one-dimensional array including several items, such as the number of epochs, learning rate, training algorithm, the number of neurons in hidden layers, and activation functions. Using the defined iterative procedure, the best performance of each produced topology after three runs is then evaluated using error metrics to represent the quality of found solution. The results then are reported back to the training algorithm to construct new topology. This procedure then was incorporated to FMA and ICA to investigate possible improvement in prediction process. To minimize the risk of getting trapped in local minima, overfitting, or early convergence, two internal loops was embedded to provide high flexibility in monitoring different training algorithms and activation functions. In this process, five training algorithms (QP quick propagation, CGD conjugate gradient descent, QN quasi-Newton, L–M Levenberg–Marquardt, MO momentum) and three activation functions (log logistic, hyt hyperbolic tangent, lin Linear) were used. The number of neurons as user defined parameter then can be arranged in diverse topologies even in similar structures, but different internal characteristics. Here, the possibilities of 16 neurons in maximum tow hidden layers were investigated. Obviously, by changing the number of neurons or defining more hidden layers, the procedure is able to capture much more topologies. Using 16 neurons, the system automatically will capture a large number of topologies (e.g., 6-16-1, 6–1-15–1, 6-2-14–1… 6-7-9-1… 6-15-1-1). Each topology then is tested by one of the training algorithms and one activation function. Accordingly, after checking all structures, it will be switched to another algorithm and subsequently activation function. This corresponds to monitoring of similar topologies subjected to different internal characteristics. All tested topologies are saved in a temporary query to be ranked using root mean square error (RMSE) and R2 to select the best optimum model. This procedure was programmed with C +  + .

Fig. 6
figure 6

Simplified diagram of hybridizing process incorporated to FMA and ICA. TA number of training algorithms, AF number of activation functions, J number of neurons

Full size image

To decrease the number of variables, value of 0.7 for learning rate was set for all implemented algorithms and the step sizes of hidden layers were changed in domain of [1.0–0.001]. The sum of squares and network root mean square error (RMSE) as well as number of epochs were also employed as output errors function and termination criteria, respectively. The priority of termination is to satisfy the RMSE and if not achieved then the number of epochs will use. Here the number of epochs was set for 500. As a result of carried out efforts, the minimum observed RMSE against the number of neurons subjected to different training algorithm and activation functions were reflected in Fig. 7A. The results of examined structures to find the optimum topology subjected to MO and Thy then was reflected in Fig. 7B. A brief summary of other training algorithms and corresponding optimum topologies is given in Table 4.

Fig. 7
figure 7

Variation of network RMSE based on the number of neurons subjected to implemented training algorithms (A) and a series of examined structures to find the optimum topology (B)

Full size image
Table 4 Results of implemented training algorithms to assess the optimized GFFN-based model
Full size table

The required parameters of ICA (Table 1) were obtained through a series of parametric analyses. Referring to the previous studies, the values of 2, π/4, and 0.02 were managed as the values for β, θ, and ζ, respectively (Abbaszadeh Shahri et al., 2020a). To capture the optimal of Ncou, Nimp, and Ndec, 12 hybrid models subjected to optimum GFFN (Table 4) were trained. Using analyzed R2 and RMSE, the values of 150, 15, and 250 were assigned to Ncou, Nimp, and Ndec, respectively (Fig. 8A–E). In case of FMA (Fig. 5), the pointed parameters in Table 2 should be tuned. This process is executed using gen-counter parameter (t) that calculates the new values for α through the function Δ = 1–10−4/0.91/max Gen and α(t+1) = 1-Δ. α(t), where Δ determines the step size of changing parameter α(t+1) and descends with the increasing of t. The required parameters for FMA then were captured through series analyses using RMSE and R2. Accordingly, values of 1, 0.2, 0.05, 0.2, and 0.5 corresponding to γ, β, Δ, α, and β0 can be selected as the most appropriate parameters to adjust FMA (Fig. 8F–H). Referring to convergence history, ICA in the number of 150 and FMA in 40 populations can optimize the GFFN model (Fig. 9). Subsequently, calculated residuals and also comparison between measured and predicted values were executed and plotted in Fig. 10.

Fig. 8
figure 8

Parametric efforts to adjust optimum internal factors of hybrid models using ICA (A–E) and FMA (F–H)

Full size image
Fig. 9
figure 9

Convergences curves of hybrid models subjected to different populations, ICA (A) and FMA (B)

Full size image
Fig. 10
figure 10

Comparing the measured and predicted values (A, C) and corresponding residuals (B)

Full size image

6 Discussion and validation

Identifying the system confusing for different classes and improved performance of generated models can be quantified and evaluated using confusion matrix [54]. The established confusion matrixes for the validation datasets of GFFN, GFFN-ICA, and GFFN-FMA were presented in Table 5. The similar process for test and train data was carried out to determine the correct classification rate (CCR) and classification error (CE) [33, 46, 50] as reflected in Table 6. According to observed results, GFFN-FMA shows 6.67% and 20% improvement regarding to GFFN-ICA and GFFN, respectively.

Table 5 Established confusion matrixes of hybrid and optimum models
Full size table
Table 6 Compared CCR, CE, and improved progress of optimized models
Full size table

The performance analyses of the models using mean absolute percentage error (MAPE), variance account for (VAF), RMSE, index of agreement (IA), and R2 criteria for validation datasets were reflected and ranked in Table 7.

Table 7 Results of statistical criteria using validate datasets to evaluate the model performance
Full size table

To check or visualize the performance of the multiclass problem at various thresholds settings, the area under the curve of receiver-operating characteristics (AUCROC) can be employed. The ROC is a probability curve showing the performance of a model at all classification thresholds and AUC represents capability of model in distinguishing between classes. Referring to ROC, the precision–recall is a useful tool to reflect the success of prediction when the classes are very imbalanced. In information retrieval, precision is a measure of result relevancy, while recall reflects the returned numbers of truly relevant. Therefore, this curve displays the relevant and corresponding number of truly predicted results. Accordingly, the curves of different models then can directly be compared for different thresholds to get the full picture of evaluating. In Fig. 11A, the AUC of precision–recall for hybrid GFFN-FMA is 2.5% and 12.5% more than GFFN-ICA and GFFN. This improvement demonstrates higher accuracy in predicted outputs of GFFN-FMA. The comparison between measured and predicted values and corresponding calculated residuals were also presented in Fig. 11B and C.

Fig. 11
figure 11

Conducted precision–recall curves (A), compared predicted values with observations (B), and calculated residuals (C) for GFFN, GFFN-FMA, and GFFN-ICA models

Full size image

Sensitivity analyses techniques as a what-if simulation for determining the effect of inputs on particular output is especially useful tool in black box processes where the output is an opaque function of several inputs [55, 56]. As presented in Eq. 12, the importance of input parameters using the cosine amplitude and partial derivative (PaD) were presented in Fig. 12.

$$\left\{ {\begin{array}{*{20}c} {{\text{cosine~amplitude}}:{\text{~}}R_{{ij}} = \frac{{\sum\limits_{{k = 1}}^{m} {\left( {x_{{ik}} \times x_{{jk}} } \right)} }}{{\sqrt {\sum\limits_{{k = 1}}^{m} {x_{{ik}}^{2} } \sum\limits_{{k = 1}}^{m} {x_{{jk}}^{2} } } }},{\text{~}}x_{i} {\text{~and~}}x_{j} :{\text{elements~of~data~pairs}}} \\ {PaD:{\text{~contribution~of~ith~variable}} = \frac{{{\text{SSD}}_{i} }}{{\sum\limits_{i} {{\text{SSD}}_{i} } }};{\text{SSD}}_{i} = \sum\limits_{p} {\left( {\frac{{\partial O_{k}^{p} }}{{\partial x_{i}^{p} }}} \right)^{2} } } \\ \end{array} } \right.$$
(12)

where Okp and xip are output and input values for pattern P, and SSDi is the sum of the squares of the partial derivatives, respectively.

Fig. 12
figure 12

Calculated importance of input parameters on predicted PPV using developed models subjected to cosine amplitude (A) and PaD (B) sensitivity analyses techniques

Full size image

Both applied sensitivity analysis methods identified the distance and total charge as the most and burden as the least effective factors on PPV.

7 Conclusion and remarks

To control and mitigate the effects of blasting on nearby vicinities, developing more accurate PPV predictive models is of great importance. In this study, two optimum hybridized structures using GFFN incorporated to FMA and ICA were presented. The optimum GFFN topology was tuned through an automated parameter setting procedure subjected to 78 monitored datasets of blasting events in Alvand–Qoly mine, Kurdistan Province-Iran. To increase the efficiency of hybrid structures, the corresponding internal variables of FMA and ICA optimally were adjusted using parametric analyses. The results of optimized hybrid architectures proved to be more accurate than the only GFFN.

Referring to conducted RMSE-iteration curves subjected to different number of populations, the higher tendency for convergence in FMA than ICA led to 11.37% and 10.42% improvements in hybrid GFFN-FMA and GFFN-ICA than GFFN. Accordingly, the R2 value of GFFN form 0.90 was updated to 0.97 (GFFN-FMA) and 0.96 (GFFN-ICA). The results of CCR showed 93.75% success for GFFN-FMA while it was decreased to 87.5% and 75% in GFFN-ICA and GFFN, respectively. Pursued accuracy performance and ranked statistical error criteria exhibited relative superiority of the GFFN-FMA than GFFN-ICA. However, the differences were not significant. The calculated AUCROC as an index of model skill demonstrated for 2.3% and 12.5% improving in predictability level of the GFFN-FMA than other models. Using different sensitivity analyses techniques, the distance, total charge, and the burden were recognized as the most and least effective factors on predicted PPV. The study showed that implementing of the FMA and ICA not only can significantly improve the robustness and performance of the GFFN model, but also provide more flexible and reliable tool for the purpose of PPV prediction. It was observed that for the current study FMA is more applicable than ICA.