Nonlinear response of an imperfect microcantilever static and dynamically actuated considering uncertainties and noise

Abstract

The motion of a slender, clamped-free, imperfect, electrically actuated microbeam is investigated. Special attention is given to the influence of imperfections and noise on the bifurcations and instabilities of the structure, a problem not tackled in the previous literature on the subject. To this end, a geometrically nonlinear theory is adopted for the microbeam retaining geometric nonlinear terms up to the third order and considering in a consistent way the effect of initial geometric imperfections. Also, additive white noise is considered to model forcing uncertainties, and the Galerkin discretization method, using as interpolating functions the linear vibration modes, is used to obtain a modal stochastic differential equation of Itô type, which is solved by the stochastic Runge–Kutta method. A parametric analysis clarifies the influence of geometric imperfections and noise level on the natural frequencies, resonance curves, and pull-in instability. Additionally, the global dynamics is examined through the generalized cell mapping, showing the effects of uncertainties on the attractor’s probability density functions and basins of attraction.

1 Introduction

Microelectromechanical systems (MEMS) are important devices with a broad range of applications [1,2,3]. Their theoretical analysis is diverse, with contributions from different fields, such as structural mechanics, electrostatics and electrodynamics, electromagnetism, piezoelectricity, electrothermal effects, and optics, to name a few. Also, these systems are rather flexible and can undergo large displacements due to their small scale in the presence of electrostatic and electrodynamic loads. Therefore, MEMS requires complex multidisciplinary analysis to correctly capture all the physical phenomena involved. For this purpose, various techniques are employed, for example, finite element and boundary element methods [1, 4, 5], shooting method [6], reduced-order models [7,8,9,10], and perturbation methods [11,12,13]. Notably, the multiple time-scales method combined with a Galerkin procedure is a powerful strategy in order to obtain theoretical internal resonances, which has been validated by experimental results [13]. Numerical techniques have also been applied in the study of microbeams, such as pseudo-arclength continuation methods with nonlocal constitutive relations [14,15,16]. These models are validated by comparing their results with experimental results and finite-element solutions available in the literature.

Younis and Nayfeh [11], Abdel-Rahman et al. [17], and Younis et al. [18] studied through an analytical approach and a reduced-order model (macromodel) the behavior of electrically actuated microbeam-based MEMS, with emphasis on their nonlinear resonant behavior. They modeled the beam as a partial integro-differential equation. Only nonlinearities due to midplane stretching and electrostatic load were considered, with displacements assumed to be small [19]. It is evident from the equation of motion that electrostatic loads result in strong nonlinearities with singularities. The analysis is carried out by dividing the actuation into a static part, due to the direct current voltage V_dc, and a dynamic part, due to an alternating current voltage V_ac. The static problem is solved numerically by the shooting method, and pull-in voltages are obtained under varying axial force. Natural frequencies are also obtained, and they exhibited a good agreement with experimental results even near the pull-in voltage. Forced vibration and various internal resonance conditions were addressed by the multiple scales method [11]. In [11, 17], the dynamic problem is considered using different Taylor-series expansion superimposed on the static solution. However, they fail to represent the electric force at voltages close to pull-in since the neglected terms in the Taylor-series expansion become significant. Younis et al. [17, 18] proposed then an alternative approach that is capable of describing the strong nonlinearities exactly, which shows better agreement with experimental data using fewer mode shapes.

The described analytic procedure is relevant to this day, being applied to other MEMS problems, as reported in a recent review paper by Hajjaj et al. [1], such as arch resonators [12, 13], arches over flexible supports [20], functionally graded viscoelastic microbeams with imperfections [21], cantilever resonators [22,23,24], narrow microbeams subject to fringing fields [4, 5, 25], and microscale beams described by the modified couple stress theory [6, 14,15,16, 19, 26,27,28]. Also, in a recent contribution, Ilyas et al. [29] investigated the response of MEMS resonators under generic electrostatic loadings theoretically. The qualitative resonant behavior was analytically demonstrated by the multiple scale method, showing that the nonlinear electrostatic load leads to softening-type nonlinearity. In a companion paper, Ilyas et al. [30] investigated the simultaneous excitation of primary and subharmonic resonances of similar strength experimentally by using different combinations of AC and DC voltages, and two potential applications are experimentally demonstrated.

Several types of uncertainties may be found in practical applications and may have a substantial influence on the behavior of MEMS, given their multi-physical nature. In [31], Vig and Kim enumerates some noise sources, including fluctuations in temperature, adsorbing/desorbing molecules, outgassing, Brownian motion, Johnson noise, drive power, and self-heating. The reduced dimension of the microbeam intensifies all noise effects and instabilities that are negligible in macro-scale devices. Experimental investigations corroborate these conclusions [9, 32, 33]. The global dynamic analysis was shown to be a powerful tool to predict and quantify finite instability, which considers, heuristically, uncertainties in initial conditions as evidenced by the works of Alsaleem et al. [33], Ruzziconi et al. [34], and Lenci et al. [35]. The influence of material parameters and their uncertainties on the nonlinear response has been highlighted in [36,37,38], and the influence of uncertainties in geometric nonlinearities in [39,40,41]. Parametric uncertainties are also of interest in the analysis of MEMS [42, 43], such as geometric [12, 15, 16] and constitutive [19] uncertainties, which can be investigated through a Monte Carlo approach, stochastic perturbation, or stochastic collocation. However, further investigation is needed to investigate the effects of uncertainties on the response of MEMs, particularly on their global dynamics, where a stochastic framework is still to be developed. The coupling between global dynamics and parametric uncertainty in a probabilistic framework is yet to be discussed.

To address these issues, in this paper an investigation has been conducted on an imperfect MEMS device constituted of an imperfect clamped-free microbeam electrostatically and electrodynamically actuated with added noise. Using Hamilton’s principle, the nonlinear equation of motion is derived by considering the nonlinear electrical load, the geometric nonlinearities up to the third order, and the geometric imperfections. Additive white noise is considered to model forcing uncertainties, and the Galerkin modal discretization is employed to generate stochastic differential equations of Itô type, which are solved by the stochastic Runge–Kutta method. Finally, the global dynamics are investigated by the generalized cell mapping [44,45,46], through which transfer operators are constructed. The effects of additive noise on resonant and non-resonant solutions are observed, changing the probability measures and basins of attraction. Special attention is given to the effect of imperfections and noise on the pull-in instability.

2 Nonlinear Euler–Bernoulli electrically actuated microbeam

The planar flexural Euler–Bernoulli beam equation with imperfections is derived through the extended Hamilton’s principle. An elastic material is considered with small elastic strains, and the classical capacitor electrostatic load is assumed [2]. Three coordinate systems are considered for the beam’s kinematic definitions, which are the reference system (X, Z), the undeformed coordinates of the imperfect beam configuration (ξ₀, ζ₀), and the deformed configuration, (ξ, ζ). The reference and undeformed systems are Lagrangian frames of reference, with the former corresponding to the perfect model. The deformed axes define an Eulerian reference frame. The undeformed axes represent the imperfect model in a stress-free configuration. A schematic of all three reference frames is given in Fig. 1, where s and $\tilde{s}$ measure the undeformed and deformed arc-lengths, respectively, and $w_{0} (x)$ is the initial geometric imperfection.

Fig. 1

Orientation of imperfect undeformed and deformed coordinate systems with respect to the reference system

The coordinates ζ₀ and ζ represent the distance between a fiber parallel to the cross-sectional centroid in the undeformed and deformed configuration, respectively. Given that the motions are restricted to the plane (X, Z) and assuming small strains, the only nonzero strain component is the axial deformation,

$$ \varepsilon _{{\xi \xi }} = \zeta \left( {\bar{\kappa }_{\eta } - \kappa _{{\eta _{0} }} } \right), $$

(1)

where the deformed and undeformed curvatures $\bar{\kappa }_{\eta }$ and $\kappa _{{\eta _{0} }}$ are defined as derivatives of the cross-sectional rotation angles $\bar{\theta }$ and $\theta _{0}$ with respect to the undeformed arc-length s,

$$ \bar{\kappa }_{\eta } = \bar{\theta }^{\prime},\quad \kappa _{{\eta _{0} }} = \theta ^{\prime}_{0} , $$

(2)

where $(\;)^{\prime} = {\rm{d}}/{\rm{d}}s$. The angles $\bar{\theta }$ and $\theta _{0}$ can be understood as transformations from the reference axes to the deformed and undeformed axes, respectively. These geometric transformations are illustrated in Fig. 2.

Fig. 2

Transformation from the material axes to the deformed and undeformed configuration

Finally, the rotation angles are assumed dependent on the vertical and axial displacements, respectively, w and u, and imperfection w₀, see Fig. 1. The expressions that relate rotations and translations are obtained through differential geometry and are given by

$$ \sin \bar{\theta } = \frac{{ - \bar{w}^{\prime}}}{{\sqrt {\left( {\sqrt {1 - w_{0}^{{\prime 2}} } + u^{\prime}} \right)^{2} + \bar{w}^{{\prime 2}} } }},\quad \cos \bar{\theta } = \frac{{\sqrt {1 - w_{0}^{{\prime 2}} } + u^{\prime}}}{{\sqrt {\left( {\sqrt {1 - w_{0}^{{\prime 2}} } + u^{\prime}} \right)^{2} + \bar{w}^{{\prime 2}} } }} $$

(3)

$$ \sin \theta _{0} = w^{\prime}_{0} ,\quad \cos \theta _{0} = \sqrt {1 + w_{0}^{{\prime 2}} } , $$

(4)

where $\bar{w} = w + w_{0}$.

By considering a linear elastic material, the strain energy is

$$ U = \int\limits_{S} {\frac{{D_{\eta } }}{2}\left( {\bar{\kappa }_{\eta } - \kappa _{\eta } } \right)^{2} {\rm{d}}s,} $$

(5)

where D_η is the flexural stiffness, the curvatures are related to transversal displacement through Eqs. (2), (3) and (4), and s is the undeformed arc-length. The kinetic energy is defined as a function of the translational and rotational velocities, that is

$$ T = \int\limits_{S} {\frac{1}{2}\left( {m{\kern 1pt} \dot{u}^{2} + m{\kern 1pt} \dot{w}^{2} + J_{\eta } \dot{\theta }^{2} } \right){\rm{d}}s,} $$

(6)

where $(\;)^{ \cdot } = {\rm{d/d}}t$, m and J_η are the linearly distributed mass and rotational inertia, respectively, and $\dot{\theta }$ is the angular velocity, where $\theta = \bar{\theta } - \theta _{0}$ since the initial rotation $\theta _{0}$ is time-independent. Assuming an inextensional model, the beam’s augmented Lagrangian, ${L} = T - U + R$, is given by

$$ {{L}} = \int\limits_{s} {\left\{ {\frac{1}{2}\left( {m{\kern 1pt} \dot{u}^{2} + m{\kern 1pt} \dot{w}^{2} + J_{\eta } \dot{\theta }^{2} } \right) - \frac{{D_{\eta } }}{2}\theta ^{{\prime 2}} + \frac{\lambda }{2}\Delta _{e} } \right\}} {\rm{d}}s, $$

(7)

where $\lambda$ is a Lagrange multiplier and the axial elongation is given by

$$ \Delta _{e} = \frac{{{\rm{d}}\tilde{s} - {\rm{d}}s}}{{{\rm{d}}{\kern 1pt} s}} = \sqrt {\left( {\sqrt {1 - w_{0}^{{\prime 2}} } + u^{\prime}} \right)^{2} + \bar{w}^{{\prime 2}} } - 1. $$

(8)

By considering the extended Hamilton’s principle, the functional

$${{H}} = \int\limits_{{t_{1} }}^{{t_{2} }} {L + W_{{{\rm{nc}}}} \;{\rm{d}}t} $$

(9)

is stationary, where W_nc represents the work of the nonconservative forces, whose variation takes the form

$$ \delta W_{{{\rm{nc}}}} = \left( {Q_{w} - c_{w} \dot{w}} \right)\delta w, $$

(10)

where Q_w is a distributed load, and c_w is the damping coefficient. From the variation of Eq. (9) and expansion of the dependent variables in Taylor series up to the third order, two coupled equations of motion are obtained,

$$ m{\kern 1pt} \ddot{u} = \left\{ {D_{\eta } \bar{w}^{\prime}{\kern 1pt} w^{\prime\prime\prime} - J_{\eta } \bar{w}^{\prime}{\kern 1pt} \ddot{w}^{\prime} + \frac{\lambda }{2}\left( {\frac{{\bar{w}^{{\prime 2}} }}{2} - 1} \right)} \right\}^{\prime } $$

(11)

$$ \begin{aligned} & m{\kern 1pt} \ddot{w} + c_{w} \dot{w} - Q_{w} = \left\{ { - D_{\eta } \left[ {\bar{w}^{\prime}w^{\prime\prime}\left( {\bar{w}^{\prime\prime} + w^{\prime\prime}_{0} } \right) + w^{\prime}w_{0}^{{\prime \prime 2}} + w^{\prime}w^{\prime\prime\prime}_{0} \left( {w^{\prime}_{0} + \frac{{w^{\prime}}}{2}} \right) + w^{\prime\prime\prime}} \right]} \right. \\ & \quad \left. { + J_{\eta } \left( {\bar{w}^{\prime}\dot{w}^{{\prime 2}} + \ddot{w}^{\prime}} \right) - \frac{\lambda }{2}\bar{w}^{\prime}} \right\}^{\prime } . \\ \end{aligned} $$

(12)

By considering the axial elongation (8) equal to zero, the model is assumed inextensional, and the axial displacement u is defined as a function of the flexural displacement w. Expanding Eq. (8) in Taylor series and retaining nonlinear polynomial terms up to the third order, the axial displacement is obtained as

$$ u = - \frac{1}{2}\int\limits_{0}^{s} {w^{{\prime 2}} + 2w^{\prime } w_{0}^{\prime } s} $$

(13)

Substituting Eq. (13) into Eq. (11), the Lagrange multiplier is obtained as

$$\lambda = 2D_{\eta }{\kern 1pt}\bar{w}^{\prime}{\kern 1pt}w^{\prime\prime\prime} -2J_{\eta } {\kern 1pt}\bar{w}^{\prime}{\kern 1pt}\ddot{w}^{\prime} +2m\int_{L}^{s}{\int_{0}^{s}{\dot{w}^{{\prime 2}}+\bar{w}^{\prime}{\kern 1pt}\ddot{w}^{\prime}{\rm{d}}s} {\kern 1pt}{\rm{d}}s} .$$

(14)

Finally, the equation of motion is obtained by substituting the Lagrange multiplier, Eq. (14), into Eq. (12), resulting in the following integro-differential equation of motion

$$\begin{aligned} & m \ddot{w} + c_{w} \dot{w} - Q_{w} = \left\{ { -D_{\eta } \left[{\bar{w}^{\prime}w^{\prime \prime}\left({\bar{w}^{\prime\prime} +w^{\prime\prime}_{0}}\right) +w^{\prime}w_{0}^{{ \prime \prime 2}} +w^{\prime}w^{\prime\prime \prime}_{0} \left({w^{\prime}_{0} +\frac{{w^{\prime}}}{2}}\right) + \left({\bar{w}^{{\prime 2}} + 1}\right)w^{\prime\prime \prime}} \right]} \right. \\&\quad \left. { + J_{\eta } \left[{\bar{w}^{\prime}\dot{w}^{{\prime 2}} +\left({\bar{w}^{{\prime 2}} + 1} \right)\ddot{w}^{\prime}} \right] -m\bar{w}^{\prime}\int_{L}^{s} {\int_{0}^{s}{\dot{w}^{\prime 2} +\bar{w}^{\prime}\ddot{w}^{\prime}{\rm{d}}s} \;{\rm{d}}s} }\right\}^{\prime } .\\\end{aligned}$$

(15)

A linear clamped-free Rayleigh beam is adopted, and the associated boundary conditions are given by,

$$ \begin{aligned} & w\left( {0,t} \right) = w^{\prime}\left( {0,t} \right) = 0, \\ & w^{\prime\prime}\left( {L,t} \right) = D_{\eta } w^{\prime\prime\prime}\left( {L,t} \right) - J_{\eta } \ddot{w}^{\prime}\left( {L,t} \right) = 0. \\ \end{aligned} $$

(16)

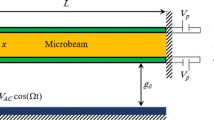
Considering a parallel plate capacitor with a rectangular cross section, the electrostatic force Q_w can be written as [2]

$$ Q_{w} = \frac{{b{\kern 1pt} \varepsilon {\kern 1pt} V^{2} }}{{2\left( {d - \bar{w}} \right)^{2} }}, $$

(17)

where b is the beam width, d is the initial gap for a perfect system, ε is the free space permittivity and V is the applied voltage.

Equation (15) is then nondimensionlized considering the following parameters

$$ \begin{aligned} & s^{*} = s/L,\quad t^{*} = t\sqrt {D_{\eta } /(m{\kern 1pt} L^{4} )} , \\ & w^{*} = w/d,\quad w_{0}^{*} = w_{0} /d,\quad Q_{w} ^{*} = Q_{w} {\kern 1pt} L^{3} /D_{\eta } , \\ & J_{\eta }^{*} = J_{\eta } /m{\kern 1pt} L^{2} ,\quad c_{w}^{*} = c_{w} L^{2} /m{\kern 1pt} D_{\eta } , \\ & \varepsilon ^{*} = \varepsilon L^{2} /D_{\eta } ,\quad d^{*} = d/L,\quad b^{*} = b/L, \\ \end{aligned} $$

(18)

resulting in

$$ \begin{aligned} & \ddot{w} + c_{w} \dot{w} - Q_{w} = \left\{ { - d^{2} \left[ {\bar{w}^{\prime}w^{\prime\prime}\left( {\bar{w}^{\prime\prime} + w^{\prime\prime}_{0} } \right) + w^{\prime}w_{0}^{{\prime \prime 2}} + w^{\prime}w^{\prime\prime\prime}_{0} \left( {w^{\prime}_{0} + \frac{{w^{\prime}}}{2}} \right) + \left( {\bar{w}^{{\prime 2}} + \frac{1}{{d^{2} }}} \right)w^{\prime\prime\prime}} \right]} \right. \\ & \quad + d^{2} \left. {J_{\eta } \left[ {\bar{w}^{\prime}\dot{w}^{{\prime 2}} + \left( {\bar{w}^{{\prime 2}} + \frac{1}{{d^{2} }}} \right)\ddot{w}^{\prime}} \right] - d^{2} \bar{w}^{\prime}\int_{1}^{s} {\int_{0}^{s} {\left( {\bar{w}^{\prime}\dot{w}^{\prime}} \right)^{ \cdot } {\rm{d}}s} \;{\rm{d}}s} } \right\}^{\prime } . \\ \end{aligned} $$

(19)

where * is dropped for brevity. The nondimensional boundary conditions are

$$ \begin{aligned} & w\left( {0,t} \right) = w^{\prime}\left( {0,t} \right) = 0, \\ & w^{\prime\prime}\left( {1,t} \right) = w^{\prime\prime\prime}\left( {1,t} \right) - J_{\eta } \ddot{w}^{\prime}\left( {1,t} \right) = 0, \\ \end{aligned} $$

(20)

and the nondimensional electrostatic load is given by

$$ Q_{w}^{*} = \frac{{b{\kern 1pt} \varepsilon {\kern 1pt} V^{2} }}{{2d^{3} \left( {1 - \bar{w}} \right)^{2} }}, $$

(21)

with the singularity now at $\bar{w} = 1$.

The total applied voltage is the sum of the direct current (V_dc) and the time-dependent alternate current (V_ac), i.e.:

$$ V\left( t \right) = V_{{{\rm{dc}}}} + V_{{{\rm{ac}}}} \left( t \right). $$

(22)

The displacement is, therefore, decomposed into its dynamic and static parts,

$$ w\left( {t,x} \right) = w_{d} \left( {t,x} \right) + w_{s} \left( x \right). $$

(23)

Considering only the DC voltage in Eq. (19), substituting Eqs. (22) and (23) into Eqs. (19) and (21) and setting to zero all time-dependent variables, the static displacement component $w_{s}$ is obtained from the following nonlinear equilibrium equation

$$ \frac{{b{\kern 1pt} \varepsilon {\kern 1pt} V_{{{\rm{dc}}}} ^{2} }}{{2d^{3} \left( {1 - \bar{w}_{s} } \right)^{2} }} = d^{2} \left\{ {\bar{w}^{\prime}w^{\prime\prime}\left( {\bar{w}^{\prime\prime} + w^{\prime\prime}_{0} } \right) + w^{\prime}w_{0}^{{\prime \prime 2}} + w^{\prime}w^{\prime\prime\prime}_{0} \left( {w^{\prime}_{0} + \frac{{w^{\prime}}}{2}} \right) + \left( {\bar{w}^{{\prime 2}} + \frac{1}{{d^{2} }}} \right)w^{\prime\prime\prime}} \right\}^{\prime } , $$

(24)

where $\bar{w}_{s} = w_{s} + w_{0}$.

The additional dynamic displacement $w_{d} \left( {t,x} \right)$ is assumed as a perturbation from the static equilibrium position, and the resulting equation of motion is obtained by substituting Eqs. (22) and (23) into Eqs. (19) and (21) and expanding in Taylor series of w_d up to the third order, resulting in

$$\begin{aligned} &\ddot{w}_{d} + c_{w}\dot{w}_{d} - \frac{{b \varepsilon }}{{d^{3}}}\left[ {\frac{{2w_{d} ^{3}V_{{{\rm{dc}}}} ^{2}}}{{\left( {1 - \bar{w}_{s} }\right)^{5} }} +\frac{{w_{d} ^{2} \left({3V_{{{\rm{dc}}}} ^{2} -2V_{{{\rm{dc}}}}V_{{{\rm{ac}}}} } \right)}}{{2\left( {1 - \bar{w}_{s} }\right)^{4} }} +\frac{{w_{d} \left({V_{{{\rm{ac}}}} +V_{{{\rm{dc}}}} }\right)^{2} }}{{\left( {1 -\bar{w}_{s} } \right)^{3} }}+ \frac{{2V_{{{\rm{dc}}}}V_{{{\rm{ac}}}} +V_{{{\rm{ac}}}} ^{2}}}{{2\left( {1 - \bar{w}_{s}} \right)^{2} }}} \right]\\&\quad = \left\{ { - d^{2}\left[ {\left({\bar{w}^{{\prime 2}} +\frac{1}{{d^{2} }}}\right)w^{\prime\prime \prime}_{d} + \frac{1}{2}w^{\prime}_{d} \left({\bar{w}^{\prime} +\bar{w}^{\prime}_{s} }\right)\left( {\bar{w}^{\prime \prime\prime}_{s} +w^{\prime\prime\prime}_{s}} \right) +\bar{w}^{\prime}w^{\prime \prime}_{d} \left({\bar{w}^{\prime\prime} +\bar{w}^{\prime\prime}_{s}} \right) + w^{\prime}_{d}\bar{w}_{s}^{{\prime \prime 2}} } \right]} \right. \\&\quad + d^{2} \left. {J_{\eta } \left[ {\bar{w}^{\prime}\dot{w}_{d}^{{\prime 2}} +\left( {\bar{w}^{{\prime }^{2}} + \frac{1}{{d^{2} }}}\right)\ddot{w}^{\prime}_{d} }\right] - d^{2}\bar{w}^{\prime}\int_{1}^{s} {\int_{0}^{s}{\dot{w}_{d}^{{\prime 2}}+ \bar{w}^{\prime}{\kern 1pt} \ddot{w}^{\prime}_{d}{\rm{d}}s} {\kern 1pt}{\rm{d}}s} } \right \}^{\prime } ,\\\end{aligned}$$

(25)

where $\bar{w}_{s} = w_{s} + w_{0}$ and $\bar{w} = w_{d} + w_{s} + w_{0}$. The sum of zeroth-order terms is set to zero since they correspond to the static equilibrium position, Eq. (24).

The Galerkin method is employed to discretize the equation of motion using as interpolation functions the linear vibration modes. The assumed mode expansion is derived from the boundary value problem considering the undamped linearized equation of motion

$$ \ddot{w} - J_{\eta } \ddot{w}^{{\prime \prime }} + w^{{iv}} = 0, $$

(26)

together with boundary conditions (20). Equation (26) corresponds to a Rayleigh beam, where the rotational inertia is considered [47]. The solution of Eq. (26) is given by

$$ w\left( {s,t} \right) = \sum\limits_{{i = 1}}^{\infty } {w^{{\left( i \right)}} \left( t \right)F_{i} \left( s \right)} $$

(27)

where w⁽ⁱ⁾ is the i-th time-dependent modal amplitude and F_i is the i-th natural vibration mode. The natural modes for the clamped-free beam are [47]

$$ F_{i} \left( s \right) = \cosh \left( {B_{i} {\kern 1pt} s} \right) - \cos \left( {A_{i} {\kern 1pt} s} \right) - \frac{{A_{i} ^{2} \cos \left( {A_{i} } \right) + B_{i} ^{2} \cosh \left( {B_{i} } \right)}}{{A_{i} {\kern 1pt} B_{i} \sin \left( {A_{i} } \right) + B_{i} ^{2} \sinh \left( {B_{i} } \right)}}\left[ {\sinh \left( {B_{i} {\kern 1pt} s} \right) - \frac{{B_{i} }}{{A_{i} }}\sin \left( {A_{i} {\kern 1pt} s} \right)} \right], $$

(28)

where

$$ A_{i} = \sqrt {\frac{{J_{\eta } }}{2}\omega _{i} ^{2} + \sqrt {\frac{{J_{\eta } ^{2} }}{4}\omega _{i} ^{4} + \omega _{i} ^{2} } } ,\quad B_{i} = \sqrt { - \frac{{J_{\eta } }}{2}\omega _{i} ^{2} + \sqrt {\frac{{J_{\eta } ^{2} }}{4}\omega _{i} ^{4} + \omega _{i} ^{2} } } , $$

(29)

and the natural flexural frequencies are the roots of the nonlinear transcendental equation

$$ \left( {B_{i} ^{4} + A_{i} ^{4} } \right)\cos \left( {A_{i} } \right)\cosh \left( {B_{i} } \right) + \left( {B_{i} ^{2} - A_{i} ^{2} } \right)A_{i} {\kern 1pt} B_{i} \sin \left( {A_{i} } \right)\sinh \left( {B_{i} } \right) + 2A_{i} ^{2} B_{i} ^{2} = 0. $$

(30)

In the Galerkin procedure, the geometric imperfection w₀, the static deflection w_s,, and the dynamic deflection w_d have the form of the first vibration mode, leading to a sdof reduced-order model, an usual procedure in the literature [2, 9, 10]. In the following analysis, for simplicity, the symbols used for the modal amplitudes are the same as those adopted for the state variables.

3 Nonlinear equilibrium and deterministic local dynamics

The nondimensional constants adopted here are the same employed in [19, 24] and are summarized in Table 1.

Table 1 Microbeam geometric and material nondimensional parameters

3.1 Static actuation

The equilibrium equation is obtained by multiplying Eq. (24) by the denominator $\left( {1 - \bar{w}_{s} } \right)^{2}$ and then applying the Galerkin method. The nonlinear equilibrium paths are obtained through a pseudo-arc-length continuation procedure together with the Newton–Raphson method [48, 49]. The stability of the static solution is verified using the minimum energy criterion. In Fig. 3, where the maximum deflection of the beam, $w_{s}$, is plotted as a function of the electrostatic forcing, $V_{{{\rm{dc}}}}$, the present results are compared with the experimental results reported in [24]. Also, for comparison purposes the results for the imperfect beam considering a small imperfection magnitude ($w_{0} = \pm 0.05$) are also shown, clarifying the influence of the imperfection uncertainties on the results. A good agreement with the experimental results is observed up to pull-in [24]. Specifically, the perfect system static pull-in actuation is 65.34, while the experimental result is 68.5. The resulting ratio is 0.953, corroborating the accuracy of the present model.

Fig. 3

Comparison of the present analytical results for the perfect and imperfect microbeam under DC actuation with the experimental results reported in [24]

Figure 4a shows the nonlinear response of the beam under DC actuation for selected levels of geometric imperfection. Here, continuous lines correspond to stable solutions, while dashed lines correspond to unstable solutions. Figure 4b shows the typical cusp catastrophe surface by introducing the imperfection magnitude as a second control parameter. The two limit points along the nonlinear equilibrium path are rather sensitive to the imperfection magnitude and sign, decreasing with positive imperfections and increasing with negative imperfections.

Fig. 4

Static response of the microbeam under DC actuation for selected levels of geometric imperfection a nonlinear equilibrium paths b cusp catastrophe surface

The pull-in instability is present in all cases, being the pull-in voltage particularly sensitive to the imperfection level and sign. The perfect system obtained pull-in voltage is 65.341 V, being in good agreement with the formula presented in [2], where the pull-in voltage is 67.443 V for the constants adopted in [19, 24]. The imperfection changes the pull-in voltage band; for w₀ > 0, the gap between the beam and the actuator plate decreases, resulting in lower pull-in voltages and a system more susceptible to this type of instability. On the other hand, the pull-in load and consequently the stability increases for w₀ < 0. This dependency is illustrated in Fig. 5.

Fig. 5

Dependency of the static pull-in voltage on the magnitude and sign of the geometric imperfection

The dependency of the natural frequency of vibration on the DC voltage is well known for microelectromechanical beams [2]. In order to investigate the combined influence of the DC voltage and geometric imperfection magnitude on the natural frequencies, Eq. (25) is linearized, and the damping coefficient and AC voltage are set to zero, resulting in

$$\begin{aligned} &\ddot{w}_{d} -\frac{{b{\kern 1pt}\varepsilon {\kern 1pt}w_{d} \left({V_{{{\rm{dc}}}} }\right)^{2} }}{{d^{3} \left({1 - \bar{w}_{s} }\right)^{3} }} = \left\{ { -d^{2} \left[ {\left({\bar{w}_{s}^{{\prime 2}}+ \frac{1}{{d^{2} }}}\right)w^{\prime\prime \prime}_{d} + \left({w^{\prime}_{d}\bar{w}^{\prime}_{s}\bar{w}^{\prime\prime}_{s}} \right)^{\prime } +\bar{w}^{\prime}_{s} \left({w^{\prime\prime}_{d}\bar{w}^{\prime\prime}_{s}+ w^{\prime}_{d}w^{\prime\prime\prime}_{s}} \right)} \right]} \right.\\&\quad + {\kern 1pt} d^{2}\left. {J_{\eta }\ddot{w}^{\prime}_{d} \left({\bar{w}_{s}^{{\prime 2}}+ \frac{1}{{d^{2} }}} \right)- d^{2}\bar{w}^{\prime}_{s}\int_{1}^{s} {\int_{0}^{s}{\bar{w}^{\prime}_{s}{\kern 1pt}\ddot{w}^{\prime}_{d}{\rm{d}}s} {\kern 1pt}{\rm{d}}s} } \right \}^{\prime } .\\\end{aligned}$$

(31)

where the influence of the imperfection and DC voltage can be observed.

Figure 6 shows the influence of the imperfection magnitude w₀ and DC voltage on the lowest natural frequency. As expected, the imperfection significantly affects the natural frequency of vibration. Furthermore, in the region of the cusp catastrophe in Fig. 4b, the system shows three distinct frequencies, two with real values (ω² > 0) and one with imaginary value (ω² < 0). The real frequencies correspond to stable solutions, while the imaginary frequency corresponds to the unstable solution. Also, for a threshold of approximately w₀ > 0.3, only one frequency persists for all DC voltages, corroborating the result presented in Fig. 5.

Fig. 6

Natural frequency of vibration dependency against DC voltage and imperfection w₀

3.2 Dynamic actuation

For the dynamic analysis, a direct current voltage V_dc = 45 V is adopted. Also, a periodic alternate voltage between the beam and the substrate,

$$ V_{{ac}} \equiv \bar{V}_{{ac}} \cos \left( {\Omega {\kern 1pt} t} \right). $$

(32)

is considered, where $\bar{V}$_ac is the forcing magnitude and $\Omega$ the forcing frequency.

Different values of static deflection w_s can be obtained depending on the imperfection magnitude, as shown in the static analysis. The static deflection for six selected levels of imperfection, varying from 0 to 0.05, is shown in Table 2.

Table 2 Static deflection as a function of the imperfection magnitude for V_dc = 45 V

Five different equations of motion are obtained from Eq. (25) by applying the Galerkin expansion for the values of V_dc, w₀, and w_s given in Table 2. For the numerical integration of the equations of motion, the fourth-order Runge–Kutta method is employed with a time-step $\Delta t = T/4000,$ where T is the period of the excitation, T = 2π/Ω. Resonance curves are obtained through a pseudo-arc-length continuation of periodic orbits [48, 49] for three values of the forcing magnitude, namely $\bar{V}$_ac = 1, 5, 10. The stability of each solution is verified through the analysis of Floquet multipliers (eigenvalues of the monodromy matrix), which also allow the characterization of the bifurcation type.

According to [19], the nonlinear response of the microbeam can be either of the softening or hardening type, depending on which type of nonlinearity prevails. The load nonlinearity leads to a softening behavior while the geometric nonlinearity, to a hardening behavior. Figure 7 displays the resonance curves of the microbeam for selected values of AC actuation and increasing imperfection level w₀ and V_dc = 45. As in the static case, continuous lines denote stable solutions and dashed lines, unstable solutions. The nonlinear response is of softening type for all values of w₀ and $\bar{V}$_ac for the chosen initial gap d (Table 1), in agreement with the experimental results in [24].

Fig. 7

Frequency–response curves for selected values of AC actuation, with V_dc = 45. SN—saddle-node bifurcation, PD—period-doubling bifurcation

As $\bar{V}$_ac increases, a pull-in bandwidth develops, thus making the system more susceptible to dynamic pull-in instability. The imperfection decreases the values of $\bar{V}$_ac for which the pull-in band appears and increases the pull-in bandwidth as illustrated in Fig. 8 for $\bar{V}$_ac = 10. Also of notice is, in all cases, the resonant peak at a forcing frequency equal to half of the natural frequency where a second pull-in band is observed for w₀ ≥ 0.03. As the imperfection level increases, the resonant peak at a third of the natural frequency also increases, leading to an additional resonance region that may influence the microbeam dynamic response.

Fig. 8

Frequency–response curves for V_dc = 45 and V_ac = 10. Pull-in bandwidth as a function of the imperfection magnitude. SN—saddle-node bifurcation

4 Global dynamics: stochastic vs deterministic analysis

The global dynamics of the dynamically actuated microbeam is now addressed. The Ulam method [50], also known as the generalized cell-mapping [44,45,46], is employed together with the equations of motion to approximate the Perron–Frobenius operator ${\mathcal{P}}_{t}$ as a probability transition matrix p_ij [50]. Then, following Lindner and Hellmann [51], the discrete Koopman operator ${\mathcal{K}}_{t}$ is considered to obtain the structure of the stochastic basin of attraction in phase space [61]. A detailed description of this procedure and the related mathematical concepts are presented in the “Appendix”.

Initially, the present implementation is first validated using the stochastically excited Duffing equation,

$$ \ddot{x} + \eta \dot{x} + \alpha x + \beta x^{3} = F\cos \left( {\omega {\kern 1pt} t} \right) + \sigma \dot{W}, $$

(33)

recently investigated in [52], where $\eta$ is the viscous damping parameter, $\alpha$ is the linear stiffness parameter, $\beta$ is the cubic stiffness parameter, F is the forcing magnitude, $\omega$ is the forcing frequency, σ is the noise amplitude and $\dot{W}$ is the white noise, which is the time derivative of the Wiener process W.

The first-order system in Langevin form is given by

$$ \begin{aligned} & {\rm{d}}x = v \\ & {\rm{d}}v = \left[ { - \eta v - \alpha x - \beta x^{3} + F\cos \left( {\omega {\kern 1pt} t} \right)} \right]{\rm{d}}t + \sigma {\rm{d}}W, \\ \end{aligned} $$

(34)

where dW is interpreted in the Itô sense. If the noise amplitude is set to zero, the equation is reduced to the deterministic Duffing equation. The chosen parameters are based on [54] and are reproduced for completeness in Table 3. The phase space is restricted to ${\mathbb{X}} = \left( {x,\dot{x}} \right) = \left[ { - 3.5,3.5} \right]^{2}$, which is divided into 300 × 300 cells for the global analysis. Twenty-five points in each cell are integrated for one period of excitation to obtain the transition probability matrix p_ij. For these parameters, the deterministic Duffing equation has two stable solutions, a periodic stable solution with the same period as the forcing and a chaotic solution, as illustrated in Fig. 9 through the basins of attraction. The color bar varies from 0 to 1, where 0 indicates regions not belonging to the depicted attractor, and 1 indicates regions belonging to the depicted attractor. The boundary between these basins is well defined, as expected in deterministic dynamical systems. The Poincaré sections are identified by the red dots. These results agree with those in [54], showing that the implementation correctly addresses the deterministic case.

Table 3 Duffing equation parameters [54]

Fig. 9

Basins of attraction for the deterministic Duffing equation, σ = 0

Figure 10 shows the steady-state probability density distribution for the Duffing equation for two values of the noise amplitude σ. For σ = 0, the probability density distribution has two well-defined separate regions, one corresponding to the periodic attractor and another corresponding to the chaotic attractor, as shown in Fig. 10a. Since there is no noise, the dynamics is deterministic, and, therefore, each phase space pair of initial conditions converges to only one attractor. Next, the system with added noise is investigated. For this, each of the 25 points per cell is evaluated 100 times. Therefore, each cell is integrated 2500 times, for one period, to construct the transient probability matrix. The attractors’ probability density distribution for σ = 0.012 is shown in Fig. 10 b, where the noisy chaotic and periodic attractors can be observed. As the noise amplitude increases, the attractors spread over significant regions of the phase space. Still, the two attractors are discernable from each other. This is more evident when analyzing the 2D and 3D views of the coexisting basins of attraction, Fig. 11, where two basins of attraction are identified, with the steady-state response associated with any initial conditions in the chaotic or periodic basin, converging to their noisy chaotic attractor or a noisy periodic attractor. However, the boundaries are no longer well defined, being blurred due to the noise. In these regions, the steady-state response of initial conditions may converge to either attractor, depending on the sampled noise. The color scale in this and the following basins are related to the probability of the response converging to each attractor, varying from 0 to 1, as clarified by the 3D views of each basin.

Fig. 10

Steady-state probability density distribution for the Duffing equation for selected values of σ

Fig. 11

Basins of attraction for the Duffing equation, σ = 0.012

Finally, we consider the Duffing equation with σ = 0.045. This noise amplitude is high enough to merge the two attractors’ probability density, as illustrated in Fig. 12. Therefore, only one attractor remains. Since only one global attractor remains, its basin is the entire phase space. As the noise level increases, jumps from the chaotic to the periodic attractor occur until a threshold value of σ = 0.05 is reached. For higher noise levels, jumps between the chaotic and periodic attractors in both directions can occur. Again, the results are in agreement with those in [52].

Fig. 12

Steady-state probability density distribution for the Duffing equation, σ = 0.045

4.1 Microcantilever analysis

With the implementation validated, the global analysis of the planar dynamics the electrostatically actuated microbeam is now investigated considering the phase space ${\mathbb{X}} = \left[ { - 3,3} \right]^{2}$, with the boundaries assumed as of the absorbing type. This region is discretized with 300 × 300 cells, with 5 × 5 initial conditions uniformly distributed within each cell. The same equations of motion used in the local dynamic analysis are considered, with parameters given in Tables 1 and 2. However, an additive stochastic excitation $\sigma {\kern 1pt} \dot{W}$ is also considered resulting in stochastic differential equations of Itô type. The white noise is added after the modal decomposition through the Galerkin method, directly into the modal equations of motion, similar to the Duffing equation [54]. A stochastic Runge–Kutta method of fourth order in drift and half order in diffusion is employed, with a time-step $\Delta t = T/4000,$ where T is the period of excitation, T = 2π/Ω. For the stochastic cases (σ ≠ 0), each initial condition is integrated 100 times, giving 2500 trajectories in each cell. The time interval of integration corresponds to one excitation period in all cases, resulting in a one-period stochastic transition matrix p_ij. Probability density distributions and (stochastic) basins of attraction are then obtained.

First, numerical simulations have been carried out for the nonlinear system with V_dc = 45, $\bar{V}$_ac = 1, and Ω = 2.8. Six combinations of the parameters w₀ and σ are considered with w₀ = 0.01, 0.02, and σ = 0, 0.01, 0.02. For these six cases, only one attractor exists, as observed in Fig. 7a, b. The stochastic basin of attraction is depicted for the selected values of w₀ and σ in Fig. 13, where the light blue region corresponds to the periodic 1 T non-resonant attractor and black to pull-in, i.e., zero probability of converging to the non-resonant attractor. This basin persists for all noise levels, with minor changes near the saddle region, suggesting that the attractor is resilient to noise for small imperfection levels and noise magnitudes. The noise effect is more evident in the attractor’s distribution. As the noise increases, the Poincaré section of the attractor spreads to larger regions in phase space, as indicated by the red region in Fig. 13.

Fig. 13

Microbeam stochastic basin of attraction for V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, low imperfection and noise levels. Light blue: non-resonant attractor, black: pull-in

The next example demonstrates the effect of higher imperfection levels on the results. As shown in Fig. 7, the softening nonlinearity increases with the imperfection magnitude. Considering again V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8 but w₀ = 0.05, the deterministic microbeam has non-resonant and resonant attractors, as shown in Fig. 7f. Figure 14 shows the stochastic basin of attraction of the non-resonant periodic attractor for σ = 0, σ = 0.01, and σ = 0.02, while Fig. 15 shows the results for the resonant attractor and Fig. 16 depicts the set of initial conditions leading to pull-in. The non-resonant attractor overall size decreases in comparison with the previous case, Fig. 13. For σ = 0.00, the basin boundary is well defined, as shown in Figs. 14a, 15a, b, and 16a, with the black regions corresponding to initial conditions leading to pull-in, demonstrating the destabilizing effect of the geometric imperfections. As the noise increases, the probability of the noisy response converging to the resonant attractor decreases, and its basin shrinks with only 10–20% of solutions asymptotically converging to this region for σ = 0.01, as observed in Fig. 15c,d. In contrast, as shown in Fig. 14b, most trials converge to the non-resonant attractor. The pull-in region remains practically unaltered except for a small region near the saddle. For σ = 0.02, only the non-resonant solution remains, comprising the regions initially occupied by the non-resonant and resonant basins. The probability density distribution evolution with the noise level clarifies this, Fig. 18, showing the collapse of the resonant solution and the spread of the noisy non-resonant attractor. For σ = 0.00, two well-defined peaks are observed, while for σ = 0.01, the noisy resonant attractor spreads to a large region with low probability and approaches noisy non-resonant attractor. Finally, for σ = 0.02, the resonant attractor completely disappears, while the remaining attractor spreads over a larger region of the phase plane, see Fig. 14c. However, the pull-in region remains largely unaffected by noise.

Fig. 14

Microbeam stochastic basin of attraction for the non-resonant attractor, with V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, w₀ = 0.05

Fig. 15

Microbeam stochastic basin of attraction for the resonant attractor, with V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, w₀ = 0.05

Fig. 16

Set of initial conditions leading to pull-in, with V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, w₀ = 0.05

In previous papers, for example, Orlando et al. [53], Silva and Gonçalves [54], and Silva et al. [55], the effect of noise on the global dynamics was investigated using the Monte Carlo method, and the cells where different samples led to different attractors were identified and excluded from the safe basins of the coexisting solutions. Here, a more refined analysis is considered where not only these cells are identified but also the probability of the ensuing response converging to one of the attractors is evaluated. Evaluation of probability through Monte Carlo approach using a large number of samples for each cell is a computationally demanding procedure. Here, the exact probability quantification of the basin boundaries and noisy attractors allows the effect of noise to be addressed more precisely and is important in various applications including the dynamic integrity analysis [35, 56].

Figures 17 and 18 show the effect of increasing noise on the time histories and Poincaré maps. The initial condition $(w_{1} ,\dot{w}_{1} ) = (0,0)$ in the non-resonant region and the initial condition $(w_{1} ,\dot{w}_{1} ) = ( - 0.1,0.6)$ in the resonant region are adopted. Time histories for initial conditions in the non-resonant region, Fig. 17, display increasing irregularity as noise increases, as illustrated by the spreading of the Poincaré map, whose size is a function of the noise intensity. Time histories for initial conditions in the resonant region, Fig. 18, also exhibit increasing irregularity with noise. For large noise levels, the response loses stability and converges to the non-resonant attractor, Fig. 18c. The probability density distribution evolution with the noise illustrates this, Fig. 19, showing the collapse of the resonant solution.

Fig. 17

Microbeam time histories, phase space projections, and Poincaré sections for V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, w₀ = 0.05 and increasing noise level. Non-resonant attractor, initial condition $\left( {w_{1} ,\dot{w}_{1} } \right) = \left( {0,0} \right)$

Fig. 18

Microbeam time histories, phase space projections, and Poincaré sections for V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, w₀ = 0.05 and increasing noise level. Resonant attractor, initial condition $\left( {w_{1} ,\dot{w}_{1} } \right) = \left( { - 0.1,0.6} \right)$

Fig. 19

Microbeam attractor’s probability density distribution for V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, high imperfection: w₀ = 0.05

The limited phase space discretization for the Ulam method can affect the quality of the results, requiring a refinement analysis to check the convergence. To verify the convergence of the stochastic response, Monte Carlo experiments were conducted, where each initial condition was integrated for 10,000 periods 5000 times, generating 5000 samples. The final histograms for σ = 0.01 and σ = 0.015 are shown in Fig. 20 for both attractors. For σ = 0.015, the paths starting in the resonant initial condition almost entirely end in the non-resonant region, as correctly addressed by the probability density distributions in Fig. 19. Although the Monte Carlo experiments and the Ulam method are conceptually different, the results are in qualitative agreement, showing the potentiality of the present strategy. Also, the present results demonstrate that the decrease in the probability of a given region directly influences its dynamic integrity [35, 56] measures, and this must be taken into account in systems with noise.

Fig. 20

Microbeam’s histograms obtained from the Monte Carlo simulation for two initial conditions at time t = 10,000 T integrated 5000 times. V_dc = 45, $\bar{V}$_ac = 1, Ω = 2.8, w₀ = 0.05. a, c non-resonant initial condition, b, d resonant initial condition

A system with a medium level of AC actuation, $\bar{V}$_ac = 5 and w₀ = 0, is now considered to demonstrate the noise impact in more detail. Again there are two coexisting periodic attractors due to a region of hysteresis (see Fig. 7). Figure 21 shows the non-resonant stochastic basin of attraction for 0 ≤ σ ≤ 0.014. There are little or no qualitative changes observed in the basin area for these noise levels, displaying the same behavior observed for $\bar{V}$_ac = 1, apart from spreading the Poincaré section, with the low probability region restricted to the long tail. However, the resonant stochastic basin, Fig. 22, changes significantly, with finger-like regions leading to pull-in (see Fig. 23) eroding the basin. These finger-like regions are similar to those observed in the escape equation due to a homoclinic tangle [57, 58]. The probability of the resonant solution along the borders of these finger-like regions decreases with the noise level, as shown by the color scale, diffusing from the boundary to the compact region. Also, a significant spread of the attractor is observed, approaching the basin boundary as the noise level increases. This also affects the probability of pull-in, as shown in Fig. 23. The color scheme is the same as in the previous figures for $\bar{V}$_ac = 1.

Fig. 21

Evolution of the microbeam non-resonant stochastic basin of attraction as a function of the noise level V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0, low noise level

Fig. 22

Evolution of the microbeam resonant stochastic basin of attraction as a function of the noise level for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0, low noise level

Fig. 23

Set of initial conditions leading to pull-in as a function of the noise level for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0, low noise level

A drastic change occurs for σ = 0.015, see Figs. 24a and 25a. For this noise level, the two basins of attraction cannot be distinguished from each other, which indicates that jumps can happen between the possible three outcomes. As the noise increases even further (σ = 0.02), no initial condition has more than a 50% probability of converging to the resonant region, Fig. 24b. For the last noise level (σ = 0.025), the resonant solution no longer exists, merging with the pull-in region, see Fig. 25c, with only the non-resonant attractor remaining. Time histories for initial conditions in the non-resonant and resonant regions together with phase space projections and respective Poincaré maps are shown in Figs. 26 and 27 to complement the analysis. As expected, the pull-in occurs for σ = 0.025, considering the initial condition in the resonant region. Furthermore, the time series with σ = 0.015, Fig. 26a, d, and σ = 0.020, Fig. 26b, e, remain separated for a long time.

Fig. 24

Evolution of the microbeam stochastic basin of attraction as a function of the noise level for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0s

Fig. 25

Set of initial conditions leading to pull-in as a function of the noise level for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0

Fig. 26

Microbeam time histories, phase space projections, and Poincaré sections for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0 and increasing noise level. Non-resonant initial condition $\left( {w_{1} ,\dot{w}_{1} } \right) = \left( {0,0} \right)$

Fig. 27

Microbeam time histories, phase space projections, and Poincaré sections for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0 and increasing noise level. Resonant initial condition $\left( {w_{1} ,\dot{w}_{1} } \right) = \left( { - 0.4,0.4} \right)$

The evolution of the probability density distribution is depicted in Fig. 28. The first notorious change happens between the deterministic case, Fig. 28a, and the first stochastic case, Fig. 28b. The deterministic case has well-defined attractors. This is expected for deterministic systems, where point attractors or Poincaré sections possess Dirac delta distributions. As the noise level increases, the resonant solution’s sensibility to noise is clearly observed, spreading the attractor over the phase space. The last cases, Fig. 28g, h, show the vanishing of the resonant solution due to the high noise level. Again, Monte Carlo experiments were conducted for verification, where each initial condition was integrated for 10,000 periods 5000 times; generating 5000 sample paths, see Fig. 29. As expected, the non-resonant attractor is stable for all three noise levels, see Fig. 29a, c, e, agreeing with the Ulam method results. The resonant attractor loses stability for the last noise case, Fig. 29f, with even some solutions converging to the non-resonant attractor. Escape is not depicted in the histogram because its time response is not located in a limited-size phase space. The percentage of escape is 81.78%, and only 11.54% of the sample are in the resonant region at time t = 10,000 T, qualitatively agreeing with the Ulam method.

Fig. 28

Microbeam attractor’s probability density distribution as a function of the noise levels for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0

Fig. 29

Microbeam’s histograms obtained from the Monte Carlo simulation for two initial conditions at time t = 10,000 T integrated 5000 times for V_dc = 45, $\bar{V}$_ac = 5, Ω = 2.8, w₀ = 0. a, c, e non-resonant initial condition, b, d, f resonant initial condition

5 Concluding remarks

The microfabrication process may produce relevant geometric imperfections. Also, the presence of noise is inevitable in real systems. Here, the theoretical investigation has been conducted on an imperfect MEMS device constituted of an imperfect clamped-free microbeam electrostatically and electrodynamically actuated with added noise. Using Hamilton’s principle, the nonlinear equation of motion is derived by considering the nonlinear electrical load, the geometric nonlinearities, the geometric imperfections, and noise. The continuous system is then discretized and reduced into a sdof system via the Galerkin method. The investigation focuses on the static and dynamic response of the microbeam in the neighborhood of the first resonance region. After introducing the formulation of the mechanical model, which takes into account the most relevant imperfection, a single-mode reduced-order model has been derived via the Galerkin technique. Both the nonlinearity of the electric force and the geometric nonlinearity of the beam are taken into account. Then, the transfer operators’ discretization used in the stochastic analysis is presented, and the stochastic differential equation of Itô type is solved by the stochastic Runge–Kutta method. Additionally, the global dynamics of the stochastic system is examined through generalized cell mapping,

The static nonlinear response of the microbeam under DC voltage displays two limit points delimiting the unstable branch of solutions that separates the two stable branches, leading to a multistability range and hysteresis. If the imperfection magnitude is added as a second control parameter, the obtained surface exhibits the typical cusp geometry, where one stable solution may suddenly jump to an alternate outcome due to the existence of competing solutions. The prevailing solution is highly dependent on imperfection and noise levels. The pull-in instability is present in most cases, being the pull-in voltage particularly sensitive to the imperfection level and sign. When the imperfection decreases the gap between the beam and the actuator plate, the pull-in voltage decreases, and the system becomes more susceptible to this type of instability. On the other hand, the pull-in load increases when the gap increases, and no static pull-in is observed after a certain threshold value. Also, the lowest natural frequency is significantly affected by the simultaneous effect of the DC voltage and geometric imperfection, becoming zero at the limit points in the region of the cusp catastrophe where it shows two distinct vibration frequencies. The resonance curves of the imperfect microbeam under AC actuation exhibit a softening response due to the fact that the load nonlinearity (which is of the softening type) is stronger than the geometric nonlinearities (which is of the hardening type) for small values of the initial gap. In these resonant regions, the coexistence of a stable non-resonant and a resonant branch is observed bending toward lower frequencies regions. As the forcing magnitude increases, it increases the multistability range and the pull-in bandwidth, thus making the system more susceptible to dynamic instability. The imperfection decreases the values at which the pull-in band is formed and increases the pull-in bandwidth. Therefore, higher imperfections increase the vulnerability of the microbeam to dynamic pull-in instability. Also of notice is in all cases, the resonant peak at a forcing frequency equals to half the natural frequency, also exhibiting a softening behavior and leading in some cases to pull-in bandwidth. As the imperfection level increases, the resonant peak at a third of the natural frequency also increases, leading to an additional resonance region that may influence the microbeam dynamic response. The formulation and results for the noisy problem are tested, comparing the results with those obtained for the Duffing equation in [52], showing excellent agreement. For the microbeam, the simulations reveal that the erosion of the basins of attraction depends not only on the amplitude and frequency of the AC voltage but also on the imperfection level and the noise magnitude. As the noise level increases, the probability density distribution along the basin boundaries spreads, which dramatically increases the sensitivity of the microbeam to initial conditions. The influence of noise on the time response of competing attractors may lead to complex responses with successive jumps between the competing attractors. Both examples show that attractors can disappear or merge depending on the noise level, having a significant influence on the nonlinear dynamics of the microbeam, and the threshold value of the intensity for noise generating a transition from the coexistence to extinction is estimated. While the present investigation concerns a specific structural system, the present framework can be employed to examine the effect of noise and uncertainties in other nonlinear problems, including higher dimensional systems.

Appendix: Stochastic dynamical systems and transfer operators

In this appendix, some essentials concepts of stochastic dynamical systems and transfer operators, necessary to understand the methodology employed in this work, are presented. Consider a measurable dynamical system $\left({{\mathbb{X}},{\mathbb{T}},\varphi _{t} } \right)$ over a phase space ${\mathbb{X}}$ (usually Euclidean), naturally endowed with a Borel σ-algebra ${\mathfrak{B}}\left({\mathbb{X}} \right)$, with a time set (additive semigroup) ${\mathbb{T}}$, continuous or discrete [59]. The flow is defined as

$$ \begin{gathered} \varphi :{\mathbb{X}} \times {\mathbb{T}} \to {\mathbb{X}} \hfill \\ \left( {x,t} \right) \mapsto \varphi _{t} {\kern 1pt} x, \hfill \\ \end{gathered} $$

(35)

with the following properties

$$\begin{array}{*{20}l} {1.}\hfill & {\varphi_{0} x ={\rm{id}}_{{\mathbb{X}}},} \hfill \\ {2.} \hfill & {\left({\varphi_{s} \circ \varphi_{t}} \right)x = \varphi_{{s + t}}x,} \hfill \\ {3.} \hfill &{\varphi_{t} x{\text{ is measurable in }}{\mathfrak{B}}\left({\mathbb{X}} \right) \otimes {\mathfrak{B}}\left({\mathbb{T}} \right),{\mathfrak{B}}\left({\mathbb{X}} \right).} \hfill \\ \end{array}$$

(36)

If the triplet $\left( {{\mathbb{X}},{\mathfrak{B}}\left( {\mathbb{X}} \right),P} \right)$ defines a probability space over the phase space, then P is its probability measure. For deterministic dynamical systems, chaotic systems, or parametric uncertain dynamical systems, P is the Dirac measure. The Dirac measure is a probability measure that represents, in terms of probability, an almost sure outcome in the sample space.

For the case of stochastic excitations, such as random noise, the dynamical system is defined as random, constituting a cocycle over the random noise space. Therefore, differences between the invariant measure structures of the deterministic and stochastic case are substantial [60]. Considering a metric dynamical system $\left( {\Omega ,({\mathfrak{F}},P),{\mathbb{T}},\theta _{t} } \right)$, such as a stochastic process, a random dynamical system $\varphi _{t}$ has the following properties:

$$ \begin{array}{*{20}l} {1.} \hfill & {\varphi {\text{ is measurable in }}{\mathfrak{F}} \otimes {\mathfrak{B}}\left( {\mathbb{T}} \right) \otimes {\mathfrak{B}}\left( {\mathbb{X}} \right),{\mathfrak{B}}\left( {\mathbb{X}} \right),} \hfill \\ {2.} \hfill & {\varphi _{t} \left( \omega \right)x:{\mathbb{X}} \to {\mathbb{X}}{\text{ form a cocyle over }}\theta _{t} {\kern 1pt} \omega :} \hfill \\ {} \hfill & {{\rm{i}}.\;\;\varphi _{0} \left( \omega \right)x = {\rm{id}}_{{\mathbb{X}}} ,\quad \forall \omega \in \Omega ,} \hfill \\ {} \hfill & {{\rm{ii}}.\;\;\varphi _{{s + t}} \left( \omega \right)x = \left( {\varphi _{s} \left( {\theta _{t} {\kern 1pt} \omega } \right) \circ \varphi _{t} \left( \omega \right)} \right)x,\quad \forall s,t \in {\mathbb{T}},\;\omega \in \Omega .} \hfill \\ \end{array} $$

(37)

The property 2.ii is also termed the cocycle property and can be rewritten as $\varphi _{{s + t}} \left( \omega \right)x = \varphi _{s} \left( {\theta _{t} {\kern 1pt} \omega } \right)\varphi _{t} \left( \omega \right)x$. An important characteristic of random dynamical systems is that they reduce to measurable dynamical systems if $\theta _{t}$ is constant over time.

The measures’ evolution of both deterministic and stochastic dynamical systems is governed by the Perron–Frobenius operator ${\mathcal{P}}_{t}$ and the Koopman operator ${\mathcal{K}}_{t}$. The Perron–Frobenius operator acts on density distributions f and is defined as

$$\begin{aligned} &{\mathcal{P}}_{t} :L_{n}\left( {\mathbb{X}} \right)\to L_{n} \left({\mathbb{X}} \right), \\&\int_{A}^{{}}{{\mathcal{P}}_{t} {\kern 1pt} f{\rm{d}}\mu } = \int_{\varphi_t^{-1}\left(A \right)}^{{}} {f{\rm{d}}\mu }, \\&\forall f \ge 0,f \in L_{n} \left( {\mathbb{X}}\right),A \in {\mathfrak{G}},\\\end{aligned}$$

(38)

where n ≥ 1. The measure μ can be the Lebesgue measure or a more complicated structure, such as a Dirac measure or a tensor product between the phase space and the stochastic space [61]. The Koopman operator is given by

$$ \begin{gathered} {\mathcal{K}}_{t} :L_{\infty } \left( {\mathbb{X}} \right) \to L_{\infty } \left( {\mathbb{X}} \right) \hfill \\ {\mathcal{K}}_{t} g = g \circ \varphi _{t} , \hfill \\ \forall g \in L_{\infty } \left( {\mathbb{X}} \right), \hfill \\ \end{gathered} $$

(39)

acting on the real-valued observables $g$ of the dynamical system φ_t. The transfer operators are dual to each other, i.e.:

$$ \left\langle {{\mathcal{P}}_{t} f,g} \right\rangle _{\mu } = \left\langle {f,{\mathcal{K}}_{t} g} \right\rangle _{\mu } . $$

(40)

Therefore, one operator can be obtained from the other without further difficulties.

The Perron–Frobenius operator ${\mathcal{P}}_{t}$ defines a functional linear dynamical system over φ_t. It follows an ensemble of trajectories, where φ_t is the evolution of only one trajectory. Complicated nonlinear flows, both deterministic and stochastic, can be represented in this manner, with each particular topology of φ_t having a counterpart of ${\mathcal{P}}_{t}$ [59].

The discretization of the transfer operators is obtained by the generalized cell mapping [44,45,46]. Guder and Kreuzer [50] proved that the generalized cell mapping is identical to the Ulam method, which approximates ${\mathcal{P}}_{t}$ by a zero-order Galerkin method. The phase space is discretized into a disjoint collection of k sets, {b₁,…,b_k}, and ${\mathcal{P}}_{t}$ is approximately given by

$$ {\mathcal{P}}_{t} \approx p_{{ij}} = \frac{{\mu \left( {\varphi _{t} ^{{ - 1}} \left( {b_{i} } \right) \cap b_{j} } \right)}}{{\mu \left( {b_{j} } \right)}}, $$

(41)

where p_ij are elements of a stochastic matrix [p_ij]. Briefly, each element p_ij corresponds to the probability of the system φ_t evolving from set b_j to set b_i. In this work, these probabilities are approximated by a Monte Carlo sampling, as in the generalized cell mapping. Also, the Koopman operator approximation is obtained by the transpose of [p_ij], [k_ij] = [p_ij]^*, due to the dual relation in Eq. (40).

Lindner and Hellmann [51] demonstrated that the fixed space of [k_ij] could be used to approximate the basin structures of φ_t. This result is explored in this study, and stochastic basins of attractions are obtained by adopting the concept of 0-absorption stability as the infinity time convergence of dynamical systems. Absorbing boundary conditions have been developed for various types of problems to truncate infinite domains in order to perform computations.