1 Introduction

Dynamics of a nonlinear system depends on the parameters chosen in the governing equation of motion. With a variation in the chosen control parameter, the qualitative behavior of nonlinear system can be drastically changed. For certain parameter ranges, a nonlinear system can exhibit chaotic behavior.

There is a large body of literature on chaotic attractors of a nonlinear system and their basins of attraction. Bifurcation theory can be used to describe the way in which different attractors are created or destroyed with the change in system parameters. There are several routes to chaos, and a positive Lyapunov exponent is indicative of chaos. After chaos is born, a further variation in system parameters can lead to interesting results that can have potential applications in controlling system dynamics. As a control parameter is varied, a sudden discontinuous change in the chaotic attractor of a dissipative dynamical system is called “crisis,” a term introduced in reference [1]. A crisis occurs when a chaotic attractor comes into contact with an unstable periodic orbit (see for example, [2, 3] for a detailed discussion). The crisis can be identified as a boundary/exterior crisis, or interior crisis, or attractor merging crisis [1, 2, 4, 5]. A 1D quadratic map can exhibit all three types of crises [2]. The forced Duffing oscillator is one of the non-autonomous systems, which can exhibit crisis [6]. The Duffing equation has been the subject of experimental and numerical investigations over a wide range of system parameter values, and different dynamics have been observed with this system including chaos, depending on the nature of the physical system being studied [7,8,9,10,11]. In the last decade, extensive results on the effect of noise on nonlinear systems dynamics have been reported [12,13,14,15]. Xu [16] has investigated the stochastic bifurcation and crisis through the global generalized cell mapping in a twin-well Duffing system subject to a harmonic excitation in the presence of noise.

Recently, in reference [15], the authors report how the introduction of noise in a Duffing oscillator can influence the frequency response curve and destroy it. Here, the authors subject chaotic trajectories to white Gaussian noise at low levels, levels that are just sufficient to cause a trajectory to escape from the basin. It is reported that there is specific escape route that the trajectory always follows—according to the authors’ experimental and computational results. Here, the boundary of the basin of the chaotic attractor is the stable manifold of a periodic orbit. This manifold is captured through a stroboscopic plotting of data. As the trajectory escapes, it is observed that it is essentially on the basin boundary. The dynamics pulls the trajectory to the fixed point on the boundary and the trajectory escapes along the unstable manifold. The experiments were repeated many times, and it was confirmed that the trajectory always escapes the basin in the same way.

In the conclusion section, the authors compare and contrast the experiments with numerical simulations. Here, the authors have compared their computational investigations with corresponding experimental studies of the influence of white Gaussian noise on the chaotic responses of a bistable Duffing oscillator. While the present study concerns a specific system with specific parameters, the authors believe that the observed phenomena is quite general and the escape route would be observed in a wide variety of nonlinear systems.

The rest of this work is organized as follows. In Sect. 2, the authors describe the experimental arrangement. In Sect. 3, the modeling efforts undertaken for the nonlinear oscillator are presented. Numerical results obtained are provided in Sect. 4. Experimental results are provided in Sect. 5. In Sect. 6, the authors present their conclusions.

Fig. 1
figure 1

Schematic of Duffing oscillator (a) and experimental arrangement (b). The separation between the magnets and their relative orientations are varied. An electromagnetic shaker is used to provide the deterministic harmonic excitation along with a white Gaussian noise input

Full size image

2 Experimental arrangement

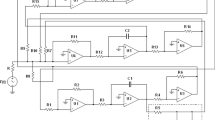
The experimental prototype of the Duffing oscillator and schematic of the experimental setup is shown in Fig. 1. The experimental arrangement consists of a cantilever steel structure with an attached tip mass magnet at its free end. The tip mass magnet is located in the magnetic field of another magnet that is fixed in a position close to it. The inter-magnet separation can be varied and the magnet orientations can be reversed to realize a nonlinear Duffing oscillator with either a hardening or a softening (monostable or bistable) characteristic. The other end of the cantilever structure is excited by an electromagnetic shaker that is used to provide the deterministic input (harmonic excitation) and the additive Gaussian noise input. The excitation provided by the shaker is along a direction normal to the longitudinal axis of the beam oscillator allowing for excitation of bending motions of the structure. Given the cantilever structure’s orientation, for the purpose of the current experimental arrangement, the influence of gravity is neglected in modeling the cantilever structure dynamics. Several means are used to gather experimental data. The free-end displacement of the cantilever structure is measured by using a strain gauge, which is secured close to the base of the cantilever structure, and the NI cDAQ-9178 with an NI 9235 module. The harmonic excitation amplitude is measured by using a 3-axis accelerometer (SparkFun ADXL337) that is attached to the shaker head at the base of the cantilever structure. A LabVIEW® program was developed to provide the deterministic harmonic excitation and Gaussian noise input to the Brüel & Kj\(\ae \)r electromagnetic shaker through NI modules. The same LabVIEW® program is also used for real-time data acquisition of the strain gauge and accelerometer signals. The natural frequencies of the system depend on the inter-magnet separation and relative orientations of the magnets.

Both hardening and softening characteristic of the nonlinear systems were realized in the experiments, as noted earlier. The experimental setup was noted to be quite sensitive to the relative spacing of the magnets. When both the magnets repel each other, the system behaves as bistable, softening nonlinear oscillator with two stable potential wells, as the zero tip deflection position is unstable. On the other hand, when the magnets attract each other, the system behaves as a monostable, nonlinear oscillator with hardening or softening characteristic and the zero tip deflection position is stable. For the purpose of this article, the authors focused on a bistable Duffing oscillator system with softening characteristics. For all of the experimental studies, the attention was on the chaotic dynamics for the deterministic case and the influence of noise in making a qualitative change.

3 Mathematical modeling and parametric identification

An equation of motion of a Duffing oscillator with a mass m, a viscous damping c, a linear stiffness \(k_1\), a nonlinear stiffness \(k_3\), a forcing amplitude F, and a forcing frequency \(\omega \) can be nondimensionalized as described in authors’ prior work [15]. The nondimensional form of equation of motion may be written as

$$\begin{aligned} \begin{aligned} \ddot{x} + \eta {\dot{x}} + \alpha x + \beta x^3 = F_0 \cos (\varOmega t). \end{aligned} \end{aligned}$$
(1)

where the different nondimensional parameters are as follows: \(\eta \) is the viscous damping, \(\alpha \) is the linear stiffness parameter, \(\beta \) is the scaled nonlinear (cubical) stiffness, \(F_0\) is the scaled forcing amplitude, \(\varOmega \) is the frequency ratio (\(\varOmega = \omega /\omega _n\)), and t represents the nondimensional time. The harmonic excitation or deterministic input is represented by \(F_{0} \cos (\varOmega t)\). Different signs of stiffness parameters \(\alpha \) and \(\beta \) correspond to different Duffing oscillator characteristics, as presented in Table 1.

In the current study, the authors have considered a bistable, Duffing oscillator with softening characteristics. For a low forcing amplitude, the Duffing oscillator represented by Eq. (1) exhibits a hysteresis behavior when the excitation frequency \(\varOmega \) is used as a control parameter in a frequency range around the system resonance (\(\varOmega = 1\)).

Table 1 Stiffness parameters and different Duffing oscillator realizations
Full size table
Table 2 Parameter identification for bistable, softening Duffing oscillator of experiments
Full size table

The linear natural frequencies \(\omega _n\) of the bistable softening Duffing oscillator are obtained from a low amplitude impulse response test about the equilibrium positions. The rest of the parameters are obtained from free oscillation data and from curve fitting of the experimental obtained deterministic frequency response curve to the analytical frequency response curve. The experimental frequency response curve is obtained by conducting quasi-static frequency sweeps for increasing and decreasing excitation frequencies. Additional information on the parametric identification can be found in the authors’ previous effort [15].

Fig. 2
figure 2

Plots of numerically obtained bifurcation diagram for softening Duffing oscillators in Eq. (1). In plot (a), the authors show a bifurcation diagram for a constant forcing amplitude (\(F_0 = 0.204\)). Plot (b) has the corresponding Lyapunov spectrum. A positive Lyapunov exponent confirms a chaotic response. Plot (c) has the bifurcation diagram for a constant forcing frequency (\(\varOmega = 0.71\))

Full size image

The parameter values, obtained through curve fitting, are listed in Table 2. For a given experimental arrangement, the parameter values of \(\eta , \alpha \), and \(\beta \) are assumed to be constant and are used to conduct further numerical and experimental studies. The parameters \(F_0\) and \(\varOmega \) are chosen as control parameters and are used in numerical simulations to produce bifurcation diagrams.

Now, on top of the harmonic excitation or deterministic input (\(F_0 \cos (\varOmega t)\)), consider a white Gaussian noise input to the system represented by \(\sigma _N {\dot{W}}(t)\). Here, \(\sigma _N\) represents the noise amplitude, W(t) represents the Wiener process, and \({\dot{W}}(t)\) represents a “mnemonic” derivative. In the presence of the noise, the Duffing oscillator equation given by Eq. (1) can be written as

$$\begin{aligned} \begin{aligned} \ddot{x} + \eta {\dot{x}} + \alpha x + \beta x^3 = F_0 \cos (\varOmega t) + \sigma _N {\dot{W}}(t). \end{aligned} \end{aligned}$$
(2)

The above equation can be rewritten into the state-space form as

$$\begin{aligned} \begin{aligned} \dot{x_1}&= x_2 \\ \dot{x_2}&= - \eta x_2 - \alpha x_1 - \beta x_1^3 + F_0 \cos (\varOmega t) + \sigma _N {\dot{W}}(t) \end{aligned} \end{aligned}$$
(3)

where \(x_1 = x\) and \(x_2 = {\dot{x}}\).

To carry out numerical studies, the above equations are written in the Langevin form of a differential equation as

$$\begin{aligned} \begin{aligned} dx_{1}&= x_2 dt \\ dx_{2}&= \Big (- \eta x_2 - \alpha x_1 - \beta x_1^3 + F_0 \cos (\varOmega t) \Big )dt + \sigma _N dW \\ \end{aligned} \end{aligned}$$
(4)

It is mentioned that in this differential form, one no longer has the derivative of the Brownian motion (which does not exist) but a differential white noise which does exist. This system is integrated as an Itô integral. It should be noted that since there is an additive (not a parametric) excitation, the Itô equations and corresponding Stratonovich equations are equivalent. The Euler–Maruyama method can be used to obtain numerical solutions of Eq. (4) as in prior work of the group (e.g., [14, 15, 17, 18]). The quantity dW, is the incremental noise, which has a mean that is equal to zero and a standard deviation that is equal to \(\sqrt{dt}\).

4 Numerical results

Getting chaos for numerical studies For the numerical simulations, the parameters have been chosen so that the deterministic response of the system shows the existence of a chaotic attractor as well as stable periodic attractor. To carry this out, after parametric identification, the forcing amplitude \(F_0\) and forcing frequency \(\varOmega \) have been varied over sufficient ranges to observe the chaotic response. The numerically obtained bifurcation diagrams along with Lyapunov spectrum are shown in Fig. 2. It is clear that the system behaves chaotically for a range of parameter values. For this article, the authors have chosen the parameter values as shown in Table 3 where the system dynamics is chaotic or periodic depending on the initial condition chosen. For these parameter values, the basin of attraction along with time series is shown in Fig. 3 and it confirms the existence of a chaotic attractor as well as a stable period-1 attractor.

Table 3 Parameter values for Duffing oscillator showing chaotic realizations
Full size table
Fig. 3
figure 3

Numerical simulations using Euler–Maruyama scheme for noise amplitude \(\sigma _N = 0\). See Table 3 for system parameter values. For the model, a chaotic attractor coexists with a periodic attractor. Plot (a) is for the stroboscopic map. Purple color (\(B_2\)) and yellow color (\(B_1\)) are used to identify the basins of attraction of the chaotic and periodic attractors, respectively. The black dots in the purple region are the (stroboscopic) chaotic attractor, while point “P” is a fixed point attractor. In plots (b) and (c), the associated time series are shown. (Color figure online)

Full size image

Numerical simulations were conducted to study any qualitative change in dynamics of the Duffing oscillator with variation of noise amplitude \(\sigma _N\) while integrating Eq. 4. When the noise amplitude \(\sigma _N\) is varied, the rest of the parameters are kept constant as shown in Table 3. The basin of attraction with these parameter values is shown in Fig. 3. The steady state response of the deterministic system (\(\sigma _N = 0\)) is chaotic or periodic depending on the initial point chosen. For any initial condition in the purple region, the system response settles down on a chaotic attractor, whereas, for any initial condition in the yellow region, the response settles down to a period-1 attractor. Both time series as well as the corresponding stroboscopic maps are shown in Fig. 3. The numerical results are obtained by integrating the stochastic differential equations, Eqs. (4), with the Euler–Maruyama scheme, as discussed in [14]. The initial conditions and parameters used (Table 3) to produce the response shown in Fig. 3, which is the deterministic case, were also used for all of the stochastic simulations as well. The numerical results are produced for more than 100 Euler–Maruyama simulations in the time domain over 1000 time periods. Each of these Euler–Maruyama simulations has the same noise amplitude \(\sigma _N\), but a different noise vector.

Fig. 4
figure 4

Numerical simulations using Euler–Maruyama scheme for noise amplitude \(\sigma _N = 0.015\). The system parameter values and basin colors are same as in Fig. 3. The black dots in the purple region are the (stroboscopic) noisy chaotic attractor, while black dots in the yellow region are the (stroboscopic) noisy periodic attractor. The black dots in plot (a) are the (stroboscopic) noisy attractor for an initial condition in the yellow region and plot (c) has the associated time series. The black dots in plot (b) are the (stroboscopic) noisy attractor for an initial condition in the purple region and plot (d) has the associated time series. The system dynamics exhibits no qualitative changes. (Color figure online)

Full size image
Fig. 5
figure 5

Contour plots of probability density of a bistable, softening Duffing oscillator (Eq. (2)). See Table 3 for system parameter values. The numerical path integration procedure based on the Gauss–Legendre integration rule is used to compute the evolution of probability density subjected to a harmonic and a white Gaussian excitation. The periodicity of probability density function implies a steady state response. With a noise amplitude \(\sigma _N < 0.02\), there is no jump in the system response from one attractor to another. With a noise amplitude \(0.02 \le \sigma _N < 0.05\), there is probability of the system response jumping from the chaotic attractor to the periodic attractor (fixed point), but there is no jump from the periodic attractor to the chaotic attractor. For a noise amplitude \(\sigma _N \ge 0.05\), there are continuous jumps from chaotic attractor to the periodic attractor

Full size image
Fig. 6
figure 6

Numerical simulations using Euler–Maruyama scheme for noise amplitude \(\sigma _N = 0.02\). The system parameter values and basin colors are same as in Fig. 3. In plot (a), the black dots in the yellow region are the (stroboscopic) periodic attractor with noise for an initial condition in the yellow region and plot (b) shows the associated time series. The periodic attractor (in yellow) exhibits no qualitative changes with the noise amplitude \(\sigma _N = 0.02\). (Color figure online)

Full size image
Fig. 7
figure 7

Numerical simulations using Euler–Maruyama scheme for noise amplitude \(\sigma _N = 0.045\). The system parameter values and basin colors are same as in Fig. 3. In plot (a), the black dots in the yellow region are the (stroboscopic) periodic attractor with noise for an initial condition in the yellow region and in plot (b), the black and green dots are the stroboscopic map with noise for an initial condition in the purple region. The green dots represent the stroboscopic map with noise for the last 200 time periods. In plot (c), a part of the associated time series with noise for an initial condition in yellow region is shown. In plot (d), a part of the associated time series with noise for an initial condition in the purple region is shown. The chaotic attractor escapes to the fixed point (periodic) attractor, but periodic attractor (in yellow) exhibits no qualitative changes with the noise amplitude \(\sigma _N = 0.045\). (Color figure online)

Full size image
Fig. 8
figure 8

Numerical simulations using Euler–Maruyama scheme for large noise amplitude (\(\sigma _N = 0.05\)). The system parameter values and basin colors are same as in Fig. 3. In plot (a), the black dots in the yellow region are the (stroboscopic) periodic attractor with noise for an initial condition in the yellow region and in plot (b), the black and green dots are the stroboscopic map with noise for an initial condition in the purple region. The green dots in plot (a) and (b) represent the stroboscopic map with noise for the last 200 time periods. In plot (c), a part of the associated time series with noise for an initial condition in yellow region is shown. In plot (d), a part of the associated time series with noise for an initial condition in the purple region is shown. A continuous jump can be seen from the chaotic attractor to the periodic attractor and periodic attractor to chaotic attractor with the noise amplitude \(\sigma _N = 0.05\). (Color figure online)

Full size image

Escaping chaos Any qualitative change in the system dynamics depends on the noise amplitude \(\sigma _N\). The numerical results show that, for a noise amplitude \(0 \le \sigma _N < \sigma _c\), with any initial condition in the chaotic or periodic basin, the steady-state response settles down on a noisy chaotic attractor or a noisy periodic attractor, respectively, as shown in Fig. 4. There are no qualitative changes observed in the system behavior. Here, \(\sigma _c\) represents the critical value of noise amplitude for which the chaotic attractor faces a crisis. At that critical noise amplitude \(\sigma _c\), the chaotic attractor comes into contact with the stable manifold at the saddle point as shown in Fig. 11b and the chaotic attractor vanishes. The features of this saddle point can be seen at the critical collapse of the chaotic attractor at the critical event, the trajectory moves rapidly toward the saddle along the stable manifold of the saddle and then escapes along its unstable manifold toward the fixed point (periodic) attractor.

The numerical path integration procedure [19, 20] based on the Gauss–Legendre integration rule has been used to find out the critical noise amplitude limit \(\sigma _c\), for which there is a jump from chaotic attractor to the periodic attractor occurs. This procedure is based on the evolution of probability density subjected to a harmonic and a white Gaussian excitation where the periodicity of the probability density function implies a steady state response. For the given parameter values in Table 3, the critical noise amplitude is found to be \(\sigma _c = 0.02\). The corresponding contour plot is shown in Fig. 5a.

With an initial condition in the chaotic attractor basin, with noise amplitude \(\sigma _N = 0.02\), all Euler–Maruyama simulations show an escape from the chaotic attractor to the periodic attractor. The steady-state trajectory stays on the noisy periodic attractor thereafter. On the other hand, for all the initial conditions in the periodic attractor basin (yellow), the trajectory remains on the noisy periodic attractor without any qualitative changes or escape. The stroboscopic map along with the time series is shown in Fig. 6.

Large noise amplitude Further, the noise amplitude is increased in the simulation of Eqs. (4). For an intermediate noise amplitude \(\sigma _c \le \sigma _N \le \sigma _0\), the chaotic attractor is destroyed and the trajectory escapes to the fixed point (periodic) attractor. On the other hand, the periodic attractor shows no qualitative changes. Here, the noise amplitude \(\sigma _0\) represents the noise limit where the jump from the periodic attractor to the chaotic attractor occurs. Again, the numerical path integration procedure has been used to find out the noise amplitude limit \(\sigma _0\). The corresponding contour plot is shown in Fig 5c, wherein the noise amplitude limit is found to be \(\sigma _0 = 0.05\). The time series results along with stroboscopic maps for the intermediate noise amplitude \(\sigma _N = 0.045 \le \sigma _0\) are shown in Fig. 7. The associated contour plot is shown in Fig. 5b. Additionally, for a large noise amplitude \(\sigma _N \ge \sigma _0\), a continuous jump from a chaotic attractor to a periodic attractor and a periodic attractor to a chaotic attractor occurs. The contour plot for a noise amplitude \(\sigma = \sigma _0 = 0.05\) is shown in Fig. 5c. The time series results and stroboscopic maps are shown in Fig. 8 which confirms the continuous jumps.

Fig. 9
figure 9

Stroboscopic map along with the time series obtained through experimental study of a forced bistable, softening Duffing oscillator showing chaotic attractor

Full size image
Fig. 10
figure 10

Stroboscopic map along with the time series obtained through experimental study of a forced bistable, softening Duffing oscillator for noise amplitude \(\sigma _E = 2.0\). In plot (a), the black dots are the stroboscopic map with noise and the red dot is the fixed point attractor for the deterministic case. In plot (b), the associated time series with noise is shown. The system dynamics shows continuous jumps from chaotic attractor to periodic attractor and periodic attractor to chaotic attractor. (Color figure online)

Full size image
Fig. 11
figure 11

The chaotic attractor is destroyed by noise and the trajectory escapes. In plot (a), the (stroboscopic) chaotic attractor (green color) along with stable (\(W_s\)) and unstable (\(W_u\)) manifold of the fixed point saddle (point “S”) for the deterministic system are shown and point “P” is a fixed point attractor. In plot (b), the numerical results for the chaotic attractor escape route (through points \(p_1\) to \(p_8\)) with noise \(\sigma _N = 0.02\) are shown. The green dots represent the stroboscopic map for the last 200 time periods. For plot (c), a stroboscopic map is obtained through an experimental study of a forced bistable, softening Duffing oscillator with noise amplitude \(\sigma _E = 1.8\). The start of the strobe for the experiments is arbitrary and is not synchronized with the clock used for plots (a) and (b). The chaotic attractor is destroyed by noise and the trajectory escapes. The chaotic attractor escape route (through points \(p_1\) to \(p_{12}\)) with noise \(\sigma _E = 1.8\) is shown. The black circles represent the stroboscopic map for the last 200 time periods. In both plots (b) and (c), the trajectory moves rapidly toward the saddle (point “S”) along the stable manifold (basin boundary) of the saddle and then escapes along its unstable manifold toward the fixed point (periodic) attractor. See Fig. 12 for the time series plot. See Sect. 6 for similarities and differences between numerical and experimental system. (Color figure online)

Full size image
Fig. 12
figure 12

The chaotic attractor is destroyed by noise and the trajectory escapes. In plot (a), numerical time series plot is shown. In plot (b), the experimental time series plot is shown. Red color is used in the time window when noise is introduced. The time series shows that the chaotic attractor escapes to the periodic attractor (fixed point). See Fig. 11 for the stroboscopic map. See Sect. 6 for similarities and differences between numerical and experimental results. (Color figure online)

Full size image

A comparison of numerical results with experimental findings is made in the next section. It should be noted that there is no direct comparison between the noise amplitude in the numerical simulations, \(\sigma _N\), and the noise amplitude in the experiments, \(\sigma _E\). The noise in numerical simulations are assumed to be white Gaussian noise, while the noise in the experiment is a complicated function of several frequency response relationships with almost a flat power density spectrum over the range of frequencies that are relevant to the context [15].

5 Experimental results

Getting chaos in experimental system The experimental studies have been conducted with a forced bistable, Duffing oscillator prototype with softening characteristic. The deterministic response shows chaotic behavior. After parametric identification through curve fitting the experimentally obtained frequency response curve to analytically obtained response curve, the numerically obtained bifurcation diagram helps to identify the forcing amplitude \(F_0\) and forcing frequency \(\varOmega \) in the chaotic region. For this study, the authors have chosen \(F_0 = 0.204\) and \(\varOmega = 0.71\). The experimental studies for these parameter values (Table 3) show chaotic dynamics. Both the time series and the stroboscopic map are shown in Fig. 9.

The numerical results are obtained by assuming noise to be a white Gaussian noise, whereas in the experimental studies, the noise is assumed to be a band-limited white noise. Due to a constant power density spectrum in the operating forcing frequency range of interest, the band limited white noise may be treated as being equivalent to a white Gaussian noise. In this section, the experimental results are qualitatively compared with numerical outcomes. For any noise amplitude \(\sigma _E\), the experiments are conducted for more than 15 runs and around 5000 time periods in each run.

Escaping chaos A small noise amplitude \(\sigma _E\) does not result in an observable qualitative change and the response is a noisy chaos. However, a further increase in the noise amplitude \(\sigma _E\) results in an eventual but sudden change in the qualitative behavior and the response escapes from the chaotic basin. Here, the noise level is just sufficient to cause the chaotic trajectory to escape to the periodic attractor within a mean time of 100 oscillation of the forced Duffing oscillator. Similar to the numerical results, the authors observed that there is a specific escape route that the trajectory always follows—the escape trajectory is essentially on the basin boundary. The dynamics pulls the trajectory toward the fixed point on the basin boundary and then, the trajectory escapes along the unstable manifold of the saddle point; that is, the branch of the unstable manifold that is outside the chaotic basin. The steady state trajectory stays on the noisy periodic attractor thereafter.

Repetitions of this experiment show that when the trajectory escapes, it always escapes the basin in the same way. One of the experimental results is shown in Fig. 11c. The experimental findings are in agreement with the numerical results shown in Fig. 11b.

Large noise amplitude For a large noise amplitude, one does not necessarily follow the above route. Hence, it is essential to keep the noise level as low as possible to observe the exit route. Similar to the numerical results shown in Fig. 8, a large noise amplitude quickly leads to continuous jumps from chaotic attractor to periodic attractor and back to the chaotic attractor, repeatedly as shown in Fig. 10. The stroboscopic map shows a cloud of points on the chaotic and periodic attractor with continuous jumps. It should be noted that a particular range of amplitude of noise \(\sigma _E\) is needed to control and terminate the chaotic response and move the response toward a stable periodic attractor.

6 Conclusions

In this paper, the authors have examined the effects of a white Gaussian noise on the chaotic and periodic responses of a harmonically forced bistable, Duffing oscillator with softening characteristics. Numerical simulation results have been carried out for more than 100 Euler–Maruyama simulations in the time domain over 1000 time periods and the experimental results are obtained for more than 15 experimental runs with 5000 time periods for each run.

Similarities and differences between numerical and experimental systems (1) The systems here are observed stroboscopically. The appearance of an experimental plot depends strongly on the phase of the strobe that is upon the instant the strobe is started. Hence, much of the difference between the numerical and experimental chaotic attractor is due to the difference in the phase of observation. (2) The parameter range for observing chaos coexisting with a periodic attractor is in a similar range for the two systems. (3) The boundary saddle S is shifted but the basin boundary in both systems is dominated by a fixed point saddle and its stable manifold. (4) There is no direct comparison between the noise amplitude in the numerical simulations, \(\sigma _N\), and the noise amplitude in the experiments, \(\sigma _E\). The noise in numerical simulations is assumed to be white Gaussian noise, while the noise in the experiments is a complicated function of several frequency response relationships with almost a flat power density spectrum over the range of frequencies that are relevant to the context. (5) For both studies, with the addition of noise, as the amplitude reaches a critical value, there is a change. A typical attractor in the chaotic regime quickly escapes to the periodic attractor. This departure is always via a special escape route: the unstable manifold of a saddle point on the basin boundary between the two basins of attraction.

The authors would like to note that the dynamics observed here can be expected in other two-dimensional cases as well. For instance, with regard to reference [1], the escape along the unstable manifold of the unstable periodic saddle located on the boundary of a basin of attraction of a chaotic attractor will be similar to that observed here with the fixed-point saddle in the present case. This would be the case, when the period of the saddle \(m = 1\). For \(m>1\), the situation would be this simple.

While the authors’ study here concerns a specific system with specific parameters, in future work, the authors plan to build on the current study and examine the effect of noise on the escape route of high dimensional nonlinear systems. These findings also suggest that a range of noise amplitude can be used to control the chaotic dynamics without any change in system parameter values.